Abstract
In the Infrastructure-as-a-Service cloud computing model, virtualized computing resources in the form of virtual machines are provided over the Internet. A user can rent an arbitrary number of computing resources to meet their requirements, making cloud computing an attractive choice for executing real-time tasks. Economical task allocation and scheduling on a set of leased virtual machines is an important problem in the cloud computing environment. This paper proposes a greedy and a genetic algorithm with an adaptive selection of suitable crossover and mutation operations (named as AGA) to allocate and schedule real-time tasks with precedence constraint on heterogamous virtual machines. A comprehensive simulation study has been done to evaluate the performance of the proposed algorithms in terms of their solution quality and efficiency. The simulation results show that AGA outperforms the greedy algorithm and non-adaptive genetic algorithm in terms of solution quality.
1. Introduction
Cloud computing, or simply “the cloud” is on-demand delivery of computing resources over the Internet on a pay-per-usage basis [1]. The pay-per-usage approach eliminates the requirement for investment in the acquisition of hardware and software making cloud computing an attractive option for many organizations [2,3]. In cloud computing, services are provisioned in the forms of Software-as-a-Service (SaaS), Platform-as-a-Service (PaaS), and Infrastructure-as-a-Service (IaaS). A cloud model in which a service provider hosts applications and makes them available to customers is referred to as SaaS. In a PaaS model, hardware and software tools are made available to the users for application development whereas an IaaS provides highly scalable virtualized computing resources that can be adjusted on-demand. That is, a user can rent an arbitrary number of computing resources to meet their requirements.
The focus of this study is on IaaS, where users can subscribe cloud resources for the execution of a set of hard real-time tasks. In cloud computing, a virtual machine (VM) provides a certain level of computational power, memory, and other resources. The VMs may have heterogeneous processing power and characteristics, providing flexible and efficient computation capabilities to the users. This makes cloud computing an attractive choice for executing applications that exhibit high task and data parallelism [4]. Many of these applications (e.g., object recognition, navigation systems, mission critical systems, financial systems, etc.) are real-time that require completion of their workload within a given deadline. An application may consist of a number of tasks each having a deadline. A task may communicate with other tasks and consequently have precedence constraint, that is, a task cannot start its execution until a set of other tasks is completed. In a cloud computing environment, tasks must be assigned and scheduled on VMs in such a way that the system resources are utilized effectively and a certain objective function is optimized [5]. To be specific, the problem considered in this paper is defined as “Given a set of real-time tasks represented as a Directed Acyclic Graph (DAG) to be executed on a set of virtual machines provided on a cloud-computing infrastructure, perform an off-line mapping of tasks to the virtual machines such that the total execution and communication cost are minimized subject to a number of system constraints”.
Scheduling of real-time tasks in distributed and grid computing platforms is an established NP-complete problem [6]. The problem becomes even more challenging when a large number of tasks are executed in a cloud computing environment [7] and hence finding the exact solutions for large problem sizes is computationally intractable. Consequently, a good solution can only be obtained through heuristics.
The task scheduling problem has been extensively studied for multiprocessor, grid, and distributed systems and numerous heuristics have been proposed [8,9,10]. These algorithms for traditional distributed and parallel systems, however, cannot work well in the new cloud computing environment [4,11]. This makes the problem of task-scheduling in cloud computing a promising research direction and has attracted several researchers to develop efficient heuristics. Most of the work on task allocation and scheduling in the cloud environment is focused on the minimization of energy consumption, makespan, and economic cost of renting virtual machines and the provision of the desired level of quality of service (QoS) [5,12,13,14,15]. However, there is not much work that explicitly deals with the allocation and scheduling of hard real-time tasks in a cloud environment to minimize execution and communication costs.
In this paper, we model the hard real-time task scheduling as an optimization problem subject to a set of constraints. The cost model includes the processing and communication costs and the constraints capture task precedence and deadline requirements. We propose an efficient greedy algorithm and an adaptive genetic algorithm. For the genetic algorithm, we propose a topology preserving two-dimensional solution encoding scheme. We also design a variety of topology preserving crossover and mutation operators that exploit the solution encoding scheme to escape from local optima, consequently resulting in high quality solutions. An adaptive strategy for the automatic selection of suitable crossover and mutation operators during the execution of a GA has also been proposed. Both adaptive and non-adaptive versions of GA, along with the proposed greedy algorithm, have been empirically studied to evaluate their performance.
The rest of the paper is organized as follows. Section 2 presents the related work. Section 3 presents our system models, objective function, and constraints. The proposed algorithms are presented in Section 4, followed by simulation results and performance comparison of the proposed algorithms in Section 5. Finally, we give the conclusion in Section 6.
2. Literature Review
Task allocation and scheduling problems have been extensively studied and efficient algorithms have been proposed for distributed systems [9,16,17,18,19,20], grid computing [6,10,21,22,23,24], and multiprocessor systems [8,25]. These studies, however, schedule tasks on a fixed number of processors and the cost of renting machines is not a dominant factor. Cloud computing, on the other hand, provides scalable resources. Virtual machines can be rented with an option of renting virtual machines that have different computing speeds and costs. The users have to pay for the rented machines even if they are not fully utilized. Therefore, the efficient use of the virtual machine is of a vital importance in the cloud computing environment. Within this context, effective and efficient scheduling algorithms are fundamentally very important [4,11,26,27]. This has attracted the attention of many researchers to study the task scheduling problem in a cloud computing environment.
Most of the work on task allocation and scheduling in a cloud environment is focused on the minimization of energy consumption, makespan, economic cost of renting virtual machines, and providing the desired level of quality of service (QoS) [5,12,13,14,15]. Wu et al. [13] proposed a task scheduling algorithm based on several quality of service (QoS) metrics. The QoS metrics include load balancing, average latency, and makespan. They calculate priorities of tasks based on a number of attributes. The tasks having higher priority are scheduled first on the machine which produces the best completion time. An algorithm to schedule workflow tasks with multi-objective QoS is proposed in [27]. The QoS parameters include the schedule time, total cost of executing tasks, as well as balancing the load among resources. A task scheduler based on a genetic algorithm is proposed by Jang et al. [28] to maximize overall QoS. They used response time and processing cost as a metric to measure QoS. Scheduling algorithms that attempt to maximize profit while providing a satisfactory level of QoS as specified by the consumer are proposed by Lee et al. [14].
Razaque et al. [29] proposed an efficient task-scheduling algorithm for workflow allocation based on the availability of network bandwidth. An algorithm based on a nonlinear programming model for divisible task scheduling was proposed to assign tasks to each VM. Min-Min and Min-Max algorithms are proposed in [30]. The Min-Min algorithm calculates the execution times for all tasks on all available resources, and then it chooses the task with the least completion time and assigns it to the corresponding executing resource. Two on-line resource allocation algorithms to schedule tasks with precedence constraints on heterogeneous cloud systems are proposed by Li et al. [31], which dynamically adjust resource allocation based on the information of the actual task execution.
Tsai et al. [32] proposed a differential evolution algorithm to schedule a set of tasks to minimize makespan and total cost. They embed the Taguchi method within a differential evolution algorithm (DEA) framework to exploit better solutions on the micro-space to be potential offspring. A hyper-heuristic algorithm is proposed by Tsai et al. [33] to schedule tasks on a cloud computing system to minimize makespan. Their algorithm uses diversity detection and improvement detection operators to dynamically select the most suitable heuristic from a pool of heuristics to find better candidate solutions. Other well-known metaheuristics such as Particle Swarm Optimization (PSO), Cuckoo Search Algorithm (CSA), and Bat algorithm have also been used to schedule tasks on cloud systems [15,34,35,36].
There are a number of papers that explicitly deal with the task allocation and scheduling of real-time tasks in a cloud environment. An algorithm to schedule non-preemptive real-time tasks to maximize the total utility was proposed by Liu et al. [37]. The proposed algorithm maximizes the total utility by accepting, scheduling, and aborting real-time services when necessary. Their simulation results show that the performance of the proposed algorithms is significantly better than the Earliest Deadline First (EDF) and the traditional utility accrual scheduling algorithms. Kumar et al. [4] formulated the real-time task allocation problem as a constrained optimization problem to minimize the economic cost of executing a set of tasks. They proposed a greedy and temporal overlap scheme to schedule the tasks. They, however, consider that only the execution cost and communication cost has not been taken into consideration. Kim et al. [38] modeled a real-time service as a real-time virtual machine request and proposed a number of algorithms to reduce power consumption. The developmental genetic programming approach has been proposed by Deniziak [39] to schedule soft real-time applications specified as a set of distributed echo algorithms. Their objective was to minimize the total costs of the IaaS services, while guaranteeing QoS.
In contrast to the above studies, this paper focuses on the minimization of total processing and communication costs for a set of tasks with hard deadlines to be executed on virtual machines. Our mathematical model provides a more realistic scenario for the cloud computing environment. Furthermore, our proposed adaptive genetic algorithm defines problem specific solution coding and algorithmic operators as well as a technique for adaptively selecting suitable GA operators from a pool during the search process. The selection of these operators is based on their performance instead of a random selection of operators. Such a scheme has not been used previously which is a novel contribution of this work. Our simulation results show that the proposed adaptive GA outperforms the classical GA and the greedy algorithm in terms of solution quality.
3. System Model and Problem Formulation
The problem considered in this paper is the allocation and scheduling of a set of hard real-time tasks on virtual machines in a cloud computing environment. In this section, we present our task model, cloud model, and problem formulation as an optimization problem. The notations and their semantics used throughout this paper are given in Table 1.

Table 1.
Notations.
3.1. Task Model
Assume that we have a set of real-time tasks, . Each task has a workload denoted by wi (measured in number of cycles) and a deadline denoted by di. A task may communicate with other tasks and hence have a precedence relationship. The tasks with a precedence constraint can be represented by a directed acyclic graph DAG(T,E), where T is the set of tasks and E represents the set of directed arcs or edges between tasks to represent dependencies. An edge between task ti and tj represents that task ti should complete its execution before tj can start. With each edge , we assign vij that represents the amount of data transmitted from ti to tj. A typical DAG is shown in Figure 1.
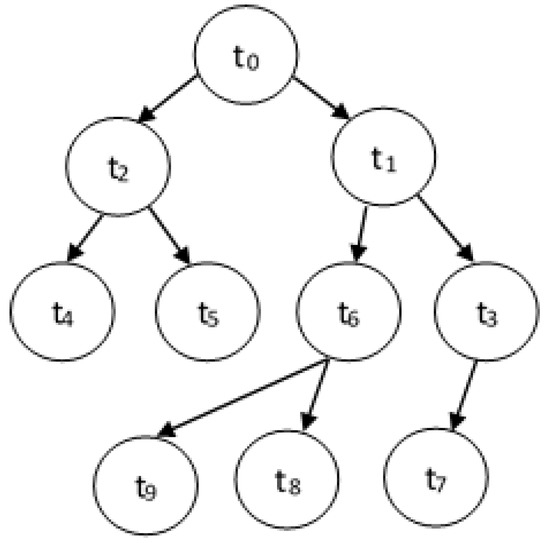
Figure 1.
A DAG with 10 tasks.
For our task model, we further define the following.
Definition 1.
In a DAG(T,E), is a set of immediate predecessors of task ti and is a set of tasks that are immediate successors of ti.
Definition 2.
If Pre(ti) is the set of predecessors of task ti, then ti cannot start its execution on a virtual machine unless all of its predecessor tasks have been executed.
Definition 3.
A set of tasks aPre(ti) = is the set of all the predecessors of task ti, if , that is, there is a direct path from tp and ti and tp does not have any predecessor.
In Figure 1, we can see that
- Succ(t4) = and Succ(t6) = {t8, t9}.
- Pre(t2) = {t0} and Pre(t5) = {t2}.
- aPre(t5) = {t0,t2} and aPre(t7) = {t0,t1,t3}.
Definition 4.
If wi is the workload of task ti T and sk is the speed of the virtual machine mk, then the time required to execute task on mk, denoted by ETik, is given by
Definition 5.
If di is the deadline and ETij is the execution time of task ti on the virtual machine mk, respectively, then the Latest Start Time (LSTi) of task ti is given by
Definition 6.
If STik and ETik are the actual start time and execution time of task ti on the virtual machine mk, respectively, then the Finish Time of task ti (FTi) is given by
Definition 7.
The earliest start time of task ti (ESTi) is given by
3.2. Cloud Model
Assume there are M virtual machines. Each virtual machine mk has a computation speed sk (number of cycles per unit time) and a cost ck. If a cloud provider charges the user on actual usage, then the cost to execute task ti on the virtual machine mk is given by
However, cloud providers charge the users a cost of Ck for leasing a virtual machine mk for a minimum of L time units (minutes, hours, etc.) regardless of the actual utilization. For example, if L = 10 min and Ck = $0.3, then a user will be charged a minimum of $0.3 even if the actual usage of the virtual machine is less than 10 min. Under this scenario, the execution cost of task ti on mk, if no other task is schedule on the same virtual machine, is given by
We assume bkl is the data communication cost per unit data volume between the virtual machines mk and ml. If two virtual machines are on the same physical machine, then the communication cost is zero.
Definition 8.
The communication cost between virtual machines can be given by
Note that B is a symmetrical matrix, where bkl = blk. The matrix also contains zeros at the diagonal representing bkk = 0. This implies the fact that the communication cost between tasks assigned to the same virtual machine is zero.
3.3. Cost Function
The total cost to execute all the tasks consists of two components: total communication cost and total execution cost. If X denotes an M×N matrix whose entry xik = 1 if task ti is scheduled on virtual machine mk, and xik = 0 otherwise, then the total communication cost (CC) is given by:
Similarly, the execution cost of all the tasks is given by:
Total cost, TC(X), is the sum of CC(X) and EC(X), that is
The task scheduling problem can now be defined as a 0–1 decision problem to find X that minimizes TC(X) under some constraints. That is,
Minimize
Subject to:
The first Constraint (10) specifies that each task should be scheduled on exactly one virtual machine. The second Constraint (11) specifies the real-time constraint and the last Constraint (12) specifies that a task cannot start before the completion of all of its predecessor tasks.
4. Proposed Algorithms
In this section, we first present an efficient greedy algorithm followed by an adaptive genetic algorithm (AGA).
4.1. Greedy Algorithm
Greedy algorithms have been extensively studied. These algorithms are best known for their simple implementation and speed. They may, however, not give the optimal solutions. Nevertheless, greedy algorithms are simpler to implement as compared to other heuristics.
The pseudo code of our proposed greedy algorithm is given in Algorithm 1. The algorithm first orders all the tasks based on increasing order of their deadlines (line 1) and initially allocates all the tasks in increasing order of their deadlines to the lowest cost virtual machine (lines 2–8). Note that if all the tasks can complete on the lowest cost machine without violating any of the constraints, then it is the optimal solution since the communication cost (CC) will be zero and the execution cost (CE) is minimal. However, if the schedule violates any of the constraints, then one or more tasks should be allocated and scheduled on other virtual machines in such a way that none of the constraints are violated. Therefore, the proposed algorithm scans the generated schedule to determine the tasks that do not meet their deadlines (lines 9–11), and relocates and reschedules them on virtual machines that incur the minimum cost provided that the rescheduled tasks meet their deadlines on the selected VMs (lines 12–17). The overall complexity of the algorithm is O(n2m).
| Algorithm 1 Pseudocode of the greedy algorithm. |
|
4.2. Proposed Adaptive Genetic Algorithm
The genetic algorithm (GA) is one of the most well-known evolutionary algorithms that is based on the concept of natural evolution [40]. The algorithm operates in an iterative manner and maintains a set of solutions, known as populations, in each iteration. Each solution in the population is referred to as a chromosome. A number of these chromosomes are selected in each iteration through a selection process and are subjected to crossover and mutation operators. The purpose of these two operators is to perturb the existing solutions and generate new solutions, where the new solutions inherit characteristics from the chromosomes in the previous iteration, in addition to introducing new characteristics in the new solutions (called offspring). At the end of the execution of the algorithm, the resulting set of solutions is reported as the best solutions found by the algorithm. In order to effectively make use of the advantage of searching global spaces to find good solutions to our problem, GA operators such as the crossover and mutation have to be altered accordingly, such that it would be applicable to the problem. In addition, the generation of the initial population consisting of feasible solutions has a large impact on its overall performance. The pseudo-code of the non-adaptive genetic algorithm for the task allocation problem is given in Algorithm 2.
In the non-adaptive genetic algorithm, only a single type of crossover and mutation (discussed later in this section) are performed. Since our solution encoding scheme enables us to define different types of crossover and mutation operators, we propose an adaptive genetic algorithm (AGA) that follows a strategy for the automatic selection of suitable crossover and mutation operators during the execution of a GA. The proposed operator selection strategy helps keep a balance between exploration and exploitation in the search process, resulting in better quality solutions. The pseudo-code of the proposed adaptive GA is given in Algorithm 3. The following subsections first describe the solution encoding and an algorithm to generate the initial population, and then presents a variety of selection, crossover, mutation, and replacement operators. We then present our proposed method for the selection of crossover and mutation operators from a pool of different types of crossover and mutation operators based on their fitness values.
| Algorithm 2 Pseudocode of non-adaptive genetic algorithm. |
|
| Algorithm 3 GA with adaptive selection of crossover and mutation. |
|
4.2.1. Solution Encoding and Generation of Initial Population
In the genetic algorithm, a schedule (solution) is represented by a chromosome. For a task scheduling problem, a chromosome can be viewed as a two dimensional array of length N, where N is the number of tasks. The first row of a chromosome is an ordered list of tasks (from left to right) and the second row represents the corresponding virtual machine number on which a task is assigned for execution, as shown in Figure 2. The latest start time, completion time, and earliest start time for each task in the schedule can be calculated using Equations (1), (3), and (4), respectively.

Figure 2.
A schedule representation as a chromosome.
In order to ensure that a schedule satisfies the precedence constraint, we scheduled the tasks by their topological order [41]. We use the algorithm given in Algorithm 4 to generate the initial population. The algorithm not only schedules the tasks by their topological order but also marks segment boundaries (tasks within a segment boundary can be executed in any order without violated precedence constraint, and therefore they can be rearranged in any sequence). These segment boundaries are required for our specialized crossover and mutation operators. Figure 3 shows three chromosomes generated by the algorithm for the given DAG.
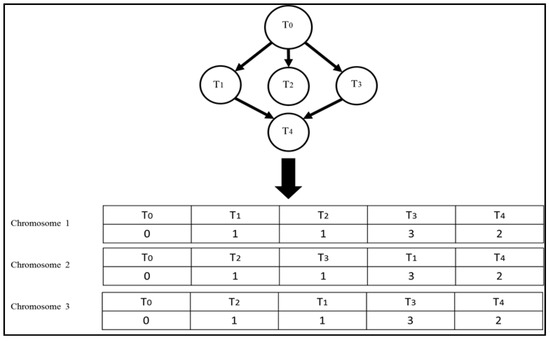
Figure 3.
An initial population generated using the initial population generation algorithm.
| Algorithm 4 The initial solution’s generation algorithm. |
|
4.2.2. Crossover Operator
In order to produce offspring, two parents are selected from the population in order to mate. The selection methods used in our work are random selection and roulette-wheel selection. For the random selection method, we randomly select two parents from the current population, whereas in the roulette-wheel method, a chromosome with a higher fitness value has higher chances of being selected for mating. The selected parents are then subjected to the crossover operator. We propose two crossover operators as explained below.
Type 1 Crossover: This crossover operator swaps corresponding randomly selected segments of two chromosomes. This ensures that the topological order in both children is preserved. Figure 4 illustrates how this crossover is performed on the second segment of the chromosomes.
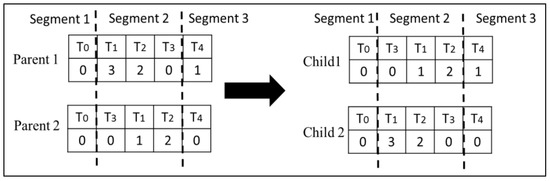
Figure 4.
Type 1 crossover performed on the second segment.
Type 2 Crossover: In type 2 crossover, we only swap the second row of the randomly selected segments, thereby changing only the VMs on which the tasks are scheduled without disturbing the schedule, as shown in Figure 5.
Figure 5.
Type 2 crossover performed on the second segment.
4.2.3. Mutation Operator
The mutation operator randomly selects a gene in a chromosome and changes it with a given probability. We propose three different types of mutations as explained below:
Type 1 Mutation: A gene in a chromosome is selected with a probability pm and the corresponding virtual machine number is changed to another randomly selected virtual machine.
Type 2 Mutation: In this mutation type, two genes which lie in the same segment are selected and swapped. The segment is selected randomly with a probability pm.
Type 3 Mutation: In this mutation, two randomly selected tasks within the same segment are swapped. The segment is selected randomly with a probability pm.
Figure 6 illustrates the operation of different types of mutation operators.
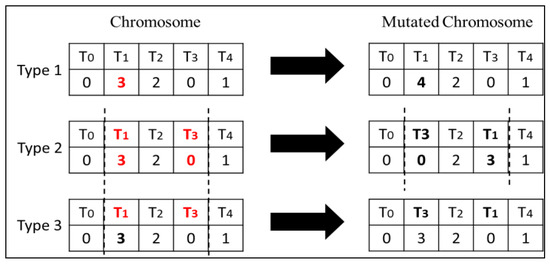
Figure 6.
Three types of mutation.
4.2.4. Replacement
A population replacement method is used to determine which solutions should be moved to the next generation. We used two techniques as discussed below.
Elitist Selection: The chromosomes with the highest fitness values are selected for the next generation.
Replacement of parents with children: In this replacement method, feasible children replace their parent chromosomes. If a child is infeasible, then the parent with the highest fitness value moves to the next generation.
4.2.5. Adaptive Selection of Crossover and Mutation
The variety of crossover and mutation operators presented in Section 4.2.3 and Section 4.2.4 have to be utilized based on the performance or fitness of the operators in the previous iterations. This can be achieved by using a roulette wheel selection technique by assigning each crossover and mutation type a probability proportional to its fitness (both crossover and mutations use a separate roulette wheel). That is, the probability of an operator being selected can be defined as
where pi is the probability of operator i being selected, Fi is the fitness of operator i, and O is the total number of operators.
We define the population diversity and local search ability to calculate the fitness of crossover and mutation types, respectively. Population diversity is used to determine the fitness of each type of crossover since it is a crucial factor in avoiding premature convergence. At each iteration, the fitness of a crossover type i is calculated by dividing the number of unique fitness values after the crossover (ua) by the number of unique fitness values before the crossover is performed (ub). That is, the finesses of a crossover operator i are given by
A selected crossover type is applied for a given number of iterations (min-itr) before making a new selection using the roulette wheel. The fitness of an operator after min-itr is taken as an exponential moving average that gives more weight to the recent performance of the operator to avoid any abrupt changes to any operator’s fitness.
On the other hand, the fitness of a mutation type i is measured based on its local search ability. This is determined by dividing the number of chromosomes produced by the mutation operator with a better fitness value (fb) by the number of chromosomes produced by the mutation operator with a lower fitness value (fw). That is
Similar to crossover, the fitness of a mutation type is the exponential moving average during its recent application in min-itr consecutive iterations.
5. Simulation Results and Discussion
We evaluated the performance of the proposed algorithms, i.e., greedy search algorithm, non-adaptive GA, and AGA. The algorithms were implemented in C++ and run on PCs with an Intel i7 processor and 8 GB RAM running on the Microsoft Windows 10 platform. This section provides details of the experimental setup and the set of experiments performed to evaluate the performance of the greedy algorithm and the non-adaptive GA and AGA in terms of their solution quality and run time.
5.1. Experimental Setup
The test data was generated randomly similar to other studies. The basic inputs to the algorithms are DAGs of varying sizes, workload and deadlines of tasks, amount of data transferred between tasks, unit data communication cost, speed of virtual machines, and cost of virtual machines.
The DAGs were generated using the TGFF utility [42]. The number of tasks were varied from 10 to 300 per task graph. The workloads for the tasks were generated within the range of [10, 4500] similar to the ones used in [4]. The execution time for a task on different machines was calculated by dividing the work load by the speed of the virtual machine. We used the technique proposed by Balbastre et al. [43] to assign the deadlines to each task in the task graph. The amount of data transmitted between dependent tasks was generated randomly in the range of [50, 1500]. The maximum number of virtual machines was taken as 50. The processing speed and cost of the virtual machine were assigned randomly from a set of typical values taken from [4,32,33]. The communication cost per unit data between two virtual machines was generated randomly in the range [1, 5].
The results were generated for the greedy and the genetic algorithms. The greedy algorithm was executed once for each input combination of virtual machines and task graphs. For genetic algorithms, the same initial population was used for all experiments for each test case, and 30 independent runs were executed following the standard practice for statistically analyzing the performance of iterative heuristics. The results for GA and AGA were statistically validated using the Wilcoxon-ranked-sum test at a 95% confidence level.
5.2. Results for Genetic Algorithm
A total of seven parameters were used for the analysis of the non-adaptive genetic algorithm in order to find the best possible parameter combinations. These parameters are the replacement methods, population size, parent selection type, crossover rate, crossover type, mutation rate, and the mutation type. Table 2 shows different parameter values used in the simulations. Different combinations of these parameter values resulted in 432 combinations. With these 432 combinations, extensive effort was made on DAGs of 10 and 20 tasks to find the best parameter setup. Consequently, four combinations as shown in Table 3 were found to generate the best quality results which were used for subsequent testing with other DAGs.

Table 2.
Parameter settings for GA.

Table 3.
Selected parameter combinations for GA. Combo = Combination, RA = replacement approach, Pop. = population size, C type = crossover type, C rate = crossover rate, M type = mutation type, and M rate = mutation rate.
Table 4 provides the results for the four combinations for each test case. It is observed from these tables that for the majority of test cases, Combination 4 produced the best results. More specifically, Combination 4 generated the minimum cost for 20, 30, 80, 100, and 200 tasks. Combination 2 produced the best results for four test cases, which were 60, 150, 250, and 300. The other two combinations produced the best results for only one test case each, making them the worst performers. Therefore, based on the results, it can be fairly claimed that Combination 4 was much better than combinations 1 and 2, while showing relatively better performance than Combination 3 as far as the quality of results is concerned.

Table 4.
Average cost for the four combinations. The best results are highlighted in bold.
With regards to the execution time, a clear trend is observed in Figure 7, favoring combination 1. While all four combinations require more or less the same execution times with smaller DAGs of 10 to 30 tasks, the difference in runtime becomes more prominent for test cases with a higher number of tasks. Therefore, while Combination 1 lags behind other combinations in terms of the quality of solutions, it outperformed the other three combinations with regards to the execution time.
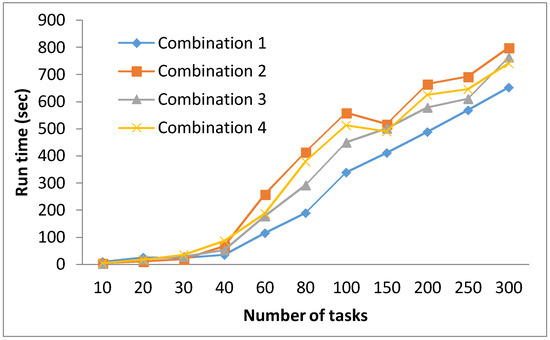
Figure 7.
Comparison of execution times for the four combinations.
5.3. Comparison of GA, Adaptive GA, and Greedy Algorithms
This section provides a comparative analysis of the greedy algorithm, GA, and AGA. For AGA, the pool of crossover and mutation operators was used as given in Table 5. Note that the pool contains the four best combinations as given in Table 3 as well as some other combinations that gave results comparable to the best four combinations. Initial fitness values for each crossover and mutation type were calculated using Equations (14) and (15), respectively, after applying each operator individually to the same initial population for a single run. The parameter min-itr was set to five iterations after experimenting with a number of other values.

Table 5.
Pool of crossover and mutation operators used in AGA.
Table 6 provides the cost obtained by each algorithm. For GA and AGA, the average cost (averaged over 30 runs) is reported. The results indicate that the greedy algorithm produced solutions of inferior quality as compared to GA and AGA, as expected. With respect to the mutual comparison of GA and AGA, the results indicate that AGA outperformed GA in all test cases. These observations are elaborated through Figure 8 which clearly indicates that AGA produced solutions with the lowest cost for all the test cases. Table 7 reflects the percentage improvement achieved by AGA with respect to the other three algorithms. The results indicate that the improvements achieved by an AGA with respect to the greedy algorithm were significantly high, in the range of 12% to over 35%. As far as a GA and AGA are concerned, the percentage improvements by an AGA were in the range of over 1.79% to 8.43%. These improvements were subjected to statistical testing. The results of this statistical testing indicated that a huge majority of improvements achieved by an AGA were statistically significant. Two exceptions were test cases with 20 and 40 tasks where the improvements were not statistically significant.

Table 6.
Cost comparison of Greedy, GA, and AGA algorithms.
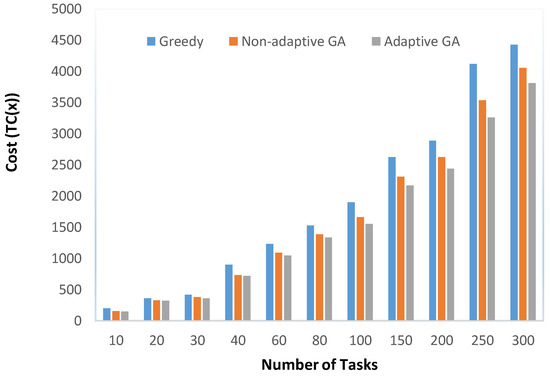
Figure 8.
Comparison of cost for Greedy, GA, and AGA.

Table 7.
Percentage improvement obtained by Adaptive GA with respect to Greedy, and GA.
Figure 9 illustrates the run time comparison of GA and AGA. It is observed in the figure that AGA takes more time as compared to GA for all test cases. This increase in time is due to the selection of the crossover and mutation operators from the pool and updating their fitness values.
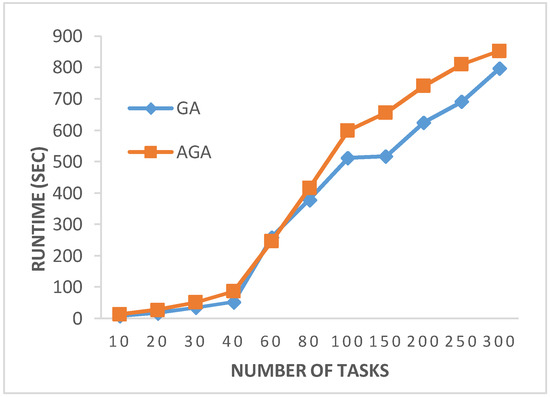
Figure 9.
Run time comparison of GA and AGA.
Another measure used to assess the effectiveness of the approach used in AGA was population diversity. Diversity is a measure used to calculate the average distance of each chromosome from the mean value. Diversity is calculated in every iteration during the execution of the algorithm [44]. The effect of the four different GA combinations as well as that of AGA on the population diversity was investigated. The purpose was to observe whether AGA was capable of reducing the possibility of premature convergence and preventing the algorithm from getting stuck in local minima. As an example, Figure 10 shows the diversity plots for one typical run for the four GA combinations as well as adaptive GA, while using the DAG of 60 tasks, and while running each algorithm for 500 iterations. The figure indicates that an AGA maintained sufficient diversity until the end of execution, while a GA with four combinations was unable to maintain diversity for longer durations. More specifically, for combinations 1 and 3, the diversity almost became zero before 330 iterations. Combinations 2 and 4 were better than the other two combinations in the sense that the diversity was maintained until around 400 iterations. However, for an AGA, the population had non-zero diversity even at the end of execution as is evident from Figure 10e. Therefore, it can be confidently claimed that an AGA was better than the other four combinations in terms of maintaining population diversity and consequently giving solutions of better quality.
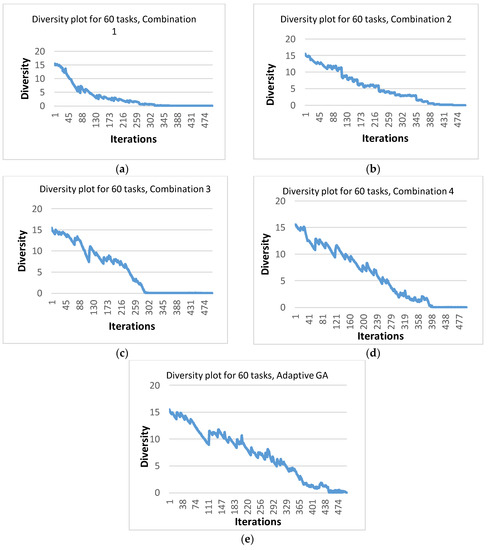
Figure 10.
Diversity plots for the typical runs for 60 tasks using (a) Combination 1; (b) Combination 2; (c) Combination 3; (d) Combination 4; and (e) AGA.
6. Conclusions
Infrastructure-as-a-Service cloud computing model is an attractive choice for economically executing real-time tasks on a set of leased virtual machines. Task allocation and scheduling on virtual machines is a well-known NP-hard problem. This paper presented an efficient greedy algorithm and a genetic algorithm with adaptive selection of crossover and mutation from a pool of crossover and mutation types. The selection of crossover and mutation is based on the previous performance of the operators. The adaptive GA uses population diversity to determine the fitness of each type of crossover while the fitness of mutation is determined in terms of its ability to find a better quality solution (i.e., intensification). The basic idea is to leverage the strength of different types of crossovers and mutations during the course of GA iterations. The simulation results show that AGA with the adaptive selection of crossover and mutation outperforms the non-adaptive version of GA and the greedy algorithm in terms of solution quality. As a future work, we will test the performance of the algorithms with larger task graphs and by increasing the size of the pool of crossover and mutation operators. Developing hyperheuristics for this problem can also be another promising direction.
Author Contributions
Amjad Mahmood worked on the theoretical development of the proposed AGA and the greedy algorithm and contributed to writing the relevant portions of the manuscript. Salman A. Khan and Rashid A. Bahlool performed the experiments, analyzed the results and contributed in writing the relevant portions of the manuscript. All authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Luo, J.Z.; Jin, J.H.; Song, A.B.; Dong, F. Cloud Computing: Architecture and Key Technologies. J. Commun. 2011, 32, 3–21. [Google Scholar]
- Abdullahi, M.; Ngadi, M. Hybrid Symbiotic Organisms Search Optimization Algorithm for Scheduling of Tasks on Cloud Computing Environment. PLoS ONE 2016, 11, 6–26. [Google Scholar]
- Armbrust, M.; Fox, A.; Griffith, R.; Joseph, A.; Katz, R.; Konwinski, A.; Zaharia, M. A view of cloud computing. Commun. ACM 2010, 53, 50–58. [Google Scholar] [CrossRef]
- Kumar, K.; Feng, J.; Nimmagadda, Y.; Lu, Y.H. Resource allocation for real-time tasks using cloud computing. In Proceedings of the IEEE 20th International Conference on Computer Communications and Networks (ICCCN), Maui, HI, USA, 31 July–4 August 2011; pp. 1–7. [Google Scholar]
- Awad, A.I.; El-Hefnawy, N.A.; Abdelkader, H.M. Enhanced Particle Swarm Optimization for Task Scheduling in Cloud Computing Environments. Procedia Comput. Sci. 2015, 65, 920–929. [Google Scholar] [CrossRef]
- Navimipour, N.J.; Khanli, L.M. The LGR method for task scheduling in computational grid. In Proceedings of the International Conference on Advanced Computer Theory and Engineering, Phuket, Thailand, 20–22 December 2008; pp. 1062–1066. [Google Scholar]
- Zhang, F.; Cao, J.; Li, K.; Khan, S.; Hwang, K. Multi-objective scheduling of many tasks in cloud platforms. Future Gener. Comput. Syst. 2014, 37, 309–320. [Google Scholar] [CrossRef]
- Davis, R.I.; Burns, A. A survey of hard real-time scheduling for multiprocessor systems. ACM Comput. Surv. 2011, 43, 35. [Google Scholar] [CrossRef]
- Braun, T.D.; Siegel, H.J.; Beck, N.; Bölöni, L.L.; Maheswaran, M.; Reuther, A.I.; Freund, R.F. A comparison of eleven static heuristics for mapping a class of independent tasks onto heterogeneous distributed computing systems. J. Parallel Distrib. Comput. 2001, 61, 810–837. [Google Scholar] [CrossRef]
- Dong, F.; Akl, S.G. Scheduling Algorithms for Grid Computing: State of The Art and Open Problems; Technical report 2006–504; Queen’s University: Kingston, ON, Canada, 2006. [Google Scholar]
- Chen, X.; Zhang, J.; Li, J. Resource management framework for collaborative computing systems over multiple virtual machines. Service Oriented Comput. Appl. 2011, 5, 225–243. [Google Scholar] [CrossRef]
- Chen, H.; Zhu, X.; Guo, H.; Zhu, J.; Qin, X.; Wu, J. Towards energy-efficient scheduling for real-time tasks under uncertain cloud computing environment. J. Syst. Softw. 2015, 99, 20–35. [Google Scholar] [CrossRef]
- Wu, X.; Deng, M.; Zhang, R.; Zeng, B.; Zhou, S. A task scheduling algorithm based on QoS-driven in cloud computing. Procedia Comput. Sci. 2013, 17, 1162–1169. [Google Scholar] [CrossRef]
- Lee, Y.C.; Wang, C.; Zomaya, A.Y.; Zhou, B.B. Profit-driven scheduling for cloud services with data access awareness. J. Parallel Distrib. Comput. 2012, 72, 591–602. [Google Scholar] [CrossRef]
- Panda, S.K.; Gupta, I.; Jana, P.K. Allocation-aware Task Scheduling for Heterogeneous Multi-cloud Systems. Procedia Comput. Sci. 2015, 50, 176–184. [Google Scholar] [CrossRef]
- Kartik, S.; Murthy, S.R. Improved task-allocation algorithms to maximize reliability of redundant distributed computing systems. IEEE Trans. Reliab. 1995, 44, 575–586. [Google Scholar] [CrossRef]
- Mahmood, A. Task allocation algorithms for maximizing reliability of heterogeneous distributed computing systems. Control Cybern. 2001, 30, 115–130. [Google Scholar]
- Hsieh, C.C. Optimal task allocation and hardware redundancy policies in distributed computing systems. Eur. J. Oper. Res. 2003, 147, 430–447. [Google Scholar] [CrossRef]
- Stavrinides, G.L.; Karatza, H.D. Scheduling multiple task graphs in heterogeneous distributed real-time systems by exploiting schedule holes with bin packing techniques. Simul. Model Pract. Theory 2011, 19, 540–552. [Google Scholar] [CrossRef]
- Zhang, Y.F.; Tian, Y.C.; Fidge, C.; Kelly, W. Data-aware task scheduling for all-to-all comparison problems in heterogeneous distributed systems. J. Parallel Distrib. Comput. 2016, 93, 87–101. [Google Scholar] [CrossRef]
- Kumar, S.; Dutta, K.; Mookerjee, V. Maximizing business value by optimal assignment of jobs to resources in grid computing. Eur. J. Oper. Res. 2009, 194, 856–872. [Google Scholar] [CrossRef]
- Kokilavani, T.; Amalarethinam, D. Load balanced min-min algorithm for static meta-task scheduling in grid computing. Int. J. Comput. Appl. 2011, 20, 43–49. [Google Scholar]
- Shojafar, M.; Pooranian, Z.; Abawajy, H.; Meybodi, M. An efficient scheduling method for grid systems based on a hierarchical stochastic Petri net. J. Comput. Sci. Eng. 2013, 7, 44–52. [Google Scholar] [CrossRef]
- Alkhanak, E.N.; Lee, S.P.; Rezaei, R.; Parizi, R.M. Cost optimization approaches for scientific workflow scheduling in cloud and grid computing: A review, classifications, and open issues. J. Syst. Softw. 2013, 113, 1–26. [Google Scholar] [CrossRef]
- Mahmood, A. A hybrid genetic algorithm for task scheduling in multiprocessor real-time systems. Stud. Inform. Control 2000, 9, 207–218. [Google Scholar]
- Liu, Z.; Qu, W.; Liu, W.; Li, Z.; Xu, Y. Resource preprocessing and optimal task scheduling in cloud computing environments. Concurr. Comput. 2015, 27, 3461–3482. [Google Scholar] [CrossRef]
- Sangwan, A.; Kumar, G.; Gupta, S. To Convalesce Task Scheduling in a Decentralized Cloud Computing Environment. Rev. Comput. Eng. Res. 2016, 3, 25–34. [Google Scholar] [CrossRef]
- Jang, S.; Kim, T.; Kim, J.; Lee, J. The study of genetic algorithm-based task scheduling for cloud computing. Int. J. Control Autom. 2012, 5, 157–162. [Google Scholar]
- Razaque, A.; Vennapusa, N.; Soni, N.; Janapati, G. Task scheduling in Cloud computing. In Proceedings of the IEEE Long Island Systems, Applications and Technology Conference (LISAT), Farmingdale, NY, USA, 29 April 2016; pp. 1–5. [Google Scholar]
- Sindhu, S. Task scheduling in cloud computing. Int. J. Adv. Res. Comput. Eng. Technol. 2015, 4, 3019–3023. [Google Scholar]
- Li, J.; Qiu, M.; Ming, Z.; Quan, G.; Qin, X.; Gu, Z. Online optimization for scheduling preemptable tasks on IaaS cloud systems. J. Parallel Distrib. Comput. 2012, 72, 666–677. [Google Scholar] [CrossRef]
- Tsai, J.T.; Fang, J.C.; Chou, J.H. Optimized task scheduling and resource allocation on cloud computing environment using improved differential evolution algorithm. Comput. Oper. Res. 2013, 40, 3045–3055. [Google Scholar] [CrossRef]
- Tsai, C.W.; Huang, W.C.; Chiang, M.H.; Chiang, M.C.; Yang, C.S. A hyper-heuristic scheduling algorithm for cloud. IEEE Trans. Cloud Comput. 2014, 2, 236–250. [Google Scholar] [CrossRef]
- Pandey, S.; Wu, L.; Guru, S.; Buyya, R. A particle swarm optimization-based heuristic for scheduling workflow applications in cloud computing environments. In Proceedings of the 24th IEEE International Conference on Advanced Information Networking and Applications (AINA), Perth, Australia, 20–23 April 2010; pp. 400–407. [Google Scholar]
- Navimipour, N.; Milani, F. Task scheduling in the cloud computing based on the cuckoo search algorithm. Int. J. Model. Opt. 2015, 5, 44. [Google Scholar] [CrossRef]
- Raghavan, S.; Sarwesh, P.; Marimuthu, C.; Chandrasekaran, K. Bat algorithm for scheduling workflow applications in cloud. In Proceedings of the 2015 International Conference Electronic Design, Computer Networks & Automated Verification (EDCAV), Shillong, India, 29–30 January 2015; pp. 139–144. [Google Scholar]
- Liu, S.; Quan, G.; Ren, S. On-line scheduling of real-time services with profit and penalty. In Proceedings of the 2011 ACM Symposium on Applied Computing, Taichung, Taiwan, 21–24 March 2011; pp. 1476–1481. [Google Scholar]
- Kim, K.H.; Beloglazov, A.; Buyya, R. Power-aware provisioning of virtual machines for real-time cloud services. Concurr. Comput. 2011, 23, 1491–1505. [Google Scholar] [CrossRef]
- Deniziak, S.; Ciopinski, L.; Pawinski, G.; Wieczorek, K.; Bak, S. Cost optimization of real-time cloud applications using developmental genetic programming. In Proceedings of the IEEE/ACM 7th International Conference on Utility and Cloud Computing (UCC), London, UK, 8–11 December 2014; pp. 774–779. [Google Scholar]
- Holland, J.H. Adaptation in Natural and Artificial Systems; University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Oh, J.; Wu, C. Genetic-algorithm-based real-time task scheduling with multiple goals. J. Syst. Softw. 2014, 71, 245–258. [Google Scholar] [CrossRef]
- Dick, R.P.; Rhodes, D.L.; Wolf, W. TGFF: Task graphs for free. In Proceedings of the 6th International Workshop on Hardware/software Codesign, Seattle, WA, USA, 15–18 March 1998; pp. 97–101. [Google Scholar]
- Balbastre, P.; Ripoll, I.; Crespo, A. Minimum deadline calculation for periodic real-time tasks in dynamic priority systems. IEEE Trans. Comput. 2008, 57, 96–109. [Google Scholar] [CrossRef]
- Khan, S.A.; Engelbrecht, A.P. A fuzzy particle swarm optimization algorithm for computer communication network topology design. Appl. Intell. 2012, 36, 161–177. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).