Optimizing Pre-Silicon CPU Validation: Reducing Simulation Time with Unsupervised Machine Learning and Statistical Analysis

Abstract

In modern processor development, extensive simulation is required before manufacturing to ensure that Central Processing Unit (CPU) designs function correctly and efficiently. This pre-silicon validation process involves running a wide range of software workloads on architectural models to identify potential issues early in the design cycle. Improving pre-silicon simulation time is critical for accelerating CPU development and reducing time-to-market for high-quality processors. This study addresses the computational challenges of validating full-system simulations by leveraging unsupervised machine learning to optimize test case selection. By identifying patterns in executed instructions, the approach reduces the need for exhaustive simulations while maintaining rigorous validation standards. Notably, the optimized subset of test cases reduced simulation time by a factor of 10 and captured 97.5% of the maximum instruction entropy, ensuring nearly the same diversity in instruction coverage as the full workload set. The combination of Principal Component Analysis (PCA) and clustering algorithms effectively distinguished compute-bound and memory-bound workloads without requiring prior knowledge of the code. Statistical Model Checking with entropy-based analysis confirmed the effectiveness of this subset. This methodology significantly reduces validation effort, expedites CPU design cycles, and improves hardware efficiency. The findings highlight the potential of machine learning-driven validation strategies to enhance pre-silicon testing, enabling faster innovation and more robust processor architectures.

1. Introduction

The growing demand for high-performance, power-efficient processors has intensified the complexity of Central Processing Unit (CPU) design and validation. Pre-silicon simulation is a critical phase in CPU development, enabling early bug detection and performance analysis before hardware fabrication. However, the increasing complexity of modern processors has significantly extended simulation time, creating a bottleneck in the validation process. As a result, CPU design teams must identify test cases that maximize validation coverage while minimizing computational overhead, ensuring efficient pre-silicon testing [1].

To address these challenges, Full-System Simulation (FSS) has become a widely used technique for pre-silicon validation. FSS enables the simulation of complete computing systems, from basic processor-memory setups to complex platforms with accelerators and I/O peripherals. Tools like Simics provide a flexible and scalable simulation environment that allows engineers to boot operating systems, run software, and identify architectural errors before fabrication [2]. Simics is widely adopted by Intel and other industry leaders for hardware and software co-development, debugging, and validation throughout the processor design cycle [3]. Comparative studies, such as [4], highlight the strengths of Simics and similar frameworks in evaluating AI accelerators and other complex hardware components. By supporting both pre-silicon and post-silicon stages, Simics enables designers to test and debug hardware models, validate firmware and operating system interactions, and evaluate system performance under a variety of workloads, all before physical prototypes are available.

Despite these capabilities, the growing complexity of Machine Learning (ML) workloads [5] has further increased simulation times. For example, the challenge of energy management optimization for multicore processors has been investigated in [6], where evaluating benchmark suites within Sniper (a pre-silicon simulator using Simics input) required 370 h—about 16 days—of simulation, demonstrating the considerable time needed for comprehensive validation.

Parallelization is often used to reduce simulation time by distributing computational tasks across multiple processor cores. However, according to [7], when simulating systems with many cores, this approach introduces additional layers of complexity. One major challenge is communication overhead; as simulations run on multiple cores, the need for these cores to exchange information can limit the overall speed-up achieved. Furthermore, while modern CPUs may contain hundreds of cores, the computers used to run simulations (host machines) typically have far fewer, which restricts the ability to scale simulations efficiently. Beyond these hardware limitations, the architecture of contemporary processors includes advanced features such as on-chip interconnects, co-processors, accelerators, and evolving instruction set architectures (ISAs). These elements add further complexity to the simulation process, increasing the computational resources and time required. Given these challenges, it becomes crucial to carefully select a subset of workloads that can provide thorough validation coverage without requiring an impractically large number of test cases or excessive simulation time.

In response to these issues, this research proposes an optimization framework leveraging unsupervised machine learning to generate an optimal subset of test cases, eliminating redundant workloads while maintaining comprehensive validation coverage. Once the reduced test set is defined, ensuring its effectiveness is crucial. Statistical Model Checking (SMC), a technique particularly suited for validating systems with stochastic behavior or vast state spaces, is employed for this purpose. The applicability of SMC in safety-critical hybrid systems is demonstrated in [8], making it a valuable tool for pre-silicon workload validation.

The paper follows a structured approach. It begins with an analysis of related works in Section 2. Section 3 describes the proposed methodology. Section 4 provides a detailed description of the workloads used in the experiments. Section 5 presents the results obtained from the methodology. Section 6 discusses the implications and significance of the findings. Section 7 outlines the limitations of the study and directions for future work. Finally, Section 8 summarizes the main conclusions.

2. Analysis of Related Works

Creating an effective test program for a CPU is a complex task that requires the review of aspects addressed during the CPU design to ensure comprehensive testing of the properties and characteristics of new CPU designs. This raises the critical question of whether the test program adequately covers all essential aspects of the device under test. If it does not, there is a significant risk of delivering defective chips to customers. Recent works, such as [9], highlight this issue and propose a post-silicon framework for analyzing the functional coverage of test programs. The proposed solution enables the analysis of test program coverage with the same efficiency as the functional verification process, requiring virtually no changes to the workflows of test program developers.

While this approach is suitable for post-silicon validation, it does not help measure the test coverage of test programs in pre-silicon. The most widely used method for coverage in simulation-based verification is code coverage [10]. Code coverage measures the proportion of source code elements executed or covered during the simulation of a test suite. Because code coverage can be easily correlated with the source code and generates minimal overhead during simulation, it is a highly popular coverage metric. However, as described by [11], the increasing complexity of new architectures, such as neuromorphic computing and specialized hardware for machine learning, generates significant verification challenges. Current test programs attempt to include full application benchmarks that simulate behavior similar to what CPUs will experience with customer applications. However, the long runtime of these programs in RTL simulation limits the feasibility of using traditional code coverage techniques.

Characterizing workloads is crucial in the design of incoming computer systems, which affects design considerations across all parts of the system, from hardware platforms to operating systems. A comprehensive understanding of workload attributes and their execution dynamics clarifies resource utilization patterns, offering insights to optimize performance on both hardware and software parts. Moreover, discerning an application’s characteristics proves invaluable in making informed decisions regarding hardware resource allocation, which makes workload characterization essential for comprehending the underlying causes of sub-optimal runtime performance on hardware platforms.

An example of workload characterization to find redundancies in test programs is presented by [12]. In this paper, the authors provide a novel way to identify redundancies among CPU17 applications, utilizing hardware performance counter statistics in addition to Principal Component Analysis (PCA) and Hierarchical Clustering. Detecting redundancies among CPU17 applications facilitates the selection of a representative subset of CPU17 applications to simplify the simulation time. This approach is only suitable for post-silicon environments, since FSS like Simics, does not expose these hardware performance counters in the pre-silicon phase.

An approach to workload characterization using pre-silicon information is demonstrated in [13], where the authors introduce a methodology for workload characterization utilizing instruction traces from the SPEC CPU 2017 suite. The instruction traces are collected using an FSS. Subsequently, the gathered instruction traces undergo instruction decomposition. This process involves segmenting the total instructions executed during workload execution on the functional simulator into distinct categories: integer instructions, floating-point instructions, branches, memory access, and pre-fetch instructions. According to the authors, instruction decomposition offers crucial insights into the instruction mix of an application. However, these experiments are conducted on a functional simulator for the UltraSPARC III architecture, rather than on an x86-64 or AMD64 architecture, two of the most widely used ISAs in data centers.

A research study that emphasizes the importance of statistical analysis of instructions executed on a functional simulator is the one conducted by [14]. This study proposes a tool to analyze benchmarks based on assembly instructions. An entropy score is calculated to facilitate an easy comparison of diversity. The results obtained from static and dynamic analysis contribute to a deeper understanding of the distribution of instructions. The tool can analyze the benchmark compiled to illustrate the predominant instructions influencing performance. High-entropy benchmarks are recommended for assessing the overall performance of functional simulators.

3. Proposed Methodology

The methodology used in this work consists of the steps described in Figure 1. In the initial stage, workloads are executed on an FSS. Specifically, the experiments were conducted using the Simics FSS, which simulates an Ice Lake Server equipped with four cores and 16 GB of RAM. The workloads described in Section 4 were simulated on the FSS simulation platform to generate instruction histograms.

This process enables the collection of instruction histograms throughout their runtime, stored in a Comma-Separated Values (CSV) file with two columns: mnemonic and count. The mnemonic column comprises executed instructions, while the count column represents their frequencies. The histogram encompasses instructions from all processes running concurrently in the OS alongside the analyzed application. This crucial step facilitates the acquisition of raw data reflective of real-world computational tasks, laying the foundation for subsequent analysis and optimization phases.

3.1. Workload Characterization

Once data collection is complete, we proceed to characterize and classify the instructions based on their functionality, as outlined in

Table 1. Classification of Instruction Types Used in Workloads.

Instruction Kind	Instruction Description
Arithmetic	CPU instructions for mathematical operations on data
I/O (Input/Output)	Instructions for data transfer between CPU and peripherals
Branch	Controlling program flow, enabling conditional jumps
Load	Instructions for fetching data from memory
Store	Instructions for saving data to memory
Vector	SIMD instructions for parallel data processing

.

3.2. Dimensionality Reduction and Clustering

Recent studies have increasingly focused on workload characterization, particularly through applying deep learning and dimensionality reduction techniques, as highlighted in recent works [15,16]. After characterizing workloads by their executed instructions, we apply PCA for dimensionality reduction. This technique, as demonstrated in previous research [17], improves the effectiveness of unsupervised machine learning algorithms such as K-means, which we use to improve the clustering accuracy in our study.

3.3. Optimal Cluster Selection (Simulation Time and SSE)

When the unsupervised ML algorithm successfully produces small clusters of workloads exhibiting similar characteristics in terms of executed instructions, it becomes feasible to determine the optimal number of sub-clusters using the Sum of Squared Error (SSE) described by [18]. The SSE is an objective function used in clustering analysis to evaluate the effectiveness of clustering algorithms. The SSE measures the dispersion or spread of data points within clusters, reflecting how well clusters are formed. The SSE is calculated by summing the squared distances between each data point and its assigned cluster centroid. This can be expressed as follows:

$$SSE=\sum _{i=1}^K\sum _{x\in C_i}dis{t}^2(m_i,x)$$

(1)

where K denotes the overall number of clusters. x denotes a data point belonging to the cluster $C_i$, with $m_i$ representing the centroid of the cluster $C_i$.

SSE consistently decreases with each iteration until it converges to a local or global minimum. Because of this, the SSE is commonly employed to determine the optimal number of clusters. A significant drop in the SSE value, accompanied by a sharper decrease, indicates a suitable number of clusters.

The work proposed by [12] uses SSE as a metric to assess clustering quality across numerous potential clusters while considering the execution time of the test case with the shortest simulation duration within each cluster.

The simulation time for each cluster is calculated during each iteration of the clustering by identifying the test case with the minimum simulation time within that cluster. This result ensures that for every cluster of test cases, the one with the shortest simulation time is chosen as the primary candidate. The sum of all minimum simulation times can be stated as follows:

$$T=\sum _{i=1}^K\underset{x\in C_i}{min}t\left(x\right)$$

(2)

where $t\left(x\right)$ represents the simulation time of each test x case within cluster $C_i$.

Following this, a graphical method involves plotting the data points representing the two lines on a graph, facilitating visual identification of the crossing point. This point is the optimal number of clusters with clustering accuracy aligned to the minimum simulation time. Subsequently, the leading candidate for each cluster can be determined, forming a list that represents a subset of test cases. This subset efficiently encapsulates the diverse range of workloads under analysis, eliminating redundant workloads.

While identifying the optimal subset of workloads for pre-silicon validation is crucial, it does not guarantee comprehensive instruction validation coverage. To overcome this challenge, the proposed methodology first includes SMC as a key component. SMC is used to assess the entropy metric to capture the variability and complexity of instruction execution across different workloads.

3.4. SMC for Instruction Coverage and Entropy Assessment

SMC can be utilized to measure the coverage of instructions executed, especially in scenarios where minimizing the set of test cases while maximizing the entropy of instructions is essential. The proposed methodology integrates insights from [14], which offers a systematic approach for dynamic analysis based on statistical analysis of executed instructions.

Once the subset of workloads with reduced execution time is selected from clusters of workloads characterized by similar instruction profiles (as provided by unsupervised machine learning) and validated by observing that the cluster separation yields minimal SSE, the next step, marking the start of the SMC process, is to calculate the execution probability for each instruction. This probability is determined by:

$$p\left(i\right)={\displaystyle \frac{e\left(i\right)}{{\sum }_{j\in B}e\left(j\right)}}$$

(3)

where for each instruction i within a workload B, the frequency of its execution $e\left(i\right)$ is calculated using the histogram generated during the Simics simulation.

Once the execution probabilities are obtained, these results can be used to calculate the entropy score. This metric is a comprehensive evaluation, considering the various instructions executed and their respective probabilities of occurrence throughout the simulation; it quantifies the uncertainty or randomness in the execution pattern of the instruction. The calculation of the entropy score provides a metric to measure the richness and effectiveness of the instruction set exercised during simulation. This is especially important for pre-silicon validation, where diverse coverage minimizes the risks of post-silicon issues by simulating a wide range of potential usage patterns in a controlled environment. The entropy formula is expressed as follows:

$$H\left(B\right)=-\sum _{i\in B}p\left(i\right)·{log}_2\left(p\left(i\right)\right)$$

(4)

In this scenario, $p\left(i\right)$ signifies the probability that instruction i appears among all instructions executed in the workload B. The entropy reaches its maximum in a benchmark with diverse instructions when the execution probabilities are evenly distributed across all instructions. Furthermore, entropy is a standard measure from information theory that quantifies the uncertainty or diversity in a probability distribution. In the context of SMC for instruction coverage, a higher entropy value indicates that the executed instructions are more evenly distributed across the instruction set, reflecting greater diversity and coverage. This formal approach ensures that the selected subset of workloads is not only minimal in size but also maximizes instruction diversity, which is critical for effective pre-silicon validation.

This approach provides a more strategic understanding of coverage, particularly when using machine learning or SSE-based optimal selection methods. A user may randomly select a few test cases without employing these methodologies. However, this random selection lacks the precision and strategic focus that a methodology-driven process offers, potentially leading to a less representative subset.

Our methodology uses entropy scores to identify subsets of workloads that maximize instruction diversity. This approach ensures broad instruction coverage with fewer workloads, reducing the need for repeated validation during new CPU design testing.

While this study focuses on ML and database workloads due to their relevance and diversity in modern datacenter environments, the proposed methodology is generalizable. The approach can be applied to other domains such as scientific computing, web services, or high-performance computing, where instruction diversity and coverage are also critical for pre-silicon validation.

4. Description of the Workloads

The workloads selected for this study consist of 13 distinct applications drawn from ML and DB domains. These choices were made to ensure coverage of critical and diverse classes of modern datacenter workloads, which are known to effectively stress both compute and memory subsystems. Within these domains, a variety of models and access patterns were included to capture both compute-bound and memory-bound behaviors. Although we recognize the potential risk of overfitting by focusing on ML and DB workloads—these were deliberately selected for their relevance and diversity. To mitigate this risk, we ensure that workloads cover a broad spectrum of behaviors. Furthermore, the substantial computational resources and time required for simulation of the full system in Simics—often several hours per workload—required a focused yet representative set for rigorous evaluation within practical resource constraints.

The corresponding identification numbers for each workload, their respective tests types (ML/DB), and the simulation time spent on the Simics FSS are listed in

Table 2. Workloads Evaluated and Associated Simulation Times.

ID	Test Name	Kind	Simulation Time (hours)
0	benchdnn_conv_avx2	ML	69
1	benchdnn_conv_bf16	ML	69
2	resnet101_throughput_amx_fp32	ML	32
3	resnet101_throughput_amx_int8	ML	61
4	resnet101_throughput_avx_fp32	ML	65
5	resnet101_throughput_avx_int8	ML	63
6	resnet50_throughput_avx_fp32	ML	201
7	resnet50_throughput_avx_int8	ML	169
8	redis_memtier_12cpu	Database	11
9	redis_memtier_16cpu	Database	13
10	redis_memtier_2cpu	Database	126
11	redis_memtier_4cpu	Database	77
12	redis_memtier_8cpu	Database	9
Total			965

. This table presents the set of workloads evaluated in this study, including their identification number, test name, workload kind (ML or DB), and the corresponding simulation time in hours. The total simulation time for all workloads is also provided, illustrating the computational effort required for comprehensive pre-silicon validation. The following subsections describe each of the workloads selected for ML applications and databases.

4.1. ML Workloads

The machine learning workloads utilized in the current experiments include ResNet-101, a convolutional neural network with 101 layers, and ResNet-50, a convolutional neural network with 50 layers. Additionally, Benchdnn is employed, which serves as a functional verification and performance benchmarking tool for the primitives provided by the oneDNN ML library. These workloads are also integral to the research conducted by [19], where the authors implement different versions of these workloads on native CUDA and with an API library that uses a CUDA backend. Their studies highlight the potential to achieve performance portability by leveraging existing building blocks designed for the target hardware.

These workloads are also used in the research conducted by [19], where the authors implement different versions of these workloads on native CUDA and with an API library that uses a CUDA backend. Their studies showcase the potential to achieve performance portability by utilizing existing building blocks designed for the target hardware.

The ongoing research implements these workloads using the oneDNN ML library. This library uses Just in Time (JIT) code generation to implement the majority of its functionalities and selects the optimal code based on detected processor features. Additionally, users can control the backend employed by oneDNN, such as compelling the library to utilize x86-64 vector instructions on an x86-64 processor.

The JIT option employed for each workload is specified as part of the workload name. For example, in the workload resnet101_throughput_amx_int8, the oneDNN library is utilized with optimizations designed for Advanced Matrix Extensions (AMX) instructions. The AMX ISA was developed to accelerate matrix operations in CPUs, aiming to improve the performance of AI/ML workloads and other applications that heavily depend on matrix operations. In contrast, in the resnet101_throughput_avx_int8 workload, the JIT option enforces the utilization of the Advanced Vector Extensions (AVX) instructions.

The suffix of the workload name specifies the data type used in the ML models, such as “int8” or “fp32”. The “int8” label signifies integers represented with 8 bits of memory, while “fp32” denotes floating-point numbers using 32 bits of memory. Additionally, “bf16” label stands for BFloat16, a floating-point format with 16 bits of precision.

4.2. Key-Value Databases Workloads

Today, software applications not only use ML systems to classify or predict, but also need to process a large amount of data produced by users. Because of this, databases became a bottleneck in software architecture. One way to improve the performance of data management and arrangement is the use of key-value databases. These databases improve the runtime performance of queries in large amounts of data by keeping an in-memory data structure mapped to data stored on disk.

Memtier is a benchmark created by Redis Labs and serves as a specialized tool designed for stress-testing key-value databases. It is frequently utilized in studies focusing on nonvolatile memory systems. For example, in [20], Memtier was used to compare performance between different nonvolatile random access memory types. The current research uses Memtier as a reference workload for characterizing key-value database applications.

5. Results

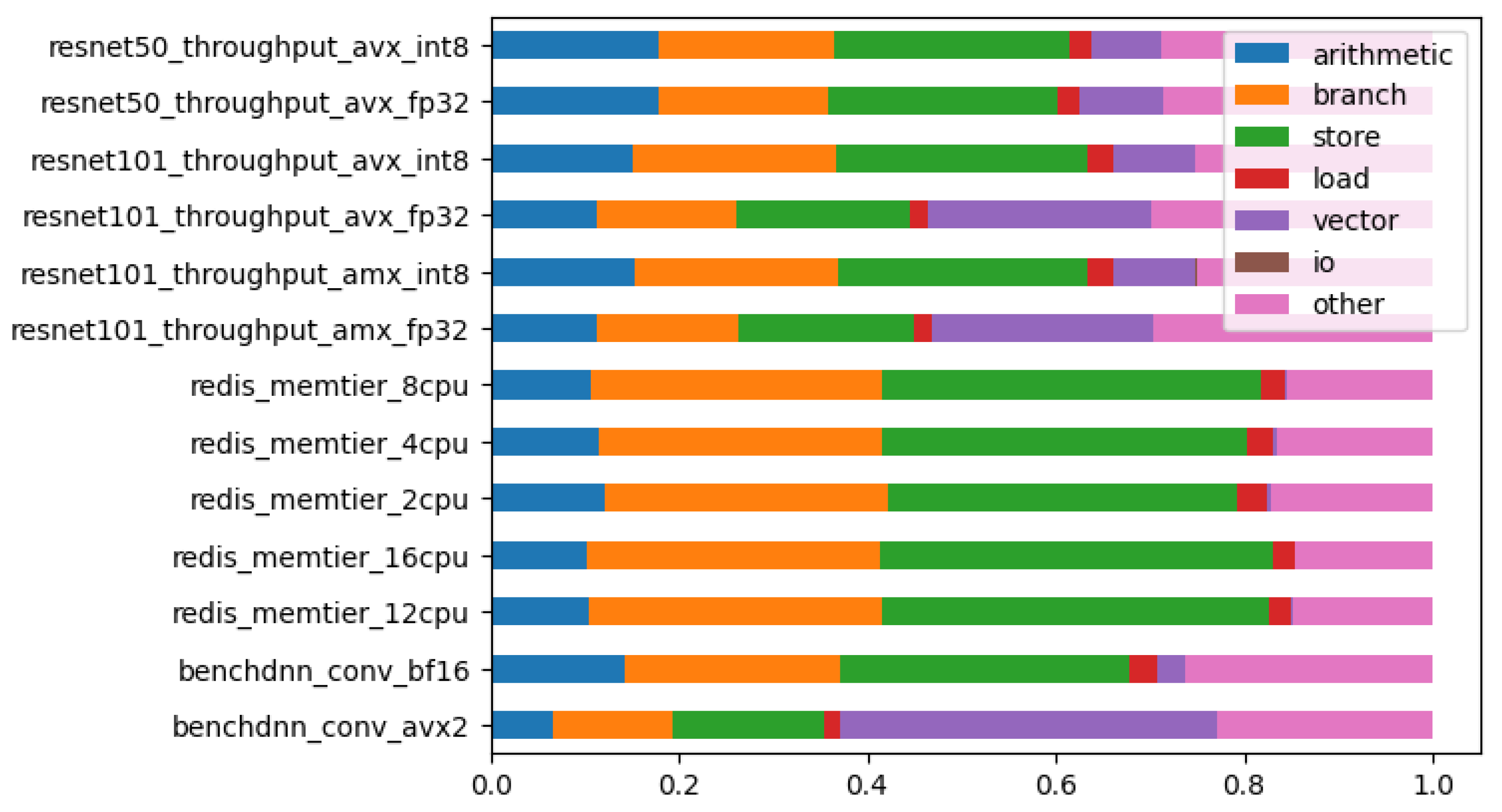
The percentages of different instruction categories on each workload can be seen in Figure 2. This image visually represents how these instructions are used in the context of each workload. This graphical representation provides insights into the interplay between instructions and test cases, thereby aiding in a more comprehensive understanding of the computation dynamics in the platform under test.

The next step of the methodology is the reduction in variables through PCA. To achieve this, it is necessary to define the number of variables that achieve an explained variance of at least 80%. The calculation of the explained variance is presented in

Table 3. Explained Variance Ratios and Cumulative Explained Variance for PCA.

PCA Index	Explained Variance Ratio (%)	Cumulative Explained Variance (%)
1	67.55	67.55
2	24.62	92.17
3	6.67	98.84
4	0.75	99.58
5	0.39	99.97
6	0.03	100.00

. This table shows the proportion of variance explained by each principal component (PCA Index) and the cumulative variance captured as additional components are included. These values guide the selection of the number of components to retain for dimensionality reduction, ensuring that most of the dataset’s variability is preserved. It is clear that using two components can attain an explained variance of nearly 93%, which aligns with the targeted goal. The incorporation of three components yields an even higher explained variance, approaching 98%. However, for this study, a deliberate decision was made to employ only two components for PCA dimensional reduction.

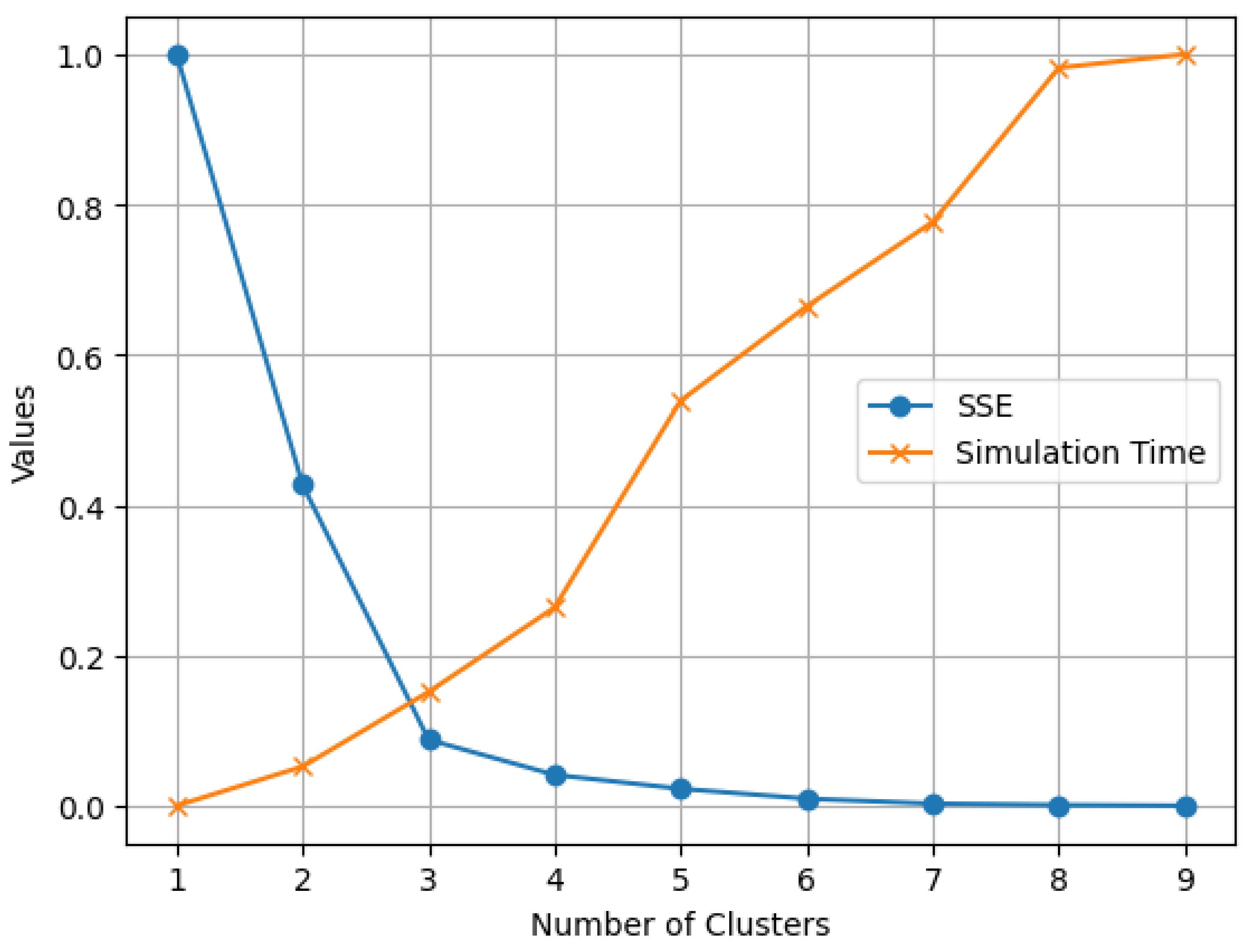
Following the application of PCA to reduce the dataset to two components, the next step involves applying unsupervised ML algorithms for clustering. However, before proceeding, it was necessary to determine the optimal number of clusters. One widely used technique in unsupervised ML clustering is the elbow method. This method suggests that the optimal number of clusters can be determined by identifying the point at which increasing the number of clusters does not substantially reduce the SSE. According to the data in Figure 3, the elbow point suggests that the optimal number of clusters is three. Figure 3 illustrates the relationship between the number of clusters and the SSE. As the number of clusters increases, the SSE decreases, but the rate of improvement diminishes after three clusters. This elbow in the curve indicates the point where adding more clusters yields minimal additional benefit, supporting the selection of three clusters as the most efficient balance between model complexity and explanatory power.

As described in Section 3, once unsupervised ML algorithms successfully produce a small cluster of workloads that exhibit similar characteristics in the executed instructions, finding the crossing point of the optimal number of clusters with a better SSE aligned with the minimum simulation time becomes feasible. The results are presented in Figure 3, which shows that the optimal number of clusters is three. The list of the best optimal candidates from these three clusters is described in

Table 4. Simulation Times and Entropy for Reduced Workloads.

Workload Name	Simulation Time (hours)	Entropy
redis_memtier_8cpu	9	4.375
resnet101_throughput_amx_int8	61	4.801
resnet101_throughput_amx_fp32	32	4.389
Total simulation time	102

. This table lists the simulation time and instruction entropy for each workload in the optimized subset selected through clustering and statistical analysis. The total simulation time for the reduced set is also provided.

To further validate the cluster selection, we computed the Calinski–Harabasz index [21] for different numbers of clusters, as shown in

Table 5. Calinski–Harabasz Index for Different Numbers of Clusters.

Number of Clusters	Calinski–Harabasz Index
2	21.46
3	70.11
4	76.25
5	120.71
6	233.18

. This table presents the Calinski–Harabasz index values calculated for cluster counts ranging from two to six, providing a quantitative measure of cluster separation quality for each configuration. These values indicate that a higher number of clusters yields better separation according to the Calinski–Harabasz index. However, considering both the SSE curve and practical constraints such as simulation time, three clusters were selected as the optimal balance between cluster quality and computational efficiency.

Once the optimal number of clusters is determined, Figure 4 visualizes the proposed clusters, and

Table 6. Workload Classification and Instruction Entropy.

Workload ID	Workload Name	Cluster ID	Entropy
0	benchdnn_conv_avx2	0	3.68
2	resnet101_throughput_amx_fp32	0	4.38
4	resnet101_throughput_avx_fp32	0	4.37
8	redis_memtier_12cpu	1	4.34
9	redis_memtier_16cpu	1	4.31
10	redis_memtier_2cpu	1	4.44
11	redis_memtier_4cpu	1	4.42
12	redis_memtier_8cpu	1	4.37
1	benchdnn_conv_bf16	2	4.80
3	resnet101_throughput_amx_int8	2	4.80
5	resnet101_throughput_avx_int8	2	4.79
6	resnet50_throughput_avx_fp32	2	4.72
7	resnet50_throughput_avx_int8	2	4.80

presents the clustering results. This table lists the workloads analyzed in the study, showing their identification number, name, assigned cluster, and calculated instruction entropy. The classification reflects the grouping of workloads based on the similarity in their instruction profiles.

The three clusters represent distinct workload groups based on their features:

• Cluster 0: Includes machine learning workloads such as BenchDNN Conv AVX2, ResNet101 Throughput AMX FP32, and ResNet101 Throughput AVX FP32, which share similar computational profiles.
• Cluster 1: Contains memory-intensive Redis MemTier database workloads (e.g., Redis MemTier 12 CPU, Redis MemTier 16 CPU, etc.), characterized by database server behaviors across varying numbers of CPU cores.
• Cluster 2: Encompasses machine learning tasks such as BenchDNN Conv BF16, ResNet101 Throughput AMX INT8, and ResNet50 Throughput AVX, which differ in precision formats or architectures (e.g., AMX, AVX, INT8) but share similar resource utilization and execution patterns.

These clusters provide valuable insights into the similarities and differences between the workloads. The confusion matrix is presented in

Table 7. Confusion Matrix for ML and DB Workload Classification.

Actual\Predicted	ML	DB
ML	8	0
DB	0	5

. This matrix shows the number of correct and incorrect predictions for each class, with rows representing actual classes and columns representing predicted classes. The results confirmed a perfect match between the predicted clusters and the actual workload groups, indicating the effectiveness and accuracy of the clustering algorithm.

Table 6 also illustrates the entropy of the executed instructions in all workloads analyzed. ML workloads exhibit higher entropy, reflecting their intricate nature and the broad spectrum of instructions required. In contrast, DB workloads demonstrate lower entropy, which indicates their reliance on a more limited array of instructions.

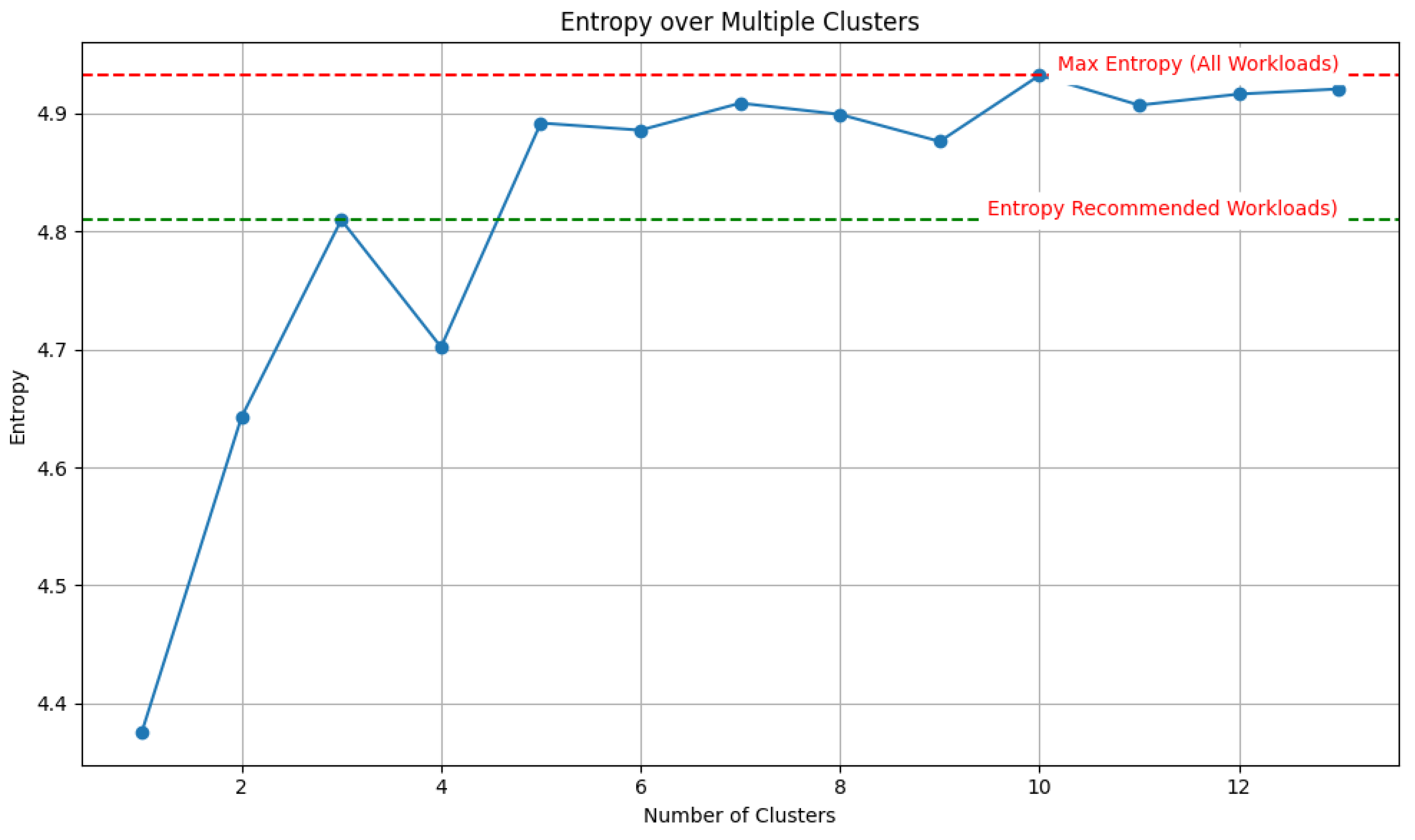
Using the entropy metric for each test case, the instruction sets of the top candidates within each cluster are combined to form a unified test case. Figure 5 shows the entropy of this aggregated histogram, and illustrates how the entropy value changes with different cluster sizes, with the x-axis representing the number of clusters and the y-axis showing the corresponding entropy values. The plot demonstrates that increasing the number of clusters leads to higher entropy, indicating greater instruction diversity. Notably, the subset of three clusters reaches 97.5% of the maximum entropy achieved with ten clusters, suggesting that dividing the test cases further yields only marginal gains in instruction diversity within the FSS under test. This finding supports the choice of three clusters as an effective balance between reducing the test set and maintaining high instruction diversity.

The entropy results indicate that three clusters retain nearly all instruction diversity. This strongly supports the hypothesis that selecting a minimal subset of workloads can achieve both substantial coverage and high entropy. By reducing the test size required for simulation systems that typically demand long hours of execution, this approach enhances testing efficiency while maintaining instruction diversity. These findings are particularly valuable for improving the efficiency of simulation-based validation in computer-aided design workflows.

6. Discussion

Simulation time in pre-silicon validation is highly demanding and resource-intensive. CPU validation engineers are challenged to select workloads that provide comprehensive coverage, yet it remains unclear how best to measure validation coverage at the pre-silicon stage. This work addresses that gap by proposing a mathematical framework for measuring test coverage using SMC.

The results demonstrate that combining PCA-based dimensionality reduction with unsupervised clustering enables the identification of a minimal yet representative subset of workloads. This subset achieves 97.5% of the maximum instruction entropy observed in the full set, indicating that exhaustive simulation is not necessary for robust validation, provided diversity in instruction coverage is maintained. The methodology thus offers substantial efficiency gains, reducing simulation time while maintaining coverage.

A key contribution of this study is the use of entropy-based metrics to quantify instruction diversity, providing a rigorous foundation for workload reduction. This statistical perspective complements ML techniques and supports more effective test case selection.

7. Limitations and Future Work

Although entropy-based assessment provides a quantitative measure of instruction diversity, it does not inherently guarantee equivalent functional or micro-architectural coverage. High instruction entropy suggests that a wide range of instructions are exercised, but it may not capture all corner cases or subtle interactions relevant for thorough CPU validation. To address this limitation, future work will focus on:

• Defect Injection Experiments: Introduce artificial bugs in specific components of the CPU design and compare the effectiveness of both the full and reduced sets of test cases in detecting these bugs. This approach will help determine whether the reduced set maintains a verification effectiveness comparable to the full set.
• Historical Bug Data Analysis: Utilize records of previously discovered bugs to assess whether the reduced test set would have successfully identified these issues. This analysis will provide practical evidence on the effectiveness of the reduced workload set.

We acknowledge that instruction entropy is a useful proxy for diversity, but it should be complemented by empirical validation to ensure robust verification. These future directions will help substantiate the practical utility of the methodology and further enhance confidence in its application for pre-silicon CPU validation.

A further limitation of this study is that all experiments were conducted using Simics on the Ice Lake Server architecture. This means that the robustness of the methodology across different architectures, ISAs, or simulation tools has not been assessed. While alternative tools such as Intel SDE [22] could be used to obtain instruction histograms, SDE is not a full-system simulator and only captures user-space instructions, omitting kernel-level and system-wide interactions. Since the workloads analyzed in this study primarily operate in user space, this approach may be suitable for similar scenarios; however, the results may not generalize to workloads with significant kernel activity or to other architectures and simulation environments.

8. Conclusions

This work presents a novel methodology for optimizing pre-silicon CPU validation by reducing simulation time while maintaining comprehensive instruction coverage and diversity. The approach leverages unsupervised machine learning and statistical analysis to streamline the validation process, addressing key challenges faced by engineers in early-stage CPU design.

Key findings and contributions include:

• Determining the optimal number of clusters by jointly considering SSE and simulation time, which enhances validation efficiency and supports more effective test case selection.
• Achieving high classification precision through the combination of PCA and unsupervised clustering, enabling accurate differentiation between database and machine learning workloads on pre-silicon FSS platforms without prior code knowledge.
• Developing an optimized subset of test cases using Statistical Model Checking and entropy analysis, which preserved instruction coverage and diversity while reducing simulation time by a factor of 9.46.
• Validating that the reduced subset achieves 97.5% of the maximum entropy, confirming its robustness and representativeness compared to the full workload set.
• Demonstrating that the refined set of test cases can significantly decrease the total hours required for pre-silicon testing, thus accelerating CPU development and validation cycles.

Overall, the research objective of enabling efficient and robust pre-silicon CPU validation was achieved.