Benchmarking Control Strategies for Multi-Component Degradation (MCD) Detection in Digital Twin (DT) Applications

Abstract

Digital Twins (DTs) have become central to intelligent asset management within Industry 4.0, enabling real-time monitoring, diagnostics, and predictive maintenance. However, implementing Prognostics and Health Management (PHM) strategies within DT frameworks remains a significant challenge, particularly in systems experiencing multi-component degradation (MCD). MCD occurs when several components degrade simultaneously or in interaction, complicating detection and isolation processes. Traditional data-driven fault detection models often require extensive historical degradation data, which is costly, time-consuming, or difficult to obtain in many real-world scenarios. This paper proposes a model-based, control-driven approach to MCD detection, which reduces the need for large training datasets by leveraging reference tracking performance in closed-loop control systems. We benchmark the accuracy of four control strategies—Proportional-Integral (PI), Linear Quadratic Regulator (LQR), Model Predictive Control (MPC), and a hybrid model—within a Digital Twin-enabled hydraulic system testbed comprising multiple components, including pumps, valves, nozzles, and filters. The control strategies are evaluated under various MCD scenarios for their ability to accurately detect and isolate degradation events. Simulation results indicate that the hybrid model consistently outperforms the individual control strategies, achieving an average accuracy of 95.76% under simultaneous pump and nozzle degradation scenarios. The LQR model also demonstrated strong predictive performance, especially in identifying degradation in components such as nozzles and pumps. Also, the sequence and interaction of faults were found to influence detection accuracy, highlighting how the complexities of fault sequences affect the performance of diagnostic strategies. This work contributes to PHM and DT research by introducing a scalable, data-efficient methodology for MCD detection that integrates seamlessly into existing DT architectures using containerized RESTful APIs. By shifting from data-dependent to model-informed diagnostics, the proposed approach enhances early fault detection capabilities and reduces deployment timelines for real-world DT-enabled PHM applications.

1. Background

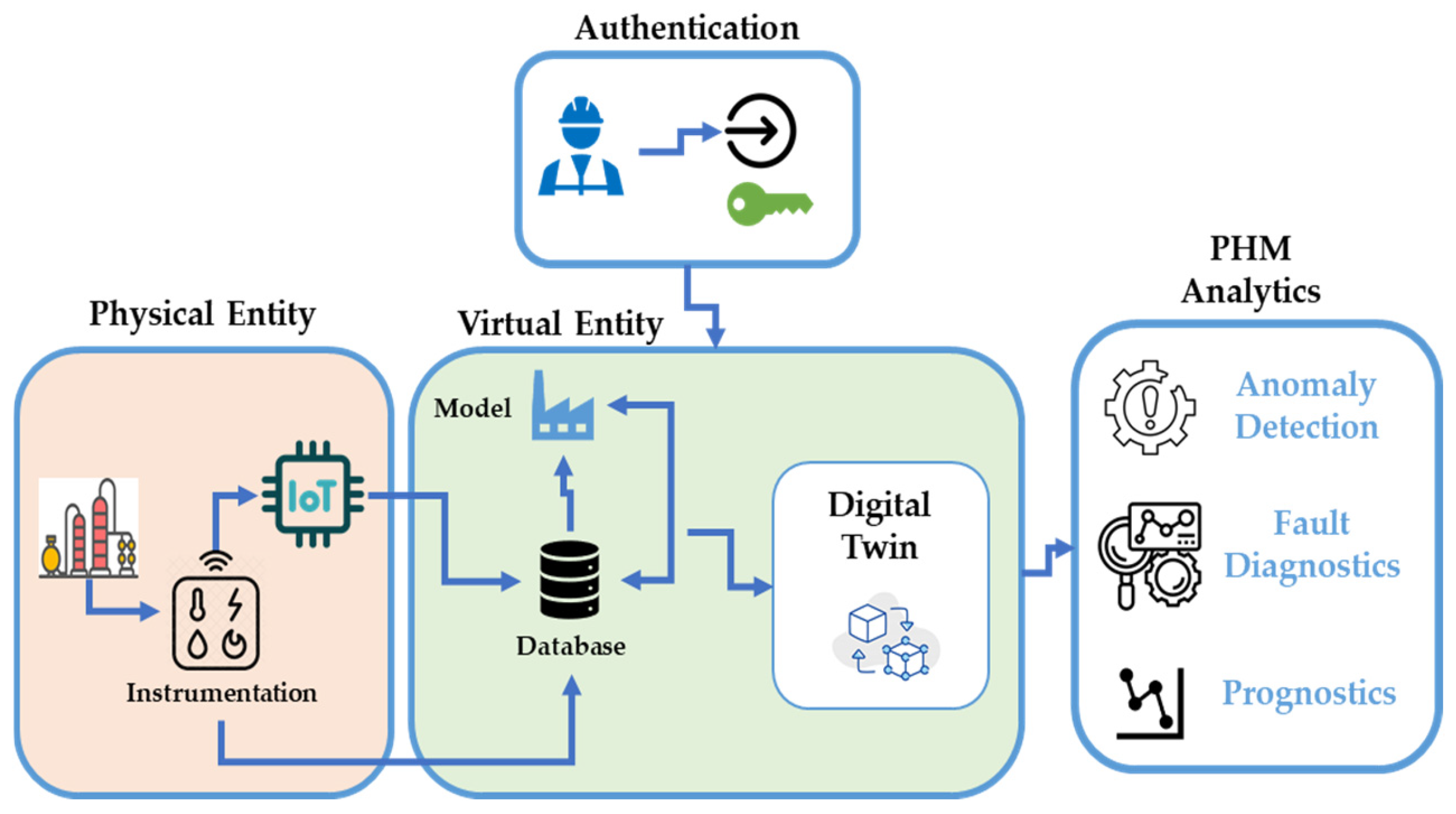
In recent years, Industry 4.0 has provided an effective approach to managing the lifecycle of industrial assets through real-time insights, predictive analytics, and intelligent maintenance strategies. A key part of this approach is the use of Digital Twins (DTs)—dynamic, virtual representations of physical assets that enable continuous monitoring, diagnostics, and prognostics [1,2]. In the context of Prognostics and Health Management (PHM), DTs serve as an enabling technology, allowing system operators to predict failures, optimize maintenance, and ensure system reliability under varying operating conditions (see Figure 1) [3,4]. However, implementing PHM strategies in complex systems presents a unique set of challenges. These systems often involve multiple interdependent components operating under varying environmental and load conditions, leading to complex multi-component degradation (MCD) phenomena. Capturing and undertaking data-driven modeling of such degradation behavior is particularly difficult due to the limited availability of high-quality degradation data, which is often expensive, time-consuming, or infeasible to obtain in real-world scenarios [5,6,7].

In response to these challenges, Physics-Informed Neural Networks (PINNs) have been explored as a way of enhancing the performance of PHM-enabled DTs, in the context of the limited availability of asset degradation data. By integrating physical constraints into neural network architectures, PINNs enforce consistency with physical behavior while still learning from the limited degradation data available [8,9,10]. However, PHM-enabled DTs that rely on PINN model analytics still require some availability of degradation data to train to predict asset performance in a multi-component degradation scenario [5]. Exploring other techniques that remove the need for degradation data will be useful in reducing the cost and time needed for developing predictive models for DT applications. Reference tracking as an idea in control systems refers to a control system’s ability to make its output follow or match a desired reference signal over time. When a control system is given a setpoint, reference tracking ensures that the system’s output behaves as closely as possible to this reference, despite disturbances or changes in system dynamics [11,12].

This paper extends this idea of reference tracking by using control strategies to track the performance of assets in a complex system by detecting MCD scenarios. This will be achieved by benchmarking control strategies used to detect MCD scenarios in a hydraulic system, with particular focus on (1) model generalizability across operating conditions, (2) robustness under simultaneous degradation events, and (3) integration within real-time DT systems. This paper contributes to DT research by developing Fault Detection and Isolation (FDI) models using control strategies for MCD detection. The results offer a non-data-driven approach to MCD model deployment. The remainder of this paper is structured as follows. Section 2 reviews multi-component degradation (MCD) detection and identifies gaps in the current methodologies. Section 3 details the proposed deployment methodology, including the reference tracking approach for DT-enabled PHM models. Section 4 presents a case study for benchmarking the performance of different control strategies. Finally, Section 5 discusses the findings and their implications, concluding with directions for future research.

2. Control-Based MCD Detection and Isolation—Review and Gaps

2.1. Introduction

As complex systems age or operate under stress, more than one part can wear out at the same time—a challenge known as multi-component degradation (MCD) [13]. Detecting such degradation early is vital to avoid system failures, especially in critical industries like aerospace, energy, and manufacturing. Digital Twins (DTs)—virtual replicas of physical systems—offer a promising way of monitoring these systems in real time [14]. Section 2 of the paper gives an overview of previous research conducted on deploying control-based fault detection and isolation analytics for MCD scenarios for DT applications.

2.2. Multi-Component Degration Detection and Isolation (MCD)

Modern engineering systems—from aircraft engines to chemical plants—often operate under harsh and dynamic conditions. Over time, various parts of these systems begin to wear out. What makes the situation especially challenging is that multiple components can degrade at the same time, often in different ways [5,15]. This phenomenon is known as multi-component degradation (MCD) [13]. Identifying MCD early is critical for maintaining safety, performance, and cost-efficiency. In the context of Digital Twin (DT) applications, detecting MCD becomes not only feasible but essential to PHM applications. This section explores how MCD is currently detected, how control systems can help, and what challenges remain.

2.2.1. Understanding Multi-Component Degradation

In real-world systems, degradation does not occur in isolation, with the degradation of one component affecting other components or systems either downstream or upstream [16,17]. For example, in a wind turbine, both the gearbox and the rotor blades may degrade simultaneously due to different loads and environmental stressors [18], or, in a hydraulic system, the failure of a filter can have a negative impact on a pump [13]. Unlike single-component degradation [3], MCD leads to overlapping symptoms, making it harder to diagnose and isolate the source of the problem even with advanced data-driven techniques [5]. Each degraded component may affect the system dynamics in unique, and sometimes interacting, ways. For instance, a slight misalignment in one component may cause increased wear in another [19]. These interdependencies mean that simple threshold-based monitoring often fails, as it may not distinguish between compounded degradation and isolated faults [5].

2.2.2. Traditional Approaches to Fault Detection and Isolation

Historically, fault detection has relied on methods like threshold analysis, signal filtering, or model-based residual generation [20,21,22]. In many cases, these techniques are tailored to detect faults in one component at a time. While effective in simple systems, they underperform when multiple faults occur simultaneously [5] or when degradation progresses gradually over time [5,23]. Model-based fault detection relies on comparing the actual behavior of a system to a predicted one [24,25]. When the difference (or residual) exceeds a certain threshold, a fault is flagged [26]. However, in MCD scenarios, multiple degradations may cause overlapping effects on the residuals, leading to false alarms or missed detections. Some researchers have explored probabilistic techniques [27,28], data-driven techniques [13,29], and physics-informed approaches [5,30] for fault detection and isolation in complex systems for MCD scenarios. These approaches, as in the former (data-driven), rely on the availability of training data, which can often be expensive, and so the latter (physics-informed) reduces this data dependency by using a physics-informed framework. Even though the physics-informed approach reduces the reliance on data, it still needs some data to model [3,5]. The ideal scenario in detecting and isolating MCD scenarios would be having analytics that do not rely on time-dependent and expensive degradation data to model and that also reduce the propensity of false positives or negatives.

2.2.3. Why Digital Twins Change the Game

Digital Twins (DTs) provide a platform for integrating real-time data with models that simulate expected behavior [1]. This duality allows engineers to not only detect faults but also predict future degradation. DTs can capture interactions between subsystems and are especially valuable in MCD scenarios, where physical dependencies play a major role. DTs enable the application of physics-informed models that go beyond black-box analytics by incorporating domain knowledge into machine learning and control algorithms [5]. The integration of these models in a DT framework such as the one presented in [3] enables the scalability of deployments to different distributed assets and systems. The DevOps approach that was employed allows for the deployment of DT-enabled analytics at scale using three-tier or microservice approaches.

2.2.4. Control-Based Detection of Multi-Component Degradation in Digital Twins

Control systems are traditionally designed to regulate the performance of engineering systems by ensuring that outputs, such as speed or temperature, follow a desired target or “reference” [31]. However, this same principle—known as reference tracking [32]—can also be used to detect early signs of degradation [33]. When components start to degrade, the system’s ability to follow its reference may decline, causing tracking errors or increased control effort. This deviation may be due to disturbances in the system [32] or control parameters not set correctly [34]. These deviations can serve as important clues for the presence of anomalies in the system. In the case of multi-component degradation (MCD), where several parts deteriorate simultaneously or in sequence, these changes are often harder to isolate [5], but control-based monitoring can still reveal valuable patterns. For example, a control system may need to work harder to maintain system performance [35] when two subsystems degrade simultaneously, and this additional control input can be used to detect changes in such complex conditions. While some studies have used control-based strategies to identify faults [36,37], very few have focused on their application to MCD scenarios, especially in Digital Twin applications. This gap is critical because DTs provide real-time feedback loops between virtual models and physical systems, allowing control strategies to be tested and adapted continuously. When combined with Digital Twins, control-based techniques can play a dual role—not only stabilizing the system [32] but also revealing complex patterns of degradation [37].

2.3. Gaps

Digital Twins (DTs) provide a unique approach in monitoring and managing complex systems by enabling the real-time tracking of physical assets through their virtual counterparts. As discussed in Section 2.3, multi-component degradation (MCD) presents a significant challenge due to overlapping and interacting faults that are difficult to detect using traditional methods. However, despite the ability of control techniques to reveal changes in system behavior that may indicate early signs of degradation the utility of combining control systems with DTs, there is a gap in how these methods are applied to MCD scenarios. Current fault detection techniques focus on single-component degradation and fail to capture the compound dynamics involved when multiple components degrade either in sequence or simultaneously. Also, even when control-based techniques are used, they are often applied in isolation or without leveraging the full potential of DT architectures.

3. Methodology—Benchmarking Control Approaches

3.1. System Description

The hydraulic system (Testbed-C103A) evaluated in this study uses a 4 mm internal diameter (ID) pipeline and incorporates key functional components including a primary fluid reservoir, an external gear pump, and a set of valves; the test bed is described in detail in a previous study [3]. The fault emulation mechanism for each component of the testbed is summarized in Appendix A.3, where healthy and faulty states for the five key critical components of the testbed are mapped against the position of the direct proportional valves (DPV) used to emulate the degradation.

3.2. Reference Tracking

3.2.1. Asset Performance Modeling

The performance of each asset in Testbed-C103A is modeled using a general transfer function $G\left(s\right)$ of a linear time-invariant (LTI) first-order system (see Equation (1)). In control systems, a first-order system is one whose behavior can be described by a first-order differential equation with one degree of freedom [32]. $K$ is the system gain with $tau \left(\tau \right)$ as the time constant and $s$ is the complex frequency variable in the Laplace domain. A time constant tau (τ = 1) means that the system responds relatively quickly [38]. Equations (2)–(7) show the derivation of state space representation of the performance model with $Y\left(s\right)$ and $U\left(s\right)$ as the input and output, respectively. 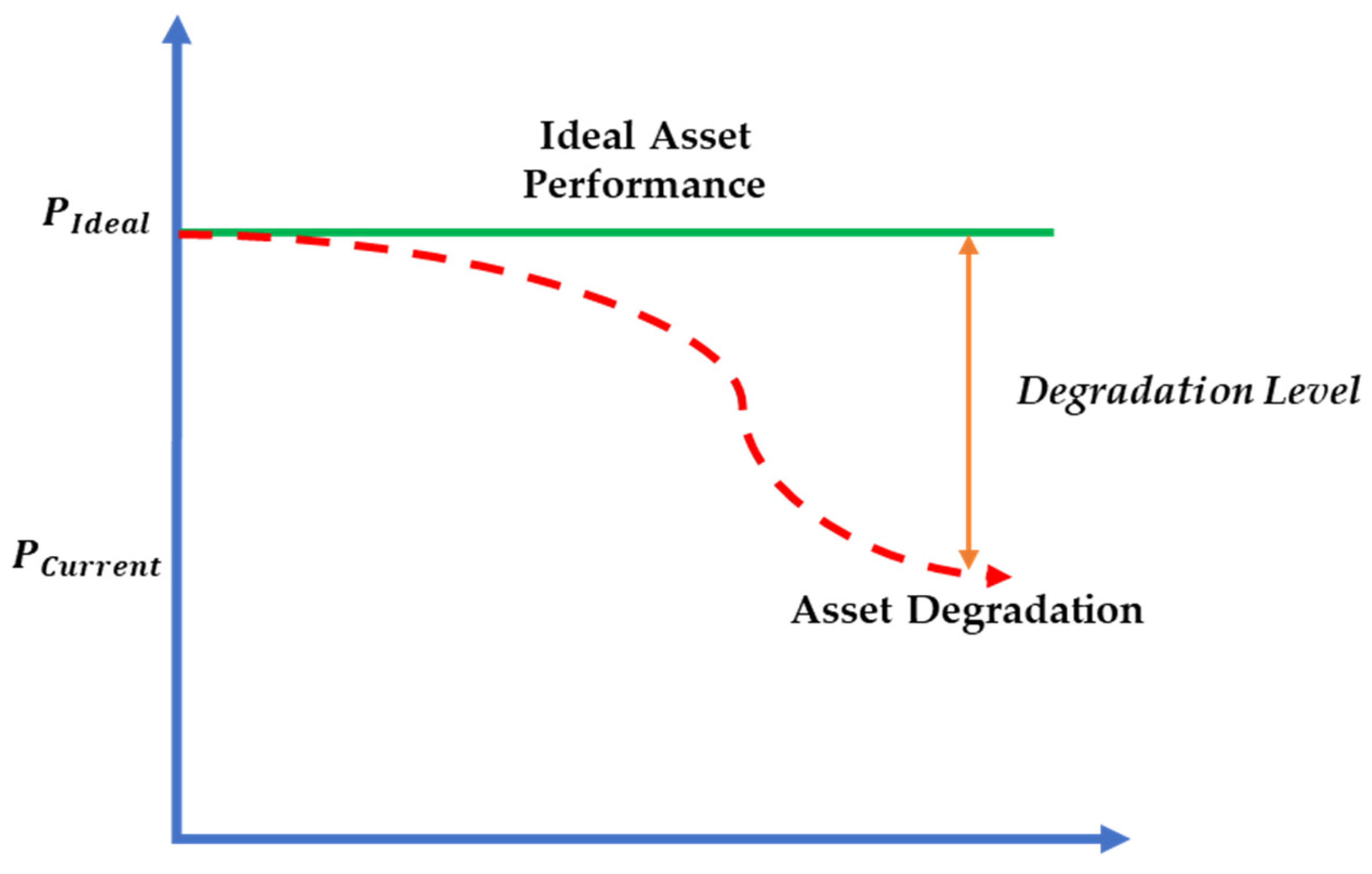Figure 2, below, shows how the deviation of the performance of an asset occurs, where its operating condition deviates from an expected reference due to a fault ultimately leading to functional failure of the asset.

$$G\left(s\right)={\displaystyle \frac{K}{\tau s+1}}$$

(1)

$$\tau s+1Y\left(s\right)=KU\left(s\right)$$

(2)

$$\begin{gathered} \dot{x}\left(t\right)=Ax\left(t\right)+Bu\left(t\right) \\ y\left(t\right)=Cx\left(t\right)+Du\left(t\right) \end{gathered}$$

(3)

$$\tau {\displaystyle \frac{dy\left(t\right)}{dt}}+y\left(t\right)-Ku\left(t\right)=0$$

(4)

$$x\left(t\right)=y\left(t\right)⟹\dot{x}\left(t\right)=\dot{y}\left(t\right)$$

(5)

$$\begin{gathered} \dot{x}\left(t\right)=-{\displaystyle \frac{1}{\tau }}x\left(t\right)+{\displaystyle \frac{K}{\tau }}u\left(t\right) \\ y\left(t\right)=x\left(t\right) \end{gathered}$$

(6)

$$A=-{\displaystyle \frac{1}{\tau }}, B={\displaystyle \frac{K}{\tau }}, C=1, D=0$$

(7)

The state $\dot{x}\left(t\right)$ to each asset on the testbed is described in

Table 1. State parameters for each asset.

Asset	LQR	PI	MPC
Filter	$∆P=P_2-P_1$	$∆P=P_2-P_1$	$P_R=P_2/P_1$
Pump	${\displaystyle \raisebox{1ex}{$P_3-P_2$}\!\left/ \!\raisebox{-1ex}{${P_3-P_2}_{Healthy}$}\right.}$	${\displaystyle \raisebox{1ex}{$P_3-P_2$}\!\left/ \!\raisebox{-1ex}{${P_3-P_2}_{Healthy}$}\right.}$	${\displaystyle \raisebox{1ex}{$P_3-P_2$}\!\left/ \!\raisebox{-1ex}{${P_3-P_2}_{Healthy}$}\right.}$
Valve	$∆P=P_4-P_3$	$∆P=P_4-P_3$	$P_R=P_4/P_3$
Nozzle	$∆P=P_5-P_4$	$∆P=P_5-P_4$	$P_R=P_5/P_4$
Pipe	${\displaystyle \raisebox{1ex}{$P_3-P_2$}\!\left/ \!\raisebox{-1ex}{${P_3-P_2}_{Healthy}$}\right.}$	${\displaystyle \raisebox{1ex}{$P_3-P_2$}\!\left/ \!\raisebox{-1ex}{${P_3-P_2}_{Healthy}$}\right.}$	${\displaystyle \raisebox{1ex}{$P_3-P_2$}\!\left/ \!\raisebox{-1ex}{${P_3-P_2}_{Healthy}$}\right.}$

below. For all the assets that degrade by gradual blockage (filter, valve, and nozzle), the pressure drop over time $∆P\left(t\right)$ is used while for the those that degrade by leaking (pump and pipe), Equation (8) is used as the states of those assets. Using negative feedback, the degradation level defined in Figure 2 above, is defined as the control effort (${\dot{C}}_{effort}$) required for move $P_{Current}$ to $P_{Ideal}$. The control effort refers to the amount of input energy (or action) required by a controller to drive a system from its current state to a desired state [39]. The resulting performance ($0\le P_{Ideal}\le 1$) of each asset is then determined using Equation (9) where $P_{Ideal}=1$.

$${Input\left(t\right)}_{leakage}={\displaystyle \raisebox{1ex}{$∆P\left(t\right)$}\!\left/ \!\raisebox{-1ex}{${∆P\left(t\right)}_{Healthy}$}\right.}$$

(8)

$$Performance=1-{\dot{C}}_{effort}$$

(9)

3.2.2. Linear Quadratic Regulator (LQR) Design

The Linear Quadratic Regulator (LQR) is an optimal control strategy used to regulate the behavior of a linear dynamic system while minimizing a cost function that balances performance and effort [32]. Using the system in Equation (1), the LQR is designed to minimize the quadratic cost function $J$ in Equation (10), where $Q\ge 0$ penalizes state deviations and $R>0$ penalizes control effort. The optimal control law is defined in Equation (12), where the gain $K$ is computed by solving the Algebraic Riccati Equation (ARE) in Equation (11).

$$J={\int }_0^{\infty }\left(x^{T}Qx+u^{T}Ru\right)dt$$

(10)

$$A^{T}S+SA-SB{R}^{-1}{B}^{T}S+Q=0$$

(11)

$$K=R^{-1}{B}^{T}S$$

(12)

At steady-state ($\dot{x}=0$), the required control input to maintain $y=r$ (y is the output and r the desired value) is derived from Equation (13), where $x_{ss}=r$ since $y=Cx=x$. Thus, the steady-state control effort $u_{ss}$ is determined using Equation (14). The closed-loop system with LQR control is shown Equation (15), with $u\left(t\right)=K(r-x)$ as the modified optimal control law for reference tracking. Finally, the goal is to tweak Q and R in Equation (11) so that the steady state error $e_{ss}\approx r-y(\infty )\approx 0$.

$$0=A{x}_{ss}+B{u}_{ss}$$

(13)

$$u_{ss}={\displaystyle \frac{r}{K}}$$

(14)

$$\dot{x}=(A-BK)x+BKr$$

(15)

3.2.3. Proportional-Integral (PI) Design

A Proportional-Integral (PI) controller is a feedback controller that ensures that a system’s output tracks a desired reference (setpoint) accurately over time, while eliminating steady-state error [32]. The objective is to track a reference signal $r\left(s\right)$ with minimal steady-state error and the Proportional-Integral (PI) controller $C\left(s\right)$ is defined in the Laplace domain (see Equation (16)), where $K_p$ and $T_i$ are proportional gain and integral time constant, respectively. The resulting closed-loop transfer function is shown in Equation (17), where the characteristic equation $\tau s^2+\left(1+K_p\right)s+K_i=0$ determines stability. The steady-state error approximates to zero ($e_{ss}\approx 0)$ for a step $r\left(s\right)= {\displaystyle \frac{1}{s}}$ (see Equation (18)). In an attempt to compute the control effort $u\left(t\right)$, to find the deviation from the healthy state, Equation (19) makes use of the real-time error information $e\left(t\right)=r\left(t\right)-y\left(t\right)$ to find the deviation from the healthy state of the asset.

$$C\left(s\right)=K_p+{\displaystyle \frac{K_i}{s}}=K_p\left(1+{\displaystyle \frac{1}{T_{i}s}}\right)$$

(16)

$$T\left(s\right)={\displaystyle \frac{K_{p}s+K_i}{\tau s^2+\left(1+K_p\right)s+K_i}}$$

(17)

$$e_{ss}=\underset{s\to 0}{\mathit{lim}} s·\left({\displaystyle \frac{1}{1+C\left(s\right)G\left(s\right)}}\right)·r\left(s\right)$$

(18)

$$u\left(t\right)=K_p\left(r\left(t\right)-y\left(t\right)\right)+K_i{\int }_0^t\left(r\left(\tau \right)-y\left(\tau \right)\right)d\tau$$

(19)

3.2.4. Model Predictive Control (MPC) Design

The design of the MPC model starts with the discrete-time state-space representation (exact discretization with time step $∆t)$ in Equation (20), where the decay per timestep is $\alpha =e^{-{\displaystyle \raisebox{1ex}{$∆t$}\!\left/ \!\raisebox{-1ex}{$\tau $}\right.}}$. The controller solves the optimization problem in Equation (21), subject to the constraints in Equations (22) and (23), where $y \in \left[\mathrm{0,1}\right]$ and $x \in \left[\mathrm{0,1}\right]$, and the prediction horizon for the model ($N=5$) and with a control weighting $\lambda =0.1$.

$$x_{k+1}=\alpha x_k+\left(1-\alpha \right)K{u}_k$$

(20)

$${y_k=x}_k$$

$$\begin{array}{c}min\\ u_{k|k,\dots ,}{u}_{k+N-1|k}\end{array}{\sum }_{i=0}^{N-1}\left[{\left(y_{k+i|k}-r_{k+i}\right)}^2+\lambda {\left(u_{k+i|k}-u_{k+i-1|k}\right)}^2\right]$$

(21)

$$y_{min}\le y_{k+i|k}\le y_{max} (0\le y\le 1)$$

(22)

$$u_{min}\le u_{k+i|k}\le u_{max} (0\le u\le 1)$$

(23)

3.2.5. Hybrid Approach

A hybrid control model is also developed using the control effort from the LQR, PID, and MPC approaches. The hybrid model control effort ${{\dot{C}}_{effort}}_{hybrid}$ is defined in Equation (24) as a weighted average of the LQR, PID, and MPC models. The defined fixed weights for LQR, PID, and MPC are 1.5, 0.8, and 0.7 respectively. The performance of the hybrid model is then benchmarked against the other controllers in Section 3.2.2 to Section 3.2.4 for the multi-component degradation scenarios.

$${{\dot{C}}_{effort}}_{hybrid}={W_{\mathrm{L}\mathrm{Q}\mathrm{R}}·{\dot{C}}_{effort}}_{\mathrm{L}\mathrm{Q}\mathrm{R}}+{W_{PI}·{\dot{C}}_{effort}}_{\mathrm{P}\mathrm{I}}+{W_{MPC}·{\dot{C}}_{effort}}_{\mathrm{M}\mathrm{P}\mathrm{C}}$$

(24)

3.3. Control-Based MCD Detection Model Implementation

Step 1: Control-Based Analytics Modeling

An application Programming interface (API) is developed by modifying the DT Implementation frame developed by Barimah et al. [3]. The sensor data from each component (see Table 1) is routed through a Thingworx^TM API to the Kubernetes cluster to obtain the output of the control-based predictive models. The feature derived from the sensor data represents the state of performance for each component. The performance modeling developed in Section 3.2.1 and the control effort for each control approach described in Section 3.2.2 to Section 3.2.5 is implemented to determine the level of degradation.

Step 2: Benchmarking Control-Based-MDC Predictive Models

The performance of all the control-based predictive models (LQR, PI, MPC, and Hybrid) are benchmarked using test data in

Table 2. Test degradation scenarios for testing control-based analytics.

MCD Test Data	Fault 1	Fault 2
T57	Pump at 60% degradation level	Nozzle at 50% degradation level
T58	Pump at 50% degradation level	Filter at 40% degradation level
T59	Pump at 60% degradation level	Valve at 50% degradation level
T60	Pump at 70% degradation level	Pipe at 50% degradation level
T62	Nozzle at 50% degradation level	Pump at 60% degradation level

below. The MCD test begins with fault 1 first for the first asset and then fault 2 in the second asset is initiated subsequently. Appendix A.1 contains the python scripts for the control-based models for the assets under consideration.

Step 3: Deployment and Monitoring

Figure 3 and Figure 4, below, summarize the methodology for deploying the control-based predictive model in a digital twin application. All operational data is sent to the Thingworx^TM platform using a Kepware server. Scheduled API requests are then sent to the Kubernetes cluster that runs the control-based analytics. Prometheus and Grafana are used for monitoring the cluster. The results from the analytics are sent back to the Thingworx^TM Digital Twin platform.

4. Case Study

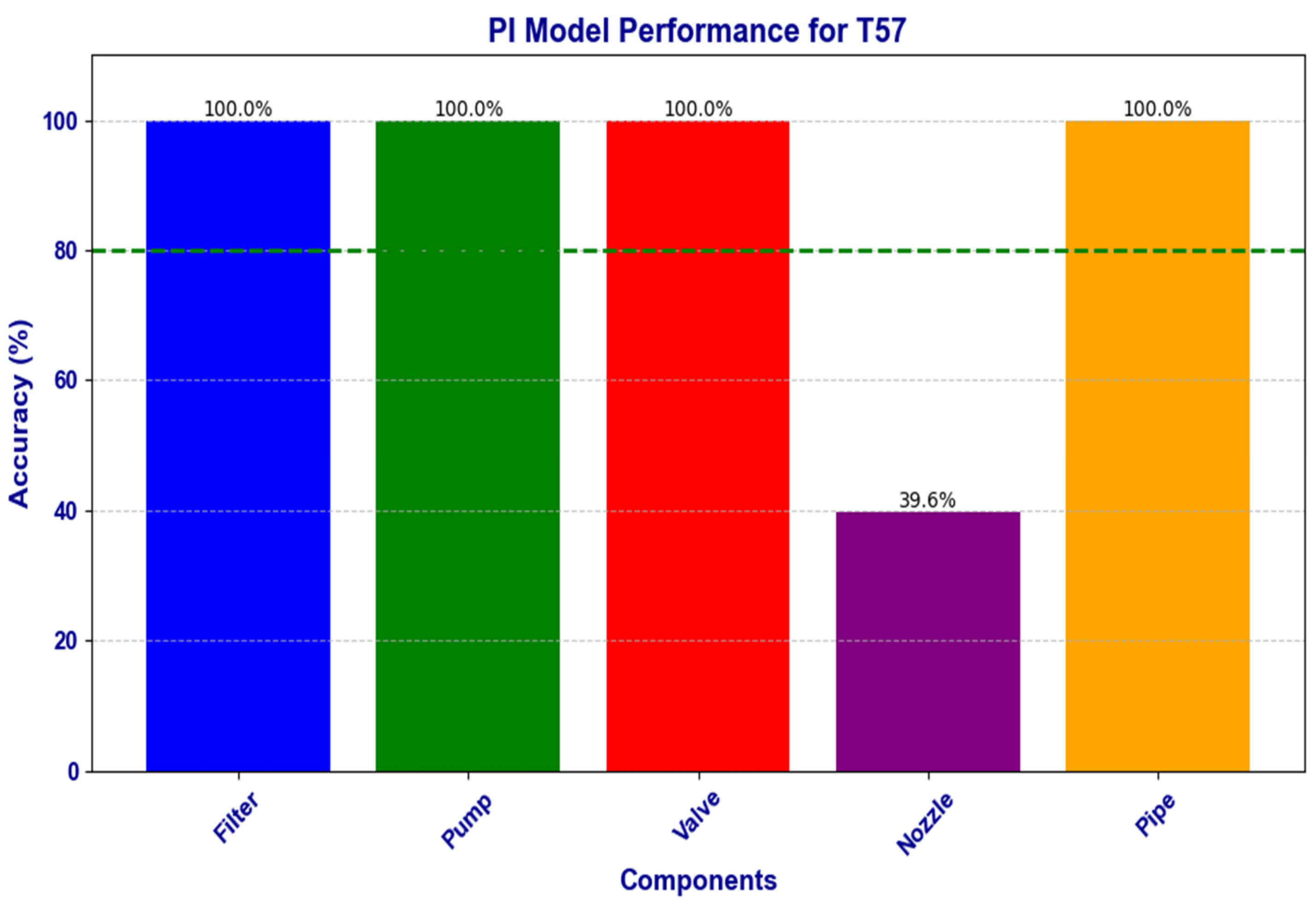
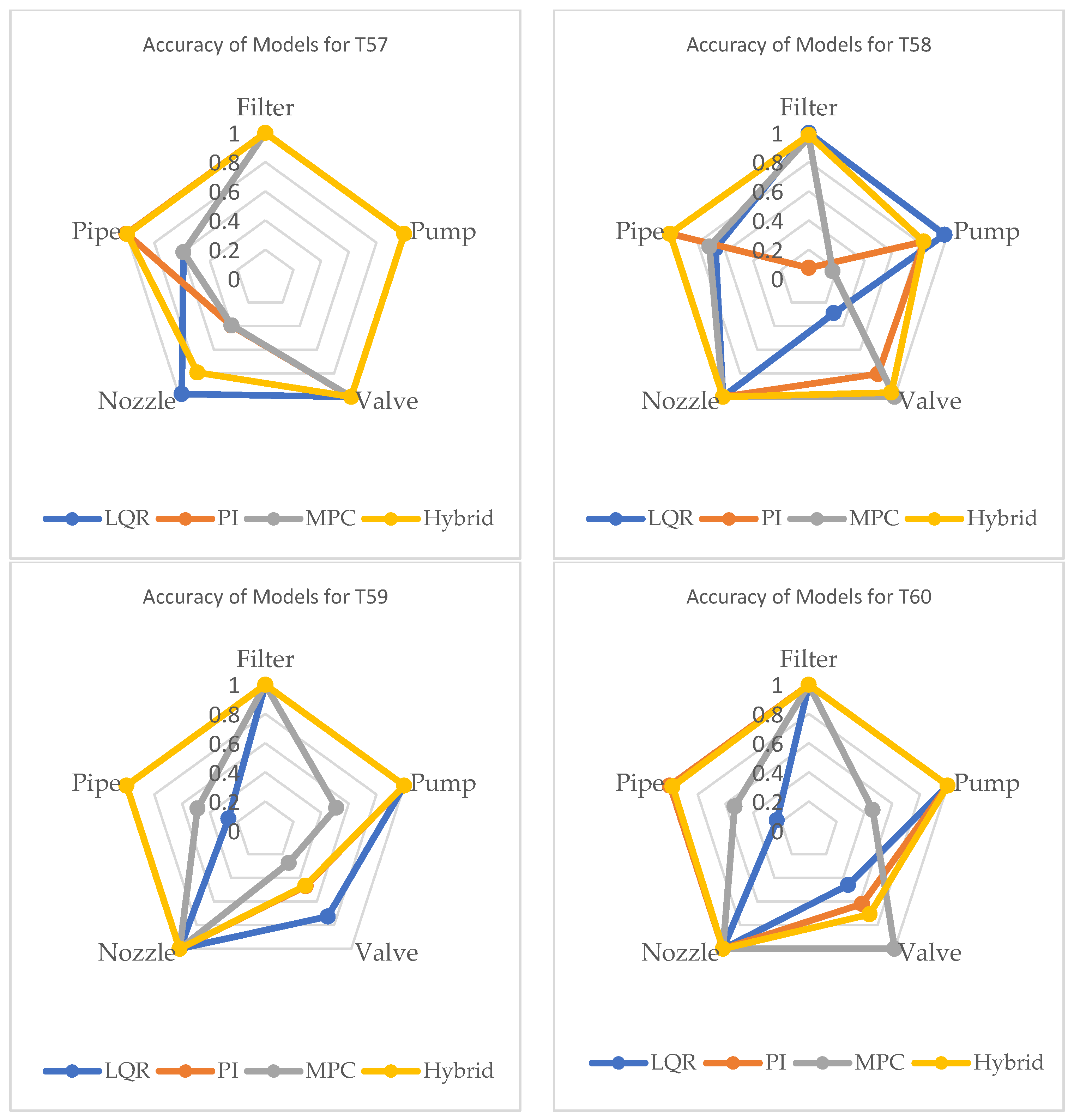
The performance of all four (4) models—LQR, PI, MPC, and hybrid—are benchmarked against the multi-component degradation scenarios shown in Table 2. The performance of the hybrid control model was better than that of the other control models. In the case of the test degradation scenario 57—pump and nozzle both at 60% and 50% degradation levels, respectively—the average accuracy of the hybrid model was 95.76% compared to the 91.32% for the LQR model, 79.7% for the MPC model, and 87.92% for the PI model. At the component or asset level, the LQR, PI, and MPC models all had 100% prediction accuracy for the filter, pump, and valve. However, the LQR was able to detect the performance in nozzle with an accuracy of 97.5% compared to about 39% in both PI and MPC models (see Figure 5 and Figure 6 as well as Appendix A.2).

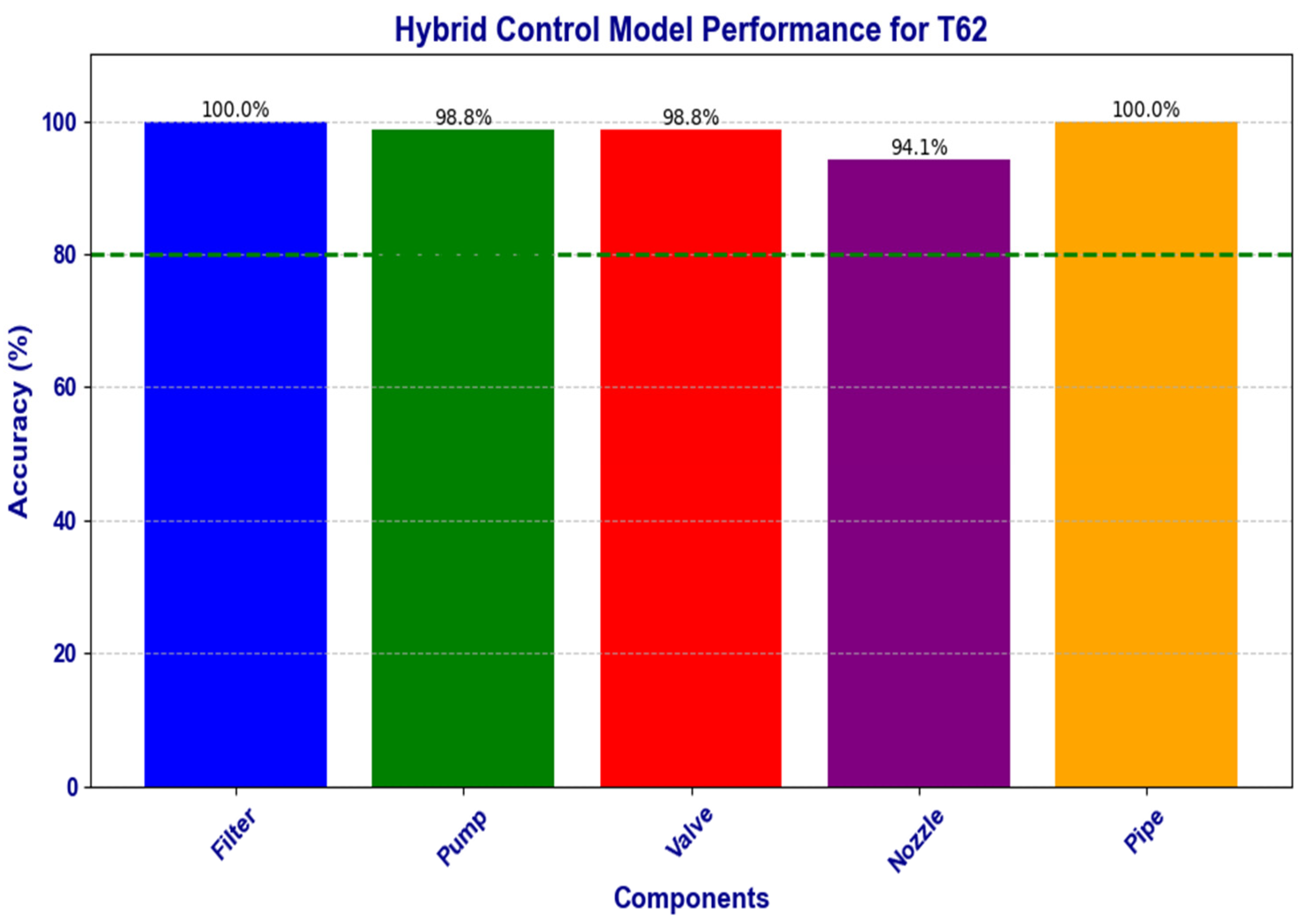
These performance levels are also seen in other degradation levels where the hybrid model compensates for the performance of the individual level. In the test degradation scenario, the sequence of the faults in Test 57 are reversed and the performance of the hybrid model also shows improved performance over the individual models (see Figure 6). The radial plots in Figure 7 show the accuracy of all the models for the rest of the test degradation scenarios. The hybrid control predictive model continued to perform better overall than the individual models, except in the case of the degraded valve in the T59 scenario and the leaking pump in the T58 scenario. The LQR model proved to be a good predictor of degradation in the both the filter and pump, as seen in Figure 7.

5. Discussion

This study explored how reference tracking using control-based predictive models can help detect and isolate multi-component degradation (MCD) in digital twin (DT) applications. The findings are promising. One of the key strengths of this approach is its ability to predict how individual components of a system will behave over time, even without direct degradation data. This makes it easier to monitor specific components and identify faults early—an important step in building smarter, more responsive digital twins. Among the models tested, the hybrid weighted approach stood out. By combining the strengths of several traditional control methods—Linear Quadratic Regulator (LQR), Model Predictive Control (MPC), and Proportional-Integral (PI) control—it was able to offset the limitations of each individual model. The LQR model, in particular, showed strong potential in predicting the performance of the hydraulic pump in Testbed-C103A, even when other components were failing at the same time.

This suggests that LQR, especially when used in a hybrid model, could be a reliable choice for monitoring pumps in systems experiencing complex degradation. However, the study also revealed that the order in which faults appear can affect model performance. For example, in test degradation data T62, the sequence of the leak and blockage faults changed how well the model could track the system’s behavior. This indicates that model effectiveness may depend not just on the type of fault, but also on when and how it occurs in relation to others. Also, the varying performance of the different models may be due to several factors that the hybrid model compensates for.

For instance, why MPC is the worst for scenario 57 and a simple PI is better than both MPC and LQR is perhaps because the MPC and LQR take a bit longer to compute the control signal. The other reason for the MPC to underperform could be that the system model and state parameters used do not completely replicate the dynamics and incorporate uncertainties for a system undergoing MCD scenarios. Finally, the system architecture presented in Figure 4 and Figure 5 demonstrate that the proposed approach can be easily scaled and integrated into digital twin platforms. Using API connections and Kubernetes clusters, it is possible to link multiple systems and components, making deployment efficient and manageable. This architecture supports real-time monitoring and could play a key role in future DT-enabled predictive maintenance strategies.

6. Conclusions

This study set out to explore how control-based reference tracking can be used to detect and isolate multi-component degradation (MCD) in Digital Twin (DT) applications—without relying on large historical degradation datasets. The results demonstrate that control strategies, particularly in hybrid form, can serve as accurate and efficient tools for fault detection in complex systems. Among the tested models, the hybrid approach consistently delivered higher accuracy across different test scenarios by combining the strengths of LQR, PI, and MPC. The LQR model also showed robust individual performance, especially in predicting degradation in key components like pumps and nozzles. A key contribution of this research is its move away from purely data-driven methods towards control-based analytics for MCD detection and isolation by eliminating the need for degradation data for training.

The study also highlights how the sequence of degradation events affects model performance, underlining the need for more adaptable strategies in dynamic environments for fault detection and isolation. The system architecture used in this work, based on REST APIs and containerized deployment, ensures that these models can be integrated into real-world applications efficiently. In summary, this research provides a new direction for PHM strategies in the context of Industry 4.0 by demonstrating how control-based reference tracking can support early, accurate, and data-efficient detection of multi-component degradation in DT-enabled systems in scalable deployment framework. The primary contributions of this work are highlighted below.

C1: A novel, control-based approach for MCD detection and isolation that eliminates the dependency on large historical datasets for training, moving beyond purely data-driven paradigms.

C2: The validation of this methodology within a scalable, containerized system architecture, demonstrating its practical viability for real-world DT deployment and integration.

Future work will focus on refining model interpretability, adapting the approach for broader system types, and exploring real-time learning mechanisms to further enhance predictive capabilities.