Abstract
Plant-parasiticnematodes represent a significant biosecurity threat in cross-border plant quarantine, necessitating precise identification for effective border control. While DL models have demonstrated success in nematode image classification based on morphological features, the limited availability of high-quality samples and the species-specific nature of nematodes result in insufficient training data, which constrains model performance. Although generative models have shown promise in data augmentation, they often struggle to balance morphological fidelity and phenotypic diversity. This paper proposes a novel few-shot data augmentation framework based on a morphology-constrained latent diffusion model, which, for the first time, integrates morphological constraints into the latent diffusion process. By geometrically parameterizing nematode morphology, the proposed approach enhances topological fidelity in the generated images and addresses key limitations of traditional generative models in controlling biological shapes. This framework is designed to augment nematode image datasets and improve classification performance under limited data conditions. The framework consists of three key components: First, we incorporate a fine-tuning strategy that preserves the generalization capability of model in few-shot settings. Second, we extract morphological constraints from nematode images using edge detection and a moving least squares method, capturing key structural details. Finally, we embed these constraints into the latent space of the diffusion model, ensuring generated images maintain both fidelity and diversity. Experimental results demonstrate that our approach significantly enhances classification accuracy. For imbalanced datasets, the Top-1 accuracy of multiple classification models improved by 7.34–14.66% compared to models trained without augmentation, and by 2.0–5.67% compared to models using traditional data augmentation. Additionally, when replacing up to 25% of real images with generated ones in a balanced dataset, model performance remained nearly unchanged, indicating the robustness and effectiveness of the method. Ablation experiments demonstrate that the morphology-guided strategy achieves superior image quality compared to both unconstrained and edge-based constraint methods, with a Fréchet Inception Distance of 12.95 and an Inception Score of 1.21 ± 0.057. These results indicate that the proposed method effectively balances morphological fidelity and phenotypic diversity in image generation.
1. Introduction
Plant-parasitic nematodes are microscopic, transparent, and colorless organisms that pose a significant threat to agriculture and forestry, often resulting in severe economic losses. Given their high-risk status in plant quarantine, accurate species identification is critical for effective biosecurity measures [1]. However, distinguishing closely related species remains a challenge due to subtle, often microscopic, morphological differences. Traditional identification methods rely on expert analysis of high-resolution microscopic images, focusing on anatomical structures such as the stylet, terminal bulb, and tail. This process, which follows a hierarchical taxonomy, demands extensive expertise and time-consuming manual examination, as illustrated in Figure 1, which shows the morphological variability in the head structures of five nematode genera.

Figure 1.
Microscopic images of the head of plant-parasitic nematodes.
Recently, deep learning-based image classification has emerged as a promising solution for nematode identification due to its ability to automatically extract complex features [2,3,4,5]. However, current methods face two key challenges. First, class imbalances in nematode datasets, caused by natural species distribution biases and sampling preferences, hinder ability of deep learning(DL) models to learn discriminative morphological features, especially for tail-related structures. Second, nematode imaging requires complex and expensive biological sample preparation, heavily reliant on operator expertise. Consequently, publicly available datasets often suffer from low resolution, morphological artifacts, and coarse annotations, limiting their utility for fine-grained morphological analysis and reducing model generalization across species [6].
To address the challenge of data imbalance due to data scarcity, researchers commonly turn to data augmentation techniques to improve model performance. Traditional augmentation methods, such as geometric transformations and color perturbations, help expand training data [7,8,9,10]. However, these methods fail to capture the nonlinear morphological variations present in nematode anatomy and may introduce feature confusion [7,8,9,10]. While generative models like Generative Adversarial Networks (GANs) and Variational Autoencoders (VAEs) have shown promise in image synthesis [11,12], they face challenges in few-shot scenarios, including mode collapse and topological distortions. These models struggle to preserve biologically important features, such as the nematode stylet and terminal bulb, which are critical for accurate classification [11,12]. More recently, Denoising Diffusion Probabilistic Models (DDPM) and their derivatives, such as Latent Diffusion Models (LDM), have shown potential for high-quality image generation through a progressive denoising process [13,14]. These models have shown strong performance in domains like medical imaging [15] and remote sensing [16]. However, their application to biological microscopic image generation remains limited, mainly due to challenges in balancing image diversity with structural fidelity. To address the dual challenges of generating high-quality and diverse nematode images, this study proposes constructing a geometry-based parametric representation of nematode morphology. This representation serves as a morphological constraint to guide the diffusion process, enabling effective control over image fidelity and mitigating dataset imbalance in few-shot scenarios.
This study presents a few-shot data augmentation framework based on a morphology-constrained LDM to enhance nematode datasets and improve fine-grained nematode classification under limited data conditions. The approach aims to systematically address the inherent limitations of existing biomedical image generation methods, particularly in maintaining topological fidelity and controlling morphological variations. We propose an innovative framework that combines fine-tuned LDM with conditionally controlled constraints. The process begins by constructing morphological constraints from nematode images that balance diversity and fidelity. Then, a LDM is employed to refine the structure, optimizing parameters under few-shot conditions through low-rank adaptive(LoRA) fine-tuning. We introduce a hierarchical attention fusion mechanism to embed the morphological constraint vector into the latent space during the noise prediction process [17,18]. The resulting synthetic nematode images are validated through data augmentation experiments, demonstrating enhanced classifier performance.
The key contributions include:
- We propose a morphology-constrained fine-tuned LDM framework, enabling stable and controlled generation of nematode images under few-shot conditions.
- We design a novel method for generating nematode morphological constraints, introducing a mechanism for mapping from nematode images to morphological constraints.
- We establish a multi-model evaluation system to assess the impact of generated data on classifiers, such as ResNet50 and DenseNet121, across different datasets. Our experiments show significant accuracy improvements over traditional methods.
2. Related Work
2.1. Data Augmentation
Deep learning-based nematode image classification tasks heavily depend on large-scale, high-quality training data. However, the scarcity of data and class imbalance severely limit model performance. Existing data augmentation methods can be categorized into traditional augmentation strategies and generative augmentation paradigms, with the core difference lying in their ability to model data distribution characteristics and morphological constraints.
2.1.1. Traditional Data Augmentation Methods
Traditional methods introduce sample diversity through geometric transformations and pixel-level perturbations, essentially expanding the data space linearly. For example, techniques like Random Erasing force the model to focus on global features by masking local regions [7], but this can obscure key anatomical structures of nematodes. CutMix generates mixed samples by replacing local regions across different samples [10], improving the robustness of the model’s classification boundaries. Similarly, MixUp creates virtual samples through feature space interpolation, helping to mitigate the risk of overfitting [9]. Although these methods improve model generalization through random combinations [8], the linear variations they generate fail to simulate the nonlinear morphological differences in nematode anatomy. This can even introduce feature confusion, leading to a degradation in classification performance.
2.1.2. Diffusion Model-Based Data Augmentation
To overcome the linear limitations of traditional methods, generative models use implicit data distribution modeling to achieve nonlinear sample expansion. However, GANs suffer from mode collapse due to their adversarial training mechanism, resulting in insufficient diversity of generated samples [11,19]. Constrained by their latent space decoupling capabilities, VAEs often produce blurry or structurally distorted images [12,20]. In contrast, DDPM approximates the data distribution through a progressive Markov chain denoising process, significantly outperforming traditional generative models in terms of fidelity and diversity evaluation metrics [13]. For high-resolution image generation, LDM compress the diffusion process into a lower-dimensional latent space and utilize pre-trained VAEs encoders for dimensionality reduction, maintaining generation quality while reducing computational complexity [14]. LDM incorporates a text-image alignment mechanism, embedding semantic prompts into cross-attention layers for fine-grained conditional generation. Despite LDM’s outstanding performance in natural image generation, challenges remain in biological morphology image synthesis. Specifically, it struggles with maintaining topological fidelity in anatomical structures (such as nematode stylet curvature and metacorpus morphology) and lacks an explicit mechanism for embedding domain prior knowledge, limiting its domain adaptation in downstream classification tasks.
2.1.3. Applications of Data Augmentation in Agriculture and Forestry
Deep learning has been widely adopted in the classification of biological images in agriculture and forestry due to its powerful feature extraction capabilities. In nematode image recognition tasks, the combination of traditional computer vision techniques with deep learning methods has significantly improved the performance of morphological feature extraction and classification [3]. To further enhance model accuracy and generalization, researchers have developed more complex deep neural networks and incorporated transfer learning strategies, achieving up to 98.82% classification accuracy across five nematode categories [21]. However, these advancements often rely on large-scale, well-balanced datasets and subjective selection of target categories. In real-world scenarios where data is limited or imbalanced, model generalization typically deteriorates. To address this, recent studies have introduced style transfer-based data augmentation techniques, which modify color information while preserving structural features of nematode images. This approach helps alleviate data imbalance issues and has shown potential for extension to other biological image domains [5]. Nevertheless, style transfer methods are inherently limited to color variation and fall short in capturing complex structural diversity within biological images. Recently, LDM have been applied in agricultural contexts, particularly in generating realistic weed images to enhance dataset diversity and fidelity [22]. While these models show promise, standard LDM still face challenges related to generation stability and controllability. As a result, the synthesized images often require substantial manual filtering before being used in downstream classification tasks.
2.2. Fine-Tuning Diffusion Models
To address the few-shot nematode image generation requirements, domain-specific fine-tuning of pre-trained diffusion models is necessary. Full Fine-Tuning updates all model parameters to inject new concepts but is prone to overfitting and catastrophic forgetting [23]. Dreambooth uses instance-driven fine-tuning by jointly optimizing classifier-free guidance and prior retention loss [24], balancing new concept learning with the retention of original knowledge, though it may reduce sample diversity in few-shot scenarios. Text Inversion optimizes text embedding vectors for concept transfer [25], but it struggles to capture complex morphological features (e.g., nematode tail markings). Recently, LoRA introduced an efficient parameter tuning strategy, freezing the backbone network weights via low-rank matrix decomposition while training only the adapter parameters [17]. This reduces memory usage and improves training stability. However, existing fine-tuning methods primarily focus on semantic concept transfer, often overlooking the geometric constraints imposed by biological morphology. As a result, generated samples struggle to maintain consistent topological fidelity.
3. Materials and Methods
This study proposes a morphology-constrained generation framework operating in two stages. Figure 2 illustrates the flowchart of the two-stage framework.
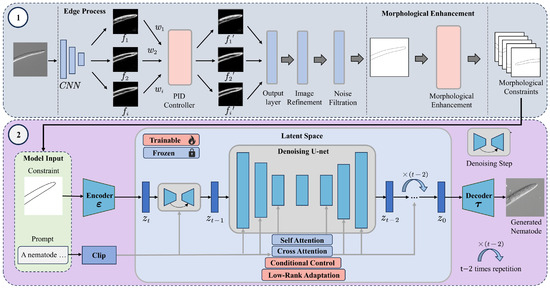
Figure 2.
Nematode Image Generation Framework Based on Morphological Constraints. This framework consists of two main stages: Stage 1 (Top): This stage establishes a mapping between nematode images and their morphological constraints. First, edge features of input nematode images are extracted using the PiDiNet convolutional network. Then, a PID controller adjusts the weight of the extracted feature map based on the error signal to optimize edge detail. The refined edge image is further processed through noise reduction and contour enhancement, resulting in a high-quality binary mask that captures morphological constraints. A subsequent morphological enhancement step introduces topological diversity to enrich the representation of nematode morphology. Stage 2 (Bottom): The generated morphological constraint is projected into the latent space via a decoder and combined with textual prompts encoded by CLIP. Within the latent space, a cross-attention mechanism embedded in the UNet guides the denoising process. During each sampling step, morphological conditions are integrated through the use of LoRA module and a conditional control unit, enabling the model to synthesize high-fidelity nematode images that conform to biological structure and variability.
3.1. Nematode Dataset
This study is based on a microscopic image dataset comprising 1550 high-resolution images of five plant-parasitic nematode genera with significant taxonomic differences. The datasets, Bnema5 and UNBnema5, are described in Table 1, with the nematode head region selected as the core area for analysis due to its inclusion of key diagnostic features. As shown in Figure 1, these genera exhibit notable morphological differences in diagnostic features, such as lip cuticle height, stylet length-to-basal bulb diameter ratio, and the morphological topology of the esophageal bulb.

Table 1.
Detailed information on five categories of nematode images in Bnema5 and UNBnema5.
All images were captured using a ZEISS Axio Imager Z1 microscopy system (Carl Zeiss Microscopy GmbH, Göttingen, Germany) equipped with a Differential Interference Contrast module [5] and a 20× objective lens, producing 16-bit grayscale images. During the preprocessing phase, the head region of interest (ROI) was first located using morphological constraints knowledge. The nematode’s anatomical boundaries were extracted using adaptive thresholding combined with contour detection algorithms. The ROI was then resampled to 512 × 512 pixels using bicubic interpolation [26], ensuring key morphological features were preserved while adapting the images to the input requirements of DL models.
3.2. Morphological Constraint Generation
This study introduces a geometry-based constraint mechanism for nematode image generation. The aim is to guide the LDM to preserve anatomical fidelity while decoupling texture details. As shown in Figure 3, constructing the morphology-constrained involves using binary masks to represent the anatomical topology of the nematode’s head region. These masks are applied to the shallow feature maps of the UNet decoder, where a channel attention mechanism adjusts the local structural weights. Meanwhile, the deeper layers of the network continue to leverage the diffusion model’s inherent ability to synthesize textures.
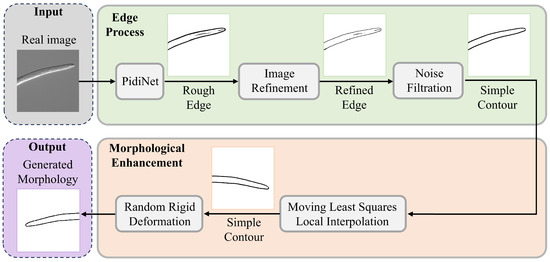
Figure 3.
Nematode Image Morphological Constraint Generation Process. The process consists of two main modules: Edge Processing (top) and Morphological Constraint Enhancement (bottom). In the edge processing module, real nematode images undergo multiple steps: initial contours are extracted using the PiDiNet edge detection network, followed by contour refinement and adaptive threshold-based noise filtering to generate fine-grained, topologically closed boundaries. In the morphological diversity enhancement module, Moving Least Squares (MLS) is employed to perform local affine deformation, while a rigid deformation kernel simulates the biological motion characteristics of nematodes. These combined techniques are used to construct a prior library of morphological constraints.
3.2.1. Binary Mask Generation
To address defocus blur and structural discontinuities in the edge extraction of microscopic nematode images [2], we combine deep learning-based edge detection with geometric-parameterized post-processing. While the Canny method is highly sensitive to noise and prone to generating false edges [27], Holistically-Nested Edge Detection (HED) overemphasizes non-structural features like cuticle textures due to its multi-scale feature fusion [28]. To overcome these limitations, we employ the direction-aware pixel difference network (PiDiNet) as the core edge detector [29]. PiDiNet operates through the collaboration of two core components: a direction-aware module and a pixel difference network. The direction-aware module enables the network to capture directional information for each pixel in the image, allowing the model to leverage spatial relationships and orientation cues for more accurate detection. The pixel difference network, on the other hand, focuses on detecting local variations by computing differences between neighboring pixels. To further enhance robustness and response stability, a PID controller is integrated into the pixel difference module. Inspired by classic feedback control systems, the PID controller refines the gradient response by balancing three terms: proportional (P), integral (I), and derivative (D). By dynamically adjusting the weights of these components, the PID mechanism helps to preserve sharp edges while suppressing spurious responses in non-edge regions. The operation of PiDiNet, as used in the first stage (top) of Figure 2, is illustrated through the edge processing pipeline. Directional feature maps are extracted via convolutional layers, followed by PID-based optimization during training to adjust feature map weights. This process improves training stability and enhances both robustness and precision in downstream detection tasks.
Figure 4 displays edge detection results for five types of nematodes using different algorithms. Panel (d) shows the result using our proposed method. The Canny method (b) is overly sensitive to epidermal textures, introducing false edges. The HED method (c) struggles with artifacts from internal myofibrils in the esophageal bulb, leading to broken contours and increased background noise. In contrast, the proposed approach (d) effectively suppresses background noise, achieving smoother contour continuity and better preserving morphological fidelity.

Figure 4.
Morphological Fidelity Comparison of Nematode Edge Detection Methods.
For the i-th edge map in PiDiNet, the loss for the j-th pixel, which has a value of , is as follows:
where is the ground truth edge probability, is a predefined threshold, meaning that a pixel is discarded and not considered to be a sample when calculating the loss if it is marked as positive by fewer than of annotators to avoid confusion. Additionally, is the percentage of negative pixel samples and .
Therefore, the total loss function is:
3.2.2. Morphological Diversity Enhancement
To address the issue of insufficient morphological diversity under topology constraints in few-shot scenarios, this study proposes a morphology-constrained enhancement method. This approach combines moving least squares(MLS) to achieve controllable morphological expansion under topological constraints [30]. The core process is outlined in Figure 5, which includes edge topology optimization, MLS-based geometric deformation modeling, and morphological constraint enhancement.
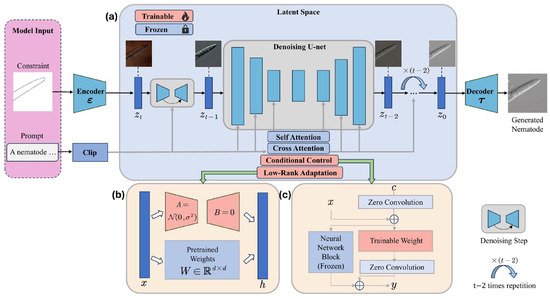
Figure 5.
Overview of proposed generative framework. Input including morphological constraint image and prompts. The entire framework consists of three main components: (a) the pre-trained text-to-image diffusion model with fixed parameters. (b) the pre-training fine-tuned model, which updates only the Adapter parameters. (c) the pre-trained conditioned control model, which incorporates zero convolution and freezes certain parameters in LDM.
First, an iterative erosion operation generates a single-pixel-wide skeleton of the nematode, denoted as S, preserving the topological connectivity between the stylet and esophageal bulb. Isolated short branches are filtered out based on a skeleton length threshold, ensuring the anatomical structure remains intact. For geometric deformation modeling, eight control points are sampled at equal intervals along the skeleton to create a set of deformation source points P. Using these points, a least-squares method is applied to fit a straight line segment representing the nematode’s skeleton . Eight points are then uniformly selected along this fitted skeleton as a set of similarity deformation points q. By modifying q while keeping the other points p fixed, the deformation function is defined in a form that enables the pre-computation of additional information:
where and are the weight and coordinates of the deformation points, respectively.After completing the parameterized deformation based on MLS, a global rigid transformation perturbation is applied to the generated mask to simulate the spatial pose variations of the nematode in its natural state. This process, which combines geometric deformation with rigid perturbation in a cascading operation, significantly enhances the phenotypic diversity of the morphology-constrained set while maintaining the topological invariance of key classification features. This approach provides an anatomically reliable morphological constraints for training generative models in few-shot scenarios.
3.3. Diffusion Model
This study aims to address the dual challenges of topological distortion and the lack of fine-grained control in generating phytopathogenic nematode images in few-shot scenarios. We propose a morphology-constrained latent diffusion generation framework to produce high-quality nematode images. The proposed generative model framework is shown in Figure 5.
3.3.1. Fine-Tuning LDM
The diffusion model seeks to learn the real image distribution through a multi-step denoising process involving normal distribution variables. This process comprises two main phases: a forward process and a reverse process. The forward diffusion process gradually transforms the data distribution into a known distribution over time, while the reverse process reconstructs new data from random noise [13].
LDM consists of an autoencoder and a UNet [31], applied for noise estimation. First, LDM trains an autoencoder to obtain the representation of images in the latent space , which are then processed through the aforementioned diffusion process to reconstruct the image . Subsequently, LDM trains a UNet denoiser to complete the image denoising process in the latent space. Text prompts are mapped to sequence embeddings using the CLIP text encoder [32], and these embeddings are used in the cross-attention layers of each transformer [33] block within the UNet. The entire optimization process can be defined as follows:
represents the noisy image input , t is the uniformly sampled timestep, and is the denoising network used to predict and remove noise added to the noisy image.
Fine-tuning allows the introduction of new concepts while leveraging the prior knowledge of the model, enabling LDM to learn nematode-related information while preserving the original model’s generation performance. This is achieved by freezing the weights of the pre-trained model and injecting a trainable low-rank decomposition matrix into each layer of the Transformer architecture [17]. For the pre-trained weight matrix , the weight update is constrained by low-rank decomposition, represented as:
3.3.2. Morphological Control
To enhance the controllability of the image generation process, we introduce conditional control by applying constraints during generation [18]. This method integrates morphological constraints into a large pre-trained multimodal generative model. By locking the pre-trained diffusion model and reusing its encoding layers, the model learns predefined conditional controls within the specified constraints. These controls influence the noise prediction in the UNet, thereby enabling more targeted and precise control over the image generation process.
After implementing conditional controls, the expression for image generation becomes:
where represents the pre-trained diffusion model, x is the input to the model, is the output of the model, and represents the model parameters. represents the zero convolution module, , and represent the parameter weights of the conditional control model.The model freezes all trained parameters in and then duplicates them into a trainable copy .
Figure 6 shows a comparative analysis of nematode image generation based on morphological constraints. Compared to the unconstrained group (b), the morphology-constrained group (c) exhibits significantly improved topological consistency and better visual naturalness in key anatomical features, such as the stylet shape, esophageal bulb curvature, and body ring texture.
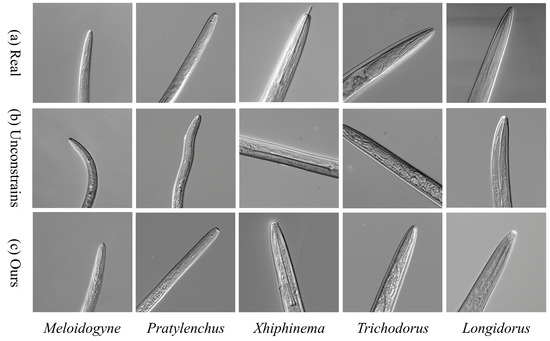
Figure 6.
Comparison of Nematode Image Generation Based on Morphological Constraints.
4. Results
4.1. Experimental Setup and Evaluation Methods
4.1.1. Fine-Tuning Configuration of LDM
In this study, we inject nematode-specific knowledge into a pre-trained LDM through fine-tuning. The base model is the publicly available Stable Diffusion v1.5, which was originally trained on high-quality subsets of the LAION-5B dataset [34]. To simulate a few-shot learning scenario, we used 200 images per nematode category for LoRA-based fine-tuning. The fine-tuning process was conducted for 500 epochs using the Adam optimizer [35]. The initial learning rate was set to , with a cosine annealing with warm restarts scheduler applied for better convergence. To prevent overfitting, the learning rate for the UNet component was set to , while the learning rate for the text encoder was set to . The LoRA rank was configured to 128, balancing the trade-off between model capacity and parameter efficiency. All experiments were conducted on a Windows 10 workstation equipped with an Intel i7-13700 CPU and an NVIDIA RTX A5000 GPU with 24GB of VRAM.
4.1.2. Configuration of Image Generation Parameters
Following the fine-tuning process, the LDM produced multiple checkpoints saved at various training stages. To determine the optimal configuration for nematode image generation, we conducted a systematic evaluation of these checkpoints under varying parameter settings, with a focus on the visual quality of the generated outputs. The core parameters considered in this process included the classifier-free guidance scale (CFG Scale), sampling algorithm (Sampler), LoRA weight, scheduler type, and the number of inference steps. To ensure experimental clarity and avoid interference between variables, each round of testing modified only one or two major parameters at a time. Parameter ranges were selected based on their priority and sensitivity to image quality, and adjustments were carried out in two phases: an initial coarse-grained search followed by a fine-grained tuning stage. Based on this iterative process, the final generation parameters were determined as follows: classifier-free guidance scale (7.5), sampler (DPM++ 2M SDE), LoRA weight (1.0), scheduler (Karras), and number of denoising steps (30).
4.1.3. Configuration of Image Classification Experiments
For the classification task, the following models were evaluated: ResNet50 [36], DenseNet121 [37], EfficientNetV2 [38], ResNeSt50 [39], and RepVGG-B1g2 [40]. All models were trained using the Stochastic Gradient Descent (SGD) optimizer with a multi-class cross-entropy loss function. Input images were resized to pixels. Training was performed for 200 epochs on an Ubuntu server (dual Intel Xeon Silver 4214 CPUs, four NVIDIA RTX 2080 Ti 12GB GPUs, 256GB DDR4 memory).
4.1.4. Evaluation Metrics
The perceptual quality, fidelity, and diversity of the generated images were assessed. Image fidelity refers to how closely the generated images resemble real ones, while image diversity measures the extent to which the generated images capture the variation present in real samples. This study used two key metrics for evaluation: Fréchet Inception Distance (FID) [41] and Inception Score (IS) [42]. FID quantifies the distribution distance between the generated and real images in the Inception-v3 [43] feature space:
where are the mean vectors of the features, and are the covariance matrices.
IS measures both the diversity of generated samples and the classification confidence. To compute IS, the Inception-v3 model is used to predict the class of all generated images, which provides the conditional label distribution. IS combines two objectives in its calculation:
where represents the predicted class probabilities, and represents the Kullback-Leibler (KL) divergence. A higher IS indicates better quality of the generated images.
In this study, we evaluate the performance of the deployed classification models using three commonly adopted metrics: Top-1 accuracy, precision, and recall. Based on comparisons with ground truth labels, each prediction is categorized as true positive , true negative , false negative , and false positive . For multiclass classification tasks, overall performance is typically summarized using two averaging methods: macro-average and micro-average. In our study, we adopt the macro-average approach, which calculates precision and recall for each class independently, and then computes the arithmetic mean across all classes. This method is more appropriate for assessing balanced performance across classes, especially under class-imbalanced conditions. Then these metrics can be calculated as follows:
4.2. Data Augmentation Under Class-Imbalanced Conditions
In this study, we applied a morphology-constrained generative augmentation strategy to the UNBnema5 dataset. As shown in Table 1, the dataset exhibits significant class imbalance, with large discrepancies in the number of nematode images across different categories. To address this, we selected 200 real images per class to fine-tune a pre-trained large-scale diffusion model using LoRA-based adaptation. Following fine-tuning, the model generated 10,000 synthetic nematode images spanning five genera. Based on morphological metrology criteria, a total of 2500 valid samples (500 per genus) were selected from the generated set. These morphology-compliant images were then used to augment the training samples of each genus, resulting in a class-balanced dataset. Under a consistent training/validation/test split of 7:2:1, the training set for each class was augmented to a uniform size of 420 images per genus. The experimental control groups included both the original (non-augmented) dataset and a RandAugment-enhanced group [8], enabling comparative evaluation of augmentation effectiveness.
As shown in Table 2, the generative augmentation strategy significantly improved classification performance across all five DL models. Among all classifiers, the study achieved the best results, with ResNet50 reaching a Top-1 accuracy of 69.33%, a 14.66% improvement over the original dataset and a 2.0% increase over the RandAugment group. The largest gain over RandAugment was observed with ResNeSt50. The macro-average precision and recall improved by 15.44% and 14.66%, respectively.

Table 2.
Metric scores for different DL models using different data augmentation methods.
4.3. Impact of Generative Image Proportions on Classification Performance
This study performed data augmentation on the Bnema5 dataset to ensure that each of the five nematode categories in the training set contained 140 samples. A certain proportion of real nematode samples were replaced by generated nematode images. Five different DL models were used for training and testing, followed by performance evaluation and comparison.
Table 3 shows the Top-1 accuracy of the Bnema5 dataset when trained with varying proportions of generated and real images. When the proportion of generated images does not exceed 25%, the classifier performance based solely on real images remains largely unchanged, highlighting the high quality of the generated samples. However, as shown in Figure 7, the performance of the DL models consistently decreases with an increasing proportion of generated images. When the training set consists entirely of generated images, all five models perform below 50%.

Table 3.
Top-1 accuracy of DL models with different proportion of generative images.
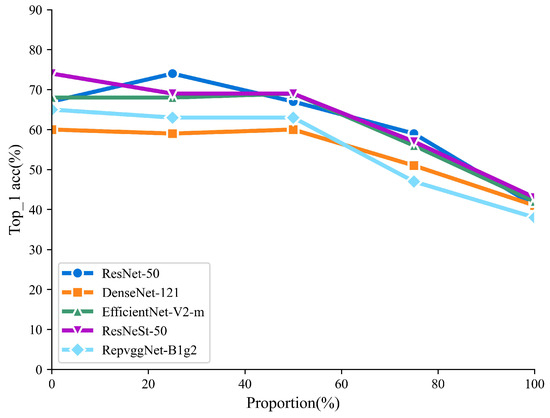
Figure 7.
Trend of Top-1 accuracy of DL models with different proportion of generative images.
4.4. Ablation Study
Section 4.2 and Section 4.3 demonstrate that the nematode images generated by our method exhibit high visual and structural quality, leading to significant improvements in deep learning model performance following data augmentation. However, it is essential to investigate the underlying relationship between this enhanced image quality and our proposed methodology. To this end, we conducted a series of ablation experiments to examine the specific contribution of morphological constraints to the effectiveness of nematode image generation. By modifying the conditional control settings related to morphological constraints within the generation model, we compared the performance of the diffusion model under three distinct generation configurations.
To assess the impact of morphological constraints on generation quality, we evaluated three generation modes using identical LDM hyperparameters: (1) baseline generation without any morphological constraints, (2) generation guided by Canny edge detection, and (3) generation guided by our proposed morphology-constrained approach. As illustrated in Figure 8, all three configurations were executed within the same generation framework to ensure a fair comparison. The baseline, unconstrained generation (b) displays topological instability, whereas the Canny-guided method (c) preserves the overall structure but introduces visual artifacts such as blurred ring patterns and jagged edges in the lip region. In contrast, our approach (d), which incorporates anatomical constraints into the noise prediction mechanism, substantially enhances the preservation of key morphological characteristics. These results highlight the ability of our framework to maintain morphological plausibility and image fidelity, with the images generated by our method clearly outperforming those of the control groups in both structural accuracy and visual realism.

Figure 8.
Comparison of Nematode Image Generation Quality Based on Morphological Constraints. (a) Real microscopic image from the Nema5 dataset; (b) Unconstrained LDM generation result; (c) Canny edge-constrained generation result; (d) Morphology-constrained generation result from this study.
The quantitative results of the ablation study, presented in Table 4, further support these findings. Our morphology-constrained strategy achieves the best performance in terms of FID with a score of 12.95, and IS of 1.21 ± 0.057. Notably, all generated samples preserve the visual characteristics typical of the ZEISS Axio Imager Z1 microscope (Carl Zeiss Microscopy GmbH, Göttingen, Germany), and the mean IS value of our method is closest to that of real microscopy images. These results confirm that our approach not only replicates biologically relevant morphological features with high fidelity but also enhances phenotypic diversity through controlled generative perturbations. Overall, the experiments demonstrate that our method successfully balances structural accuracy and diversity in nematode image generation.

Table 4.
Quantitative assessment of nematode images generated under different constraint conditions.
5. Conclusions
This study proposes a LDM generation framework enhanced by morphology constraints and LoRA fine-tuning. By embedding morphology constraints extracted from real nematode images into the noise prediction process of a fine-tuned latent diffusion model, we improve the performance of few-shot nematode datasets. Experimental results demonstrate that, under real-world imbalanced data conditions, the generated samples boost the Top-1 classification accuracy of five mainstream deep learning models, including ResNet50, by up to 14.66%, significantly outperforming conventional augmentation strategies. This improvement establishes a reliable data foundation for fine-grained nematode identification, particularly in critical applications such as plant quarantine and biosecurity inspection. Furthermore, under balanced data conditions, replacing up to 25% of real images with generated samples leads to negligible loss in classification performance, validating the quality and consistency of the generated data. Quantitative evaluation of the ablation study demonstrates that, under different constraint conditions, the proposed framework achieves the best performance compared to alternative methods, with a FID of 12.95 and an IS of 1.21 ± 0.057. These results indicate that our method effectively balances morphological fidelity and phenotypic diversity in the generation of nematode images.
The morphology-constrained generative framework proposed in this study not only enables the synthesis of high-quality biological images but also offers a transferable and generalizable solution for a wide range of image-based recognition tasks in agricultural and biological domains. This makes the approach a valuable and scalable tool for applications such as biosecurity screening and automated identification systems. However, a current limitation of the framework lies in the morphology constraint mechanism, which is primarily derived from the morphological characteristics of nematodes. As such, the constraint formulation may not be directly applicable to organisms with fundamentally different anatomical structures. Future research will focus on developing more universal morphological control strategies to enhance the adaptability and robustness of generative models across diverse biological imaging tasks.
Author Contributions
Conceptualization, X.O. and J.Z.; Data curation, J.G.; Formal analysis, X.O., J.Z. and S.Y.; Investigation, X.O. and S.Y.; Methodology, X.O. and S.Y.; Project administration, J.Z.; Resources, J.G.; Supervision, J.Z.; Validation, X.O. and S.Y.; Visualization, X.O.; Writing—original draft, X.O.; Writing—review & editing, J.Z., J.G. and S.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key R&D Program of China (NO. 2022YFF0608804), by Zhejiang Provincial Natural Science Foundation, China (NO. LQ23F050002).
Data Availability Statement
Data will be made available on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Nicol, J.M. Important nematode pests. In Bread Wheat: Improvement and Production; FAO Plant Production and Protection Series: Rome, Italy, 2002; pp. 345–366. [Google Scholar]
- Liu, M.; Wang, X.; Zhang, H. Taxonomy of multi-focal nematode image stacks by a CNN based image fusion approach. Comput. Methods Programs Biomed. 2018, 156, 209–215. [Google Scholar] [CrossRef]
- Thevenoux, R.; Le, V.L.; Villessèche, H.; Buisson, A.; Beurton-Aimar, M.; Grenier, E.; Folcher, L.; Parisey, N. Image based species identification of Globodera quarantine nematodes using computer vision and deep learning. Comput. Electron. Agric. 2021, 186, 106058. [Google Scholar] [CrossRef]
- Abade, A.; Porto, L.F.; Ferreira, P.A.; de Barros Vidal, F. NemaNet: A convolutional neural network model for identification of soybean nematodes. Biosyst. Eng. 2022, 213, 39–62. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhuang, J.; Ye, S.; Xu, N.; Xiao, J.; Gu, J.; Fang, Y.; Peng, C.; Zhu, Y. Domain generalization in nematode classification. Comput. Electron. Agric. 2023, 207, 107710. [Google Scholar] [CrossRef]
- Zhou, B.T.; Nah, W.L.; Lee, K.W.; Baek, J.H. A General Image Based Nematode Identification System Design. In Proceedings of the International Conference on Computational Intelligence and Security, Xi’an, China, 15–19 December 2005. [Google Scholar]
- DeVries, T.; Taylor, G.W. Improved regularization of convolutional neural networks with cutout. arXiv 2017, arXiv:1708.04552. [Google Scholar]
- Cubuk, E.D.; Zoph, B.; Shlens, J.; Le, Q.V. Randaugment: Practical automated data augmentation with a reduced search space. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Seattle, WA, USA, 14–19 June 2020; pp. 3008–3017. [Google Scholar]
- Zhang, H.; Cisse, M.; Dauphin, Y.N.; Lopez-Paz, D. mixup: Beyond empirical risk minimization. arXiv 2017, arXiv:1710.09412. [Google Scholar]
- Yun, S.; Han, D.; Oh, S.J.; Chun, S.; Choe, J.; Yoo, Y.J. CutMix: Regularization Strategy to Train Strong Classifiers With Localizable Features. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 6022–6031. [Google Scholar]
- Chen, H. Challenges and Corresponding Solutions of Generative Adversarial Networks (GANs): A Survey Study. J. Phys. Conf. Ser. 2021, 1827, 012066. [Google Scholar] [CrossRef]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Ho, J.; Jain, A.; Abbeel, P. Denoising diffusion probabilistic models. Adv. Neural Inf. Process. Syst. 2020, 33, 6840–6851. [Google Scholar]
- Rombach, R.; Blattmann, A.; Lorenz, D.; Esser, P.; Ommer, B. High-Resolution Image Synthesis with Latent Diffusion Models. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 10674–10685. [Google Scholar]
- Zhou, T.; Chen, X.; Shen, Y.; Nieuwoudt, M.; Pun, C.M.; Wang, S. Generative AI Enables EEG Data Augmentation for Alzheimer’s Disease Detection Via Diffusion Model. In Proceedings of the 2023 IEEE International Symposium on Product Compliance Engineering—Asia (ISPCE-ASIA), Shanghai, China, 4–5 November 2023; pp. 1–6. [Google Scholar]
- Liu, L.Q.; Chen, B.W.; Chen, H.; Zou, Z.X.; Shi, Z.W. Diverse Hyperspectral Remote Sensing Image Synthesis With Diffusion Models. IEEE Trans. Geosci. Remote. Sens. 2023, 61, 1–16. [Google Scholar] [CrossRef]
- Hu, J.E.; Shen, Y.; Wallis, P.; Allen-Zhu, Z.; Li, Y.; Wang, S.; Chen, W. LoRA: Low-Rank Adaptation of Large Language Models. arXiv 2021, arXiv:2106.09685. [Google Scholar]
- Zhang, L.; Rao, A.; Agrawala, M. Adding Conditional Control to Text-to-Image Diffusion Models. In Proceedings of the 2023 IEEE/CVF International Conference on Computer Vision (ICCV), Paris, France, 1–6 October2023; pp. 3813–3824. [Google Scholar]
- Wang, K.; Gou, C.; Duan, Y.; Lin, Y.; Zheng, X.; Wang, F.Y. Generative adversarial networks: Introduction and outlook. IEEE/Caa J. Autom. Sin. 2017, 4, 588–598. [Google Scholar] [CrossRef]
- Tomczak, J.M.; Welling, M. VAE with a VampPrior. arXiv 2017, arXiv:1705.07120. [Google Scholar]
- da Silva Abade, A.; Faria Porto, L.; Afonso Ferreira, P.; de Barros Vidal, F. Nemanet: A convolutional neural network model for identification of nematodes soybean crop in brazil. arXiv 2021, arXiv:2103.03717. [Google Scholar]
- Chen, D.; Qi, X.; Zheng, Y.; Lu, Y.; Huang, Y.; Li, Z. Synthetic data augmentation by diffusion probabilistic models to enhance weed recognition. Comput. Electron. Agric. 2024, 216, 108517. [Google Scholar] [CrossRef]
- Ding, N.; Qin, Y.; Yang, G.; Wei, F.; Yang, Z.; Su, Y.; Hu, S.; Chen, Y.; Chan, C.M.; Chen, W.; et al. Parameter-efficient fine-tuning of large-scale pre-trained language models. Nat. Mach. Intell. 2023, 5, 220–235. [Google Scholar] [CrossRef]
- Ruiz, N.; Li, Y.; Jampani, V.; Pritch, Y.; Rubinstein, M.; Aberman, K. DreamBooth: Fine Tuning Text-to-Image Diffusion Models for Subject-Driven Generation. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 17–24 June 2022; pp. 22500–22510. [Google Scholar]
- Gal, R.; Alaluf, Y.; Atzmon, Y.; Patashnik, O.; Bermano, A.H.; Chechik, G.; Cohen-Or, D. An image is worth one word: Personalizing text-to-image generation using textual inversion. arXiv 2022, arXiv:2208.01618. [Google Scholar]
- Keys, R. Cubic convolution interpolation for digital image processing. IEEE Trans. Acoust. Speech Signal Process. 1981, 29, 1153–1160. [Google Scholar] [CrossRef]
- Canny, J. A Computational Approach to Edge Detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, PAMI-8, 679–698. [Google Scholar] [CrossRef]
- Xie, S.; Tu, Z. Holistically-Nested Edge Detection. Int. J. Comput. Vis. 2015, 125, 3–18. [Google Scholar] [CrossRef]
- Su, Z.; Liu, W.; Yu, Z.; Hu, D.; Liao, Q.; Tian, Q.; Pietikäinen, M.; Liu, L. Pixel Difference Networks for Efficient Edge Detection. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 11–17 October 2021; pp. 5097–5107. [Google Scholar]
- Schaefer, S.; McPhail, T.; Warren, J.D. Image deformation using moving least squares. ACM Trans. Graph. 2006, 25, 533–540. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. arXiv 2015, arXiv:1505.04597. [Google Scholar]
- Radford, A.; Kim, J.W.; Hallacy, C.; Ramesh, A.; Goh, G.; Agarwal, S.; Sastry, G.; Askell, A.; Mishkin, P.; Clark, J.; et al. Learning Transferable Visual Models From Natural Language Supervision. In Proceedings of the International Conference on Machine Learning, Online, 18–24 July 2021. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. arXiv 2017, arXiv:1706.03762. [Google Scholar]
- Schuhmann, C.; Beaumont, R.; Vencu, R.; Gordon, C.; Wightman, R.; Cherti, M.; Coombes, T.; Katta, A.; Mullis, C.; Wortsman, M.; et al. LAION-5B: An open large-scale dataset for training next generation image-text models. arXiv 2022, arXiv:2210.08402. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Huang, G.; Liu, Z.; Weinberger, K.Q. Densely Connected Convolutional Networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2016; pp. 2261–2269. [Google Scholar]
- Tan, M.; Le, Q.V. EfficientNetV2: Smaller Models and Faster Training. In Proceedings of the International Conference on Machine Learning, Virtual, 18–24 July 2021. [Google Scholar]
- Zhang, H.; Wu, C.; Zhang, Z.; Zhu, Y.; Zhang, Z.L.; Lin, H.; Sun, Y.; He, T.; Mueller, J.W.; Manmatha, R.; et al. ResNeSt: Split-Attention Networks. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), New Orleans, LA, USA, 19–20 June 2022; pp. 2735–2745. [Google Scholar]
- Ding, X.; Zhang, X.; Ma, N.; Han, J.; Ding, G.; Sun, J. RepVGG: Making VGG-style ConvNets Great Again. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 13728–13737. [Google Scholar]
- Heusel, M.; Ramsauer, H.; Unterthiner, T.; Nessler, B.; Hochreiter, S. GANs Trained by a Two Time-Scale Update Rule Converge to a Local Nash Equilibrium. In Proceedings of the Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Salimans, T.; Goodfellow, I.J.; Zaremba, W.; Cheung, V.; Radford, A.; Chen, X. Improved Techniques for Training GANs. arXiv 2016, arXiv:1606.03498. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.E.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).