High-Dimensional Cross Parity Codes and Parities from Lower Than (d − 1)-Dimensional Hyperplanes

Abstract

Cross parity codes are mostly used as 2-dimensional codes, and sometimes as 3-dimensional codes. We argue that higher dimensions can help to reduce the number of parity bits, and thus deserve further investigation. As a start, we investigate parities from $(d-2)$-dimensional hyperplanes in d-dimensional parity codes, instead of parities from $(d-1)$-dimensional hyperplanes as usual.

1. Introduction

Cross parity codes have been used for a long time [1] as part of channel coding to achieve forward error correction due to their simplicity and fast correction circuits, although the number of parity bits is higher than for other block codes [2]. Mostly, 2-dimensional parity codes have been used with row and column parities, and they have been extended to correct at least a fraction of 2-bit errors [3]. We are not aware of a systematic study of higher dimensions; only [2] mention that they performed experiments, and [1] mentions that higher than three dimensions are possible.

As the minimum code weight is restricted to $min(4,d+1)$, it seems useless to investigates dimensions $d>3$, yet there are other parameters to be considered as well, such as the number of parity bits.

We therefore first investigate the optimal parity code dimension for a given data size, with respect to the number of parity bits. As the results indicate that higher dimensions can be useful, we investigate higher dimensions with regard to the question of if they can correct a part of the 2-bit errors. To this end, we consider a variant that is only useful in higher dimensions: while the normal d-dimensional cross parity code computes parities from $(d-1)$-dimensional hyperplanes, we consider parities from $(d-2)$-dimensional hyperplanes. We have not been able to locate literature that investigates this variant. The first dimension where this is useful is $d=3$. 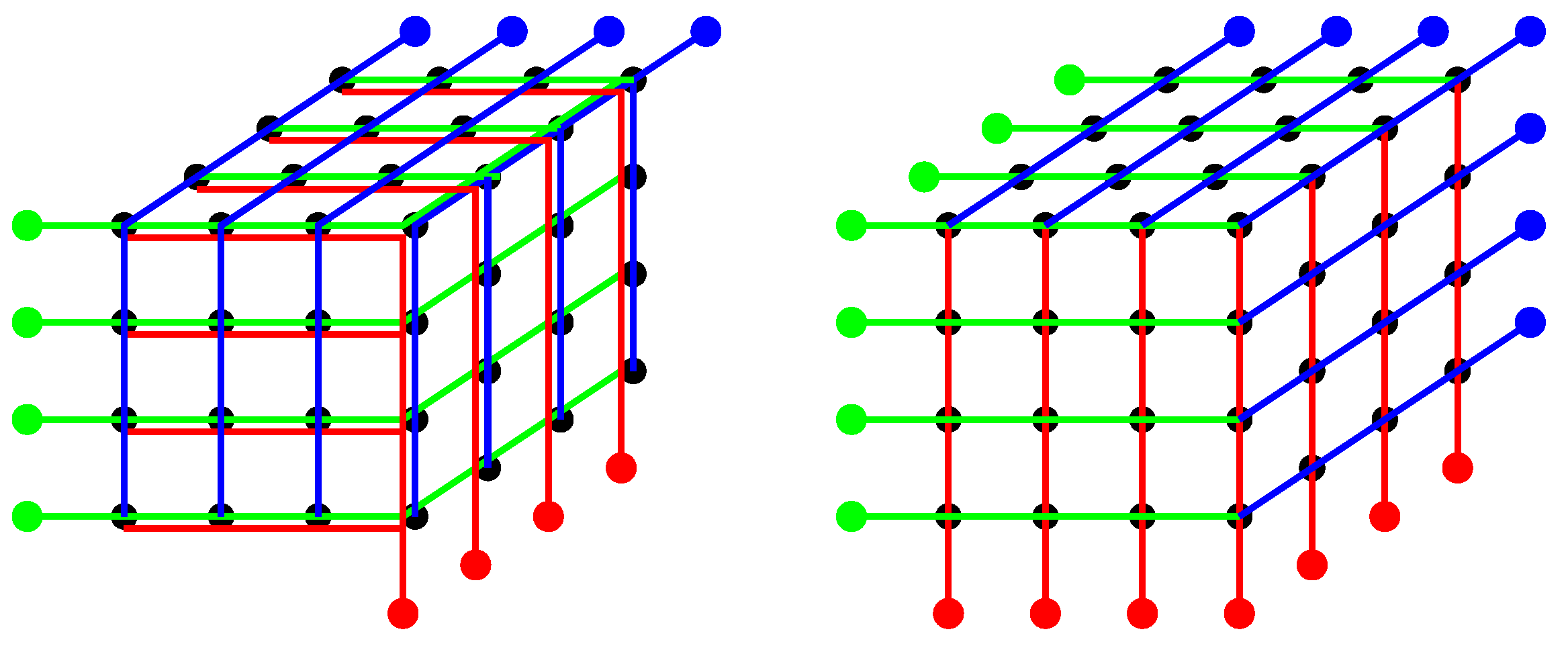Figure 1 depicts $64=4^3$ data bits arranged in a 3-dimensional cube. On the left side, the usual cross parity code with $3·4=12$ parity bits from 2-dimensional planes is shown. On the right side, 1-dimensional parities are used, resulting in $\left({\displaystyle \genfrac{}{}{0pt}{}{3}{2}}\right)·4^2=48$ parity bits. While the number of parity bits is much higher, the promise is that a larger fraction of 2-bit errors can be corrected.

Our analysis indicates that using higher-dimension parity codes can help to reduce the number of parity bits, and that with the proposed variant, all 2-bit errors can be corrected, in contrast to 2-dimensional parity codes.

The remainder of this article is structured as follows. Section 2 provides some background on cross parity codes. Section 3 demonstrates that cross parity codes of higher dimensions can reduce the number of parity bits needed and should therefore be investigated further. Section 4 investigates a variant that becomes possible with higher dimensions: computing the parities not from $(d-1)$-dimensional hyperplanes as usual, but using $(d-2)$-dimensional hyperplanes. Section 5 reports on simulation experiments. Section 6 discusses related work, and Section 7 provides conclusions and an outlook for future work.

2. Background

In this research, we consider error-correction codes, i.e., codes that add redundancy to information to be transmitted during channel coding to achieve forward error correction. The sender of the information adds the redundant information to form the message to be transmitted. The receiver of the message, i.e., information plus redundant information, can detect if an error in the form of one or several bit flips for binary information (on which we will focus) has occurred during transmission. For a limited number of bit flips, the receiver can even correct these errors, i.e., recover the original information. In particular, we consider systematic codes that leave the information (message) unchanged and merely add redundancy bits.

Let N be the number of information or data bits, to which T redundancy bits are added. Then, each data word $x\in {\{0,1\}}^N$ is extended by redundancy bits $c\left(x\right)\in {\{0,1\}}^D$ to form a code word $x,c\left(x\right)$ or message of length $N+T$ bits to be transmitted. Let $C=\left\{(x,c\left(x\right))\right|x\in {\{0,1\}}^N\}$ be the set of code words. The code distance $d_{min}$ is the minimum Hamming distance between any two different code words. Then, at least $d_{min}$ bit flips during transmission are necessary to convert a code word into another code word. If fewer than $d_{min}$ bit errors occur, this will be detected, as the receiver will not receive a valid code word, i.e., the receiver receives a tuple $(\tilde{x},\tilde{c})$ for which $\tilde{c}\ne c\left(\tilde{x}\right)$. Also, if fewer than $d_{min}/2$ bit flips occur, these errors can be corrected by the receiver by finding the unique code word $(x,c(x\left)\right)$ with a Hamming distance less than $\lfloor d_{min}/2\rfloor$ to the received tuple $(\tilde{x},\tilde{c})$. Block codes are often characterized by a tuple message length, information length, and code distance, possibly extended by the size of the alphabet used (2 in our case of binary information), i.e., ${(N+T,N,d_{min})}_2$.

As an example, we consider a ${(3,1,3)}_2$-code, i.e., $N=1$ data bit and $T=2$ redundancy bits. The redundancy bits simply replicate the data bit. Then, only two valid code words 000 and 111 exist with Hamming distance $d_{min}=3$. If 1 or 2 bit errors occur, e.g., errors on the first and last bits will convert 000 into 101, then this can be detected as no valid code word is received. However, in our example $\lfloor d_{min}/2\rfloor =1$, and therefore this 2-bit error cannot be corrected, as the unique code word with Hamming distance 1 from 101 will be 111.

As adding redundancy consumes part of the available bandwidth and thus reduces the effective bandwidth for message information, the code rate of an error-correction code [4], defined as $N/(N+T)$, is an important measure (next to the code distance, which defines the number of correctable and detectable errors) to compare codes. If the code rate is close to 1, then the overhead from the redundancy bits is not high.

A final measure to compare codes is the decoding time, i.e., the receiver’s effort to check if an error occurred during transmission and to correct it if possible. For some codes, the decoding can be quite complex and might even necessitate a software algorithm, cf. for instance the Berlekamp–Massey algorithm for Reed–Solomon Codes [4], while for cross parity codes (see below) it is very short and can be performed in hardware, which allows applications like error correction in memories.

An important class of error-correction block codes are linear codes that can be defined via a binary $(N+T)\times N$-matrix M, where for systematic codes the top part is the $N\times N$-identity matrix so that $x,c\left(x\right)=M·x$.

Please note that in many cases, one cannot choose the data size N arbitrarily. Hamming codes are linear codes where N is of the form $N=2^t-t-1$ and $T=t$ redundancy bits are added [4], resulting in a message of length $2^t-1$ and a code rate of $1-t/(2^t-1)$, which is close to 1. $d_{min}=3$, i.e., one error can be corrected and two errors can be detected. Our (3,1,3)-code above is the simplest form of a Hamming code. For BCH codes with 2-bit error correction (so-called double-error correction or DEC-BCH codes) [5], $N=2^t-2t-1$ data bits can be used and $T=2t$ redundancy bits are added. Please note that the number N of data bits is always slightly smaller than a power of 2, which means that the case where $N=2^u$, i.e., N is a power of 2, must be treated by using a code for $2^{u+1}-(u+1)-1$ data bits, where the remaining data bits are assumed to be 0, and there are $2(u+1)$ redundancy bits.

Let $N=n^d$ for integers $n\ge 2$ and $d\ge 3$. Let $I=\{0,\dots ,n-1\}$, $D=\{0,\dots ,d-1\}$ and $D^{\left(2\right)}=\{(k_1,k_2)\in D^2|k_1<k_2\}$.

Let $x\in {\left({\{0,1\}}^n\right)}^d$ be binary data of N bits in total, oriented in a d-dimensional cube of side length n. Each data bit is denoted as $x_{i_0,\dots ,i_{d-1}}$, where $i_j\in I$ for $j\in D$, in short: $x_{i_j:j\in D}$.

The usual cross parity code defines $d·n$ parity bits via all possible $(d-1)$-dimensional planes, of which there is n in each dimension and d dimensions to choose from:

$$\begin{array}{ccc}\hfill p_{k,l}& =& \sum _{i_j\in I:j\in D\setminus \left\{k\right\}}{x}_{i_j:j<k,l,i_j:j>k}\hfill \\ & =& \sum _{i_0,\dots ,i_{k-1},i_{k+1},\dots ,i_{d-1}\in I^{d-1}}{x}_{i_0,\dots ,i_{k-1},l,i_{k+1}\dots i_{d-1}}\hfill \end{array}$$

where $k\in D$, $l\in I$ and ∑ means addition modulo 2, i.e., exclusive or. The number of redundancy bits $T=dn$ is thus proportional to $N^{1/d}$ and thus notably higher than for Hamming or BCH codes. The resulting code rate is $n^d/(n^d+dn)$ and thus depends on the chosen dimension, see the next section.

All 1-bit errors can be corrected, and 2-bit errors can be detected, as the minimum code weight is $min(d+1,4)$ [2]. Yet, for $d=2$, no 2-bit errors can be corrected. This, however, can be achieved via an extension with a few additional parity bits [3].

3. Choosing Dimension

Wong and Shea [2] give the minimum code weight as $min(d+1,4)$, which seems to suggest that only dimensions $d=2$ and $d=3$ are of interest, and there is also no research known to us that systematically investigates parity codes of higher dimensions.

For a given N, the number of parity bits is solely a function of d. If we consider N a constant and $f\left(d\right)=d·N^{1/d}$ as a function on real d with domain $[2,{log}_{2}N]$, then we can calculate the derivation $f^{\prime }\left(d\right)=N^{1/d}-lnN·N^{1/d}/d$ and see that there is a $d^{*}$ in the domain with $f^{\prime }\left(d^{*}\right)=0$, and the sign of $f^{\prime }$ goes from negative to positive, i.e., f will be minimal at $d^{*}$. As d really is an integer, the minimum will be reached at either $\lceil d^{*}\rceil$ or $\lfloor d^{*}\rfloor$. Still, not all integral values of d might be possible because $n=N^{1/d}$ must also be integral as well, or at least nearly integral so as not to waste too many bits through using $\tilde{N}={\tilde{n}}^d$ with $\tilde{n}=\lceil N^{1/d}\rceil$ and ignoring $\tilde{N}-N$ bits.

As an example, we might consider again the $N=64$ data bits from Figure 1. If we arrange them in $d=2$ dimensions, we obtain $n=8$ and thus $d·n=2·8=16$ parity bits, i.e., more than for $d=3$, where we had 12 parity bits (cf. Section 1). Yet, an arrangement in $d=4$ dimensions with side length 3 is also possible. As $3^4=81$, we waste some bits, yet the number of parity bits is still $4·3=12$, and the “superfluous” bits could be ignored by assuming them to be 0 or could be used to add further redundancy. While $d=5$ seems not to be interesting as $2^5=32$ is too small and $3^5$ cannot be better than $3^4$, we finally consider $d=6$, leading to a cube of side length 2 with $2·6=12$ parity bits. The difference to smaller dimensions is that for $d=6$, each parity bit is computed over 32 data bits, while for $d=3$, each parity bit is computed over 16 data bits. The code rates for $d=2,3,4,6$ are $0.80,0.84,0.84,0.84$, respectively.

The following examples demonstrate that already for quite moderate values of N, the minimum number of parity bits is reached in higher dimensions, and the same holds if we use modified cross parity codes that add $2^d$ parity bits from half planes in each dimension (called quadrants for $d=2$ [3]) to be able to correct some of the 2-bit errors.

For $N=2^{10}=1024$, at least $d=2$ and $d=5$ are possible. The minimum is reached at $d^{*}\approx 7$, and the number of parity bits are 64 for $d=2$ yet only 20 for $d=5$, resulting in code rates of $0.94$ and $0.98$, respectively. For $N=2^{12}=4096$, at least $d=2,3,4,6$ are possible, as $d=5$ would lead to $\tilde{n}=6$ and $\tilde{N}=7776$, i.e., almost twice as large as N. The minimum is reached at $d^{*}\approx 8.3$; the function values are given in the upper row of

Table 1. Number of parity bits and code rates for $N=4096$ data bits depending on dimension d, with ($g\left(d\right)$) and without ($f\left(d\right)$) extended parities.

Dim.	No. Parity	Code	No. Ext.	Code
d	Bits  $\mathit{f}\left(\mathit{d}\right)$	Rate	Bits  $\mathit{g}\left(\mathit{d}\right)$	Rate
2	128	0.969	132	0.969
3	48	0.988	56	0.986
4	32	0.992	48	0.988
6	24	0.994	88	0.978

together with the achieved code rates.

If we add $2^d$ parity bits to obtain the extended cross parity code, function $g\left(d\right)=f\left(d\right)+2^d$ has the derivation $g^{\prime }\left(d\right)=f^{\prime }\left(d\right)+2^d·ln2$, which also goes from negative to positive in the domain. For $N=1024$, the number of parity bits is 68 for $d=2$ and 52 for $d=5$. For $N=4096$, the minimum is reached at $d^{*}\approx 3.85$. The number of parity bits is shown in the lower row of Table 1 together with the achieved code rates.

This observation indicates that parity codes of higher dimension deserve further investigation, e.g., with respect to their merits for extended cross parity codes.

We also see that these higher-dimensional cross parity codes are not impractical. While the code rates do not reach the level of a 2-bit correcting BCH code (26 redundancy bits for 4096 data bits, achieving code rate 0.994), they are also not far away and lead to simpler decoding functions.

4. Parities from ($d-2$)-Dimensional Hyperplanes

The usual cross parity codes compute parity from $(d-1)$-dimensional hyperplanes, which seems plausible for $d=2$ and $d=3$. However, as the previous section suggests, higher dimensions might also be of interest. Then, the question arises if parities from lower-dimensional hyperplanes also have some merit, although their number will be higher than in the usual cross parity code.

In this article, we consider parities from $(d-2)$-dimensional hyperplanes. As an example, one may imagine line parities in a cube for $d=3$ (cf. Figure 1(right)), which cover the three visible surfaces, i.e., there are $3n^2$ parity bits.

Formally, we define $\left({\displaystyle \genfrac{}{}{0pt}{}{d}{2}}\right)·n^2$ parity bits via

$$\begin{array}{ccc}\hfill p_{k_1,k_2,l_1,l_2}& =& \sum _{i_j\in I:j\in D\setminus \{k_1,k_2\}}{x}_{i_j:j<k_1,l_1,i_j:k_1<j<k_2,l_2,i_j:j>k_2}\hfill \\ & =& \sum _{i_0,\dots ,i_{k_1-1},i_{k_1+1},\dots ,i_{k_2-1},i_{k_2+1},\dots i_{d-1}\in I^{d-2}}{x}_{i_0,\dots ,i_{k_1-1},l_1,i_{k_1+1},\dots ,i_{k_2-1},l_2,i_{k_2+1},\dots i_{d-1}}\hfill \end{array}$$

where $(k_1,k_2)\in D^{\left(2\right)}$ and $l_1,l_2\in I$.

Please note that in the following, we do not consider bit errors on parity bits, and hence do not specify how these are protected. As protecting the parity bits can be performed in the same manner as for data bits (yet with a smaller size and smaller dimension), we see this as acceptable.

If a single bit error occurs in bit $x_{i_0,\dots ,i_{d-1}}$, then this shows in $\left({\displaystyle \genfrac{}{}{0pt}{}{d}{2}}\right)$ parities: for each $(k_1,k_2)\in D^{\left(2\right)}$, it shows in $p_{k_1,k_2,i_{k_1},i_{k_2}}$.

More formally, the receiver computes

$$\Delta p_{k_1,k_2,l_1,l_2}=p_{k_1,k_2,l_1,l_2}+\sum _{i_j\in I:j\in D\setminus \{k_1,k_2\}}{x}_{i_j:j<k_1,l_1,i_j:k_1<j<k_2,l_2,i_j:j>k_2}$$

(1)

for each $(k_1,k_2)\in D^{\left(2\right)}$ and $l_1,l_2\in I$, and for each $i_0,\dots ,i_{d-1}\in I^d$ computes

$$\Delta x_{i_0,\dots ,i_{d-1}}=\prod _{(k_1,k_2)\in D^{\left(2\right)}}\Delta p_{k_1,k_2,i_{k_1},i_{k_2}}.$$

(2)

For completeness, i.e., to separate from multi-bit errors, one could additionally multiply with $\overline{\Delta p_{k_1,k_2,l_1,l_2}}$, where either $l_1\ne k_1$ or $l_2\ne k_2$, or both, for all $(k_1,k_2)\in D^{\left(2\right)}$.

In the case of a single bit error in bit $x_{i_0,\dots ,i_{d-1}}$, $\Delta x_{i_0,\dots ,i_{d-1}}=1$ and all $\Delta x_{i_0^{\prime },\dots ,i_{d-1}^{\prime }}=0$ for $(i_0^{\prime },\dots ,i_{d-1}^{\prime })\in I^d\setminus \left\{(i_0,\dots ,i_{d-1})\right\}$.

Assume as an example that two-bit errors occur at two bits on a line in one of the dimensions, w.l.o.g. $x_{2,i_1,\dots ,i_{d-1}}$ and $x_{3,i_1,\dots ,i_{d-1}}$. The errors show in parities $\Delta p_{0,k_2,2,i_{k_2}}$ and $\Delta p_{0,k_2,3,i_{k_2}}$ for each $k_2\in D\setminus \left\{0\right\}$. These errors can be distinguished from 1-bit errors and thus corrected.

Now assume the general case that two-bit errors occur at $x_{i_0,\dots ,i_{d-1}}$ and $x_{i_0^{\prime },\dots ,i_{d-1}^{\prime }}$, where $i_j\ne i_j^{\prime }$ for $j\in J\subseteq D$ and $i_j=i_j^{\prime }$ for $j\in D\setminus J$. Please note that $J\ne \varnothing$, because otherwise $(i_0,\dots ,i_{d-1})=(i_0^{\prime },\dots ,i_{d-1}^{\prime })$, yet all sets J with $1\le \left|J\right|\le d$ are possible. The case $\left|J\right|=1$ has been treated in the example; thus, we assume $\left|J\right|\ge 2$ in the sequel.

For $k_1,k_2\in D\setminus J$ with $k_1<k_2$ (if $|D\setminus J|\ge 2$), all $\Delta p_{k_1,k_2,l_1,l_2}=0$, as for $l_1=i_{k_1}$ and $l_2=i_{k_2}$ both errors are counted, and none are counted otherwise.

For $k_1,k_2\in J$ with $k_1<k_2$, $\Delta p_{k_1,k_2,i_{k_1},i_{k_2}}=1$ and $\Delta p_{k_1,k_2,i_{k_1}^{\prime },i_{k_2}^{\prime }}=1$, while $\Delta p_{k_1,k_2,l_1,l_2}=0$ for $(l_1,l_2)\ne (i_{k_1},i_{k_2})$ and $(l_1,l_2)\ne (i_{k_1}^{\prime },i_{k_2}^{\prime })$.

For $k_1\in J$ and $k_2\in D\setminus J$ with $k_1<k_2$ (if $|D\setminus J|\ge 1$), $\Delta p_{k_1,k_2,i_{k_1},i_{k_2}}=1$ and $\Delta p_{k_1,k_2,i_{k_1}^{\prime },i_{k_2}^{\prime }}=1$, while $\Delta p_{k_1,k_2,l_1,l_2}=0$ for $(l_1,l_2)\ne (i_{k_1},i_{k_2})$ and $(l_1,l_2)\ne (i_{k_1}^{\prime },i_{k_2}^{\prime })$ (please note that $i_{k_2}=i_{k_2}^{\prime }$ here).

The same holds for $k_2\in J$ and $k_1\in D\setminus J$ with $k_1<k_2$.

Thus, for each $k\in J$, the following $2(d-1)$ parities have value 1: $\Delta p_{k_1,k,i_{k_1},i_k}=1$ and $\Delta p_{k_1,k,i_{k_1}^{\prime },i_k^{\prime }}=1$ for $k_1=0,\dots ,k-1$, and $\Delta p_{k,k_2,i_k,i_{k_2}}=1$ and $\Delta p_{k,k_2,i_k^{\prime },i_{k_2}^{\prime }}=1$ for $k_2=k+1,\dots ,d-1$.

For each pair $(k_1,k_2)\in D^{\left(2\right)}$ with $k_1,k_2\in J$, parities $\Delta p_{k_1,k_2,...}$ are counted twice, so that the total number of parities with value 1 is $2(d-1)\left|J\right|-2\left({\displaystyle \genfrac{}{}{0pt}{}{\left|J\right|}{2}}\right)$.

From the number of $\Delta p$ with value 1, the different sizes of J can be distinguished, and for a particular size of J, the different possibilities for J that correspond to the different error positions can be distinguished. Thus, 2-bit errors are correctable.

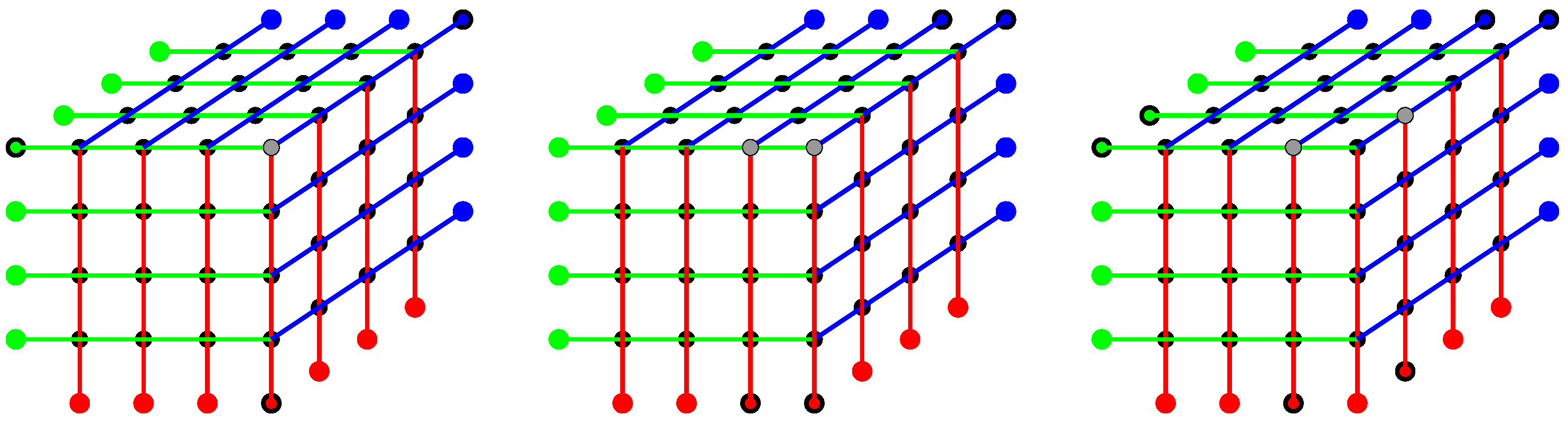
We illustrate this with our example from the right side of Figure 1. For one error, e.g., on the upper right front corner, three line parity bits (one in each dimension) do not match the re-computed parities, cf. the left side of Figure 2. If two errors occur in a line, e.g., on the upper right front corner and left to it, four line parity bits do not match the re-computed parities, cf. mid of Figure 2. If two errors occur yet not in a line, e.g., the two neighbors of the upper right corner, then six parity bits are affected, cf. right side of Figure 2. If we switch the error bits to the other two data bits in the $2\times 2$-square on the top right, then the affected parities in blue and green would remain the same, yet the red parities would differ.

The code rates for such cross parity codes from $(d-2)$-dimensional hyperplanes for different values of N and the value $d_{opt}$ of the dimension that leads to best code rate for the given N are depicted in

Table 2. Code rates for $N=64$, 256, 1024 and 4096 data bits and cross parity codes using $(d-2)$-dimensional data hyperplanes with code rate-optimal dimension $d_{opt}\in \{3,\dots ,6\}$ for given N.

No. Data Bits N	${\mathit{d}}_{\mathbf{opt}}$	Code Rate
64	3	0.571
256	4	0.727
1024	5	0.865
4096	6	0.945

. The code rates at least for the largest value of N are competitive with DEC-BCH codes (0.945 vs. 0.994), given that decoding for cross parity codes is quite fast.

5. Simulation Experiments

We implemented a simulation for $n=4$ and $d=3$, i.e., $N=4^3=64$ data bits. We systematically injected all possible 1-bit and 2-bit errors and computed the error syndromes. We found that each syndrome is unique, i.e., that all 1-bit and 2-bit errors can be recognized and distinguished and thus are correctable.

The simulation starts by computing the parity bits of a data word by the sender, i.e., by computing the code word. Then, all 64 possible 1-bit error positions and all 2016 2-bit error positions are enumerated. Each error is injected at the pre-computed position by the sender, the modified code word is given to the receiver, and then the parity bits are re-computed by the receiver. More exactly, in each case the receiver computes and stores the 48 $\Delta p$ values according to Equation (1) and the 48 $\Delta x$ values according to Equation (2). When this has been performed for all errors, the receiver checks if for any pair of errors, the subsets of the $\Delta p$s with values 1 are equal. If this occurs, these two errors cannot be distinguished. As this does not occur, the receiver matches each subset with the position(s) of the injected error(s) that lead to this subset. If the same subset occurs in the future, then the receiver can flip the data bits at the error positions and thus correct the error.

6. Related Work

There are only few works that deal with cross parity codes.

While already Rubinoff [1] mentions n-dimensional codes, he neither discusses the choice of dimension nor the use of lower-dimensional planes for parities.

Hsiao and Tou [6] compare parity codes with other error-correcting codes but do not seem to go beyond three dimensions.

Wong et al. [2] mention that they performed experiments with higher dimensions, but they also do not discuss the choice of dimension nor the use of lower-dimensional planes for parities.

Poolakkaparambil et al. [7] combine other types of block codes with cross parity codes, yet also seem not discuss higher dimensions.

Interestingly, Vertat and Dudacek [8] define 3-dimensional parity codes with 2-dimensional planes of 1-dimensional line parities, yet do not analyze them but construct 5-dim. and 6-dimensional parity codes as 2-dim. and 3-dimensional constructions, respectively, of those 3-dimensional building blocks with additional parity blocks, i.e., they perform a hierarchical construction.

Standard textbooks like Lin and Costello [4] or Tomlinson et al. [9] do not discuss them in detail.

7. Conclusions

Cross parity codes have been used for a long time, but a systematic investigation of parity codes in higher dimensions seems missing. As a first result, we have demonstrated that higher dimensions can help to reduce the number of parity bits to achieve competitive code rates, and are thus a useful field for further studies, especially in view of extended cross parity codes that can correct at least part of 2-bit errors.

Beyond this, we have investigated a variant that is only possible for higher dimensions. Instead of computing parity bits from $(d-1)$-dimensional hyperplanes, we presented parities from $(d-2)$-dimensional hyperplanes. While this increases the number of parity bits, we demonstrated that—in contrast to 2-dimensional parity codes—2-bit errors can be corrected, and code rates are competitive with DEC-BCH codes, at least for large N.

Future work will comprise more detailed investigations on higher-dimensional codes with respect to their behavior on burst errors, their potential for extensions like [3], and the possibilities to reduce the number of parity bits, e.g., by using $(d-2)$-dimensional hyperplanes only in some dimensions and $(d-1)$-dimensional hyperplanes to compute fewer parity bits in the remaining dimensions. This might be further improved by moving from cubes to cuboids, i.e., having different side lengths in different dimensions: a smaller side length in dimensions with $(d-2)$-dimensional hyperplanes will help to further reduce the number of parity bits.