SMS3D: 3D Synthetic Mushroom Scenes Dataset for 3D Object Detection and Pose Estimation
Abstract
1. Introduction
- We introduce a novel synthetic dataset generation pipeline tailored for the mushroom industry, providing detailed annotations for various computer vision tasks.
- Our data generation pipeline uses real 3D-scanned mushroom models and high-resolution soil images, enhancing dataset relevance.
- We validate our dataset through quantitative and qualitative analysis, benchmarking machine learning models on relevant tasks to demonstrate its potential for advancing automation in the mushroom industry.
- We propose a state-of-the-art 3D object detection and pose estimation pipeline for use in robotic mushroom harvesting applications.
2. Related Work
2.1. Mushroom Detection and Segmentation in Agriculture
2.2. Synthetic Datasets for Agricultural Applications
2.3. 3D Pose Estimation Using Point Clouds
2.4. Deep Learning Models for Point Cloud Processing
2.5. Pose Estimation with RGB-D Data
2.6. Robotic Systems for Mushroom Harvesting
2.7. Limitations of Existing Works and Our Contributions
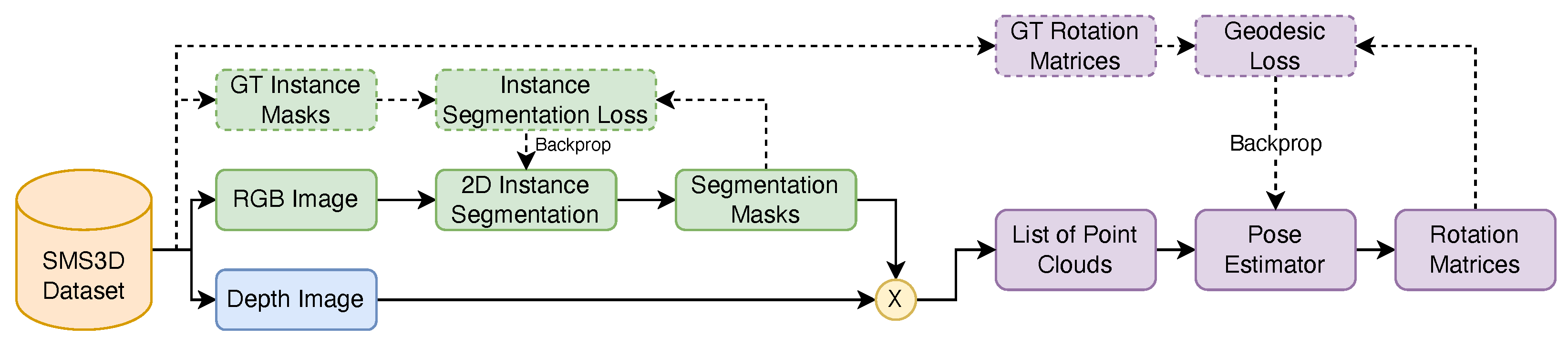
3. Methodology
3.1. Synthetic Scene Generation
3.1.1. Ground Plane Generation
- A is the amplitude controlling the height variation;
- s is the scaling factor affecting the frequency of the noise;
- is the base elevation (set to zero in our case);
- is the Perlin noise function, defined as follows:where
- -
- O is the number of octaves controlling the level of detail;
- -
- p is the persistence determining the amplitude reduction at each octave;
- -
- is a smooth noise function.
3.1.2. Mushroom Placement
- Roll (): sampled from a Gaussian distribution .
- Pitch (): sampled from a Gaussian distribution .
- Yaw (): uniformly sampled from .
3.1.3. Mushroom Placement Algorithm
| Algorithm 1 Mushroom Placement Process. |
Output Ground plane mesh, list of mushroom models, maximum attempts M, overlap threshold
|
- M is the maximum placement attempts (set to 100) to balance computational cost and placement success;
- is the overlap threshold (5% IoU), ensuring minimal collisions, where larger can yield unrealistic overlaps and stricter thresholds reduce feasibility;
- Transformations (position, orientation, size) ensure unique, realistic mushroom instances;
- Collision detection uses mesh intersection volumes, checked against .
3.2. Pose Estimation Model Training
4. Results
4.1. Evaluation of Pose Estimation
4.1.1. Effect of Number of Points
4.1.2. Effect of Rotation Representation
4.1.3. Effect of Including RGB Information
4.1.4. Model Performance and Inference Time
4.1.5. Final Model Performance
4.1.6. Comparison with State-of-the-Art Methods
- The use of the 6D rotation representation with the Gram–Schmidt process ensures continuity and avoids the ambiguities inherent in other representations, facilitating more accurate rotation predictions.
- The adoption of the Point Transformer network [15] allows for the effective capture of both local and global geometric features within the point cloud data through self-attention mechanisms.
- The combination of 2D object detection and instance segmentation with 3D pose estimation isolates individual mushrooms, reducing the complexity introduced by overlapping objects and background clutter.
- Extensive training on a comprehensive synthetic dataset that closely mimics real-world conditions enhances the model’s generalization capabilities.
4.2. 2D Object Detection and Instance Segmentation Results
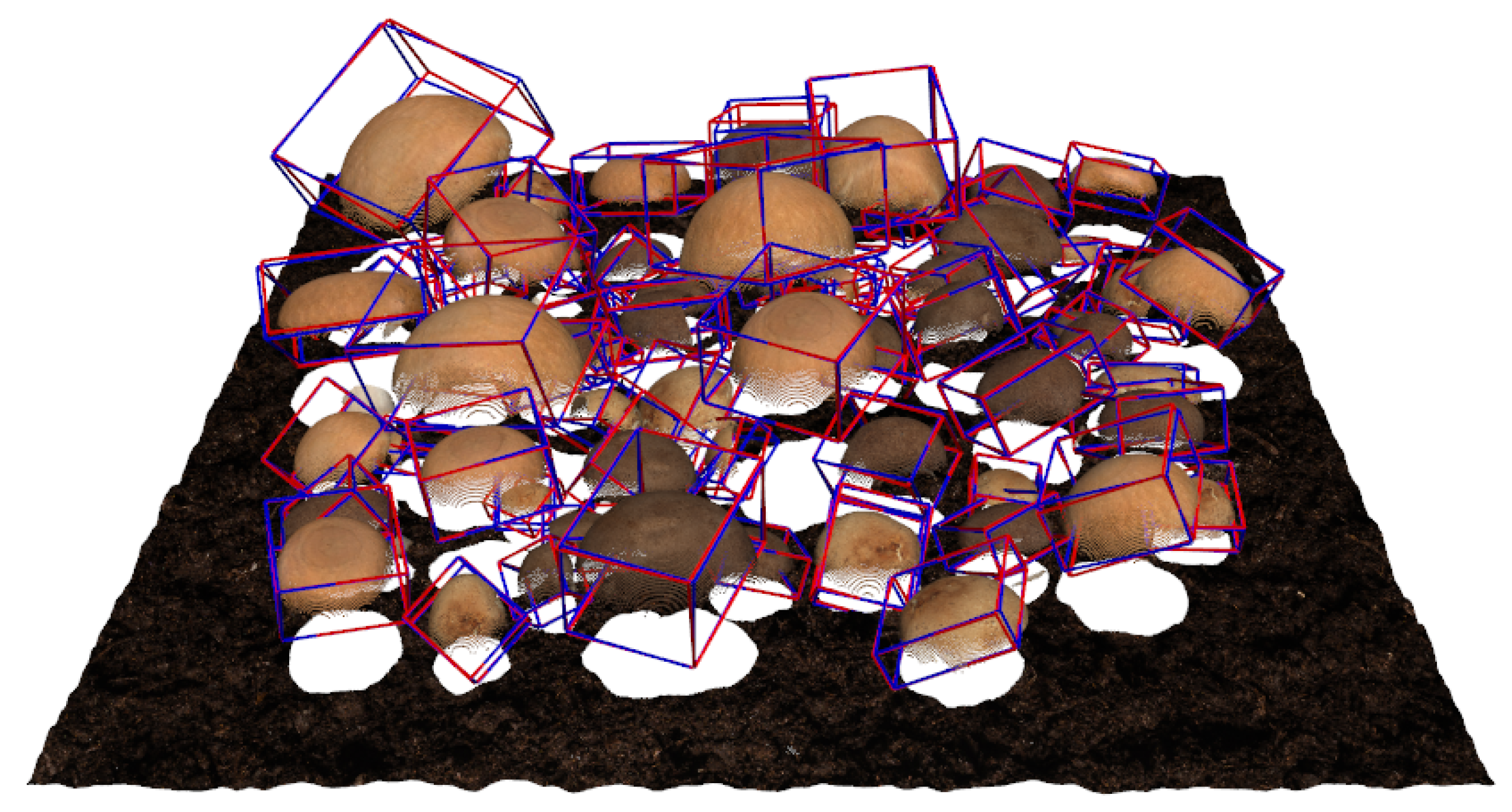
4.3. Application to Real-World Data
4.3.1. Quantitative Evaluation on Real M18K Images
4.3.2. Qualitative Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Anagnostopoulou, D.; Retsinas, G.; Efthymiou, N.; Filntisis, P.; Maragos, P. A Realistic Synthetic Mushroom Scenes Dataset. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Vancouver, BC, Canada, 17–24 June 2023. [Google Scholar] [CrossRef]
- Retsinas, G.; Efthymiou, N.; Maragos, P. Mushroom Segmentation and 3D Pose Estimation From Point Clouds Using Fully Convolutional Geometric Features and Implicit Pose Encoding. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023. [Google Scholar]
- Wee, B.S.; Chin, C.S.; Sharma, A. Survey of Mushroom Harvesting Agricultural Robots and Systems Design. IEEE Trans. Agrifood Electron. 2024, 2, 59–80. [Google Scholar] [CrossRef]
- Qian, Y.; Jiacheng, R.; Pengbo, W.; Zhan, Y.; Changxing, G. Real-time detection and localization using SSD method for oyster mushroom picking robot. In Proceedings of the 2020 IEEE International Conference on Real-Time Computing and Robotics (RCAR), Asahikawa, Japan, 28–29 September 2020; pp. 158–163. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, J.; Yuan, J. A High-Accuracy Contour Segmentation and Reconstruction of a Dense Cluster of Mushrooms Based on Improved SOLOv2. Agriculture 2024, 14, 1646. [Google Scholar] [CrossRef]
- Shi, C.; Mo, Y.; Ren, X.; Nie, J.; Zhang, C.; Yuan, J.; Zhu, C. Improved Real-Time Models for Object Detection and Instance Segmentation for Agaricus bisporus Segmentation and Localization System Using RGB-D Panoramic Stitching Images. Agriculture 2024, 14, 735. [Google Scholar] [CrossRef]
- Zakeri, A.; Fawakherji, M.; Kang, J.; Koirala, B.; Balan, V.; Zhu, W.; Benhaddou, D.; Merchant, F.A. M18K: A Comprehensive RGB-D Dataset and Benchmark for Mushroom Detection and Instance Segmentation. arXiv 2024, arXiv:cs.CV/2407.11275. [Google Scholar]
- Károly, A.I.; Galambos, P. Automated Dataset Generation with Blender for Deep Learning-based Object Segmentation. In Proceedings of the 2022 IEEE 20th Jubilee World Symposium on Applied Machine Intelligence and Informatics (SAMI), Poprad, Slovakia, 2–5 March 2022. [Google Scholar] [CrossRef]
- Cieslak, M.; Govindarajan, U.; Garcia, A.; Chandrashekar, A.; Hädrich, T.; Mendoza-Drosik, A.; Michels, D.L.; Pirk, S.; Fu, C.C.; Pałubicki, W. Generating Diverse Agricultural Data for Vision-Based Farming Applications. In Proceedings of the 2024 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Seattle, WA, USA, 17–18 June 2024. [Google Scholar] [CrossRef]
- Gao, G.; Lauri, M.; Wang, Y.; Hu, X.; Zhang, J.; Frintrop, S. 6D Object Pose Regression via Supervised Learning on Point Clouds. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020. [Google Scholar] [CrossRef]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. PointNet++: Deep hierarchical feature learning on point sets in a metric space. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Red Hook, NY, USA, 4–9 December 2017. NIPS’17. [Google Scholar]
- Dang, Z.; Wang, L.; Guo, Y.; Salzmann, M. Learning-Based Point Cloud Registration for 6D Object Pose Estimation in the Real World. In Proceedings of the Computer Vision–ECCV 2022; Avidan, S., Brostow, G., Cissé, M., Farinella, G.M., Hassner, T., Eds.; Springer: Cham, Germany, 2022. [Google Scholar] [CrossRef]
- Chen, W.; Duan, J.; Basevi, H.; Chang, H.J.; Leonardis, A. PointPoseNet: Point Pose Network for Robust 6D Object Pose Estimation. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Snowmass Village, CO, USA, 1–5 March 2020. [Google Scholar]
- Charles, R.Q.; Su, H.; Kaichun, M.; Guibas, L.J. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar] [CrossRef]
- Zhao, H.; Jiang, L.; Jia, J.; Torr, P.H.; Koltun, V. Point Transformer. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, BC, Canada, 10–17 October 2021; pp. 16259–16268. [Google Scholar]
- Soltan, S.; Oleinikov, A.; Demirci, M.F.; Shintemirov, A. Deep Learning-Based Object Classification and Position Estimation Pipeline for Potential Use in Robotized Pick-and-Place Operations. Robotics 2020, 9, 63. [Google Scholar] [CrossRef]
- Baisa, N.L.; Al-Diri, B. Mushrooms Detection, Localization and 3D Pose Estimation using RGB-D Sensor for Robotic-picking Applications. arXiv 2022. [Google Scholar] [CrossRef]
- Mavridis, P.; Mavrikis, N.; Mastrogeorgiou, A.; Chatzakos, P. Low-cost, accurate robotic harvesting system for existing mushroom farms. In Proceedings of the 2023 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Seattle, WA, USA, 27 June–1 July 2023. [Google Scholar] [CrossRef]
- Lin, A.; Liu, Y.; Zhang, L. Mushroom Detection and Positioning Method Based on Neural Network. In Proceedings of the 2021 IEEE 5th Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 12–14 March 2021; Volume 5, pp. 1174–1178. [Google Scholar] [CrossRef]
- Development of a Compact Hybrid Gripper for Automated Harvesting of White Button Mushroom. Volume 7: 48th Mechanisms and Robotics Conference (MR). In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Washington, DC, USA, 25–28 August 2024; Available online: https://asmedigitalcollection.asme.org/IDETC-CIE/proceedings-pdf/IDETC-CIE2024/88414/V007T07A036/7403466/v007t07a036-detc2024-143056.pdf (accessed on 31 January 2025). [CrossRef]
- Koirala, B.; Kafle, A.; Nguyen, H.C.; Kang, J.; Zakeri, A.; Balan, V.; Merchant, F.; Benhaddou, D.; Zhu, W. A Hybrid Three-Finger Gripper for Automated Harvesting of Button Mushrooms. Actuators 2024, 13, 287. [Google Scholar] [CrossRef]
- Koirala, B.; Zakeri, A.; Kang, J.; Kafle, A.; Balan, V.; Merchant, F.A.; Benhaddou, D.; Zhu, W. Robotic Button Mushroom Harvesting Systems: A Review of Design, Mechanism, and Future Directions. Appl. Sci. 2024, 14, 9229. [Google Scholar] [CrossRef]
- Zhou, Y.; Barnes, C.; Lu, J.; Yang, J.; Li, H. On the Continuity of Rotation Representations in Neural Networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Perlin, K. An Image Synthesizer; ACM SIGGRAPH Computer Graphics: New York, NY, USA, 1985; Volume 19, pp. 287–296. [Google Scholar] [CrossRef]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask R-CNN. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2980–2988. [Google Scholar] [CrossRef]
- Huynh, D.Q. Metrics for 3D Rotations: Comparison and Analysis. J. Math. Imaging Vis. 2009, 35, 155–164. [Google Scholar] [CrossRef]
- Retsinas, G.; Efthymiou, N.; Anagnostopoulou, D.; Maragos, P. Mushroom Detection and Three Dimensional Pose Estimation from Multi-View Point Clouds. Sensors 2023, 23, 3576. [Google Scholar] [CrossRef] [PubMed]










| Number of Points | Geodesic Loss Value | Mean (degrees) | Inference Time (ms) |
|---|---|---|---|
| 64 | 0.628 | 11.99 | 2.561 |
| 256 | 0.505 | 9.64 | 3.481 |
| 1024 | 0.421 | 8.04 | 5.536 |
| Rotation Representation | Geodesic Loss Value | Mean (degrees) |
|---|---|---|
| 6D Gram–Schmidt | 0.421 | 8.04 |
| 9D Rotation Matrix | 1.595 | 30.46 |
| Quaternion | 0.622 | 11.88 |
| Euler Angles | 1.169 | 22.33 |
| Model Configuration | Geodesic Loss Value | Mean (degrees) |
|---|---|---|
| Without RGB | 0.421 | 8.04 |
| With RGB | 1.610 | 30.75 |
| Method | IoU Threshold | (degrees) |
|---|---|---|
| Retsinas et al. [2] | 25% | 4.22 |
| Baisa and Al-Diri [17] | - | 13.5 |
| Retsinas et al. [27] | 25% | 8.70 |
| Retsinas et al. [27] | 50% | 7.27 |
| This Work (Synthetic) | - | 1.67 |
| This Work (Real, 10 Images) | - | 3.68 |
| Dataset | Detection | Segmentation | ||||
|---|---|---|---|---|---|---|
| F1 | AP | AR | F1 | AP | AR | |
| SMS3D | 0.927 | 0.901 | 0.955 | 0.919 | 0.907 | 0.933 |
| M18K | 0.891 | 0.876 | 0.905 | 0.881 | 0.866 | 0.896 |
| M18K (Pre-Trained on SMS3D) | 0.905 | 0.889 | 0.922 | 0.915 | 0.901 | 0.931 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zakeri, A.; Koirala, B.; Kang, J.; Balan, V.; Zhu, W.; Benhaddou, D.; Merchant, F.A. SMS3D: 3D Synthetic Mushroom Scenes Dataset for 3D Object Detection and Pose Estimation. Computers 2025, 14, 128. https://doi.org/10.3390/computers14040128
Zakeri A, Koirala B, Kang J, Balan V, Zhu W, Benhaddou D, Merchant FA. SMS3D: 3D Synthetic Mushroom Scenes Dataset for 3D Object Detection and Pose Estimation. Computers. 2025; 14(4):128. https://doi.org/10.3390/computers14040128
Chicago/Turabian StyleZakeri, Abdollah, Bikram Koirala, Jiming Kang, Venkatesh Balan, Weihang Zhu, Driss Benhaddou, and Fatima A. Merchant. 2025. "SMS3D: 3D Synthetic Mushroom Scenes Dataset for 3D Object Detection and Pose Estimation" Computers 14, no. 4: 128. https://doi.org/10.3390/computers14040128
APA StyleZakeri, A., Koirala, B., Kang, J., Balan, V., Zhu, W., Benhaddou, D., & Merchant, F. A. (2025). SMS3D: 3D Synthetic Mushroom Scenes Dataset for 3D Object Detection and Pose Estimation. Computers, 14(4), 128. https://doi.org/10.3390/computers14040128











