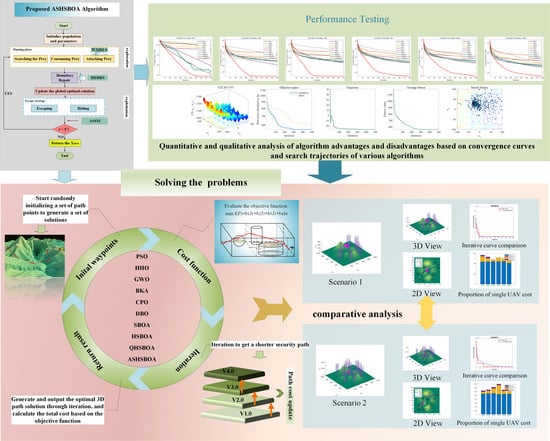
Simulation Application of Adaptive Strategy Hybrid Secretary Bird Optimization Algorithm in Multi-UAV 3D Path Planning
Abstract
1. Introduction
- A novel Adaptive Strategy Hybrid Secretary Bird Optimization Algorithm (ASHSBOA) is proposed, which integrates three innovative improvement strategies into the original Secretary Bird Optimization Algorithm (SBOA). This enhancement aims to boost the algorithm’s capability in solving practical application problems.
- The ASHSBOA is subjected to multi-angle and multi-time tests on two sets of benchmark functions, namely CEC2017 and CEC2022, to evaluate its performance both quantitatively and qualitatively. Additionally, the Wilcoxon test and the Friedman test are serviced to assess the statistically significant differences between the ASHSBOA and the others.
- A multi-UAV path planning model is constructed to test the performance of ASHSBOA in real-world application issues.
2. Related Work
3. Preliminary
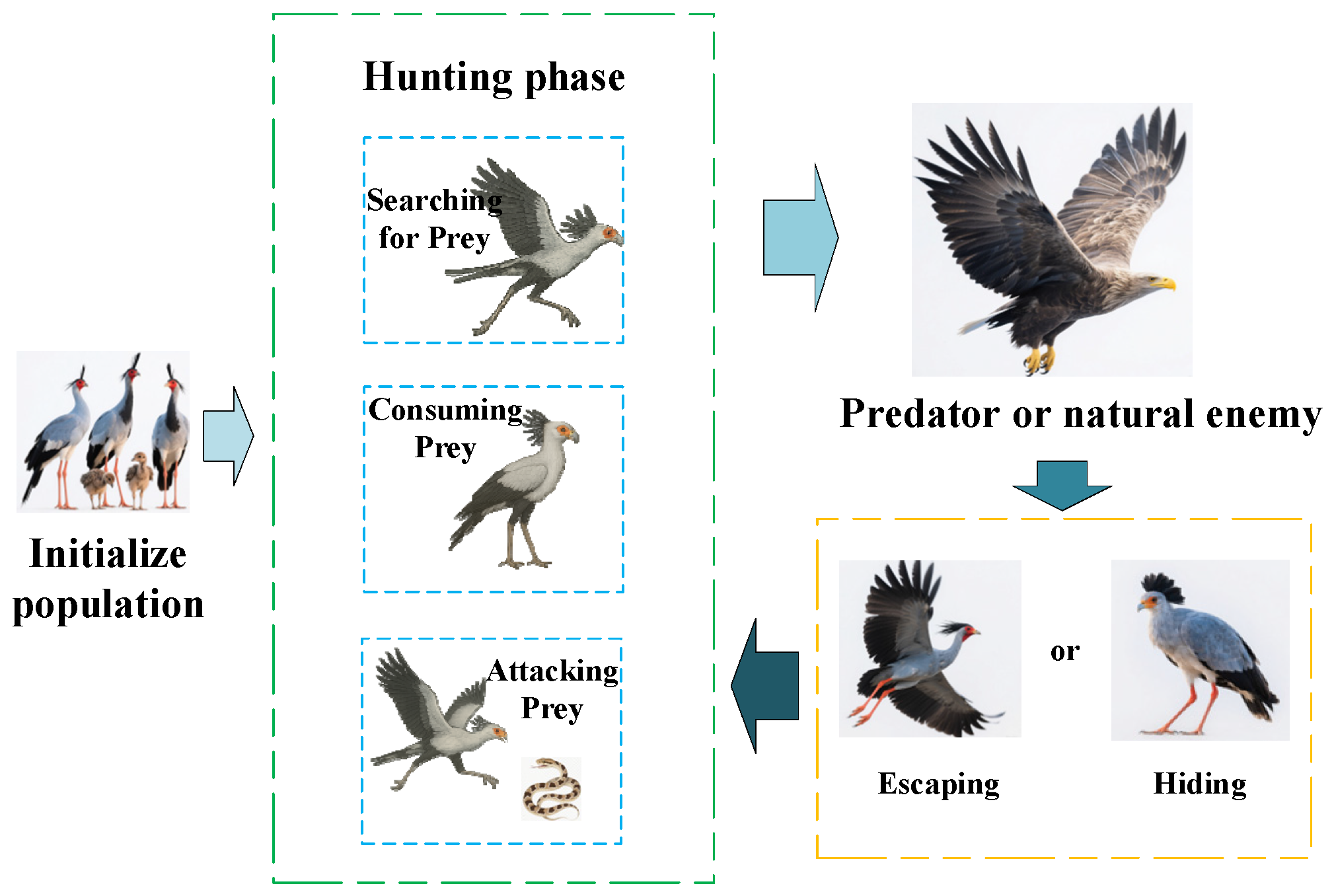
3.1. Secretary Bird Optimization Algorithm
3.1.1. Initialization
3.1.2. Exploration Phase (Hunting Strategy)
3.1.3. Exploitation Phase (Escape Strategy)
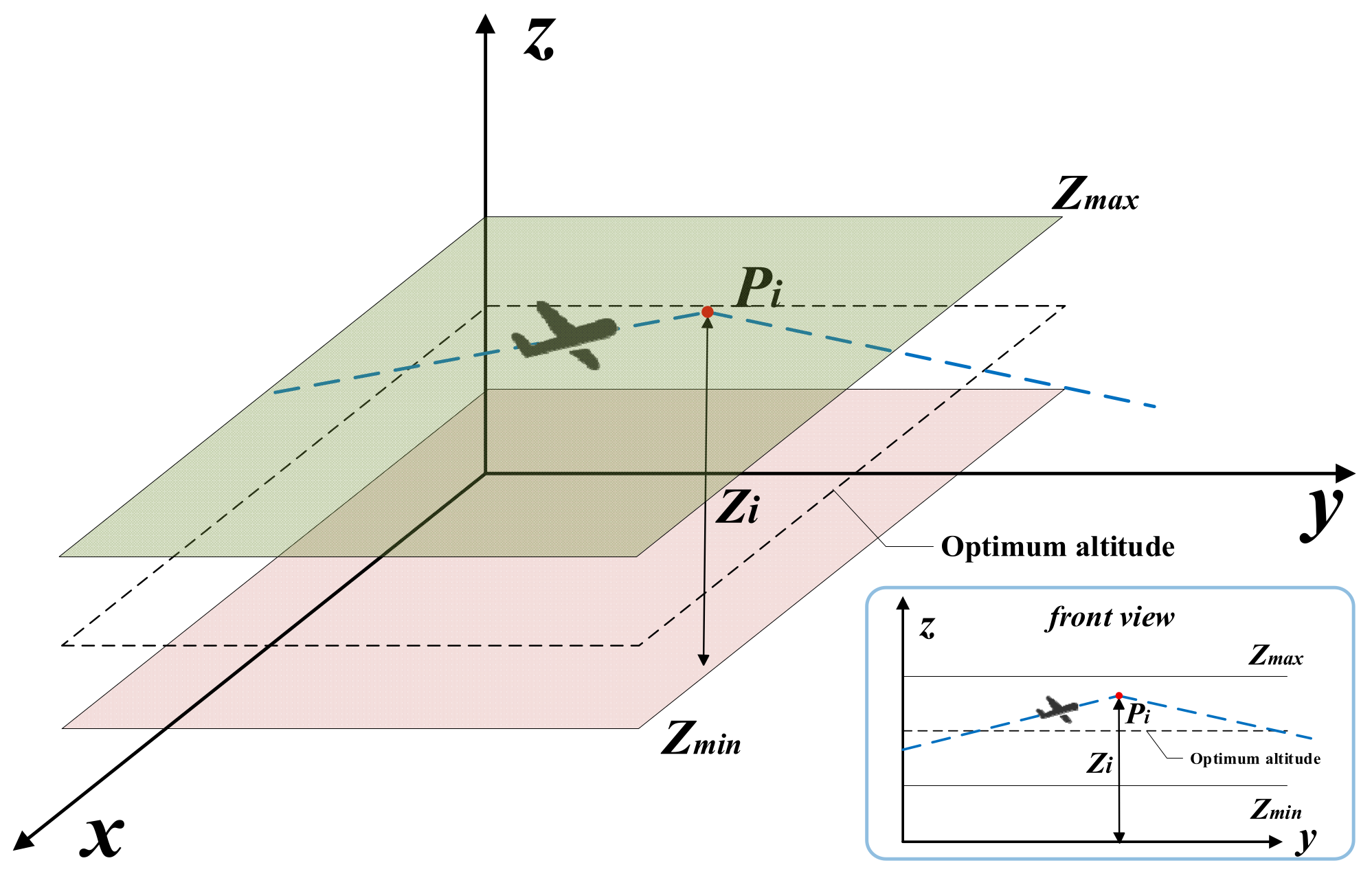
3.2. Multi-UAV Path Planning Model
3.2.1. Path Length Cost
3.2.2. Threat and Obstacle Avoidance Costs
3.2.3. High Deviation Cost
3.2.4. Smoothness Costs
- is the objective function;
- , , , are the weight coefficients;
- , , , are the sub-objectives.
4. Proposed Algorithm
4.1. Weighted Multi-Directional Dynamic Learning Strategy (WMDLS)
4.2. Adaptive Strategy Selection Mechanism (ASSM)
4.3. Hybrid Elite-Guided Boundary Repair Strategy (HEBRS)
- (1)
- Elite-Guided repair (40% probability): pulls the transgressing dimension towards the global optimal solution, as in Equation (27).
- (2)
- Reflection processing (40% probability): simulates physical reflection behavior as in Equation (28).
- (3)
- Random reset (20% probability): random initialization of the severely out-of-bounds dimension, as in Equation (29).
4.4. Pseudocode
| Algorithm 1: ASHSBOA (Adaptive Strategy Hybrid Secretary Bird Optimization Algorithm) |
| Input: population size: N; problem dimension: D; search boundary: [lb, ub]; max iterations: T; fitness function: f(x) Output: Optimal position: X_best |
| 1. Initialize population X[i] for i = 1 … N with random values in [lb, ub] 2. Evaluate f(X[i]), set Xbest 3. p_search = 1/3, p_approach = 1/3, p_attack = 1/3. // Initialize strategy probabilities 4. Initialize counters for strategy adaptation (success and failure) 5. learning_period = L 6. for t = 1 to T: 7. for each individual i = 1 to N: 8. // Adaptive Strategy Selection (Equation (26)) 9. r = random(0, 1) 10. if r < p_search: 11. // Search Prey Stage (exploration) 12. X_new = SearchPreyUpdate(X, i) 13. elif r < p_search + p_approach: 14. // Approach Prey Stage (transition) 15. X_new = ApproachPreyUpdate(X, i, X_best) 16. else: 17. // Apply Weighted Multi-directional Dynamic Learning Strategy: (Equation (24)) 18. Let X_best = global best, X_worst = worst in population 19. Let X_r1, X_r2 = two random distinct individuals 20. Compute adaptive weights w1 … w4 // per Equation (25) 21. Update individual position: X_new 22. f_new = Fitness(X_new) 23. // Record success/failure for strategy adaptation 24. if f_new < f(X[i]): 25. if r <= p_search: succ_search += 1 26. elif r <= p_search + p_approach: succ_approach += 1 27. else: succ_attack += 1 28. else: 29. if r <= p_search: fail_search += 1 30. elif r <= p_search + p_approach: fail_approach += 1 31. else: fail_attack += 1 32. if f_new < f(X[i]): 33. X[i] = X_new 34. f(X[i]) = f_new 35. // Hybrid Elite-Guided Boundary Repair (HEBRS, Strategy 3, Equations (27)–(30)) 36. // For j of X[i] that is out of bounds, apply HEBRS: 37. for j = 1 to D: 38. if X[i][j] < lb[j] or X[i][j] > ub[j]: 39. β = random choice weighted {0.4, 0.4, 0.2} 40. if β < 0.4: 41. X[i][j] = X_best[j] − rand() × |X[i][j] − X_best[j]| // Elite-guided repair, (Equation (27)) 42. elif β < 0.8: 43. X[i][j] = lb[j] + (ub[j] − X[i][j]) // Reflect repair, (Equation (28)) 44. else: 45. X[i][j] = lb[j] + rand() × (ub[j] − lb[j]) // Random reset, (Equation (29)) 46. end for 47. end for 48. Update X_best with best X[i] in population 49. if t mod L == 0: 50. Update strategy application probabilities p_search, p_approach, p_attack based on success rates 51. Reset counters to avoid accumulation 52. end for 53. return X_best |
4.5. Complexity Analysis
5. CEC Test
5.1. CEC 2017
5.1.1. CEC2017 Wilcoxon and Friedman Test
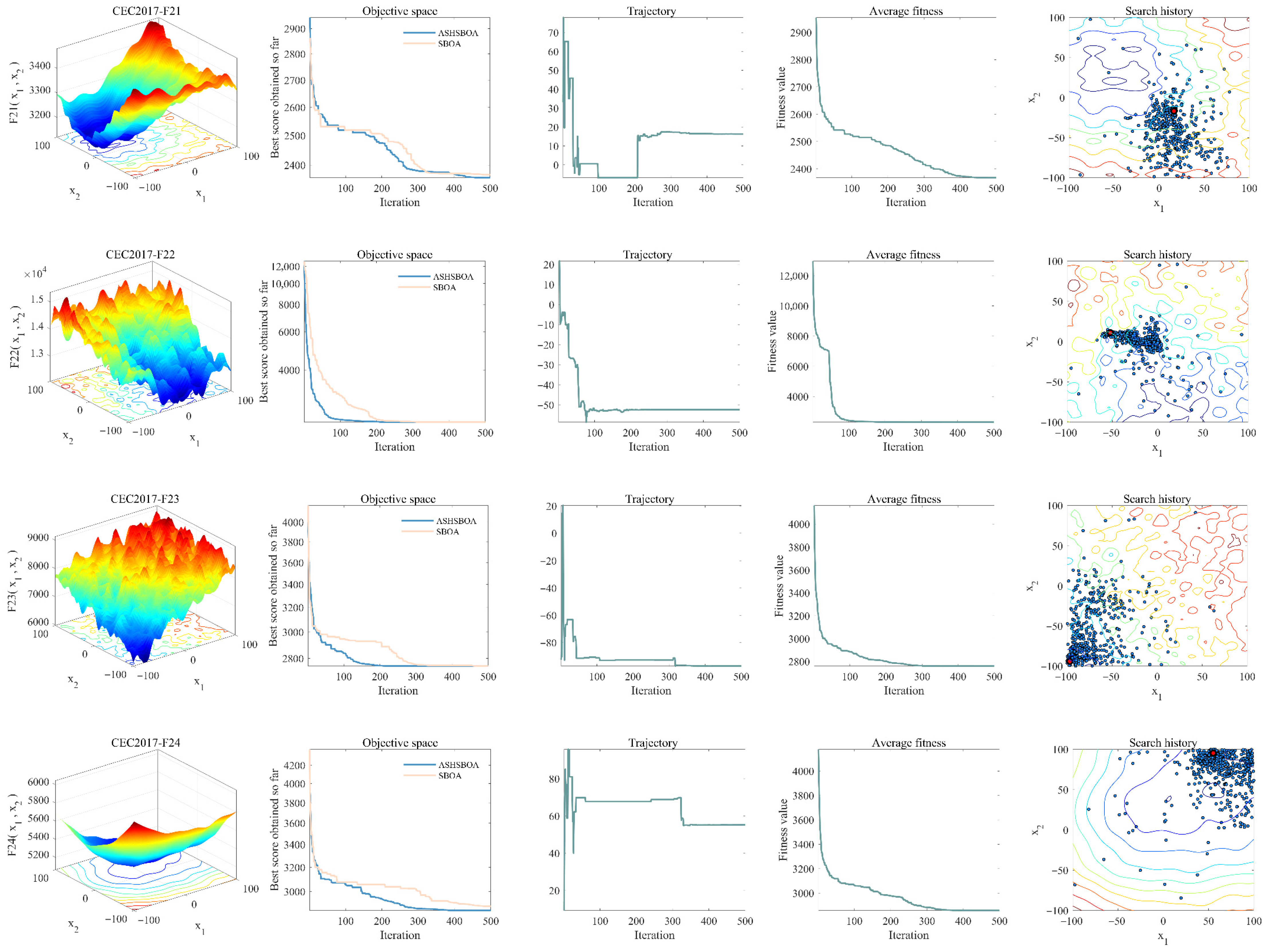
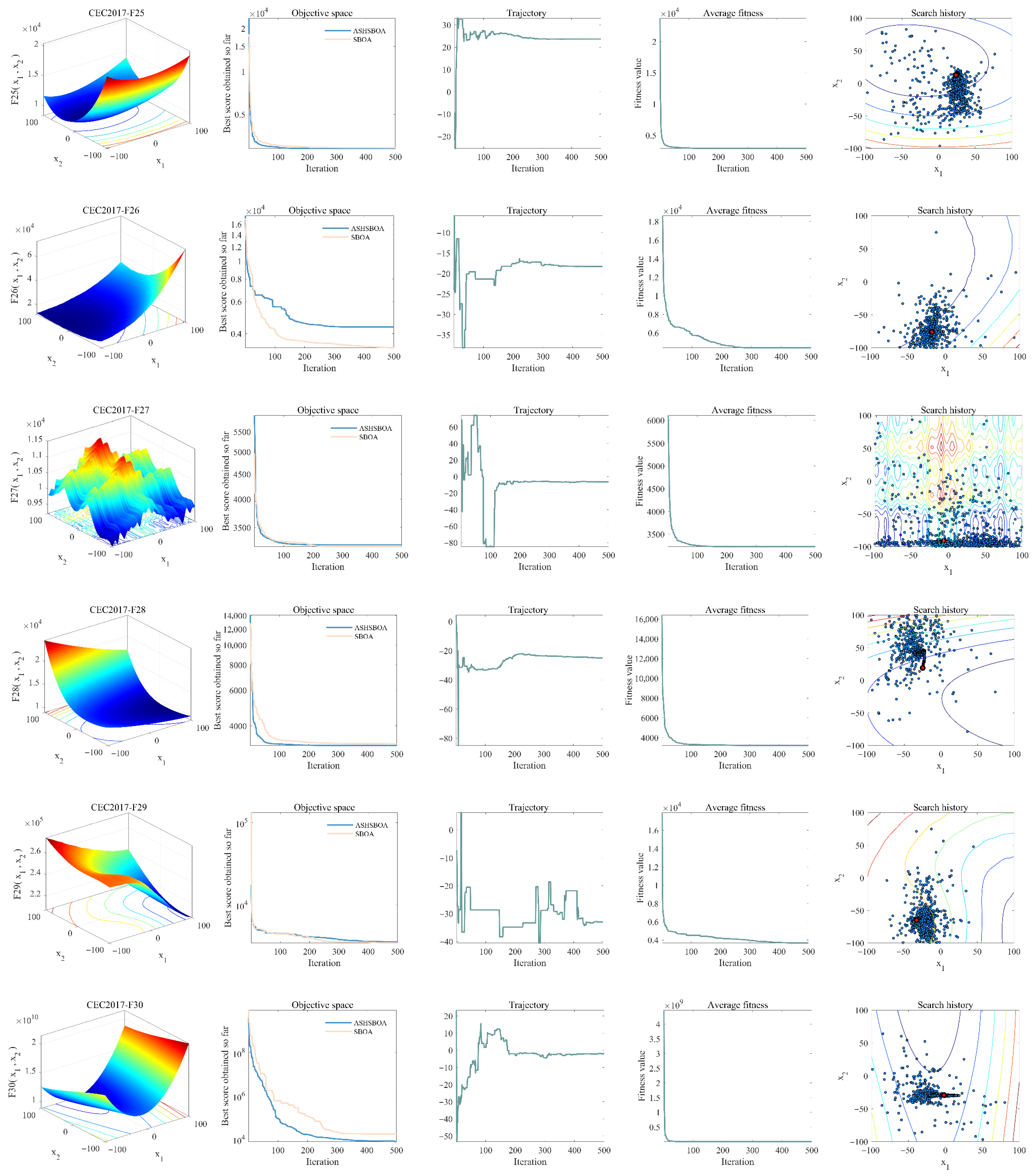
5.1.2. Qualitative Analysis
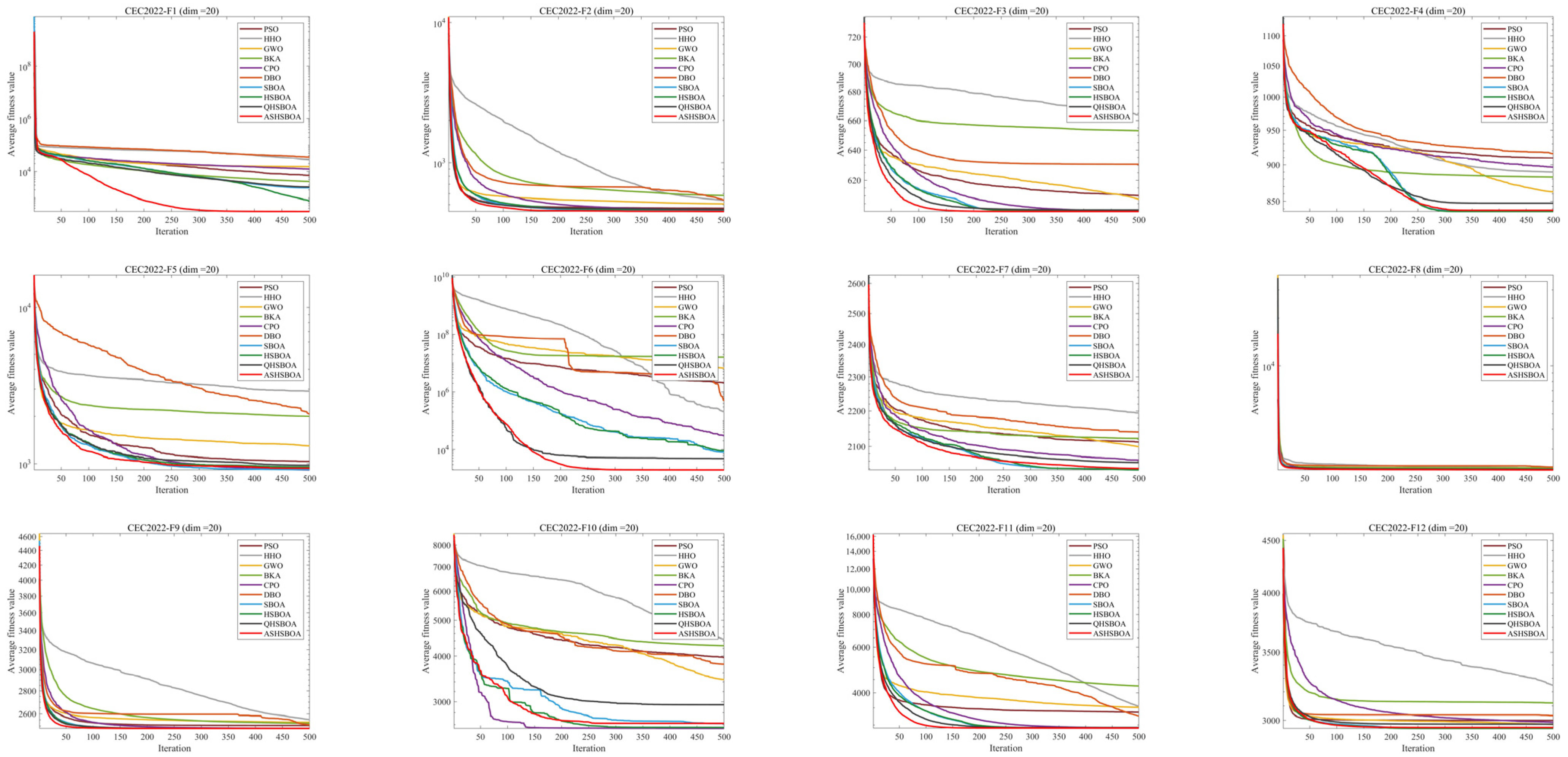
5.2. CEC 2022
CEC 2022 Wilcoxon and Friedman Test
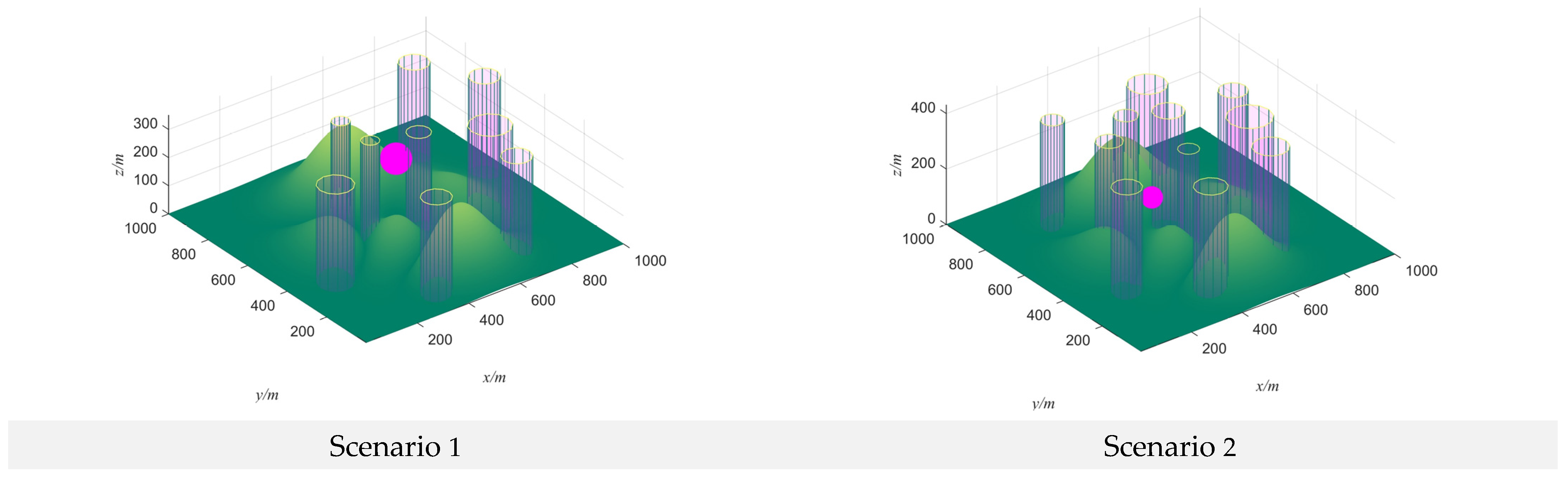
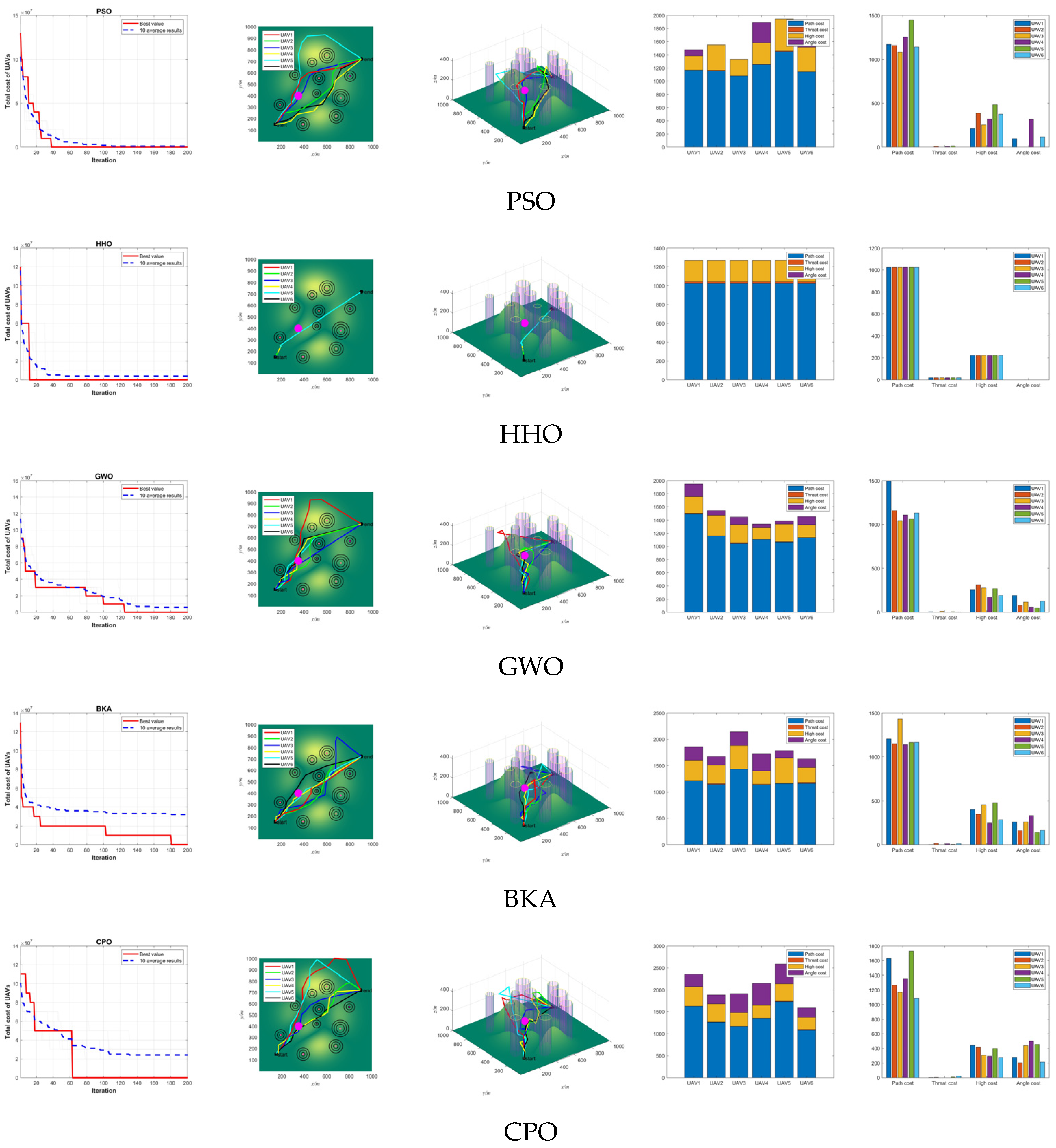
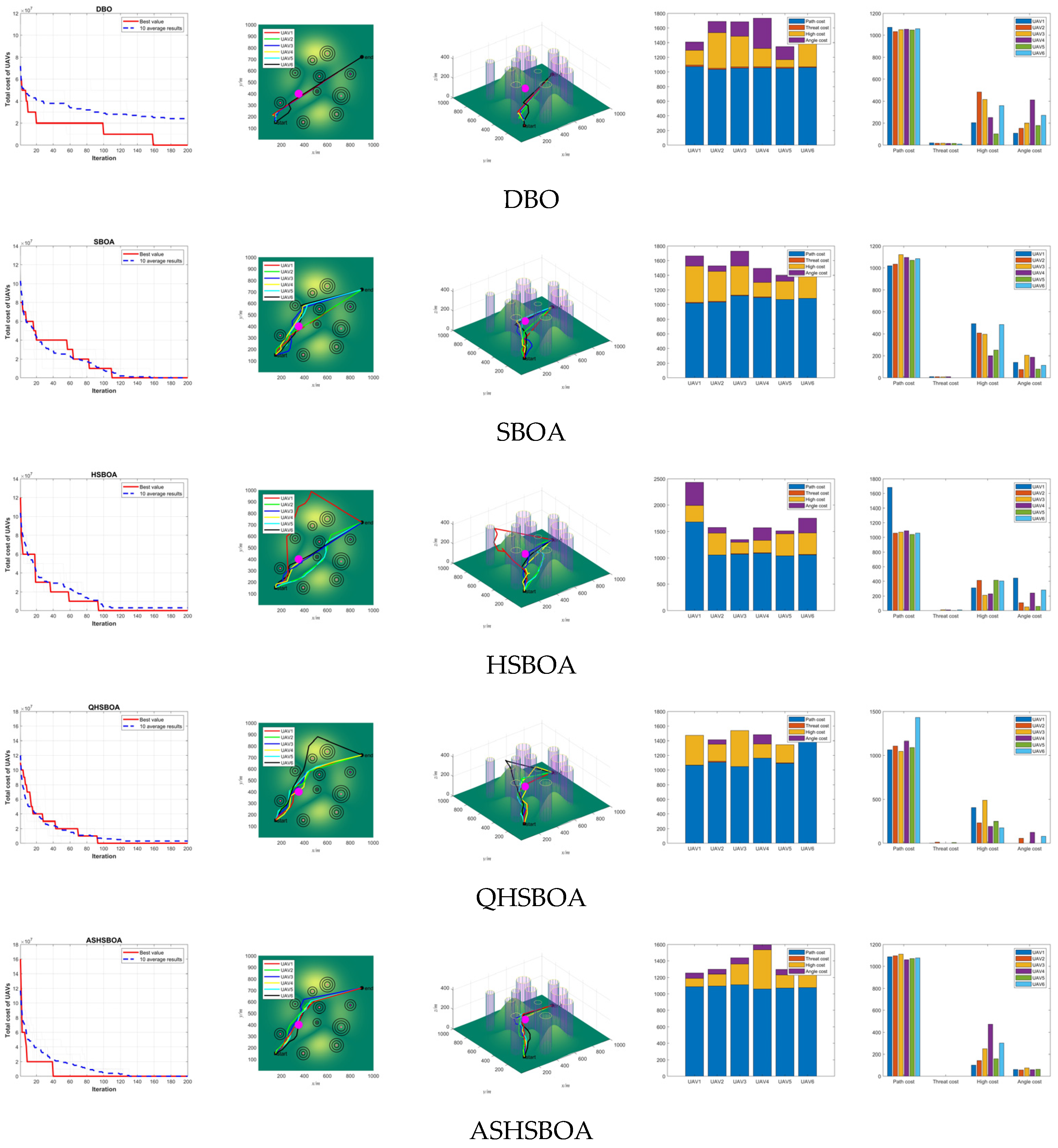
6. Experimental Results and Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sullivan, J.M. Evolution or revolution? The rise of UAVs. IEEE Technol. Soc. Mag. 2006, 25, 43–49. [Google Scholar]
- Kunovjanek, M.; Wankmüller, C. Containing the COVID-19 pandemic with drones-Feasibility of a drone enabled back-up transport system. Transp. Policy 2021, 106, 141–152. [Google Scholar] [CrossRef]
- Benarbia, T.; Kyamakya, K. A literature review of drone-based package delivery logistics systems and their implementation feasibility. Sustainability 2021, 14, 360. [Google Scholar] [CrossRef]
- Shehadeh, M.A.; Kůdela, J. Benchmarking global optimization techniques for unmanned aerial vehicle path planning. Expert Syst. Appl. 2025, 293, 128645. [Google Scholar] [CrossRef]
- Wang, Y.; Mulvaney, D.; Sillitoe, I.; Swere, E. Robot navigation by waypoints. J. Intell. Robot. Syst. 2008, 52, 175–207. [Google Scholar] [CrossRef]
- Li, J.; Xiong, Y.; She, J. UAV path planning for target coverage task in dynamic environment. IEEE Internet Things J. 2023, 10, 17734–17745. [Google Scholar] [CrossRef]
- Kamate, S.; Yilmazer, N. Application of object detection and tracking techniques for unmanned aerial vehicles. Procedia Comput. Sci. 2015, 61, 436–441. [Google Scholar] [CrossRef]
- Sziroczak, D.; Rohacs, D.; Rohacs, J. Review of using small UAV based meteorological measurements for road weather management. Prog. Aerosp. Sci. 2022, 134, 100859. [Google Scholar] [CrossRef]
- Giordan, D.; Manconi, A.; Remondino, F.; Nex, F. Use of unmanned aerial vehicles in monitoring application and management of natural hazards. Geomat. Nat. Hazards Risk 2017, 8, 1–4. [Google Scholar] [CrossRef]
- Yang, T.; Jiang, Z.; Sun, R.; Cheng, N.; Feng, H. Maritime search and rescue based on group mobile computing for unmanned aerial vehicles and unmanned surface vehicles. IEEE Trans. Ind. Inform. 2020, 16, 7700–7708. [Google Scholar] [CrossRef]
- Ibrahim, A.W.N.; Ching, P.W.; Seet, G.L.G.; Lau, W.S.M.; Czajewski, W. Moving objects detection and tracking framework for UAV-based surveillance. In Proceedings of the 2010 Fourth Pacific-Rim Symposium on Image and Video Technology, Singapore, 14–17 November 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 456–461. [Google Scholar]
- Kim, J.; Kim, S.; Ju, C.; Son, H.I. Unmanned aerial vehicles in agriculture: A review of perspective of platform, control, and applications. Ieee Access 2019, 7, 105100–105115. [Google Scholar] [CrossRef]
- Phung, M.D.; Ha, Q.P. Safety-enhanced UAV path planning with spherical vector-based particle swarm optimization. Appl. Soft Comput. 2021, 107, 107376. [Google Scholar] [CrossRef]
- Meng, Q.; Qu, Q.; Chen, K.; Yi, T. Multi-UAV Path Planning Based on Cooperative Co-Evolutionary Algorithms with Adaptive Decision Variable Selection. Drones 2024, 8, 435. [Google Scholar] [CrossRef]
- Debnath, D.; Hawary, A.F.; Ramdan, M.I.; Alvarez, F.V.; Gonzalez, F. QuickNav: An effective collision avoidance and path-planning algorithm for UAS. Drones 2023, 7, 678. [Google Scholar] [CrossRef]
- Debnath, D.; Vanegas, F.; Sandino, J.; Hawary, A.F.; Gonzalez, F. A review of UAV path-planning algorithms and obstacle avoidance methods for remote sensing applications. Remote Sens. 2024, 16, 4019. [Google Scholar] [CrossRef]
- Dechter, R.; Pearl, J. Generalized best-first search strategies and the optimality of A. J. ACM (JACM) 1985, 32, 505–536. [Google Scholar] [CrossRef]
- Dijkstra, E.W. A note on two problems in connexion with graphs. In Edsger Wybe Dijkstra: His Life, Work, and Legacy; Association for Computing Machinery: New York, NY, USA, 2022; pp. 287–290. [Google Scholar]
- Cobb, H.G.; Grefenstette, J.J. Genetic Algorithms for Tracking Changing Environments; Morgan Kaufmann Publishers Inc.: Burlington, MA, USA, 1993. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory; MHS’95. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; IEEE: Piscataway, NJ, USA, 1995; pp. 39–43. [Google Scholar]
- Storn, R.; Price, K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Colorni, A.; Dorigo, M.; Maniezzo, V. Distributed Optimization by Ant Colonies. In Proceedings of the European Conference on Artificial Life, ECAL’91, Paris, France, 11–13 December 1991; Varela, F., Bourgine, P., Eds.; Elsevier Publishing: Amsterdam, The Netherlands; pp. 134–142. [Google Scholar]
- Geng, L.; Zhang, Y.F.; Wang, J.; Fuh, J.Y.H.; Teo, S.H. Cooperative mission planning with multiple UAVs in realistic environments. Unmanned Syst. 2014, 2, 73–86. [Google Scholar] [CrossRef]
- Bai, X.; Jiang, H.; Cui, J.; Lu, K.; Chen, P.; Zhang, M. UAV path planning based on improved A∗ and DWA algorithms. Int. J. Aerosp. Eng. 2021, 2021, 4511252. [Google Scholar] [CrossRef]
- Tianzhu, R.; Rui, Z.; Jie, X.; Zhuoning, D. Three-dimensional path planning of UAV based on an improved A* algorithm. In Proceedings of the 2016 IEEE Chinese Guidance, Navigation and Control Conference (CGNCC), Nanjing, China, 12–14 August 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 140–145. [Google Scholar]
- Wu, X.; Xu, L.; Zhen, R.; Wu, X. Bi-directional adaptive A* algorithm toward optimal path planning for large-scale UAV under multi-constraints. IEEE Access 2020, 8, 85431–85440. [Google Scholar] [CrossRef]
- Chen, J.; Li, M.; Yuan, Z.; Gu, Q. An improved A* algorithm for UAV path planning problems. In Proceedings of the 2020 IEEE 4th Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chongqing, China, 12–14 June 2020; IEEE: Piscataway, NJ, USA, 2020; Volume 1, pp. 958–962. [Google Scholar]
- Sun, S.; Wang, H.; Xu, Y.; Wang, T.; Liu, R.; Chen, W. A Fusion Approach for UAV Onboard Flight Trajectory Management and Decision Making Based on the Combination of Enhanced A* Algorithm and Quadratic Programming. Drones 2024, 8, 254. [Google Scholar] [CrossRef]
- De Filippis, L.; Guglieri, G.; Quagliotti, F. Path planning strategies for UAVS in 3D environments. J. Intell. Robot. Syst. 2012, 65, 247–264. [Google Scholar] [CrossRef]
- Maini, P.; Sujit, P.B. Path planning for a UAV with kinematic constraints in the presence of polygonal obstacles. In Proceedings of the 2016 International Conference on Unmanned Aircraft Systems (ICUAS), Arlington, VA, USA, 7–10 June 2016; IEEE: Arlington, VA, USA, 2016; pp. 62–67. [Google Scholar]
- Li, G.; Li, Y. UAV path planning based on improved ant colony algorithm. In Proceedings of the Second International Conference on Algorithms, Microchips, and Network Applications (AMNA 2023), Zhengzhou, China, 13–15 January 2023; SPIE: Bellingham, WA, USA, 2023; Volume 12635, pp. 59–63. [Google Scholar]
- Huan, L.; Ning, Z.; Qiang, L. UAV path planning based on an improved ant colony algorithm. In Proceedings of the 2021 4th International Conference on Intelligent Autonomous Systems (ICoIAS), Wuhan, China, 14–16 May 2021; IEEE: Arlington, VA, USA, 2021; pp. 357–360. [Google Scholar]
- Song, H.; Jia, M.; Lian, Y.; Liang, K. UAV path planning based on an improved ant colony algorithm. J. Electron. Res. Appl. 2022, 6, 10–25. [Google Scholar] [CrossRef]
- Zhang, M.; Han, Y.; Chen, S.; Liu, M.; He, Z.; Pan, N. A multi-strategy improved differential evolution algorithm for UAV 3D trajectory planning in complex mountainous environments. Eng. Appl. Artif. Intell. 2023, 125, 106672. [Google Scholar] [CrossRef]
- Huang, C.; Zhou, X.; Ran, X.; Wang, J.; Chen, H.; Deng, W. Adaptive cylinder vector particle swarm optimization with differential evolution for UAV path planning. Eng. Appl. Artif. Intell. 2023, 121, 105942. [Google Scholar] [CrossRef]
- Yu, X.; Jiang, N.; Wang, X.; Li, M. A hybrid algorithm based on grey wolf optimizer and differential evolution for UAV path planning. Expert Syst. Appl. 2023, 215, 119327. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, X. UAV path planning based on hybrid differential evolution with fireworks algorithm. In International Conference on Swarm Intelligence, Proceedings of the 13th International Conference, ICSI 2022, Xi’an, China, 15–19 July 2022; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2022; Volume 13344, pp. 354–364. [Google Scholar]
- Nayeem, G.M.; Fan, M.; Akhter, Y. A time-varying adaptive inertia weight based modified PSO algorithm for UAV path planning. In Proceedings of the 2021 2nd International Conference on Robotics, Electrical and Signal Processing Techniques (ICREST), Dhaka, Bangladesh, 5–7 January 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 573–576. [Google Scholar]
- Majeed, A.; Hwang, S.O. A multi-objective coverage path planning algorithm for UAVs to cover spatially distributed regions in urban environments. Aerospace 2021, 8, 343. [Google Scholar] [CrossRef]
- Shivgan, R.; Dong, Z. Energy-efficient drone coverage path planning using genetic algorithm. In Proceedings of the 2020 IEEE 21st International Conference on High Performance Switching and Routing (HPSR), Newark, NJ, USA, 11–14 May 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar]
- Silva Arantes, J.D.; Silva Arantes, M.; Motta Toledo, C.F.; Júnior, O.T.; Williams, B.C. Heuristic and genetic algorithm approaches for UAV path planning under critical situation. Int. J. Artif. Intell. Tools 2017, 26, 1760008. [Google Scholar] [CrossRef]
- Galvez, R.L.; Dadios, E.P.; Bandala, A.A. Path planning for quadrotor UAV using genetic algorithm. In Proceedings of the 2014 International Conference on Humanoid, Nanotechnology, Information Technology, Communication and Control, Environment and Management (HNICEM), Palawan, Philippines, 12–16 November 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1–6. [Google Scholar]
- Noreen, I.; Khan, A.; Habib, Z. Optimal path planning using RRT* based approaches: A survey and future directions. Int. J. Adv. Comput. Sci. Appl. 2016, 7, 97–107. [Google Scholar] [CrossRef]
- Yang, K.; Keat Gan, S.; Sukkarieh, S. A Gaussian process-based RRT planner for the exploration of an unknown and cluttered environment with a UAV. Adv. Robot. 2013, 27, 431–443. [Google Scholar] [CrossRef]
- Meng, L.I.; Qinpeng, S.U.N.; Mengmei, Z.H.U. UAV 3-dimension flight path planning based on improved rapidly-exploring random tree. In Proceedings of the 2019 Chinese Control and Decision Conference (CCDC), Nanchang, China, 3–5 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 921–925. [Google Scholar]
- Moon, S.; Oh, E.; Shim, D.H. An integral framework of task assignment and path planning for multiple unmanned aerial vehicles in dynamic environments. J. Intell. Robot. Syst. 2013, 70, 303–313. [Google Scholar] [CrossRef]
- Hao, G.; Lv, Q.; Huang, Z.; Zhao, H.; Chen, W. UAV path planning based on improved artificial potential field method. Aerospace 2023, 10, 562. [Google Scholar] [CrossRef]
- San Juan, V.; Santos, M.; Andújar, J.M. Intelligent UAV map generation and discrete path planning for search and rescue operations. Complexity 2018, 2018, 6879419. [Google Scholar] [CrossRef]
- Liu, Y.; Zheng, Z.; Qin, F.; Zhang, X.; Yao, H. A residual convolutional neural network based approach for real-time path planning. Knowl.-Based Syst. 2022, 242, 108400. [Google Scholar] [CrossRef]
- He, L.; Aouf, N.; Song, B. Explainable Deep Reinforcement Learning for UAV autonomous path planning. Aerosp. Sci. Technol. 2021, 118, 107052. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Wang, J.; Wang, W.; Hu, X.; Qiu, L.; Zang, H.F. Black-winged kite algorithm: A nature-inspired meta-heuristic for solving benchmark functions and engineering problems. Artif. Intell. Rev. 2024, 57, 98. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Abouhawwash, M. Crested Porcupine Optimizer: A new nature-inspired metaheuristic. Knowl.-Based Syst. 2024, 284, 111257. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. Dung beetle optimizer: A new meta-heuristic algorithm for global optimization. J. Supercomput. 2023, 79, 7305–7336. [Google Scholar] [CrossRef]
- Yuan, C.; Zhao, D.; Heidari, A.A.; Liu, L.; Chen, Y.; Chen, H. Polar lights optimizer: Algorithm and applications in image segmentation and feature selection. Neurocomputing 2024, 607, 128427. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Molina, D.; Poyatos, J.; Ser, J.D.; García, S.; Hussain, A.; Herrera, F. Comprehensive taxonomies of nature-and bio-inspired optimization: Inspiration versus algorithmic behavior, critical analysis recommendations. Cogn. Comput. 2020, 12, 897–939. [Google Scholar] [CrossRef]
- Fu, Y.; Liu, D.; Chen, J.; He, L. Secretary bird optimization algorithm: A new metaheuristic for solving global optimization problems. Artif. Intell. Rev. 2024, 57, 123. [Google Scholar] [CrossRef]
- Sanjalawe, Y.; Al-E’mari, S.; Abualhaj, M.; Makhadmeh, S.N.; Alsharaiah, M.A.; Hijazi, D.H. Recent advances in secretary bird optimization algorithm, its variants and applications. Evol. Intell. 2025, 18, 65. [Google Scholar] [CrossRef]
- Lyu, L.; Kong, G.; Yang, F.; Li, L.; He, J. Augmented gold rush optimizer is used for engineering optimization design problems and UAV path planning. IEEE Access 2024, 12, 134304–134339. [Google Scholar] [CrossRef]
- Jia, C.; He, L.; Liu, D.; Fu, S. Path planning and engineering problems of 3D UAV based on adaptive coati optimization algorithm. Sci. Rep. 2024, 14, 30717. [Google Scholar] [CrossRef]
- Zheng, S.; Huo, J.; Yang, J.; Cao, F. An energy-efficient multi-hop routing protocol for 3D bridge wireless sensor network based on secretary bird optimization algorithm. IEEE Sens. J. 2024, 24, 38045–38060. [Google Scholar] [CrossRef]
- Maurya, P.; Tiwari, P.; Pratap, A. Enhanced secretary bird optimization algorithm for enhanced DG deployment and reconfiguration in electrical distribution networks to improve power system efficiency. Evol. Intell. 2025, 18, 52. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhang, M.; Huang, Q.; Wu, X.; Wan, L.; Huang, J. Secretary bird optimization algorithm based on quantum computing and multiple strategies improvement for KELM diabetes classification. Sci. Rep. 2025, 15, 3774. [Google Scholar] [CrossRef]
- Zheng, X.; Liu, R.; Li, S. A Novel Improved Dung Beetle Optimization Algorithm for Collaborative 3D Path Planning of UAVs. Biomimetics 2025, 10, 420. [Google Scholar] [CrossRef]
- Hellwig, M.; Beyer, H.G. Benchmarking evolutionary algorithms for single objective real-valued constrained optimization—A critical review. Swarm Evol. Comput. 2019, 44, 927–944. [Google Scholar] [CrossRef]
- García-Martínez, C.; Gutiérrez, P.D.; Molina, D.; Lozano, M.; Herrera, F. Since CEC 2005 competition on real-parameter optimisation: A decade of research, progress and comparative analysis’s weakness. Soft Comput. 2017, 21, 5573–5583. [Google Scholar] [CrossRef]
- Kudela, J.; Matousek, R. New benchmark functions for single-objective optimization based on a zigzag pattern. IEEE Access 2022, 10, 8262–8278. [Google Scholar] [CrossRef]
- Tan, L.; Zhang, H.; Liu, Y.; Yuan, T.; Jiang, X.; Shang, Z. An adaptive Q-learning based particle swarm optimization for multi-UAV path planning. Soft Comput. 2024, 28, 7931–7946. [Google Scholar] [CrossRef]
- Zhang, H.; Tan, L.; Liu, Y.; Yuan, T.; Zhao, H.; Liu, H. Energy-Efficient Multi-UAV Collaborative Path Planning using Levy Flight and Improved Gray Wolf Optimization. In Proceedings of the 2024 International Joint Conference on Neural Networks (IJCNN), Yokohama, Japan, 30 June–5 July 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1–8. [Google Scholar]
- Tan, L.; Zhang, H.; Shi, J.; Liu, Y.; Yuan, T. A robust multiple Unmanned Aerial Vehicles 3D path planning strategy via improved particle swarm optimization. Comput. Electr. Eng. 2023, 111, 108947. [Google Scholar] [CrossRef]









| Algorithm | Parameter |
|---|---|
| PSO | |
| HHO | |
| GWO | |
| BKA | |
| CPO | |
| DBO | |
| SBOA | |
| HSBOA | |
| QHSBOA | |
| ASHSBOA |
| PSO | HHO | GWO | BKA | CPO | DBO | SBOA | HSBOA | QHSBOA | ASHSBOA | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| mean | F1 | 1.43 × 109 | 4.65 × 108 | 2.36 × 109 | 1.31 × 1010 | 6.37 × 105 | 2.90 × 108 | 3.70 × 104 | 5.16 × 104 | 1.28 × 104 | 5.58 × 103 |
| F3 | 6.10 × 104 | 5.76 × 104 | 6.26 × 104 | 3.52 × 104 | 6.60 × 104 | 9.20 × 104 | 2.59 × 104 | 1.57 × 104 | 2.74 × 104 | 1.58 × 103 | |
| F4 | 6.53 × 102 | 7.64 × 102 | 6.68 × 102 | 1.89 × 103 | 5.15 × 102 | 6.92 × 102 | 5.08 × 102 | 5.16 × 102 | 5.16 × 102 | 4.87 × 102 | |
| F5 | 7.10 × 102 | 7.70 × 102 | 6.28 × 102 | 7.51 × 102 | 6.95 × 102 | 7.39 × 102 | 5.88 × 102 | 5.87 × 102 | 5.93 × 102 | 5.81 × 102 | |
| F6 | 6.24 × 102 | 6.69 × 102 | 6.13 × 102 | 6.62 × 102 | 6.02 × 102 | 6.48 × 102 | 6.03 × 102 | 6.03 × 102 | 6.03 × 102 | 6.01 × 102 | |
| F7 | 9.97 × 102 | 1.31 × 103 | 9.18 × 102 | 1.23 × 103 | 9.40 × 102 | 1.05 × 103 | 8.55 × 102 | 8.67 × 102 | 8.48 × 102 | 8.24 × 102 | |
| F8 | 1.00 × 103 | 9.84 × 102 | 9.05 × 102 | 9.87 × 102 | 9.86 × 102 | 1.03 × 103 | 8.75 × 102 | 8.71 × 102 | 8.88 × 102 | 8.75 × 102 | |
| F9 | 1.69 × 103 | 8.78 × 103 | 2.53 × 103 | 5.62 × 103 | 1.34 × 103 | 6.73 × 103 | 1.46 × 103 | 1.38 × 103 | 1.24 × 103 | 1.25 × 103 | |
| F10 | 7.32 × 103 | 6.13 × 103 | 5.37 × 103 | 5.57 × 103 | 7.58 × 103 | 6.91 × 103 | 4.43 × 103 | 4.39 × 103 | 4.16 × 103 | 4.33 × 103 | |
| F11 | 1.49 × 103 | 1.55 × 103 | 2.60 × 103 | 1.67 × 103 | 1.28 × 103 | 1.85 × 103 | 1.23 × 103 | 1.22 × 103 | 1.22 × 103 | 1.20 × 103 | |
| F12 | 7.51 × 107 | 8.69 × 107 | 9.30 × 107 | 2.10 × 108 | 9.97 × 105 | 9.38 × 107 | 1.04 × 106 | 1.21 × 106 | 8.24 × 105 | 4.20 × 104 | |
| F13 | 6.17 × 106 | 1.32 × 106 | 1.82 × 107 | 1.58 × 108 | 2.06 × 104 | 1.41 × 107 | 2.15 × 104 | 2.26 × 104 | 1.50 × 104 | 1.50 × 104 | |
| F14 | 1.33 × 105 | 9.02 × 105 | 4.85 × 105 | 1.13 × 104 | 3.34 × 103 | 5.73 × 105 | 2.62 × 104 | 2.79 × 104 | 3.46 × 104 | 1.50 × 103 | |
| F15 | 2.22 × 105 | 1.15 × 105 | 1.47 × 106 | 4.88 × 104 | 4.69 × 103 | 6.21 × 104 | 1.51 × 104 | 1.08 × 104 | 7.05 × 103 | 1.92 × 103 | |
| F16 | 3.09 × 103 | 3.74 × 103 | 2.68 × 103 | 3.17 × 103 | 3.08 × 103 | 3.29 × 103 | 2.35 × 103 | 2.36 × 103 | 2.35 × 103 | 2.31 × 103 | |
| F17 | 2.23 × 103 | 2.80 × 103 | 2.15 × 103 | 2.37 × 103 | 2.05 × 103 | 2.65 × 103 | 1.98 × 103 | 1.94 × 103 | 2.00 × 103 | 1.92 × 103 | |
| F18 | 1.44 × 106 | 3.37 × 106 | 1.96 × 106 | 6.35 × 105 | 1.41 × 105 | 4.14 × 106 | 4.51 × 105 | 5.77 × 105 | 4.53 × 105 | 1.95 × 103 | |
| F19 | 3.97 × 105 | 1.89 × 106 | 8.63 × 105 | 2.97 × 106 | 5.69 × 103 | 2.57 × 106 | 9.48 × 103 | 1.67 × 104 | 9.19 × 103 | 2.00 × 103 | |
| F20 | 2.53 × 103 | 2.84 × 103 | 2.53 × 103 | 2.51 × 103 | 2.46 × 103 | 2.76 × 103 | 2.28 × 103 | 2.25 × 103 | 2.39 × 103 | 2.26 × 103 | |
| F21 | 2.51 × 103 | 2.60 × 103 | 2.41 × 103 | 2.55 × 103 | 2.48 × 103 | 2.57 × 103 | 2.36 × 103 | 2.37 × 103 | 2.38 × 103 | 2.35 × 103 | |
| F22 | 5.53 × 103 | 7.58 × 103 | 5.12 × 103 | 6.28 × 103 | 2.31 × 103 | 4.78 × 103 | 2.52 × 103 | 2.65 × 103 | 2.43 × 103 | 2.63 × 103 | |
| F23 | 2.98 × 103 | 3.30 × 103 | 2.81 × 103 | 3.12 × 103 | 2.85 × 103 | 2.99 × 103 | 2.73 × 103 | 2.73 × 103 | 2.73 × 103 | 2.72 × 103 | |
| F24 | 3.10 × 103 | 3.54 × 103 | 2.94 × 103 | 3.29 × 103 | 3.03 × 103 | 3.21 × 103 | 2.89 × 103 | 2.91 × 103 | 2.89 × 103 | 2.87 × 103 | |
| F25 | 2.98 × 103 | 3.01 × 103 | 3.02 × 103 | 3.26 × 103 | 2.92 × 103 | 3.00 × 103 | 2.90 × 103 | 2.91 × 103 | 2.91 × 103 | 2.89 × 103 | |
| F26 | 5.26 × 103 | 8.52 × 103 | 4.78 × 103 | 7.53 × 103 | 4.86 × 103 | 6.99 × 103 | 4.08 × 103 | 4.21 × 103 | 4.10 × 103 | 4.31 × 103 | |
| F27 | 3.27 × 103 | 3.63 × 103 | 3.26 × 103 | 3.39 × 103 | 3.28 × 103 | 3.34 × 103 | 3.22 × 103 | 3.22 × 103 | 3.25 × 103 | 3.22 × 103 | |
| F28 | 3.35 × 103 | 3.48 × 103 | 3.51 × 103 | 3.80 × 103 | 3.27 × 103 | 3.56 × 103 | 3.26 × 103 | 3.25 × 103 | 3.25 × 103 | 3.22 × 103 | |
| F29 | 4.22 × 103 | 5.12 × 103 | 3.96 × 103 | 4.77 × 103 | 4.05 × 103 | 4.56 × 103 | 3.64 × 103 | 3.65 × 103 | 3.69 × 103 | 3.63 × 103 | |
| F30 | 2.69 × 106 | 1.29 × 107 | 1.09 × 107 | 1.50 × 107 | 1.28 × 105 | 3.52 × 106 | 2.20 × 104 | 3.99 × 104 | 1.66 × 104 | 1.16 × 104 | |
| std | F1 | 8.98 × 108 | 2.44 × 108 | 1.45 × 109 | 1.31 × 1010 | 4.50 × 105 | 2.09 × 108 | 5.66 × 104 | 6.15 × 104 | 9.03 × 103 | 5.60 × 103 |
| F3 | 1.99 × 104 | 6.34 × 103 | 1.42 × 104 | 1.43 × 104 | 1.28 × 104 | 2.09 × 104 | 8.97 × 103 | 5.70 × 103 | 6.40 × 103 | 1.13 × 103 | |
| F4 | 2.04 × 102 | 1.63 × 102 | 1.30 × 102 | 2.78 × 103 | 2.35 × 101 | 1.25 × 102 | 2.75 × 101 | 2.77 × 101 | 2.07 × 101 | 3.10 × 101 | |
| F5 | 2.51 × 101 | 2.81 × 101 | 4.17 × 101 | 4.57 × 101 | 1.39 × 101 | 5.21 × 101 | 2.62 × 101 | 2.28 × 101 | 2.38 × 101 | 2.54 × 101 | |
| F6 | 1.13 × 101 | 6.50 × 100 | 4.48 × 100 | 7.38 × 100 | 6.53 × 10−1 | 1.01 × 101 | 2.19 × 100 | 2.58 × 100 | 2.17 × 100 | 1.83 × 100 | |
| F7 | 2.51 × 101 | 8.24 × 101 | 6.42 × 101 | 7.33 × 101 | 1.81 × 101 | 1.02 × 102 | 4.33 × 101 | 4.66 × 101 | 3.95 × 101 | 3.52 × 101 | |
| F8 | 2.78 × 101 | 2.54 × 101 | 2.84 × 101 | 5.49 × 101 | 1.74 × 101 | 6.07 × 101 | 1.99 × 101 | 1.52 × 101 | 2.28 × 101 | 1.88 × 101 | |
| F9 | 6.07 × 102 | 1.20 × 103 | 8.80 × 102 | 1.19 × 103 | 3.87 × 102 | 1.80 × 103 | 4.65 × 102 | 4.80 × 102 | 3.91 × 102 | 3.99 × 102 | |
| F10 | 7.72 × 102 | 7.39 × 102 | 1.53 × 103 | 1.18 × 103 | 3.15 × 102 | 1.24 × 103 | 5.59 × 102 | 5.87 × 102 | 7.10 × 102 | 7.50 × 102 | |
| F11 | 7.40 × 101 | 1.23 × 102 | 1.14 × 103 | 9.54 × 102 | 2.22 × 101 | 4.30 × 102 | 4.47 × 101 | 4.14 × 101 | 3.52 × 101 | 3.51 × 101 | |
| F12 | 4.90 × 107 | 6.49 × 107 | 1.03 × 108 | 8.86 × 108 | 6.23 × 105 | 1.91 × 108 | 8.28 × 105 | 9.75 × 105 | 5.71 × 105 | 3.92 × 104 | |
| F13 | 4.56 × 106 | 8.60 × 105 | 4.07 × 107 | 6.50 × 108 | 9.25 × 103 | 2.44 × 107 | 2.02 × 104 | 1.90 × 104 | 1.90 × 104 | 1.74 × 104 | |
| F14 | 8.63 × 104 | 1.52 × 106 | 5.60 × 105 | 1.69 × 104 | 5.87 × 103 | 1.08 × 106 | 3.46 × 104 | 2.67 × 104 | 3.31 × 104 | 1.32 × 101 | |
| F15 | 2.64 × 105 | 5.72 × 104 | 3.77 × 106 | 3.51 × 104 | 3.00 × 103 | 5.16 × 104 | 1.42 × 104 | 1.69 × 104 | 6.96 × 103 | 6.43 × 102 | |
| F16 | 3.62 × 102 | 4.45 × 102 | 3.82 × 102 | 5.38 × 102 | 2.06 × 102 | 4.21 × 102 | 2.60 × 102 | 3.11 × 102 | 2.72 × 102 | 2.27 × 102 | |
| F17 | 1.52 × 102 | 3.26 × 102 | 1.99 × 102 | 2.70 × 102 | 1.51 × 102 | 3.19 × 102 | 1.62 × 102 | 1.40 × 102 | 1.88 × 102 | 1.17 × 102 | |
| F18 | 1.23 × 106 | 3.26 × 106 | 2.64 × 106 | 2.84 × 106 | 1.81 × 105 | 5.04 × 106 | 3.29 × 105 | 3.89 × 105 | 3.72 × 105 | 5.27 × 101 | |
| F19 | 6.86 × 105 | 2.21 × 106 | 8.07 × 105 | 1.11 × 107 | 3.13 × 103 | 4.87 × 106 | 8.51 × 103 | 1.65 × 104 | 7.73 × 103 | 1.74 × 102 | |
| F20 | 1.48 × 102 | 2.52 × 102 | 1.69 × 102 | 1.58 × 102 | 1.17 × 102 | 1.65 × 102 | 1.12 × 102 | 1.76 × 102 | 1.59 × 102 | 1.10 × 102 | |
| F21 | 2.60 × 101 | 6.30 × 101 | 2.36 × 101 | 5.05 × 101 | 1.44 × 101 | 4.55 × 101 | 1.52 × 101 | 1.76 × 101 | 2.97 × 101 | 1.36 × 101 | |
| F22 | 3.19 × 103 | 1.23 × 103 | 2.11 × 103 | 1.66 × 103 | 4.17 × 100 | 2.18 × 103 | 8.11 × 102 | 1.09 × 103 | 6.93 × 102 | 1.03 × 103 | |
| F23 | 9.17 × 101 | 1.42 × 102 | 5.97 × 101 | 1.06 × 102 | 1.75 × 101 | 8.93 × 101 | 2.72 × 101 | 1.89 × 101 | 2.76 × 101 | 2.34 × 101 | |
| F24 | 7.41 × 101 | 1.46 × 102 | 4.58 × 101 | 1.10 × 102 | 1.78 × 101 | 9.22 × 101 | 1.74 × 101 | 2.77 × 101 | 2.88 × 101 | 1.65 × 101 | |
| F25 | 4.61 × 101 | 3.08 × 101 | 5.88 × 101 | 4.90 × 102 | 2.11 × 101 | 7.71 × 101 | 1.96 × 101 | 2.07 × 101 | 2.07 × 101 | 1.50 × 101 | |
| F26 | 1.06 × 103 | 1.17 × 103 | 5.05 × 102 | 1.63 × 103 | 1.20 × 103 | 9.46 × 102 | 7.79 × 102 | 8.17 × 102 | 1.12 × 103 | 9.70 × 102 | |
| F27 | 4.43 × 101 | 1.81 × 102 | 2.62 × 101 | 8.43 × 101 | 1.20 × 101 | 5.57 × 101 | 1.16 × 101 | 1.06 × 101 | 2.12 × 101 | 1.23 × 101 | |
| F28 | 3.80 × 101 | 9.07 × 101 | 1.85 × 102 | 8.17 × 102 | 2.61 × 101 | 5.31 × 102 | 2.86 × 101 | 2.67 × 101 | 2.54 × 101 | 3.26 × 101 | |
| F29 | 2.76 × 102 | 6.56 × 102 | 2.06 × 102 | 7.19 × 102 | 1.49 × 102 | 3.92 × 102 | 1.70 × 102 | 1.86 × 102 | 1.63 × 102 | 1.69 × 102 | |
| F30 | 1.65 × 106 | 1.10 × 107 | 8.27 × 106 | 5.26 × 107 | 7.40 × 104 | 4.27 × 106 | 1.67 × 104 | 5.12 × 104 | 6.90 × 103 | 4.39 × 103 |
| PSO | HHO | GWO | BKA | CPO | DBO | SBOA | HSBOA | QHSBOA | ASHSBOA | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| mean | F1 | 6.31 × 109 | 5.20 × 109 | 1.30 × 1010 | 4.61 × 1010 | 1.82 × 108 | 1.31 × 1010 | 1.49 × 108 | 5.78 × 107 | 4.06 × 107 | 5.48 × 107 |
| F3 | 2.12 × 105 | 1.73 × 105 | 1.70 × 105 | 1.01 × 105 | 1.77 × 105 | 2.62 × 105 | 1.07 × 105 | 9.88 × 104 | 1.06 × 105 | 3.18 × 104 | |
| F4 | 1.20 × 103 | 1.76 × 103 | 1.54 × 103 | 7.20 × 103 | 7.09 × 102 | 1.57 × 103 | 6.22 × 102 | 6.55 × 102 | 6.27 × 102 | 5.72 × 102 | |
| F5 | 9.55 × 102 | 9.49 × 102 | 7.81 × 102 | 9.37 × 102 | 9.29 × 102 | 9.72 × 102 | 7.15 × 102 | 7.10 × 102 | 7.14 × 102 | 6.95 × 102 | |
| F6 | 6.43 × 102 | 6.79 × 102 | 6.25 × 102 | 6.74 × 102 | 6.12 × 102 | 6.68 × 102 | 6.14 × 102 | 6.13 × 102 | 6.12 × 102 | 6.07 × 102 | |
| F7 | 1.33 × 103 | 1.88 × 103 | 1.17 × 103 | 1.73 × 103 | 1.24 × 103 | 1.39 × 103 | 1.11 × 103 | 1.14 × 103 | 1.10 × 103 | 1.04 × 103 | |
| F8 | 1.26 × 103 | 1.25 × 103 | 1.07 × 103 | 1.24 × 103 | 1.23 × 103 | 1.32 × 103 | 1.02 × 103 | 1.03 × 103 | 1.02 × 103 | 9.93 × 102 | |
| F9 | 1.71 × 104 | 3.12 × 104 | 1.26 × 104 | 1.86 × 104 | 8.08 × 103 | 3.00 × 104 | 5.73 × 103 | 7.04 × 103 | 6.31 × 103 | 4.45 × 103 | |
| F10 | 1.32 × 104 | 1.03 × 104 | 8.24 × 103 | 9.40 × 103 | 1.37 × 104 | 1.15 × 104 | 7.46 × 103 | 7.61 × 103 | 7.45 × 103 | 6.82 × 103 | |
| F11 | 2.58 × 103 | 3.19 × 103 | 7.21 × 103 | 4.51 × 103 | 1.93 × 103 | 4.20 × 103 | 1.45 × 103 | 1.48 × 103 | 1.52 × 103 | 1.34 × 103 | |
| F12 | 3.05 × 109 | 8.66 × 108 | 1.53 × 109 | 9.58 × 109 | 1.82 × 107 | 9.65 × 108 | 1.50 × 107 | 1.44 × 107 | 1.09 × 107 | 1.64 × 106 | |
| F13 | 2.78 × 108 | 4.70 × 107 | 3.72 × 108 | 1.71 × 109 | 1.60 × 104 | 1.21 × 108 | 9.80 × 103 | 1.10 × 104 | 6.90 × 103 | 9.01 × 103 | |
| F14 | 1.76 × 106 | 7.19 × 106 | 1.85 × 106 | 3.89 × 105 | 1.73 × 105 | 5.29 × 106 | 2.05 × 105 | 2.99 × 105 | 2.54 × 105 | 1.66 × 103 | |
| F15 | 7.78 × 106 | 3.71 × 106 | 7.99 × 107 | 2.12 × 108 | 1.26 × 104 | 5.88 × 107 | 1.36 × 104 | 1.41 × 104 | 1.00 × 104 | 1.00 × 104 | |
| F16 | 4.26 × 103 | 4.97 × 103 | 3.27 × 103 | 4.92 × 103 | 4.44 × 103 | 4.72 × 103 | 2.98 × 103 | 3.06 × 103 | 3.01 × 103 | 2.85 × 103 | |
| F17 | 3.73 × 103 | 3.95 × 103 | 3.23 × 103 | 3.74 × 103 | 3.53 × 103 | 4.15 × 103 | 2.82 × 103 | 2.85 × 103 | 2.86 × 103 | 2.80 × 103 | |
| F18 | 6.60 × 106 | 9.56 × 106 | 1.02 × 107 | 3.65 × 106 | 1.85 × 106 | 1.16 × 107 | 2.65 × 106 | 2.49 × 106 | 1.73 × 106 | 3.32 × 104 | |
| F19 | 7.79 × 106 | 2.20 × 106 | 6.62 × 106 | 3.35 × 107 | 2.15 × 104 | 4.92 × 106 | 1.81 × 104 | 1.52 × 104 | 1.70 × 104 | 2.03 × 104 | |
| F20 | 3.56 × 103 | 3.58 × 103 | 3.16 × 103 | 3.25 × 103 | 3.68 × 103 | 3.75 × 103 | 2.83 × 103 | 2.86 × 103 | 2.84 × 103 | 2.81 × 103 | |
| F21 | 2.77 × 103 | 2.96 × 103 | 2.57 × 103 | 2.92 × 103 | 2.70 × 103 | 2.89 × 103 | 2.48 × 103 | 2.49 × 103 | 2.48 × 103 | 2.45 × 103 | |
| F22 | 1.46 × 104 | 1.25 × 104 | 1.04 × 104 | 1.13 × 104 | 1.34 × 104 | 1.25 × 104 | 9.03 × 103 | 8.88 × 103 | 8.16 × 103 | 6.58 × 103 | |
| F23 | 3.38 × 103 | 3.95 × 103 | 3.04 × 103 | 3.79 × 103 | 3.18 × 103 | 3.49 × 103 | 2.94 × 103 | 2.94 × 103 | 2.92 × 103 | 2.90 × 103 | |
| F24 | 3.59 × 103 | 4.37 × 103 | 3.22 × 103 | 3.84 × 103 | 3.35 × 103 | 3.74 × 103 | 3.10 × 103 | 3.14 × 103 | 3.07 × 103 | 3.04 × 103 | |
| F25 | 3.46 × 103 | 3.76 × 103 | 4.02 × 103 | 7.50 × 103 | 3.24 × 103 | 3.81 × 103 | 3.16 × 103 | 3.17 × 103 | 3.19 × 103 | 3.11 × 103 | |
| F26 | 8.30 × 103 | 1.19 × 104 | 7.18 × 103 | 1.27 × 104 | 7.53 × 103 | 1.02 × 104 | 6.35 × 103 | 6.40 × 103 | 6.60 × 103 | 5.75 × 103 | |
| F27 | 3.66 × 103 | 5.03 × 103 | 3.71 × 103 | 4.29 × 103 | 3.74 × 103 | 4.02 × 103 | 3.41 × 103 | 3.39 × 103 | 3.55 × 103 | 3.40 × 103 | |
| F28 | 3.86 × 103 | 4.99 × 103 | 4.61 × 103 | 6.58 × 103 | 3.73 × 103 | 5.86 × 103 | 3.46 × 103 | 3.48 × 103 | 3.50 × 103 | 3.38 × 103 | |
| F29 | 5.67 × 103 | 7.41 × 103 | 5.00 × 103 | 8.64 × 103 | 5.18 × 103 | 6.10 × 103 | 4.08 × 103 | 4.17 × 103 | 4.32 × 103 | 4.03 × 103 | |
| F30 | 8.90 × 107 | 1.32 × 108 | 1.98 × 108 | 3.98 × 108 | 1.01 × 107 | 7.61 × 107 | 1.26 × 106 | 1.27 × 106 | 1.16 × 106 | 1.48 × 106 | |
| std | F1 | 3.12 × 109 | 1.55 × 109 | 5.29 × 109 | 2.21 × 1010 | 6.69 × 107 | 2.17 × 1010 | 4.96 × 108 | 6.64 × 107 | 8.26 × 107 | 2.83 × 108 |
| F3 | 4.97 × 104 | 1.88 × 104 | 2.43 × 104 | 3.15 × 104 | 2.02 × 104 | 6.57 × 104 | 1.92 × 104 | 1.94 × 104 | 1.73 × 104 | 1.02 × 104 | |
| F4 | 5.05 × 102 | 3.92 × 102 | 4.73 × 102 | 6.31 × 103 | 5.49 × 101 | 2.00 × 103 | 5.53 × 101 | 6.71 × 101 | 6.58 × 101 | 5.43 × 101 | |
| F5 | 5.31 × 101 | 3.95 × 101 | 5.97 × 101 | 8.63 × 101 | 2.86 × 101 | 9.77 × 101 | 4.65 × 101 | 3.74 × 101 | 3.78 × 101 | 4.17 × 101 | |
| F6 | 1.30 × 101 | 5.76 × 100 | 5.96 × 100 | 8.51 × 100 | 2.70 × 100 | 9.33 × 100 | 5.92 × 100 | 4.94 × 100 | 7.36 × 100 | 2.87 × 100 | |
| F7 | 5.75 × 101 | 9.16 × 101 | 9.18 × 101 | 1.37 × 102 | 4.55 × 101 | 1.32 × 102 | 6.16 × 101 | 7.25 × 101 | 8.70 × 101 | 7.59 × 101 | |
| F8 | 4.65 × 101 | 3.49 × 101 | 5.82 × 101 | 8.15 × 101 | 2.60 × 101 | 9.09 × 101 | 4.21 × 101 | 3.84 × 101 | 4.52 × 101 | 3.72 × 101 | |
| F9 | 9.58 × 103 | 3.32 × 103 | 5.22 × 103 | 6.33 × 103 | 2.88 × 103 | 8.17 × 103 | 1.83 × 103 | 2.84 × 103 | 2.67 × 103 | 1.60 × 103 | |
| F10 | 9.48 × 102 | 1.28 × 103 | 1.52 × 103 | 1.32 × 103 | 3.83 × 102 | 2.59 × 103 | 1.03 × 103 | 1.05 × 103 | 8.48 × 102 | 1.12 × 103 | |
| F11 | 3.66 × 102 | 8.48 × 102 | 2.60 × 103 | 2.48 × 103 | 3.36 × 102 | 2.65 × 103 | 1.18 × 102 | 1.04 × 102 | 1.66 × 102 | 6.74 × 101 | |
| F12 | 2.76 × 109 | 6.79 × 108 | 1.54 × 109 | 1.41 × 1010 | 7.85 × 106 | 5.95 × 108 | 9.26 × 106 | 1.06 × 107 | 9.76 × 106 | 1.07 × 106 | |
| F13 | 6.31 × 108 | 1.25 × 108 | 9.25 × 108 | 4.86 × 109 | 8.84 × 103 | 1.74 × 108 | 9.69 × 103 | 1.01 × 104 | 4.26 × 103 | 7.80 × 103 | |
| F14 | 3.06 × 106 | 7.01 × 106 | 1.86 × 106 | 1.10 × 106 | 1.54 × 105 | 5.26 × 106 | 1.37 × 105 | 1.97 × 105 | 2.16 × 105 | 4.09 × 101 | |
| F15 | 8.25 × 106 | 6.69 × 106 | 3.16 × 108 | 6.54 × 108 | 5.72 × 103 | 2.22 × 108 | 8.04 × 103 | 8.08 × 103 | 6.79 × 103 | 6.15 × 103 | |
| F16 | 5.28 × 102 | 5.44 × 102 | 3.62 × 102 | 1.73 × 103 | 3.34 × 102 | 5.99 × 102 | 4.10 × 102 | 3.68 × 102 | 4.40 × 102 | 3.33 × 102 | |
| F17 | 4.43 × 102 | 4.90 × 102 | 5.09 × 102 | 6.49 × 102 | 2.70 × 102 | 4.37 × 102 | 2.74 × 102 | 3.39 × 102 | 3.01 × 102 | 2.19 × 102 | |
| F18 | 2.96 × 106 | 8.53 × 106 | 8.83 × 106 | 6.75 × 106 | 1.20 × 106 | 1.39 × 107 | 1.36 × 106 | 1.74 × 106 | 8.66 × 105 | 2.81 × 104 | |
| F19 | 4.74 × 106 | 1.45 × 106 | 1.06 × 107 | 1.74 × 108 | 8.57 × 103 | 6.75 × 106 | 1.20 × 104 | 1.02 × 104 | 1.17 × 104 | 1.40 × 104 | |
| F20 | 3.48 × 102 | 3.30 × 102 | 4.27 × 102 | 2.72 × 102 | 2.57 × 102 | 4.38 × 102 | 3.03 × 102 | 3.17 × 102 | 3.24 × 102 | 2.79 × 102 | |
| F21 | 5.48 × 101 | 8.37 × 101 | 7.78 × 101 | 1.28 × 102 | 2.87 × 101 | 8.16 × 101 | 2.89 × 101 | 3.60 × 101 | 4.25 × 101 | 3.13 × 101 | |
| F22 | 2.20 × 103 | 1.11 × 103 | 2.46 × 103 | 1.44 × 103 | 4.58 × 103 | 1.98 × 103 | 2.04 × 103 | 2.44 × 103 | 2.58 × 103 | 3.08 × 103 | |
| F23 | 1.37 × 102 | 2.21 × 102 | 8.59 × 101 | 1.89 × 102 | 3.14 × 101 | 1.27 × 102 | 3.01 × 101 | 5.59 × 101 | 4.18 × 101 | 4.74 × 101 | |
| F24 | 1.58 × 102 | 2.50 × 102 | 9.47 × 101 | 1.82 × 102 | 3.07 × 101 | 1.44 × 102 | 5.67 × 101 | 4.76 × 101 | 4.79 × 101 | 3.33 × 101 | |
| F25 | 2.88 × 102 | 2.35 × 102 | 3.69 × 102 | 3.22 × 103 | 4.94 × 101 | 1.65 × 103 | 4.26 × 101 | 4.19 × 101 | 5.03 × 101 | 3.12 × 101 | |
| F26 | 1.94 × 103 | 1.43 × 103 | 7.88 × 102 | 1.84 × 103 | 2.13 × 103 | 2.00 × 103 | 1.71 × 103 | 1.30 × 103 | 1.92 × 103 | 1.53 × 103 | |
| F27 | 1.82 × 102 | 6.29 × 102 | 1.30 × 102 | 4.23 × 102 | 7.62 × 101 | 3.05 × 102 | 7.35 × 101 | 5.31 × 101 | 1.21 × 102 | 5.92 × 101 | |
| F28 | 6.16 × 102 | 4.18 × 102 | 5.58 × 102 | 1.79 × 103 | 8.98 × 101 | 2.22 × 103 | 6.67 × 101 | 4.77 × 101 | 7.34 × 101 | 4.34 × 101 | |
| F29 | 5.07 × 102 | 1.68 × 103 | 4.23 × 102 | 4.54 × 103 | 2.83 × 102 | 7.91 × 102 | 3.92 × 102 | 3.40 × 102 | 3.37 × 102 | 2.48 × 102 | |
| F30 | 3.39 × 107 | 6.66 × 107 | 1.52 × 108 | 9.73 × 108 | 4.53 × 106 | 6.97 × 107 | 6.77 × 105 | 4.25 × 105 | 2.98 × 105 | 5.41 × 105 |
| PSO | HHO | GWO | BKA | CPO | DBO | SBOA | HSBOA | QHSBOA | ASHSBOA | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| mean | F1 | 3.53 × 1010 | 5.07 × 1010 | 5.68 × 1010 | 1.60 × 1011 | 1.34 × 1010 | 6.75 × 1010 | 1.46 × 1010 | 4.61 × 109 | 1.13 × 1010 | 5.61 × 109 |
| F3 | 5.88 × 105 | 3.54 × 105 | 5.41 × 105 | 2.77 × 105 | 4.45 × 105 | 6.58 × 105 | 3.36 × 105 | 3.28 × 105 | 3.21 × 105 | 2.03 × 105 | |
| F4 | 4.21 × 103 | 9.83 × 103 | 5.93 × 103 | 2.78 × 104 | 2.29 × 103 | 1.23 × 104 | 1.64 × 103 | 1.54 × 103 | 1.69 × 103 | 1.27 × 103 | |
| F5 | 1.72 × 103 | 1.68 × 103 | 1.25 × 103 | 1.57 × 103 | 1.66 × 103 | 1.78 × 103 | 1.17 × 103 | 1.19 × 103 | 1.20 × 103 | 1.13 × 103 | |
| F6 | 6.71 × 102 | 6.92 × 102 | 6.46 × 102 | 6.81 × 102 | 6.43 × 102 | 6.78 × 102 | 6.38 × 102 | 6.40 × 102 | 6.41 × 102 | 6.34 × 102 | |
| F7 | 2.46 × 103 | 3.76 × 103 | 2.23 × 103 | 3.42 × 103 | 2.36 × 103 | 2.96 × 103 | 2.27 × 103 | 2.41 × 103 | 2.21 × 103 | 2.18 × 103 | |
| F8 | 2.03 × 103 | 2.14 × 103 | 1.57 × 103 | 2.00 × 103 | 1.98 × 103 | 2.14 × 103 | 1.50 × 103 | 1.53 × 103 | 1.49 × 103 | 1.44 × 103 | |
| F9 | 6.33 × 104 | 6.96 × 104 | 4.57 × 104 | 3.81 × 104 | 4.70 × 104 | 7.58 × 104 | 2.72 × 104 | 3.30 × 104 | 2.99 × 104 | 2.77 × 104 | |
| F10 | 2.96 × 104 | 2.45 × 104 | 2.04 × 104 | 2.06 × 104 | 3.06 × 104 | 2.87 × 104 | 1.80 × 104 | 1.94 × 104 | 1.73 × 104 | 1.70 × 104 | |
| F11 | 7.90 × 104 | 1.43 × 105 | 9.24 × 104 | 6.27 × 104 | 9.21 × 104 | 2.24 × 105 | 3.85 × 104 | 2.22 × 104 | 4.09 × 104 | 9.57 × 103 | |
| F12 | 1.17 × 1010 | 1.24 × 1010 | 1.18 × 1010 | 5.97 × 1010 | 8.79 × 108 | 7.19 × 109 | 3.50 × 108 | 3.60 × 108 | 4.36 × 108 | 1.62 × 108 | |
| F13 | 1.15 × 109 | 1.83 × 108 | 1.80 × 109 | 8.52 × 109 | 2.14 × 105 | 3.06 × 108 | 1.05 × 106 | 5.71 × 104 | 3.07 × 104 | 1.71 × 104 | |
| F14 | 1.39 × 107 | 1.12 × 107 | 1.12 × 107 | 4.87 × 106 | 4.67 × 106 | 1.82 × 107 | 3.47 × 106 | 4.09 × 106 | 2.66 × 106 | 8.92 × 104 | |
| F15 | 3.61 × 108 | 2.40 × 107 | 5.32 × 108 | 3.69 × 109 | 9.42 × 103 | 1.07 × 108 | 8.28 × 103 | 8.29 × 103 | 6.72 × 103 | 4.57 × 103 | |
| F16 | 1.00 × 104 | 1.05 × 104 | 6.84 × 103 | 1.00 × 104 | 1.04 × 104 | 9.46 × 103 | 5.69 × 103 | 5.77 × 103 | 5.57 × 103 | 5.31 × 103 | |
| F17 | 8.24 × 103 | 8.71 × 103 | 5.52 × 103 | 7.60 × 105 | 6.95 × 103 | 8.93 × 103 | 4.94 × 103 | 5.13 × 103 | 4.70 × 103 | 4.76 × 103 | |
| F18 | 1.68 × 107 | 1.02 × 107 | 8.76 × 106 | 7.37 × 106 | 5.20 × 106 | 3.23 × 107 | 4.34 × 106 | 5.89 × 106 | 4.00 × 106 | 4.69 × 105 | |
| F19 | 4.85 × 108 | 3.54 × 107 | 3.88 × 108 | 3.19 × 109 | 1.32 × 104 | 1.16 × 108 | 6.60 × 103 | 1.38 × 104 | 6.37 × 103 | 6.90 × 103 | |
| F20 | 6.94 × 103 | 6.28 × 103 | 5.42 × 103 | 5.59 × 103 | 7.29 × 103 | 7.08 × 103 | 5.12 × 103 | 4.86 × 103 | 4.93 × 103 | 4.55 × 103 | |
| F21 | 3.73 × 103 | 4.41 × 103 | 3.09 × 103 | 4.13 × 103 | 3.40 × 103 | 4.00 × 103 | 2.97 × 103 | 3.01 × 103 | 2.92 × 103 | 2.88 × 103 | |
| F22 | 3.24 × 104 | 2.75 × 104 | 2.26 × 104 | 2.43 × 104 | 3.31 × 104 | 3.13 × 104 | 2.07 × 104 | 2.19 × 104 | 1.94 × 104 | 1.99 × 104 | |
| F23 | 4.85 × 103 | 5.88 × 103 | 3.69 × 103 | 5.22 × 103 | 3.99 × 103 | 4.82 × 103 | 3.41 × 103 | 3.42 × 103 | 3.44 × 103 | 3.33 × 103 | |
| F24 | 5.83 × 103 | 8.45 × 103 | 4.49 × 103 | 6.77 × 103 | 4.56 × 103 | 6.14 × 103 | 4.08 × 103 | 4.10 × 103 | 3.98 × 103 | 3.95 × 103 | |
| F25 | 5.52 × 103 | 6.81 × 103 | 7.23 × 103 | 1.29 × 104 | 4.91 × 103 | 1.07 × 104 | 4.33 × 103 | 4.20 × 103 | 4.52 × 103 | 4.15 × 103 | |
| F26 | 2.05 × 104 | 3.15 × 104 | 1.75 × 104 | 3.77 × 104 | 2.16 × 104 | 2.73 × 104 | 1.74 × 104 | 1.74 × 104 | 1.81 × 104 | 1.66 × 104 | |
| F27 | 4.06 × 103 | 7.03 × 103 | 4.30 × 103 | 6.03 × 103 | 4.21 × 103 | 4.81 × 103 | 3.77 × 103 | 3.76 × 103 | 3.97 × 103 | 3.78 × 103 | |
| F28 | 6.63 × 103 | 9.70 × 103 | 9.69 × 103 | 1.99 × 104 | 6.07 × 103 | 1.88 × 104 | 4.82 × 103 | 4.46 × 103 | 4.92 × 103 | 4.31 × 103 | |
| F29 | 1.09 × 104 | 1.30 × 104 | 9.19 × 103 | 5.04 × 104 | 1.03 × 104 | 1.22 × 104 | 7.57 × 103 | 7.34 × 103 | 7.76 × 103 | 7.02 × 103 | |
| F30 | 1.40 × 109 | 8.32 × 108 | 1.74 × 109 | 7.29 × 109 | 6.59 × 106 | 2.90 × 108 | 7.35 × 105 | 1.11 × 106 | 8.11 × 105 | 2.90 × 105 | |
| std | F1 | 1.03 × 1010 | 8.11 × 109 | 1.16 × 1010 | 4.73 × 1010 | 3.86 × 109 | 4.81 × 1010 | 8.26 × 109 | 1.04 × 109 | 5.19 × 109 | 3.70 × 109 |
| F3 | 9.61 × 104 | 5.97 × 104 | 1.06 × 105 | 3.60 × 104 | 6.18 × 104 | 3.16 × 105 | 2.02 × 104 | 3.36 × 104 | 2.12 × 104 | 2.09 × 104 | |
| F4 | 1.59 × 103 | 2.05 × 103 | 1.78 × 103 | 2.02 × 104 | 2.87 × 102 | 1.17 × 104 | 3.78 × 102 | 1.96 × 102 | 4.22 × 102 | 1.60 × 102 | |
| F5 | 8.59 × 101 | 6.01 × 101 | 6.21 × 101 | 1.75 × 102 | 6.05 × 101 | 2.11 × 102 | 7.33 × 101 | 5.64 × 101 | 7.21 × 101 | 7.81 × 101 | |
| F6 | 1.26 × 101 | 3.82 × 100 | 5.01 × 100 | 8.79 × 100 | 6.38 × 100 | 1.04 × 101 | 5.34 × 100 | 6.33 × 100 | 6.73 × 100 | 6.30 × 100 | |
| F7 | 1.30 × 102 | 1.48 × 102 | 1.67 × 102 | 2.31 × 102 | 1.18 × 102 | 2.31 × 102 | 1.79 × 102 | 1.77 × 102 | 1.83 × 102 | 1.76 × 102 | |
| F8 | 7.75 × 101 | 7.33 × 101 | 7.87 × 101 | 1.47 × 102 | 3.89 × 101 | 2.41 × 102 | 5.95 × 101 | 9.43 × 101 | 8.01 × 101 | 9.01 × 101 | |
| F9 | 1.65 × 104 | 3.94 × 103 | 1.12 × 104 | 9.75 × 103 | 5.83 × 103 | 1.07 × 104 | 4.60 × 103 | 5.74 × 103 | 5.34 × 103 | 5.34 × 103 | |
| F10 | 1.21 × 103 | 1.79 × 103 | 5.37 × 103 | 3.13 × 103 | 6.94 × 102 | 4.50 × 103 | 1.52 × 103 | 1.66 × 103 | 1.63 × 103 | 1.45 × 103 | |
| F11 | 2.24 × 104 | 3.58 × 104 | 1.69 × 104 | 1.34 × 104 | 1.44 × 104 | 5.25 × 104 | 1.08 × 104 | 4.17 × 103 | 1.08 × 104 | 3.53 × 103 | |
| F12 | 6.85 × 109 | 3.41 × 109 | 5.12 × 109 | 4.70 × 1010 | 2.76 × 108 | 2.20 × 109 | 3.46 × 108 | 1.04 × 108 | 5.59 × 108 | 3.50 × 108 | |
| F13 | 8.33 × 108 | 8.70 × 107 | 1.31 × 109 | 7.55 × 109 | 2.09 × 105 | 2.19 × 108 | 5.54 × 106 | 4.80 × 104 | 4.51 × 104 | 1.04 × 104 | |
| F14 | 6.29 × 106 | 3.00 × 106 | 6.20 × 106 | 1.30 × 107 | 1.55 × 106 | 1.04 × 107 | 2.05 × 106 | 1.93 × 106 | 1.13 × 106 | 6.56 × 104 | |
| F15 | 4.35 × 108 | 4.71 × 107 | 9.19 × 108 | 5.66 × 109 | 2.81 × 103 | 1.09 × 108 | 4.69 × 103 | 6.85 × 103 | 4.29 × 103 | 3.06 × 103 | |
| F16 | 1.16 × 103 | 1.16 × 103 | 8.81 × 102 | 2.02 × 103 | 4.04 × 102 | 1.48 × 103 | 7.51 × 102 | 8.35 × 102 | 7.03 × 102 | 6.94 × 102 | |
| F17 | 8.91 × 102 | 1.96 × 103 | 6.17 × 102 | 1.87 × 106 | 3.67 × 102 | 1.32 × 103 | 5.76 × 102 | 4.85 × 102 | 4.64 × 102 | 5.97 × 102 | |
| F18 | 7.02 × 106 | 5.76 × 106 | 3.64 × 106 | 1.35 × 107 | 1.68 × 106 | 1.85 × 107 | 2.50 × 106 | 3.03 × 106 | 1.61 × 106 | 2.53 × 105 | |
| F19 | 6.99 × 108 | 1.40 × 107 | 6.69 × 108 | 7.22 × 109 | 6.71 × 103 | 1.18 × 108 | 4.58 × 103 | 3.39 × 104 | 5.09 × 103 | 4.99 × 103 | |
| F20 | 4.96 × 102 | 5.50 × 102 | 7.58 × 102 | 5.80 × 102 | 2.65 × 102 | 8.53 × 102 | 4.13 × 102 | 6.02 × 102 | 5.35 × 102 | 4.95 × 102 | |
| F21 | 1.54 × 102 | 2.06 × 102 | 7.82 × 101 | 2.89 × 102 | 3.98 × 101 | 1.65 × 102 | 8.69 × 101 | 7.89 × 101 | 7.43 × 101 | 6.81 × 101 | |
| F22 | 1.23 × 103 | 1.36 × 103 | 5.14 × 103 | 3.67 × 103 | 7.46 × 102 | 3.86 × 103 | 1.64 × 103 | 1.93 × 103 | 3.90 × 103 | 3.32 × 103 | |
| F23 | 2.58 × 102 | 4.21 × 102 | 1.03 × 102 | 3.88 × 102 | 6.74 × 101 | 2.20 × 102 | 7.29 × 101 | 6.18 × 101 | 1.09 × 102 | 6.97 × 101 | |
| F24 | 4.72 × 102 | 7.96 × 102 | 1.74 × 102 | 4.46 × 102 | 8.84 × 101 | 5.39 × 102 | 1.14 × 102 | 1.17 × 102 | 1.08 × 102 | 1.03 × 102 | |
| F25 | 7.93 × 102 | 4.56 × 102 | 1.10 × 103 | 3.51 × 103 | 2.84 × 102 | 6.60 × 103 | 3.05 × 102 | 1.55 × 102 | 3.43 × 102 | 3.84 × 102 | |
| F26 | 1.83 × 103 | 2.66 × 103 | 1.58 × 103 | 7.43 × 103 | 1.53 × 103 | 3.81 × 103 | 4.77 × 103 | 3.96 × 103 | 4.47 × 103 | 3.89 × 103 | |
| F27 | 2.95 × 102 | 9.66 × 102 | 2.56 × 102 | 1.22 × 103 | 1.68 × 102 | 5.69 × 102 | 1.51 × 102 | 1.14 × 102 | 1.52 × 102 | 1.16 × 102 | |
| F28 | 1.95 × 103 | 8.63 × 102 | 1.50 × 103 | 7.04 × 103 | 5.96 × 102 | 5.73 × 103 | 5.58 × 102 | 1.51 × 102 | 3.77 × 102 | 2.68 × 102 | |
| F29 | 8.35 × 102 | 1.23 × 103 | 8.62 × 102 | 1.11 × 105 | 4.14 × 102 | 2.24 × 103 | 6.53 × 102 | 7.45 × 102 | 6.65 × 102 | 6.60 × 102 | |
| F30 | 1.10 × 109 | 4.97 × 108 | 1.35 × 109 | 9.53 × 109 | 2.72 × 106 | 1.70 × 108 | 3.42 × 105 | 6.16 × 105 | 5.34 × 105 | 1.74 × 105 |
| Function | PSO | HHO | GWO | BKA | CPO | DBO | SBOA | HSBOA | QHSBOA |
|---|---|---|---|---|---|---|---|---|---|
| F1 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 4.69 × 10−8 | 3.20 × 10−9 | 3.99 × 10−4 |
| F3 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.69 × 10−11 | 3.02 × 10−11 |
| F4 | 9.92 × 10−11 | 3.34 × 10−11 | 4.50 × 10−11 | 3.02 × 10−11 | 9.21 × 10−5 | 1.21 × 10−10 | 2.38 × 10−3 | 1.58 × 10−4 | 1.87 × 10−5 |
| F5 | 3.69 × 10−11 | 3.02 × 10−11 | 8.20 × 10−7 | 3.02 × 10−11 | 3.02 × 10−11 | 3.69 × 10−11 | 2.46 × 10−1 | 3.04 × 10−1 | 2.61 × 10−2 |
| F6 | 3.02 × 10−11 | 3.02 × 10−11 | 4.98 × 10−11 | 3.02 × 10−11 | 1.17 × 10−3 | 3.02 × 10−11 | 4.03 × 10−3 | 4.22 × 10−4 | 3.77 × 10−4 |
| F7 | 3.02 × 10−11 | 3.02 × 10−11 | 1.85 × 10−8 | 3.02 × 10−11 | 3.69 × 10−11 | 5.49 × 10−11 | 2.16 × 10−3 | 3.37 × 10−5 | 6.67 × 10−3 |
| F8 | 3.02 × 10−11 | 3.02 × 10−11 | 1.43 × 10−5 | 3.34 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 9.47 × 10−1 | 4.73 × 10−1 | 1.70 × 10−2 |
| F9 | 1.53 × 10−5 | 3.02 × 10−11 | 1.55 × 10−9 | 3.02 × 10−11 | 1.15 × 10−1 | 3.02 × 10−11 | 2.32 × 10−2 | 1.96 × 10−1 | 9.23 × 10−1 |
| F10 | 3.69 × 10−11 | 1.17 × 10−9 | 1.77 × 10−3 | 4.42 × 10−6 | 3.02 × 10−11 | 2.87 × 10−10 | 5.20 × 10−1 | 4.20 × 10−1 | 3.48 × 10−1 |
| F11 | 3.02 × 10−11 | 3.69 × 10−11 | 3.02 × 10−11 | 8.15 × 10−11 | 4.20 × 10−10 | 3.02 × 10−11 | 2.27 × 10−3 | 2.81 × 10−2 | 4.51 × 10−2 |
| F12 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.69 × 10−11 | 3.02 × 10−11 | 5.49 × 10−11 | 4.62 × 10−10 | 4.50 × 10−11 |
| F13 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 2.50 × 10−3 | 8.89 × 10−10 | 1.15 × 10−1 | 3.64 × 10−2 | 9.00 × 10−1 |
| F14 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 |
| F15 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 6.12 × 10−10 | 3.02 × 10−11 | 1.41 × 10−9 | 2.67 × 10−9 | 9.53 × 10−7 |
| F16 | 1.29 × 10−9 | 3.02 × 10−11 | 1.64 × 10−5 | 2.03 × 10−9 | 4.98 × 10−11 | 7.39 × 10−11 | 5.59 × 10−1 | 5.89 × 10−1 | 8.07 × 10−1 |
| F17 | 5.97 × 10−9 | 4.08 × 10−11 | 2.15 × 10−6 | 4.18 × 10−9 | 1.17 × 10−3 | 4.98 × 10−11 | 2.17 × 10−1 | 6.52 × 10−1 | 1.19 × 10−1 |
| F18 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 |
| F19 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 4.08 × 10−11 | 3.02 × 10−11 | 1.09 × 10−10 | 7.38 × 10−10 | 1.21 × 10−10 |
| F20 | 4.18 × 10−9 | 1.21 × 10−10 | 7.69 × 10−8 | 3.35 × 10−8 | 1.25 × 10−7 | 3.34 × 10−11 | 5.20 × 10−1 | 2.84 × 10−1 | 3.18 × 10−4 |
| F21 | 3.02 × 10−11 | 3.02 × 10−11 | 9.92 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 9.93 × 10−2 | 1.77 × 10−3 | 1.00 × 10−3 |
| F22 | 2.92 × 10−9 | 5.49 × 10−11 | 2.92 × 10−9 | 2.61 × 10−10 | 2.38 × 10−7 | 3.50 × 10−9 | 1.17 × 10−2 | 1.56 × 10−2 | 1.09 × 10−1 |
| F23 | 3.02 × 10−11 | 3.02 × 10−11 | 1.56 × 10−8 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 2.23 × 10−1 | 5.37 × 10−2 | 4.84 × 10−2 |
| F24 | 3.02 × 10−11 | 3.02 × 10−11 | 3.16 × 10−10 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 4.08 × 10−5 | 1.03 × 10−6 | 1.76 × 10−2 |
| F25 | 9.92 × 10−11 | 3.34 × 10−11 | 5.49 × 10−11 | 3.02 × 10−11 | 2.83 × 10−8 | 2.03 × 10−9 | 6.97 × 10−3 | 3.50 × 10−3 | 2.25 × 10−4 |
| F26 | 5.57 × 10−3 | 1.33 × 10−10 | 1.77 × 10−3 | 9.26 × 10−9 | 7.62 × 10−3 | 1.55 × 10−9 | 7.96 × 10−1 | 8.07 × 10−1 | 7.62 × 10−1 |
| F27 | 1.60 × 10−7 | 3.02 × 10−11 | 3.20 × 10−9 | 3.02 × 10−11 | 3.02 × 10−11 | 7.39 × 10−11 | 4.46 × 10−1 | 7.48 × 10−2 | 5.46 × 10−6 |
| F28 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 1.16 × 10−7 | 3.34 × 10−11 | 3.83 × 10−6 | 4.35 × 10−5 | 1.75 × 10−5 |
| F29 | 2.15 × 10−10 | 3.02 × 10−11 | 8.35 × 10−8 | 3.02 × 10−11 | 8.10 × 10−10 | 3.02 × 10−11 | 5.59 × 10−1 | 6.31 × 10−1 | 1.33 × 10−1 |
| F30 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 2.84 × 10−4 | 1.43 × 10−5 | 3.34 × 10−3 |
| Function | PSO | HHO | GWO | BKA | CPO | DBO | SBOA | HSBOA | QHSBOA |
|---|---|---|---|---|---|---|---|---|---|
| F1 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 5.57 × 10−10 | 4.08 × 10−11 | 2.02 × 10−8 | 5.97 × 10−9 | 3.35 × 10−8 |
| F3 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.69 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.34 × 10−11 | 3.34 × 10−11 |
| F4 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 1.07 × 10−9 | 3.02 × 10−11 | 6.91 × 10−4 | 4.42 × 10−6 | 2.27 × 10−3 |
| F5 | 3.02 × 10−11 | 3.02 × 10−11 | 3.65 × 10−8 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 7.24 × 10−2 | 9.63 × 10−2 | 4.21 × 10−2 |
| F6 | 3.02 × 10−11 | 3.02 × 10−11 | 3.34 × 10−11 | 3.02 × 10−11 | 1.61 × 10−6 | 3.02 × 10−11 | 2.49 × 10−6 | 7.74 × 10−6 | 2.05 × 10−3 |
| F7 | 3.34 × 10−11 | 3.02 × 10−11 | 8.20 × 10−7 | 3.02 × 10−11 | 7.39 × 10−11 | 4.08 × 10−11 | 4.46 × 10−4 | 3.37 × 10−5 | 2.81 × 10−2 |
| F8 | 3.02 × 10−11 | 3.02 × 10−11 | 6.01 × 10−8 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.78 × 10−2 | 1.68 × 10−3 | 2.92 × 10−2 |
| F9 | 1.29 × 10−9 | 3.02 × 10−11 | 2.15 × 10−10 | 3.02 × 10−11 | 7.60 × 10−7 | 3.02 × 10−11 | 3.50 × 10−3 | 3.01 × 10−4 | 4.03 × 10−3 |
| F10 | 3.02 × 10−11 | 6.07 × 10−11 | 5.97 × 10−5 | 9.76 × 10−10 | 3.02 × 10−11 | 5.57 × 10−10 | 3.51 × 10−2 | 9.47 × 10−3 | 2.15 × 10−2 |
| F11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 4.50 × 10−11 | 3.02 × 10−11 | 8.29 × 10−6 | 7.09 × 10−8 | 1.16 × 10−7 |
| F12 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 4.50 × 10−11 | 4.62 × 10−10 | 9.92 × 10−11 |
| F13 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 5.56 × 10−4 | 3.02 × 10−11 | 4.20 × 10−1 | 3.79 × 10−1 | 8.65 × 10−1 |
| F14 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 |
| F15 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 1.02 × 10−1 | 4.98 × 10−11 | 7.98 × 10−2 | 2.32 × 10−2 | 9.23 × 10−1 |
| F16 | 4.50 × 10−11 | 3.02 × 10−11 | 6.36 × 10−5 | 1.33 × 10−10 | 3.02 × 10−11 | 3.02 × 10−11 | 1.96 × 10−1 | 6.35 × 10−2 | 1.91 × 10−1 |
| F17 | 2.61 × 10−10 | 4.50 × 10−11 | 1.78 × 10−4 | 1.78 × 10−10 | 1.96 × 10−10 | 3.02 × 10−11 | 9.23 × 10−1 | 4.83 × 10−1 | 3.04 × 10−1 |
| F18 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 |
| F19 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 5.79 × 10−1 | 4.98 × 10−11 | 6.31 × 10−1 | 2.06 × 10−1 | 4.92 × 10−1 |
| F20 | 9.76 × 10−10 | 8.10 × 10−10 | 1.95 × 10−3 | 3.52 × 10−7 | 1.61 × 10−10 | 5.07 × 10−10 | 9.00 × 10−1 | 4.92 × 10−1 | 8.42 × 10−1 |
| F21 | 3.02 × 10−11 | 3.02 × 10−11 | 1.09 × 10−10 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 2.50 × 10−3 | 2.84 × 10−4 | 1.91 × 10−2 |
| F22 | 2.37 × 10−10 | 3.69 × 10−11 | 1.29 × 10−6 | 1.78 × 10−10 | 3.81 × 10−7 | 2.37 × 10−10 | 3.77 × 10−4 | 6.20 × 10−4 | 1.44 × 10−2 |
| F23 | 3.02 × 10−11 | 3.02 × 10−11 | 5.07 × 10−10 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 1.78 × 10−4 | 2.62 × 10−3 | 4.84 × 10−2 |
| F24 | 3.02 × 10−11 | 3.02 × 10−11 | 6.70 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 5.46 × 10−6 | 8.89 × 10−10 | 1.77 × 10−3 |
| F25 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 4.50 × 10−11 | 5.49 × 10−11 | 5.19 × 10−7 | 2.68 × 10−6 | 2.03 × 10−7 |
| F26 | 6.28 × 10−6 | 5.49 × 10−11 | 1.53 × 10−5 | 4.98 × 10−11 | 5.56 × 10−4 | 4.57 × 10−9 | 1.15 × 10−1 | 2.32 × 10−2 | 6.35 × 10−2 |
| F27 | 1.10 × 10−8 | 3.02 × 10−11 | 3.02 × 10−11 | 3.69 × 10−11 | 3.02 × 10−11 | 4.50 × 10−11 | 6.73 × 10−1 | 7.62 × 10−1 | 9.06 × 10−8 |
| F28 | 6.70 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 1.03 × 10−6 | 9.26 × 10−9 | 1.69 × 10−9 |
| F29 | 3.02 × 10−11 | 3.02 × 10−11 | 9.92 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 4.50 × 10−11 | 9.47 × 10−1 | 9.93 × 10−2 | 3.99 × 10−4 |
| F30 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 9.88 × 10−3 | 5.94 × 10−2 | 7.29 × 10−3 |
| Function | PSO | HHO | GWO | BKA | CPO | DBO | SBOA | HSBOA | QHSBOA |
|---|---|---|---|---|---|---|---|---|---|
| F1 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 2.02 × 10−8 | 3.02 × 10−11 | 3.32 × 10−6 | 9.23 × 10−1 | 1.25 × 10−5 |
| F3 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 1.46 × 10−10 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.34 × 10−11 | 3.02 × 10−11 |
| F4 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 2.13 × 10−5 | 4.42 × 10−6 | 6.74 × 10−6 |
| F5 | 3.02 × 10−11 | 3.02 × 10−11 | 4.80 × 10−7 | 3.02 × 10−11 | 3.02 × 10−11 | 3.34 × 10−11 | 3.78 × 10−2 | 1.77 × 10−3 | 1.37 × 10−3 |
| F6 | 3.02 × 10−11 | 3.02 × 10−11 | 7.77 × 10−9 | 3.02 × 10−11 | 3.09 × 10−6 | 3.02 × 10−11 | 5.83 × 10−3 | 4.98 × 10−4 | 1.41 × 10−4 |
| F7 | 7.69 × 10−8 | 3.02 × 10−11 | 4.38 × 10−1 | 3.02 × 10−11 | 7.66 × 10−5 | 3.69 × 10−11 | 5.37 × 10−2 | 3.16 × 10−5 | 6.31 × 10−1 |
| F8 | 3.02 × 10−11 | 3.02 × 10−11 | 4.74 × 10−6 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 2.42 × 10−2 | 1.00 × 10−3 | 4.21 × 10−2 |
| F9 | 3.34 × 10−11 | 3.02 × 10−11 | 8.35 × 10−8 | 3.08 × 10−8 | 7.39 × 10−11 | 3.02 × 10−11 | 5.01 × 10−1 | 4.46 × 10−4 | 1.71 × 10−1 |
| F10 | 3.02 × 10−11 | 3.02 × 10−11 | 6.20 × 10−4 | 4.11 × 10−7 | 3.02 × 10−11 | 1.09 × 10−10 | 1.70 × 10−2 | 6.53 × 10−7 | 3.18 × 10−1 |
| F11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 1.46 × 10−10 | 3.02 × 10−11 |
| F12 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 5.57 × 10−10 | 3.02 × 10−11 | 5.00 × 10−9 | 9.76 × 10−10 | 1.85 × 10−8 |
| F13 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 8.48 × 10−9 | 3.50 × 10−9 | 6.20 × 10−4 |
| F14 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 |
| F15 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 9.83 × 10−8 | 3.02 × 10−11 | 9.51 × 10−6 | 1.25 × 10−4 | 1.17 × 10−3 |
| F16 | 3.02 × 10−11 | 3.02 × 10−11 | 4.31 × 10−8 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 5.01 × 10−2 | 3.78 × 10−2 | 1.33 × 10−1 |
| F17 | 3.02 × 10−11 | 3.02 × 10−11 | 4.35 × 10−5 | 5.49 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 2.64 × 10−1 | 1.56 × 10−2 | 6.95 × 10−1 |
| F18 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.69 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 |
| F19 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 1.58 × 10−4 | 3.02 × 10−11 | 4.55 × 10−1 | 1.58 × 10−1 | 6.41 × 10−1 |
| F20 | 3.02 × 10−11 | 5.49 × 10−11 | 3.83 × 10−6 | 1.01 × 10−8 | 3.02 × 10−11 | 3.02 × 10−11 | 3.83 × 10−5 | 5.75 × 10−2 | 9.07 × 10−3 |
| F21 | 3.02 × 10−11 | 3.02 × 10−11 | 1.61 × 10−10 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 1.11 × 10−4 | 1.07 × 10−7 | 4.68 × 10−2 |
| F22 | 3.02 × 10−11 | 3.02 × 10−11 | 1.12 × 10−1 | 5.53 × 10−8 | 3.02 × 10−11 | 3.02 × 10−11 | 2.97 × 10−1 | 1.86 × 10−3 | 5.49 × 10−1 |
| F23 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 2.53 × 10−4 | 1.02 × 10−5 | 2.77 × 10−5 |
| F24 | 3.02 × 10−11 | 3.02 × 10−11 | 3.34 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 6.36 × 10−5 | 5.86 × 10−6 | 3.11 × 10−1 |
| F25 | 3.16 × 10−10 | 3.02 × 10−11 | 3.34 × 10−11 | 3.02 × 10−11 | 5.46 × 10−9 | 4.50 × 10−11 | 4.23 × 10−3 | 4.36 × 10−2 | 5.86 × 10−6 |
| F26 | 7.66 × 10−5 | 3.34 × 10−11 | 3.51 × 10−2 | 3.02 × 10−11 | 9.51 × 10−6 | 2.61 × 10−10 | 2.64 × 10−1 | 2.71 × 10−1 | 1.58 × 10−1 |
| F27 | 5.86 × 10−6 | 3.02 × 10−11 | 1.09 × 10−10 | 3.02 × 10−11 | 1.61 × 10−10 | 5.49 × 10−11 | 9.00 × 10−1 | 2.84 × 10−1 | 1.86 × 10−6 |
| F28 | 6.70 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 2.28 × 10−5 | 4.23 × 10−3 | 1.73 × 10−7 |
| F29 | 3.02 × 10−11 | 3.02 × 10−11 | 1.46 × 10−10 | 3.02 × 10−11 | 3.02 × 10−11 | 3.69 × 10−11 | 1.11 × 10−3 | 7.98 × 10−2 | 1.41 × 10−4 |
| F30 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 9.83 × 10−8 | 4.18 × 10−9 | 1.49 × 10−6 |
| Test Functions and Dimensions | Algorithm and the Friedman Test | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Algorithm | PSO | HHO | GWO | BKA | CPO | DBO | SBOA | HSBOA | QHSBOA | ASHSBOA | |
| CEC2017-30D | Friedman | 7.231 | 8.756 | 6.546 | 7.633 | 5.014 | 7.955 | 3.230 | 3.290 | 3.299 | 2.046 |
| Rankings | 7 | 10 | 6 | 8 | 5 | 9 | 2 | 3 | 4 | 1 | |
| CEC2017-50D | Friedman | 7.436 | 8.380 | 6.399 | 7.772 | 5.623 | 7.971 | 3.111 | 3.215 | 3.118 | 1.974 |
| Rankings | 7 | 10 | 6 | 8 | 5 | 9 | 2 | 4 | 3 | 1 | |
| CEC2017-100D | Friedman | 7.467 | 8.152 | 6.070 | 7.751 | 6.070 | 8.137 | 3.166 | 3.252 | 3.067 | 1.870 |
| Rankings | 7 | 10 | 5.5 | 8 | 5.5 | 9 | 3 | 4 | 2 | 1 | |
| PSO | HHO | GWO | BKA | CPO | DBO | SBOA | HSBOA | QHSBOA | ASHSBOA | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| mean | F1 | 4.24 × 102 | 1.15 × 103 | 3.07 × 103 | 6.96 × 102 | 3.87 × 102 | 1.44 × 103 | 3.00 × 102 | 3.00 × 102 | 3.00 × 102 | 3.00 × 102 |
| F2 | 4.26 × 102 | 4.45 × 102 | 4.30 × 102 | 4.20 × 102 | 4.01 × 102 | 4.41 × 102 | 4.06 × 102 | 4.08 × 102 | 4.11 × 102 | 4.07 × 102 | |
| F3 | 6.03 × 102 | 6.38 × 102 | 6.02 × 102 | 6.27 × 102 | 6.00 × 102 | 6.10 × 102 | 6.00 × 102 | 6.00 × 102 | 6.00 × 102 | 6.00 × 102 | |
| F4 | 8.25 × 102 | 8.27 × 102 | 8.13 × 102 | 8.20 × 102 | 8.21 × 102 | 8.33 × 102 | 8.11 × 102 | 8.11 × 102 | 8.14 × 102 | 8.14 × 102 | |
| F5 | 9.05 × 102 | 1.42 × 103 | 9.41 × 102 | 1.13 × 103 | 9.00 × 102 | 1.01 × 103 | 9.00 × 102 | 9.00 × 102 | 9.00 × 102 | 9.00 × 102 | |
| F6 | 6.52 × 103 | 6.53 × 103 | 5.50 × 103 | 2.81 × 103 | 1.83 × 103 | 5.59 × 103 | 4.03 × 103 | 4.50 × 103 | 3.07 × 103 | 1.80 × 103 | |
| F7 | 2.03 × 103 | 2.09 × 103 | 2.03 × 103 | 2.05 × 103 | 2.01 × 103 | 2.04 × 103 | 2.01 × 103 | 2.01 × 103 | 2.02 × 103 | 2.01 × 103 | |
| F8 | 2.26 × 103 | 2.23 × 103 | 2.23 × 103 | 2.23 × 103 | 2.22 × 103 | 2.23 × 103 | 2.22 × 103 | 2.22 × 103 | 2.23 × 103 | 2.22 × 103 | |
| F9 | 2.54 × 103 | 2.61 × 103 | 2.59 × 103 | 2.55 × 103 | 2.53 × 103 | 2.56 × 103 | 2.53 × 103 | 2.53 × 103 | 2.53 × 103 | 2.53 × 103 | |
| F10 | 2.57 × 103 | 2.59 × 103 | 2.57 × 103 | 2.60 × 103 | 2.52 × 103 | 2.56 × 103 | 2.55 × 103 | 2.51 × 103 | 2.56 × 103 | 2.53 × 103 | |
| F11 | 2.76 × 103 | 2.78 × 103 | 2.79 × 103 | 2.72 × 103 | 2.61 × 103 | 2.82 × 103 | 2.71 × 103 | 2.68 × 103 | 2.76 × 103 | 2.69 × 103 | |
| F12 | 2.87 × 103 | 2.93 × 103 | 2.87 × 103 | 2.87 × 103 | 2.87 × 103 | 2.87 × 103 | 2.86 × 103 | 2.86 × 103 | 2.87 × 103 | 2.86 × 103 | |
| std | F1 | 7.14 × 101 | 5.78 × 102 | 2.14 × 103 | 1.41 × 103 | 6.41 × 101 | 1.42 × 103 | 4.03 × 10−1 | 2.71 × 10−1 | 2.39 × 10−2 | 2.36 × 10−14 |
| F2 | 7.12 × 101 | 3.66 × 101 | 2.42 × 101 | 4.77 × 101 | 1.78 × 100 | 6.16 × 101 | 3.42 × 100 | 1.25 × 101 | 2.24 × 101 | 1.26 × 101 | |
| F3 | 1.45 × 100 | 1.23 × 101 | 1.81 × 100 | 9.51 × 100 | 2.75 × 10−3 | 8.66 × 100 | 3.04 × 10−4 | 9.90 × 10−4 | 3.10 × 10−1 | 1.05 × 10−1 | |
| F4 | 8.22 × 100 | 8.85 × 100 | 6.24 × 100 | 7.89 × 100 | 5.51 × 100 | 1.24 × 101 | 5.11 × 100 | 3.73 × 100 | 5.86 × 100 | 6.65 × 100 | |
| F5 | 3.23 × 100 | 1.55 × 102 | 6.64 × 101 | 1.14 × 102 | 3.84 × 10−4 | 1.31 × 102 | 1.18 × 10−1 | 2.41 × 10−1 | 7.15 × 10−1 | 2.13 × 10−1 | |
| F6 | 3.30 × 103 | 3.34 × 103 | 2.62 × 103 | 1.69 × 103 | 2.90 × 101 | 2.21 × 103 | 1.88 × 103 | 2.10 × 103 | 1.43 × 103 | 2.57 × 100 | |
| F7 | 5.28 × 100 | 3.64 × 101 | 1.28 × 101 | 1.83 × 101 | 5.22 × 100 | 1.97 × 101 | 1.00 × 101 | 9.79 × 100 | 3.97 × 101 | 8.88 × 100 | |
| F8 | 5.51 × 101 | 1.23 × 101 | 3.01 × 101 | 2.13 × 101 | 4.45 × 100 | 5.53 × 100 | 8.47 × 100 | 7.37 × 100 | 3.26 × 101 | 9.20 × 100 | |
| F9 | 4.50 × 101 | 3.98 × 101 | 4.04 × 101 | 4.44 × 101 | 4.57 × 10−3 | 4.26 × 101 | 1.46 × 10−13 | 2.07 × 10−13 | 6.38 × 10−13 | 2.68 × 101 | |
| F10 | 6.29 × 101 | 9.34 × 101 | 5.82 × 101 | 1.68 × 102 | 4.49 × 101 | 6.97 × 101 | 5.51 × 101 | 3.78 × 101 | 5.70 × 101 | 5.03 × 101 | |
| F11 | 1.36 × 102 | 1.39 × 102 | 1.50 × 102 | 1.75 × 102 | 5.48 × 101 | 1.96 × 102 | 1.35 × 102 | 1.10 × 102 | 1.47 × 102 | 1.44 × 102 | |
| F12 | 1.06 × 101 | 5.22 × 101 | 7.95 × 100 | 4.00 × 100 | 8.84 × 10−1 | 1.08 × 101 | 1.98 × 100 | 2.06 × 100 | 4.75 × 100 | 1.38 × 100 |
| PSO | HHO | GWO | BKA | CPO | DBO | SBOA | HSBOA | QHSBOA | ASHSBOA | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| mean | F1 | 7.06 × 103 | 2.81 × 104 | 1.54 × 104 | 4.12 × 103 | 1.23 × 104 | 3.53 × 104 | 2.37 × 103 | 7.67 × 102 | 2.55 × 103 | 3.00 × 102 |
| F2 | 4.72 × 102 | 5.36 × 102 | 5.07 × 102 | 5.82 × 102 | 4.61 × 102 | 5.40 × 102 | 4.55 × 102 | 4.60 × 102 | 4.62 × 102 | 4.47 × 102 | |
| F3 | 6.10 × 102 | 6.64 × 102 | 6.08 × 102 | 6.53 × 102 | 6.00 × 102 | 6.31 × 102 | 6.00 × 102 | 6.00 × 102 | 6.01 × 102 | 6.00 × 102 | |
| F4 | 9.10 × 102 | 8.90 × 102 | 8.63 × 102 | 8.83 × 102 | 8.97 × 102 | 9.16 × 102 | 8.38 × 102 | 8.37 × 102 | 8.48 × 102 | 8.38 × 102 | |
| F5 | 1.03 × 103 | 2.92 × 103 | 1.30 × 103 | 2.00 × 103 | 9.13 × 102 | 2.08 × 103 | 9.18 × 102 | 9.53 × 102 | 9.78 × 102 | 9.37 × 102 | |
| F6 | 2.11 × 106 | 2.10 × 105 | 6.68 × 106 | 1.62 × 107 | 2.98 × 104 | 4.95 × 105 | 8.07 × 103 | 9.06 × 103 | 4.85 × 103 | 1.96 × 103 | |
| F7 | 2.11 × 103 | 2.19 × 103 | 2.10 × 103 | 2.12 × 103 | 2.06 × 103 | 2.14 × 103 | 2.04 × 103 | 2.04 × 103 | 2.06 × 103 | 2.04 × 103 | |
| F8 | 2.28 × 103 | 2.28 × 103 | 2.26 × 103 | 2.30 × 103 | 2.23 × 103 | 2.32 × 103 | 2.23 × 103 | 2.23 × 103 | 2.25 × 103 | 2.22 × 103 | |
| F9 | 2.50 × 103 | 2.55 × 103 | 2.53 × 103 | 2.52 × 103 | 2.48 × 103 | 2.51 × 103 | 2.48 × 103 | 2.48 × 103 | 2.48 × 103 | 2.48 × 103 | |
| F10 | 3.97 × 103 | 4.44 × 103 | 3.45 × 103 | 4.27 × 103 | 2.54 × 103 | 3.80 × 103 | 2.62 × 103 | 2.55 × 103 | 2.94 × 103 | 2.62 × 103 | |
| F11 | 3.37 × 103 | 3.55 × 103 | 3.52 × 103 | 4.25 × 103 | 2.93 × 103 | 3.25 × 103 | 2.92 × 103 | 2.93 × 103 | 2.94 × 103 | 2.92 × 103 | |
| F12 | 3.00 × 103 | 3.25 × 103 | 2.97 × 103 | 3.12 × 103 | 2.99 × 103 | 3.03 × 103 | 2.95 × 103 | 2.95 × 103 | 2.97 × 103 | 2.95 × 103 | |
| std | F1 | 5.09 × 103 | 9.33 × 103 | 6.93 × 103 | 2.79 × 103 | 3.15 × 103 | 1.13 × 104 | 2.36 × 103 | 5.12 × 102 | 1.65 × 103 | 8.06 × 10−2 |
| F2 | 2.03 × 101 | 5.25 × 101 | 3.45 × 101 | 4.06 × 102 | 9.49 × 100 | 1.04 × 102 | 1.67 × 101 | 1.69 × 101 | 1.53 × 101 | 1.88 × 101 | |
| F3 | 3.88 × 100 | 9.54 × 100 | 5.62 × 100 | 7.95 × 100 | 1.31 × 10−1 | 1.16 × 101 | 4.14 × 10−1 | 4.93 × 10−1 | 2.25 × 100 | 1.81 × 10−1 | |
| F4 | 1.89 × 101 | 1.20 × 101 | 2.70 × 101 | 2.55 × 101 | 1.16 × 101 | 3.67 × 101 | 1.28 × 101 | 1.64 × 101 | 1.68 × 101 | 1.46 × 101 | |
| F5 | 1.24 × 102 | 3.73 × 102 | 3.27 × 102 | 2.28 × 102 | 2.01 × 101 | 4.61 × 102 | 2.30 × 101 | 1.00 × 102 | 1.46 × 102 | 9.54 × 101 | |
| F6 | 1.88 × 106 | 1.20 × 105 | 1.83 × 107 | 6.91 × 107 | 2.92 × 104 | 1.40 × 106 | 5.87 × 103 | 7.72 × 103 | 3.52 × 103 | 4.89 × 102 | |
| F7 | 4.35 × 101 | 7.21 × 101 | 4.90 × 101 | 4.89 × 101 | 9.67 × 100 | 5.45 × 101 | 1.02 × 101 | 9.37 × 100 | 3.95 × 101 | 1.33 × 101 | |
| F8 | 6.59 × 101 | 8.53 × 101 | 5.03 × 101 | 9.41 × 101 | 2.02 × 100 | 9.20 × 101 | 2.90 × 100 | 2.94 × 100 | 4.50 × 101 | 2.20 × 100 | |
| F9 | 2.77 × 101 | 4.90 × 101 | 4.81 × 101 | 7.73 × 101 | 5.81 × 10−1 | 2.53 × 101 | 6.41 × 10−3 | 4.80 × 10−3 | 6.25 × 10−3 | 1.47 × 10−6 | |
| F10 | 1.07 × 103 | 6.60 × 102 | 7.98 × 102 | 1.03 × 103 | 7.66 × 101 | 1.19 × 103 | 2.35 × 102 | 1.13 × 102 | 3.79 × 102 | 1.88 × 102 | |
| F11 | 2.82 × 102 | 7.85 × 102 | 3.62 × 102 | 1.19 × 103 | 4.70 × 101 | 7.42 × 102 | 7.62 × 101 | 4.68 × 101 | 1.87 × 102 | 7.74 × 101 | |
| F12 | 4.34 × 101 | 2.05 × 102 | 1.91 × 101 | 1.62 × 102 | 1.01 × 101 | 4.40 × 101 | 8.27 × 100 | 8.72 × 100 | 4.87 × 101 | 1.10 × 101 |
| Function | PSO | HHO | GWO | BKA | CPO | DBO | SBOA | HSBOA | QHSBOA |
|---|---|---|---|---|---|---|---|---|---|
| F1 | 5.14 × 10−12 | 5.14 × 10−12 | 5.14 × 10−12 | 5.14 × 10−12 | 5.14 × 10−12 | 5.14 × 10−12 | 5.14 × 10−12 | 5.14 × 10−12 | 5.14 × 10−12 |
| F2 | 1.97 × 10−4 | 2.06 × 10−7 | 7.80 × 10−8 | 3.77 × 10−1 | 3.18 × 10−2 | 2.21 × 10−5 | 1.45 × 10−1 | 4.78 × 10−2 | 3.32 × 10−1 |
| F3 | 2.96 × 10−11 | 2.96 × 10−11 | 5.95 × 10−11 | 2.96 × 10−11 | 6.67 × 10−6 | 3.27 × 10−11 | 7.73 × 10−1 | 4.73 × 10−1 | 1.76 × 10−1 |
| F4 | 1.24 × 10−5 | 1.28 × 10−6 | 4.64 × 10−1 | 3.18 × 10−3 | 2.52 × 10−4 | 3.97 × 10−9 | 1.37 × 10−1 | 6.56 × 10−2 | 8.30 × 10−1 |
| F5 | 2.23 × 10−11 | 2.23 × 10−11 | 2.41 × 10−10 | 2.23 × 10−11 | 6.61 × 10−1 | 2.23 × 10−11 | 2.61 × 10−1 | 2.14 × 10−1 | 1.16 × 10−2 |
| F6 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 4.50 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 |
| F7 | 1.17 × 10−9 | 3.02 × 10−11 | 8.89 × 10−10 | 3.69 × 10−11 | 2.46 × 10−1 | 1.09 × 10−10 | 4.68 × 10−2 | 3.27 × 10−2 | 4.21 × 10−2 |
| F8 | 2.87 × 10−10 | 3.02 × 10−11 | 1.46 × 10−10 | 4.50 × 10−11 | 4.86 × 10−3 | 2.61 × 10−10 | 8.77 × 10−2 | 2.75 × 10−3 | 1.44 × 10−2 |
| F9 | 3.69 × 10−11 | 3.32 × 10−11 | 4.10 × 10−11 | 4.10 × 10−11 | 4.56 × 10−11 | 1.00 × 10−7 | 3.38 × 10−1 | 5.76 × 10−2 | 6.44 × 10−9 |
| F10 | 5.86 × 10−6 | 6.05 × 10−7 | 8.56 × 10−4 | 1.29 × 10−6 | 7.96 × 10−3 | 6.28 × 10−6 | 3.04 × 10−1 | 5.11 × 10−1 | 3.92 × 10−2 |
| F11 | 1.23 × 10−4 | 2.70 × 10−5 | 2.52 × 10−4 | 3.56 × 10−4 | 5.68 × 10−3 | 2.22 × 10−5 | 2.52 × 10−4 | 8.16 × 10−4 | 4.00 × 10−5 |
| F12 | 4.21 × 10−8 | 4.35 × 10−11 | 1.76 × 10−1 | 4.29 × 10−1 | 2.17 × 10−1 | 1.97 × 10−6 | 7.11 × 10−7 | 8.20 × 10−5 | 8.76 × 10−1 |
| Function | PSO | HHO | GWO | BKA | CPO | DBO | SBOA | HSBOA | QHSBOA |
|---|---|---|---|---|---|---|---|---|---|
| F1 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 |
| F2 | 1.61 × 10−6 | 4.08 × 10−11 | 8.89 × 10−10 | 1.21 × 10−10 | 4.64 × 10−5 | 2.78 × 10−7 | 1.56 × 10−2 | 1.58 × 10−4 | 1.64 × 10−5 |
| F3 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 1.60 × 10−7 | 3.02 × 10−11 | 3.99 × 10−4 | 2.75 × 10−3 | 1.09 × 10−5 |
| F4 | 3.69 × 10−11 | 6.70 × 10−11 | 7.22 × 10−6 | 1.29 × 10−9 | 4.98 × 10−11 | 8.99 × 10−11 | 9.23 × 10−1 | 6.10 × 10−1 | 2.42 × 10−2 |
| F5 | 4.69 × 10−8 | 3.02 × 10−11 | 2.03 × 10−9 | 3.02 × 10−11 | 3.04 × 10−1 | 3.69 × 10−11 | 8.77 × 10−2 | 4.64 × 10−3 | 2.75 × 10−3 |
| F6 | 3.02 × 10−11 | 3.02 × 10−11 | 3.34 × 10−11 | 4.08 × 10−11 | 3.69 × 10−11 | 5.49 × 10−11 | 1.21 × 10−10 | 1.21 × 10−10 | 2.15 × 10−10 |
| F7 | 7.39 × 10−11 | 3.02 × 10−11 | 1.55 × 10−9 | 2.37 × 10−10 | 6.01 × 10−8 | 8.99 × 10−11 | 2.84 × 10−1 | 3.71 × 10−1 | 6.79 × 10−2 |
| F8 | 3.02 × 10−11 | 3.02 × 10−11 | 8.10 × 10−10 | 6.07 × 10−11 | 1.96 × 10−10 | 6.12 × 10−10 | 3.03 × 10−3 | 2.13 × 10−4 | 4.23 × 10−3 |
| F9 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 |
| F10 | 5.19 × 10−7 | 4.98 × 10−11 | 1.61 × 10−6 | 2.19 × 10−8 | 2.17 × 10−1 | 1.11 × 10−6 | 3.55 × 10−1 | 9.47 × 10−1 | 1.68 × 10−4 |
| F11 | 1.29 × 10−9 | 5.07 × 10−10 | 8.15 × 10−11 | 3.02 × 10−11 | 3.99 × 10−4 | 9.53 × 10−7 | 1.11 × 10−3 | 3.99 × 10−4 | 7.62 × 10−3 |
| F12 | 2.57 × 10−7 | 3.02 × 10−11 | 2.88 × 10−6 | 1.29 × 10−9 | 8.15 × 10−11 | 6.70 × 10−11 | 4.51 × 10−2 | 1.76 × 10−2 | 1.63 × 10−2 |
| Test Functions and Dimensions | Algorithm and the Friedman Test | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Algorithm | PSO | HHO | GWO | BKA | CPO | DBO | SBOA | HSBOA | QHSBOA | ASHSBOA | |
| CEC2022-10D | Friedman | 7.083 | 8.783 | 6.822 | 6.619 | 4.264 | 7.596 | 3.453 | 3.536 | 4.090 | 2.753 |
| Rankings | 8 | 10 | 7 | 6 | 5 | 9 | 2 | 3 | 4 | 1 | |
| CEC2022-20D | Friedman | 7.139 | 8.781 | 6.800 | 7.539 | 5.111 | 7.717 | 3.047 | 2.975 | 3.839 | 2.053 |
| Rankings | 7 | 10 | 6 | 8 | 5 | 9 | 3 | 2 | 4 | 1 | |
| Algorithms | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Mean | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Scenario 1 | PSO | 10,423.8 | 10,008,703.2 | 8249.2 | 8766.0 | 9697.0 | 9344.5 | 9707.0 | 8913.2 | 8462.6 | 9604.9 | 1,009,187.1 |
| HHO | 7856.1 | 10,779.8 | 8668.5 | 7674.1 | 10,008,918.7 | 8950.1 | 7640.6 | 7694.9 | 7673.8 | 10,222.3 | 1,008,607.9 | |
| GWO | 8406.4 | 8741.3 | 8697.6 | 8559.3 | 8099.7 | 9146.9 | 8456.2 | 8373.0 | 8169.6 | 8097.9 | 8474.8 | |
| BKA | 8987.0 | 9160.9 | 9797.8 | 9017.5 | 9391.3 | 10,014,197.9 | 10,008.2 | 8858.7 | 10,915.8 | 8833.0 | 1,009,916.8 | |
| CPO | 10,208.2 | 10,403.7 | 9946.0 | 8892.7 | 9118.5 | 9632.8 | 9909.8 | 9770.1 | 10,212.7 | 10,180.8 | 9827.5 | |
| DBO | 10,307.0 | 12,081.1 | 10,478.8 | 10,878.3 | 10,986.7 | 9781.6 | 9501.4 | 10,742.6 | 9974.1 | 8951.4 | 10,368.3 | |
| SBOA | 8398.9 | 8639.3 | 8322.5 | 8978.2 | 8146.7 | 8600.6 | 8159.9 | 9191.6 | 8141.6 | 8137.6 | 8471.7 | |
| HSBOA | 9454.3 | 8620.5 | 8848.1 | 8476.5 | 8194.1 | 8471.8 | 8893.7 | 8714.7 | 8450.1 | 8585.9 | 8671.0 | |
| QHSBOA | 8265.3 | 8670.2 | 8548.4 | 8647.8 | 7910.4 | 7662.6 | 8771.3 | 8408.1 | 7581.1 | 8071.7 | 8253.7 | |
| ASHSBOA | 8066.3 | 8600.6 | 8263.8 | 7655.9 | 8370.7 | 7702.2 | 8026.5 | 7882.5 | 8672.2 | 8046.9 | 8128.8 | |
| Scenario 2 | PSO | 10,391.2 | 11,414.4 | 10,952.0 | 10,648.6 | 10,011,203.5 | 10,002.5 | 10,312.5 | 11,807.0 | 9848.5 | 10,759.4 | 1,010,733.9 |
| HHO | 7620.7 | 8010.8 | 10,007,871.8 | 7622.1 | 7626.2 | 7764.7 | 30,008,116.7 | 7597.0 | 7866.0 | 7849.6 | 4,007,794.6 | |
| GWO | 9254.6 | 9126.5 | 10,009,718.2 | 9431.2 | 10,009,498.5 | 10,009,330.6 | 11,073.6 | 10,008,894.5 | 10,009,942.3 | 10,009,387.6 | 6,009,565.8 | |
| BKA | 50,009,526.7 | 10,009,065.7 | 40,009,158.8 | 10,009,333.7 | 60,009,499.9 | 40,009,262.4 | 20,012,471.3 | 30,011,804.9 | 10,818.6 | 60,009,499.9 | 32,010,044.2 | |
| CPO | 20,010,465.3 | 20,010,150.8 | 20,011,750.7 | 40,011,503.2 | 30,012,529.1 | 30,009,572.0 | 20,010,610.5 | 30,009,970.3 | 12,491.9 | 30,009,956.8 | 24,010,900.1 | |
| DBO | 50,009,315.2 | 20,009,067.5 | 50,009,403.4 | 20,009,296.6 | 9561.7 | 10,009,921.9 | 20,009,481.2 | 20,009,829.0 | 30,009,349.1 | 20,009,189.3 | 24,009,441.5 | |
| SBOA | 10,099.1 | 11,942.9 | 11,068.9 | 9499.5 | 10,526.0 | 10,999.6 | 10,290.6 | 10,369.6 | 10,986.4 | 9881.3 | 10,566.4 | |
| HSBOA | 11,018.4 | 10,198.0 | 10,010,130.9 | 10,256.9 | 11,323.7 | 10,010,787.8 | 11,105.5 | 10,010,235.4 | 10,534.3 | 11,332.0 | 3,010,692.3 | |
| QHSBOA | 9429.9 | 9525.2 | 8939.3 | 10,651.5 | 10,428.5 | 10,009,972.2 | 9576.1 | 11,038.3 | 20,009,208.2 | 11,842.7 | 3,010,061.2 | |
| ASHSBOA | 10,285.5 | 9757.2 | 9544.9 | 8698.1 | 9093.1 | 8786.7 | 8255.0 | 10,323.4 | 9349.6 | 10,191.1 | 9428.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, X.; Liu, R.; Liu, X. Simulation Application of Adaptive Strategy Hybrid Secretary Bird Optimization Algorithm in Multi-UAV 3D Path Planning. Computers 2025, 14, 439. https://doi.org/10.3390/computers14100439
Zheng X, Liu R, Liu X. Simulation Application of Adaptive Strategy Hybrid Secretary Bird Optimization Algorithm in Multi-UAV 3D Path Planning. Computers. 2025; 14(10):439. https://doi.org/10.3390/computers14100439
Chicago/Turabian StyleZheng, Xiaojun, Rundong Liu, and Xiaoyang Liu. 2025. "Simulation Application of Adaptive Strategy Hybrid Secretary Bird Optimization Algorithm in Multi-UAV 3D Path Planning" Computers 14, no. 10: 439. https://doi.org/10.3390/computers14100439
APA StyleZheng, X., Liu, R., & Liu, X. (2025). Simulation Application of Adaptive Strategy Hybrid Secretary Bird Optimization Algorithm in Multi-UAV 3D Path Planning. Computers, 14(10), 439. https://doi.org/10.3390/computers14100439