Measure Student Aptitude in Learning Programming in Higher Education—A Data Analysis

Abstract

Analyzing student performance in Introductory Programming courses in Higher Education is critical for early intervention and improved learning outcomes. This study explores the potential of a cognitive test for student success in an Introductory Programming course by analyzing data from 180 students, including Freshmen and Repeating Students, using descriptive statistics, correlation analysis, Categorical Principal Component Analysis and Item Response Theory models analysis. Analysis of the cognitive test revealed that some reasoning questions presented a statistically significant correlation, albeit of weak magnitude, with the course grades, particularly for freshman students. The development of models for predicting student performance in Introductory Programming using cognitive tests is also being explored. This study found that reasoning skills, namely logical reasoning and sequence completion, were more predictive of success in programming than general ability. The study also showed that a Programming Cognitive Test can be a useful tool for identifying students at risk of failure, particularly for freshmen students.

1. Introduction

Introductory Programming (IP) remains a challenge for students who start programming for the first time [1,2,3,4], with a high failure rate in the first programming subject in higher education [5,6]. Due to this, research was done around the factors that influence the learning process and the ways and strategies to overcome them [7]. Several factors were found in the literature to explain this problem, such as the ability to think abstractly [8], previous experience of programming [9,10], the effect of teaching approaches that consider students’ motivational strategies and learning preferences and learning styles [11,12], mathematics skills [13], or problem-solving skills [14].

Quite a few experiments and studies have also been conducted with the goal of investigating the problem and helping to minimize it [15]. Numerous tools and strategies were developed to contribute to the solution of this problem, some of which included the development of specialized platforms to help students in the process of learning and understanding how to program [16,17,18,19], and even the use of new technologies, such as robots, was analyzed and tested to see if they help students learn to program [20], and while each has its advantages, none of them have yet solved it completely. However, there is a lack of consensus on the most effective methods, and the role of student aptitude remains largely unexplored. This study aims to contribute to the ongoing discussion by evaluating the potential of a Programming Cognitive Test (PCT) as an instrument for early diagnosis and prediction of student performance in Introductory Programming (IP). The study focuses on Freshmen Students (FS) and Repeating Students (RS) to identify those who may benefit from additional academic support.

The first curricular unit of programming is extremely important to aspiring computer engineers because it serves as the foundation on which their entire educational and professional path is built [9,10]. Programming aptitude is not only a prerequisite but also an essential skill that serves as the foundation for a future engineer’s abilities. This skill lays the groundwork for understanding complex algorithms, problem-solving methodologies, and the fundamentals of software development [21]. Early intervention is crucial for addressing these challenges and improving student learning outcomes [22,23]. For this purpose, we needed to collect data from tests that measured students’ aptitude for learning programming as soon as possible, along with additional background information deemed relevant [12,13]. The purpose of this work was to make an exploratory analysis of this data and then enable its visualization and analysis. This involved exploring data using graphs and descriptive statistics to identify patterns, trends, and correlations between variables [10,14,24]. Additionally, it involved identifying relevant features by selecting the most impactful variables that may affect students’ academic performance in their initial programming subject [9,25,26].

Predicting the skills required for success in programming is a topic that has been studied for many years and explored by several authors, yet a consensus has not been reached. Recently, research has focused on developing and validating aptitude tests for programming [22,27]. Most of these tests require related skills, such as mathematics and logic [28]. The IBM Programmer Aptitude Test is the most well-known early test for predicting programming aptitude. The test was widely used in industry to evaluate job applicants and assess their potential to learn programming [29]. We used PCT with questions in the following categories: Verbal questions, Reasoning questions, and Aptitude questions (Appendix A). This paper presents an exploratory analysis of data collected from this test.

Over the past two years, the emergence of Generative Artificial Intelligence (GenAI) tools such as GitHub Copilot, ChatGPT, and Amazon CodeWhisperer has transformed the way students approach introductory programming courses. These technologies enable the automatic generation of code, explanations of complex snippets, and even the solution of complete exercises. While these tools offer valuable opportunities to reduce initial barriers, they also raise concerns about the effective acquisition of fundamental cognitive skills such as logical reasoning, abstraction, and problem-solving. In this new context, it becomes even more important to understand the extent to which cognitive skills, as assessed by the Programming Cognitive Test (PCT), continue to be valid predictors of academic success, and to consider how to adapt them to the current reality.

Recent studies have highlighted the impact of GenAI on programming education. For example, papers presented at conferences such as SIGCSE and ITiCSE from 2023 to 2025 have addressed the potential benefits and drawbacks of employing Large Language Models (LLMs) in academic settings. Research indicates that students can gain confidence and reduce initial frustration when using AI-based programming assistants. However, they risk becoming overly dependent on them, which can compromise the development of reasoning and debugging skills. Studies [30,31] have explored how AI-mediated exercises can support early interventions. Other authors have argued for the need for new diagnostic tools that explicitly consider the interaction between cognitive skills and the use of GenAI [32]. Thus, the recent literature highlights the urgent need to rethink not only teaching methods, but also how we assess programming skills in the context of an educational ecosystem transformed by generative AI.

One of the aims of this study was to determine whether this type of aptitude prediction technique is relevant and has an impact on the field, which necessitates ensuring that the test is effective and continually improved. We believe that the analyses carried out can contribute to this development.

The remainder of this paper is structured as follows. Section 2 describes the methodology used, including the sample and test description. Section 3 presents the results analysis, and Section 4 discusses the results. Finally, Section 5 presents the conclusions and future research.

2. Materials and Methods

We collected data from the PCT answers, designed to assess students’ aptitude for learning IP, as well as any additional background information deemed relevant.

Data were collected from first-year students of the “Introduction to Programming” curricular unit, who were learning the C programming language as part of the Computer Engineering (CE) Bachelor’s degree at the Coimbra Institute of Engineering (ISEC) of the Polytechnic University of Coimbra (IPC) in Portugal.

In this section, a description of the study participants and data collection methods is provided, followed by a brief explanation of the PCT.

2.1. Sample

During the first week of classes in the first semester of the 2023/2024 academic year, which began in September 2023, a test was distributed to assess students’ aptitude for programming. A total of 217 students answered the test.

The curricular unit has a total grade of 20 marks, including grades from two tests and a final exam at the end of the semester. The assessment of the curricular unit consisted of the following components: 1st test (5 marks), 2nd test (6 marks), and a final exam (9 marks), totaling 20 marks. For students to take the exam, they needed to achieve a minimum of 25% on each test and attend a minimum of 7 out of 15 practical classes. In the exam, they also required a minimum of 25%. If the student obtains a grade of 9.5 or higher after all these requirements, the student has passed.

It is important to note that the final grade for this course is based on a combination of various assessment components, rather than solely on a single exam. Specifically, final performance comprised the weighted sum of two written exams (the first exam accounting for 25% of the final grade, and the second for 30%), as well as a final exam (accounting for 45% of the final grade). Furthermore, passing required meeting attendance criteria and achieving a minimum score in each component. Therefore, the final grade used in this study provides a comprehensive assessment of student performance throughout the semester. However, it does not capture performance in purely practical programming tasks in isolation. We acknowledge this limitation and emphasize that future research may benefit from using more specific metrics, such as results in programming assignments or practical laboratory exercises, to assess programming capabilities more directly.

For statistical analysis, students who did not get a final grade because they did not fulfill the requirements were removed from the sample. Thus, out of a total of 217 students, only 180 participated in all three evaluation methods and received a final grade. The final dataset consisted of 180 instances, each corresponding to the students’ information about the test answers and the course grades.

2.2. Programming Cognitive Test Description

Our test consisted of three independent parts: a Verbal question [33], Reasoning questions [34], and Aptitude questions [35], designed to test programming aptitude. Each part, from our perspective, assessed a crucial skill or competency needed for success in programming.

Programmers need to read and understand complex documentation, articulate problems effectively, and collaborate with team members. Verbal questions can assess skills such as language comprehension and clarity of thought. In programming, this translates, for instance, into understanding the problem description, writing clear code comments, and understanding error messages.

Programmers must be able to break down problems into smaller, manageable parts, think critically about solutions, and debug efficiently. Reasoning questions tests a person’s ability to apply logic, analyze situations, and make sound decisions—skills that are fundamental to coding, designing algorithms, and troubleshooting.

Programming requires not only existing knowledge but the ability to grasp new concepts quickly, making aptitude testing relevant. Aptitude questions could measure numerical ability, spatial reasoning, or abstract thinking, which are critical when dealing with algorithms, data structures, and computational logic.

The questions used were taken from online tests and are similar to those used by International Business Machines Corporation (IBM) in the recruitment process. Only the Verbal question part was considered a little complex and misaligned with our intentions. Therefore, the researchers involved used triangulation, opting to use a single Verbal question, which proved to be effective [36] and has already been used in several studies to assess individual qualities such as decision-making [37].

Therefore, we considered the chosen Verbal question to test the test-taker’s general language skills, grammatical knowledge, and vocabulary base, determining cognitive abilities. Reasoning questions assessed the test-taker’s problem-solving abilities, decision-making skills, and analytical, numerical, and logical capabilities. Aptitude questions were in the form of visual problems to be solved based on the test-taker’s mathematical knowledge and numerical abilities.

The test consisted of 21 multiple-choice questions, divided into three categories: 1 Verbal question (P1), 10 Reasoning questions (P2 to P11), and 10 Aptitude questions (P12 to P21). The Verbal question presented a logical problem; the Reasoning questions were based on sequences of numbers or letters that must be completed, and the Aptitude questions presented some mathematical problems.

Each group of PCT items tests a set of capabilities, such as abstraction and logical reasoning. These capabilities have been identified as key competencies in important scientific articles presented at major initiatives in this area. Examples of these initiatives include conferences such as SIGCSE and ITiCSE. Abstraction is considered one of the pillars of computing and is essential for modeling problems, designing algorithms, and building clean, reusable code. Logical reasoning is equally vital for understanding conditions, control flows, and algorithmic structures.

Thus, the Verbal question (P1), which consists of the Wason Selection Task, tests conditional and deductive reasoning, which is fundamental to understanding if-else and while statements in programming, i.e., logical reasoning.

The Reasoning questions (P2–P11) include items such as numerical or alphabetic series, logical matrices, and analogies. These questions require the ability to identify underlying patterns (P3, P5, P8, and P10) and apply step-by-step rules to reach a solution (P2, P4, P7, P9, and P11). These skills correspond directly to algorithm analysis, recognizing loop invariants, and the ability to decompose complex problems.

The Aptitude question (P12–P21) includes items that test logical reasoning (P13, P19–P21) and items that test mechanical calculation without apparent abstraction.

2.3. Methods

We used descriptive statistics to examine the characteristics of the dataset and to characterize the two groups of students (FS—Freshman Students and RS—Repeating Students). This allowed us to identify potential differences in their performance. Correlation analysis allowed us to identify the strength and direction of associations, enabling us to determine whether the test was, in fact, correlated with the grades and which types of questions (Verbal, Reasoning, or Aptitude) were more predictive of programming success. Another important analysis was the Categorical Principal Component Analysis (CATPCA), which was used to reduce the dimensionality of the categorical data. This allowed us to identify the variables with the most significant impact on the students’ final grades, helping us to determine the most important questions on the test. CATPCA was extremely useful in reformulating and adjusting the test questions because it ensured their relevance to the test’s central objective. Item Response Theory (IRT) models will also be used to assess the difficulty and discrimination of individual questions.

3. Results Analysis

The following sections are structured as follows: a detailed analysis of the PCT using descriptive statistics, a correlation analysis, a CATPCA and an IRT model analysis are presented.

3.1. Descriptive Statistics

The test results were divided into two groups: FS and RS. This is because RS may already be influenced or biased by some undesirable backgrounds or programming experiences. In addition, students were asked about their level of experience with programming. FS all reported having basic or no knowledge of any of the programming languages, which we considered to be nonexistent. As our objective was to predict the performance of at-risk students in the initial phase of learning programming, we made this separation.

The number of RS was 32, from a total of 180.

Table 1. Descriptive statistics—RS (Repeating Students).

	Students	Total Grade	Minimum	Maximum	Average	Std. Deviation
Verbal	32	1	0	1	0.34	0.483
Reasoning	32	10	0	10	5.81	2.402
Aptitude	32	10	2	8	4.41	1.663
T_grade	32	21	6	16	10.56	2.994
C_grade	32	20	8	16	12.56	2.395

presents the descriptive statistics for the RS. In this table, it is possible to analyze the number of RS that responded to the test, as well as the minimum, maximum, mean, and standard deviation observed in all three question categories (Verbal, Reasoning and Aptitude), all tests (T_grade) and IP course final grade (C_grade) for those students. It was considered that each question in the test weighs one point (despite not having the same complexity).

Table 2. Descriptive statistics—FS (Freshmen Students).

	Students	Total Grade	Minimum	Maximum	Average	Std. Deviation
Verbal	148	1	0	1	0.49	0.502
Reasoning	148	10	1	10	6.70	2.072
Aptitude	148	10	1	9	5.03	1.682
T_grade	148	21	5	18	12.21	3.069
C_grade	148	20	5	20	12.77	3.281

shows the descriptive statistics for the FS. There were 148 FS out of 180.

Based on Table 1 and Table 2, the overall grades were better in the FS group, as evidenced by the average across all categories, and the average test scores were higher than those in the RS group. In terms of course grades, the average was close in both cases. Based on the mean number of correct answers, it can be concluded that the category of Aptitude questions caused the most difficulty for the students, as the average in both groups is lower in this category than in the category of Reasoning questions. The fact that there was only one question in the Verbal questions category, assessed as correct or incorrect, did not allow us to draw many conclusions about the average in this category.

To determine if there was a correlation between the two groups of students (FS and RS) and their grades in the five components, we used the point-biserial correlation. This type of correlation enables us to assess the quality of the answers between the two student groups. In other words, measured the relationship between a continuous variable (grades) and a dichotomous variable (FS or RS).

The correlation with the Verbal category was r = 0.109 with p-value = 0.143, that with the Reasoning category was r = 0.157 with p-value = 0.035, that with the Aptitude category was r = 0.141 with p-value = 0.059, that with the test grade was r = 0.203 with p-value = 0.006 and that with the course grade was r = 0.025 with p-value = 0.735. Only for the Reasoning category and the test grade was the correlation considered statistically significant, indicating a significant association between the group and the grades in these two components. When the correlations are above zero, as they were in all cases, this indicates that FS tended to receive better grades than RS in these five components. However, the relationships were relatively weak in all five cases.

To understand if the difference between the average grades of FS and RS was statistically significant, four t-tests were conducted. These tests covered the Verbal, Reasoning, Aptitude, and course average categories. The t-tests indicated that there was no statistically significant difference, because the significance reached was not less than 0.05 in the Verbal category grades, Aptitude category grades and course grades (p-value = 0.143, p-value = 0.059 and p-value = 0.680, respectively); on the other hand, the Reasoning category grade achieved a p-value = 0.035, meaning that there was a statistically significant difference. To complement the t-test, the sample’s effect sizes were calculated using Cohen’s d with the associated standard error. The results were: Verbal category, Cohen’s d = 0.498 with std error = 0.1967; Reasoning category, Cohen’s d = 2.133 with std error = 0.225; Aptitude category, Cohen’s d = 1.679 with std error = 0.214; and course grades, Cohen’s d = 3.145 with std error = 0.256.

Although the t-tests showed that, in most categories, there were no statistically significant differences between the grades of FS and RS, the effect sizes indicated that, for several categories, there were considerable differences in terms of magnitude. The fact that large effect sizes were observed (as in the case of the course grade and the Aptitude category) suggested essential differences. Still, the p-value did not reach significance, possibly due to the small number of RS.

3.2. Answers per Question Analysis

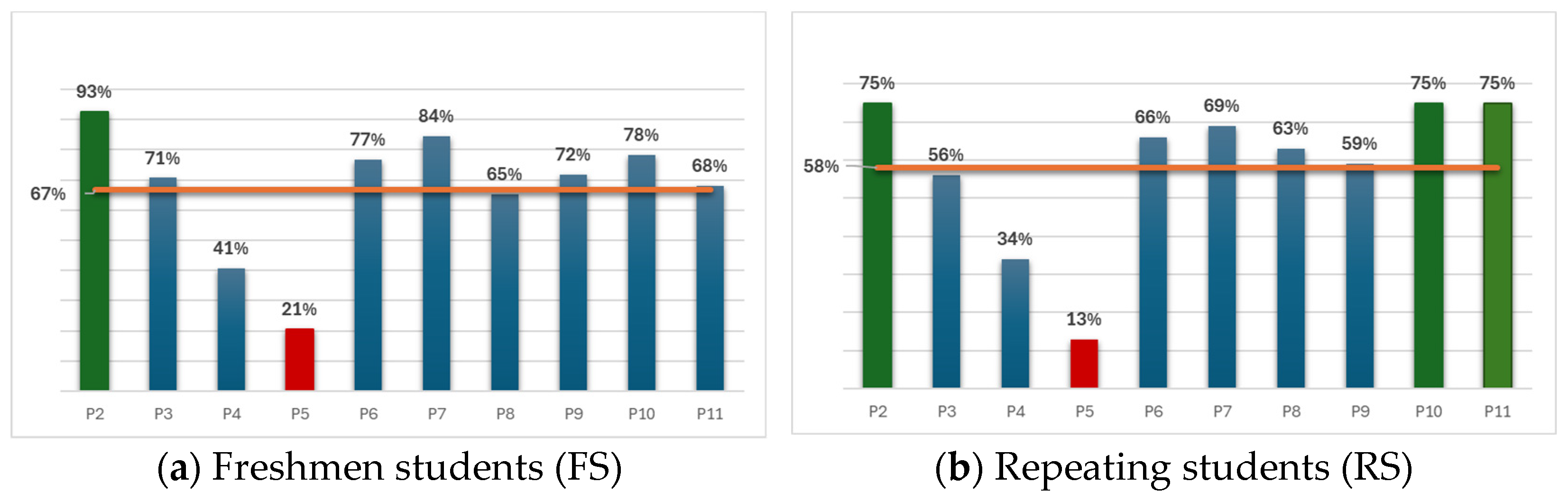
The test results were divided into two groups: FS and RS. This is because RS may already be influenced by previous knowledge. Figure 1 shows the percentage of correct answers per question in the category of Aptitude questions (P22 to P11) for both FS and RS, and the respective average number of correct answers in this category.

The green bars represent the questions with the most correct answers, and the red bars indicate the questions with the fewest correct answers. In both cases, question P2 had the most correct answers (along with question P10 in the RS group). The question with the most incorrect answers in both cases was P5. The t-tests conducted in the Reasoning questions category indicated that only question P2 had a statistically significant difference between the FS and RS. All the other questions had, statistically, no significant difference.

Figure 2 shows the percentage of correct answers per question in the category of Aptitude questions (P12 to P21) for both FS and RS, and the respective average number of correct answers in this category. The green bars represent the questions with the most correct answers, and the red bars indicate the questions with the fewest correct answers. In this category, questions P13 and P21 had the most correct answers for RS and P21 for FS, respectively. As for the question with the highest number of incorrect answers, P16 was the one in both cases, with only 13 correct answers overall. The t-tests conducted in the Aptitude questions category indicated that questions P16, P17 and P18 had statistically significant differences. The remaining questions showed no statistically significant difference, indicating that the answering patterns in those questions were similar in both FS and RS.

The fact that there were questions with such high incorrect response rates may suggest that these questions were not sufficiently relevant to the context of the problem. Only with this analysis was it still very premature to draw firm conclusions. However, it allowed us to flag some questions (P5 and P16) that may have had a low impact and needed to be replaced or removed. The following analyses, including correlation and CATPCA, allowed us to identify the importance of these questions for the test more concretely.

3.3. Correlations

This section analyses the correlation between the test questions, test grades, and course grades. To do this, Pearson’s correlation was used. Pearson’s correlation is a statistical measure that assesses the strength of the relationship between two variables. It provides a coefficient ranging from −1 to +1, indicating the direction (negative or positive) and strength of the association between the variables. When the coefficient is close to +1, it means a strong positive correlation. On the other hand, a coefficient close to −1 suggests a strong negative correlation, indicating that the variables move inversely to each other. A coefficient close to 0 indicates no correlation.

The correlation analysis aimed to identify which questions in the test were most strongly associated with academic performance in the course, providing an initial insight into how different aspects of verbal, reasoning and aptitude skills relate to grades. The correlations were conducted considering the two groups of students (FS and RS). Within each group, the analysis focused on three main parts: part I corresponded to the correlation between the test grade (T_grade) and the course grade (C_grade); part II corresponded to the correlation between the test grade (T_grade) and each of the Verbal question (P1) and the Reasoning questions (P2 to P11); part III corresponded to the correlation between the test grade (T_grade) and each one of the Aptitude questions (P12 to P21).

Besides providing an overview of the relationship between the factors assessed by the test and the student’s performance, this analysis was also crucial for identifying the relationship between the test grades and the course grades. From the correlation coefficients, we could determine which areas of knowledge (Verbal, Reasoning or Aptitude) impacted students’ success in the course. This provided valuable insights for redefining and adjusting the test questions to meet the students’ specific needs, maximizing the test’s effectiveness as a tool for predicting programming aptitude.

Starting with the correlations for the FS, the correlation between the test and course grades (part I) was r = 0.141, indicating a very weak positive correlation with low statistical significance (p-value = 0.087). This shows a slight tendency for test answers to be associated with better grades in the course, although the relationship was very weak.

Table 3. Freshmen students’ course grade correlation with questions (part II).

	P1	P2	P3	P4	P5	P6	P7	P8	P9	P10	P11
C_grade	0.073	0.114	0.022	0.066	0.031	0.099	−0.087	0.199 *	0.012	0.008	0.152
	P12	P13	P14	P15	P16	P17	P18	P19	P20	P21
C_grade	0.103	−0.068	0.130	0.076	−0.022	0.031	0.159	−0.018	0.077	−0.131

* Correlation is significant (p-value < 0.05).

presents the correlation between all 21 questions and the final course grade for the FS group (parts II and III). The question P8 was the only one that had a statistically significant correlation with the course grade.

For the RS, the correlation between the test and course grades (part I) was r = 0.305, indicating a slightly positive correlation with low statistical significance (p-value = 0.089). This meant there was a somewhat stronger tendency for better test grades to be associated with better grades in the course for RS than for FS, but this relationship was still weak.

Table 4. Repeating students’ course grade correlation with questions (part II).

	P1	P2	P3	P4	P5	P6	P7	P8	P9	P10	P11
C_grade	0.023	0.138	0.371 *	0.061	0.010	0.117	0.046	0.185	0.116	0.168	0.385 *
	P12	P13	P14	P15	P16	P17	P18	P19	P20	P21
C_grade	0.150	0.318	0.230	−0.018	a.	0.021	−0.189	−0.015	0.073	−0.021

* Correlation is significant (p-value < 0.05). a. Cannot be computed because at least one of the variables is constant.

presents the correlation between all 21 questions and the final course grade for the RS group (parts II and III). In this case, questions P3 and P11 were the only ones with a statistically significant correlation with the course grade.

For both FS and RS groups, the questions that most correlated with the course grade were from the Reasoning category, where the questions were intended to complete the sequence based on past information. These questions assessed the students’ problem-solving abilities, decision-making skills, and analytical, numerical, and logical capabilities. Although the test captured some aspects related to course performance, it likely did not account for a significant portion of the variation in students’ grades. Weak correlations, as determined, suggest that the test, in its current state, is insufficient to predict grades in the course. The relationship between the test and course grades was not strong enough to say that students who performed better on the test will necessarily have better course grades.

3.4. Principal Components Analysis for Categorical Data

The test consisted of a total of 21 questions. As observed throughout this statistical analysis, specific questions on the test may have had little to no impact on predicting a student’s aptitude for programming. We, therefore, decided to specifically identify the questions that had the greatest effect on the test results and those with the least impact. In the case of questions with the least impact, identifying them will enable us to remove or modify them, ensuring the test is more effective.

For this analysis, we decided to carry out a dimensionality reduction, which allowed us to determine the weight of each variable within the test. Considering that the variables in question were the scores for each question, i.e., 0 if the answer was incorrect and 1 if the answer was correct, then the dataset contained binary data. CATPCA was used to try to reduce dimensionality and preserve maximum sample variability in uncorrelated variables. It is a statistical technique used to analyze categorical data that can handle binary data. The main idea behind it is to find a linear combination of the original categorical variables that maximizes the total variance without assuming linear relationships among the data. To apply CATPCA, an initial requirement was to define the number of dimensions. The number of dimensions considered was 1, as the main objective here was to determine which questions weighed most in each category (Reasoning and Aptitude categories). This analysis did not consider the Verbal category because it only has one question. This analysis also considered both groups (FS and RS).

• CATPCA applied to Freshmen Students

For the Reasoning questions category, the internal consistency coefficient, Cronbach’s Alpha, obtained during this analysis, achieved a value of 0.69, indicating an acceptable level of internal consistency in the data. Regarding the Aptitude questions category, the internal consistency coefficient obtained a value of 0.569, indicating poor internal consistency of the data. 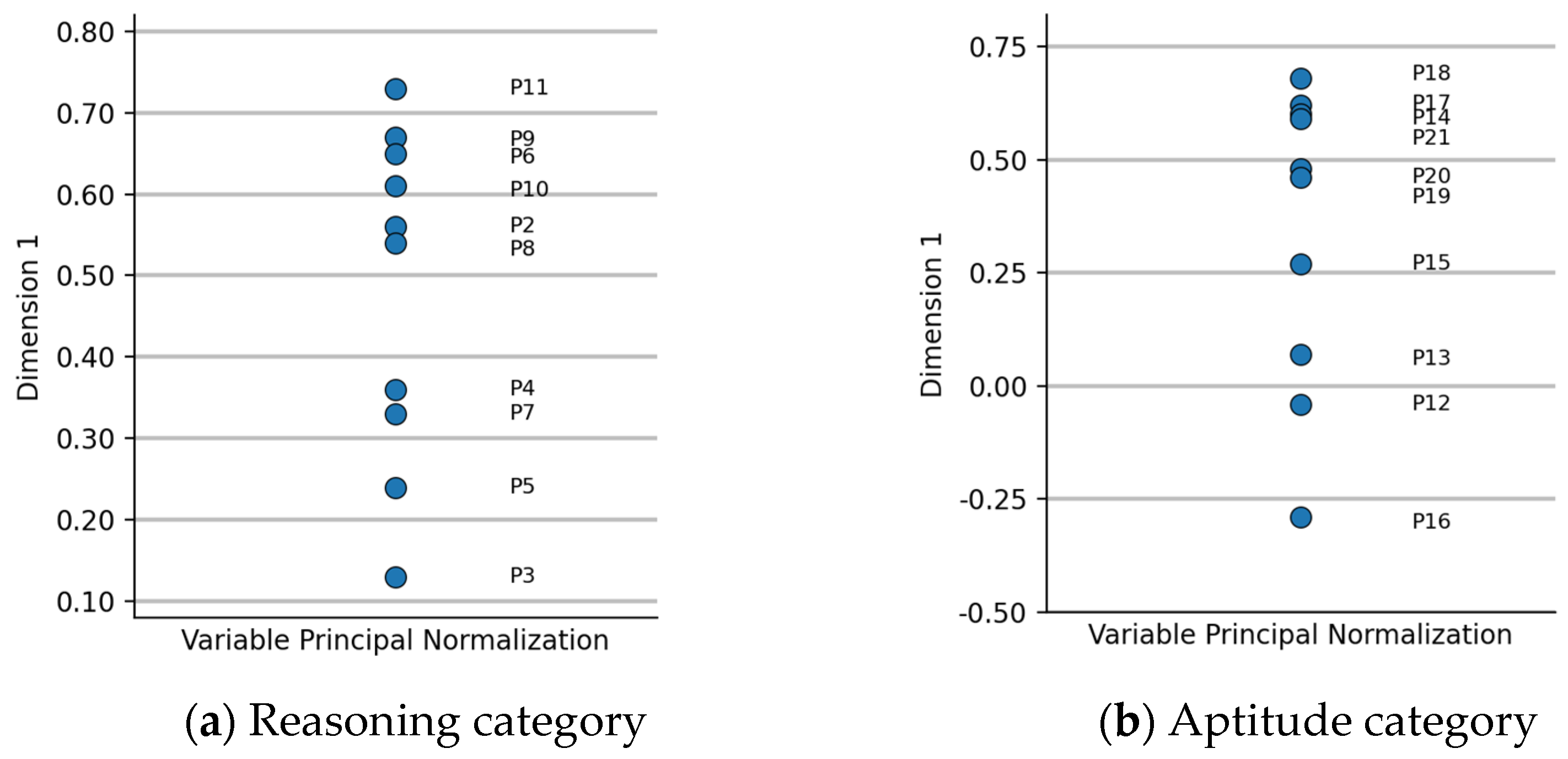The component loadings graphs in Figure 3 show the distribution of the questions in the Reasoning category (a) and Aptitude category (b) for the FS.

In this type of graph, it is possible to see the most relevant/impactful variables in the dimension. Within this dimension, it is possible to see which question had the most weight. For the Reasoning category, question P11 carried the most weight in the FS group, while question P3 carried the least weight. As for the Aptitude category, question P18 had the most weight, while P16 had the least weight. Questions P12 and P16 had a negative position in the dimension, most likely because they were among the questions with the most incorrect answers.

• CATPCA applied to Repeating Students

Regarding the RS group, the execution steps were the same. First, the internal consistency coefficient, Cronbach’s Alpha, for the Reasoning questions category, with a value of 0.742, indicated an acceptable level of internal consistency in the data. For the Aptitude questions category, the internal consistency coefficient achieved a value of 0.575, indicating poor internal consistency of the data.

The component loadings graphs in Figure 4 show the distribution of the questions in the Reasoning category (a) and Aptitude category (b) for the RS. In the RS group, for the Reasoning category question, P9 had the most weight, while P11 had the least weight. With only 32 instances, the dataset may not have sufficient statistical power to accurately capture the relationships between the variables, which might be one reason why questions P3 and P11 had a weak weight in the CATPCA and still showed some correlation with the course grade. For the Aptitude category, question P17 had the most weight, while P12 had the least weight.

Based on the CATPCA results of the two groups of students, questions P3, P12 and P16 were identified as capturing less variance in the data and having less weight within the dimension. These results may suggest that these questions were less important for the test’s purpose or were not well aligned with the main factors intended to be measured.

3.5. Item Response Theory Analysis

IRT was used to analyze the performance of FS and RS based on their answers to two distinct groups of questions: the Reasoning category and the Aptitude category. IRT provided a framework for examining the extent to which questions within these categories measure students’ underlying abilities, such as reasoning skills and aptitude for programming. This analysis helped determine which items effectively differentiated students of different skills and which might need revision or removal in future assessments.

Before developing this analysis, we needed to choose our model. There are three different models: 1 parameter model, 2 parameters model, and 3 parameters model. Since the analysis was done by differentiating the two groups of questions, we could consider that the questions were all relatively consistent (within each category), and we did not expect much variability in discrimination. In any case, to be sure, the Akaike Information Criterion (AIC) and the Bayesian Information Criterion (BIC) were calculated for each of the three types of models, and the best values (lower AIC and BIC values) were obtained when using the 1-parameter model. Therefore, we used the Rasch model, a 1-parameter IRT model.

• IRT for Freshmen Students applied in the Reasoning category

IRT analysis allowed us to calculate a variable called difficulty that represents the level of skill an individual needs to have to have a 50% chance of answering a question correctly. In the analysis of this variable, there was no upper or lower limit for the values obtained; instead, positive or negative values were assigned to each question. The lower the values, the less complex the question, while the higher the values, the greater the difficulty. 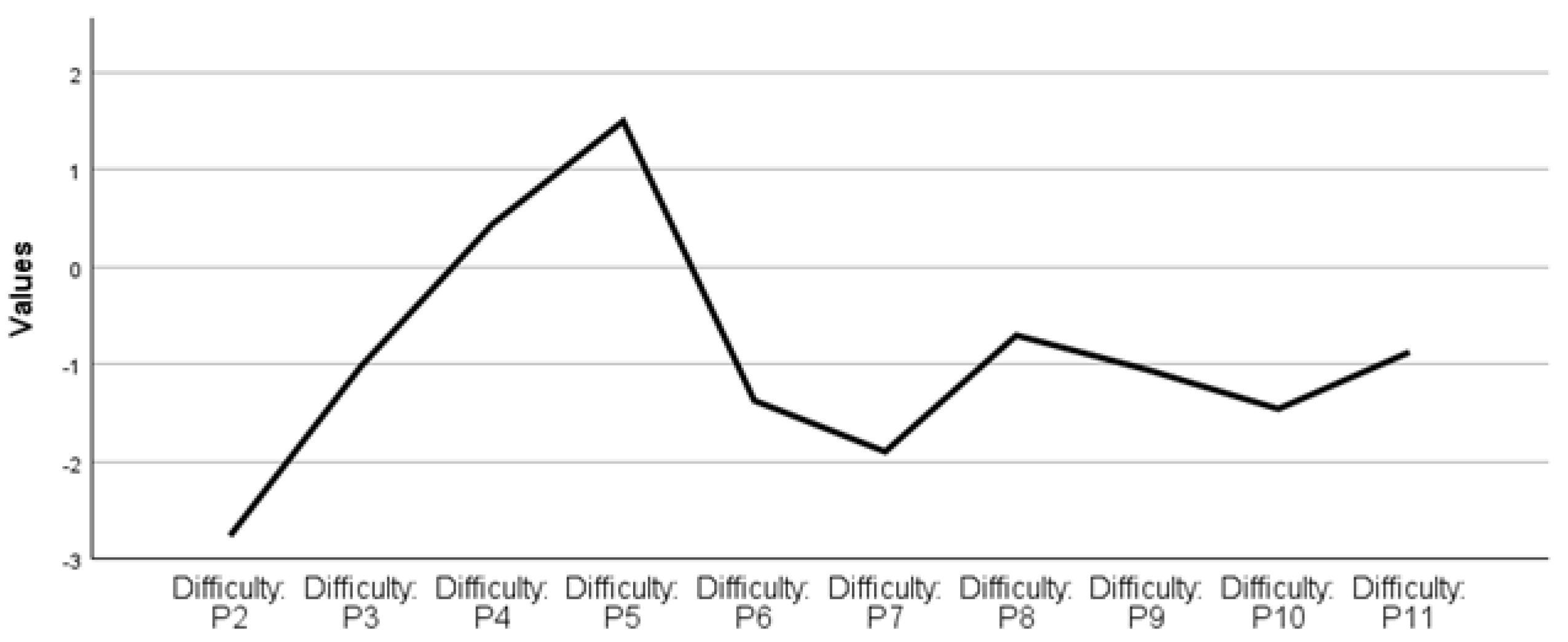In Figure 5, it is possible to conclude that the IRT analysis defined questions P4 and P5 as the most difficult ones, while P2, P7, and P10 were considered the easiest ones.

The Rash model also calculated the overall discrimination value for the Reasoning category. The discrimination value evaluated how well a question or set of questions differentiated between individuals with different levels of ability. High discrimination values (>1.0) indicate that the item is effective at separating individuals with high and low skills. Low values (close to 0) indicate that the item does not discriminate well between different ability levels and may not be highly informative. For the FS, the Reasoning category obtained a discrimination of 1.079, indicating that this set of questions was effective at separating individuals with high and low abilities.

The IRT model used provided us with the Item Characteristics Curve (ICC), a graphical tool that illustrates the relationship between the probability of a student answering a question correctly and that student’s skill level. In Figure 6, it is evident that question P2 is, in fact, the question that requires the least ability to answer correctly; conversely, question P5 is shown to require the most ability to answer correctly.

• IRT for Freshmen Students applied in the Aptitude category

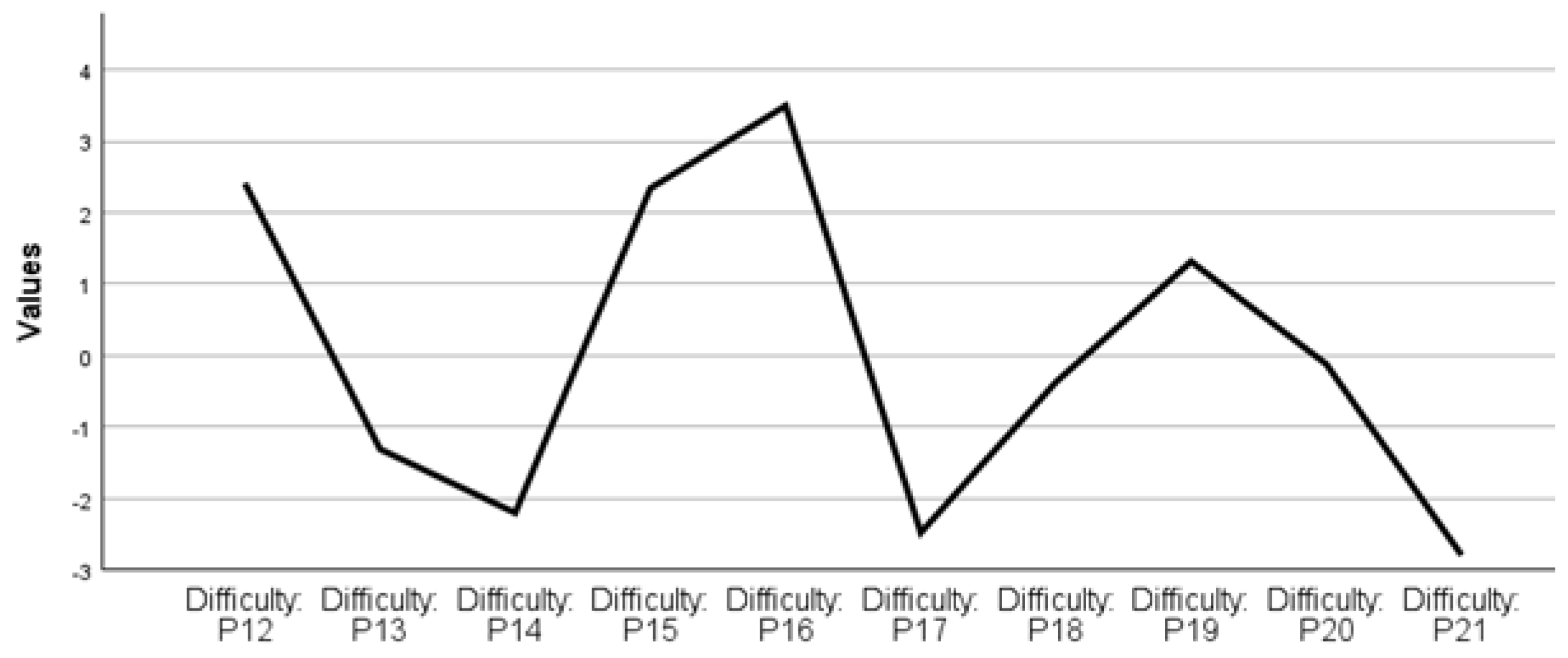
The analysis of the Aptitude category in the FS group was basically the same. In Figure 7, it is shown that questions P12, P15, and P16 were calculated as the most difficult ones, while questions P14, P17, and P21 were calculated as the easiest ones.

For the FS, the Aptitude category obtained a discrimination of 0.730, indicating that this set of questions did not discriminate well between different ability levels and might not be the most informative.

In Figure 8, it is evident that question P21 requires the least ability to answer correctly, while question P16 requires the most ability to answer correctly.

• IRT for Repeating Students applied in Reasoning and in Aptitude categories

In the group of RS, the IRT analysis could be slightly affected by the reduced size of the sample. However, we performed the same analysis and observed that the results were similar, generally following the same pattern with minor variations.

Like in the FS group, for RS, the most difficult questions in the Reasoning category were P4 and P5, with questions P2 and P10 being the easiest ones. We obtained an overall discrimination of 1.229, indicating that this set of questions was effective at separating individuals with high and low abilities, even better than with the FS. From the ICC graph, we can see that P2 and P10 were the Reasoning category questions that required the least ability to get them correct, while question P5 was the one that needed the most ability to get the answer correct for RS.

The analysis was basically the same for the Aptitude category in the RS group. Questions P12, P16 and P19 were calculated as the hardest ones, while questions P13 and P21 were calculated as the easiest ones. The extremely high difficulty calculated for question P16 can be explained by the fact that there was no single correct answer to that question. For the RS, the Aptitude category obtained a discrimination of 0.675, indicating that this set of questions did not discriminate well between different ability levels and might not be the most informative. Questions P13 and P21 were the ones that required less ability to get the answer correct, while question P16 (with zero correct answers) was the one that needed the most ability to get the answer correct.

Overall, the IRT analysis corroborated the conclusions of the previous analyses, namely in defining the questions that caused the greatest difficulties for the students and in determining that the category of Aptitude questions might not be the most suitable for assessing the students’ abilities.

4. Discussion

This study investigated the extent to which a PCT, composed of Verbal, Reasoning, and Aptitude items, could predict student success in an introductory programming course, with a particular focus on first-time students (FS). The analyses provided key insights into how specific cognitive skills relate to academic performance in programming contexts. Reasoning items—especially those pertaining to sequence completion (e.g., P3, P8, and P11)—demonstrated weak to moderate, yet statistically significant, correlations with final course grades (r = 0.371, 0.199, and 0.385, respectively). These questions assessed logical thinking, pattern recognition, and abstract reasoning, foundational skills for programming tasks, such as algorithmic thinking and debugging. These findings highlight the relevance of reasoning ability in the early stages of programming education. In contrast, the Aptitude component (items P12–P21), which focused on mathematical, spatial, and numerical reasoning, showed limited predictive utility. Several items, such as P16—an abstract, multi-step mathematical problem—received no correct responses. Both IRT and CATPCAs identified these items as lacking discriminative power. Similarly, item P5, a matrix logic task, showed extremely low accuracy, suggesting that the cognitive demand was excessive and misaligned with the foundational level of the course. These results raise questions about the construct validity of the Aptitude category and suggest that substantially revising or removing these items may be necessary to improve the PCT’s overall psychometric robustness. The Verbal component, limited to a single item (P1), which was adapted from the Wason Selection Task [36], did not provide sufficient data to assess its predictive potential. Although including this item lends credibility, as it was selected from a validated question previously used in educational aptitude assessments, relying on a single question limits the reliability and interpretability of the Verbal subscore. Expanding this component is essential for capturing the verbal reasoning dimension more comprehensively.

A comparative analysis of freshman students (FS) and repeating students (RS) revealed significant performance differences, suggesting that the PCT may be particularly informative for FS, those engaging with programming for the first time. This segmentation was deliberate, aiming to explore how prior exposure to programming might influence cognitive and academic outcomes. Interestingly, RS scored lower than FS in both the PCT components and final course grades, despite their prior experience with programming content. This counterintuitive result suggests that RS may face additional challenges, such as decreased motivation, reduced self-confidence, or unaddressed learning gaps. Conversely, FS may benefit from the higher motivation and engagement levels associated with a fresh academic start, which could enhance their performance. These findings underscore the importance of differentiated pedagogical interventions. For the RS group, tailored support should address affective factors—such as motivation and self-efficacy—alongside instructional reinforcement of foundational concepts. Practice-based activities that aim to strengthen problem-solving skills may also help close performance gaps and foster more equitable learning outcomes.

Importantly, the PCT demonstrated higher predictive validity for FS, suggesting that RSs may be affected by external factors (e.g., prior failure, anxiety, or decreased motivation) that the test does not capture. These findings underscore the importance of complementing cognitive assessments with broader diagnostic frameworks that address the full range of student needs.

From a measurement perspective, CATPCA confirmed the weak contribution of the Aptitude items to overall test performance. Items such as P12, P15, and P16 showed the lowest factor loadings, suggesting limited alignment with the cognitive constructs under investigation. Discrimination indices derived from the FS and RS groups also indicated that the Aptitude category had a poor ability to differentiate among students with varying abilities. The Rasch model corroborated these findings by showing that students needed a disproportionately high level of ability to answer these items correctly, which reduces their practical relevance in assessing programming aptitude. In contrast, Reasoning items consistently demonstrated stronger psychometric properties. These questions, especially those focused on logical inference and pattern completion, were more effective at distinguishing between students across a range of cognitive abilities. IRT results supported these conclusions, reinforcing the usefulness of Reasoning-based assessments in identifying students’ readiness for programming coursework.

Despite its contributions, this study has several limitations. First, the total sample size was 180 students, but the RS subgroup was relatively small (n = 32), which may limit the generalizability of subgroup analyses. Additionally, the study only examined cognitive test scores and course grades without considering potentially influential variables such as demographic background, learning styles, motivational profiles, or pedagogical approaches. Additionally, the Aptitude category showed low internal consistency, with Cronbach’s alpha values of 0.569 (FS) and 0.575 (RS). This highlights the necessity of a thorough review and potential redesign of this component. Another point to consider is that the study used the course’s final grade as the main performance indicator. Although this grade integrates theoretical and practical assessments, it does not explicitly distinguish between programming skills, commitment, attendance, and other assessment factors. Therefore, we recognize that using the final grade exclusively may introduce noise into the analysis of the relationship between cognitive aptitude and programming performance. Future work should explore alternative metrics, such as performance in practical programming tasks, code correction, or lab projects, to more directly capture students’ programming skills.

In summary, the PCT showed modest predictive value, especially for first-time students. This offers preliminary evidence of its usefulness in providing early academic diagnostics in programming education. However, continued refinement is necessary for it to be effective. Future research should prioritize the revision of Aptitude items to better align with programming-relevant constructs and explore the integration of affective and contextual factors into predictive models. IRT results, especially those highlighting item difficulty and discrimination, provide a solid foundation for improving the test’s design.

Although PCT should not be used alone to determine programming aptitude or risk, it offers a promising framework for the early identification of cognitive strengths and weaknesses. With targeted refinement, PCT has the potential to make meaningful contributions to data-informed teaching strategies and student support systems in computing education.

When interpreting the results of this study, it is important to consider their context within the current GenAI era. While AI tools can alleviate some of the initial difficulties in programming, they can also obscure cognitive gaps that traditional tests still manage to highlight. The PCT remains relevant because it directly assesses logical reasoning and pattern recognition, measuring fundamental human capabilities that cannot be replaced by the simple use of automated tools. However, it will also be necessary to adapt and enrich the instrument to assess students’ ability to interact critically with AI-generated code, for example, by checking for errors, identifying limitations, or restructuring solutions. Therefore, our analysis reinforces the idea that, in the GenAI era, the measurement of cognitive aptitudes must be complemented with tasks that integrate real-world AI use cases more than ever.

5. Pedagogical Recommendations

Based on the findings of this study, we offer the following evidence-based pedagogical recommendations to improve student success in Introductory Programming courses.

First, reasoning skill development should be prioritized. Since Reasoning items (e.g., P3, P8, P11) had a modest correlation with programming success, we recommend integrating logical reasoning and pattern-recognition exercises early in the course. These exercises may include puzzles, sequence analysis, and activities that require algorithmic thinking.

Another aspect is using cognitive diagnostics for early support rather than for student selection. The PCT can serve as an early screening tool to identify students who may benefit from tailored support, particularly those who are struggling with abstract reasoning. However, this approach should be accompanied by mentoring, active learning techniques, and positive reinforcement.

Testing a revision that removes low-impact items can also be considered. Items such as P5 (matrix logic) and P16 (overly complex arithmetic) were identified as not aligned with programming skills at this stage. Eliminating or redesigning these types of questions will improve the relevance and discriminatory power of future tests.

The Verbal section can also be extended. Understanding documentation, interpreting error messages, and communicating code effectively require strong verbal reasoning skills. Currently, the test includes only one item (P1), but this could be expanded to include multiple items tailored to programming-specific verbal tasks.

The Aptitude items could also be redesigned with a programming context. Although traditional aptitude tasks (e.g., arithmetic, spatial reasoning) did not demonstrate a strong link to programming outcomes, redesigned versions that incorporate computational logic could be more effective. For example, one could incorporate pseudocode-based problems or logic table tasks.

Since programming success is influenced by various factors, including motivation, learning environment, prior experience, and teaching quality, we can make this type of identification rather than relying solely on PCT results to define student potential.

These recommendations align with our empirical findings and provide clear guidance on how to improve assessment design and teaching interventions in programming education. However, we propose a set of pedagogical recommendations that teachers can also use to translate the findings into tangible improvements in teaching and learning practices.

First and foremost, we emphasize the critical importance of conducting early cognitive assessments at the beginning of introductory programming courses. These assessments should aim to identify students who may face challenges or show reduced aptitude in key areas such as logical reasoning and problem-solving. Early identification of these difficulties enables timely intervention, preventing students from falling behind and fostering a more inclusive learning environment.

Based on these assessments, tailored tutoring programs or mentoring sessions can be developed to provide personalized support to students identified as at risk. It is hoped that this ongoing support, which can be adjusted as progress is made, will significantly increase students’ confidence and self-esteem, ultimately leading to more effective and meaningful learning outcomes.

Central to this process is the integration of diverse teaching strategies. These strategies include the use of adaptive methods, such as practical and collaborative approaches, tailored to accommodate different student profiles. These profiles can be identified through the initial use of learning style assessments. Specifically, the authors used the Index of Learning Styles (ILS) in their research [38], as it was developed by engineering researchers specifically for engineering students. Furthermore, it is expected that these strategies will increase student engagement and foster a more dynamic and inclusive learning environment.

To ensure the effectiveness of these strategies, frequent and personalized feedback is essential. With this in mind, some authors began developing an e-learning platform several years ago that proposes activities tailored to the preferred learning styles and cognitive levels of students. By generating automated feedback, the platform facilitates the creation of alternative learning paths to achieve the same objectives. Moreover, these strategies could be extended to other engineering courses facing similar challenges, fostering interdepartmental collaboration to share best practices and resources that support students of different abilities. This approach not only promotes a more inclusive learning environment but also addresses a broader range of student needs.

The further integration of educational technologies, such as adaptive learning platforms and programming simulators, offers the potential to personalize individual learning experiences. These tools facilitate student learning by providing continuous support and automatically adapting content and resources to align with each student’s abilities. Group members bring valuable expertise to this area, not only as programming educators but also as contributors to the development of innovative educational tools designed to enhance programming education.

Given that these curricular units involve numerous teachers with different pedagogical approaches, a factor that can have a significant impact on student motivation, we also recommend organizing training workshops for teachers. These workshops would focus on interpreting and using cognitive test results to adjust teaching strategies and incorporate active learning methodologies. Such training will enhance teachers’ ability to implement targeted and effective interventions based on the data collected, ultimately improving learning outcomes. This set of approaches will allow for continuous improvement and refinement of teaching practices, ensuring that introductory programming courses effectively support all students.

6. Ethical Considerations

All participants were first-year students enrolled in the “Introductory Programming” course at the Polytechnic University of Coimbra. Participation in the cognitive test was voluntary, and the purpose of the study was explained to the students. The test was administered during the first week of class and had no impact on final grades or evaluation. All data were anonymized at the point of collection.

Informed consent was obtained from all participants. No personal or identifiable data was collected. Consent was obtained at the time of test administration, and participation did not influence course grades or evaluation. The research protocol followed institutional guidelines for ethical conduct in educational studies.

We also recognize the ethical implications of using aptitude tests to identify “at-risk” students. Although the intention is to provide support, care must be taken to avoid labeling or stigmatizing students. We emphasize that cognitive tests should be used for diagnostic purposes in conjunction with pedagogical support, not for exclusionary purposes.

To mitigate ethical concerns, we suggest that the PCT be administered in an aggregated and anonymous manner in future. This would allow teachers to obtain an overview of their class’s cognitive potential without labeling or stigmatizing individual students. This collective approach can help adapt teaching strategies to the needs of the group while respecting privacy and equity in the educational process.

7. Conclusions and Future Work

This study examined the predictive potential of the Programming Cognitive Test (PCT) in predicting success in an introductory programming course, with a particular focus on first-time students (FS). The PCT, which is structured around three cognitive domains—Verbal, Reasoning, and Aptitude—was administered to a sample of 180 students, including both FS and returning students (RS).

The findings suggest that reasoning skills, especially those involving logical thinking and pattern recognition, are the most promising cognitive predictors of programming performance. Items such as P3 (alphabetic sequence), P8 (analogies), and P11 (numerical deduction) exhibited modest, yet statistically significant, correlations with final course grades. Analyses using both the CATPCA and the Rasch model confirmed that Reasoning items have superior discriminative power compared to Aptitude or Verbal items. In contrast, the Aptitude section, which focused on mathematical and spatial reasoning, demonstrated low reliability and poor alignment with student performance. Some items, like P16, were challenging and lacked diagnostic value. The Verbal component, limited to a single item, was insufficient for meaningful evaluation of verbal reasoning.

A key contribution of this study is its ability to differentiate between FS and RS. The PCT was notably more predictive for FS, suggesting that cognitive assessments are particularly effective in identifying students at risk of academic setbacks or motivational declines before they occur. In contrast, RS performance appears to be influenced by external factors—such as prior failure, anxiety, or reduced self-efficacy—that the test does not capture.

Although PCT does not currently predict success in IP courses, it lays the groundwork for developing more precise, domain-specific diagnostic tools. Reasoning questions were found to be the most psychometrically robust and educationally relevant, thus supporting their prioritization in future iterations of the test. In contrast, the Aptitude section requires substantial revision to improve its internal consistency and alignment with programming-specific cognitive demands.

However, this study has some limitations. The small number of RS participants may have reduced the statistical power of the subgroup analyses. Additionally, influential non-cognitive factors, such as prior programming knowledge, socio-economic background, motivation, learning styles, and pedagogical variations, were not considered. Future research must address these limitations to develop a more comprehensive understanding of student performance in programming. Despite these constraints, this study makes a significant contribution to the literature, demonstrating the comparative utility of cognitive domains in predicting programming success, introducing CATPCA as a valuable tool for evaluating cognitive test structure, and applying IRT to identify the items that are most and least effective in differentiating student abilities.

As future work, we intend to focus on refining the PCT by removing or replacing underperforming items—particularly in the Aptitude domain—and expanding the Verbal section to improve reliability. Additionally, a redesigned PCT centered on reasoning skills and validated with larger, more diverse student samples across different instructional contexts could enhance early identification and support strategies in programming education.

As future work, we also propose extending the PCT to contexts where GenAI plays an active role in the learning process. This could involve creating tasks that require students to evaluate, debug, and improve the output generated by AI assistants, thereby distinguishing between critical thinking and mere passive technology use. Furthermore, we plan to comparatively investigate student performance in scenarios with and without access to generative AI tools better to understand the interaction between cognitive aptitude and technological dependence. Finally, we believe it is crucial to expand the sample size and replicate this study across different institutions to assess the generalizability of the results to a global context of programming education in the GenAI era.