Hardware–Software System for Biomass Slow Pyrolysis: Characterization of Solid Yield via Optimization Algorithms

Abstract

Biofuels represent a sustainable alternative that supports global energy development without compromising environmental balance. This work introduces a novel hardware–software platform for the experimental characterization of biomass solid yield during the slow pyrolysis process, integrating physical experimentation with advanced computational modeling. The hardware consists of a custom-designed pyrolizer equipped with temperature and weight sensors, a dedicated control unit, and a user-friendly interface. On the software side, a two-step kinetic model was implemented and coupled with three optimization algorithms, i.e., Particle Swarm Optimization (PSO), Genetic Algorithm (GA), and Nelder–Mead (N-M), to estimate the Arrhenius kinetic parameters governing biomass degradation. Slow pyrolysis experiments were performed on wheat straw (WS), pruning waste (PW), and biosolids (BS) at a heating rate of 20 °C/min within 250–500 °C, with a 120 min residence time favoring biochar production. The comparative analysis shows that the N-M method achieved the highest accuracy (100% fit in estimating solid yield), with a convergence time of 4.282 min, while GA converged faster (1.675 min), with a fit of 99.972%, and PSO had the slowest convergence time at 6.409 min and a fit of 99.943%. These results highlight both the versatility of the system and the potential of optimization techniques to provide accurate predictive models of biomass decomposition as a function of time and temperature. Overall, the main contributions of this work are the development of a low-cost, custom MATLAB-based experimental platform and the tailored implementation of optimization algorithms for kinetic parameter estimation across different biomasses, together providing a robust framework for biomass pyrolysis characterization.

1. Introduction

Due to the growing need to transition to a sustainable energy system, solid biofuels such as biochar have been positioned as promising alternatives to partially replace fossil fuels [1]. Where accurate prediction of biomass yields through data synthesis is critical to ensuring efficient supply chains [2]. Lignocellulosic biomass, including agricultural residues (with yields predictable via machine learning [3]), forestry waste, and sewage sludge (convertible via advanced thermochemical pathways [4]), constitutes an abundant renewable resource for biofuel production. Biomass currently supplies around 14% of global energy [5], and recent policies are promoting its use within the framework of the circular economy. According to the International Energy Agency (IEA), bioenergy could meet 20% of global energy demand by 2050, playing a strategic role in the decarbonization of industry and transportation [6]. In agricultural regions such as Guanajuato, Mexico, the utilization of wheat straw, pruning residues, and biosolids represents a strategic opportunity to produce biochar while improving local waste management.

Among the thermochemical processes employed for biomass conversion under controlled (inert or oxygen-free) atmospheres, torrefaction and pyrolysis are effective techniques for optimizing the energy yield and physicochemical properties of the resulting solid products [7]. These technologies enable biomass decomposition over different temperature ranges (200–800 °C). Depending on temperature, each process yields specific products: torrefaction (200–300 °C) produces low-temperature biochar [8,9], while pyrolysis (300–800 °C) produces biochar along with liquid and gaseous fractions [10,11,12]. These processes allow tailoring of biochar composition and quality by adjusting temperature, heating rate, and residence time [13,14]. Pyrolysis is further classified into two types: slow pyrolysis (300–650 °C), with residence times of up to 12 h and heating rates of 10–30 °C/min, yields biochar at 30–40% [14,15]; and fast pyrolysis (>500 °C), with residence times of up to 2 s and heating rates up to 1000 °C/min, yields 10–30% solids and 15–20% liquids [16,17]. In both cases, the resulting biochar exhibits high chemical stability, can be used as a soil amendment, contributes to carbon sequestration, and improves soil fertility [18,19,20,21].

To investigate biomass-to-biochar degradation behavior, kinetic analysis is typically employed using thermal treatments at elevated temperatures to accelerate reaction rates [22]. Several thermal analysis techniques are available, including thermogravimetry (TG) [23], differential scanning calorimetry (DSC) [24], differential thermal analysis (DTA) [25], and Fourier-transform infrared spectroscopy (FTIR) [26]. The most common of these is thermogravimetric analysis (TGA), which measures weight loss characteristics and allows quantification of the solid yield fraction during biochar production via biomass dehydration and decomposition [27,28]. Accurate characterization of solid yield during slow pyrolysis requires advanced kinetic models capable of capturing the complex nature of thermal decomposition [29]. In this regard, several techniques are applied to study biomass decomposition, including single-step, multi-step, and reaction mechanism-based approaches, as reviewed by Skrzyniarz et al. [22], which also details the biomass types used in each study. The two-step kinetic model proposed by Di Blasi and Lanzetta [30] separates the decomposition stages of cellulose and lignin [31]. This scheme, based on first-order kinetics and Arrhenius laws, simplifies the complex evolution observed in TGA data from lignocellulosic samples [32]. While this model has been widely applied to torrefaction studies, its implementation in slow pyrolysis remains relatively unexplored.

Recent studies have enriched this approach with advanced optimization tools.

Table 1. Summary of studies on two-step kinetic model fitting with optimization algorithms for solid yield prediction.

Biomass	Temperature Profiles			Optimization Algorithm	Fit (%)	Ref.
	Temperature (°C)	Heating Rate (°C/min)	Residence Time (min)
Wood Waste	225–375	5, 10, 20, 30, and 40	60	N-M	0.9996	[33]
Wood Waste	200–300	20	60		0.99	[34]
Ashe Juniper	210–380	6 and 7	160		>0.98	[35]
Eucalyptus Grandis	210–290	5	80		--	[36]
Poplar and Fir	200–230	0.2	1740		0.9997	[37]
Poplar and Xylan	200–240	1	600		>0.97	[38]
Wheat Straw	250–300	10 and 50	100		--	[39]
Wheat Straw	250–325	20	100	PSO	>0.98	[40]
Xylan	200–300	20	120		>0.98	[41]
Sorghum residue	200–300	20	60		>0.8469	[42]
Pequi Seed (PS) and oil-PS	200–300	7–15	80	L-M	0.97	[43]
Spruce and Birch	220–300	--	120	SSE	>0.971	[44]
Beech, Pine, Wheat, and Willow	200–300	--	100	LSR	--	[45]

shows the different optimization algorithms used alongside the two-step kinetic model, such as Nelder–Mead (N-M) [33,34,35,36,37,38,39], Particle Swarm Optimization (PSO) [40,41,42], Levenberg–Marquardt (L-M) [43], Sum of Squared Errors (SSE) [44], and Least Squares Regression (LSR) [45], each delivering promising results for different biomasses and temperature profiles in torrefaction processes. Controlling variable heating rates (0.1–50 °C/min), treatment temperatures (200–800 °C) and adjustable residence times (minutes to hours) enables identification of optimal torrefaction/pyrolysis conditions that maximize solid yield and biochar quality, as demonstrated by Chen et al. [41] for wood (118% energy density increase compared to fixed conditions).

Although TGA is widely used to characterize thermal decomposition kinetics of milligram-scale samples, it presents critical limitations in predicting solid yields for torrefaction and slow pyrolysis when extrapolated to industrial reactors. First, scale and heat/mass transfer effects (≈10 mg) do not replicate real reactor conditions, underestimating mass loss by up to 15% in fibrous biomasses (e.g., wood residues) due to the absence of internal thermal gradients [33,35,37]. Second, the lack of vapor–solid interactions and insufficient residence times in TGA oversimplifies secondary recombination mechanisms, causing deviations in solid yields of over 12% compared to pilot-scale systems [34,36,44]. These factors demand validation using larger-scale reactors for reliable industrial applications [40,43]. Given that various algorithms have been reported with different biomasses and temperature profiles, implementing an autonomous system that integrates thermal profile control (heating rates, temperatures, and residence times) with optimization algorithms into a single platform would be highly valuable. Such a system could meet different needs depending on the application or biomass type and extend the process to slow pyrolysis. Moreover, it would complement commercial equipment such as TGA.

The quality of biochar that has undergone a thermal process is expressed in terms of its higher heating value (HHV) and a lower atomic ratio of H/C and O/C [40], which are determined through elemental analysis and calorimetry. These studies are conducted using specialized equipment outside the slow pyrolysis thermal process.

This work presents a comprehensive hardware–software system for slow pyrolysis of biomass, incorporating automated control and optimization algorithms (PSO, Genetic Algorithms–GA, and N-M) for the kinetic characterization of biochar yield, representing a significant extension of our previous approach [40]. Three biomass species abundant in the region were selected as case studies, and their degradation kinetics were modeled using three optimization algorithms. The software, developed in MATLAB 2023b, includes advanced thermokinetic characterization capabilities, while the hardware integrates a control and monitoring platform, a pyrolyzer with predictive control to compensate for process delays [46,47,48], as well as real-time temperature and weight sensors. The software module accurately estimates the global kinetic parameters of two steps (including biochar yield) using particle swarm optimization (PSO), genetic algorithms (GA), and the Nelder–Mead (N-M) method. These algorithms serve as optimization tools (N-M) and computational intelligence (PSO and GA) that transform experimental data into predictive models for thermochemical conversion. These algorithms estimate the parameters required for the two-step kinetic model based on experimental data. While methodological comparisons of this type have been reported in isolated cases in the literature, as summarized in Table 1, the integration of these techniques with a predictive control system represents a significant advancement. Unlike previous isolated studies, this system combines predictive control strategies with evolutionary and deterministic optimization methods, establishing a methodological framework that demonstrates the potential of optimization and computational intelligence tools in renewable energy processes. By considering three types of locally available residual biomass (wheat straw—WS, pruning waste—PW, and sewage biosolids—BS), the study provides both experimental validation and modeling in the context of Guanajuato, Mexico, supporting its applicability to agro-industrial energy systems. Overall, this hybrid approach (advanced control + optimization and computational intelligence tools-based multi-method kinetic fitting) offers an innovative platform for optimizing biochar and bioenergy production, directly contributing to the digitization, efficiency, and resilience of biomass-based renewable energy systems.

2. Materials and Methods

This section describes the three types of biomass used in this study, selected for their relevance to the Guanajuato region in Mexico. It then presents the fundamentals of the Smith predictive controller, which is essential for compensating time delays in temperature control systems, as well as the two-step kinetic model that characterizes biomass degradation kinetics. Finally, the section introduces the optimization algorithms employed, i.e., PSO, GA, and the N-M method, for predicting solid yield.

2.1. Use of Biomass for Sustainability

In recent years, Guanajuato, Mexico, has become the third-largest national producer of wheat, with average yields of 6.4 tons/ha and more than 400,000 tons annually, generating a significant volume of wheat straw (WS), of which less than 30% is used for animal feed [49]. In addition to this residual biomass, urban pruning residues (PW) and biosolids (BS) from wastewater treatment plants, whose management is regulated by NOM-004-SEMARNAT-2002 [50,51], represent additional resources. These biomass types offer a strategic opportunity for valorization through slow pyrolysis, a process that produces biochar with applications in soil improvement, greenhouse gas mitigation, and environmental remediation [52,53] by reducing carbon emissions [54].

In this study, as shown in Figure 1, WS samples were collected in the municipality of Penjamo (cropland located at 20°25′52″ N, 101°43′20″ W), PW in Irapuato and Celaya (20°40′27″ N, 101°20′51″ W, and 20°31′44″ N, 100°48′54″ W, respectively), and BS in León (21°07′22″ N, 101°41′00″ W). This collection strategy aligns with state-level circular economy policies and the National Program for the Sustainable Use of Bioenergy [55,56].

Property Characterization

The WS, PW, and BS were ground to a uniform powder and sieved with a No. 20 mesh sieve. The proximate analysis was based on the standard procedure of the American Society for Testing and Materials. The results of the analysis of the feedstocks wheat straw (WS), pruning waste (PW), and biosolids (BS) are detailed in

Table 2. Characteristics of the feedstocks.

Biomass Characteristics	WS	PW	BS	Method
Proximate analysis (wt.%) (dry basis)
VCM	76.51 ± 0.256	85.75 ± 0.200	63.16 ± 0.332	ASTM E871-82
Ash	3.52 ± 0.351	5.15 ± 0.100	27.70 ± 0.235	E1775
FC	19.97 ± 1.670	9.06 ± 0.159	9.14 ± 0.398	E871-82
Ultimate Analysis (wt.%)
C	46.205	42.167	34.178	Thermo Scientific iCAP 74000 ICP-OES analyzer, CA-USA
H	6.275	5.275	4.966
N	3.612	2.179	6.304
S	0.000	0.000	0.452
O*	43.908	50.379	54.100
O:C	0.714	0.896	1.187
H:C	1.629	1.501	1.743

.

2.2. Theoretical Background

2.2.1. Smith Predictive Control

In pyrolysis thermal systems, a key variable to control is the set point temperature to optimize biochar yields. However, regulating the heating rate (<5 °C/min) poses a complex challenge due to dynamic delays (>45 s) [57], thermal nonlinearities, and disturbances in biomass feed flow. The Smith predictive controller addresses these limitations by integrating a 30% improvement in dead-time compensation compared to conventional controllers [46], achieving a 40% reduction in the Integral of Absolute Error (IAE) during ramp profiles [47], and providing better disturbance rejection in industrial plants [48]. One of the main features of the Smith predictor is its capability to compensate for dead time [47], which makes it an ideal control strategy for thermal systems [46,48].

The structure of the Smith predictor is shown in Figure 2. It can be divided into two parts: the controller C(s) and the predictor structure, which consists of a transfer function G_m(s) and a dead-time model given by e^−Ls. The model error (e_p) is defined as the difference between the process output (y) and the model output (y_pm). The variable y_m(t + L) represents the predicted process output in open-loop. G_m(s) is used for open-loop prediction, and the model is expressed in

$$P_m\left(s\right)=G_m{e}^{-Ls}$$

(1)

The closed-loop dynamics of the system are given by Equation (2), where τ is a design parameter representing the desired system response time.

$$G_d\left(s\right)={\displaystyle \frac{e^{-Ls}}{\tau s+1}}$$

(2)

2.2.2. Two-Step Kinetic Model

To describe the biomass degradation kinetics up to the formation of biochar, expressed as the instantaneous solid yield at each study temperature SY^(T)(t), the instantaneous weight measurement w_i(t), and the initial weight w₀ are used as defined in

$$S{Y}^{(T)}\left(t\right)={\displaystyle \frac{w_i\left(t\right)}{w_0}}$$

(3)

where t (min) represents the time and T (°C) is the treatment temperature.

Based on the model proposed by Di Blasi and Lanzetta [30], the two-step kinetic model given in Equation (4) is employed, which simplifies the thermal decomposition of biomass into two parallel and independent reactions. The first stage corresponds to the rapid decomposition of cellulose and hemicellulose, while the second stage represents the slower degradation of lignin. This is modeled through the decomposition of solid pseudo-components A, B, and C, and volatile fractions V1 and V2. Solid A corresponds to raw biomass, B is the intermediate solid, and C is the generated biochar, with each reaction releasing volatiles V1 and V2. The initial conditions for the kinetic rates were obtained following the same criteria as in [40], where (−20 < k_i < 0 dB) defines the search range for the optimization algorithms.

$$1^{st} step:\left\{\begin{array}{c}A\stackrel{k_1}{\to }B\\ A\stackrel{k_{V1}}{\to }V1\end{array}\right. 2^{nd} step:\left\{\begin{array}{c}B\stackrel{k_2}{\to }C\\ B\stackrel{k_{V2}}{\to }V2\end{array}\right.$$

(4)

where k_i (min⁻¹, i = 1, 2, V1, V2) are the kinetic rate constants, defined by the Arrhenius law in Equation (5). Here, A_0,i (min⁻¹) is the pre-exponential factor, E_a,i (J·mol⁻¹) is the activation energy, T (K) is the isothermal temperature, and R (J·mol⁻¹·K⁻¹) is the universal gas constant [32].

$$k_i=A_{0,i}\exp \left({\displaystyle \frac{-E_{a,i}}{RT}}\right)$$

(5)

The sum of the solid pseudo-components A, B, and C represents the evolution of SY^(T)(t), as described in Equation (6), while the evolution of the volatile yields V1 and V2 is given by Equation (7). At the beginning of the slow pyrolysis process (t = 0), the raw material described by pseudo-component A corresponds to the fraction 1.0 (m_A = 1.0) of SY^(T)(t = 0).

$$S{Y}^{\left(T\right)}\left(t\right)=Y_A^{\left(T\right)}\left(t\right)+Y_B^{\left(T\right)}\left(t\right)+Y_B^{\left(T\right)}\left(t\right)$$

(6)

$$Y{V}^{\left(T\right)}\left(t\right)=Y_{V1}^{\left(T\right)}\left(t\right)+Y_{V2}^{\left(T\right)}\left(t\right)$$

(7)

Equations (8)–(12) are used to model the time evolution of pseudo-components A, B, C, V1, and V2.

$$Y_A^{\left(T\right)}\left(t\right)=\frac{d{m}_A\left(t\right)}{dt}=-\left(k_1+k_{V1}\right)\times m_A\left(t\right)$$

(8)

$$Y_B^{\left(T\right)}\left(t\right)=\frac{d{m}_B\left(t\right)}{dt}=k_1\times m_A\left(t\right)-\left(k_2+k_{V1}\right)\times m_B\left(t\right)$$

(9)

$$Y_C^{\left(T\right)}\left(t\right)=\frac{d{m}_C\left(t\right)}{dt}=k_2\times m_B\left(t\right)$$

(10)

$$Y_{V1}^{\left(T\right)}\left(t\right)=\frac{d{m}_{V1}\left(t\right)}{dt}=k_{V1}\times m_A\left(t\right)$$

(11)

$$Y_{V2}^{\left(T\right)}\left(t\right)=\frac{d{m}_{V2}\left(t\right)}{dt}=k_{V2}\times m_B\left(t\right)$$

(12)

To minimize, min, the error between experimental data and the predicted thermodegradation curves, the Least Squares Method (LSM) [40] is applied as the Objective Function (OF), as defined in

$$\min : O{F}^{\left(T\right)}={{\displaystyle \sum _{j=1}^n\left[{\left(SY\right)}_{\exp ,j}^{\left(T\right)}\left(t\right)-{\left(SY\right)}_{sim,j}^{\left(T\right)}\left(t\right)\right]}}^2$$

(13)

where ${\left(SY\right)}_{\exp ,\mathrm{t}}^{\left(T\right)}\left(t\right)$ is the j-th experimental datapoint of solid yield, ${\left(SY\right)}_{\mathrm{sim},\mathrm{t}}^{\left(T\right)}\left(t\right)$ is the calculated solid yield, T is the isothermal temperature, and n is the number of experimental points. The fit quality is calculated using [41,42]:

$$fit\left(\%\right)=\left[1-{\displaystyle \frac{\sqrt{\frac{OF}{n}}}{{\left({\left(SY\right)}_{\exp ,\mathrm{j}}^{\left(T\right)}\left(t\right)\right)}_{\max }}}\right]\times 100\%$$

(14)

The calculation of the kinetic parameters A_0,i and E_a,i of the Arrhenius Equation (5) in a thermal degradation process using the two-step kinetic model described in Equations (8)–(12) represents a complex problem that involves integral equations. Therefore, optimization algorithms are well-suited for solving nonlinear problems with high-dimensional search spaces. In this work, three optimization algorithms: PSO, GA, and N-M, are applied to solve this parameter estimation problem.

2.2.3. Particle Swarm Optimization (PSO) Algorithm

PSO is known as a metaheuristic algorithm, which is inspired by social behaviors observed in natural systems. It is particularly effective for identifying kinetic parameters in nonlinear models due to its simplicity and convergence properties [58]. The procedure, as illustrated in Figure 3a, begins with the initialization of a swarm of particles. The search space is defined in a range from −20 to 0 dB regardless of the selected biomass [40]. Each particle i is defined by its position $x_i\left(0\right)$ and velocity $v_i\left(0\right)$, randomly generated within the predefined parameter bounds.

At each iteration t, the following five steps are performed:

• Evaluation of the objective function: Each particle’s position corresponds to a candidate set of kinetic parameters of the two-step model, and the quality of the solution is evaluated by employing the Objective Function (OF), Equation (13), between the experimental data ${\left(SY\right)}_{\exp ,\mathrm{j}}^{\left(T\right)}\left(t\right)$ and model predictions ${\left(SY\right)}_{\mathrm{sim},\mathrm{j}}^{\left(T\right)}\left(t\right)$. It ensures that the OF reflects the average discrepancy between experimental and simulated values, regardless of the dataset size.
• Update of personal and global bests: After the evaluation, each particle updates its personal best position $p_i^{best}$, and the swarm updates the global best position $g^{best}$ if the current solution yields better performance.
• Velocity update: The velocity of each particle is updated according to

  $$v_i\left(t+1\right)=\omega \times v_i\left(t\right)+c_1·r_1·rand()·\left(p_i^{best}-x\left(t\right)\right)+c_2·r_2·\left(g^{best}-x_i\left(t\right)\right)$$

  (15)

  where ω is the inertia weight, c₁ and c₂ are acceleration coefficients (cognitive and social, respectively), and r₁, r₂ are random numbers in the range [0, 1].
• Position update: Once the velocity is updated, the new position of the particle is calculated as follows:

  $$x_i\left(t+1\right)=x_i\left(t\right)+v_i\left(t+1\right)$$

  (16)
• Stopping criterion: The algorithm ends when a stopping condition is met, i.e., a maximum number of iterations T_max, or when the OF drops below a predefined threshold ε:

  $$f t\ge T_{\max } or O{F}^{\left(T\right)}\le \epsilon , then stop$$

  (17)

2.2.4. Genetic Algorithm (GA)

GAs are evolutionary computation techniques inspired by the principles of natural selection and genetics, initially proposed by [59]. In particular, a GA mimics the evolutionary process by iteratively improving a population of candidate solutions through mechanisms analogous to biological evolution. As illustrated in Figure 3b, the basic operations of a GA follow a sequential flow consisting of initialization, fitness evaluation, selection, crossover, mutation, and a stopping criterion. Each of these steps is described below.

• Initialization: The initial population of N individuals is defined as

  $$P\left(0\right)=\left\{x_1\left(0\right),x_2\left(0\right),\dots ,x_N\left(0\right)\right\}$$

  (18)

  Each individual, denoted as x_i(0), is a candidate solution encoded as a real-valued vector (Arrhenius kinetic parameters). It is worth noting that these vectors are initialized randomly within specified bounds for each parameter, the search space is defined in a range from −20 to 0 dB regardless of the selected biomass.
• Fitness evaluation: Later, each individual is evaluated using a fitness function designed to quantify the degree of agreement between the model and experimental data. In kinetic parameter estimation, OF^(T) Equation (13) is used for this task.
• Selection: Following fitness evaluation, individuals are selected to form a mating pool. The probability of selection is typically biased toward individuals with superior fitness. One common method is roulette wheel selection, where the selection probability of the i-th individual is calculated as

  $$p_i={\displaystyle \frac{f\left(x_i\right)}{{\displaystyle \sum _{k=1}^{N}f\left(x_k\right)}}}$$

  (19)

  when solving minimization problems, a scaling or transformation of the fitness function is applied to ensure proper selection dynamics.
• Crossover: Selected individuals are paired and recombined to produce new offspring. For real-coded chromosomes, arithmetic crossover can be utilized:

  $$\begin{array}{l}Offsprin{g}_1=\alpha ·x_i+\left(1-\alpha \right)·x_j\\ Offsprin{g}_2=\left(1-\alpha \right)·x_i+\alpha ·x_j\end{array}$$

  (20)

  where α ∈ [0, 1] is a crossover coefficient randomly selected for each pair.
• Mutation: In order to introduce variability and prevent premature convergence, mutation is applied by perturbing individual genes as follows:

  $$x_{i,k}^{mutated}=x_{i,k}+\delta$$

  (21)

  where x_i,k is the k-th gene of chromosome x_i, and δ is a small random noise sampled from a predefined distribution (e.g., Gaussian).
• Replacement and termination: The new generation, composed of the offspring, replaces the current population. This iterative cycle is repeated until a termination condition is satisfied, such as reaching a maximum number of generations G_max or achieving a minimum fitness threshold ε:

  $$if g\ge G_{\max } or \min \left(f\left(x\right)\right)\le \epsilon , thens stop$$

  (22)

  The best-performing individual at the final generation is considered the optimal solution.

2.2.5. Nelder–Mead Algorithm (N-M)

N-M algorithm, introduced by [60], is a direct search optimization method commonly used for unconstrained minimization of nonlinear objective functions. Unlike gradient-based methods, N-M does not require the calculation of derivatives, making it particularly useful for tasks that are noisy, discontinuous, or not differentiable. It operates on a geometrical figure called a simplex, which in an n-dimensional space consists of n + 1 vertices. Each vertex corresponds to a candidate solution. The algorithm iteratively moves and reshapes this simplex in the search space to find a local minimum of the objective function.

The typical flow of the N-M algorithm, as outlined in Figure 3c, includes the following operations:

• Simplex initialization and ordering: An initial simplex S = {x₁ + x₂ + … + x_m+1} is formed using n + 1 points in the parameter space, and the objective function f(x_i) is evaluated at each vertex. The points are then sorted such that

  $$f\left(x_1\right)\le f\left(x_2\right)\le \dots \le f\left(x_{n+1}\right)$$

  (23)

  where x₁ denotes the best solution and x_n+1 the worst within the current simplex.
• Centroid and transformation: The centroid x_c of all points except the worst one is computed as

  $$x_c={\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n{x}_i}$$

  (24)

  Using x_c, the algorithm attempts reflection, and if necessary, expansion or contraction, which are estimated as follows:
  Reflection: a reflection point x_r is generated by reflecting the worst point through the centroid:

  $$x_r=x_c+\alpha \left(x_c-x_{n+1}\right)$$

  (25)

  Expansion: it is applied if x_r is better than the best as follows:

  $$x_e=x_c+\gamma \left(x_r-x_c\right)$$

  (26)

  Contraction: it is employed if x_r is worse as follows:

  $$x_c^{\prime }=x_c+\beta \left(x_{worst}-x_c\right)$$

  (27)

  It is worth noting that the parameter values α = 1, γ = 2, and β = 0.5 are commonly used, as they have been shown to yield suitable results in optimization problems [61].
• Shrinkage: If no transformation improves the simplex, it is contracted around the best point:

  $$x_i=x_1+\delta \left(x_i-x_1\right) \mathrm{for} i=2,\dots ,n+1$$

  (28)

  with δ = 0.5.
• Convergence check: The iteration continues until the spread of function values or vertex distances falls below a threshold ε:

  $$\underset{i}{\max }‖x_i-x_1‖<\epsilon \mathrm{or} \underset{i}{\max }‖f\left(x_i\right)-f\left(x_1\right)‖<\epsilon$$

  (29)

Once the stop and end conditions of each algorithm are met, a set of Arrhenius kinetic parameters (A_0,i and E_a,i) is established by the two-step kinetic model, as shown in the orange boxes in Figure 3.

3. Methodology

The methodology developed in this proposal integrates a hybrid hardware–software system designed for control, data acquisition, and kinetic modeling of the slow pyrolysis process of lignocellulosic biomass aimed at biomass-to-biochar conversion, as shown in Figure 4. The proposed approach consists of two main components: (i) Hardware System, comprising the design and implementation of a physical thermal control system for a pyrolyzer, and monitoring of weight loss with a scale, and (ii) Software System, consisting of a computational module for temperature control in the pyrolyzer, biomass weight-loss monitoring, and kinetic parameter fitting and prediction using the two-step kinetic model and optimization algorithms based on PSO, GA, and N–M. The details of the physical elements are provided in Section 4.1.

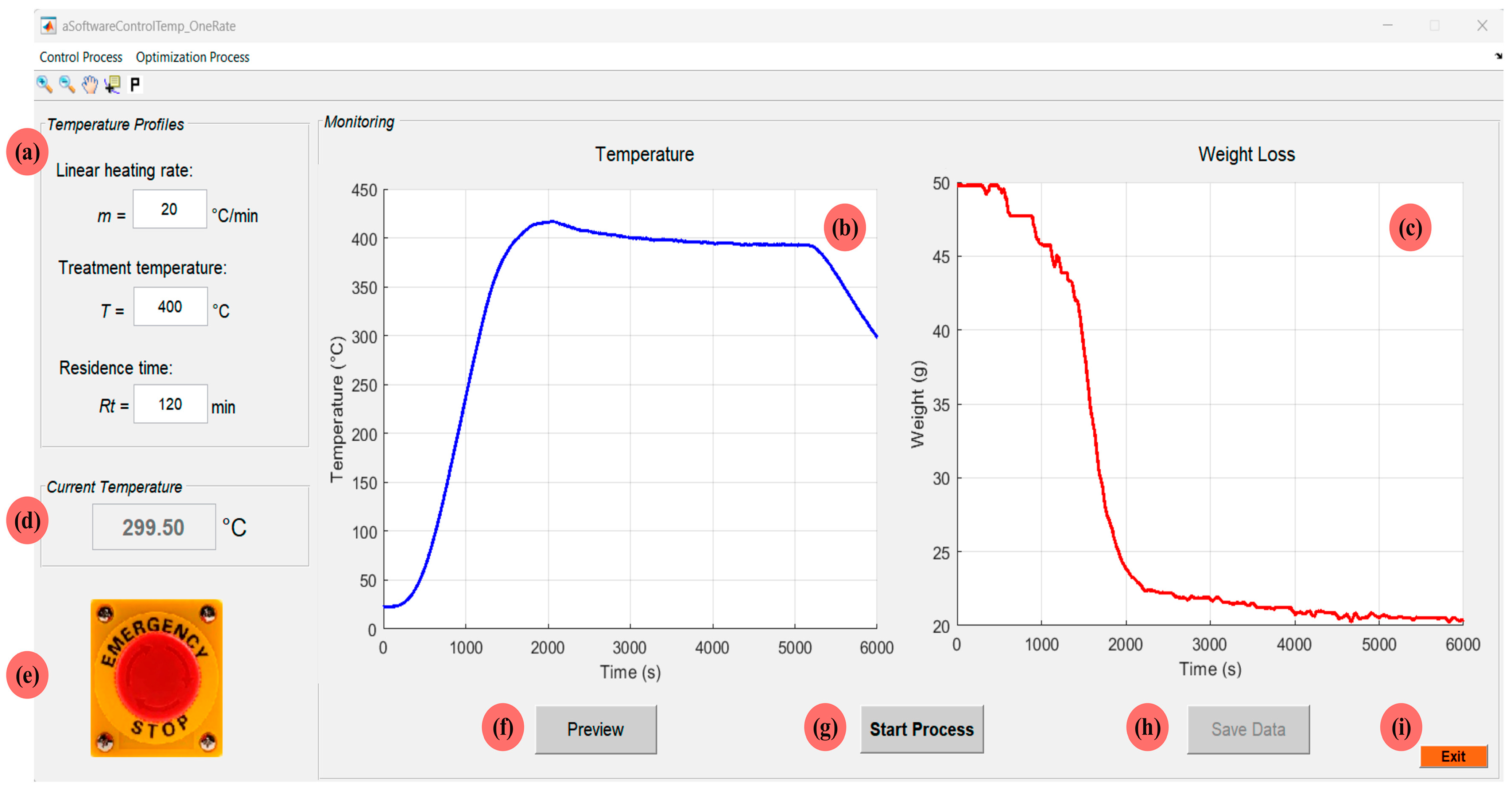
3.1. Hardware System

The pyrolyzer is designed to process raw biomass and obtain a solid product (biochar) after slow pyrolysis. The system includes a commercial scale connected to a computer via RS232, enabling real-time weight-loss recording, which is essential for kinetic analysis. The core of the physical subsystem consists of a microcontroller acting as an interface between process sensors, control elements, and the computer, as shown in Figure 4a. The microcontroller receives temperature data from a thermocouple connected to an amplifier, ensuring accurate digital readings of the pyrolyzer’s thermal profiles. This thermal signal is used by a power driver that regulates voltage to a medium-power band heater (220 V_AC, 3000 W). This resistive heating element is responsible for reaching the required temperatures to induce the thermochemical decomposition of biomass. Sensor data are transmitted to the software for visualization, storage, and subsequent processing.

3.2. Software System

Figure 5 presents a flow diagram of the graphical user interface (GUI), developed as part of a computational system that integrates thermal control of the biomass slow pyrolysis reactor with the implementation of optimization algorithms for kinetic fitting of experimental data based on the two-step kinetic model. The interface supports two main processes: (a) Pyrolyzer Control, (b) Optimization Algorithms for modeling the thermochemical processes associated with lignocellulosic biomass degradation. In both cases, it is important to establish: (c) Selection of the thermal profile according to the heating rate (°C/min): (i) linear and (ii) double, a target temperature (°C), and residence time (min).

Figure 5a corresponds to the Pyrolyzer Control Module, where the user defines the temperature profile applied to the reactor. The system allows the manipulation of temperature profiles data: heating rate (m), and treatment temperature (T). The user also specifies the residence time (Rt) of the process. Once configured, the system starts the experiment, activating real-time monitoring of key variables: temperature (°C) and weight loss (g). In addition, the user can select the Preview button to view the temperature profile before starting a control test. These variables are displayed in dynamic plots and stored using the Save Data function for later analysis. If an error occurs during operation, the process can be stopped via the STOP button.

In parallel, the interface supports a manual analysis stage, where the user selects experimental datasets containing temperature (°C), solid yield (%), and acquisition time (min). For the last two variables, at least four points are required for each studied temperature. Solid yield is normalized according to the weight-loss relationship (m/m₀) from Equation (3). This step is necessary for preprocessing adjustments before running the optimization algorithms.

Figure 5b describes the Optimization Algorithm Process Flow, where experimental thermal profiles are imported, and the biomass type is selected. Once completed, the interface automatically generates experimental plots used as input for the fitting algorithms.

Figure 5c shows the thermal profiles that can be programmed into the proposed hardware–software system: heating rate m (°C/min) and operating temperature T (°C). T_amb (°C) is the ambient temperature, and residence time (R_t (min)) corresponds to the duration of each slow pyrolysis run.

The system supports the execution of three optimization algorithms, i.e., PSO, GA, and N–M, aimed at optimizing the kinetic parameters of the two-step model using experimental solid yield (SY^(T)) data, which describe biomass thermal conversion as the combination of two parallel reactions with their respective rate constants. The objective function minimizes the error (Equation (13)) between experimental data and model predictions in terms of conversion and weight loss. Upon confirmation (RUN Algorithms), the system calculates the optimal kinetic parameters and displays them in the interface. Otherwise, the user may clear plots and data via the Clear Plots & Data button. Final results can be exported using the Save Data function.

The GUIs were developed to facilitate the visualization of temperature curves (°C) and weight loss (g), as well as the selection of the type of biomass to be analyzed. This integration allows for closing the cycle between data acquisition, processing, and analysis within a single platform. The graphical interfaces were implemented in MATLAB 2023b. Figure 6 shows the main interface where the user can choose between the pyrolyzer control process and the optimization algorithms.

Figure 7 presents the design of the GUI corresponding to the pyrolyzer control process, which includes: (a) defining temperature profiles (also shown in Figure 5c), (b) temperature graph, (c) weight loss graph, (d) current temperature monitoring display, (e) STOP button, (f) temperature profile Preview button, (g) Process Start button, (h) button to Save Data (temperature profiles and weight loss), and (i) an Exit button from the control process screen.

Figure 8 shows the GUI for the Optimization Algorithms process. This interface is divided into Experimental Data and Optimization Algorithms. For the first section: (a) loading data of temperature profiles as case studies, (b) solid yield data to be fitted to the two-step kinetic model, (c) instantaneous solid yield time data, (d) biomass type selector, (e) temperature profile graphs, (f) solid yield data graphs, and (g) a button to generate experimental graphs. In the second section, the graphs and results of the kinetic parameters obtained from the fitting by PSO, GA, and N-M with the two-step kinetic model are shown, as well as the values of the objective functions and fits calculated according to Equations (13) and (14). The subsections include: (h) graphs of the model and experimental data obtained by PSO, (i) Arrhenius curves by PSO, (j) values of kinetic parameters obtained by PSO from Equations (5) and (8)–(12), as well as the fit and OF values; (k) graphs of the model and experimental data obtained by GA, (l) Arrhenius curves by GA, (m) values of kinetic parameters obtained by GA from Equations (5) and (8)–(12), as well as the fit and OF values; (n) graphs of the model and experimental data obtained by N-M, (o) Arrhenius curves by N-M, (p) values of kinetic parameters obtained by N-M from Equations (5) and (8)–(12), as well as the fit and OF values. This section also includes the (q) RUN algorithms button, (r) the Clear Plots and Data button for when the adjustments are not as expected by the user, (s) the Save Data button, and (t) the Exit button from the Optimization window.

4. Experimentation and Results

4.1. Experimental Setup and Test Design

In Figure 9, a physical experimental setup is shown. Figure 9a shows a hardware–software system consisting of a pyrolysis-type reactor made of AISI 304 stainless steel with dimensions of 10.16 cm × 25.0 cm × 0.602 cm and a capacity of 0–2 kg of biomass, equipped with a 220 V_AC, 3000 W clamp-type electric heater. Both the pyrolyzer and the heater were custom-made, designed to operate under slow pyrolysis conditions. Thermal control is achieved through a type-K temperature sensor [62], whose signal is conditioned by a MAX6675 amplifier with a resolution of 0.25 °C [63]. This signal is digitally interpreted by an ATmega328P microcontroller [64] and then modulated to regulate the heater power via an Autonics SPC1-50 power driver, 220 V_AC~50/60 Hz [65]. Temperature data are sent to an external computer via a USB port. A Smith predictive control system with a delay of L = 225 s, Equations (1) and (2), was implemented in MATLAB 2023b software, enabling the pyrolyzer temperature to be controlled within a range from ambient temperature (T_amb) to 700 °C, heating rates between 5 and 50 °C/min, and residence times set by the user according to the test requirements. The plant transfer function, G_m(s), is shown in Equation (30), and the controller transfer function, C(s), is shown in Equation (31). For continuous monitoring of weight loss during the slow pyrolysis process, a commercial digital scale, Rhino Baco-30, with a capacity of 0–30 kg and ±1 g resolution [66], was used, communicating with the computer via RS232 protocol. The software system was implemented on an HP OMEN Intel^® Core™ i7-9750H CPU @ 2.60 GHz, 8.0 GB RAM, 2 TB storage, and 4 GB graphics card. During each slow pyrolysis test, the system records temperature (°C) and weight loss (g) data at a sampling frequency of 1 Samples/s, generating an experimental data base. To standardize the experiments, the initial weights (w₀ = 50 g) were established for each of the biomass samples under study. Figure 9b shows the schematic diagram of the reaction system consisting of: A: hardware–software system; B: interfaces (temperature, power driver, RS232); C: scale; D: thermocouple; E: clamp resistor; F: reactor; G: exhaust gas pipe; H: condenser; I: tars; J: thermal insulator; K: biomass; and L: N₂ tank.

$$G_m\left(s\right)={\displaystyle \frac{1082.1}{767.24s+1}}$$

(30)

$$C\left(s\right)={\displaystyle \frac{0.036652\mathrm{s}+0.000290173884}{s}}$$

(31)

Figure 10 shows the evolution of the three biomass types used in this research: wheat straw (WS), pruning waste (PW), and biosolids (BS) during the slow pyrolysis process at different temperatures, starting from a raw state (w₀ = 50 g) to the formation of biochar.

Nitrogen (N₂) is injected at a flow rate of 50 mL/min before starting the experiment for 5 min to eliminate any trace of air (oxidizing agent) into the reactor when the sample has been previously placed.

All samples were processed with a heating rate of 20 °C/min and a residence time of 120 min. Figure 10a depicts WS treated at 250, 275, 300, and 325 °C, where a color change from light to deep black can be observed, indicating an initial torrefaction stage followed by advanced carbonization. Figure 10b corresponds to PW treated at 300, 400, and 500 °C, showing a more gradual change from brown to black biochar with a more compact structure. In the case of BS, as shown in Figure 10c, treated at 300, 400, and 500 °C, the transformation progresses from gray to dark, dense biochar.

For each biomass under study, solid yield data (%) were obtained from weight-loss curves (with a minimum of four data points per temperature). These points were normalized (m/m_o) according to Equation (3), and the corresponding time instants were recorded. To validate the methodology,

Table 3. Experimental design based on 50 g of initial weight for each biomass: wheat straw (WS), pruning waste (PW), and biosolids (BS).

Biomass	Heating Rate (°C/min)	Residence Time (min)	Set of Temperatures (°C)	Solid Yield (%), Equation (3)	Instantaneous Solid Yield Time (min)	Heat Treatment
WS	20	120	250	1, 0.834, 0.746, and 0.638	1, 33, 53, and 83	Torrefaction and Slow Pyrolysis
			275	1, 0.748, 0.645, and 0.543	1, 40, 60, and 80
			300	1, 0.604, 0.504, and 0.469	1, 48, 68, and 88
			325	1, 0.478, 0.471, and 0.450	1, 57, 77, and 97
PW			300	1, 0.614, 0.552, and 0.552	1, 51, 76, and 101	Slow Pyrolysis
			400	1, 0.436, 0.413, and 0.408	1, 51, 76, and 101
			500	1, 0.384, 0.368, and 0.331	1, 51, 76, and 101
BS			300	1, 0.958, 0.719, 0.645, and 0.620	1, 26, 51, 76, and 101	Slow Pyrolysis
			400	1, 0.810, 0.551, 0.530, and 0.511	1, 26, 51, 76, and 101
			500	1, 0.782, 0.437, 0.431, and 0.429	1, 26, 51, 76, and 101

summarizes the experimental design applied to the three biomass types (WS, PW, and BS), subjected to slow pyrolysis under controlled conditions of 20 °C/min heating rate, 120 min residence time, temperatures between 250 °C and 500 °C, along with the solid yield (%) and instantaneous conversion times (min) obtained from the thermal treatment. Biomass weight loss was monitored in real-time via the integrated system’s scale, with initial and final weighings performed to validate measurement consistency.

4.2. Analysis of Biomass Data from the Optimization Process

The collected information is captured in the software, as shown in Section 3.2, Figure 8, within the Experimental Data section, where it is displayed and used as input for kinetic model fitting and optimization algorithms. For the PSO algorithm configuration, the initial parameters were set to 500 particles, 500 iterations, and social and cognitive parameters c₁ = 2 and c₂ = 2. For the GA case, the configuration parameters used included the crossover function defined by MATLAB’s @crossoverheuristic with a scaling factor of 8 to avoid local optima, a population size per generation of 100, a maximum number of iterations of 1000, and a tolerance function of 1 × 10⁻¹². Finally, for the N-M case, the configuration parameters used were MATLAB’s fminsearch function with a maximum of 2000 iterations, a maximum of 3000 function evaluations, and a tolerance function of 1 × 10⁻⁶. The search space varies depending on the biomass type and optimization algorithm, although the limits were always set to satisfy the condition −20 < k_i < 0 dB, relating the natural logarithm on both sides of Equation (5), and the maximum and minimum temperatures established for each practical case study, as shown in [40]. For WS: the search space ranged from 1 × 10¹ to 1 × 10²⁰ for A₀, while the range for E_a was from 1 × 10⁴ to 9 × 10⁶. For PW: the search space for A₀ ranged from 1 × 10⁻¹ to 1 × 10²⁰, while the search range for E_a ranged from 1 × 10⁴ to 9 × 10⁵. Finally, for BS: the search range for A₀ was from 1 × 10⁻¹ to 9 × 10²⁰, and for E_a the search range was from 1 × 10⁰ to 9 × 10⁶. For each biomass, the search ranges for A₀ and E_a remain independent of the optimization algorithm used. To obtain the Arrhenius kinetic parameters, namely the A₀ and E_a, according to Equation (5), for the different biomasses under study, the following presents the fitting of experimental data to the two-step kinetic model (which relates the rate constants k₁, k_V1, k₂, and k_V2, Equations (8)–(12)) using the optimization algorithms.

4.2.1. Wheat Straw (WS)

Table 4. Arrhenius kinetic parameters of wheat straw obtained using PSO, GA, and N-M algorithms, along with fitting accuracy and processing times.

Algorithms	Temperatures (°C)	Arrhenius Constants (s−1)	Arrhenius Parameters		Fit (%)	Processing Time (min)
			A0 (s−1)	Ea (J·mol−1)
PSO	250, 275, 300, and 325	k1	1.141 × 1011	1.310 × 105	99.999	6.280
		kV1	9.789 × 105	8.087 × 104
		k2	9.724 × 106	9.762 × 104
		kV2	6.763 × 105	8.557 × 104
GA		k1	5.321 × 101	1.994 × 104	99.996	1.870
		kV1	2.455 × 102	3.764 × 104
		k2	1.852 × 103	5.453 × 104
		kV2	2.307 × 103	5.492 × 104
N-M		k1	6.090 × 108	1.080 × 105	100.000	4.053
		kV1	3.660 × 103	5.710 × 104
		k2	7.450 × 103	6.280 × 104
		kV2	2.980 × 103	5.900 × 104

summarizes the kinetic parameters of the two-step model applied to WS, fitted using three optimization algorithms: PSO, GA, and N-M. The N-M algorithm achieved the best fit at 100% accuracy in 4.053 min, while PSO reached 99.999% accuracy but required more computational time (6.280 min). GA was the fastest algorithm (1.870 min), with slightly lower accuracy (99.996%). According to Table 4, the performance hierarchy in relation to fit (N-M > PSO > GA) observed in this biomass suggests that its pyrolysis kinetics are governed by relatively well-behaved reactions in a predominantly convex parameter space. The homogeneous lignocellulosic structure of WS, with balanced proportions of cellulose, hemicellulose, and lignin, generates an optimization landscape with a well-defined global minimum. This feature allows efficient local search algorithms such as N-M to converge rapidly to the optimal solution with high accuracy, while population-based algorithms (PSO and GA), although competent, are slightly less efficient in this moderately complex scenario.

The set of kinetic constants obtained using the PSO and N-M algorithms shows very similar activation energy values (with a difference of less than 10%). The highest value in the equation is related to the decomposition of solid matter, while the lower values correspond to the cracking of volatile compounds and the second stage of the model. Regarding the pre-exponential factor, high values indicate a strong molecular structure and the potential for a reaction to occur more frequently, resulting from effective molecular collisions based on the arrangement of molecules. Therefore, the obtained value using GA suggests a solution not valid for physical interpretation.

Figure 11 shows the curves of the two-step kinetic model (solid lines) alongside the experimental solid yield data (points) for WS, highlighting some nuances depending on the optimization algorithm used. In Figure 11a(i,ii), the PSO algorithm provides a close match to the experimental data, exhibiting minor errors during intermediate stages (275–300 °C), as well as increased dispersion in the Arrhenius plot, suggesting sensitivity to the swarm parameter selection. Figure 11b(i,ii) show GA producing smoother fitting curves. Finally, Figure 11c(i,ii) demonstrate that N-M achieves the best Arrhenius linearity, although its performance heavily depends on initial conditions, which could lead to convergence to local minima that do not accurately represent the true kinetics. For all three algorithms, the fits show a consistent relationship in the Arrhenius plots, where k₁ > k_V1 > k₂ > k_V2, indicating that the first stage of slow pyrolysis proceeds faster than the second, and that volatile release processes are slower than solid conversion.

Figure 12 shows the correlation between the experimental values of biochar yield and the values predicted by the optimization models (PSO, GA, and N-M) for wheat straw. The data were obtained under a constant heating rate of 20 °C/min, a residence time of 120 min, and a slow pyrolysis temperature range of 250, 275, 300, and 325 °C. Each data point represents an individual experimental condition, allowing for direct visual evaluation of model performance. For each item, the solid orange line (y) represents the ideal perfect correlation, where the predicted values would match the experimental values exactly. The proximity of the data cloud to this ideal line demonstrates the high accuracy of the optimization algorithm developed to predict solid yield. In all cases, a strong correlation between the hardware system data and the software predictions validates the overall effectiveness of the proposed system. However, the degree of accuracy varies between algorithms, as evident in the three sections analyzed. Figure 12a illustrates the correlations with PSO, demonstrating a good fit with an R-squared value of 0.990. Figure 12b corresponds to the correlations with GA with R² = 0.994. Finally, Figure 12c shows the correlations with the N-M method with R² = 0.996. In all three cases, the value of R² suggests high efficiency in the search for the global optimum for the kinetic parameters of the model. For the temperature of 275 °C, there is a slight dispersion of data for PSO and GA; however, N-M achieves a better fit.

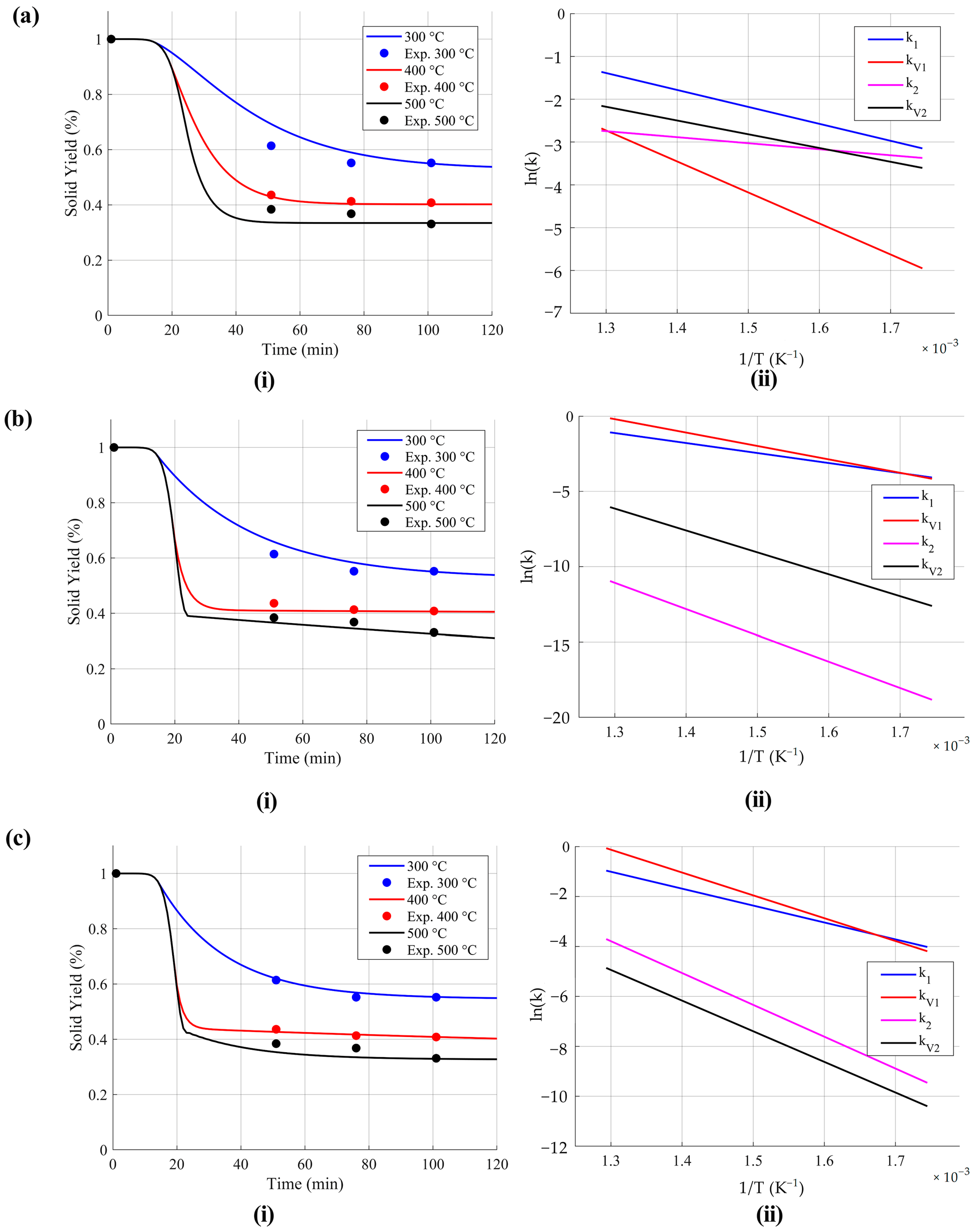
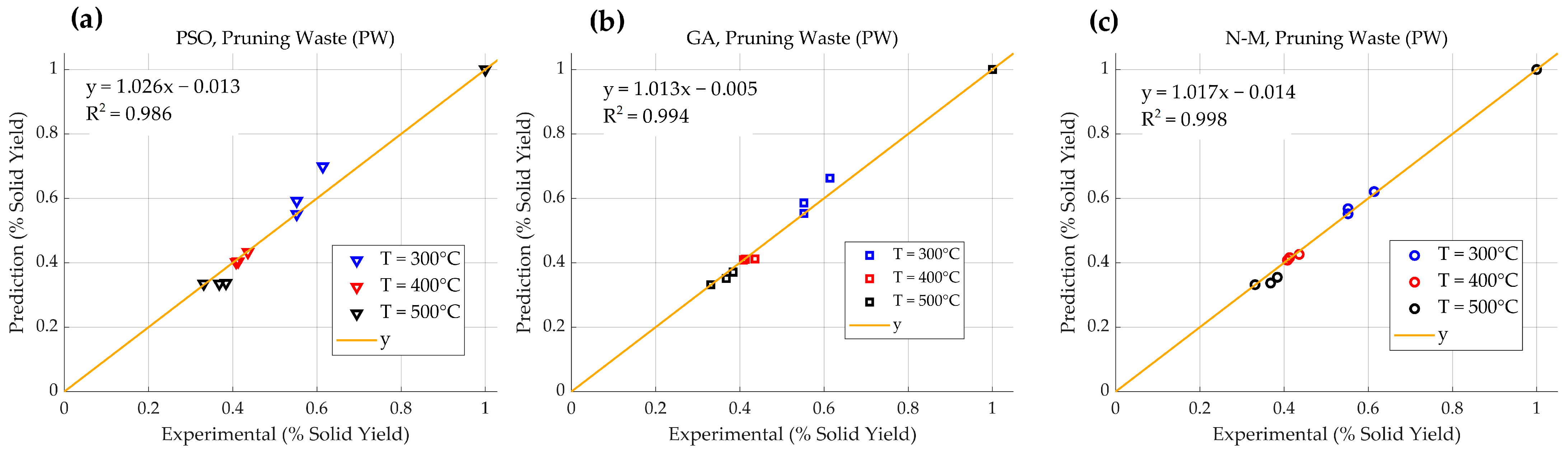
4.2.2. Pruning Waste (PW)

Table 5. Arrhenius kinetic parameters of Pruning Waste obtained using PSO, GA, and N-M algorithms, along with fitting accuracy and processing times.

Algorithms	Temperatures (°C)	Arrhenius Constants (s−1)	Arrhenius Parameters		Fit (%)	Processing Time (min)
			A0 (s−1)	Ea (J·mol−1)
PSO	300, 400, and 500	k1	4.280 × 101	3.290 × 104	99.830	6.426
		kV1	7.990 × 102	6.020 × 104
		k2	4.000 × 10−1	1.170 × 104
		kV2	7.380 × 100	2.670 × 104
GA		k1	1.861 × 103	5.526 × 104	99.999	1.805
		kV1	8.839 × 104	7.408 × 104
		k2	1.090 × 105	1.454 × 105
		kV2	3.546 × 105	1.214 × 105
N-M		k1	3.438 × 103	5.630 × 104	100.000	2.345
		kV1	1.810 × 105	7.597 × 104
		k2	5.062 × 105	1.058 × 105
		kV2	8.553 × 104	1.021 × 105

presents the kinetic parameters obtained for PW through fitting the two-step model using PSO, GA, and N-M algorithms. The activation energies (E_a) and frequency factors (A₀) for the Arrhenius constants are included, along with the percentage of fit and computational time. The N-M algorithm showed the best performance with a 100% fit achieved in 2.345 min, followed by GA (99.999%, 1.805 min) and PSO (99.830%, 6.426 min). Table 5 showed a performance hierarchy in relation to fit (N-M > GA > PSO) for this biomass, with a more robust overall fit. It is attributed to the greater presence of structural components such as lignin, which confers a more predictable but slightly more complex decomposition kinetics than WS. The consistently lignocellulosic nature of PW generates a sufficiently regular search space where local search methods maintain their advantage, while population methods show a slight excess of computational capacity for this specific application.

For the case of PW, the N-M and GA methods offer the best fit parameters, such as activation energy and the pre-exponential factor, as they yield high values, which support the interpretation of their physical significance. In contrast, the PSO method is discarded, firstly due to its lower accuracy in the fitting process, and secondly because it yields parameter values that are too small (physically not valid).

Figure 13 displays the fitting curves of the two-step kinetic model (solid lines) alongside the experimental solid yield data (points) for PW according to the different optimization algorithms. In Figure 13a(i,ii), corresponding to PSO, there is a close match with the experimental data at 400 °C, with minor errors at 300 °C and 500 °C. The Arrhenius plots indicate that the first stage of slow pyrolysis is slightly faster than the second. On the other hand, Figure 13b(i,ii), show that GA produces smooth fits at 300 °C and 400 °C, while the fit at 500 °C appears forced; however, the Arrhenius curves demonstrate that the volatile decomposition stages are slower than the solid conversion, which is a characteristic of slow pyrolysis. Finally, Figure 13.c, i, and ii, show that N-M achieves a very good fit at 300 °C and 400 °C, exhibiting rapid decomposition during minutes 15–22. This is reflected in the Arrhenius plots, where the first stage of solid decomposition occurs much faster than the second stage.

The models were evaluated under slow pyrolysis conditions with a heating ramp of 20 °C/min, a residence time of 120 min, and target temperatures of 300, 400, and 500 °C, and four experimental data points per temperature. Figure 14 shows the correlation between the experimental data and the predicted data. The solid orange line represents the ideal correlation (y). Figure 14 compares the performance of three optimization algorithms for predicting biochar yield from pruning waste. Unlike the results obtained for wheat straw, the three algorithms demonstrated higher and very similar performance for this biomass, as confirmed by the coefficients of determination (R²) very close to 1. The N-M algorithm, Figure 14c, presented the highest statistical correlation, with an R² of 0.998, indicating that its predictions explain 99.8% of the variance in the experimental data. It was closely followed by GA, Figure 14b, with an R² of 0.994, and finally PSO, Figure 14a, with an equally excellent value of 0.986. The close clustering of all data points around the orange line in the three graphs strongly validates the accuracy and robustness of the hardware–software system developed to characterize the pyrolysis of pruning waste. The fact that even the simplest algorithm (N-M) achieved the most accurate prediction suggests that the response surface of the model for this specific type of biomass is well-behaved and allows for robust optimization even with direct methods.

4.2.3. Biosolids (BS)

For the case of BS,

Table 6. Arrhenius kinetic parameters of Biosolids obtained using PSO, GA, and N-M algorithms, along with fitting accuracy and processing times.

Algorithms	Temperatures (°C)	Arrhenius Constants (s−1)	Arrhenius Parameters		Fit (%)	Processing Time (min)
			A0 (s−1)	Ea (J·mol−1)
PSO	300, 400, and 500	k1	2.865 × 102	5.017 × 104	100.000	6.520
		kV1	3.637 × 100	2.968 × 104
		k2	7.620 × 10−1	1.857 × 100
		kV2	8.298 × 102	4.584 × 104
GA		k1	6.721 × 101	3.566 × 104	99.921	1.351
		kV1	4.174 × 101	3.760 × 104
		k2	5.273 × 10−1	1.675 × 104
		kV2	8.609 × 100	3.737 × 104
N-M		k1	4.145 × 103	5.677 × 104	100.000	6.449
		kV1	2.471 × 103	5.707 × 104
		k2	4.501 × 102	4.967 × 104
		kV2	8.244 × 104	8.648 × 104

presents the kinetic parameters obtained by fitting the two-step model using PSO, GA, and N-M algorithms. Activation energies (Ea) and frequency factors (A₀) for the Arrhenius constants are included, along with the percentage of fit and computational time. In this case, the PSO and N-M algorithms showed the best performance with 100% fit achieved in 6.520 and 6.449 min, respectively, while GA reached 99.921% in 1.351 min. For BS, the performance hierarchy of the fit (PSO = N-M > GA) reflects the unique chemical complexity of this biomass. Its high inorganic content (ash), presence of metals, and extreme heterogeneity of its organic composition generate a non-convex search space with multiple local minima. In this scenario, the PSO algorithm proved to be the most robust, leveraging its population-based and stochastic nature to effectively explore the parameter space and avoid local optima. The surprising performance of N-M, outperforming GA, suggests that in certain initial configurations, this local search method can find competitive solutions in complex spaces, albeit with less consistency than PSO. The relatively inferior performance of GA could be attributed to a less efficient exploration of the search space compared to PSO, possibly due to premature convergence or a suboptimal selection of operating parameters for this specific biomass.

The PSO and N-M methods offer the best fit parameters. However, high values for the activation energy and the pre-exponential factor support the interpretation of their physical significance, making N-M stand out compared to PSO and GA.

Figure 15 shows the fitting curves of the two-step kinetic model (solid lines) to the experimental solid yield data (points) of BS using the different optimization algorithms presented, reflecting the thermal complexities of this biomass. In Figure 15a(i,ii), the PSO algorithm produces a noticeable accuracy in the solid yield profile, although in the 20–35 min range there is a fitting error, possibly due to the coexistence of organic and mineral fractions with different reactivities. The Arrhenius plots maintain good linearity with slight deviations in the second stage (k₂), which may reflect the influence of inorganic compounds on the kinetics. In Figure 15b(i,ii), the GA fit is acceptable but shows notable errors around minute 26; however, the Arrhenius plots indicate rapid decomposition in the first stage compared to the second. In contrast, Figure 15c(i,ii) show that N–M achieves a smooth fit but has less ability to capture the experimental inflections around minute 26, evidencing less stability in the kinetic slopes in the Arrhenius curves.

Figure 16 compares the effectiveness of three optimization algorithms for predicting biochar yield from biosolids, with five experimental data points per temperature. The analysis reveals a clear gradient in predictive performance among the methods evaluated. The PSO algorithm, Figure 16a, proved to be the most robust and accurate for this specific biomass and conditions, achieving a coefficient of determination (R²) of 0.980. This indicates that the model explains 98.0% of the variance in the experimental data, with the data points clustered closely around the ideal orange line (y). GA in Figure 16b performed well, although with slightly lower accuracy (R² = 0.955). Moderate dispersion of the points is observed, suggesting that the algorithm was able to capture the general trend but with some more significant prediction errors at specific points. The N-M algorithm, Figure 16c, presented the least accurate fit (R² = 0.860). The greater dispersion of the data indicates a difficulty in consistently converging towards the global optimal solution for this particular problem, possibly becoming stuck in local optima or being more susceptible to the influence of the initial parameter configuration. This performance hierarchy (PSO > GA > N-M) validates the selection of robust metaheuristics such as PSO for the optimization of kinetic parameters in complex pyrolysis models, where the search space can be nonlinear and multimodal.

4.3. Quantitative Comparison of Biochar Yield

For a quantitative comparison of biochar yield among biomasses,

Table 7. Experimental and predicted biochar yields at the maximum slow pyrolysis temperature.

Biomass	Tmax (°C)	Final Solid Yields (%)
		Exp.	Algorithms/Predictions
			PSO	GA	N-M
WS	325	0.450	0.449	0.449	0.455
PW	500	0.331	0.335	0.332	0.332
BS	500	0.429	0.429	0.431	0.429

presents the experimental and predicted values at the maximum pyrolysis temperature for each material. WS exhibited the highest solid yield (45.0% at 325 °C), followed by BS (42.9% at 500 °C) and PW (33.1% at 500 °C). This hierarchy can be attributed to the higher proportion of structural components (e.g., lignin) in WS, which promotes biochar formation.

5. Discussion

Slow pyrolysis emerges as a key technology for the circular economy, transforming residual biomass into biochar, bio-oils, and high-energy gases while promoting carbon sequestration. In this context, the proposed integrated hardware–software system allowed the kinetic evaluation of three representative biomasses from Guanajuato, Mexico, i.e., WS, PW, and BS, applying the two-step kinetic model that distinguishes consecutive reactions of solid and volatile formation. The selection of these three biomasses responds to strategic criteria of regional abundance (>400,000 tons/year of WS alone in Guanajuato [49], 18% of municipal urban PW [67], 120 ktons/year (equivalent to 1.2 × 10⁸ kg per year) of BS generated in local treatment plants [50]), compositional diversity (lignin 12% WS, 28% PW, 18% BS; cellulose: 42.5% WS, 31.3% PW, 22.66% BS; and ash: 5.1% WS, 8.9% PW, 18.4%), and potential for industrial scalability. This triad allows extrapolation of results to more than 15 additional Mexican biomasses (corn, agave, sorghum, etc.) through pre-loaded composition libraries. The hardware–software platform thus establishes an extrapolable framework for designing slow pyrolysis biorefineries, where the composition determines the optimal operating parameters through optimization algorithms such as PSO, GA, and N-M, comparing their accuracy and computational efficiency [68].

Figure 17 shows bar charts depicting the three different biomasses with the three optimization algorithms implemented. From Figure 17a, results demonstrated that for wheat straw, N-M achieved the best fit at 100%, while GA showed the lowest fit at 99.996%. For pruning residues, N-M provided the best fit at 100%, and the lowest was PSO with 99.830%. For biosolids, PSO and N-M yielded similar results at 100%, and GA gave 99.921% fit. Visually, GA exhibited smoother behavior in terms of fitting on the solid yield curves as seen in Figure 11, Figure 13 and Figure 15. Among the studied biomasses, wheat straw showed higher efficiency in biochar generation, associated with its high lignin content. Regarding the adjustment of optimization algorithms, Figure 17b shows that it is independent of the type of biomass, with PSO being consistently the most accurate for complex biomasses such as BS (R² = 0.980), N-M is the most accurate for WS (R² = 0.996), while for PW, all three algorithms showed excellent correlation with a slight advantage for N-M (R² = 0.998). These results validate that the selection of the optimal algorithm must consider the specific nature of the biomass, highlighting the robustness of the hardware and software system developed to efficiently characterize the performance of biochar in slow pyrolysis. Finally, Figure 17c displays the processing times (t_p) obtained for the three biomasses with the different algorithms. In all cases, GA showed the fastest processing times (1.351 < t_p < 1.870 min) compared to PSO and N-M, while PSO required the longest processing times in all cases (6.280 < t_p < 6.520 min).

Table 8. Performance hierarchy for R², fit, and processing time (t_p) for different biomasses and optimization algorithms.

Biomass	Standard Metrics	Algorithms			Performance Hierarchy
		PSO	GA	N-M
WS	R2	0.990	0.994	0.996	N-M > GA > PSO
	fit (%)	99.999	99.996	100	N-M > PSO > GA
	tp (min)	6.280	1.870	4.053	GA < N-M < PSO
PW	R2	0.986	0.994	0.998	N-M > GA > PSO
	fit (%)	99.830	99.999	100	N-M > GA > PSO
	tp (min)	6.426	1.805	2.435	GA < N-M < PSO
	R2	0.980	0.955	0.860	PSO > GA > N-M
BS	fit (%)	100	99.921	100	PSO = N-M > GA
	tp (min)	6.520	1.351	6.449	GA < N-M < PSO

shows the performance hierarchy for R², fit, and processing time (t_p) for the different biomasses and optimization algorithms, demonstrating that in terms of R² and fit for biomasses such as WS and PW, the N-M algorithm is the best, while for more complex biomasses such as BS, the best algorithm is PSO.

Among the advantages of the proposed system are its reconfigurability, since the model and algorithms can adapt to different biomasses and operational conditions without requiring structural modifications. The use of efficient algorithms reduces simulation time, resulting in. Additionally, the methodology is scalable to other thermochemical processes with low computational cost [69], such as gasification or combustion. The system can be adapted to study co-pyrolysis, where the feedstock consists of biomass and plastic mixtures, which could help generate biofuels with higher calorific value and industrial applications. Technically, the proposed hardware–software system allows configuration of different heating rates (5–50 °C/min), residence times, and temperature ranges (T_amb to 700 °C), as well as handling larger biomass quantities (0–2 kg), while other systems sometimes handle very small amounts (on the order of mg). It includes three different optimization algorithms (PSO, GA, and N-M) to compare the best fit curves and kinetic parameters obtained. However, other optimization algorithms and kinetic models can also be incorporated.

Despite these advantages, the hardware–software system presents some limitations such as a limited temperature range (<700 °C), which could be improved by installing a higher power heating element to reach a wider pyrolysis temperature range. The precision of the weight loss monitoring system is ±1 g, which could be enhanced with a higher-resolution system. The system lacks a cooling mechanism, so the time between tests can be prolonged (up to twice the residence time). Installing pressure valves and nitrogen flow controls would help maintain a regulated inert atmosphere. Also, although biomass weight loss was monitored in real time using the scale integrated into the hardware–software system, and each sample was weighed independently at the beginning and end of each test to verify measurement consistency, this study lacks experimental replicates. Therefore, future research will incorporate systematic replicates to enhance statistical robustness through uncertainty quantification.

Beyond solid yield, the integrated hardware–software system is uniquely positioned to optimize biochar quality. Future iterations will incorporate post-process analysis of elemental composition (C, H, O). O/C and H/C ratios are key indicators of biochar stability and carbon sequestration potential. By correlating these parameters with the optimized kinetic conditions found by the algorithms (PSO, GA, N-M), the system can generate a comprehensive dataset. This high-quality data is ideal for developing machine learning models that predict not only yield but also biochar quality based on biomass feedstock and pyrolysis conditions, ultimately enabling multi-objective optimization for tailored biochar production.

Although this work lays a solid foundation for optimizing slow pyrolysis of biomass within an integrated hardware–software system, several lines warrant further investigation:

(a)

Integration of Real-Time Product Characterization: Future system iterations could incorporate online analytical techniques (e.g., FTIR, GC-MS) for simultaneous monitoring of bio-oil and syngas composition, enabling comprehensive mass balance closure and product valorization assessment.

(b)

Machine Learning Enhancement: Expanding beyond traditional optimization algorithms to incorporate machine learning approaches (e.g., neural networks, random forests) could improve prediction accuracy across diverse biomass types and mixed feedstocks.

(c)

Economic and Environmental Impact Assessment: Subsequent research should integrate techno-economic analysis (TEA) and life cycle assessment (LCA) to evaluate the economic viability and environmental benefits of implementing the optimized parameters identified by the system.

(d)

Expansion to Co-Pyrolysis and Catalytic Pyrolysis: The platform’s adaptability provides opportunities to explore synergistic effects in co-pyrolysis of biomass-plastic mixtures and catalytic pyrolysis for enhanced bio-oil quality.

5.1. Unique Value of Integrated Hardware–Software Platform for Slow Biomass Pyrolysis Research

The hardware–software platform offers unique value by addressing research questions that commercial systems cannot efficiently solve. While standard equipment is limited to generic characterization under predefined conditions, the integrated system allows:

• Automated optimization for biomass: Determines optimal kinetic parameters (A, E_a) under operating conditions (m, T, R_t) to maximize yield and quality of biochar in biomass (WS, PW, BS), using computational intelligence algorithms (PSO, GA) and optimization (N-M) that explore multimodal search spaces.
• Advanced validation of kinetic models: Evaluates the behavior of complex kinetic models (e.g., two-step) under customized conditions and unconventional or region-specific biomasses, through full integration between hardware (data generation) and software (real-time adjustment).
• Rational selection of algorithms: Establishes practical guidelines for choosing the optimal algorithm (PSO, GA, N-M) according to the type of biomass, balancing accuracy, speed, and computational cost.
• Accessibility and generalization of advanced research: The platform promotes cutting-edge pyrolysis research for institutions with limited budgets by offering an accessible solution specialized in the study of local biomass, overcoming the limitations of traditional commercial systems.

The platform transcends conventional characterization by integrating characterization, optimization, and validation into a single workflow, laying the foundation for the design of decentralized biorefineries tailored to specific feedstocks—a critical capability for the circular economy that commercial systems do not offer.

5.2. Selection of Optimization Algorithms for Slow Pyrolysis Kinetics

Based on the hardware–software system and the evaluation of three optimization algorithms (PSO, GA, N-M) targeting three different types of biomasses (WS, PW, BS), a practical guide is provided here for researchers who need to select an algorithm for the characterization of slow pyrolysis kinetics:

• Selection according to biomass type:
  • For homogeneous lignocellulosic biomass (e.g., wheat straw—WS, pruning waste—PW): The N-M algorithm is recommended, as it achieved good accuracy (R² = 0.996 and 0.998), making it the optimal choice for these systems with convex search spaces.
  • For complex and heterogeneous biomass (e.g., biosolids—BS), PSO and N-M show a similar fit. However, the kinetic parameters obtained with N-M exhibit greater physical consistency with actual thermal decomposition mechanisms, offering not only optimization but also a relevant thermochemical interpretation.
• Selection based on objective (Accuracy vs. Speed):
  • For maximum accuracy (especially in complex biomasses): PSO is the preferred option, despite its higher computational cost.
  • For maximum speed and efficiency (in homogeneous biomasses): N-M offers the best performance, providing exceptional accuracy with minimal resource consumption.
  • For a balance between accuracy and speed: GA is a robust option, although in this work, it was consistently outperformed by PSO or N-M in one of the two aspects.
• Selection based on computational resources:
  • For limited resources: N-M is the most efficient alternative.
  • For sufficient resources: PSO justifies its computational investment in complex systems.

6. Conclusions

The proposed hardware–software system enabled the evaluation of slow pyrolysis kinetics of three residual biomasses through a two-step kinetic model optimized with three algorithms. The average results showed that the N-M method achieved the highest accuracy (100% fit in estimating solid yield) with a convergence time of 4.282 min, while GA converged faster (1.675 min) with a fit of 99.972%, and PSO had the slowest convergence time at 6.409 min and a fit of 99.943%. Confirming the effectiveness of hybrid deterministic–evolutionary approaches for kinetic parameter prediction. Wheat straw exhibited the highest biochar yield, highlighting its potential role in carbon sequestration and soil enhancement. The hardware–software system is capable of accurately predicting biochar yield for different biomasses, with wheat straw (WS) being the material with the highest solid yield (45.0% at 325 °C), followed by biosolids (42.9% at 500 °C) and pruning waste (33.1% at 500 °C). This difference in yields is related to the distinctive structural composition of each biomass.

Beyond accurate parameter fitting, the system establishes an optimization and computational intelligence tools-driven methodological framework that integrates optimization algorithms into an automated and reproducible platform for thermochemical characterization. This approach provides not only precise process control but also adaptability to diverse biomasses and operating conditions, ensuring robust and scalable applications in energy systems. By leveraging optimization and computational intelligence tools, the system contributes to the resilience of energy infrastructures, offering digital tools that can support decision-making in the valorization of biomass waste under varying environmental conditions.

Key advantages include reconfigurability, low computational cost, and scalability, while limitations involve the need for broader validation across heterogeneous biomasses and composition variability.

Although this work successfully demonstrated the effectiveness of a hardware–software system coupled with optimization algorithms to characterize the performance of biochar in the slow pyrolysis of various biomasses, true predictive capability and physical relevance require external validation with temperatures withheld from the parameter estimation process. Therefore, future experiments will include independent validation points to forecast solid yield under out-of-calibration temperature data, thereby verifying predictive performance and enhancing parameter reliability under extended operating conditions.