Do LLMs Offer a Robust Defense Mechanism Against Membership Inference Attacks on Graph Neural Networks?

Abstract

Graph neural networks (GNNs) are deep learning models that process structured graph data. By leveraging their graphs/node classification and link prediction capabilities, they have been effectively applied in multiple domains such as community detection, location sharing services, and drug discovery. These powerful applications and the vast availability of graphs in diverse fields have facilitated the adoption of GNNs in privacy-sensitive contexts (e.g., banking systems and healthcare). Unfortunately, GNNs are vulnerable to the leakage of sensitive information through well-defined attacks. Our main focus is on membership inference attacks (MIAs) that allow the attacker to infer whether a given sample belongs to the training dataset. To prevent this, we introduce three LLM-guided defense mechanisms applied at the posterior level: posterior encoding with noise, knowledge distillation, and secure aggregation. Our proposed approaches not only successfully reduce MIA accuracy but also maintain the model’s performance on the node classification task. Our findings, validated through extensive experiments on widely used GNN architectures, offer insights into balancing privacy preservation with predictive performance.

1. Introduction

The recent achievements of Deep Neural Networks (DNNs) have transformed the domain of machine learning (ML), particularly in machine translation [1,2], speech recognition [3], and object detection [4,5] tasks. This revolution is ascribed to the progress of deep learning (DL) architectures, including Convolutional Neural Networks (CNNs) [6], Recurrent Neural Networks (RNNs) [7], and autoencoders [8]. The input representation is acquired alongside the downstream job in the deep learning framework. This collaborative learning obviates the necessity for manually engineered features, as is typical in conventional machine learning. The effectiveness of these neural architectures is primarily due to advancements in processing resources, enabling the development of more intricate and deeper models. Furthermore, the accessibility of comprehensive training datasets has enhanced learning and generalization across many tasks. These networks proficiently extract latent representations from Euclidean data, such as photos, text, and videos, enhancing their adaptability and performance across various applications. Convolutional Neural Networks (CNNs) have been particularly pivotal in comprehending and using the characteristics of image data. Convolutional Neural Networks (CNNs) utilize translation invariance and local connectivity to extract pertinent features for various image processing applications [9].

However, the constraints of traditional deep learning architectures become apparent when addressing graph-structured data, as machine learning models evolve. Graphs are omnipresent in our daily lives and depict a wide variety of facts, such as chemical structures in chemistry and social interactions. The conventional assumptions of machine learning, such as instance independence, are not upheld in the graph domain, leading to significant challenges in applying typical deep learning architectures to graph data [10,11].

Graph neural networks (GNNs) proficiently manage diverse tasks by utilizing the complex graph architecture and associated node attributes. Furthermore, GNNs exhibit adaptability across several scales of graph analysis. At the node level, they employ message passing and graph convolutions to derive representative node embeddings, generally leveraging softmax or multilayer perceptron layers for final predictions [12,13]. Edge-level tasks utilize node representations alongside learned similarity metrics or neural architectures for link prediction and edge classification [14]. Graph-level analysis combines pooling and readout operations to produce comprehensive graph representations appropriate for classification problems [15].

Despite their efficacy, GNNs have substantial security issues, especially concerning data privacy [16]. Their message passing characteristics render them susceptible to various attack vectors, such as membership inference [17], attribute inference [18], and property inference [19]. These vulnerabilities require improved security standards and protective measures, particularly for apps handling sensitive data.

This work concentrates on membership inference attacks targeting GNNs in node classification tasks. Membership inference attacks pose a considerable risk to privacy, seeking to ascertain whether a specific data piece was included in the training dataset utilized for the GNN. These attacks exploit particular attributes of the model, including its confidence levels or output variances, to deduce sensitive information regarding the training data. In the context of GNNs, it pertains to the identification of a particular node or edge within a training graph, which could compromise confidential information.

Defense techniques against GNN vulnerabilities, particularly membership inference attacks, have developed through various methodologies. This encompasses probability encoding techniques that disguise class links and graph perturbation methods that implement controlled alterations to network structure and node attributes. Although these defenses demonstrate potential in reducing attacks, they inevitably entail a fundamental trade-off between security improvement and model efficacy. The equilibrium between defensive strength and computational efficiency is a crucial factor in the design of protective strategies for GNN implementations.

We propose three LLM-guided approaches to encode the posteriors of graph neural networks to defend against membership inference attacks. These attacks enable adversaries to determine whether a particular data point was part of the training set. Our approaches aim to obscure membership signals in the model’s predictions.

Posterior Encoding with Noise: This approach perturbs the output posterior probabilities by adding noise, making it difficult for attackers to distinguish between members and non-members. The noise is calibrated with a parameter $ϵ$ to control the perturbation level.

Knowledge Distillation: A teacher GNN model generates soft labels, which are then used to train a student model. This helps generalize the outputs and reduces overfitting to the training data, making it harder for attackers to infer membership.

Secure Aggregation: Multiple independently trained GNN models aggregate their predictions, followed by noise perturbation. This makes it harder for an adversary to exploit individual model outputs and reduces the risk of successful MIAs.

All three approaches ensure that the index of the highest value in the posterior remains the highest. These approaches collectively obscure membership information while preserving node classification accuracy. Our experiments show that they effectively mitigate MIAs on various GNN architectures and datasets.

The paper is structured as follows: An examination of pertinent literature and prior research is presented in Section 2. The introduction of our suggested defensive mechanism, outlined in Section 3, is succeeded by a comprehensive account of the experimental techniques and parameters in Section 4. The outcomes of our results are detailed and analyzed in Section 5. The work concludes in Section 6, summarizing principal findings and suggesting avenues for future research.

2. Related Works

2.1. Background

Graph neural networks have emerged as powerful tools for learning representations of graph-structured data. Unlike traditional neural networks that operate on grid-structured data, GNNs are designed to handle irregular interconnected data, making them suitable for tasks such as node classification, link prediction, and graph classification. A GNN leverages the inherent structure and relationships within graphs to capture complex patterns and dependencies. Graph neural networks employ various layers to process and learn from graph-structured data. Three fundamental types of layers in GNNs are the Convolutional Layer, Attention Layer, and Message Passing Layer. These layers play distinct roles in capturing and updating node representations within a graph.

• Convolutional Layers used in GCN, ARMA, and ChebNet update node representations through neighborhood aggregation:

  $${\mathbf{h}}_i^t=\varphi \left({\mathbf{h}}_i^{t-1},\underset{j\in {\mathcal{N}}_i}{⨁}{c}_{ij}\psi \left({\mathbf{h}}_j^{t-1}\right)\right)$$

  (1)

  where $\psi$ processes neighboring nodes and $c_{ij}$ weights their contributions.
• Attention Layers (used in GATs, MoNet, GaAN) implement dynamic neighbor weighting:

  $${\mathbf{h}}_i^t=\varphi \left({\mathbf{h}}_i^{t-1},\underset{j\in {\mathcal{N}}_i}{⨁}a\left({\mathbf{h}}_i^{t-1},{\mathbf{h}}_j^{t-1}\right)\psi \left({\mathbf{h}}_j^{t-1}\right)\right)$$

  (2)

  where a determines neighbor importance through learned attention mechanisms.
• Message Passing Layers (used in GraphSAGE, MPNNs) control information flow between nodes:

  $${\mathbf{h}}_i^t=\varphi \left({\mathbf{h}}_i^{t-1},\underset{j\in {\mathcal{N}}_i}{⨁}\psi \left({\mathbf{h}}_i^{t-1},{\mathbf{h}}_j^{t-1}\right)\right)$$

  (3)

  where $\psi$ defines the message content passed between nodes.

2.2. Membership Inference Attacks and Defense Mechanisms

In this section, we explore the emerging challenges posed by MIAs targeting GNNs, along with the state-of-the-art protection mechanisms designed to mitigate these threats.

The investigation of membership inference attacks (MIAs) in graph-based models has advanced considerably. Preliminary investigations [20] identified intrinsic vulnerabilities in knowledge graph applications, laying the groundwork for ensuing privacy breach evaluations. A significant advancement was made by [21], who presented a graph-specific membership inference attack methodology employing shadow datasets and models to ascertain training set membership. He et al. [22] improved this framework by including multi-hop confidence vectors into the training process of the attack model, resulting in higher inference accuracy. Subsequent advancements enhanced the comprehension of GNN weaknesses. The authors of [23] illustrated exploitation techniques targeting robust GNN architectures, whilst [24] revealed weaknesses in unsupervised graph representation learning. Disparate vulnerability patterns in link inference attacks were identified in [25].

In response to these weaknesses, defense solutions against MIAs in GNN node classification were developed along three principal approaches. Encoding-based strategies modify output probability distributions to improve resistance against membership inference attacks (MIAs) using several techniques. One-hot encoding [26] employs a binary vector representation that retains just the highest class probabilities while ensuring similarity in representation among nodes. The ReLU-based transformation [27] selectively nullifies probability values except for the highest class, whereas posterior shuffling [28] preserves the highest probability while randomizing the indices of the remaining classes. The top-k selection [29] limits the output to the classes with the highest probabilities. Perturbation-based methodologies, as demonstrated by [30], include controlled noise into graph representations. They generally utilize graph autoencoders (GAEs) to modify node embeddings while preserving structural integrity via adjacency matrix reconstruction. In addition to these methods, regularization techniques emphasize the mitigation of overfitting, chiefly through dropout [31], which intermittently disables neurons during training to diminish reliance on particular neurons. Figure 1 provides a taxonomy of defenses against membership inference attacks in GNNs.

According to the recent survey [32], defense mechanisms against attacks on GNNs can be broadly classified into three classes: (i) Before training, where data and graph preprocessing are applied to mitigate adversarial perturbations. (ii) During training, where techniques such as adversarial training, architectural modifications, differential privacy (DP), and federated learning (FL) are integrated into the training pipeline. (iii) After training, including post hoc defenses such as detection mechanisms and output perturbation. Our proposed method, LLM-guided posterior encoding, naturally belongs to the after-training/postprocessing family, since it operates directly on posterior vectors after model training. However, it introduces a novel twist that is not captured in the existing taxonomy. Instead of static or hand-crafted perturbations, our method leverages transformer-based optimization to adaptively encode posteriors while preserving the index of the maximum probability. This ensures utility retention while suppressing membership signals, offering a new direction within the after-training category of the survey. Compared to DP and FL defenses (placed under the “during training” stage), our approach avoids the weaknesses noted in the survey: DP’s tendency to degrade utility due to excessive noise injection, and FL’s high communication overhead and vulnerability to gradient leakage. In contrast, our method does not require retraining or a distributed setup, relying only on low-dimensional posterior vectors (dimensions depending on the number of classes in a dataset). This makes it lightweight, adaptive, and computationally efficient, aligning with the survey’s call for methods that balance privacy, robustness, and environmental well-being in trustworthy GNNs.

On the other hand, encoding-based strategies reduce the amount of posterior information exposed, but at the cost of rigid transformations that harm accuracy. Perturbation-based defenses improve resistance but require retraining with graph autoencoders, introducing computational overhead. Regularization-based methods such as dropout mitigate overfitting but only provide indirect protection, and are insufficient against strong membership inference attacks. Compared with these approaches, our method departs in two critical ways. First, instead of fixed transformations or heavy retraining, LLM-guided posterior encoding introduces adaptive perturbations to posteriors while explicitly preserving the class with maximum probability, thus minimizing the accuracy–privacy trade-off. Second, unlike differential privacy (which injects large amounts of noise and severely impacts utility) and federated learning (which suffers from communication overhead and gradient leakage risks), our method is lightweight and purely post hoc, requiring no modification to the training process. This design ensures computational efficiency, adaptability, and robustness to membership inference, which positions our approach as a distinct advancement within the broader landscape of trustworthy GNNs.

Although these defense strategies effectively diminish MIA vulnerability, they inevitably affect model performance. This trade-off between security and usefulness underpins our proposed methodology, elaborated in the subsequent section, which seeks to attain an optimal equilibrium between MIA resistance and classification efficacy.

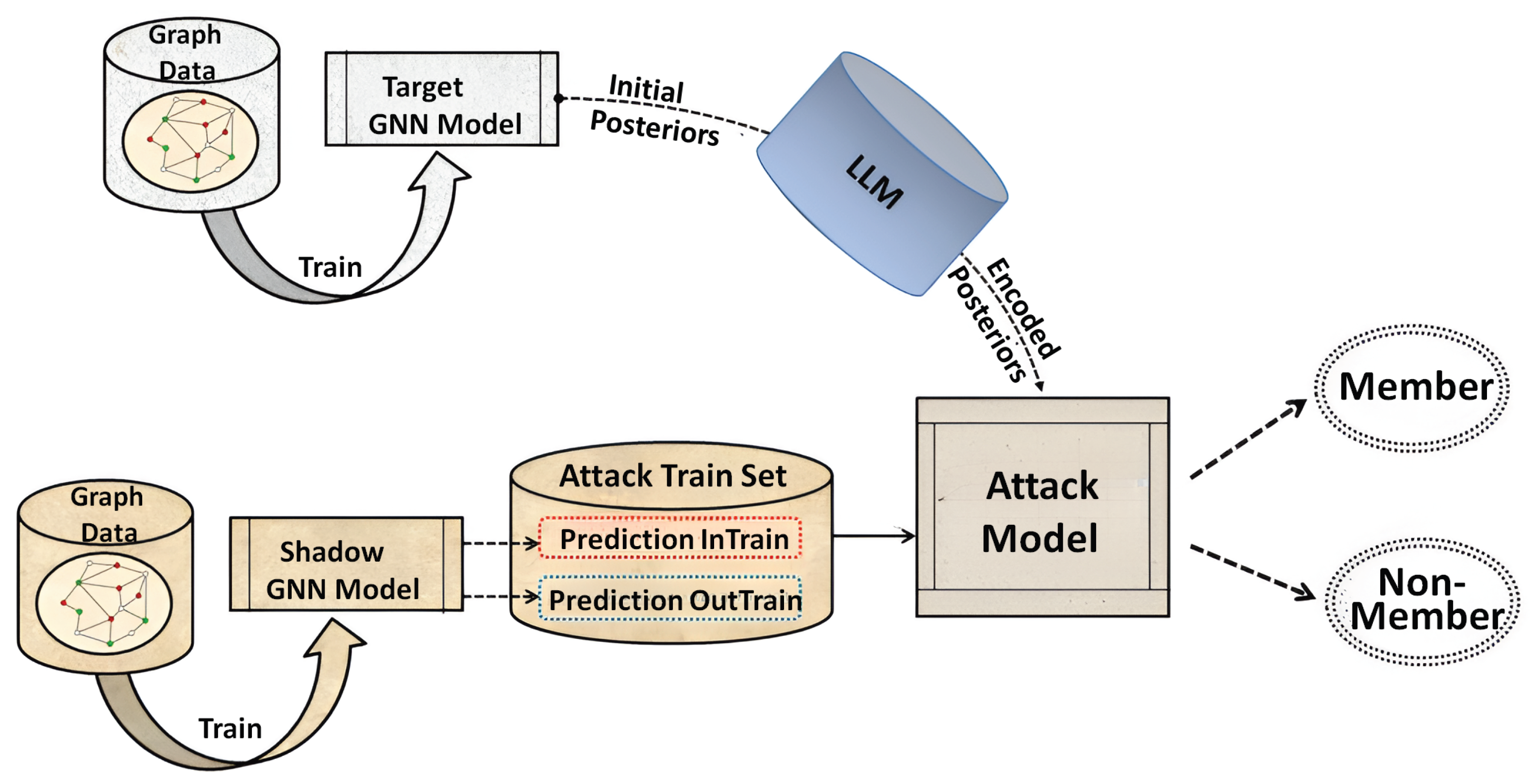
3. Proposed Model

3.1. Attack Methodology

A membership inference attack is a binary classification task aimed at determining whether a specific node v with attributes $X_v$ is part of the GNN’s training dataset. Initially, we designate our attack classifier as $\mathcal{A}$. Subsequently, we employ an accuracy metric to evaluate the attacker’s inference capacity, wherein accuracy quantifies the proportion of predicted member nodes that are actual members of the training dataset.

To train classifier $\mathcal{A}$, we construct a labeled training dataset containing ground truth information. Specifically, we construct a shadow model that replicates the behavior of the target model. We assume that the shadow model employs the same GNN architecture and hyperparameters as the target model. Our attack comprises three phases, as shown in Figure 2:

1/Shadow model No indent formatting of these three paragraphs is necessary training involves the attacker employing an identical model architecture to that of the target model, thereafter training the shadow model on a graph neural network dataset that exhibits a comparable distribution to that utilized for the target’s training. The attacker use a dataset $D_{shadow}$ comprising two subsets: $D_{shadow}^{train}$ for training and $D_{shadow}^{test}$ for testing.

2/To develop the attack model (binary classifier) $\mathcal{A}$, the attacker solicits predictions from the trained shadow model to obtain the associated output class posterior probability. The posterior probabilities of samples from $D_{shadow}^{train}$ are designated as members, while the posterior probabilities of samples from $D_{shadow}^{test}$ are designated as non-members. The designated labels serve as ground truth data for the attack model. Subsequently, all the generated posterior probabilities and labels are utilized in training the attack model.

3/Membership inference: To ascertain the membership of a certain sample, the attacker interrogates the target model regarding the candidate sample’s posterior probabilities. The attacker subsequently inputs the posteriors into the attack model $\mathcal{A}$ to ascertain the membership status (member/non-member). To enhance the MIA for a certain category of datasets, one may select an adaptive classifier. Consequently, a particular machine learning classification algorithm will be selected depending on its efficacy. We utilize various classifiers (attack models $\mathcal{A}$), including MLP [33], XGB [34], and Random Forest [35]. We choose the most powerful.

3.2. Proposed Defense Methodologies

As shown in Figure 3, we propose three LLM-guided posterior encoding defense methodologies that protect graph neural networks (GNNs) from membership inference attacks (MIAs). These defenses focus on perturbing the class probabilities or posteriors during the inference phase, making it harder for attackers to infer membership information, while also ensuring that the classification accuracy is maintained. In our framework, we utilize an LLM architecture not as an external assistant, but as an embedded transformer module that operates on internal GNN outputs (e.g., logits or posteriors) to dynamically generate secure distributions. The role of the LLM is to learn an adaptive mapping from GNN outputs to perturbed posteriors in order to confuse adversarial inference. By leveraging LLM architectures as internal modules that operate on class logits or posteriors, we obtain adaptive, learnable, and context-sensitive defenses that outperform static noise or heuristic-based strategies.

3.2.1. Posterior Encoding Using LLM-Guided Knowledge Distillation

Knowledge distillation is a classical technique where a student model learns from a teacher model by matching its output distributions. Traditionally, the teacher’s logits are softened using a temperature parameter $\tau$, and the student mimics:

$${\tilde{\mathbf{p}}}_v^{\left(t\right)}=\mathrm{softmax}\left({\displaystyle \frac{{\mathbf{z}}_v^{\left(t\right)}}{\tau }}\right)$$

However, static temperature smoothing cannot adapt to variations in overconfidence, class imbalance, or local graph structure.

In our defense methodology, the teacher model is trained on the dataset, and its class probabilities are softened using a temperature parameter $\tau$, resulting in “soft labels” that are used to train the student model. By utilizing soft labels rather than hard classification outputs, the student model learns a smoother representation of the data distribution, making it less likely to overfit to any particular training example.

To enhance this process, we integrate an LLM-based transformer $g_{\varphi }$ that takes the logits of the teacher model ${\mathbf{z}}_v^{\left(t\right)}\in {\mathbb{R}}^C$ for each node v and produces softened posteriors ${\tilde{\mathbf{p}}}_v=g_{\varphi }\left({\mathbf{z}}_v^{\left(t\right)}\right)$. The student is trained to match ${\tilde{\mathbf{p}}}_v$ via KL divergence while maximizing entropy:

$${\mathcal{L}}_{\mathrm{distill}}=\mathrm{KL}({\tilde{\mathbf{p}}}_v \Vert \mathrm{softmax}({\mathbf{z}}_v^{\left(t\right)}/\tau ))-\lambda ·\mathcal{H}\left({\tilde{\mathbf{p}}}_v\right)$$

This architecture allows dynamic, node-specific smoothing, protecting nodes that might otherwise leak membership signals. To further obfuscate the class membership, noise is introduced to the posterior probabilities during inference. This noise prevents the attacker from making definitive inferences about the membership of a node based solely on its predicted probabilities. The noise is generated by a specific noise function parameterized by $ϵ$, and is added to all class probabilities, ensuring that the final prediction remains uncertain and difficult for adversaries to exploit.

3.2.2. Posterior Encoding Using LLM-Guided Secure Aggregation

Secure aggregation leverages outputs from multiple independently trained GNNs to mask membership signals. Conventionally, aggregation uses a simple mean:

$${\overline{\mathbf{p}}}_v={\displaystyle \frac{1}{K}}\sum _{k=1}^K{\mathbf{p}}_v^{\left(k\right)}$$

However, this treats all nodes and models equally, failing to account for model agreement, node risk, or class imbalance.

In our defense methodology, multiple independent GNN models are trained, and the class probabilities for each node are generated by each model. These predictions are then aggregated by taking their average, making it harder for an attacker to rely on any single model’s output for membership inference.

Instead of simple averaging, we employ an LLM-based model $g_{\varphi }$ that receives as input a stacked tensor of logits from all models ${\mathbf{Z}}_v=[{\mathbf{z}}_v^{\left(1\right)},\dots ,{\mathbf{z}}_v^{\left(K\right)}]\in {\mathbb{R}}^{K\times C}$ and outputs an aggregated posterior:

$${\tilde{\mathbf{p}}}_v=\mathrm{softmax}(g_{\varphi }\left({\mathbf{Z}}_v\right)+\mathit{\eta }),\mathit{\eta }\sim \mathcal{N}(0,{\sigma }^{2}I)$$

This transformer learns to exploit inter-model disagreement and apply adaptive smoothing to obscure confident predictions that could leak membership. The module is trained using

$${\mathcal{L}}_{\mathrm{agg}}=\mathrm{CE}({\tilde{\mathbf{p}}}_v,y_v)-\lambda ·\mathcal{H}\left({\tilde{\mathbf{p}}}_v\right)$$

Noise is added to the aggregated posterior values to further obscure the individual model predictions, reducing the precision of the class probabilities. The final prediction is made based on the highest probability in the perturbed distribution, after it is normalized to ensure valid probability values. This process ensures that attackers cannot exploit the aggregated posterior to discern the original membership.

3.2.3. Posterior Encoding with LLM-Guided Noise Injection

Noise injection defends against MIAs by adding randomness to output probabilities. Traditional methods apply fixed Gaussian or Laplacian noise:

$${\tilde{\mathbf{p}}}_v=\mathrm{softmax}({\mathbf{z}}_v+\mathit{\eta }),\mathit{\eta }\sim \mathcal{N}(0,{\sigma }^{2}I)$$

However, fixed noise is blind to node context, class confidence, and vulnerability.

In our defense methodology, a single GNN model is trained on the dataset, and during the inference phase, noise is added directly to the class probabilities (posteriors) of each node. This noise, generated based on a noise function parameterized by $ϵ$, is added to each class probability, making the final posterior less deterministic and more uncertain.

Our LLM-based method trains a transformer $g_{\varphi }$ to generate context-aware noise:

$${\mathit{\eta }}_v=g_{\varphi }\left({\mathbf{z}}_v\right)$$

$${\tilde{\mathbf{p}}}_v=\mathrm{softmax}({\mathbf{z}}_v+{\mathit{\eta }}_v)$$

This adaptive noise preserves the top-1 class while maximizing entropy where needed. The training objective is

$${\mathcal{L}}_{\mathrm{noise}}=\mathrm{CE}({\tilde{\mathbf{p}}}_v,y_v)-\lambda ·\mathcal{H}\left({\tilde{\mathbf{p}}}_v\right)$$

After the noise is added, we perform a normalization of the posteriors to ensure that they represent valid probability distributions. To ensure that the noise does not drastically change the predicted class, we swap the highest probability class with any other class that may have been perturbed, maintaining the original class prediction when the noise does not change the outcome. The final output is then based on the highest perturbed probability.

These defenses approaches offer robust protection against membership inference attacks without substantially sacrificing the performance of the GNN on the node classification task.

3.3. LLM Architectural Details

The architecture of LLMs (the Generative Pre-trained Transformer) is based on a decoder-only transformer model, originally designed for autoregressive language modeling tasks. This architecture operates on input sequences by mapping them into vector representations and applying self-attention mechanisms to learn contextual dependencies between elements in the sequence. The model is particularly well-suited for tasks requiring flexible posterior transformations, making it an ideal choice for implementing privacy-preserving defenses in graph neural networks.

The input representation to the LLM varies depending on the defense strategy being deployed. For knowledge distillation, the input consists of a single posterior vector, denoted as $X=\left[{\mathbf{p}}_v^{\left(t\right)}\right]$, corresponding to the soft label from a teacher model. In the context of secure aggregation, the input is extended to include multiple posterior vectors from an ensemble of models, represented as $X=[{\mathbf{p}}_v^{\left(1\right)},\dots ,{\mathbf{p}}_v^{\left(K\right)}]$. For noise injection techniques, the input is a single posterior vector $X=\left[{\mathbf{p}}_v\right]$, which will be perturbed by the model. In all cases, optional positional encodings $p_t\in {\mathbb{R}}^d$ may be added to incorporate order information into the input sequence.

At the core of the LLM is the self-attention mechanism. Each input at layer l is linearly projected into query, key, and value spaces using learned weight matrices $W_Q$, $W_K$, and $W_V$, respectively. The attention weights are computed via scaled dot-product attention, where $d_k$ is the dimensionality of the key vectors:

$$Q=h_{l-1}{W}_Q,K=h_{l-1}{W}_K,V=h_{l-1}{W}_V$$

$$\mathrm{Attention}(Q_t,K,V)=\sum _{j=1}^T{\alpha }_{t,j}{V}_j,{\alpha }_{t,j}=\mathrm{softmax}\left({\displaystyle \frac{Q_t{K}_j^{\top }}{\sqrt{d_k}}}\right)$$

Here, $h_{l-1}$ represents the hidden state from the previous layer, and T is the number of tokens in the sequence. This mechanism enables the model to selectively focus on relevant elements across the input sequence, enhancing its ability to model complex dependencies.

Following the attention block, each layer contains a position-wise feedforward network (FFN), which further transforms the input using a two-layer perceptron with ReLU activation:

$$\mathrm{FFN}\left(x\right)=\mathrm{ReLU}(x{W}_1+b_1)W_2+b_2$$

The output of the attention and feedforward sub-layers is combined using residual connections and normalized using layer normalization, yielding the final layer output:

$$h_l^t=\mathrm{LayerNorm}(\mathrm{Attention}+\mathrm{FFN})$$

where $W_1,W_2$ are feedforward weights, and $b_1,b_2$ are the corresponding bias terms.

The output layer varies based on the defense strategy. For knowledge distillation, the final hidden state is mapped to class probabilities using a softmax transformation, ${\tilde{\mathbf{p}}}_v=\mathrm{softmax}\left(W_{out}{h}_L\right)$, where $W_{out}$ is the output projection matrix and $h_L$ is the final hidden representation from the last layer L. In secure aggregation, a special classification token (denoted as [CLS]) is prepended to the input sequence, and its final embedding is used for output computation: ${\tilde{\mathbf{p}}}_v=\mathrm{softmax}\left(W_{out}\left[\mathtt{CLS}\right]\right)$. For noise injection, the model directly predicts an additive noise vector ${\mathit{\eta }}_v=W_{out}{h}_L$, which is added to the original posterior before applying the softmax: ${\tilde{\mathbf{p}}}_v=\mathrm{softmax}({\mathbf{p}}_v+{\mathit{\eta }}_v)$.

The use of an LLM in this context offers several key advantages. It enables the learning of complex, nonlinear transformations of logits and posterior distributions, which can obscure membership signals. The model is also capable of dynamically adjusting its transformations based on node-specific risk profiles, allowing adaptive privacy-preserving behavior. Finally, because it is trained from end to end, the model can explicitly optimize for a trade-off between prediction accuracy and privacy protection.

4. Experiments

4.1. Datasets

We conducted our experiments on three widely used benchmark datasets for graph learning: Cora, CiteSeer, and PubMed.

• Cora: a citation dataset consisting of machine learning papers grouped into seven classes. The nodes represent papers, and the edges represent citation links.
• CiteSeer: another citation network, with publications categorized into six classes. Features are expressed as binary-valued word vectors.
• PubMed: a biomedical dataset of abstracts of medical papers classified into three classes.

Details about these three datasets are given in

Table 1. Dataset statistics.

Dataset	Nodes	Edges	Features	Classes
Cora	2708	10,565	1433	7
CiteSeer	3327	9104	3703	6
PubMed	19,717	88,648	500	3

.

We selected these datasets for three main reasons. Firstly, they are standard benchmarks in the literature on graph neural networks (GNNs) and membership inference attacks, which ensures that our results are comparable with prior work. In addition, they cover different scales and feature dimensions: Cora is relatively small, CiteSeer is medium-sized, and PubMed is significantly larger, with nearly 20,000 nodes. This diversity allows us to evaluate the scalability and robustness of our proposed defenses under varying graph sizes and feature complexities.

In order to design the target and shadow GNN architectures for the MIA, we split our dataset into two equivalent sets, maintaining the same number of node classes in each set. We represented the first set as the target model dataset $D_{Target}$ and the second as the shadow model dataset $D_{Shadow}$. To obtain training and test sets for the target model and the shadow model, we split $D_{Shadow}$ and $D_{Target}$ into two subsets. We eventually obtained four subsets, $D_{shadow}^{train}$, $D_{test}^{train}$, $D_{target}^{train}$, and $D_{target}^{test}$, on which the training and testing of the models were conducted.

4.2. Proposed Approach

We employed GPT-4 as the chosen LLM to guide the posterior encoding process in GNNs. We implemented three different LLM-guided approaches to enhance the robustness of GNN models against membership inference attacks. In our experiments, we utilized a two-layer architecture across the following GNN models: Graph Attention Network (GAT), Graph Convolutional Network (GCN), GraphSAGE, ChebNet, and ARMA models. Both shadow and target models were trained for 200 epochs. These configurations were essential for understanding the experimental setup and replicating our results in mitigating MIAs on GNNs. The LLM module does not process raw text or graph features but instead operates directly on the posterior vectors produced by the final GNN layer. Each posterior corresponds to the class probability distribution of a node, with dimensionality equal to the number of classes in the dataset (3 for PubMed, 6 for CiteSeer, and 7 for Cora). The transformer module encodes these vectors using a small stack of self-attention layers (4 layers, hidden size 256, 8 heads), producing context-aware perturbations that are applied back to the posteriors. By focusing only on posterior encoding, our approach remains lightweight (≈12 M parameters) and efficient, while still leveraging the expressive capacity of transformer architectures for adaptive defense.

4.3. Experimental Setup

The experimental setup was meticulously designed to optimize performance and efficiency. The system was configured to leverage TPU (32 GB RAM) acceleration for material computations, facilitated by TensorFlow (version 2.13.0), a prominent open source machine learning library developed by Google that automatically harnesses available TPUs. Elevated RAM was also used to handle large datasets and computations efficiently. Python (version 3.10.12) was the primary programming language employed, and the experiment utilized a variety of libraries and tools. Alongside these, specific PyTorch Geometric libraries (PyTorch 2.3.1), such as torch-scatter, torch-sparse, torch-cluster, torch-spline-conv, and torch-geometric, were integrated to support the complex requirements of graph neural networks. These libraries provide essential functionalities for efficient graph data structure manipulation, message passing algorithms, and various specialized GNN layers, ensuring robust and effective experimentation.

4.4. Metrics

In evaluating the effectiveness of the defense mechanisms and the performance of the GNN architectures, we report three standard metrics: accuracy, precision, and F1 score.

Accuracy measures the overall proportion of correctly classified instances. Precision quantifies the proportion of positive predictions that are correct, while F1 score provides the harmonic mean of precision and recall, capturing the balance between these two aspects.

By including these complementary metrics, our evaluation offers a more complete assessment of the proposed defense strategies and their impact on model performance.

5. Results and Discussion

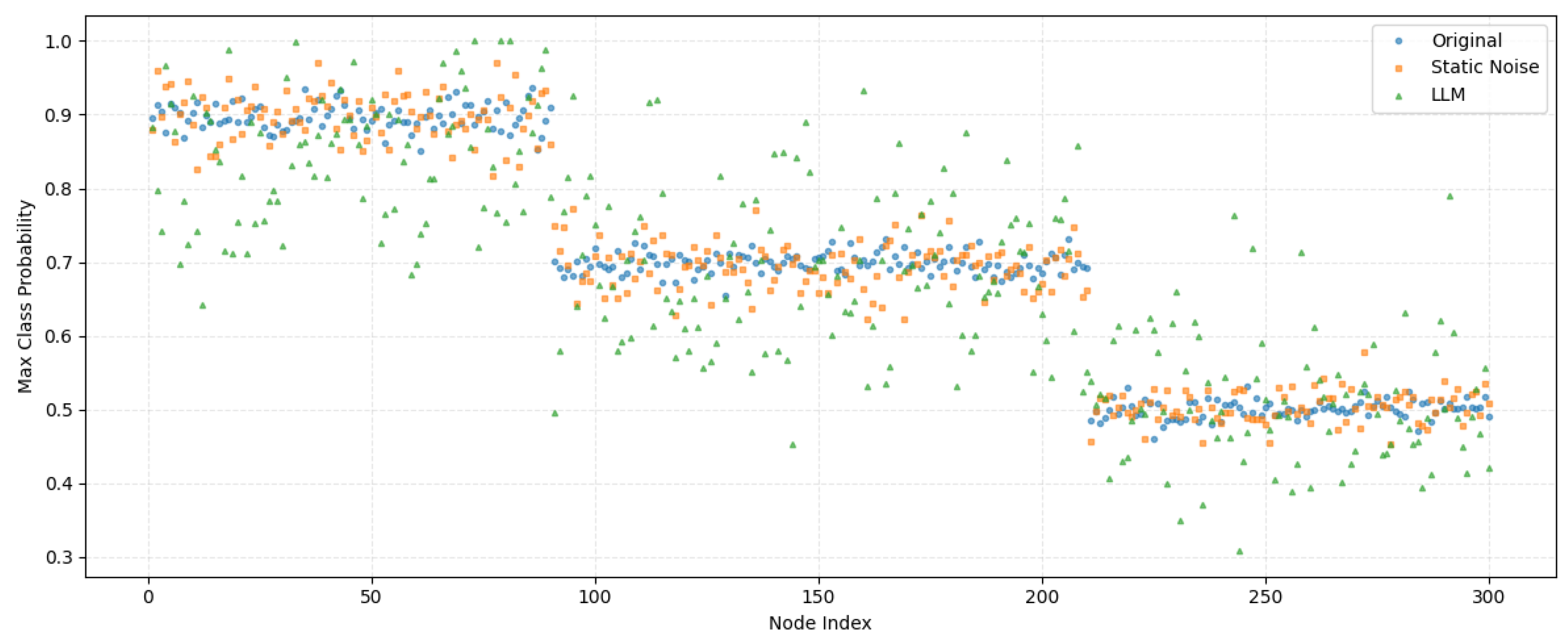
5.1. Reduction of Membership Inference Attack Accuracy Using Three LLM-Guided Defense Strategies

We now analyze the empirical results obtained for our three LLM-guided defenses: LLM* noise injection, LLM** secure aggregation, and LLM*** knowledge distillation, as illustrated in Figure 4. The evaluation spans three benchmark datasets (Cora, PubMed, and CiteSeer) and five representative GNN architectures (GCNs, ARMA, GATs, ChebNet, and GraphSAGE). The y-axis denotes the membership inference attack (MIA) accuracy, where a lower value indicates stronger privacy protection. For reference, random guessing yields an accuracy of 50%; hence, defenses achieving values near or below this threshold can be considered effective.

Overall, all three LLM-based strategies reduce MIA accuracy compared to the unprotected baseline (approximately 96–98%), confirming the success of posterior encoding mechanisms guided by LLMs. Among them, the LLM with guided knowledge distillation defense demonstrates the most robust and consistent performance across datasets and models. Its average MIA accuracy remains below 48% in most settings, with minima reaching 42.8% on Cora (ARMA) and 40.9% on PubMed (ChebNet), indicating strong confusion induced at the decision boundary level without degrading classification utility. This effectiveness is attributed to the ability of the LLM module to adaptively soften posteriors while preserving top-1 predictions and increasing posterior entropy.

The LLM with guided secure aggregation performs secure aggregation of multiple GNN posteriors, and also provides strong protection, achieving MIA accuracies between 43% and 47%. The transformer-based aggregation model learns to amplify inter-model disagreement and suppress overconfident predictions, and is particularly effective on CiteSeer (e.g., 43.3% on GCN and 44.0% on ChebNet). This confirms that ensemble-level reasoning guided by an LLM can yield high privacy robustness.

Finally, the LLM with guided noise injection into posteriors yields slightly higher MIA accuracies (around 45–48%) but still maintains privacy well below the baseline. Its slightly weaker performance is explained by the fact that noise injection may not always introduce sufficient structured uncertainty without impacting utility. Nonetheless, this method remains attractive due to its simplicity and the capacity of the LLM module to generate node- and class-specific perturbations.

In summary, these results validate our hypothesis that LLMs, when integrated as posterior transformers, offer adaptive learnable defenses that generalize well across datasets and architectures. They outperform fixed noise or heuristic-based methods by injecting uncertainty where it matters most, ultimately achieving a reliable balance between utility and privacy.

5.2. Outperforming Previous Defense Approaches

Our findings demonstrate that the three proposed LLM-guided posterior encoding approaches effectively enhance the security of graph neural networks (GNNs) against membership inference attacks across all five GNN architectures and the three datasets evaluated. Among these, LLM-guided posterior encoding using knowledge distillation proved to be the most robust, achieving the greatest reduction in membership inference attack accuracy. This was followed by LLM-guided posterior encoding using secure aggregation, with LLM-guided posterior encoding with noise ranking third in effectiveness. In some cases, our methods were able to reduce attack accuracy to as low as 0.4, outperforming alternative posterior encoding strategies such as one-hot encoding, ReLU transformations, shuffling, dropout, top-k selection, and variational autoencoders (VAEs), as well as graph perturbation methods like Graph Perturbation 1 (based on graph variational autoencoders) and Graph Perturbation 2 (based on graph autoencoders).

As shown in

Table 2. Accuracy of membership inference attack after employing different defense approaches (LLM*: encoding with noise, LLM**: secure aggregation, LLM***: knowledge distillation). Bold values indicate the lowest MIA accuracy (most robust), and underlined values indicate the second-lowest MIA accuracy (second most robust).

Datasets	Defenses			GNNs
	Approaches	GCN	Arma	GAT	Cheb	Sage
	MIA	97.30	93.50	98.30	98.40	96.10
	Shuffle ENC.	52.90	58.30	58.00	59.10	54.70
	Dropout	57.10	54.80	56.30	62.80	54.40
	One-Hot ENC.	50.00	50.00	50.00	50.00	50.00
	RELU	63.40	58.10	60.10	63.90	60.30
Cora	K TOP	67.30	70.20	63.80	66.20	63.50
	VAE	57.30	57.50	55.40	54.70	54.90
	Graph per 1	55.10	55.70	54.70	56.20	54.90
	Graph per 2	54.90	55.20	54.30	55.30	53.80
	LLM*	47.20	48.10	47.00	48.40	47.20
	LLM**	44.30	47.40	45.10	44.90	43.70
	LLM***	42.80	45.60	46.00	42.90	43.40
	MIA	87.30	85.60	94.60	96.40	92.30
	Shuffle ENC.	58.10	53.50	61.10	54.10	54.70
	Dropout	61.80	57.70	63.40	52.20	56.60
	One-Hot ENC.	50.00	50.00	50.00	50.00	50.00
	RELU	64.60	59.10	63.10	55.20	56.80
PubMed	K TOP	67.50	66.40	69.80	61.30	63.10
	VAE	57.10	58.70	57.70	56.40	53.90
	Graph per 1	56.20	56.30	54.90	56.50	56.20
	Graph per 2	56.10	55.50	54.10	55.70	55.10
	LLM*	45.00	45.20	47.30	48.60	46.50
	LLM**	42.80	44.90	45.40	46.10	47.30
	LLM***	42.30	45.10	42.30	45.00	43.60
	MIA	96.00	94.10	98.40	99.70	96.40
	Shuffle ENC.	53.60	56.40	57.20	54.80	55.70
	Dropout	56.90	59.70	60.80	58.80	57.70
	One-Hot ENC.	50.00	50.00	50.00	50.00	50.00
	RELU	57.80	62.10	64.60	60.80	59.90
CiteSeer	K TOP	63.30	64.80	65.90	62.90	64.30
	VAE	56.10	57.10	56.30	5.570	58.10
	Graph per 1	54.80	55.70	54.60	55.30	54.80
	Graph per 2	54.70	54.60	54.20	54.10	54.30
	LLM*	47.00	47.80	48.30	48.90	47.70
	LLM**	44.60	45.40	46.70	47.30	43.20
	LLM***	43.30	46.70	45.50	46.00	44.10

, the lowest accuracy of membership inference attacks after employing our defense approaches is marked in bold.

The superior performance of our approaches can be attributed to their ability to introduce structured uncertainty into the posterior probabilities while preserving the integrity of node classification tasks. Unlike conventional encoding techniques, which either fail to sufficiently obfuscate membership signals or introduce excessive noise that degrades model performance, our LLM-based encoding methods strike a balance between security and predictive accuracy.

A key observation is that knowledge distillation outperforms all other techniques, including secure aggregation and direct noise perturbation. This can be explained by the inherent ability of knowledge distillation to smooth the decision boundary of the student model, reducing overfitting and making it more resistant to membership inference attacks. By leveraging soft labels generated by the teacher model, the student GNN learns a generalized representation of the data, minimizing the risk of exposing membership-sensitive information. Furthermore, the addition of noise to the distilled posteriors ensures that adversarial models cannot reliably infer membership, providing an additional layer of protection.

Secure aggregation, while also effective, relies on ensemble learning to dilute membership signals across multiple independently trained GNN models. Although it enhances security, its effectiveness is slightly lower than knowledge distillation because it still retains some degree of model-specific biases in the aggregated predictions. Lastly, posterior encoding with noise alone, while improving security over baseline methods, lacks the structured knowledge transfer seen in distillation, making it comparatively less robust.

Overall, our LLM-guided posterior encoding approaches outperform traditional encoding and graph perturbation techniques, offering a novel and effective paradigm for securing GNNs against membership inference attacks. The results underscore the importance of leveraging knowledge distillation in enhancing model robustness, providing a strong foundation for future research in privacy-preserving GNNs.

Figure 5 and Figure 6 present the estimated precision and F1 scores for membership inference attacks across all three datasets, comparing baseline defenses with our proposed LLM-guided methods. The results highlight several key trends.

First, defenses such as dropout, ReLUs, and top-k generally achieve relatively high precision and F1 values. This indicates that, while these methods offer some obfuscation of membership signals, they still allow the attack model to distinguish members from non-members with considerable confidence. Similarly, approaches like Shuffle Encoding and one-hot encoding show only limited reductions, often keeping precision and F1 around the 50–60% range, which corresponds to moderate attack effectiveness.

In contrast, our three LLM-guided defenses consistently yield the lowest precision and F1 scores across Cora, PubMed, and CiteSeer. For instance, in the CiteSeer dataset, precision for the proposed approaches drops close to 42–46%, while F1 values are reduced to 41–44%. Comparable trends are observed for Cora and PubMed, where precision is lowered below $47\%$ and F1 values remain in the mid-$40\%$ range. All five GNN architectures tested (GCNs, ARMA, GATs, Chebyshev, and GraphSAGE) consistently experience these reductions.

The decrease in precision and F1 achieved by our methods reflects their stronger resistance to membership inference attacks by introducing structured uncertainty into the posterior probabilities through mechanisms such as posterior noise injection, secure aggregation, and knowledge distillation. This prevents adversarial models from reliably identifying true members, even though it lowers precision and F1 compared to weaker defenses.

Among the three LLM-based strategies, knowledge distillation consistently shows the most robust suppression of attack performance, followed closely by secure aggregation, with posterior encoding using noise ranking third. This ranking mirrors the findings from the accuracy evaluation (Table 2), further confirming that distillation provides the most balanced trade-off between privacy preservation and utility.

Overall, the precision and F1 results reinforce the conclusion that our proposed LLM-guided approaches substantially outperform traditional defenses. By driving precision and F1 toward the chance level (≈50%), they ensure that membership inference attacks cannot gain a reliable advantage, thereby offering stronger privacy guarantees for GNN-based applications.

5.3. Maintaining Node Classification Accuracy in GNN

Our experimental results, shown in Figure 7, indicate that all three of our proposed methods maintain the accuracy of the GNN model, even when encoding posterior probabilities. In contrast, other widely used defense approaches such as dropout, variational autoencoders (VAEs), graph variational autoencoders (GVAEs), and graph autoencoders (GAEs) demonstrate accuracy degradation in the node classification task. Specifically, accuracy reductions range from $30.1\%$ to 42.3% for dropout, from 7.5% to 13.2% for VAEs, from 15.4% to 22.3% for GVAEs (Graph Perturbation 1), and from 20% to 30% for GAEs (Graph Perturbation 2).

Furthermore, standard techniques such as one-hot encoding, ReLU, and top-k methods also maintain the classification accuracy of the GNN model, as they preserve the index of the highest value in the class probabilities, even after encoding. These methods are effective in maintaining the integrity of the classification outcome because the highest probability index remains consistent, ensuring that the correct class is still identified. However, while these methods offer some level of robustness, our proposed approaches surpass them in terms of resilience against membership inference attacks. By incorporating advanced techniques such as knowledge distillation and secure aggregation, our models not only retain high classification accuracy but also provide enhanced protection against adversarial probing of model membership.

5.4. Computational Overhead and Practical Deployment

A key reason our three LLM-guided defenses are more practical than prior approaches lies in their storage and time efficiency. Our proposed approaches operate only on posterior vectors (3–7 dimensions depending on the dataset). They avoid the heavy memory costs of graph reconstruction methods such as GAEs and VGAEs, which require storing and regenerating full adjacency matrices (scaling as $O\left(N^2\right)$). The resulting lightweight transformer has approximately 12 M parameters, compared to ensembles that require 5–10 full GNNs or VGAE/GAE models that double parameter counts through encoder–decoder duplication.

Training efficiency is also improved. Our LLM-guided defenses introduce only ∼8–10% extra training time relative to baseline GNNs. By comparison, a VGAE adds ∼25–30% runtime overhead due to variational sampling, GAE and graph perturbation approaches increase training time by 40–60%, and ensembles impose a 5–10× overhead. Despite their efficiency, our LLMs achieve the lowest membership inference attack success rates (42–45%), surpassing both lightweight but weak defenses (dropout, Shuffle) and heavy but less robust approaches (VGAEs, GAEs, ensembles). This demonstrates that our proposed approaches, when applied to posteriors, achieve superior security efficiency trade-offs and are well-suited for deployment.

5.5. Why LLMs?

To mitigate the vulnerability of overconfident posteriors in node classification tasks, particularly against membership inference attacks (MIAs), various defense strategies have been proposed. Classical approaches such as temperature scaling, label smoothing, and Gaussian noise introduce fixed mathematical transformations to the predicted probability distributions. However, these techniques are inherently global. They apply uniform adjustments across all nodes without regard for the specific characteristics or risk profiles of individual predictions. As a result, they often fail to effectively flatten highly confident outputs while simultaneously preserving the uncertainty of less confident ones, leading to suboptimal privacy protection and potential degradation in model utility.

Large language models (LLMs) offer a more adaptive and context-aware alternative. Instead of applying the same perturbation to all predictions, LLMs learn to modulate their transformations based on the shape, entropy, and interclass relationships of each posterior distribution. This allows them to selectively apply stronger perturbations to sharply peaked distributions, often indicative of overconfidence, while minimally adjusting already uncertain predictions. As a result, the output distributions become smoother and less predictable, making it harder for adversaries to infer sensitive information from the output confidence values.

Figure 8 shows the effect of different perturbation mechanisms on the top-1 class probability (i.e., the maximum class probability) for each node in a graph of 300 nodes. Each point represents a node’s most confident class after classification, and the x-axis corresponds to the node index. Original predictions (blue dots) show clusters of high-confidence values, reflecting strong certainty in class assignments. When static Gaussian noise is added (orange squares), these confidences are slightly perturbed but largely maintain their global structure and relative magnitude. In contrast, the LLM-based approach (green triangles) produces more varied and less concentrated top-1 confidences, effectively smoothing the posteriors in a node-specific way. This irregularity in the LLM-transformed confidences reduces the risk that consistent patterns are exploited by inference attacks. To illustrate the difference more concretely, consider a posterior vector such as [0.95, 0.02, 0.03]. A static noise mechanism might yield [0.96, 0.03, 0.01], which remains highly overconfident. In contrast, an LLM could output a transformed vector like [0.65, 0.20, 0.15], redistributing the probability mass in a way that reduces certainty while preserving the semantic content of the label distribution. This transformation is not predefined but learned, enabling the defense to generalize across a wide variety of input distributions and structural settings.

Overall, the plot highlights the limitation of static mathematical defenses and demonstrates the strength of LLM-based approaches in reshaping posterior distributions at a finer granularity. By learning context-specific transformations, LLMs provide a more robust and adaptive defense framework, capable of mitigating overconfidence and enhancing the privacy of node classification systems without requiring explicit assumptions about the data distribution or graph topology.

6. Conclusions

Our proposed LLM-guided posterior encoding methods enhance the security of graph neural networks (GNNs) against membership inference attacks while preserving the accuracy of node classification tasks. Compared to traditional defense approaches, such as dropout, VAEs, GVAEs, and GAEs, our methods offer superior robustness, maintain high classification accuracy, and provide better protection against adversarial probing. Knowledge distillation, in particular, stands out as the most effective strategy, ensuring that membership inference attacks are effectively mitigated without compromising model performance.

Our future work will expand on these findings by exploring the use of multiple types of large language models (LLMs) beyond GPT-4, broadening the applicability of our defense methods. In addition, we plan to expand our research to include graph classification and edge prediction tasks, further enhancing the versatility of our approach. Finally, we aim to investigate encoding strategies not only for posterior probabilities but also within the architecture of the GNN itself, striving for even more comprehensive defenses against adversarial threats.