Design of Morlet Wavelet Neural Networks for Solving the Nonlinear Van der Pol–Mathieu–Duffing Oscillator Model

Abstract

The motivation behind this study is to simplify the complex mathematical formulations and reduce the time-consuming processes involved in traditional numerical methods for solving differential equations. This study develops a computational intelligence approach with a Morlet wavelet neural network (MWNN) to solve the nonlinear Van der Pol–Mathieu–Duffing oscillator (Vd-PM-DO), including parameter excitation and dusty plasma studies. The proposed technique utilizes artificial neural networks to model equations and optimize error functions using global search with a genetic algorithm (GA) and fast local convergence with an interior-point algorithm (IPA). We develop an MWNN-based fitness function to predict the dynamic behavior of nonlinear Vd-PM-DO differential equations. Then, we apply a novel hybrid approach combining WCA and ABC to optimize this fitness function, and determine the optimal weight and biases for MWNN. Three different variants of the Vd-PM-DO model were numerically evaluated and compared with the reference solution to demonstrate the correctness of the designed technique. Moreover, statistical analyses using twenty trials were conducted to determine the reliability and accuracy of the suggested MWNN-GA-IPA by utilizing mean absolute deviation (MAD), Theil’s inequality coefficient (TIC), and mean square error (MSE).

1. Introduction

The theory of nonlinear systems can be applied to solve problems in various fields, including economics, astronomy, nerve physiology, chemistry, heartbeat control, cryptography, electronic circuits, and many others. Most systems in the modern world are, by nature, nonlinear [1,2]. Furthermore, many researchers have been interested in nonlinear oscillations because most vibration problems are nonlinear. Thus, nonlinear differential equations (NLDEs) are very useful in understanding scientific and engineering problems, which often take the form of nonlinear types. The significance of mathematical computations was emphasized in numerous research studies and literature works that deal with NLDEs that arise in a variety of scientific and engineering fields [3]. While a large number of NLDEs can be numerically studied, very few of them can be solved directly. Several approximation methods have been employed in the literature to investigate the relationship between the amplitude and frequency of the nonlinear oscillators (NOSs) such as the homotopy perturbation technique [4,5], variational iteration method [6], energy balance approach [7,8], Akbari Ganji method [9], Adomain decomposition technique [10], and many others.

In recent years, there has also been a lot of research on the use of artificial neural networks (ANNs) to solve nonlinear differential equations. Yang et al. [11] proposed physics-informed generative adversarial networks as one data-driven method for handling stochastic differential equations (SDEs) using sparse observations. Raissi [12] investigated the application of deep learning methods for solving coupled SDEs. Mattheakis et al. [13] constructed physics-based neural networks (NNs) to analyze the DEs that describe the dynamic behavior of systems. The NNs integrate the Hamiltonian formulation utilizing a loss function, which ensures the energy efficiency of the solutions. The predictions made by the network are used to build this loss function in its entirety, and no outside data are required. Piscopo et al. [14] studied a particular technique for determining fully differentiable solutions for ordinary, partial, and coupled equations containing analytical solutions. Hagge et al. [15] designed a novel technique for estimating unknown functions in iterated DEs with high precision, without the need for sensitivity equation solutions. This novel approach eliminates the requirement to run a differential equation solver the package at each time step, resulting in faster backpropagation. Mattheakis et al. [16] employed an ANN technique to solve nonlinear DEs and developed a symplectic neural network that gives predictions based on energy conservation using the idea of hub neurons. Raissi et al. [17] proposed the concept of physics-informed neural networks (PINNs), which are ANNs that may be trained to execute supervised learning tasks according to the nonlinear partial differential equations (PDEs) that govern physical laws. Over the years, the “curse of dimensionality” has made it difficult to build algorithms for solving high-dimensional partial DEs. In a paper, Han and Jentzen [18] demonstrated a deep learning-based method that can handle universal high-dimensional parabolic partial DEs. PDEs are transformed into stochastic DEs, and neural networks are used to approximate the gradient of the unknown solutions. This process is similar to deep reinforcement learning, where the gradient behaves as the policy function.

Mosta and Sibanda [19] developed the linearization approach to solve the Van der Pol bimodal problem. Njah and Vincent [20] proposed an active control technique for the double-well Duffing–Van der Pol oscillator. Kimiaeifar [21] provided an outstanding description of the chaotic behavior of the Van der Pol–Mathieu–Duffing oscillator under various excitations. Hu and Chung explored the stability evaluation of the Van der Pol equation [22]. In recent years, researchers have developed several approaches [23,24] to solve the well-known nonlinear oscillator models. Numerical approaches require precise step sizes and iterations, resulting in considerable computing costs.

To address these limitations, researchers have developed artificial neural network algorithms in recent years to predict the solutions for dynamical models. The motivation for this study is to address the complex mathematical formulation and the time-intensive nature of traditional numerical methods for solving differential equations. This research seeks an alternative approach to achieve more efficient and simplified solutions. Here, we tackle the key challenge of predicting the behavior of oscillators without relying on intricate strategies or time-consuming simulations. This study aims to design a Morlet wavelet neural network to solve the Van der Pol–Mathieu–Duffing oscillator (Vd-PM-DO) for the first time, encompassing parameter excitation and dusty plasma studies. The optimization process uses a combination of global and local search methods, notably the genetic algorithm (GA) and the interior-point algorithm (IPA). The results produced by the proposed methodology are compared with reference solutions. Furthermore, a statistical analysis is conducted to assess the accuracy, efficiency, and reliability of the method.

The key features of the suggested MWNN-GA-IPA, for significant contributions and unique insights, are outlined as follows:

• A novel design of an integrated algorithm MWNN-GA-IPA that uses a feed-forward ANN with a Morlet wavelet activation function within hidden neurons to solve the nonlinear Van der Pol–Mathieu–Duffing oscillator (Vd-PM-DO) models and optimize using GA and IPA algorithms.
• The correctness of overlapping outcomes with the reference results establish the accuracy and stability of the proposed algorithm MWNN-GA-IPA.
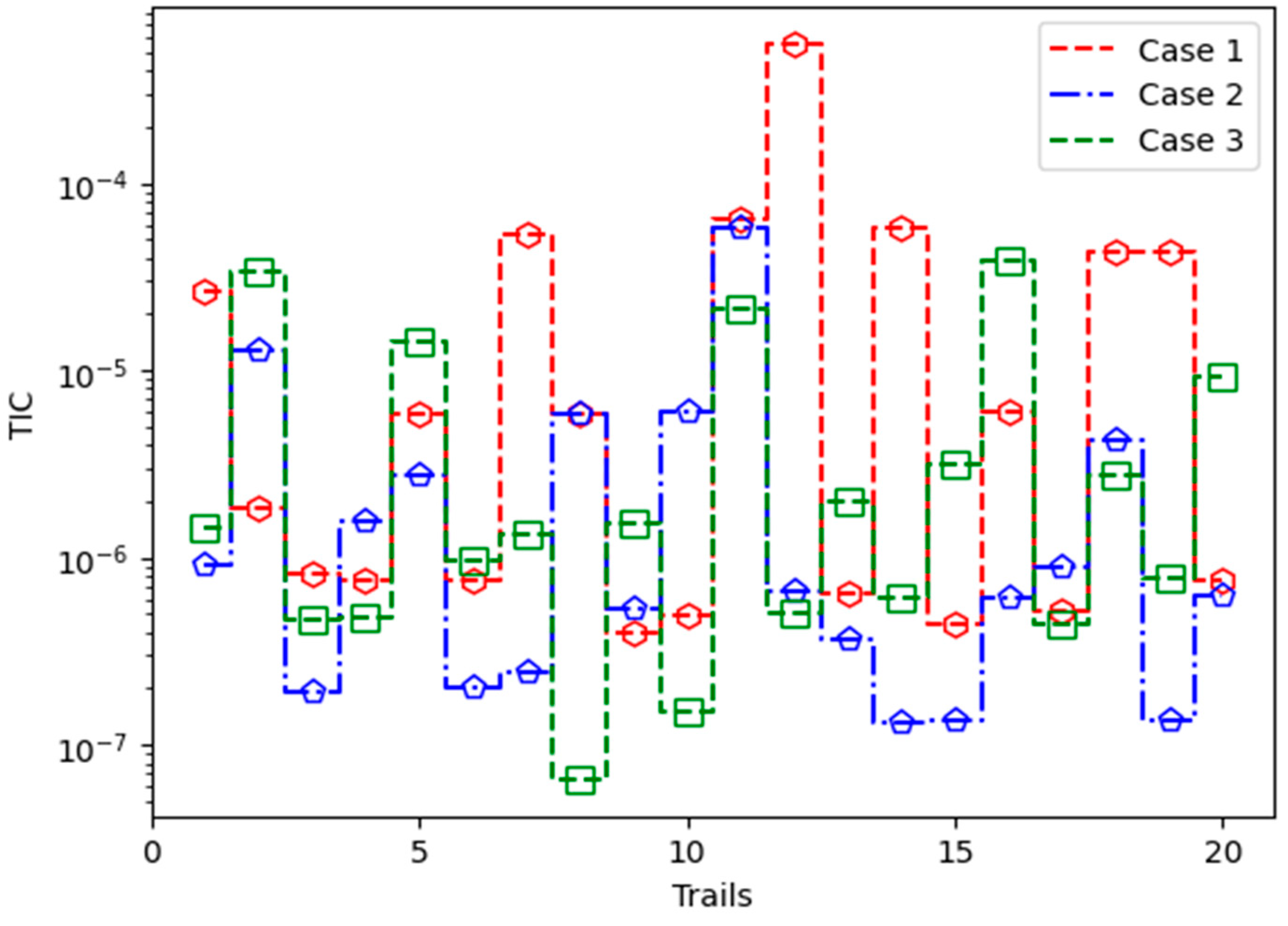
• The MWNN-GA-IPA model effectively handles Vd-PM-DO models using 10 neurons and achieves reasonable accuracy in mean square error (MSE), Theil’s inequality coefficient (TIC), and mean absolute deviation (MAD) indices across multiple runs to validate the performance.
• The proposed MWNN-GA-IPA technique has several advantages, including adaptability, ease of understanding, smooth implementation, and broad applicability, and efficiently tackles intricate, nonlinear, and singular problems.

2. Problem Formulation

It is very useful and significant to investigate the behavior of nonlinear dynamical systems. The nonlinear Van der Pol–Mathieu–Duffing oscillator (Vd-PM-DO) equation is expressed as follows [25]:

$$\left\{\begin{array}{c}{h}^{″}\left(t\right)+ϵ\left[\left(\mu -\alpha h^2\right)h^{\prime }\left(t\right)+\theta hcos\left(\mathsf{\Omega }t\right)\right]-{\omega }^{2}h+\beta h^3-ϵ\sigma h\eta \left(t\right)=0,\\ h\left(0\right)=a,\hspace{1em}{h}^{\prime }\left(0\right)=b\end{array}\right.$$

(1)

where $h\left(t\right)$ denotes the displacement of the equilibrium position, $\beta >0$ is the nonlinear term, and $\mathsf{\Omega }$ and $\theta$ represent the frequency and intensity coefficient. All other notations express the different physical characteristics of the above equation.

3. Methodology: MWNNs

Morlet wavelet neural networks (MWNNs) are a cutting-edge hybrid technology that combines the efficiency of artificial neural networks (ANNs) with the reliability of wavelet transforms, particularly the Morlet wavelet. This integration enables more effective handling of complicated and nonlinear problems, particularly in areas such as signal processing and time series. MWNNs outperform typical neural networks because they combine wavelet theory and machine learning, particularly when data vary significantly over time. MWNNs capture both local and global data features, allowing for a more complete and dynamic approach to solving problems in a number of scientific and engineering fields. MWNNs can be developed for stable, accurate, and consistent solutions in different domains. The fitness function is formulated based on the differential equation and initial conditions. The optimization configuration of GA-IPA is also defined.

3.1. MWNN Modeling

The mathematical formulation of the nonlinear Van der Pol–Mathieu–Duffing oscillator (Vd-PM-DO) equation with feed-forward MWNNs along with the designed solution and their nth-order derivatives are expressed as:

$$\widehat{h}\left(t\right)=\sum _{j=1}^m{u}_{j}S(w_{j}t+v_j)$$

(2)

$${\widehat{h}}^{\left(n\right)}\left(t\right)=\sum _{j=1}^m{u}_j{S}^{\left(n\right)}(w_{j}t+v_j)$$

(3)

In Equation (3), S represents the set of neurons with unknown weight vectors. W is defined as $W=[u,w,v]$.

$$u=\left[u_1,u_2,u_3,\dots u_m\right],\hspace{1em}w=\left[w_1,w_2,w_3,\dots w_m\right]\hspace{1em}and v=[v_1,v_2,v_3,\dots v_m]$$

The proposed method has not been developed nor applied before to find the solution of the Vd-PM-DO equation. The mathematical form of the Morlet wavelet is given as [26,27,28,29]:

$$\widehat{S}\left(t\right)=\sum _{j=1}^m\cos \left(1.75t\right)e^{-0.5t^2},$$

(4)

The updated form of Equation (4) utilizing the Morlet wavelet (MW) function is expressed as follows:

$$\widehat{S}\left(t\right)=\sum _{j=1}^m\cos \left(1.75t\right)e^{-0.5t^2},$$

$$\widehat{S}\left(t\right)=\sum _{j=1}^m{u}_j\cos \left(1.75(w_{j}t+v_j)\right)e^{-0.5{(w_{j}t+v_j)}^2}$$

$$\begin{array}{c}\hfill {\widehat{S}}^{\prime }\left(t\right)={\displaystyle \sum _{j=1}^m}({-u}_j{w}_j{e}^{-0.5{\left(w_{j}t+v_j\right)}^2})(\sin \left(1.75\left(w_{j}t+v_j\right)\right)\\ \hfill +1.75\left(w_{j}t+v_j\right)\mathrm{c}\mathrm{o}\mathrm{s}(1.75\left(w_{j}t+{\gamma }_j\right)\left)\right)\end{array}$$

$${\widehat{S}}^{″}\left(t\right)=\sum _{j=1}^m{-u}_j{w}_j^2{e}^{-0.5{(w_{j}t+v_j)}^2}\left(\begin{array}{c}-3.0625\cos (1.75\left(w_{j}t+v_j\right)\\ +3.5(w_{j}t+v_j)\sin \left(1.75\left(w_{j}t+v_j\right)\right)\\ +(-1+{\left(w_{j}t+v_j\right)}^2)\cos \left(1.75\left(w_{j}t+v_j\right)\right)\end{array}\right)$$

The fitness function is written as:

$$e=e_1+e_2,$$

(5)

where $e_1$ and $e_2$ indicate the error function connected with the nonlinear Vd-PM-DO equation with initial conditions demonstrated as follows:

$$e_1={\displaystyle \frac{1}{N}}\sum _{j=1}^m{\left({\widehat{h}}^{″}\left(t\right)+ϵ\left[\left(\mu -\alpha {\widehat{h}}^2\right)h^{\prime }\left(t\right)+\theta \widehat{h}cos\left(\mathsf{\Omega }t\right)\right]-{\omega }^2\widehat{h}+\beta {\widehat{h}}^3-ϵ\sigma \widehat{h}\eta \left(t\right)\right)}^2$$

(6)

$$e_2={\displaystyle \frac{1}{2}}\left({({\widehat{h}}_0-a)}^2+{\left({\displaystyle \frac{d{\widehat{h}}_0}{dt}}-b\right)}^2\right)$$

(7)

where $N={\displaystyle \frac{1}{h}},{\widehat{h}}_j=h\left(t_j\right), and t_j=jh$.

The solution of Vd-PM-DO can be determined with the weights. As the error function $e\to 0,$ the approximated outcomes overlap with the numerical solution of the proposed model, $\widehat{h}\left(t\right)\to h\left(t\right).$

3.2. Optimization Process: GA-IPA

This section describes the GA-IPA hybrid optimization algorithms for solving the Vd-PM-DO differential model.

The genetic algorithm (GA) is the first stochastic population-based optimization technique introduced in the literature. This algorithm is utilized through the operator known as selection, mutation, and crossover. GA can be used to optimize constrained and unconstrained issues. GA is now widely used in various applications, including heart diagnosis systems [30], astrophysics singular systems [31], a prediction structure for air blasts [32], nonlinear electric circuit designs [33], and Painleve-equation-based nonlinear optic systems [34]. The potential implementations of the genetic algorithm motivated the authors to handle the Vd-PM-DO equation in order to determine the decision variables for MWNNs.

The interior-point algorithm optimizes stiff, intricate, and convex structures using local search techniques. This algorithm is used in various applications, including image renewal [35], risk-resistant optimization systems [36], power system state prediction [37], and many other fields [38,39,40,41,42].

4. Performance Catalogues

In this section, we present the statistical techniques of absolute deviation (MAD), Theil’s inequality coefficient (TIC), and mean square error (MSE) used for the Vd-PM-DO model. The mathematical indices of MSE, MAD, and TIC are demonstrated as given:

$$\mathrm{M}\mathrm{S}\mathrm{E}=\sum _{\mathrm{j}=1}^n{(h_{\mathrm{j}}-{\widehat{h}}_{\mathrm{j}})}^2,$$

(8)

$$\mathrm{T}.\mathrm{I}.\mathrm{C}={\displaystyle \frac{\sqrt{\frac{1}{\mathrm{n}}\sum _{\mathrm{j}=1}^{\mathrm{n}}{(h_{\mathrm{j}}-{\widehat{h}}_{\mathrm{j}})}^2}}{\sqrt{\frac{1}{n}\sum _{\mathrm{j}=1}^{\mathrm{n}}{\left(h_{\mathrm{j}}\right)}^2}+\sqrt{\frac{1}{\mathrm{n}}\sum _{\mathrm{j}=1}^{\mathrm{n}}{\left({\widehat{h}}_{\mathrm{j}}\right)}^2}}},$$

(9)

$$\mathrm{M}\mathrm{A}\mathrm{D}={\displaystyle \frac{1}{\mathrm{n}}}\sum _{\mathrm{j}=1}^n\left|h_{\mathrm{j}}-{\widehat{h}}_{\mathrm{j}}\right|$$

(10)

5. Results and Discussion

This section presents a numerical analysis of the proposed algorithm to handle the Vd-PM-DO equation. Three different cases, each based on varying constant coefficient parameters and the excitation function of the Vd-PM-DO in Equation (1), have been considered to evaluate the robust, accurate, and reliable performance of MWNN-GA-IPA across a variety of problems. Furthermore, these cases are designed to identify and observe specific properties or behaviors of the proposed MWNN-GA-IPA in different scenarios.

Problem 1 (For excitation function $\eta \left(t\right)=1$)

Consider the Vd-PM-DO equation; using $ϵ=0.3, \mu =0.5,\theta =0.5, \omega =1, \sigma =1, \mathsf{\Omega }=1,\beta =0.1, \alpha =0.7,$ Equation (1) can be rewritten as:

$$\left\{\begin{array}{c}{h}^{″}\left(t\right)+0.3\left[(0.5{-0.7h^2)h}^{\prime }\left(t\right)+0.5hcos\left(t\right)\right]-1^{2}h+0.1h^3-0.3h=0,\\ h\left(0\right)=1,\hspace{1em}{h}^{\prime }\left(0\right)=0\end{array}\right.$$

(11)

A merit function is given as:

$$\begin{array}{c}e={\displaystyle \frac{1}{N}}{\displaystyle \sum _{m=1}^N}{\left({\displaystyle \frac{d^2{\widehat{h}}_m}{d{t}_m^2}}+0.3\left[\left(0.5-0.7{\widehat{h}}^2\right){\widehat{h}}_m^{\prime }+0.5{\widehat{h}}_{m}cos\left(t\right)\right]-{\left(1.0\right)}^2{\widehat{h}}_m+0.1{\widehat{h}}^3-0.3h_m\right)}^2\\ +{\displaystyle \frac{1}{2}}\left({({\widehat{h}}_0-1)}^2+{\left({\displaystyle \frac{d{\widehat{h}}_0}{dt}}\right)}^2\right)\end{array}$$

(12)

Problem 2 (For excitation function $\eta \left(t\right)=1$)

In this case, we consider the following Vd-PM-DO equation with different parametric values $ϵ=0.2, \mu =0.5,\theta =0.6, \omega =0.7, \sigma =1.5, \mathsf{\Omega }=0.3,\beta =0.4, \alpha =0.6$, and the equation can be expressed as follows:

$$\left\{\begin{array}{c}{h}^{″}\left(t\right)+0.2\left[(0.5{-0.6h^2)h}^{\prime }\left(t\right)+0.6hcos\left(0.3t\right)\right]-{0.7}^{2}h+0.4h^3-0.3\left(1.5\right)h=0,\\ h\left(0\right)=0,\hspace{1em}{h}^{\prime }\left(0\right)=1\end{array}\right.$$

(13)

The error function is expressed as follows:

$$\begin{array}{c}e={\displaystyle \frac{1}{N}}{\displaystyle \sum _{m=1}^N}{\left({\displaystyle \frac{d^2{\widehat{h}}_m}{d{t}_m^2}}+0.2\left[\left(0.5-0.6{\widehat{h}}^2\right){\widehat{h}}_m^{\prime }+0.6{\widehat{h}}_{m}cos\left(0.3t\right)\right]-{\left(0.7\right)}^2{\widehat{h}}_m+0.4{\widehat{h}}^3-0.3\left(1.5\right)h_m\right)}^2\\ +{\displaystyle \frac{1}{2}}\left({\left({\widehat{h}}_0\right)}^2+{\left({\displaystyle \frac{d{\widehat{h}}_0}{dt}}-1\right)}^2\right)\end{array}$$

(14)

Problem 3 (For excitation function $\eta \left(t\right)=t$)

Consider the Vd-PM-DO equation; using $ϵ=0.3, \mu =0.1,\theta =0.5, \omega =0.4, \sigma =1, \mathsf{\Omega }=0.5,\beta =0.6, \alpha =0.2$, Equation (1) is given as:

$$\left\{\begin{array}{c}{h}^{″}\left(t\right)+0.3\left[(0.1{-0.2h^2)h}^{\prime }\left(t\right)+0.5hcos\left(0.5t\right)\right]-{0.4}^{2}h+0.6h^3-0.3ht=0,\\ h\left(0\right)=0,\hspace{1em}{h}^{\prime }\left(0\right)=1\end{array}\right.$$

(15)

The fitness function is given as:

$$\begin{array}{c}e={\displaystyle \frac{1}{N}}{\displaystyle \sum _{m=1}^N}{\left({\displaystyle \frac{d^2{\widehat{h}}_m}{d{t}_m^2}}+0.3\left[\left(0.1-0.2{\widehat{h}}^2\right){\widehat{h}}_m^{\prime }+0.5{\widehat{h}}_{m}cos\left(0.5t\right)\right]-{\left(0.4\right)}^2{\widehat{h}}_m+0.6{\widehat{h}}^3-0.3h_m\right)}^2\\ +{\displaystyle \frac{1}{2}}\left({\left({\widehat{h}}_0\right)}^2+{\left({\displaystyle \frac{d{\widehat{h}}_0}{dt}}-1\right)}^2\right)\end{array}$$

(16)

The MWNN-GA-IPA optimization performance for 20 independent executions of the Vd-PM-DO equation utilizing 10 neurons is presented. Figure 1 shows the best weights for the predicted outcomes of the proposed methodology for 10 neurons. The comparison of the proposed results with the reference solution for all cases of the Vd-PM-DO equation is shown in Figure 2. The overlapping results for 10 neurons improve the performance of the developed MWNN-GA-IPA in solving the Vd-PM-DO equation.

The MWNN-GA-IPA optimization technique is employed to calculate the solution of the nonlinear Vd-PM-DO over twenty runs, with adaptable network parameters. The present scheme is conducted to determine the unknown weights, which are expressed as given below:

$$\begin{array}{c}{\widehat{h}}_1\left(t\right)=-12.9444\mathrm{c}\mathrm{o}\mathrm{s}\left({\displaystyle \frac{7}{4}}\left(4.1206\mathrm{t}-7.6041\right)\right)e^{-{\displaystyle \frac{1}{2}}{\left(4.1206\mathrm{t}-7.6041\right)}^2}\hfill \\ +1.3731\mathrm{c}\mathrm{o}\mathrm{s}\left({\displaystyle \frac{7}{4}}\left(1.2631\mathrm{t}-3.3279\right)\right)e^{-{\displaystyle \frac{1}{2}}{\left(1.2631\mathrm{t}-3.3279\right)}^2}\hfill \\ +\dots 15.0000\mathrm{c}\mathrm{o}\mathrm{s}\left({\displaystyle \frac{7}{4}}\left(3.8497\mathrm{t}-8.2868\right)\right)e^{-{\displaystyle \frac{1}{2}}{\left(3.8497\mathrm{t}-8.2868\right)}^2},\hfill \end{array}$$

$$\begin{array}{c}{\widehat{h}}_2\left(t\right)=14.9415\mathrm{c}\mathrm{o}\mathrm{s}\left({\displaystyle \frac{7}{4}}\left(-1.2886\mathrm{t}+4.1493\right)\right)e^{-{\displaystyle \frac{1}{2}}{\left(-1.2886\mathrm{t}+4.1493\right)}^2}\hfill \\ +5.4407\mathrm{c}\mathrm{o}\mathrm{s}\left({\displaystyle \frac{7}{4}}\left(-0.0245\mathrm{t}+4.2205\right)\right)e^{-{\displaystyle \frac{1}{2}}{\left(-0.0245\mathrm{t}+4.2205\right)}^2}\hfill \\ +\dots 1.4169\mathrm{c}\mathrm{o}\mathrm{s}\left({\displaystyle \frac{7}{4}}\left(-2.0448\mathrm{t}-4.1910\right)\right)e^{-{\displaystyle \frac{1}{2}}{\left(-2.0448\mathrm{t}-4.1910\right)}^2},\hfill \end{array}$$

$$\begin{array}{c}{\widehat{h}}_3\left(t\right)=-0.0605\mathrm{c}\mathrm{o}\mathrm{s}\left({\displaystyle \frac{7}{4}}\left(1.0811\mathrm{t}+2.6331\right)\right)e^{-{\displaystyle \frac{1}{2}}{\left(1.0811\mathrm{t}+2.6331\right)}^2}\hfill \\ -7.2952\mathrm{c}\mathrm{o}\mathrm{s}\left({\displaystyle \frac{7}{4}}\left(-0.7410\mathrm{t}-3.9485\right)\right)e^{-{\displaystyle \frac{1}{2}}{\left(-0.7410\mathrm{t}-3.9485\right)}^2}\hfill \\ +\dots -4.9470\mathrm{c}\mathrm{o}\mathrm{s}\left({\displaystyle \frac{7}{4}}\left(14.9990\mathrm{t}+10.2985\right)\right)e^{-{\displaystyle \frac{1}{2}}{\left(14.9990\mathrm{t}+10.2985\right)}^2}\hfill \end{array}$$

The Van der Pol–Mathieu–Duffing oscillator (Vd-PM-DO) is a mathematical model that combines nonlinear dynamics and parametric forcing. It is commonly used to represent systems with complicated nonlinear behavior. Dusty plasma research involves charged dust particles suspended in plasma, which results in unique collective phenomena such as wave propagation, self-organization, and nonlinear oscillations. The Vd-PM-DO and dusty plasma investigations are linked by the use of nonlinear dynamics to describe and understand dusty plasma behavior. Dusty plasmas frequently exhibit nonlinear oscillatory behavior due to the interaction of electrostatic forces, plasma waves, and dust-particle dynamics. The Vd-PM-DO captures nonlinear and parametric interactions, making it an effective analog for simulating oscillations and instabilities in dusty plasma. The Mathieu component of the Vd-PM-DO may describe parametric resonances, which are useful for understanding wave–particle interactions in dusty plasma. The Duffing component of the Vd-PM-DO, with its double-well potential and chaotic dynamics, successfully simulates such instabilities.

Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8 represent the convergence graphics utilizing MSE, TIC, and MAD metrics, as well as histograms (HGs) and boxplots (BPs) for the Vd-PM-DO model. The best-MSE values are ${10}^{-6}–{10}^{-8}$, ${10}^{-5}–{10}^{-8}$, and ${10}^{-5}–{10}^{-7}$ for the Vd-PM-DO model. The TIC operator values lie within the ranges of ${10}^{-3}–{10}^{-6}$, ${10}^{-4}–{10}^{-6}$, and ${10}^{-4}–{10}^{-7}$ for problems 1–3, respectively. Additionally, the MAD values within the ranges of ${10}^{-3}–{10}^{-7}$, ${10}^{-5}–{10}^{-7}$, and ${10}^{-4}–{10}^{-8}$ for examples 1–3 of the Vd-PM-DO system. These optimal measures obtained through statistical gauges validate the accuracy of the MWNN–GA-IPA scheme.

6. Conclusions

The present research aims to develop a Morlet wavelet neural network to solve the Van der Pol–Mathieu–Duffing oscillator model. The Vd-PM-DO equation has gained a lot of interest among researchers and scientists due to its numerous applications in mathematics and engineering, such as in the detection of weak signals, mechanical breakdown signals, and the inverted pendulum. The combination of global and local operators called GA-IPA is utilized for optimization purposes. To validate the accuracy of the MWNN-GA-IPA, numerical outcomes are compared to the reference solution for each problem in the Vd-PM-DO model. To assess the accuracy of the MWNN-GA-IPA approach, 20 trials are conducted using 10 neurons, utilizing various statistical measures. It is also significant that the obtained outcomes closely matched with the reference solutions across all neurons. In the future, the designed stochastic scheme, MWNN-GA-IPA, has the potential to be used as an efficient, reliable, and powerful computing scheme to solve problems in fields such as nanotechnology, fluid dynamics, and electric machines.