Design of Morlet Wavelet Neural Networks for Solving the Nonlinear Van der Pol–Mathieu–Duffing Oscillator Model
Abstract
1. Introduction
- A novel design of an integrated algorithm MWNN-GA-IPA that uses a feed-forward ANN with a Morlet wavelet activation function within hidden neurons to solve the nonlinear Van der Pol–Mathieu–Duffing oscillator (Vd-PM-DO) models and optimize using GA and IPA algorithms.
- The correctness of overlapping outcomes with the reference results establish the accuracy and stability of the proposed algorithm MWNN-GA-IPA.
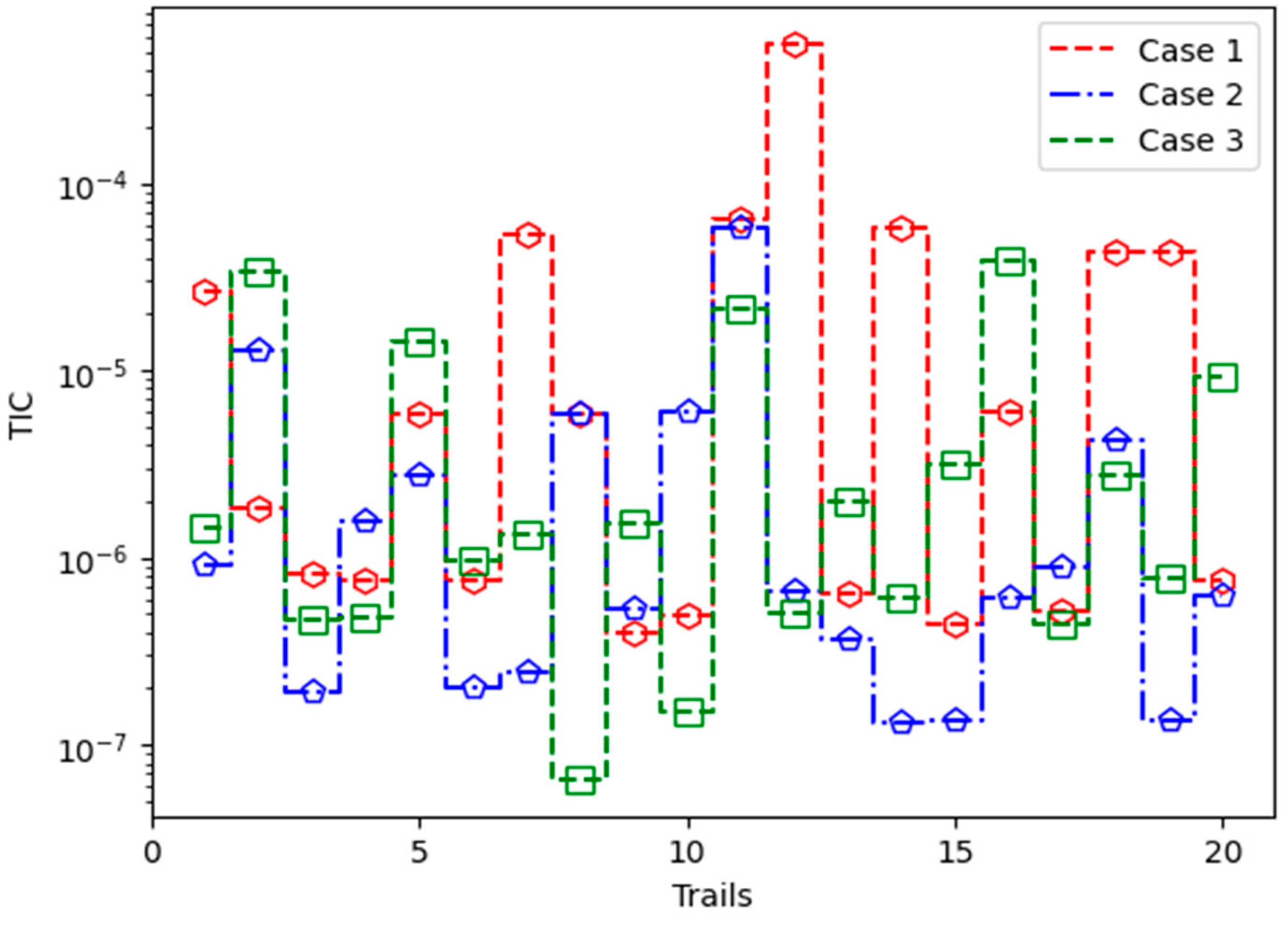
- The MWNN-GA-IPA model effectively handles Vd-PM-DO models using 10 neurons and achieves reasonable accuracy in mean square error (MSE), Theil’s inequality coefficient (TIC), and mean absolute deviation (MAD) indices across multiple runs to validate the performance.
- The proposed MWNN-GA-IPA technique has several advantages, including adaptability, ease of understanding, smooth implementation, and broad applicability, and efficiently tackles intricate, nonlinear, and singular problems.
2. Problem Formulation
3. Methodology: MWNNs
3.1. MWNN Modeling
3.2. Optimization Process: GA-IPA
4. Performance Catalogues
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Brown, P.N.; Saad, Y. Hybrid Krylov methods for nonlinear systems of equations. SIAM J. Sci. Stat. Comput. 1990, 11, 450–481. [Google Scholar] [CrossRef]
- Drazin, P.G. Nonlinear Systems; No. 10; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Kumar, D.; Singh, J.; Baleanu, D. A hybrid computational approach for Klein–Gordon equations on Cantor sets. Nonlinear Dyn. 2017, 87, 511–517. [Google Scholar] [CrossRef]
- He, J.-H. A coupling method of a homotopy technique and a perturbation technique for non-linear problems. Int. J. Non-linear Mech. 2000, 35, 37–43. [Google Scholar] [CrossRef]
- Biazar, J.; Eslami, M. A new homotopy perturbation method for solving systems of partial differential equations. Comput. Math. Appl. 2011, 62, 225–234. [Google Scholar] [CrossRef]
- Amir, M.; Ashraf, A.; Haider, J.A. The Variational Iteration Method for a Pendulum with a Combined Translational and Rotational System. Acta Mech. Autom. 2024, 18, 48–54. [Google Scholar] [CrossRef]
- Koochi, A.; Goharimanesh, M. Nonlinear oscillations of CNT nano-resonator based on nonlocal elasticity: The energy balance method. Rep. Mech. Eng. 2021, 2, 41–50. [Google Scholar] [CrossRef]
- Mehdipour, I.; Ganji, D.; Mozaffari, M. Application of the energy balance method to nonlinear vibrating equations. Curr. Appl. Phys. 2010, 10, 104–112. [Google Scholar] [CrossRef]
- Samadi, H.; Mohammadi, N.S.; Shamoushaki, M.; Asadi, Z.; Ganji, D.D. An analytical investigation and comparison of oscillating systems with nonlinear behavior using AGM and HPM. Alex. Eng. J. 2022, 61, 8987–8996. [Google Scholar] [CrossRef]
- Adomian, G. Solving Frontier Problems of Physics: The Decomposition Method; Springer: Dordrecht, The Netherlands, 1994; Volume 60. [Google Scholar]
- Yang, L.; Zhang, D.; Karniadakis, G.E. Physics-informed generative adversarial networks for stochastic differential equations. SIAM J. Sci. Comput. 2020, 42, A292–A317. [Google Scholar] [CrossRef]
- Raissi, M. Forward–backward stochastic neural networks: Deep learning of high-dimensional partial differential equations. In Peter Carr Gedenkschrift: Research Advances in Mathematical Finance; World Scientific: Singapore, 2024; pp. 637–655. [Google Scholar]
- Mattheakis, M.; Sondak, D.; Dogra, A.S.; Protopapas, P. Hamiltonian neural networks for solving equations of motion. Phys. Rev. E 2022, 105, 065305. [Google Scholar] [CrossRef]
- Piscopo, M.L.; Spannowsky, M.; Waite, P. Solving differential equations with neural networks: Applications to the calculation of cosmological phase transitions. Phys. Rev. D 2019, 100, 016002. [Google Scholar] [CrossRef]
- Hagge, T.; Stinis, P.; Yeung, E.; Tartakovsky, A.M. Solving differential equations with unknown constitutive relations as recurrent neural networks. arXiv 2017, arXiv:1710.02242. [Google Scholar]
- Mattheakis, M.; Protopapas, P.; Sondak, D.; Di Giovanni, M.; Kaxiras, E. Physical symmetries embedded in neural networks. arXiv 2019, arXiv:1904.08991. [Google Scholar]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Han, J.; Jentzen, A.; E, W. Solving high-dimensional partial differential equations using deep learning. Proc. Natl. Acad. Sci. USA 2018, 115, 8505–8510. [Google Scholar] [CrossRef] [PubMed]
- Motsa, S.S.; Sibanda, P. A note on the solutions of the Van der Pol and Duffing equations using a linearisation method. Math. Probl. Eng. 2012, 2012, 693453. [Google Scholar] [CrossRef]
- Njah, A.; Vincent, U. Chaos synchronization between single and double wells Duffing–Van der Pol oscillators using active control. Chaos Solitons Fractals 2008, 37, 1356–1361. [Google Scholar] [CrossRef]
- Kimiaeifar, A. An analytical approach to investigate the response and stability of Van der Pol-Mathieu-Duffing oscillators under different excitation functions. Math. Methods Appl. Sci. 2010, 33, 1571–1577. [Google Scholar] [CrossRef]
- Hu, K.; Chung, K.-W. On the stability analysis of a pair of van der Pol oscillators with delayed self-connection, position and velocity couplings. AIP Adv. 2013, 3, 112118. [Google Scholar] [CrossRef]
- Fan, Q.; Leung, A.Y.T.; Lee, Y.Y. Periodic and quasi-periodic responses of van der pol–Mathieu system subject to various excitations. Int. J. Nonlinear Sci. Numer. Simul. 2016, 17, 29–40. [Google Scholar] [CrossRef]
- Jadoon, I.; Raja, M.A.Z.; Junaid, M.; Ahmed, A.; Rehman, A.U.; Shoaib, M. Design of evolutionary optimized finite difference based numerical computing for dust density model of nonlinear Van-der Pol Mathieu’s oscillatory systems. Math. Comput. Simul. 2021, 181, 444–470. [Google Scholar] [CrossRef]
- Sahoo, A.K.; Chakraverty, S. A neural network approach for the solution of Van der Pol-Mathieu-Duffing oscillator model. Evol. Intell. 2024, 17, 1425–1435. [Google Scholar] [CrossRef]
- Sabir, Z.; Wahab, H.A.; Umar, M.; Sakar, M.G.; Raja, M.A.Z. Novel design of Morlet wavelet neural network for solving second order Lane–Emden equation. Math. Comput. Simul. 2020, 172, 1–14. [Google Scholar] [CrossRef]
- Sabir, Z.; Raja, M.A.Z.; Guirao, J.L.; Shoaib, M. A novel design of fractional Meyer wavelet neural networks with application to the nonlinear singular fractional Lane-Emden systems. Alex. Eng. J. 2021, 60, 2641–2659. [Google Scholar] [CrossRef]
- Sabir, Z.; Raja, M.A.Z.; Baleanu, D. Fractional mayer Neuro-swarm heuristic solver for multi-fractional order doubly singular model based on lane–emden Equation. Fractals 2021, 29, 2140017. [Google Scholar] [CrossRef]
- Sabir, Z.; Raja, M.A.Z.; Shoaib, M.; Aguilar, J.F.G. FMNEICS: Fractional Meyer neuro-evolution-based intelligent computing solver for doubly singular multi-fractional order Lane–Emden system. Comput. Appl. Math. 2020, 39, 303. [Google Scholar] [CrossRef]
- Reddy, G.T.; Reddy, M.P.K.; Lakshmanna, K.; Rajput, D.S.; Kaluri, R.; Srivastava, G. Hybrid genetic algorithm and a fuzzy logic classifier for heart disease diagnosis. Evol. Intell. 2020, 13, 185–196. [Google Scholar] [CrossRef]
- Sabir, Z.; Saoud, S.; Raja, M.A.Z.; Wahab, H.A.; Arbi, A. Heuristic computing technique for numerical solutions of nonlinear fourth order Emden–Fowler equation. Math. Comput. Simul. 2020, 178, 534–548. [Google Scholar] [CrossRef]
- Jahed Armaghani, D.; Hasanipanah, M.; Mahdiyar, A.; Abd Majid, M.Z.; Bakhshandeh Amnieh, H.; Tahir, M.M. Airblast prediction through a hybrid genetic algorithm-ANN model. Neural Comput. Appl. 2018, 29, 619–629. [Google Scholar] [CrossRef]
- Mehmood, A.; Zameer, A.; Ling, S.H.; Rehman, A.U.; Raja, M.A.Z. Integrated computational intelligent paradigm for nonlinear electric circuit models using neural networks, genetic algorithms and sequential quadratic programming. Neural Comput. Appl. 2020, 32, 10337–10357. [Google Scholar] [CrossRef]
- Ahmad, I.; Ahmad, S.; Awais, M.; Ahmad, S.U.I.; Raja, M.A.Z. Neuro-evolutionary computing paradigm for Painleve equation-II in nonlinear optics. Eur. Phys. J. Plus 2018, 133, 184. [Google Scholar] [CrossRef]
- Bertocchi, C.; Chouzenoux, E.; Corbineau, M.-C.; Pesquet, J.-C.; Prato, M. Deep unfolding of a proximal interior point method for image restoration. Inverse Probl. 2020, 36, 034005. [Google Scholar] [CrossRef]
- Garreis, S.; Surowiec, T.M.; Ulbrich, M. An interior-point approach for solving risk-averse PDE-constrained optimization problems with coherent risk measures. SIAM J. Optim. 2021, 31, 1–29. [Google Scholar] [CrossRef]
- Pesteh, S.; Moayyed, H.; Miranda, V. Favorable properties of interior point method and generalized correntropy in power system state estimation. Electr. Power Syst. Res. 2020, 178, 106035. [Google Scholar] [CrossRef]
- Hansen, T.L.; Jensen, T.L. A fast interior-point method for atomic norm soft thresholding. Signal Process. 2019, 165, 7–19. [Google Scholar] [CrossRef]
- Mangoni, D.; Tasora, A.; Garziera, R. A primal–dual predictor–corrector interior point method for non-smooth contact dynamics. Comput. Methods Appl. Mech. Eng. 2018, 330, 351–367. [Google Scholar] [CrossRef]
- Qiu, S.; Chen, Z. An interior point method for nonlinear optimization with a quasi-tangential subproblem. J. Comput. Appl. Math. 2018, 334, 77–96. [Google Scholar] [CrossRef]
- Ahmad, I.; Bakar, A.A.; Ali, I.; Haq, S.; Yussof, S.; Ali, A.H. Computational Analysis of Time-Fractional Models in Energy Infrastructure Applications. Alex. Eng. J. 2023, 82, 426–436. [Google Scholar] [CrossRef]
- Alebraheem, J.; Ibrahim, T.Q.; Arif, G.E.; Hamdi, A.A.; Bazighifan, O.; Ali, A.H. The Stabilizing Effect of Small Prey Immigration on Competitive Predator-Prey Dynamics. Math. Comput. Model. Dyn. Syst. 2024, 30, 605–625. [Google Scholar] [CrossRef]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, A.H.; Amir, M.; Rahman, J.U.; Raza, A.; Arif, G.E. Design of Morlet Wavelet Neural Networks for Solving the Nonlinear Van der Pol–Mathieu–Duffing Oscillator Model. Computers 2025, 14, 14. https://doi.org/10.3390/computers14010014
Ali AH, Amir M, Rahman JU, Raza A, Arif GE. Design of Morlet Wavelet Neural Networks for Solving the Nonlinear Van der Pol–Mathieu–Duffing Oscillator Model. Computers. 2025; 14(1):14. https://doi.org/10.3390/computers14010014
Chicago/Turabian StyleAli, Ali Hasan, Muhammad Amir, Jamshaid Ul Rahman, Ali Raza, and Ghassan Ezzulddin Arif. 2025. "Design of Morlet Wavelet Neural Networks for Solving the Nonlinear Van der Pol–Mathieu–Duffing Oscillator Model" Computers 14, no. 1: 14. https://doi.org/10.3390/computers14010014
APA StyleAli, A. H., Amir, M., Rahman, J. U., Raza, A., & Arif, G. E. (2025). Design of Morlet Wavelet Neural Networks for Solving the Nonlinear Van der Pol–Mathieu–Duffing Oscillator Model. Computers, 14(1), 14. https://doi.org/10.3390/computers14010014





