Abstract
Aiming at the difficulty in effectively identifying critical quality features in the complex machining process, this paper proposes a critical quality feature recognition method based on a machining process network. Firstly, the machining process network model is constructed based on the complex network theory. The LeaderRank algorithm is used to identify the critical processes in the machining process. Secondly, the Entropy-CRITIC method is used to calculate the weight of the quality features of the critical processes, and the critical quality features of the critical processes are determined according to weight ranking results. Finally, the feasibility and effectiveness of the method are verified by taking the medium-speed marine diesel engine coupling rod machining as an example. The results show that the method can still effectively identify the critical quality features in the case of small sample data and provide support for machining process optimization and quality control, thus improving product consistency, reliability, and machining efficiency.
1. Introduction
Processing quality is determined by multiple processes and is affected by the generation, transmission, and accumulation of error sources in multiple processes [1]. According to the Pareto principle, the unqualified processing quality of a small number of processes causes most quality problems in product processing [2]. Only the critical quality features of a few critical processes can be monitored centrally to achieve overall quality control. Therefore, extracting the critical quality features of critical processes is essential to ensure the quality of product processing.
Many scholars have recently researched identifying critical quality features in multi-process mechanical product processing. Yang et al. [3] established a structural model of critical process quality features through hierarchical analysis and achieved the identification of critical quality features. He et al. [4] proposed a three-layer quality feature structure and constructed an association tree to identify critical features based on rough set and fuzzy sorting methods. Zhang et al. [5] proposed an extraction and optimization model to identify critical features by calculating importance and mapping weights. Wang et al. [6] used weighted grey objective decision-making methods to cope with information uncertainty and identify critical features. Li et al. [7] used fuzzy linear regression to construct the redesign quality feature importance degree equation to identify critical quality features. Most of the above research methods are based on product design and process information analysis to identify critical quality features from the quality management perspective. However, as the complexity of machining processes and structures of mechanical products increases, the number of quality features increases, and the sample data often show high dimensionality and multiple correlations. As a result, it is not easy to comprehensively analyze product design and process information for complex workpieces, which ultimately reduces the efficiency and accuracy of quality feature identification.
To address the challenges of reduced efficiency and accuracy in quality feature identification caused by high dimensionality and multiple correlations in data, some scholars have turned to data-driven methods. Using statistical regression and machine learning, they have established models that relate the final product quality to quality features based on the online collection of product processing data, which allows for identifying crucial quality features that significantly impact the final product. Qiao [8] uses the B-K-Lasso algorithm to reduce the data dimension and identify critical quality features. Ma et al. [9] used entropy weight and Mahalanobis–Taguchi methods to identify critical quality features. Wang [10] identified the critical quality features in small sample data by improving the elastic network algorithm. Jin et al. [11] established a regression model based on the covariance matrix to identify critical features. Wang et al. [12] used mutual information and the IGSA algorithm for critical quality features. He et al. [13] used the decomposed multi-objective particle swarm optimization algorithm to identify critical quality features. Wang et al. [14] identified critical features through the mutation transmission model and partial least squares regression. With the continuous development of inspection technology, data-driven methods based on statistical regression and machine learning have achieved significant results in large-scale, standardized production. These methods can effectively process large amounts of data and accurately identify critical features that significantly impact product quality. However, in the manufacturing environment of single-piece, small-lot flexibility production, the limitation of sample data leads to such methods being inaccurate and unreliable. Therefore, it is necessary to explore new approaches to address the problem of quality feature identification for complex workpieces [15].
Complex network theory is an effective modeling method for complex systems, and it is widely used in mechanical processing, communication networks, ecosystems, financial networks, and transportation systems [16]. It can reveal the critical features of these systems, such as dynamic behavior, propagation mechanism, and system stability [16]. Su et al. [17] proposed a network recovery metric and dynamic resilience model based on complex network theory to evaluate infrastructure resilience to destructive events. Ibne et al. [18] used Bayesian networks to evaluate the resilience of smart grids and determine critical variables. Tan et al. [19] used Bayesian networks to evaluate the resilience of smart grids and identify critical variables and mitigation techniques. Complex network theory also identifies critical processes and quality features in machining. Qu et al. [20] established a processing network model through process nodes and used the PageRank algorithm to identify critical processes. Yu et al. [21] constructed an adaptive network describing the relationship between error and machining in manufacturing, using the weighted LeaderRank algorithm to identify critical features. Jiang et al. [22] proposed a real-time monitoring model based on an error transfer network to improve processing stability. However, these methods have achieved some results in applying complex network theory to identify critical processes and quality features in machining. These studies often only consider the network structure features in the machining process without entirely using the actual machining data, which may lead to biased identification results.
Given the above problems, this paper proposes a recognition method based on complex network theory and the Entropy-CRITIC method. Firstly, according to the coupling relationship of machining quality in the workpiece machining process, a machining process network model describing the relationship between machining features, machining elements, and quality features is constructed using complex network theory. The LeaderRank algorithm is used to identify the critical processes in the machining process. Then, based on the actual processing data of the quality features of the critical processes, the Entropy-CRITIC method is used to calculate the weight of the quality features of the critical processes. According to the weight ranking results, the critical quality features are determined. Finally, the proposed method is verified by taking the connecting rod machining of a medium-speed marine diesel engine as an example.
2. Establishment of Machining Process Network Based on Complex Networks
Complex network theory is an effective method used to analyze coupling relationships in complex systems, so establishing a machining process network model based on the evolution of machining features based on complex network theory can be used to effectively identify the critical processes in the network [23,24]. In order to establish the machining process network, the process information needs to be extracted and processed according to the part’s process information and machining features to abstract the nodes of the part machining process network and the transfer relationship between the nodes [25].
2.1. The Definition of Processing Technology Network Node
Machining quality can be described by the output of various processes’ quality feature values. The quality feature values typically include surface quality, dimensional accuracy, and form and location tolerances. In order to better describe the relationship between the processing process and the output quality features, each process of the processing object is decomposed into multiple processing features, each corresponding to one or more quality features. According to the process information and processing features of the processing object, each feature is abstracted into a network node in the network model, which mainly includes processing features, quality features, and processing elements of three categories, which are defined as follows:
- (1)
- Machining Feature (MF)
- Machining features are the basic unit of part processing used to describe the geometry and topological affinity of the workpiece surface. In the machining process, the state of machining features constantly changes, essentially the evolution of quality features.
- (2)
- Quality Feature (QF)
- The quality feature contains information containing nominal requirements, tolerances, and actual error parameters. It is categorized into two types of quality features with and without datum reference.
- (3)
- Machining Element (ME)
- The machining element is the direct error source that causes the error in process quality features. It mainly includes machine tools (MT), cutting tools (CT), and fixtures (FT).
In order to facilitate the establishment of the machining process relationship network, it is necessary to code according to the process information and machining features of the parts. The coding rules are shown in Table 1 below:

Table 1.
Coding rules of processing technology relationship network nodes.
2.2. Definition of Edge Relationship between Nodes in Machining Process Network
The directed solid line in the machining process relationship network describes the coupling relationship between different nodes, and this coupling relationship is defined as the inter-node edge relationship. The edge relationship between nodes can be mainly divided into four forms: evolutionary relationship, positioning relationship, processing relationship, and attribute relationship, which are defined as follows:
- (1)
- Evolutionary relationship (ER)
- The evolution of a processing feature at different stages is called an evolutionary relationship.
- (2)
- Location relationship (LR)
- In multi-process machining, the localization between workpiece datums is called the localization relationship.
- (3)
- Processing relationship (PR)
- The relationship between different processing stages using different elements is called processing relationship.
- (4)
- Attribute relation (AR)
- A machining feature usually contains one or more quality features, and this coupling relationship between a machining quality feature and its plural quality features is defined as an attribute relationship.
2.3. Construction of Processing Technology Network
During the processing of the workpiece, the quality of each process is not only affected by the machine tools, fixtures, tools, and other elements of the current process but also by the quality error of the previous process [26]. In order to analyze the coupling relationship between the machining features, quality features, and processing elements of each process in the machining process, the complex network theory is used for reference. It is abstracted as a node by extracting the information in the processing process. According to the relationship between nodes, different nodes are connected into edges. A directed graph model describing each process’s machining features, quality features, and processing elements is established.
The machining process network model of the workpiece mainly includes three types of network nodes: processing features, quality features, and processing elements, as well as the connection edges between different nodes. The model can be defined as:
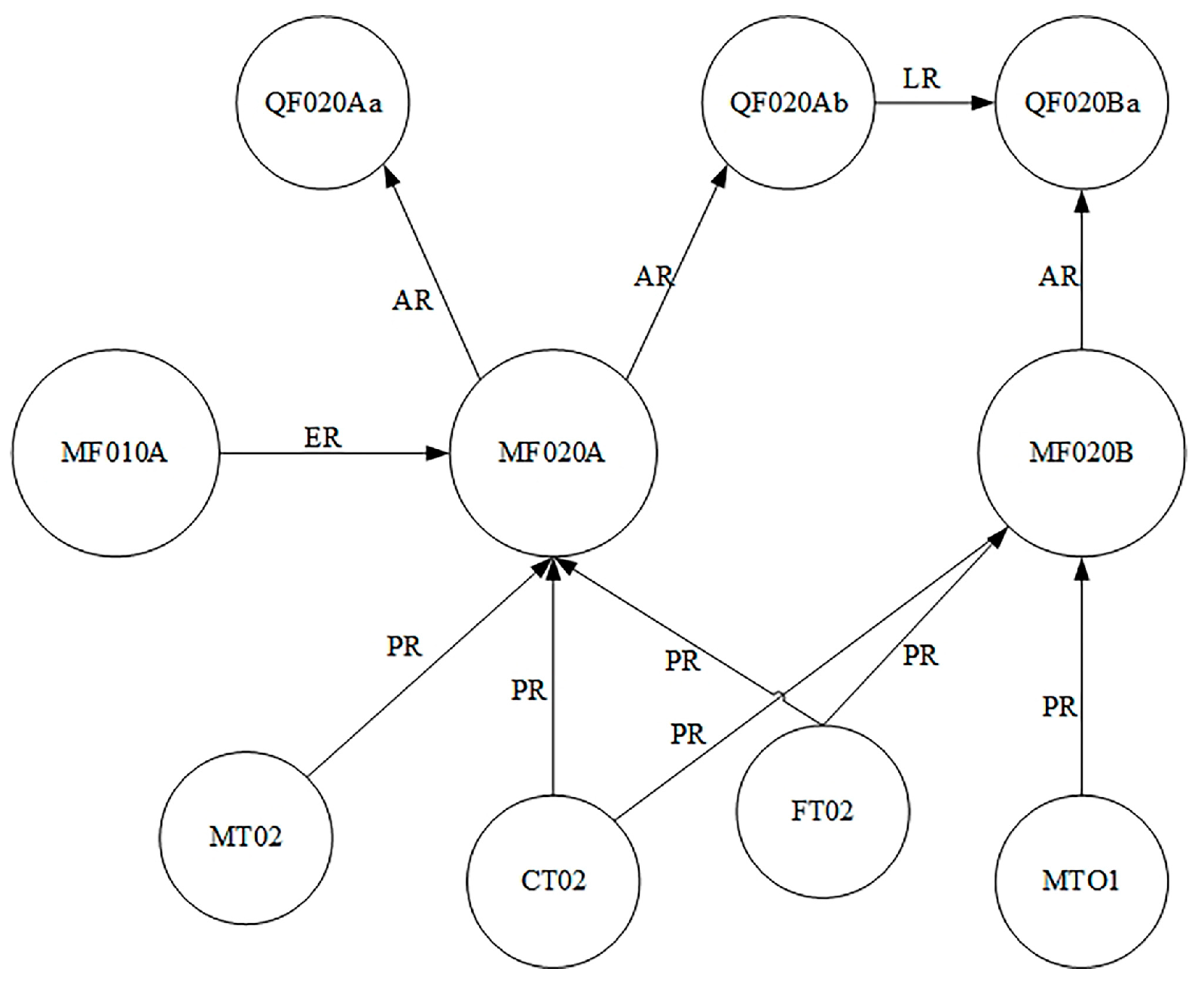
where represents the collection of nodes of different processing elements in the workpiece processing process. represents the collection of nodes of processing features obtained from the decomposition of the workpiece processing process. represents the collection of nodes of quality features output from the workpiece processing features. denotes the set of directed edges in the workpiece machining process network between machining qualities or machining qualities, machining elements of the role of the relationship between the set of directed edges. According to the above definition of the machining process, network nodes and edge relationships can be established as shown in Figure 1, machining process sub-network.
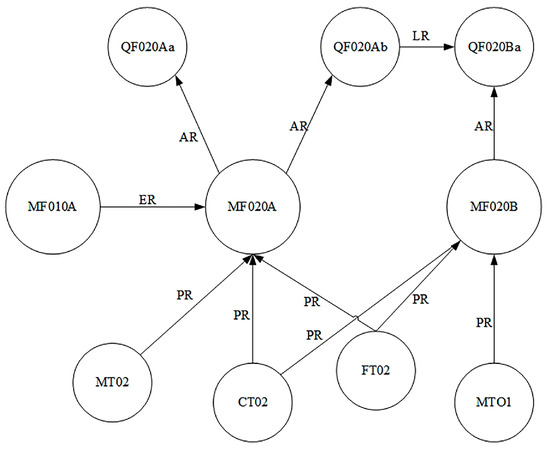
Figure 1.
Processing sub-network.
According to Figure 1, each sub-network is merged according to the processing sequence of workpiece processing quality, thus forming a complete machining process network model. Through this method, the machining features, quality features, and the coupling relationship between the machining elements of each process of complex parts in the machining process can be visualized, laying a solid foundation for the identification of subsequent critical processes.
3. Critical Process Identification Based on the Machining Process Network
For analyzing objects with complex processing technology and various processes, it is tough to screen out the critical processes only by analyzing the processing technology. Therefore, the LeaderRank (LR) algorithm is introduced to evaluate the importance of each quality node in the machining process network, and the quality nodes are sorted according to their importance to determine the critical processes of the connecting rod.
The LR algorithm is developed on the basis of the PageRank (PR) algorithm, whose basic idea is to add a background node to a known directed network to obtain a directed network with N + 1 node [27]. This background node is mainly used for the existence of bi-directional connections with other nodes in the network to ensure that the out-degree and in-degree of all nodes are greater than 0. This avoids the appearance of isolated nodes in a complex network to ensure convergence of the algorithms [28]. The in-degree denotes the sum of the number of other nodes pointing to a particular node, while the out-degree represents the total number of other nodes pointing to the other nodes from that node.
Initially, an initial value is assigned to the background node g. Each node in the original network is assigned a value of 1 unit of LR, , . According to the out-degree, the nodes distribute the LR value equally to the nodes in the multi-temporal phase. The process is iterated until each node LR value in the network reaches a stable state. The nodes are equivalent to constantly wandering throughout the iteration process, represented by the random matrix Q = (qij):
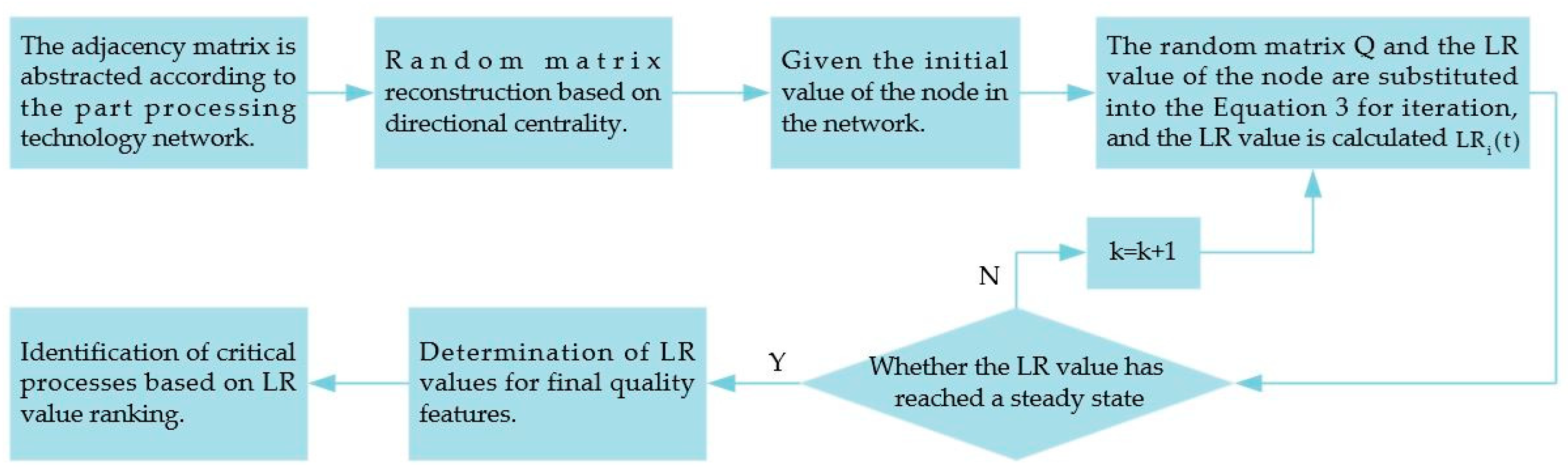
The original LR algorithm is constructed only by the out-degree of the nodes, and the background nodes are calculated iteratively using a uniform distribution. This method ignores the influence of the node’s in-degree on the system and the influence of the correlation between the nodes, which sometimes leads to a significant error. Similarly, the importance of the network nodes directly affects the machining process network. Suppose the weights of the background nodes are uniformly assigned. In that case, they may not reflect the network structure’s intrinsic connections and information flow, thus reducing the algorithm’s accuracy. In order to avoid the limitations of a single structure and uniform allocation, this paper makes it more reasonable by reconstructing the random matrix Q and redistributing the weights of the background nodes in proportion to the LR values of the nodes in the stable state of the network. The improved LR algorithm is used to identify the critical process flow, and its specific steps are shown in Figure 2.
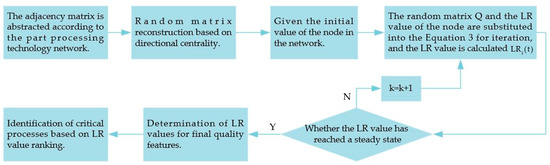
Figure 2.
Flow chart of critical process identification based on improved LR algorithm.
The critical steps are described as follows:
- (1)
- Random matrix Q reconstruction based on directional centrality
- In order to better represent the directionality of nodes in a machining process network, a directional centrality degree is proposed to quantify the importance of each machining quality node in a directed network system. The directional centrality degree can be used to measure the coupling relationship between each quality feature, expressed through a node’s in-degree and out-degree. Equation (5) can express the stochastic matrix of node based on directional centrality degree.where represents the set of nodes of node , and .
- (2)
- Determination of final quality feature LR values
- When the number of iterations is stabilized or the maximum number of iterations is reached, the background node values are assigned according to the proportion of LR values of each node.
Calculate the influence degree value of each node, and according to the size sorting, the critical process can be obtained by clustering them with the process number. Identifying critical processes verifies the value of applying complex network theory in the analysis of the machining process of mechanical products but also provides a scientific basis for optimizing the process in actual production.
4. Determination of Critical Quality Features
The LR algorithm can determine the critical processes in the connecting rod machining process network. However, these processes involve a variety of quality features, such as nominal dimensions, form tolerances, and surface roughness, which increase the difficulty of machining control. Critical quality features must be strictly controlled, and they directly affect the machining quality. Extracting critical quality features in critical processes can help optimize the machining process [29] to objectively evaluate the importance of each quality feature in the machining process and to prevent the preference for a single evaluation method [30]. In this section, the Entropy-CRITIC method is used to calculate the weights of the quality features in the critical processes to extract the most influential quality features for determining the critical quality features in the critical processes.
4.1. Determination of Critical Quality Features Based on Entropy Weight Method
In the traditional evaluation of quality features, weight determination often depends on expert experience and subjective judgment, which may introduce bias. As an objective weighting method, the weight calculation of the entropy weight method is wholly based on the data distribution to improve the objectivity and accuracy of evaluation. The specific methods are as follows:
- (1)
- When a batch of parts has n samples and m quality features for the h quality feature, the information entropy can be expressed:where n denotes the number of samples, m denotes the number of quality features, p is the probability matrix. Each element in is the proportion of each sample under the h-th quality feature.
- (2)
- The information utility value can be expressed:
- (3)
- The more significant the utility value of the information, the more the corresponding information. The information utility value is normalized to obtain the entropy weight of each quality feature, which can be expressed as follows:
The quality features of the critical process of the connecting rod to be extracted above are taken as the evaluation object, and the error fluctuation of each quality feature index reflects the degree of variation in the machining process. The information entropy can effectively quantify this variability. The lower the information entropy of a quality feature, the greater the variability of the quality feature among different samples. The more significant the impact on the final processing quality, the more the quality feature can be regarded as critical.
4.2. Determination of Critical Quality Features Based on the CRITIC Method
The entropy weight method only considers the degree of dispersion of each quality feature among different samples and does not directly address the correlation between quality features. When there is a strong correlation between quality features, considering only the variability may not be sufficient to reflect the quality features’ importance accurately. For example, two quality features with high variability may be strongly correlated, and their importance may be overestimated based solely on the entropy weighting method. For this reason, the CRITIC weight method becomes a complement and extension of the entropy weight method due to its consideration of the correlation between quality features, especially when the correlation between quality features is significant. The specific method is as follows:
- (1)
- When a batch of parts has n samples and m quality features, the standard deviation of each quality feature is . The standard deviation measures the contrast strength. The larger the standard deviation is, the more significant the machining error fluctuation of each quality feature index is, and the corresponding weight will be higher.where is the standardized value of the h sample under the quality feature l, is the average value of all standardized values h of the quality feature l, and n is the total number of samples.
- (2)
- Calculate the correlation coefficient A between the quality features; the Pearson correlation coefficient often measures the linear relationship between two random variables.
- (3)
- Calculate the conflictability between qualitative featureswhere the correlation coefficient expresses the correlation between quality features. The stronger the correlation between a quality feature and other quality features, the less conflictive it is, reflecting more of the same information. This weakens the importance of the quality feature to a certain extent, so the weight assigned to the quality feature should be reduced.
- (4)
- Calculate the amount of information Chwhere Ch represents the information on the quality feature h. The larger the Ch, the more influential the h quality feature is in all quality features.
- (5)
- Calculate the quality feature weight
For the comprehensive evaluation of multi-index objects, the CRITIC weight method reduces the overlap of information between indicators by eliminating the influence of some indicators with solid correlations. It provides a more balanced perspective for the weight distribution of each quality feature in the process of part processing. This helps to identify the critical quality features that significantly impact the final product quality, thus providing more robust support for processing quality control and optimization.
4.3. Determination of Critical Quality Features Based on Entropy-CRITIC Method
In practical application, the entropy weight method focuses on the internal information entropy of the index but ignores the interaction between the indexes. Although the CRITIC method considers the correlation between indicators, it only partially considers the independence of indicators. Therefore, to more accurately determine the importance of various quality features in the machining process of connecting rods, this paper employs combination weighting, integrating the two objective evaluation methods for weight assignment [31]. The combination weighting method aims at maximizing the range of the index score. It considers the weight value obtained by the entropy weight method and the CRITIC method as the constraint to optimize the final weight of the quality feature index. The specific method is as follows:
- (1)
- Single weighting method. The m quality features are computed using x assignment methods to construct the weight matrix D.where is the weight of the quality feature evaluation index y calculated by the z weighting method, .
- (2)
- Combination weight interval. According to the weight matrix D, the value interval of the combined weight can be defined. Where , , represents the combined weight of the quality feature evaluation index .
- (3)
- Quality feature evaluation object score Z.
- (4)
- Combination weight. The combination weight optimization model can be determined by using extreme variance maximization to maximize the variance of the score Z of each evaluation object.where is the comprehensive evaluation variance, is the value of evaluation index y, is the mean value of evaluation index y.
5. Instance Analysis
In order to illustrate the practicability and applicability of this method, the machining process of a specific type of medium-speed marine diesel engine connecting rod is taken as an example to realize the critical quality features in its critical processes. For the connecting rod of a marine diesel engine, its structure is relatively complex, the process is various, and the processing process involves multiple equipment, stations, and benchmarks. It is not only affected by the state of process resources such as machine tools, tools, and fixtures, but it may also affect the quality of the subsequent process due to the output quality error of the previous process. In production, it is difficult to objectively and effectively identify the critical quality feature control points in the vital process, resulting in insufficient final quality control. If the processing technology is reasonably determined, it is necessary to determine the critical quality features in the process. The connecting rod model of the marine diesel engine is shown in Figure 3.

Figure 3.
Connecting rod model of marine diesel engine.
The marine diesel engine connecting rod machining process is complex, containing 30 processing features, 128 quality features, and 85 processing elements. In order to more accurately describe the transfer relationship between the various processes in the connecting rod machining process, between the process and the output quality, each process of the connecting rod is decomposed into multiple machining features. Each machining feature corresponds to its unique quality features, machining equipment, tools, and connecting rod fixtures. In order to facilitate the modeling of the machining process network, the nodes of the machining process network are coded according to the coding rules of the nodes of the machining process network given in Table 1, and the correspondence is shown in Table 2.

Table 2.
Connecting rod machining features, quality features, and processing elements coding table.
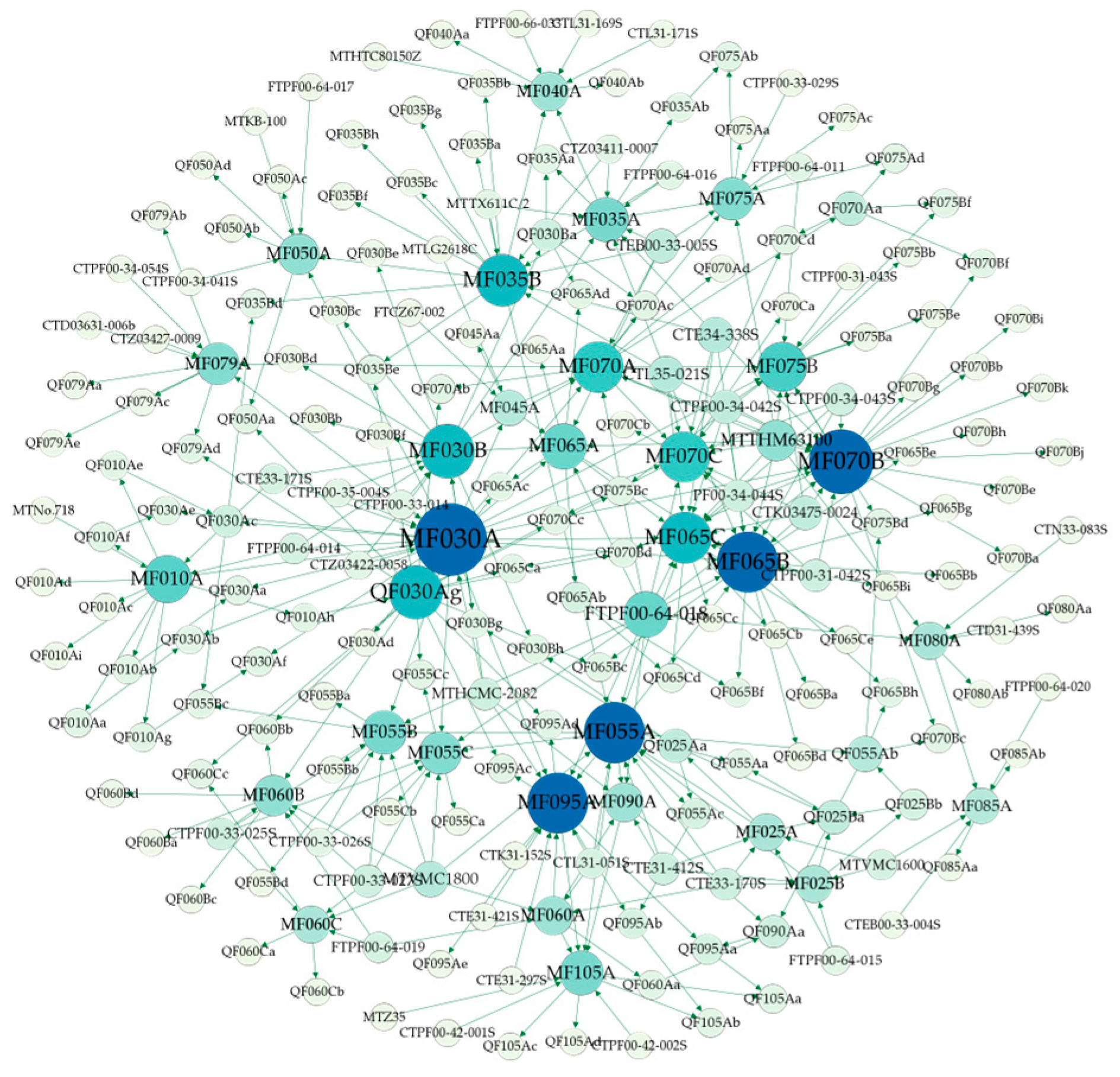
In order to intuitively and accurately locate the critical processes, it is necessary to establish sub-networks by the machining sequence between the machining qualities of the connecting rods and merge them to form a complete machining process network model. Iterative calculations are performed according to Equations (2) and (3) until convergence to a stable value to obtain the final LR value of each node in the network. The connecting rod machining process visualization network is reconstructed according to the size of the LR value of each node. As shown in Figure 4, the size of the network nodes represents the size of the LR value, and the more significant the network node, the darker its colour and the higher its influence.
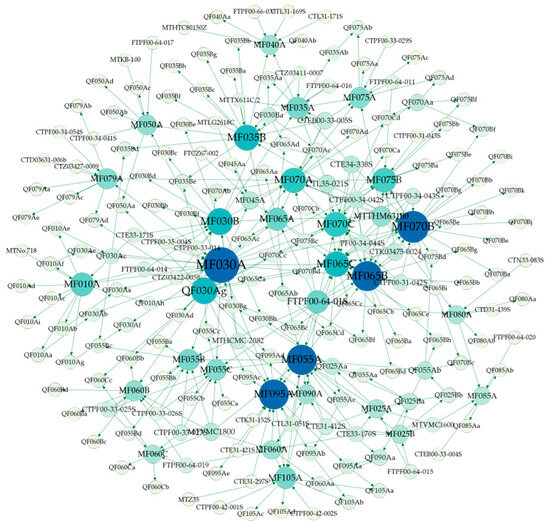
Figure 4.
Visual network model of diesel engine connecting rod processing technology.
The machining feature nodes with larger LR values are defined as critical machining features for the connecting rod machining process. According to Figure 4, the size or colour intensity of the machining feature nodes indicates that the LR values of nodes MF030A, MF055A, MF065B, MF070B, and MF095A are relatively large. We can obtain the process by clustering them by process number, and the corresponding process of critical machining features are 030, 055, 065, 070, and 095, respectively. The corresponding contents of the above processes are acceptable milling the upper and lower part of the connecting rod, semi-finish boring of the size of the head hole, machining of the large end cap bolt holes, fine boring of the size of the head hole, honing of the size of the head hole, respectively. According to the experience of the factory process engineers in the formulation of the process, with regard to the processing experience of the technicians, the analysis results are consistent with the actual processing of the connecting rod.
After the above preliminary screening, 24 quality features were obtained in the critical process. In order to facilitate the further screening of the critical quality features in the critical process, 24 quality features need to be numbered, and the corresponding quality features are coded, as shown in Table 3.

Table 3.
Critical process corresponding to the quality feature numbering table.
Record 50 sets of historical processing data under the same lot corresponding to the above 24 quality features, as shown in Table 4.

Table 4.
Historical processing data of connecting rod.
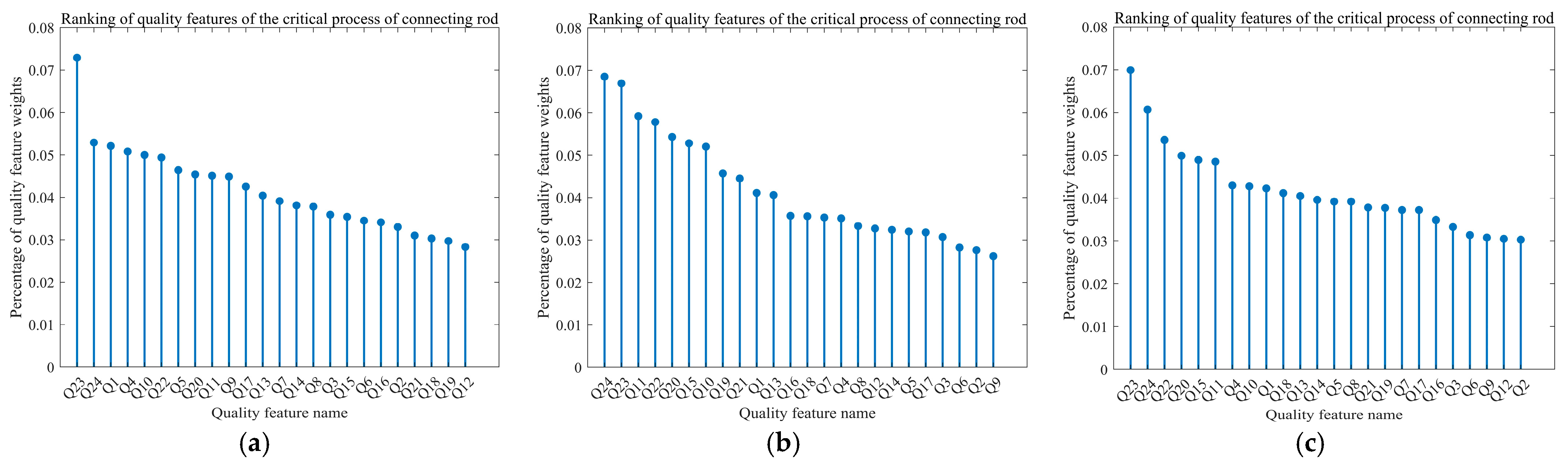
Regarding Table 4, connecting rod historical processing number and connecting rod processing process network, respectively, using the entropy weight method, CRITIC method, and Entropy-CRITIC method, allows us to calculate the weight of each quality feature in the processing process network. According to the weight size ranking of each quality feature calculated, the critical quality features of the connecting rod essential process under the entropy weight, CRITIC, and Entropy-CRITIC methods can be extracted. The ordering of the quality features of the connecting rod critical process is shown in Figure 5.
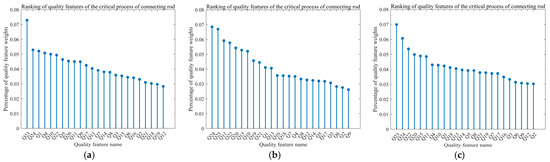
Figure 5.
Ranking of critical quality features of connecting rod: (a) Entropy weight method; (b) CRITIC method; (c) Entropy-CRITIC method.
Figure 5 shows the weight distribution of each quality feature in the critical process of connecting rod machining according to the entropy weight method, CRITIC method, and Entropy-CRITIC method. The results of the entropy weight method show that the weights of Q23 (the diameter of the large head hole of the fine boring hole) and Q24 (the diameter of the small head hole of the fine boring hole) are significantly higher than other features, indicating that they are dominant in quality control. The CRITIC method considers the correlation and variability between features, changes the weight distribution, reduces the weight of highly correlated features, and provides a new perspective on the balanced distribution of quality features. The results of the Entropy-CRITIC method are similar to the former two, and the weight of each quality feature is more reasonably allocated. Specifically, the weight of Q1 (the upper surface of the fine milling big head hole) in the entropy weight method is more significant. However, it is smaller in the CRITIC method because the entropy weight method only considers the machining error fluctuation of Q1 and does not consider the correlation between Q1 and subsequent processing. The critical quality features screened using this method correspond not only to the objectives focused on in the actual processing of the production enterprise but also by comprehensively analyzing the correlation and volatility between the features. Overall, the Entropy-CRITIC method can allocate the weight of each quality feature more reasonably. In addition, through theoretical analyses and technical exchanges with production enterprises, the critical quality features given by relevant experts are consistent with the screening results of the model, which verifies the effectiveness of the proposed method.
The entropy weight method emphasizes the degree of discreteness within the quality features. It extracts the weights from the distributional variability of the data. In contrast, the CRITIC method complements the correlation and conflict analysis between the quality features and does not consider the independence between the quality features. The combination of the two makes the evaluation results more objective and comprehensive. Therefore, the multi-angle evaluation calculation based on the Entropy-CRITIC method ensures that all information is used in the weight calculation and is more suitable for extracting critical quality features in marine diesel engine connecting rod machining.
6. Conclusions
This paper researches and discusses the identification method of critical quality features in the machining process of complex mechanical products, which is verified with the example of machining the connecting rod of a marine diesel engine for medium-speed machines. The results show that the proposed method can effectively identify the critical processes in the machining process and determine the critical quality features in these processes. The crucial nodes in the machining network, i.e., the critical processes, are identified through the LeaderRank algorithm. Subsequently, using the Entropy-CRITIC method, the Extreme Difference Maximization analysis successfully identified the critical quality features. These features significantly impact the quality of connecting rod machining and provide a clear direction for optimizing the machining process.
In addition, even with small sample data, the method still has high effectiveness and feasibility. It can screen out the quality features critical to product quality under complex process conditions. However, the results will be more accurate and reasonable with more sample data on quality features and more in-depth analyses of the coupling relationship between features. Therefore, this method is especially suitable for cases of rich sample data, which can significantly improve the consistency, reliability, and processing efficiency of products.
Author Contributions
Conceptualization, D.Q. and W.L.; Data curation, Y.Z. (Yuting Zhang), C.G., G.Z. and Y.Z. (Yong Zhan); Formal analysis, Y.Z. (Yuting Zhang), C.G., G.Z. and Y.Z. (Yong Zhan); Investigation, C.G.; Methodology, D.Q. and W.L.; Software, D.Q., W.L. and Y.Z. (Yuting Zhang); Supervision, Y.Z. (Yuting Zhang) and Y.Z. (Yong Zhan); Validation, W.L. and Y.Z. (Yuting Zhang); Visualization, C.G.; Writing—original draft, D.Q.; Writing—review and editing, W.L. and Y.Z (Yong Zhan). All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by designing and verifying key technologies of marine engines’ high reliability in the major special project ship research program of MIIT, Number CBG5N21-2-1. The authors are grateful for the financial support.
Data Availability Statement
The data that support the findings of this study are available on request from the corresponding author, Yong Zhan, upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chen, Q.; Liu, W.; Jiang, X.; Xu, S.; Wang, Y.; Liu, O. Identification and clustering analysis of critical processes for multi-variety and small-batch manufacturing processes. Comput. Integr. Manuf. Syst. 2022, 28, 812–825. [Google Scholar]
- Lu, C. Study on Prediction of Surface Quality in Machining Process. J. Mater. Process. Technol. 2008, 205, 439–450. [Google Scholar] [CrossRef]
- Yang, C.; Zhang, Q.; Li, H.; Xie, Q. Research on the decision-making of crucial process quality control points based on the AHP method. Min. Mach. 2004, 2, 57–59+5. [Google Scholar]
- He, H.; Tang, X. Product quality assurance design based on critical quality features. J. Aeronaut. 2007, 6, 1468–1481. [Google Scholar]
- Zhang, G.; Ji, F.; Ren, X.; Ge, H.; Zhang, S. A model for extracting critical quality features of complex electromechanical products. J. Chongqing Univ. 2010, 32, 8–14. [Google Scholar]
- Wang, H.; Fang, Z.; Wang, D.; Liu, S. An integrated fuzzy QFD and grey decision-making approach for supply chain collaborative quality design of large complex products. Comput. Ind. Eng. 2020, 140, 106212. [Google Scholar] [CrossRef]
- Li, L.; Jing, J.; Jiang, X.; Song, B. Identification method of critical quality features for the redesign of used machine tools. Mach. Des. Manuf. 2018, 5, 151–154. [Google Scholar]
- Qiao, P. Research on Complex Product Quality Prediction Based on Improved LASSO-RF. Master’s Thesis, Zhengzhou University, Zhengzhou, China, 2019. [Google Scholar]
- Ma, L.; Mao, J. Research on the identification of critical quality features based on the entropy weight method and Mahalanobis-Taguchi method. Light Ind. Mach. 2017, 35, 101–105. [Google Scholar]
- Wang, N.; Yan, N.; Xu, Y.; Yang, J. Identification of crucial quality features in complex multi-process manufacturing process. Stat. Decis.-Mak. 2021, 37, 177–180. [Google Scholar]
- Jin, N.; Zhou, S. Data-driven variation source identification for manufacturing process using the eigenspace comparison method. Nav. Res. Logist. 2010, 53, 383–396. [Google Scholar] [CrossRef]
- Wang, H.; Liang, L.; Niu, Z.; He, Z. Identification of CTQs for complex products based on mutual information and improved gravitational search algorithm. Math. Probl. Eng. 2015, 2015, 765985. [Google Scholar] [CrossRef]
- He, Z.; Hu, H.; Zhang, M.; Zhang, Y.; Li, A.-D. A Decomposition-Based Multi-Objective Particle Swarm Optimization Algorithm with a Local Search Strategy for Key Quality Characteristic Identification in Production Processes. Comput. Ind. Eng. 2022, 172, 108617. [Google Scholar] [CrossRef]
- Wang, N.; Xu, C.; Yang, F. Method of Identifying Key Quality Characteristics in Multistage Manufacturing Process Based on PLSR. Appl. Mech. Mater. 2012, 217, 2580–2584. [Google Scholar] [CrossRef]
- Zhang, F.; Jiang, P. A review of research on applying complex network theory to discrete shop floor production processes. Ind. Eng. 2016, 19, 1–8. [Google Scholar] [CrossRef]
- Özel, T.; Karpat, Y. Predictive Modeling of Surface Roughness and Tool Wear in Hard Turning Using Regression and Neural Networks. Int. J. Mach. Tools Manuf. 2005, 45, 467–479. [Google Scholar] [CrossRef]
- Su, Y.; Ye, W. The protection and recovery strategy development of dynamic resilience analysis and cost consideration in the infrastructure network. J. Comput. Des. Eng. 2022, 9, 168–186. [Google Scholar] [CrossRef]
- Ibne Hossain, N.U.; Nagahi, M.; Jaradat, R.; Shah, C.; Buchanan, R.; Hamilton, M. Modeling and Assessing Cyber Resilience of Smart Grid Using Bayesian Network-Based Approach: A System of Systems Problem. J. Comput. Des. Eng. 2020, 7, 352–366. [Google Scholar] [CrossRef]
- Tan, F.; Wu, J.; Xia, Y.; Tse, C.K. Traffic Congestion in Interconnected Complex Networks. Phys. Rev. E 2014, 89, 062813. [Google Scholar] [CrossRef]
- Qu, D.; Li, C.; Gu, C.; Yao, Y.; Zhan, Y. Research on Identification of Key Processes in Machining Process Based on PageRank Algorithm. Adv. Mech. Eng. 2024, 16, 16878132241229988. [Google Scholar] [CrossRef]
- Yu, J.; Zhu, P. Weighted Self-Regulation Complex Network-Based Variation Modeling and Error Source Diagnosis of Hybrid Multistage Machining Processes. IEEE Access 2019, 7, 36033–36044. [Google Scholar] [CrossRef]
- Jiang, P.; Jia, F.; Wang, Y.; Zheng, M. Real-time quality monitoring and predicting model based on error propagation networks for multistage machining processes. J. Intell. Manuf. 2014, 25, 521–538. [Google Scholar] [CrossRef]
- Liu, D.; Jiang, P. The complexity analysis of a machining error propagation network and its application. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2009, 223, 623–640. [Google Scholar] [CrossRef]
- Zhang, F.; Jiang, P. Complexity analysis of distributed measuring and sensing network in multistage machining processes. J. Intell. Manuf. 2013, 24, 55–69. [Google Scholar] [CrossRef]
- Jiang, P.; Wang, Y.; Wang, H.; Zheng, M. Multi-process machining quality prediction based on assignment-based error transfer network. J. Mech. Eng. 2013, 49, 160–170. [Google Scholar] [CrossRef]
- Jia, F.; Jiang, P.; Liu, D.; Zheng, M. Error propagation control method for blade batch processing. CIMS 2012, 18, 76–86. [Google Scholar] [CrossRef]
- Ma, N.; Guan, J.; Zhao, Y. Bringing PageRank to the citation analysis. Inf. Process. Manag. 2008, 44, 800–810. [Google Scholar] [CrossRef]
- Li, Q.; Zhou, T.; Lu, L.; Chen, D. Identifying influential spreaders by weighted LeaderRank. Phys. A Stat. Mech. Its Appl. 2014, 404, 47–55. [Google Scholar] [CrossRef]
- Yuan, Q. Key Process and Quality Characteristic Identification for Manufacturing Systems Using Dynamic Weighting Function and DS Evidence Theory. Int. J. Perform. Eng. 2018, 14, 1651. [Google Scholar] [CrossRef]
- Lu, Z.; Liu, C.; Liao, C.; Zhu, J.; Liu, H.; Chen, Y. Conceptual design and optimization of polymer gear system for low-thrust turbofan aeroengine accessory transmission. J. Comput. Des. Eng. 2024, 11, 212–229. [Google Scholar] [CrossRef]
- Jing, L.; Sheng, G.; Wang, W.; Wu, J.; Xu, X. Research on spot market monitoring and evaluation based on range maximization AHP-CRITIC. J. North China Electr. Power Univ. (Nat. Sci. Ed.) 2022, 49, 110–117. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).