Self-Adaptive Evolutionary Info Variational Autoencoder
Abstract
1. Introduction
- We combine the implementation of the InfoVAE model ELBO objective with the evolution strategy of the eVAE model to create a new eInfoVAE model.
- We improve on the evolution strategy from eVAE, by implementing the higher search power self-adaptive simulated binary crossover, to introduce the novel SA-eInfoVAE model.
- We comprehensively analyse and validate the improved performance of the proposed SA-eInfoVAE model on the MNIST dataset against existing models. Performance metrics include reconstructive, generative and disentanglement performance and latent encoding strength.
- We assess the performance of the SA-eInfoVAE model on a complex dataset to determine its applicability and capability to improve on aerodynamic optimisation problems that are being solved using machine learning algorithms.
2. Related Works
2.1. The Variational Autoencoder
2.2. Issues with Variational Autoencoders
2.3. Modified Variational Autoencoder Models
2.3.1. The -VAE Model
2.3.2. The InfoVAE Model
2.3.3. The Evolutionary Variational Autoencoder Model
2.4. Genetic Algorithms and Evolution Strategies
2.4.1. Simulated Binary Crossover and Cauchy Distributional Mutation
2.4.2. Self-Adaptive Simulated Binary Crossover
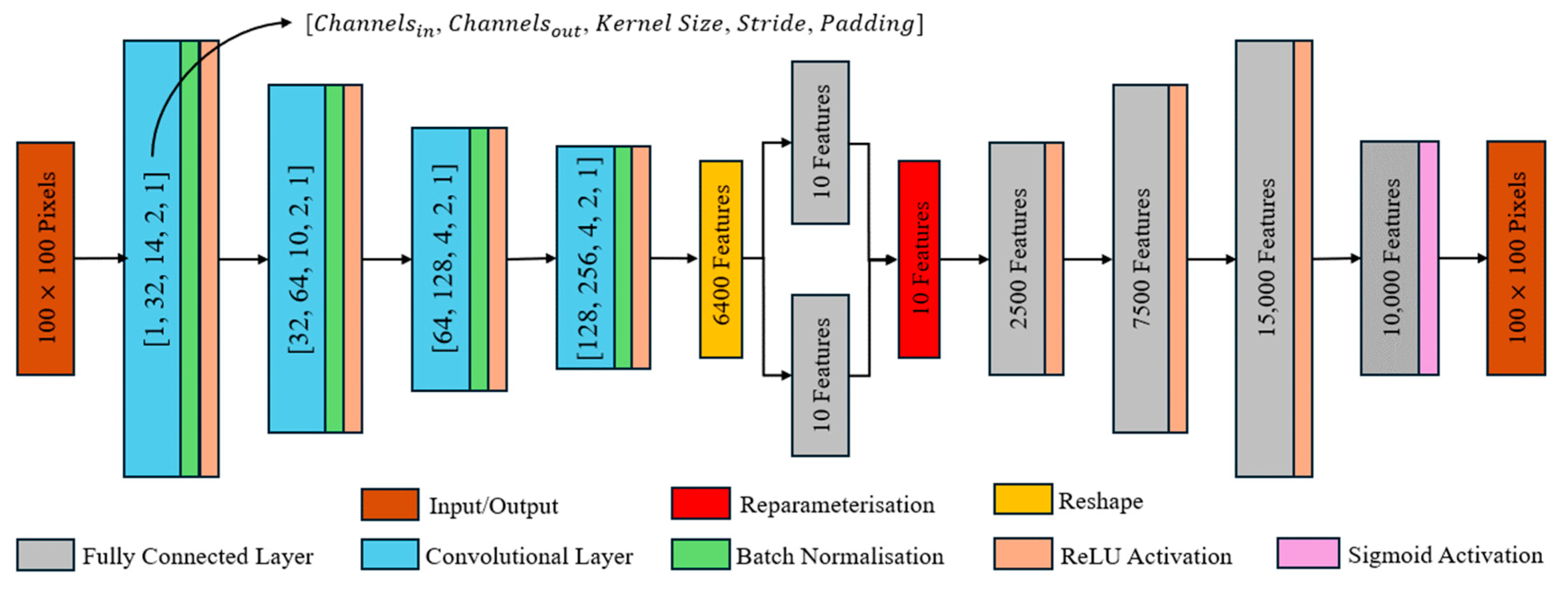
3. The Self-Adaptive Evolutionary Info Variational Autoencoder Model
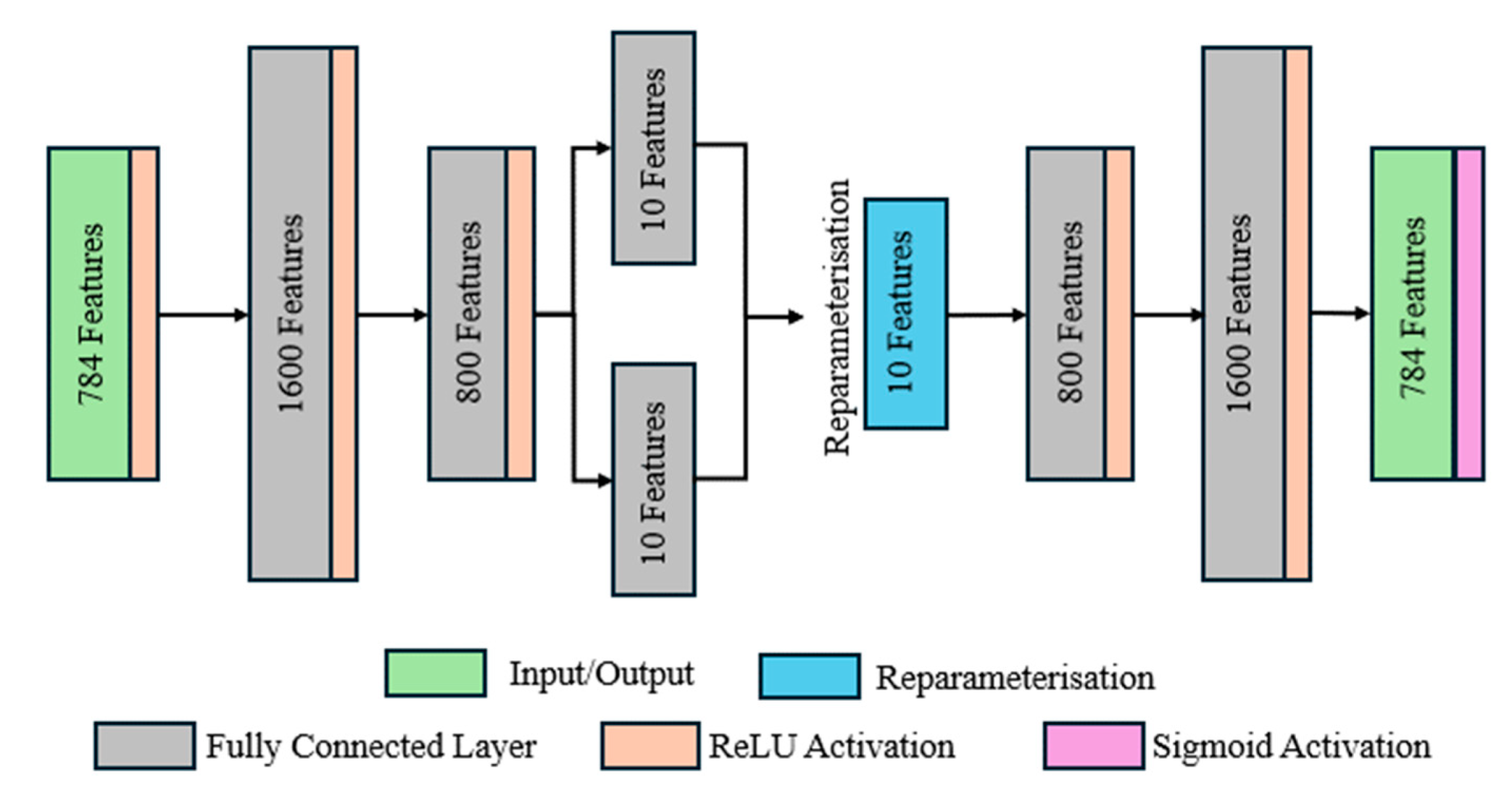
3.1. Implementation of the InfoVAE ELBO Objective
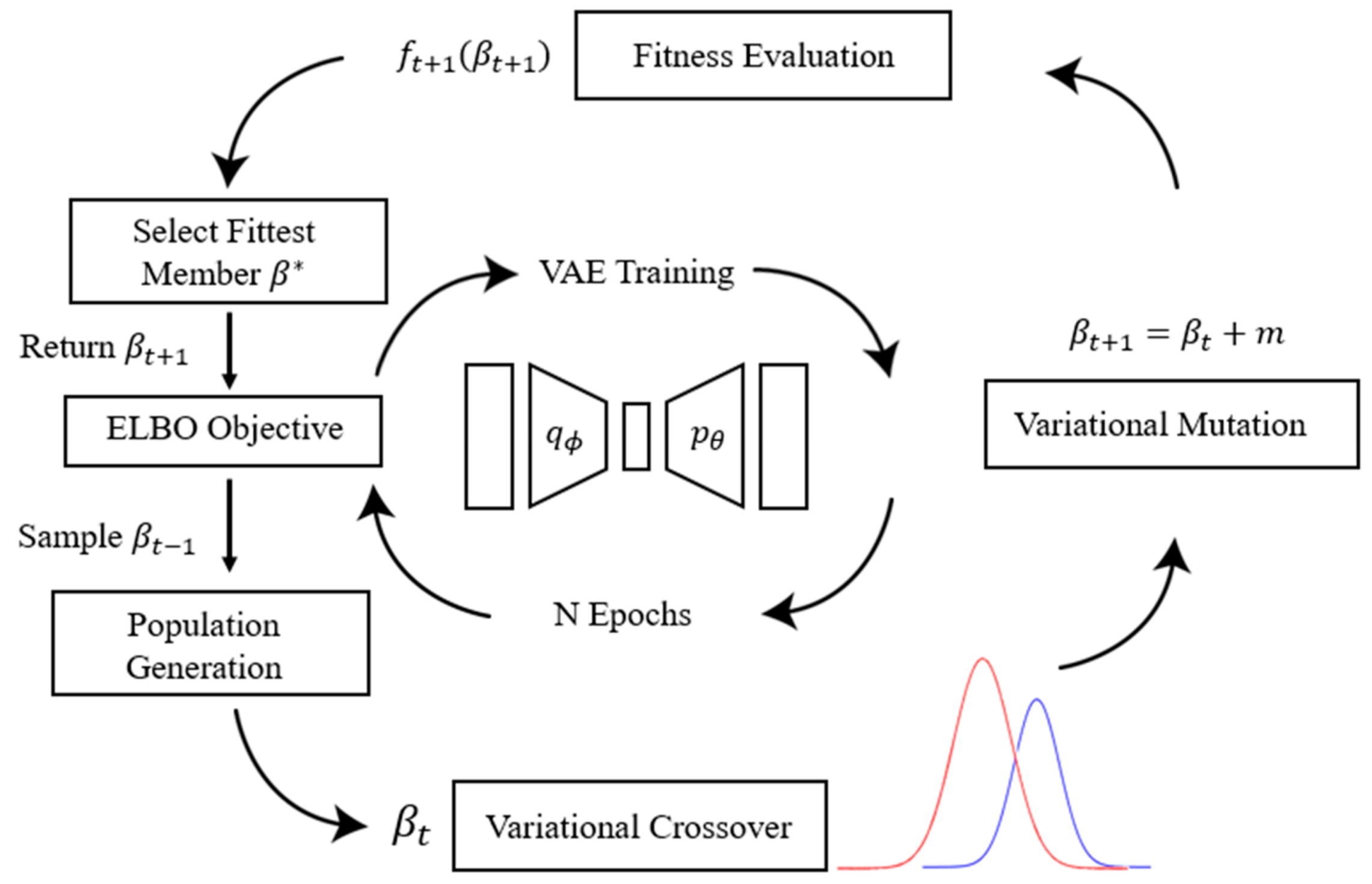
3.2. Implementation of Evolution Strategy
- Sample randomly from the uniform distribution .
- Calculate from Equation (11) below.
- Calculate the two child solutions by blending the current population member with the previous value , shown by Equation (12) below.
- Evaluate the fitness, , of both child solutions according to the fitness function in Equation (13) and select the fitter child solution to be passed to the final population.
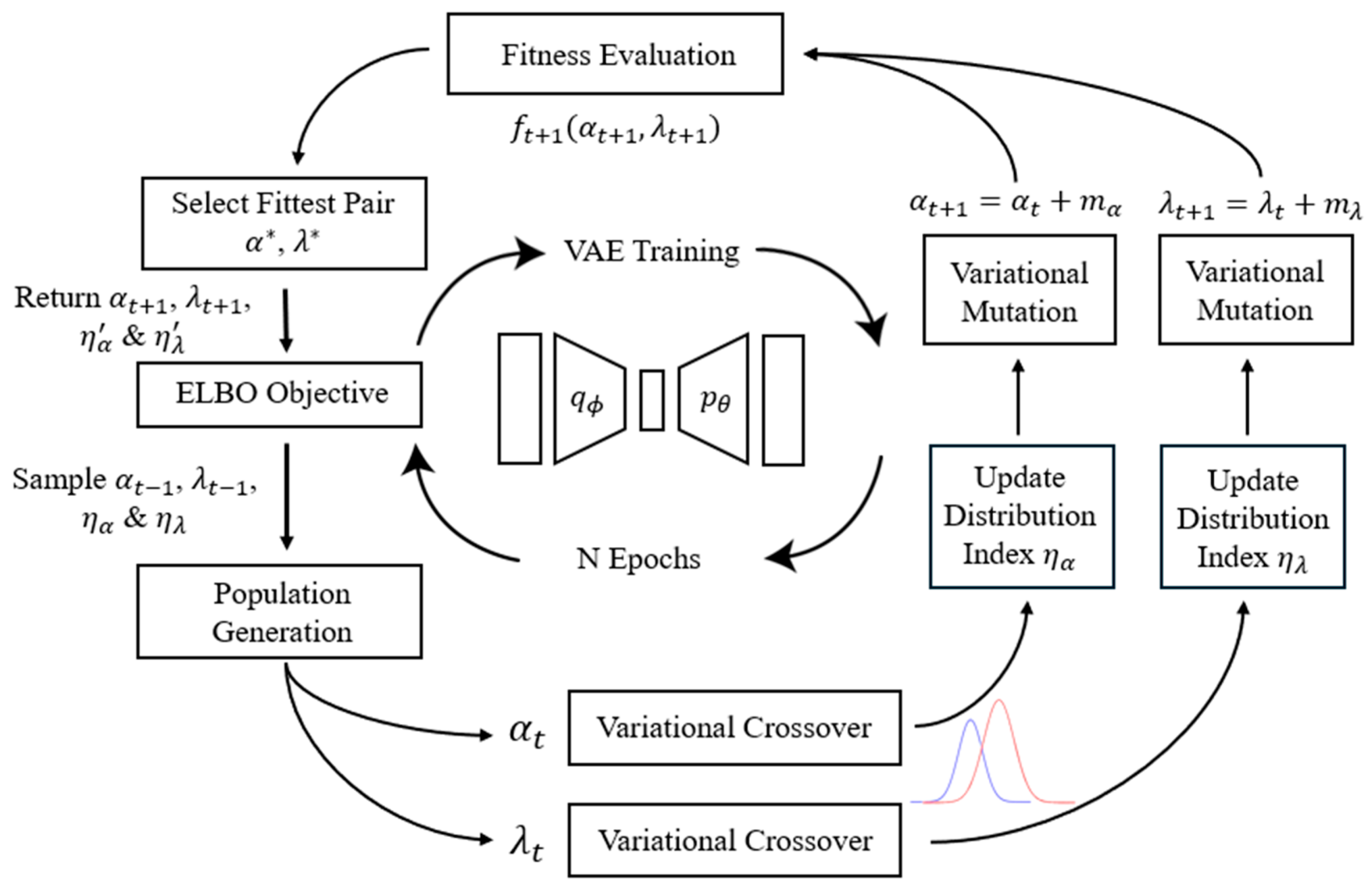
- Set the exponent update factor .
- Calculate the spread factor according to Equation (14) below.
- Evaluate the fitness of , and according to the fitness function in Equation (13).
- Determine whether the child solution lies within the region bounded by the parents or outside of this region. In the latter case, the nearest parent must also be determined.
- Update the distribution index using the appropriate equation determined by the following set of rules detailed by Deb et al. [37]. If the child solution lies outside of the region bounded by the parents and is a better solution compared to the nearest parent, the updated distribution index is calculated using Equation (15) below.
- If the child solution lies outside the region bounded by the parents and is a worse solution compared to the nearest parent, is calculated using Equation (16) below.
- If the child solution lies in the region bounded by the two parents and is a better solution compared to either parent, is calculated using Equation (17) below.
- If the child solution lies in the region bounded by the two parents and is a worse solution compared to either parent, is calculated using Equation (18) below.
3.3. Implementation of Qualitative Comparisons and Quantitative Performance Metrics
3.3.1. Loss Function Logging and Generated Images
3.3.2. Reconstructive Performance Metrics
3.3.3. Visualisation of the Latent Space
3.3.4. The Disentanglement Metric
- Randomly select the latent variable to be fixed, where represents the number of latent dimensions.
- Generate two latent vectors, and by sampling each variable randomly and enforcing .
- Use the decoder to generate images and from the latent vectors and .
- Pass the generated images and to the encoder and infer the latent vectors and .
- Compute , the absolute difference between the inferred latent representations.
- Repeat the process for a batch of samples.
- Compute the average and report this as a percentage disentanglement score.
3.4. Experimental Setups
3.4.1. Experimental Setup on the MNIST Dataset
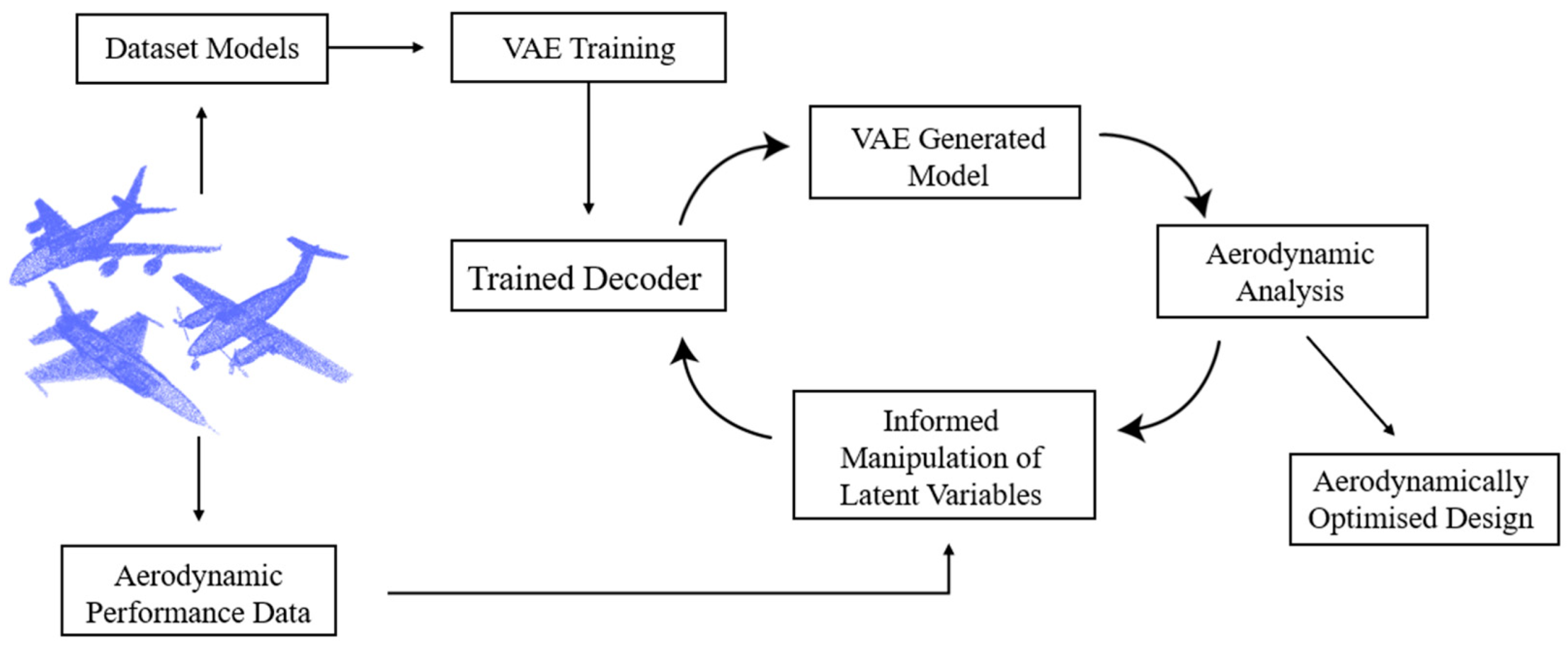
3.4.2. Experimental Setup on the Aircraft Image Dataset
4. Results
4.1. Validation on the MNIST Dataset
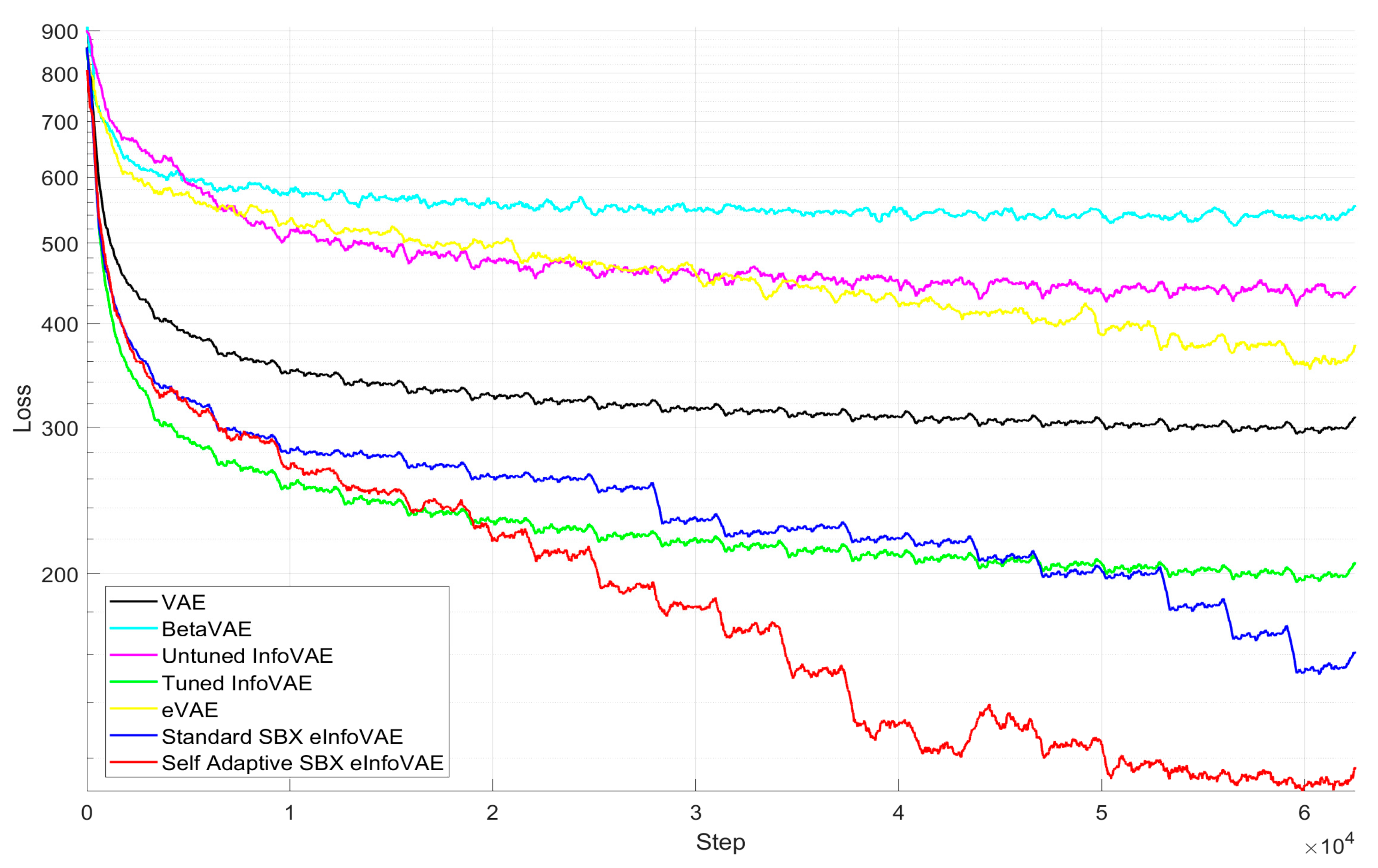
4.1.1. Loss Function and Hyperparameter Evolution
4.1.2. Generative Performance
4.1.3. Reconstructive Performance
4.1.4. Disentanglement Performance
4.1.5. Comparison of the Latent Space
4.1.6. Final Remarks on the MNIST Dataset
4.2. Results on the ShapeNetCore Aircraft Image Dataset
5. Conclusions and Discussion
6. Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, J.; Xiasong, D.; Martins, J.R.R.A. Machine Learning in Aerodynamic Shape Optmisation. Prog. Aeronaut. Sci. 2022, 134, 100849. [Google Scholar] [CrossRef]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. arXiv 2013, arXiv:13.12.6114. [Google Scholar] [CrossRef]
- Rezende, D.J.; Mohammed, S.; Wierstra, D. Stochastic Backpropagation and Approximate Inference in Deep Generative Models. In Proceeding of the 31st International Conference on Machine Learning, Beijing, China, 21–26 June 2014. [Google Scholar]
- Burda, Y.; Grosse, R.; Salakhutdinov, R. Importance Weighted Autoencoders. arXiv 2015, arXiv:1509.00519. [Google Scholar] [CrossRef]
- Saha, S.; Minku, L.; Yao, X.; Sendhoff, B.; Menzel, S. Exploiting 3D variational autoencoders for interactive design. Proc. Des. Soc. 2022, 2, 1747–1756. [Google Scholar] [CrossRef]
- Rios, T.; Stein, B.V.; Wollstadt, P.; Back, T.; Sendhoff, B.; Menzel, S. Exploiting Local Geometric Features on Vehicle Design Optimization with 3D Point Cloud Autoencoders. In Proceeding of the 2021 IEEE Congress on Evolutionary Computation (CEC), Krakow, Poland, 28 June–1 July 2021. [Google Scholar] [CrossRef]
- Mrosek, M.; Othmer, C.; Radepsiel, R. Variational Autoencoders for Model Order Reduction in Vehicle Aerodynamics. In Proceeding of the AIAA Aviation Forum, Virtual, 2–6 August 2021. [Google Scholar] [CrossRef]
- Higgins, I.; Matthey, L.; Pal, A.; Burgess, C.; Glorot, X.; Botvnick, M.; Mohamed, S.; Lerchner, A. Beta-VAE: Learning Basic Visual Concepts with a Constrained Variational Framework. In Proceeding of the 5th International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Zhao, S.; Song, J.; Ermon, S. InfoVAE: Balancing Learning and Inference in a Variational Autoencoders. In Proceedings of the 31st AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019. [Google Scholar] [CrossRef]
- Shao, H.; Yao, S.; Sun, D.; Zhang, A.; Liu, S.; Liu, D.; Wang, J.; Abdelzaher, T. ControlVAE: Controllable Variational Autoencoder. In Proceedings of the 37th International Conference on Machine Learning, Virtual, 13–18 July 2020. [Google Scholar]
- Bond-Taylor, S.; Leach, A.; Long, Y.; Willcocks, C.G. Deep Generative Modelling: A Comparative Review of VAEs, GANs, Normalizing Flows, Energy-Based and Autoregressive Models. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 7327–7347. [Google Scholar] [CrossRef]
- Seong, J.Y.; Ji, S.; Choi, D.; Lee, S.; Lee, S. Optimizing Generative Adversarial Network (GAN) Models for Non-Pneumatic Tire Design. Appl. Sci. 2023, 13, 10664. [Google Scholar] [CrossRef]
- Andriyanov, N.A.; Vasiliev, K.K.; Dementiev, V.E.; Belyanchikov, A.V. Restoration of Spatially Inhomogeneous Images Based on a Doubly Stochastic Model. Optoelectron. Instrument. Proc. 2022, 58, 465–471. [Google Scholar] [CrossRef]
- Bamford, T.; Keane, A.; Toal, D. SDF-GAN: Aerofoil Shape Parameterisation via an Adversarial Auto-Encoder. In Proceedings of the AIAA Aviation Forum and Ascend 2024, Las Vegas, NV, USA, 29 July–2 August 2024. [Google Scholar] [CrossRef]
- Du, X.; He, P.; Martins, J.R.R.A. A B-Spline-based Generative Adversarial Network Model for Fast Interactive Airfoil Aerodynamic Optimization. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar] [CrossRef]
- Chen, W.; Chiu, K.; Fuge, M. Aerodynamic Design Optimization and Shape Exploration using Generative Adversarial Networks. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar] [CrossRef]
- Yu, X.; Zhang, X.; Cao, Y.; Xia, M. VAEGAN: A Collaborative Filtering Framework based on Adversarial Variational Autoencoders. In Proceedings of the 28th International Conference on Artificial Intelligence, Macao, China, 10–16 August 2019. [Google Scholar]
- Wang, Y.; Shimada, K.; Farimani, A.B. Airfoil GAN: Encoding and synthesizing airfoils for aerodynamic shape optimization. J. Comput. Des. Eng. 2023, 10, 1350–1362. [Google Scholar] [CrossRef]
- Blei, D.M.; Kucukelbir, A.; McAuliffe, J.D. Variational Inference: A Review for Statisticians. J. Am. Stat. Assoc. 2017, 112, 859–877. [Google Scholar] [CrossRef]
- Shlens, J. Notes on Kullback-Leibler Divergence and Likelihood Theory. arXiv 2014, arXiv:1404.2000. [Google Scholar] [CrossRef]
- Doersch, C. Tutorial on Variational Autoencoders. arXiv 2016, arXiv:1606.05908. [Google Scholar]
- Tomczak, J.M.; Welling, M. VAE with VampPrior. In Proceedings of the International Conference on Artificial Intelligence and Statistics (AISTATS), Playa Blanca, Spain, 9–11 April 2018. [Google Scholar]
- Van Den Oord, A.; Kalchbrenner, N.; Kavukcuoglu, K. Pixel Recurrent Neural Networks. In Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016. [Google Scholar]
- Gulrajani, I.; Kumar, K.; Ahmed, F.; Taiga, A.A.; Visin, F.; Vazquez, D.; Courville, A. PixelVAE: A Latent Variable Model for Natural Images. arXiv 2016, arXiv:1611.05013. [Google Scholar] [CrossRef]
- Razavi, A.; Van Den Oord, A.; Poole, B.; Vinyals, O. Preventing Posterior Collapse with delta-VAEs. arXiv 2019, arXiv:1901.03416. [Google Scholar] [CrossRef]
- Wu, Z.; Cao, L.; Qi, L. eVAE: Evolutionary Variational Autoencoder. IEEE Trans. Neural Netw. Learn. Syst. 2024, accepted. [Google Scholar] [CrossRef] [PubMed]
- Fu, H.; Li, C. Cyclical Annealing Schedule: A simple Approach to Mitigating KL Vanishing. In Proceedings of the Annual Conference of the North American Chapter of the Association for Computational Linguistics, Minneapolis, MN, USA, 2–7 June 2019. [Google Scholar]
- Liu, Z.; Luo, P.; Wang, X.; Tang, X. Deep Learning Face Attributes in the Wild. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 3730–3738. [Google Scholar]
- Aubry, M.; Maturana, D.; Efros, A.A.; Russell, B.C.; Sivic, J. Seeing 3D Chairs: Exemplar Part-based 2D-3D Alignment using a Large Dataset of CAD Models. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014; pp. 3762–3769. [Google Scholar]
- Paysan, P.; Knothe, R.; Amberg, B.; Romdhani, S.; Vetter, T. A 3D Face Model for Pose and Illumination Invariant Face Recognition. In Proceedings of the 2009 Sixth IEEE International Conference on Advanced Video and Signal Based Surveillance, Genova, Italy, 2–4 September 2009; pp. 296–301. [Google Scholar] [CrossRef]
- Chen, X.; Duan, Y.; Houthooft, R.; Schulman, J.; Sutskever, I.; Abbeel, P. InfoGAN: Interpretable Representation Learning by Information Maximizing Generative Adversarial Nets. In Proceedings of the Advances in Neural Information Processing Systems 29 (NIPS), Barcelona, Spain, 5–10 December 2016. [Google Scholar]
- Kulkarni, T.D.; Whitney, W.F.; Kohli, P.; Tenenbaum, J. Deep Convolutional Inverse Graphics Network. In Proceedings of the Advances in Neural Information Processing Systems 28 (NIPS), Montreal, QC, Canada, 7–12 December 2015. [Google Scholar]
- Alemi, A.; Poole, B.; Fischer, I.; Dillon, J.; Saurous, R.A.; Murphy, K. Fixing a Broken ELBO. In Proceedings of the 35th International Conference on Machnine Learning, Stockholm, Sweden, 10–15 July 2018. [Google Scholar]
- Gretton, A.; Borgwardt, K.M.; Rasch, J.M.; Schölkopf, B.; Smola, A. A Kernel Two-Sample Test. J. Mach. Learn. Res. 2012, 13, 723–773. [Google Scholar]
- Deb, K.; Agrawal, R.B. Simulated Binary Crossoer for Continuous Search Space. Complex Syst. 1995, 9, 115–148. [Google Scholar]
- Chacón, J.; Segura, C. Analysis and Enhancement of Simulated Binary Crossover. In Proceedings of the 2018 IEEE Congress on Evolutionary Computation (CEC), Rio de Janeiro, Brazil, 8–13 July 2018. [Google Scholar] [CrossRef]
- Deb, K.; Sindhiya, K.; Okabe, T. Self-Adaptie Simulated Binary Crossover for Real-Parameter Optimization. In Proceedings of the 9th Annual Conference on Genetic and Evolutionary Computation, London, UK, 7 July 2007. [Google Scholar]
- NVIDIA T4 Tensor Core GPU. Available online: https://www.nvidia.com/en-gb/data-center/tesla-t4/ (accessed on 10 April 2024).
- Fadel, S.; Ghoniemy, S.; Abdallah, M.; Abu Sorra, H.; Ashour, A.; Ansary, A. Investigating the Effect of Different Kernal Functions on the Performance of SVM for Recognizing Arabic Characters. Int. J. Adv. Comput. Sci. Appl. 2016, 7, 446–450. [Google Scholar]
- What is W&B? Available online: https://docs.wandb.ai/guides (accessed on 24 January 2024).
- Węglarczyk, S. Kernel Density Estimation and its Application. ITM Web Conf. 2018, 23, 00037. [Google Scholar] [CrossRef]
- Rani, E.G.; Sakthimohan, M.; Abhigna, R.G.; Selvalakshmi, D.; Keerthi, T.; Raja Sekar, R. MNIST Handwritten Digit Recognition using Machine Learning. In Proceedings of the 2022 2nd International Conference on Advance Computing and Innovative Technologies in Engineering (ICACITE), Greater Nodia, India, 28–29 April 2022. [Google Scholar] [CrossRef]
- Chang, A.X.; Funkhouser, T.; Guibas, L.; Hanrahm, P.; Huang, Q.; Li, Z.; Savarese, S.; Savva, M.; Song, S.; Su, H.; et al. ShapeNet: An Information-Rich 3D Model Repository. arXiv 2015, arXiv:1512.03012. [Google Scholar]
- Wellner, P.D. Adaptive Thresholding for the Digital Desk; EuroPARC Technical Report EPC-93-110; Xerox: Norwalk, CT, USA, 1993. [Google Scholar]
- Van Der Maaten, L.; Hinton, G. Visualizing Data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- The CIFAR-10 Dataset. Available online: https://www.cs.toronto.edu/~kriz/cifar.html (accessed on 3 August 2024).










| Network Parameter | Learning Rate | Batch Size | Latent Dimensions | Training Epochs |
|---|---|---|---|---|
| Value | 0.00035 | 16 | 10 & 2 | 20 |
| Hyperparameter | |||||||
|---|---|---|---|---|---|---|---|
| Model | Crossover Rate | Mutation Rate | |||||
| VAE | - | - | - | - | - | - | - |
| -VAE | - | - | 4 | - | - | - | - |
| Untuned InfoVAE | 0 | 1000 | - | - | - | - | - |
| Tuned InfoVAE | 0.7 | 100 | - | - | - | - | - |
| eVAE | - | - | 0.3 | 0.2 | - | - | |
| Standard SBX eInfoVAE | (Initially) | (Initially) | - | 0.3 | 0.2 | 8 | 3 |
| Self-Adaptive SBX eInfoVAE | (Initially) | (Initially) | - | 0.3 | 0.2 | 8 (Initially) | 3 (Initially) |
| Network Parameter | Learning Rate | Batch Size | Latent Dimensions | Training Epochs |
|---|---|---|---|---|
| Value | 0.00035 | 16 | 10 & 2 | 20 |
| Parameters | Initialisations | ||||
|---|---|---|---|---|---|
| Crossover Rate | Mutation Rate | ||||
| 0.3 | 0.2 | 8 | 3 | ||
| Digit Mean-Square Error (×10−1) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Model | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Average |
| VAE | 0.133 | 0.032 | 0.159 | 0.127 | 0.231 | 0.389 | 0.116 | 0.131 | 0.154 | 0.147 | 0.162 |
| Untuned InfoVAE | 0.193 | 0.077 | 0.454 | 0.238 | 0.245 | 0.426 | 0.286 | 0.147 | 0.254 | 0.322 | 0.264 |
| Tuned InfoVAE | 0.116 | 0.046 | 0.163 | 0.125 | 0.118 | 0.287 | 0.094 | 0.065 | 0.123 | 0.119 | 0.126 |
| -VAE | 0.213 | 0.117 | 0.406 | 0.308 | 0.291 | 0.528 | 0.218 | 0.173 | 0.224 | 0.372 | 0.285 |
| eVAE | 0.187 | 0.087 | 0.252 | 0.267 | 0.163 | 0.426 | 0.121 | 0.160 | 0.241 | 0.260 | 0.216 |
| Standard SBX eInfoVAE | 0.089 | 0.032 | 0.122 | 0.100 | 0.080 | 0.184 | 0.066 | 0.058 | 0.120 | 0.102 | 0.095 |
| Self-Adaptive SBX eInfoVAE | 0.090 | 0.022 | 0.130 | 0.084 | 0.069 | 0.173 | 0.045 | 0.063 | 0.108 | 0.079 | 0.086 |
| Model | VAE | Untuned InfoVAE | Tuned InfoVAE | -VAE | eVAE | Standard SBX eInfoVAE | Self-Adaptive SBX eInfoVAE |
|---|---|---|---|---|---|---|---|
| Disentanglement Performance/% | 85.4 | 90.8 | 90.3 | 45.7 | 57.1 | 91.1 | 96.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Emm, T.A.; Zhang, Y. Self-Adaptive Evolutionary Info Variational Autoencoder. Computers 2024, 13, 214. https://doi.org/10.3390/computers13080214
Emm TA, Zhang Y. Self-Adaptive Evolutionary Info Variational Autoencoder. Computers. 2024; 13(8):214. https://doi.org/10.3390/computers13080214
Chicago/Turabian StyleEmm, Toby A., and Yu Zhang. 2024. "Self-Adaptive Evolutionary Info Variational Autoencoder" Computers 13, no. 8: 214. https://doi.org/10.3390/computers13080214
APA StyleEmm, T. A., & Zhang, Y. (2024). Self-Adaptive Evolutionary Info Variational Autoencoder. Computers, 13(8), 214. https://doi.org/10.3390/computers13080214







