Abstract
In recent research in computer-aided geometric design (CAGD), one of the most popular concerns has been the creation of new basis functions for the Bézier curve. Bézier curves with high degrees often overshoot, which makes it challenging to maintain control over the ideal length of the curved trajectory. To get around this restriction, free-form surfaces and curves can be created using the Caputo Fabrizio basis function. In this study, the Caputo Fabrizio fractional order derivative is used to construct the Caputo Fabrizio basis function, which contains fractional parameter and shape parameters. The Caputo Fabrizio Bézier curve and surface are defined using the Caputo Fabrizio basis function, and their geometric properties are examined. Using fractional and shape parameters in the implementation of the Caputo Fabrizio basis function offers an alternative perspective on how the Caputo Fabrizio basis function can construct complicated curves and surfaces beyond a limited formulation. Curves and surfaces can have additional shape and length control by adjusting a number of fractional and shape parameters without affecting their control points. The Caputo Fabrizio Bézier curve’s flexibility and versatility make it more effective in creating complex engineering curves and surfaces.
1. Introduction
The Bézier curve’s geometric properties make it a topic that is frequently explored in CAGD [1,2]. Control points are what distinguish Bézier curves from other curves. The control points can be manipulated to modify the shape of the Bézier curve. Shape parameters allow the construction of a curve without requiring any changes to the control points. An integral method was used by Wang et al. [3] to create a Bézier basis using shape parameters. The trigonometric polynomial curve containing shape parameters was first presented by Han [4,5]. A technique for modifying curves with n shape parameters was given by Yang and Zeng [6]. Hu et al. [7] offered a shape-modifiable generalized Bézier (GB) curve that takes into account several shape parameters and explained its applicability to engineering surface modeling. Maqsood et al. [8] developed generalized trigonometric (GT) basis containing two distinct form parameters by applying the recurrence technique to improve the geometric features of GT Bézier surfaces and curves. The modifying alternatives that result from showing a rational Bézier curve in barycentric form are examined by Ramanatoanina et al. [9]. Bulut [10] presented a novel approach and identified the local and global paths for avoiding collisions in dynamic scenarios using cubic Bézier curves having three shape parameters. A novel class of kth-degree generalized trigonometric Bernstein (GT-Bernstein) basis incorporating two form parameters was proposed by Ammad et al. [11]. In addition, a number of real-world applications of GT-Bézier curves are covered, including the freehand geometric modeling of complex curves and the approximation of certain conic curves. Shape parameters are used in the construction of quintic trigonometric Bézier-like basis functions by Ammad et al. [12]. They also produce biquintic Bézier surfaces, which combine the fundamental characteristics of a traditional Bézier surface with remarkable shape-changing flexibility by incorporating four form parameters. The Arabic word (Allah) was creatively created by Omar et al. [13], applying a trigonometric Bézier curve that included shape parameters. To create a C-shaped model, Ziatdinov et al. [14] coupled multiples of log-aesthetic curves (LAC) by continuity. This model was then used to model track and gear designs. The geometric continuity of the general Bézier curve containing n number of shape parameters up to and the parametric continuity up to was studied by Qin et al. [15]. Using two different form parameters, rational quadratic trigonometric Bézier (RQTB) curves were presented by Bashir et al. [16]. Additionally, they used and continuity to link these curves. Generalized hybrid trigonometric Bézier (GHTB) curves with a variety of shapes and font styles were constructed by Bibi et al. [17]. They calculated their curvature by using different continuity criteria as well.
Any real- or complex-order integrals and derivatives are used in fractional calculus. Debnath [18] provides an outline of the many uses of fractional calculus in science and technology. Fractional calculus was used by Sebaa et al. [19] to describe the viscous interplay between solid and fluid structures. Furthermore, Blot’s theory was utilized to create the transmission and reflection scattering operators for a segment of bone in a flexible frame that had a cancellous structure. A few brief summaries by renowned experts in the field of fractional calculus were offered by Sun et al. [20]. For the human liver, Baleanu et al. presented a unique fractional model that incorporates the Caputo Fabrizio (CF) fractional order derivative [21]. The homotopy analysis transform method was used to create this mathematical model; its convergence was also examined, and numerical experiments were conducted to provide a clearer understanding of the outcomes. Arora et al. [22] provided an in-depth study of fractional-order derivative-based computer vision algorithms. This work also emphasized the challenges and possible uses of fractional calculus in computer vision and provided evidence of its usefulness in these fields. De Oliveira and Tenreiro Machado [23] examined the definitions of fractional integrals and derivatives. Li [24] generalized the wavelet collocation technique for fractional differential equations (FDEs) by means of a cubic B-spline wavelet. An analytical formula in the Caputo fractional-order derivative sense was provided for cubic B-spline functions. The approach’s primary feature is its ability to transform these kinds of issues into an algebraic equation system that can be used with computer programming. Kirmani et al. [25] presented the fractional order shape preserving the Kirmani Norhaida Riaz (KNR) cubic spline by applying the Caputo fractional time derivative. Using the Riemann–Liouville fractional integral, Said Mad Zain et al. [26] produced the fractional basis function and the fractional Bézier curve including fractional and shape parameters. Furthermore, their work presented fractional continuity, a novel form of continuity.
Remarkably little research in CAGD addresses fractional calculus’s function in Bézier curve building. When more complex curves are used for interpolation or fitting a big number of points, the Bézier curve has a tendency to overshoot. One approach to prevent this issue is to manage the curve’s optimal length. In this study, a fractional parameter is used to overcome this problem. For the Caputo Fabrizio Bézier curve, the Caputo Fabrizio basis function is generated using the Caputo Fabrizio (CF) fractional order derivative. Moreover, the characteristics of the Caputo Fabrizio Bézier curve and basis are discussed in detail. The Caputo Fabrizio Bézier curve’s length and shape can be changed by adjusting the fractional and shape parameters, respectively, without affecting the curve’s range or control points.
The overall structure of this study is as follows. The idea of Caputo Fabrizio (CF) fractional derivatives is discussed in Section 2. Next, the properties of the Caputo Fabrizio basis functions are discussed, along with the creation of the Caputo Fabrizio basis function for the Caputo Fabrizio Bézier curve. Section 3 discusses the creation and display of the Caputo Fabrizio Bézier curve’s different properties. The influence of fractional and shape parameters is covered in Section 4. The Caputo Fabrizio Bézier curve is used in Section 5 to create a few simple surfaces, including surface rotation and extruded surface. Section 6 deals with the application of the Caputo Fabrizio Bézier curve. Finally, Section 7 addresses the conclusion and suggestions for further research.
2. Caputo Fabrizio Basis Function with Fractional and Shape Parameters
In this section, we address how the Caputo Fabrizio fractional order derivative is used to create the Caputo Fabrizio basis function with fractional and shape parameters.
Definition 1.
For an a integrable function over the interval , the Caputo fractional time derivative of order is [27]
where , , and
Now (1) has the following form if and ,
Now by replacing the kernel in (2) with and with , we obtain the Caputo Fabrizio fractional derivative of order .
is the normalization function having condition .
In this work, we take and specifically. Using the substitution method and simplifying (3), we obtain
The fractional parameter is represented by .
2.1. The Construction of the Caputo Fabrizio Basis Function
Definition 2.
The classical Bernstein basis function is defined as [28]
The Caputo Fabrizio fractional time derivative as defined in (3) is used to construct the Caputo Fabrizio basis function with fractional parameter and form (shape) parameters .
Here,
Depending on the degree of basis, a different number of shape parameters are needed; for instance, two or three shape parameters are needed for the quadratic and cubic Caputo Fabrizio basis functions. For every degree of Caputo Fabrizio basis functions, there is an extra parameter, known as the fractional parameter.
2.2. Properties of Caputo Fabrizio Basis Function
- (i)
- Partition of unity.
- (ii)
- Terminal property.
- (iii)
- Non-negativity.
- (i) Partition of unity.
For any value of () and , we have to prove .
Proof.
□
- (ii) Terminal property.
Case (i): .
In Bernstein basis functions for , , () and , . In the case of Caputo Fabrizio basis functions we obtain similar results as above, which means that the starting point is the same for both (Bernstein and Caputo Fabrizio) basis functions at .
Case (ii): .
For , , () and , , but in the case of the Caputo Fabrizio basis, the end point is not fixed and depends on fractional parameter . Figure 1, Figure 2 and Figure 3 show that the starting point of all the Caputo Fabrizio basis functions is fixed and the ending point in not fixed at different values of ().
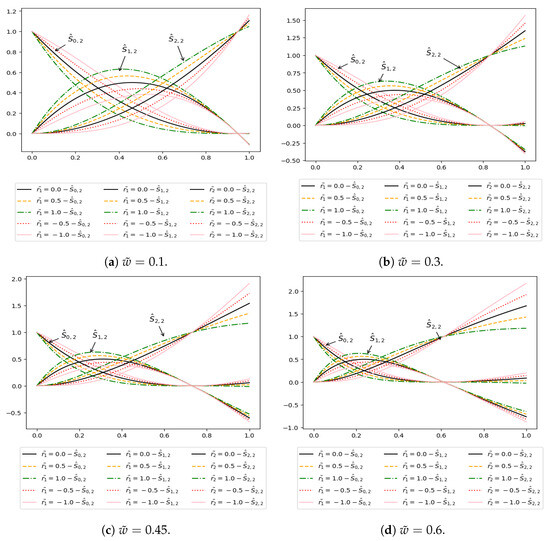
Figure 1.
Quadratic Caputo Fabrizio basis with different values of shape parameters (, ) and fractional parameter ().
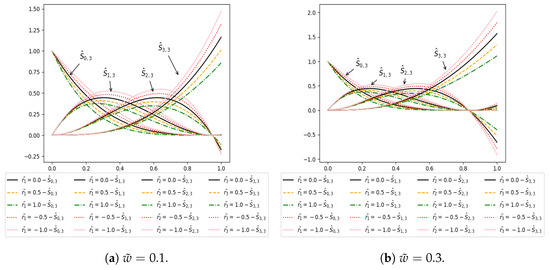
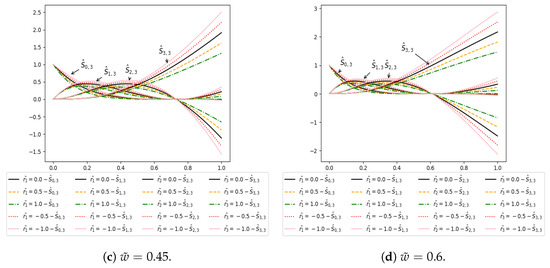
Figure 2.
Cubic Caputo Fabrizio basis with different values of (fractional parameter) and , , (shape parameters).
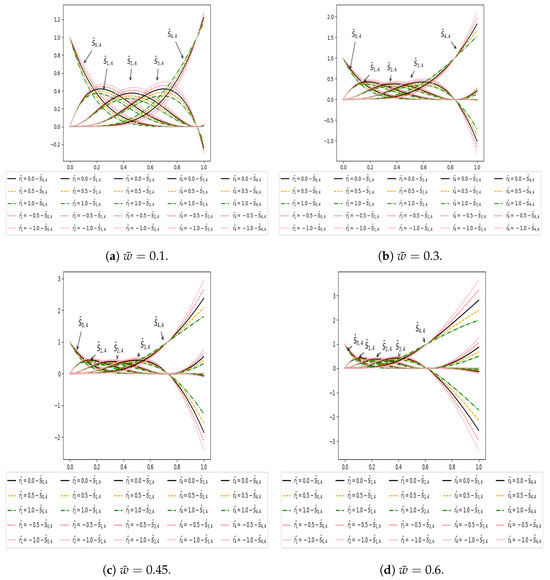
Figure 3.
Quartic Caputo Fabrizio basis with different values of (fractional parameter) and , , , (shape parameters).
- (iii) Non-negativity.
Case (i): and ,
⇒.
Case (ii): and ,
⇒.
3. Caputo Fabrizio Bézier Curve with Fractional and Shape Parameters
Definition 3.
The fractional parameter and shape parameters define the Caputo Fabrizio Bézier curve of degree as
Here, ∈ are the control points and is the Caputo Fabrizio basis as defined in (6).
Now using (7), we define the quadratic and cubic Caputo Fabrizio Bezier curves for and .
Definition 4.
A quadratic curve based on the Caputo Fabrizio fractional time derivative with two shape parameters is
Definition 5.
A cubic curve based on the Caputo Fabrizio fractional time derivative with three shape parameters is
Properties of Caputo Fabrizio Bézier Curve with Fractional and Shape Parameters
- Endpoint terminal.
- Convex hull.
- Symmetry.
- Geometric invariance.
- Shape-adjustable property.
- Curve’s length-adjustable property.
- i. Endpoint terminal.
Case (i): .
Hence, (10) indicates that at and , the endpoint of the Caputo Fabrizio Bézier curve is independent of the fractional parameter .
Case (ii): .
Compared to a conventional Bézier curve, the endpoint of a Caputo Fabrizio Bézier curve for is not defined by its last control point. This indicates that the parameter determines the endpoint of the Caputo Fabrizio Bézier curve at . It is simple to compute the location of the endpoint terminal at by inserting the value of in (11). When varies, this endpoint terminal characteristic for the Caputo Fabrizio Bézier curve will give the tractable particle path.
- ii. Convex hull.
The convex polygon whose vertices are the control points forms the convex hull. When a Bezier curve is used, the entire curve is included within the convex hull; however, when a Caputo Fabrizio Bezier curve is used, the curve falls partially outside the convex hull (see Figure 4 and Figure 5).
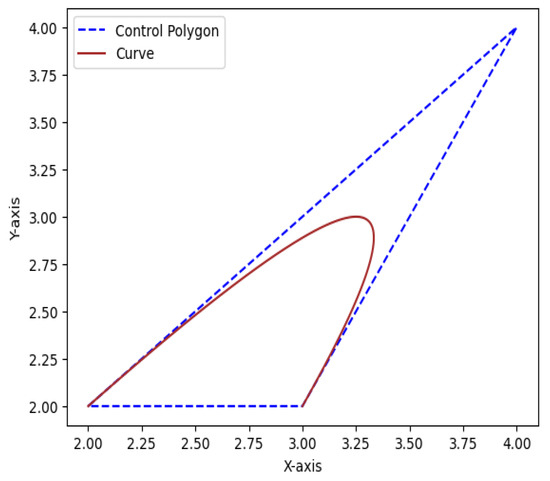
Figure 4.
Classical quadratic Bézier curve.
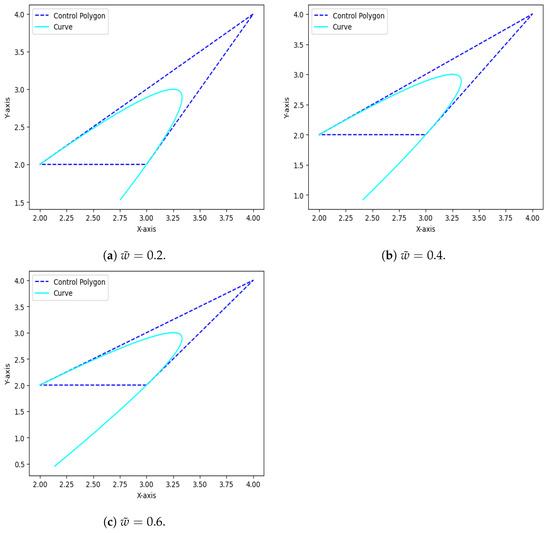
Figure 5.
Quadratic Caputo Fabrizio Bézier curve at , , and .
- iii. Symmetry.
The symmetry characteristics become partially symmetrical when ; hence, the Caputo Fabrizio Bézier curve will keep the same feature as the symmetrical form but on a different scale. It is evident from Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 that the symmetry qualities are fully formed when approaches to 1.
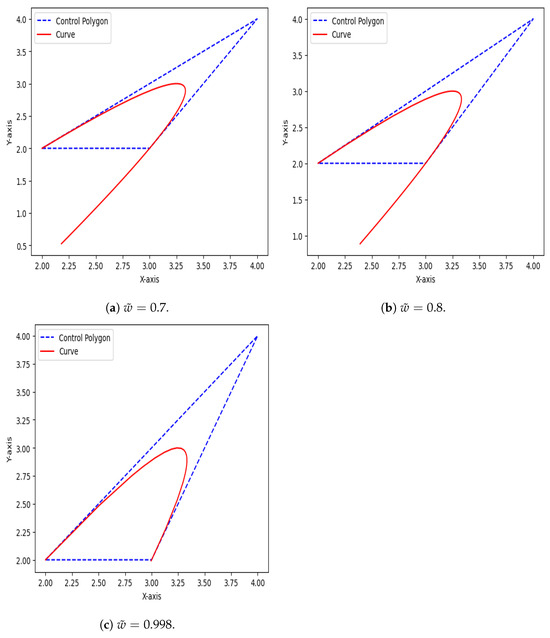
Figure 6.
Quadratic Caputo Fabrizio Bézier curve at , , and .
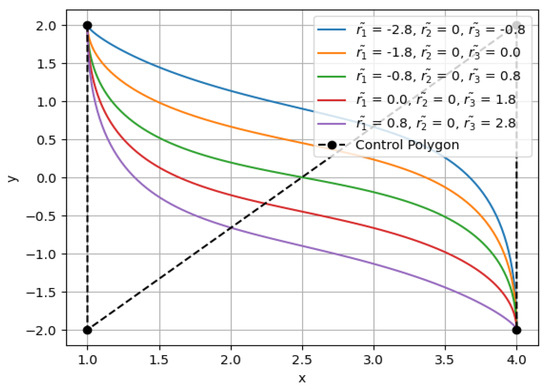
Figure 7.
Classical Cubic Bézier curve.
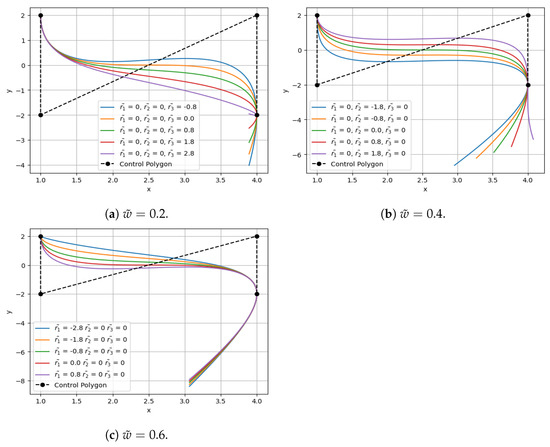
Figure 8.
Cubic Caputo Fabrizio Bézier curves at different values of fractional parameter and shape parameters , , and .
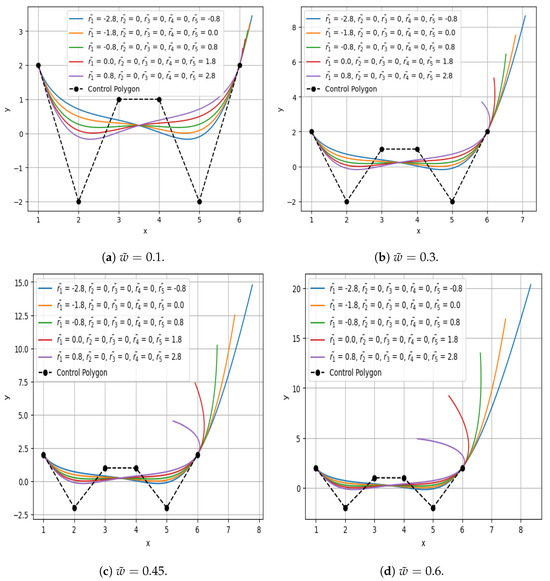
Figure 9.
Quintic Caputo Fabrizio Bézier curves at various values of fractional parameter and shape parameters , , , , and .
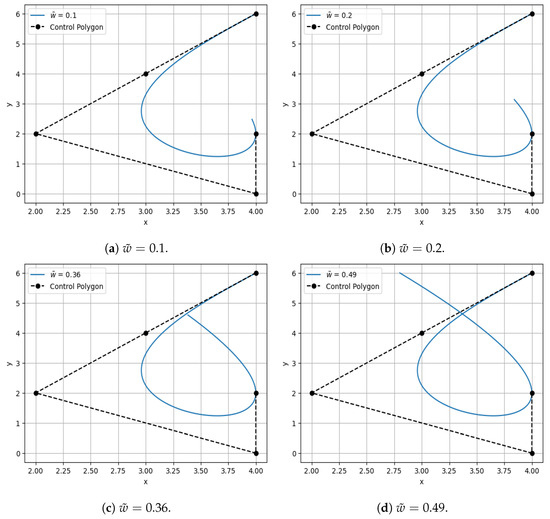
Figure 10.
Quartic Caputo Fabrizio Bézier curves with various values of fractional parameter = 0.1, 0.2, 0.36, and 0.49.
- iv. Geometric invariance.
This property holds for an arbitrary matrix with dimensions m × m (m = 2, 3) and an arbitrary vector in or .
Affine transformations have no effect on Caputo Fabrizio Bézier curves.
- v. Curve’s shape-adjustable property.
There is a conventional Bézier curve located inside the convex hull. A traditional Bézier curve’s disadvantage is that it cannot be changed without changing the control points. To get around this limitation, the Caputo Fabrizio fractional-order Bézier basis functions with shape (form) arguments is used. The number of degrees has an impact on how many form parameters are constructed. The curve’s i-th degree in this instance will have (shape) form parameters. The curve may be made more flexible by employing the different values of without changing the control points.
- vi. Curve’s length-adjustable property.
The disadvantage of the classical Bézier curve is that it is not possible to modify the curve without altering the control points. Caputo Fabrizio Bézier curves can be used to overcome this constraint. Fractional and form parameters are the two categories of parameters for the Caputo Fabrizio Bézier curve. The length of the curve is controlled by a fractional parameter. Section 4 provides more details on this attribute. The created curve’s length is adjusted and managed using the fractional parameter .
Example 1.
From the above Figure 5 and Figure 6, it is clear that the curve length is increased when and decreased when . Specifically, at , the terminal point of the quadratic Caputo Fabrizio Bézier curve (approximately 2.9959, 1.9919) closely aligns with the terminal point (3, 2) of the classical quadratic Bézier curve. This convergence implies that as approaches 1, the endpoint of the quadratic Caputo Fabrizio Bézier curve tends toward that of the classical quadratic Bézier curve. However, it is noteworthy that the quadratic Caputo Fabrizio Bézier curve loses its smoothness beyond , indicating a departure from its smooth trajectory.
Example 2.
Example 3.
Take the values , , , , , and . The quintic Caputo Fabrizio Bézier curves made from various quantities of and are shown in Figure 9.
4. The Curve’s Geometric Effect on Fractional and Shape Parameters
When there are a larger number of control points and they are situated in close contact with each another, the length of the curve becomes gradually difficult to manage; if we attempt to lengthen the curve by modifying the control points, the continuity and smoothness of the curve are affected. The fractional parameter is presented as a solution to this problem. Keeping the control points the same, the length of the Caputo Fabrizio Bézier curve is controlled by its fractional parameter. While retaining the essential features of a Bézier curve, engineers can design the required curve with greater flexibility in length and shape by using the fractional parameter . Figure 10a–d demonstrate how we can lengthen the curve using a fractional parameter without altering the control points. Figure 11 illustrates how the curve’s length can be increased at various values of the fractional parameter while maintaining the same path and control points. The length of the curve is increased when (see Figure 5) and decreased in the range (see Figure 6).
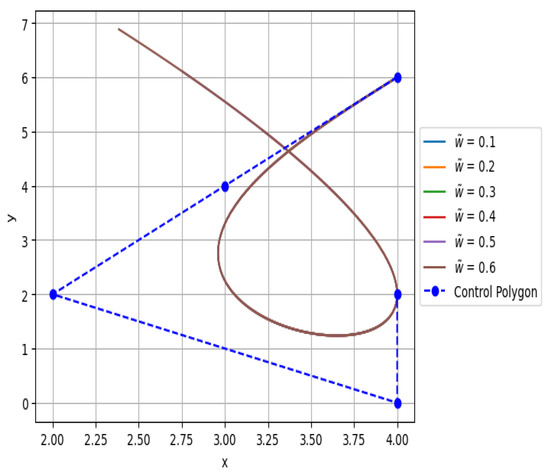
Figure 11.
Quartic Caputo Fabrizio Bézier curves with various values of fractional parameter = 0.1, 0.2, 0.3, 0.4, 0.5, and 0.6.
The option of a curve to modify its shape while maintaining the properties of a conventional Bézier curve and not requiring modifications to its management points has led to a notable increase in the use of shape preservation parameters in CAGD in recent times. Without changing control points, shape parameters are essential for modifying the physical shape of Caputo Fabrizio Bézier curves. The degree of the Caputo Fabrizio Bézier curves is determined by the number of shape parameters it possesses. For example, quartic and quintic Caputo Fabrizio Bézier curves have four and five shape parameters, respectively. Normally, two parameters are associated with the center of the shape, and one parameter is associated with its end. As a result, two control points are linked to one parameter. For , a shape parameter is often associated with the and control points. The curve will converge towards as increases. In Figure 8, shape parameter is linked to and ; the shape parameter is linked to and , and the form parameter is linked to and control points. As rises in value, the curve will move in the direction of point . The result will be the same for and .
5. Construction of Surfaces Using Caputo Fabrizio Bézier Curves
Curves are a useful tool for creating surfaces. Using Caputo Fabrizio Bézier curves, a few basic surface types are produced in this section.
5.1. Surface Revolution
By rotating the created curve around an axis, a surface can be produced from it. The resultant surface, known as the surface of revolution along the specific axis, always possesses azimuthal symmetry. The cubic Caputo Fabrizio Bezier curve used in this work to generate the surface is described as follows:
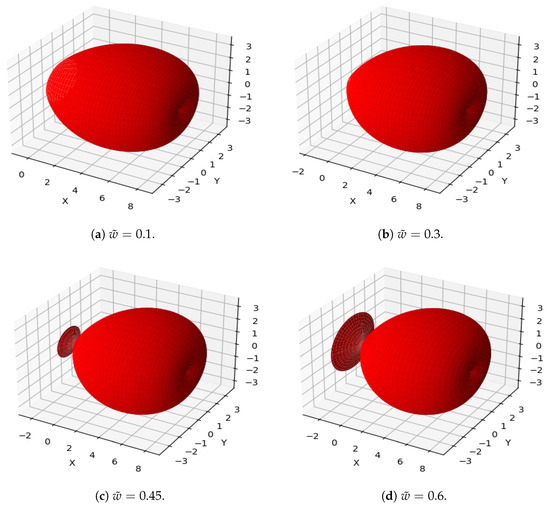
Figure 12.
Surface of revolution of cubic Caputo Fabrizio Bézier curve at various values of fractional parameter .
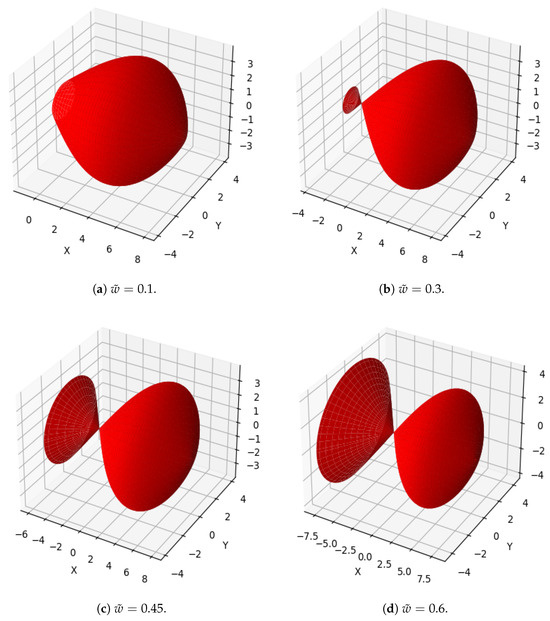
Figure 13.
Surface of revolution of cubic Caputo Fabrizio Bézier curve at various values of and shape parameters , , and .
Example 4.
Let , , , and . By using various values of , , and and along the x axis, a surface of revolution is produced.
5.2. Extruded Surface
A surface that results from extruding a curve along a scalar vector is called an extruded surface. For a Parametric curve in the direction (), an extruded surface is defined as
where is a scalar and a is a vector.
Example 5.
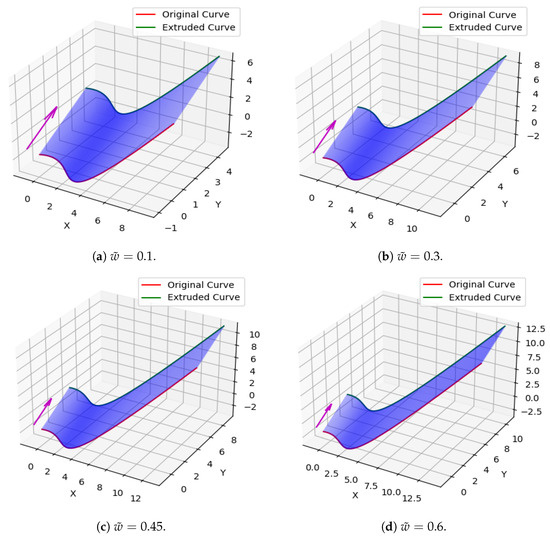
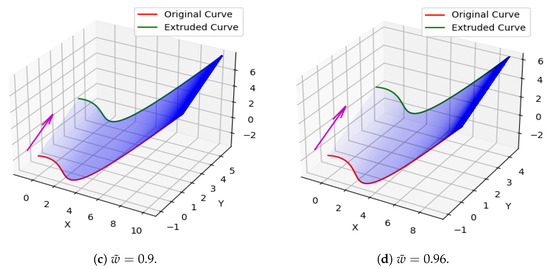
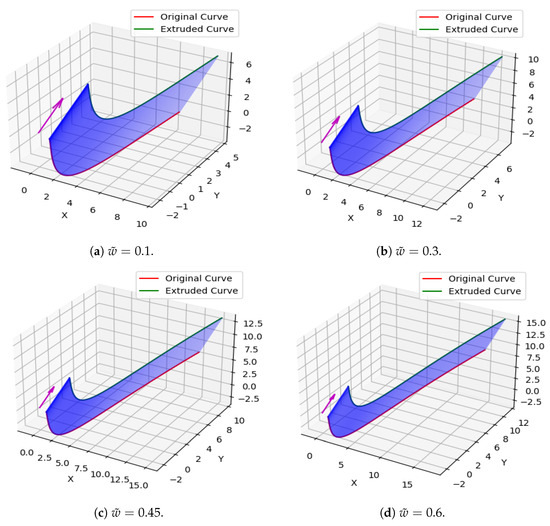
Take , , , and . The surfaces are generated and displayed in Figure 14, Figure 15 and Figure 16 using (13) and the vector for extrusion.

Figure 14.
Extruded surface created by using a cubic Caputo Fabrizio Bézier curve at = 0.1, 0.3, 0.45, 0.6.


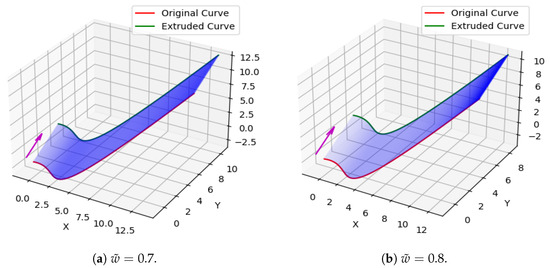
Figure 15.
Extruded surface created by using a cubic Caputo Fabrizio Bézier curve at = 0.7, 0.8, 0.9, 0.96.

Figure 16.
Extruded surface created by using a cubic Caputo Fabrizio Bézier curve at = 0.1, 0.3, 0.45, 0.6 and shape parameters values , , and .
6. Application of Caputo Fabrizio Bézier Curve
Caputo Fabrizio Bézier curves can be used to overcome hurdles in a range of situations, including molecular dynamics, protein folding, and other applications in chemistry and biology, by producing flexible and smooth routes that can go around barriers. The following are some situations in which Caputo Fabrizio Bézier curves can be applied:
- Caputo Fabrizio Bézier curves can be used in molecular dynamics to simulate possible trajectories for a molecule as it travels across a potential energy landscape. In this case, regions of high energy that the molecule must avoid could constitute obstacles.
- Proteins’ smooth folding paths can be modeled using Caputo Fabrizio Bézier curves, which help prevent high-energy misfolded states.
- Caputo Fabrizio Bézier curves can be used in chemical reactions to discover the most efficient path from reactants to products and to navigate potential energy surfaces by avoiding high-energy obstacles.
Figure 17, Figure 18 and Figure 19 show paths that navigate around obstacles, created using quintic Caputo Fabrizio Bézier curves with varying shape and fractional parameters. Obstacles are represented as rectangles. Shape parameters allow manipulation of the curve to follow the desired path, while fractional parameters enable length adjustment without altering control points. This flexibility and length control make Caputo Fabrizio Bézier curves ideal for modeling complex pathways in high-dimensional energy landscapes, efficiently avoiding obstacles.
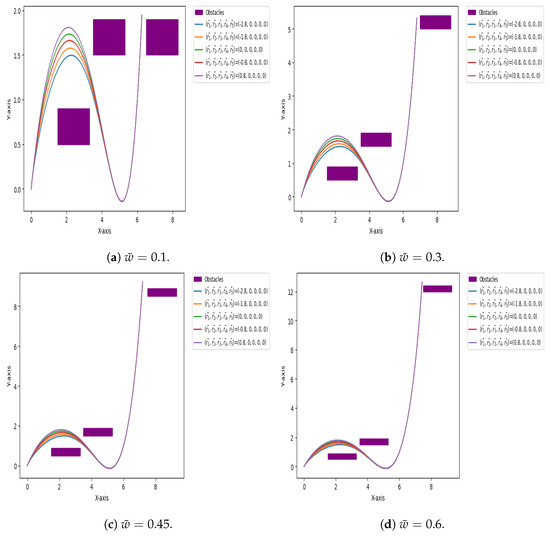
Figure 17.
Paths that navigate around obstacles, created using quintic Caputo Fabrizio Bézier curves with varying shape and fractional parameters.
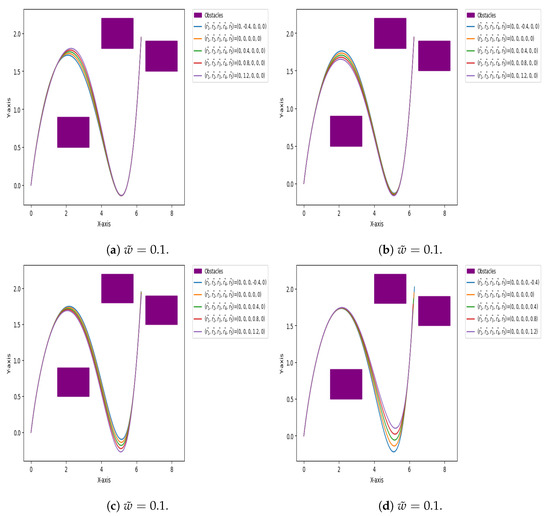
Figure 18.
Paths that navigate around obstacles, created using quintic Caputo Fabrizio Bézier curves at (fractional parameter) and different values of shape parameters , , , , and .
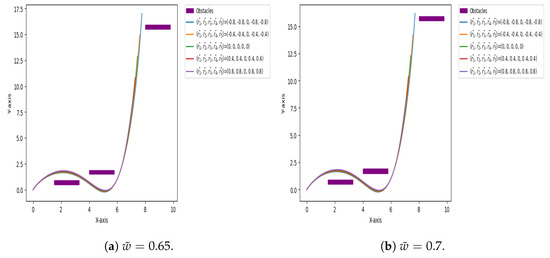
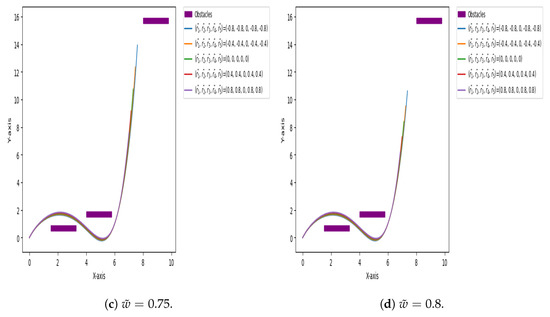
Figure 19.
Paths that navigate around obstacles, created using quintic Caputo Fabrizio Bézier curves at , , , and (fractional parameter) and different values of shape parameters , , , , and .
7. Conclusions
A Caputo Fabrizio Bézier curve incorporating fractional and shape parameters is constructed using the Caputo Fabrizio fractional-order derivative. The length of the curve becomes increasingly challenging to control when there are more control points that are close to one another; if we try to lengthen the curve by changing the control points, it will overshoot and deviate from the curve trajectory. The fractional parameter is presented as a solution to this problem. Keeping the control points the same, the length of the Caputo Fabrizio Bézier curve is controlled by its fractional parameter. Without changing the control points, the curve can be formed in a variety of ways while keeping the characteristics of a traditional Bézier curve by using shape parameters. While retaining the essential features of a Bézier curve, engineers can design the required curve with greater flexibility in length and shape by using the fractional parameter and shape parameters . The fractional parameter very productively controls the optimal length of the curve in the range (). The main advantages of this innovative type of Caputo Fabrizio Bézier curves are its flexibility and elasticity, especially in path and trajectory problems. The Caputo Fabrizio Bézier curves represent an incredibly effective solution to the overshooting issue.
The limitation of the Caputo Fabrizio Bézier curve is that the curve does not remain smooth for values of ; therefore, the results are valid when (). This study can be expanded in the future to address the parametric and geometric continuity of the proposed Caputo Fabrizio Bézier curves.
Author Contributions
Conceptualization, M.A. and S.K.N.K.; methodology, M.A.; software, M.A. and R.A.; validation, M.A. and S.K.N.K.; formal analysis, R.A. and M.R.; writing—original draft preparation, M.A.; visualization, R.A. and M.R.; supervision, S.K.N.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
There is no data set and material involved in this research.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Prautzsch, H.; Boehm, W.; Paluszny, M. Bézier and B-Spline Techniques; Springer: Berlin/Heidelberg, Germany, 2002; Volume 6. [Google Scholar]
- Farin, G.E.; Farin, G. Curves and Surfaces for CAGD: A Practical Guide; Morgan Kaufmann: Burlington, MA, USA, 2002. [Google Scholar]
- Wen-Tao, W.; Guo-Zhao, W. Bézier curves with shape parameter. J. Zhejiang-Univ.-Sci. A 2005, 6, 497–501. [Google Scholar] [CrossRef]
- Han, X. Quadratic trigonometric polynomial curves with a shape parameter. Comput. Aided Geom. Des. 2002, 19, 503–512. [Google Scholar] [CrossRef]
- Han, X. Cubic trigonometric polynomial curves with a shape parameter. Comput. Aided Geom. Des. 2004, 21, 535–548. [Google Scholar] [CrossRef]
- Yang, L.; Zeng, X.M. Bézier curves and surfaces with shape parameters. Int. J. Comput. Math. 2009, 86, 1253–1263. [Google Scholar] [CrossRef]
- Hu, G.; Wu, J.; Qin, X. A novel extension of the Bézier model and its applications to surface modeling. Adv. Eng. Softw. 2018, 125, 27–54. [Google Scholar] [CrossRef]
- Maqsood, S.; Abbas, M.; Hu, G.; Ramli, A.L.A.; Miura, K.T. A novel generalization of trigonometric Bézier curve and surface with shape parameters and its applications. Math. Probl. Eng. 2020, 2020, 4036434. [Google Scholar] [CrossRef]
- Ramanantoanina, A.; Hormann, K. New shape control tools for rational Bézier curve design. Comput. Aided Geom. Des. 2021, 88, 102003. [Google Scholar] [CrossRef]
- Bulut, V. Path planning of mobile robots in dynamic environment based on analytic geometry and cubic Bézier curve with three shape parameters. Expert Syst. Appl. 2023, 233, 120942. [Google Scholar] [CrossRef]
- Ammad, M.; Misro, M.Y.; Ramli, A. A novel generalized trigonometric Bézier curve: Properties, continuity conditions and applications to the curve modeling. Math. Comput. Simul. 2022, 194, 744–763. [Google Scholar] [CrossRef]
- Ammad, M.; Misro, M.Y. Construction of local shape adjustable surfaces using quintic trigonometric Bézier curve. Symmetry 2020, 12, 1205. [Google Scholar] [CrossRef]
- Omar, A.; Ahmed, I.; Abuzaiyan, F. The Quadratic Trigonometric Bézier like Curve with two Shape Parameters. J. Pure Appl. Sci. 2023, 22, 215–221. [Google Scholar]
- Ziatdinov, R.; Yoshida, N.; Kim, T.W. Fitting G2 multispiral transition curve joining two straight lines. Comput.-Aided Des. 2012, 44, 591–596. [Google Scholar] [CrossRef]
- Qin, X.; Shen, X.; Yang, Y. A novel extension to the polynomial basis functions describing Bézier curves and surfaces of degree n with multiple shape parameters. Appl. Math. Comput. 2013, 223, 1–16. [Google Scholar] [CrossRef]
- Bashir, U.; Abbas, M.; Ali, J.M. The G2 and C2 rational quadratic trigonometric Bézier curve with two shape parameters with applications. Appl. Math. Comput. 2013, 219, 10183–10197. [Google Scholar] [CrossRef]
- Bibi, S.; Abbas, M.; Miura, K.T.; Misro, M.Y. Geometric modeling of novel generalized hybrid trigonometric Bézier-like curve with shape parameters and its applications. Mathematics 2020, 8, 967. [Google Scholar] [CrossRef]
- Debnath, L. Recent applications of fractional calculus to science and engineering. Int. J. Math. Math. Sci. 2003, 2003, 3413–3442. [Google Scholar] [CrossRef]
- Sebaa, N.; Fellah, Z.E.A.; Lauriks, W.; Depollier, C. Application of fractional calculus to ultrasonic wave propagation in human cancellous bone. Signal Process. 2006, 86, 2668–2677. [Google Scholar] [CrossRef]
- Sun, H.; Zhang, Y.; Baleanu, D.; Chen, W.; Chen, Y. A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonlinear Sci. Numer. Simul. 2018, 64, 213–231. [Google Scholar] [CrossRef]
- Baleanu, D.; Jajarmi, A.; Mohammadi, H.; Rezapour, S. A new study on the mathematical modelling of human liver with Caputo–Fabrizio fractional derivative. Chaos Solitons 2020, 134, 109705. [Google Scholar] [CrossRef]
- Arora, S.; Mathur, T.; Agarwal, S.; Tiwari, K.; Gupta, P. Applications of fractional calculus in computer vision: A survey. Neurocomputing 2022, 489, 407–428. [Google Scholar] [CrossRef]
- De Oliveira, E.C.; Tenreiro Machado, J.A. A review of definitions for fractional derivatives and integral. Math. Probl. Eng. 2014, 2014, 1–7. [Google Scholar] [CrossRef]
- Li, X. Numerical solution of fractional differential equations using cubic B-spline wavelet collocation method. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 3934–3946. [Google Scholar] [CrossRef]
- Kirmani, S.; Bilal Riaz, M. Shape preserving fractional order KNR C1 cubic spline. Eur. Phys. J. Plus 2019, 134, 319. [Google Scholar] [CrossRef]
- Said Mad Zain, S.A.A.A.; Misro, M.Y.; Miura, K.T. Generalized fractional Bézier curve with shape parameters. Mathematics 2021, 9, 2141. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Tan, J. The Mechanical Meaning of Bernstein Basis Function. Int. J. Appl. Math. Control. Eng. 2018, 1, 47–54. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).