Abstract
The modeling of real objects digitally is an area that has generated a high demand due to the need to obtain systems that are able to reproduce 3D objects from real objects. To this end, several techniques have been proposed to model objects in a computer, with the fringe profilometry technique being the one that has been most researched. However, this technique has the disadvantage of generating Moire noise that ends up affecting the accuracy of the final 3D reconstructed object. In order to try to obtain 3D objects as close as possible to the original object, different techniques have been developed to attenuate the quasi/periodic noise, namely the application of convolutional neural networks (CNNs), a method that has been recently applied for restoration and reduction and/or elimination of noise in images applied as a pre-processing in the generation of 3D objects. For this purpose, this work is carried out to attenuate the quasi/periodic noise in images acquired by the fringe profilometry technique, using a modified CNN-Multiresolution network. The results obtained are compared with the original CNN-Multiresolution network, the UNet network, and the FCN32s network and a quantitative comparison is made using the Image Mean Square Error E (IMMS), Peak Signal-to-Noise Ratio (PSNR), Structural Similarity Index (SSIM), and Profile (MSE) metrics.
Keywords:
3D object; computer vision; CNN; fringe profilometry; filter; Moire noise; PSNR; synthetic objects 1. Introduction
Sensors and cameras detect the world in two dimensions and without depth, unlike humans who perceive the world in three dimensions and with depth, thus detecting details of the surrounding world. However, modern techniques make it possible to obtain 3D information from objects by means of sensors and cameras, thus observing the surrounding world with near-realistic accuracy. One of these techniques is to obtain 3D information of objects by means of 2D images using phase shift profilometry (PSP) on objects [1,2]. However, this technique produces noise in the images, known as Moire noise, due to the use of a fringe pattern projected on the object, which affects the accuracy and final reconstruction of the object to be reconstructed and the extraction of 3D information [3,4]. The reduction and/or elimination of periodic or quasi/periodic noise, known as Moire noise, began as soon as the first digital images could be obtained; however, it was not until it was analyzed as to how such noise was produced that research began on ways to attenuate or eliminate it from the images. Once the noise present in the images was analyzed, it was found that they are formed in a repetitive pattern, and that they are of different nature, as is shown in Figure 1. Recent techniques make use of deep learning to deal with restoration of images. A deep learning model is a set of layers made up of linearly stacked neurons and are widely used in different areas, such as computer vision tasks, language processing, signal processing, and time series processing, among others [5,6,7,8,9,10,11,12]. Convolutional neural networks are a type of deep learning model for computer vision tasks, and have many applications in this field, since their potential has been demonstrated in areas of low-level computer vision and image processing tasks. Many of these tasks involve object recognition, classification, segmentation, restoration, and image denoising and/or attenuation [13,14,15,16,17,18,19,20]. In this paper, we propose and compare a filter based on a deep convolutional neural network to reduce the quasi/periodic noise in images affected by this noise as pre-processing of images, in the 3D reconstruction of objects by means of fringe profilometry. The deep learning network proposed in this article was based on the Multiresolution-CNN proposed by Sun [21] for periodic noise reduction in digital images, using as a comparison the same network used as the original Multiresolution-CNN base, the UNet network [22], and the FCN32s network [23], whose characteristics will be described below. The results obtained will be described, along with a brief discussion, in Section 3, and the conclusions will be presented in Section 4. It should be noted that two experiments were carried out: the first one with the parameters of their respective authors adapted to the task of denoising, and the second one with the best parameters reached and adjusted to each CNN model to make a fair comparison.

Figure 1.
Images with different type of periodic noise. (a) Image without noise. (b) Image with periodic noise. (c) Image with quasi/periodic noise.
2. Materials and Methods
The development of the fringe profilometry system emulation environment, the training of the proposed Convolutional Neural Network (CNN), and the CNNs used for comparison are performed on a personal computer with an I7-10750H processor @2.60 GHz, with 16 Gb of RAM and an NVIDIA GeForce RTX 3060 graphics card with 6 Gb of RAM. The experiments and tests were also performed with the above mentioned computer and Matlab 2020a. The images used for the experiments were created by emulating a 3-step fringe profilometry system in the open source software Blender, version 2.95.5. The fringe projector is represented by a lamp, while the camera has a focal length setting of 28 mm [24]. The 3D object models used are acquired from platforms such as TurboSquid, which are also free to use. To perform the training, the 345 images were divided in proportion of 70% for training, 10% for validation and 20% for testing, following the methodology proposed by Sun [21]. Some images of the database can be seen in Figure 2; both the image with quasi/periodic noise and its corresponding target image preprocessed with the algorithm developed to attenuate the quasi/periodic noise, which is shown in detail in Section 2.1.
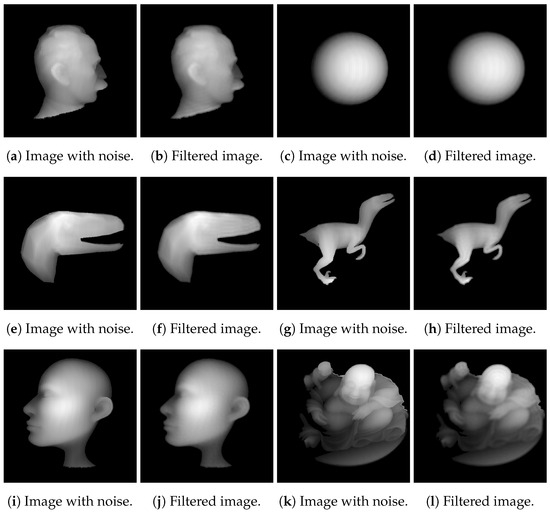
Figure 2.
Database images generated for Convolutional Neural Network (CNN) training.
Figure 3 indicates the steps followed to prepare the database of images, the sets of training, validation, and testing, and the procedure performed for each convolutional neural network architecture used.
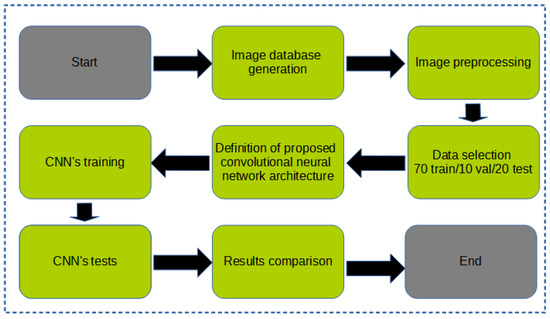
Figure 3.
Methodology used.
2.1. Pre-Processing of Database Images
Once the images necessary for the training of the CNNs have been obtained, it is necessary to pre-process them in order to obtain the set of images used as source and target. To achieve this, a phase unwrapping algorithm is used to obtain the absolute phase to obtain the source set. A filtering algorithm is then applied to obtain the set of images to be used as target images [25]. The methodology shown in Figure 4 shows the steps followed to filter and remove quasi/periodic noise using an adaptive filtering algorithm based on the frequency domain (ATBF) [26] as a basis.
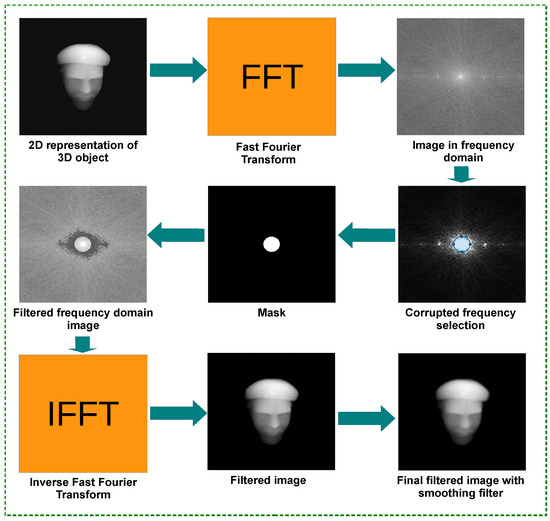
Figure 4.
Methodology used to remove noise from the images created in the database.
In summary, the step series are described below:
- An absolute phase image is obtained by an unwrapping algorithm which contains the 3D information of an object or surface in the spatial domain.
- The absolute phase image is transformed to the frequency domain using the fast Fourier transform.
- A convolution with a Laplacian kernel of size is applied to the image in the frequency domain to highlight the pixels that contain corrupted frequencies.
- A second image is created from the original frequency domain image as a mask, in order to preserve the central region which contain most of information of the image.
- After the convolution, the pixels with frequencies corrupted are replaced by the mean of their neighbors pixels, and the mask is applied to recover the original central region completing with this the process of filtering.
- An inverse fast Fourier transform is then applied to the frequency domain image filtered to obtain an image in the spatial domain.
- The filtered image in the spatial domain it is then processed by a smoothing filter in order to reduce the noise remaining.
- Finally, a filtered image from an image with quasi/periodic noise is added to a database.
A detailed explanation can be found in our previous work [25].
2.2. Construction of Convolutional Neural Network Model
Three Convolutional Neural Networks, in addition to the proposed one based on the Multiresolution-CNN [21], were evaluated, and two experiments were carried out.
In the first experiment, the features proposed by the original author of each Convolutional Neural Network were used, which are summarized in Table 1. U-Net, FCN32s, and Multiresolution-CNN [21] while similar to Multiresolution-CNN in the proposed model, changed the size of images and the input based in grayscale.

Table 1.
Hyperparameters used during training of networks for comparison.
The U-Net and FCN32s architecture used in this work were used in the same way as the original authors, changing the hyperparameters to be adapted to infer complete images instead of segmented images. This was obtained by changing the optimizer, training and validation loss, and using the target and as an output and a convolution instead of classification, as can be observed in Figure 5 and Figure 6. The Multiresolution-CNN and Modified Multiresolution-CNN models preserved the hyperparameters proposed by Sun et al. [21], because they demonstrated the best performance with these hyperparamters.
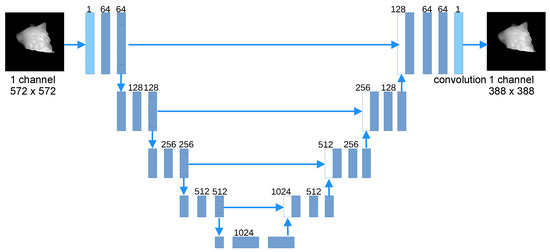
Figure 5.
U-Net network architecture [22].
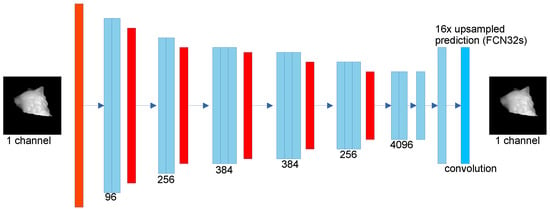
Figure 6.
FCN32s network architecture [23].
Finally, all inferences were cropped to the size of the inference produced by the U-Net network, because the original architecture produces a image of size pixels so as to make a fair comparison, and the cut was made from the center of the image. The optimizer RMSprop() [27,28] was used for the U-Net and FCN32s models,
where E is the error and w, the weight change. The gist of RMSprop is to maintain a moving average of the square gradients and divide the gradient by the root of this average. The optimizer Adam() was the hyperparameter used for Multiresolution-CNN and Modified Multiresolution-CNN,
where is the gradient evaluated a timestep t, is the moving average, is the squared gradient, and and are the decay rates for the moment estimates. Optimizer Adam is based on adaptive estimation of first-order and second-order moments, and is computationally efficient and has little memory requirements [27,29].
The MSELoss() function [30] was used to calculate the training and validation loss for models U-Net, Mutiresolution-CNN, and Modified Multiresolution-CNN
where N is the batch size, x and y are tensors of arbitrary shapes with a total of n elements each.
The second experiment was carried out proposing similar hyperparameters, which are summarized in Table 2, so as to make a fair comparison and so as to obtain the best results from each Convolutional Neural Network model trained.

Table 2.
Parameters used during network training for comparison.
2.3. U-Net Network
The U-Net convolutional network is a network commonly used for segmentation tasks. This network takes advantage of the use of data augmentation to perform the segmentation task using a limited number of images and achieving good results. The architecture of the network shows a shrinking path to capture the context of the feature map and an asymmetric expansion path that enables accurate feature localization. The U-Net network was originally created for segmentation tasks in the biomedical area, having achieved its purpose with a limited number of images; however, the authors claim that it can be useful for other tasks [22]. The architecture of the U-Net network used in this work is shown in Figure 5.
2.4. FCN32s Network
The FCN32s network is a Convolutional Neural Network that takes a deep learning network model for classification, and uses that classification to produce a feature map that allows for image segmentation. The vision of the creators was to take a network that would allow for classification of any given image size and be able to perform inference with good efficiency. The network comprises a hop that adds to the VGG16 network a FCN in order to segment according to the results obtained directly from the output of the classification network [23]. The network architecture used is shown in Figure 6.
2.5. Multiresolution-CNN
The Mutiresolution Convolutional Neural Network is a fully convolutional network trained to remove Moire pattern noise from photos by nonlinear analysis at different resolutions from a contaminated input image before calculating how to cancel the Moire artifacts in each frequency band present in the image. The neural network is intended to eliminate Moire noise in images acquired by cellular phones taken from screens, in which Moire noise is produced at different frequencies due to the difference between the camera sensor and the pixels displayed on the screens [21]. The image in Figure 7 shows the architecture of the Multiresolution convolutional network adapted to this work.
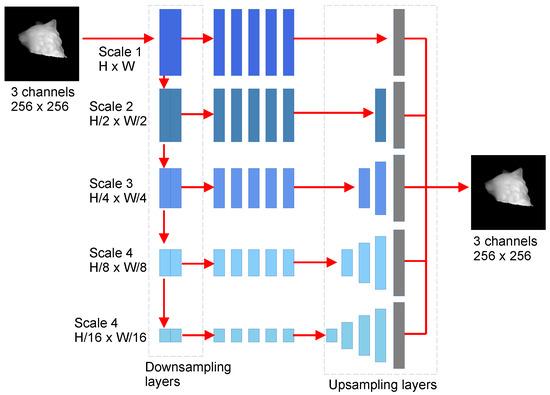
Figure 7.
Multiresolution network architecture [21].
2.6. Modified Multiresolution-CNN Network Proposed
The proposed network for pre-processing images with quasi/periodic noise is based on the network proposed by Sun [21], adding an extra layer that receives images from one (1) kernel of and a single channel, and another layer of similar characteristics at the output, in order to keep the original network intact. The network architecture is shown in Figure 8.
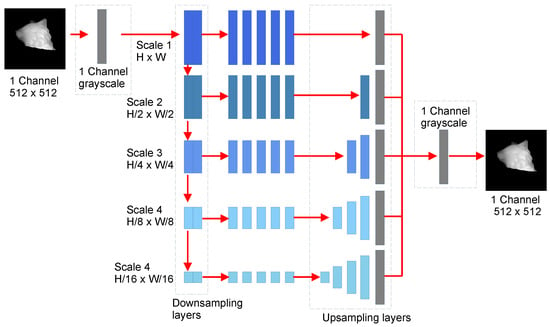
Figure 8.
Proposed Modified Multiresolution-CNN Network Architecture.
3. Results and Discussion
The experiments were carried out using the parameters proposed by their respective authors. However, it should be noted that for the UNet network [22] and FCN32s network [23], some parameters were changed from those that the optimizer originally used, while the proposed Modified Multiresolution network and the Multiresolution-CNN network [21] used the parameters of the latter, only changing the architecture of the modified network. Instead of using an optimizer to measure the pixel classification performance, a more convenient optimizer was used for both cases to measure the noise difference between the quasi/periodic noisy image and the target image. In addition, for this first training and experiment, the pre-trained weights of the VGGNet network were used. As a second experiment, it was performed with the parameters that obtained the best result of the proposed CNN network architecture, and would be adjusted to the other CNN models for comparison.
3.1. Experiment 1: Parameters Proposed by the Authors of Each CNN
The hyperparameters used in each convolutional neural network for the first experiment are shown in Table 1.
The training was performed with 50 epochs, in which the model was saved if the resulting loss function was lower than the previously obtained value, and was strongly penalized otherwise. The graphs in Figure 9 show the evolution of the training loss and validation loss of the four trained CNN models, scaled logarithmically for a better appreciation of the loss.
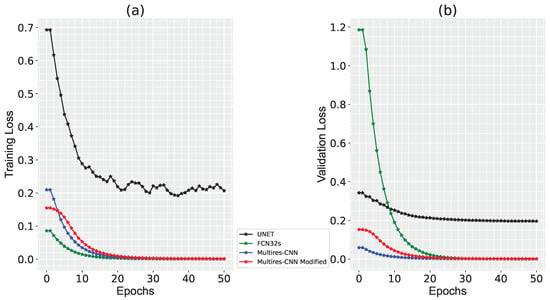
Figure 9.
Evolution of (a) training loss and (b) validation loss.
The graphs in Figure 10 show the evolution of the training and validation loss for each trained CNN. It can be seen how these values evolve as expected to be able to make correct inferences in the case of the Multiresolution [21] and Modified Multiresolution networks. That is, the model fits the training set correctly, and the loss decreases as when validation is performed, so when testing the newly trained model, the inference error is minimal.
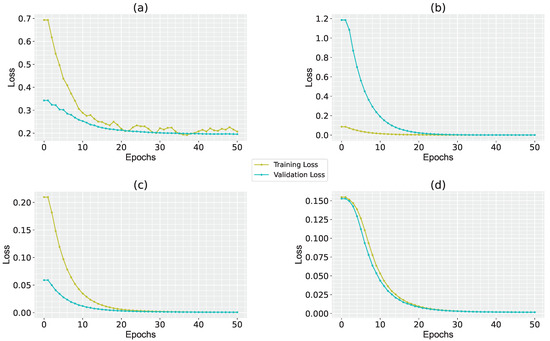
Figure 10.
Evolution of training and validation loss for (a) U-Net model, (b) FCN32s model, (c) Multiresolution-CNN, and (d) Multiresolution-CNN Modified.
The results of applying the trained models of the networks to images contaminated with quasi/periodic noise obtained by fringe profilometry show superior performance when performing inference in the case of Multiresolution [21] and Modified Multiresolution networks. This is achieved by attenuating the noise present in the images, in addition to the fact that the loss of object information is lower, as shown in the images in Figure 11. Although the evolution of the losses shows a strange behavior in some models during training, these are taken into account, because an evaluation of their performance is made not only considering this evolution and the loss achieved by them, but also the quantitative and visual metrics, with the latter being the most important, since it is intended to generate an inference as close as possible to the 3D object to be reconstructed.

Figure 11.
Close-up view of 3D objects after processing with multiple CNNs and object with quasi/periodic noise. (a) 2D representation of filtered object using UNet model. (b) 2D representation of filtered object using FCN32s model. (c) 2D representation of filtered object using Multires-CNN model. (d) 2D representation of filtered object using Modified Multires-CNN model. (e) 2D representation of object with noise. (f) 2D representation of original object.
The training and validation loss values and training time for each model are shown in Table 3. It is observed that the training time is a little more than 19 min for the Multires-CNN model, and a little more than 21 min for the Modified Multires-CNN case; however, better inferences are produced for the latter model.

Table 3.
Training results with proposed convolutional neural network and CNNs for comparison.
After obtaining the inferences with the different trained models, the figures are scaled [31] in order to obtain a height estimation and perform measurements such as profile analysis, which allows us to quantify the similarity between the inferences obtained and the original 3D object. The reconstruction of the 3D object is shown in Figure 12, in which Figure 12d shows a greater similarity and smoothness in shape, contrary to Figure 12a–c.
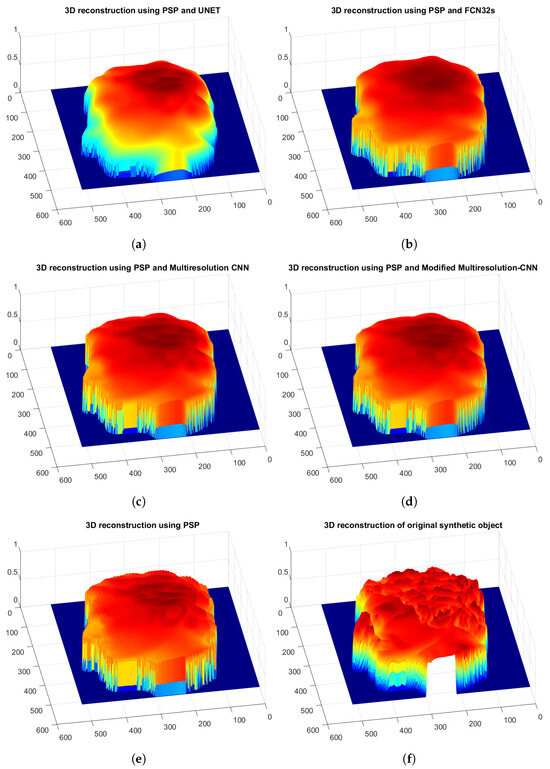
Figure 12.
Close-up view of 3D objects after processing with multiple CNNs and objects with quasi-periodic noise. (a) 3Dç reconstruction of filtered object using UNet model. (b) 3D reconstruction of filtered object using FCN32s model. (c) 3D reconstruction of filtered object using Multiresolution-CNN model. (d) 3D reconstruction of filtered object using Modified Multiresolution-CNN model. (e) 3D reconstruction of object with noise. (f) 3D reconstruction of original object.
A profile analysis shows that the inference generated by the proposed network model approximates the original 3D object, as well as presenting a smoother shape, as shown in the profiles shown in Figure 13. Also shown are the profiles of the compared CNNs, the profile of the original object and the profile contaminated with quasi-periodic noise.
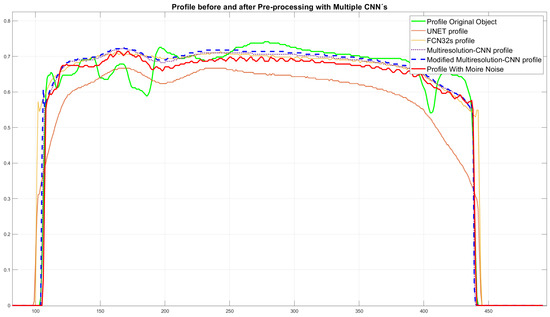
Figure 13.
Profile analysis of the inferred objects using CNNs, the original object, and the object contaminated with quasi/periodic noise.
The quantitative results are shown in Table 4, and were obtained using the image of the original 3D object. The measurements were performed using the inferences obtained by the trained CNNs and cropping those inferences to the smaller size that is obtained by the UNet Network [22], as shown in Figure 11a, in order to obtain the same regions to be compared.

Table 4.
Quantitative results of the proposed and compared training networks.
3.2. Experiment 2: Best Parameters Obtained with the Proposed Convolutional Neural Network and Applied to the Other CNNs
The parameters used in each convolutional neural network for the second experiment are shown in Table 2.
The training progress and validation loss shown in the graphs in Figure 14 demonstrate that the model training is more consistent with what was expected, which means that the models fit the training set better, generating better inferences than those generated in the previous experiment.
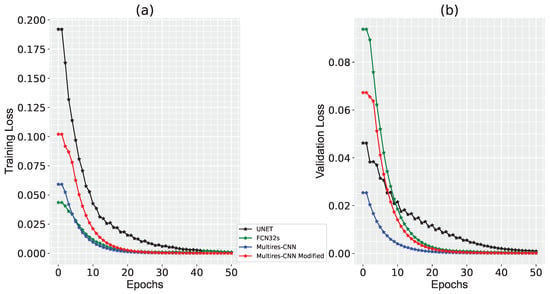
Figure 14.
Evolution of training and validation loss.
The evolution of loss by validation and training of each CNN shows a behavior whereby the model fits better with the hyperparameters selected as the general ones for the four models; in addition, it is observed that there is no overtraining or undertraining, and that the value of the losses tends to reduce, as expected when training a CNN, thus improving the generated inferences. The graphs in Figure 15 show this evolution for each CNN.
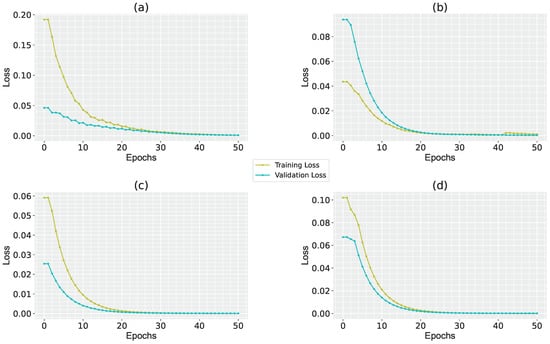
Figure 15.
Evolution of training and validation loss for (a) U-Net model, (b) FCN32s model, (c) Multiresolution-CNN, and (d) Multiresolution-CNN Modified.
As in the previous experiment, we obtained the generated inferences shown in their 2D representation, as shown in the images in Figure 16. With the new parameters, a considerable change is observed in the generated inferences, generating complete objects and better preserving the information; however, there is still a loss of information in the inferences generated by the UNet network [22] and FCN32s [23], as shown in Figure 16a,b.

Figure 16.
Close-up view of objects after inferences made with multiple convolutional neural networks, object with quasi/periodic noise and original object. (a) 2D representation of filtered object using UNet model. (b) 2D representation of filtered object using FCN32s model. (c) 2D representation of filtered object using Multiresolution-CNN model. (d) 2D representation of filtered object using Modified Multiresolution-CNN model. (e) 2D representation of object with noise. (f) 2D representation of original object.
The training and validation loss values, as well as the training time for each model obtained in this experiment, are shown in Table 5.

Table 5.
Training results of proposed network model and comparison network models.
The reconstructions of the 3D objects performed with the inferences obtained from the application of the trained models show a closer and smoother reconstruction in the case of the Multiresolution-CNN [21] and Modified Multiresolution-CNN models, as can be seen in Figure 17.
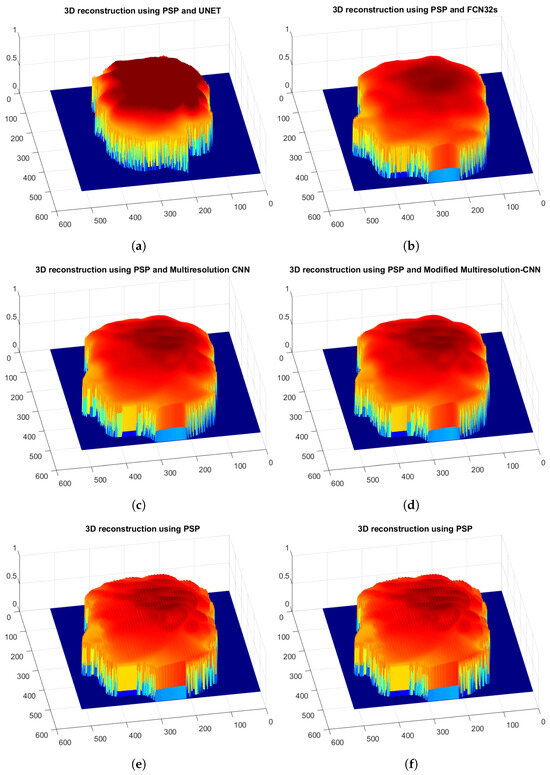
Figure 17.
Close-up view of 3D objects after inferences made with multiple convolutional neural networks, object with quasi/periodic noise and original object. (a) 3D reconstruction of filtered object using UNet model. (b) 3D reconstruction of filtered object using FCN32s model. (c) 3D reconstruction of filtered object using Multiresolution-CNN model. (d) 3D reconstruction of filtered object using Modified Multiresolution-CNN model. (e) 3D reconstruction of object with noise. (f) 3D reconstruction of original object.
A profile analysis performed shows the smoothness formed by the inference generated by the proposed trained model, as shown in Figure 18.
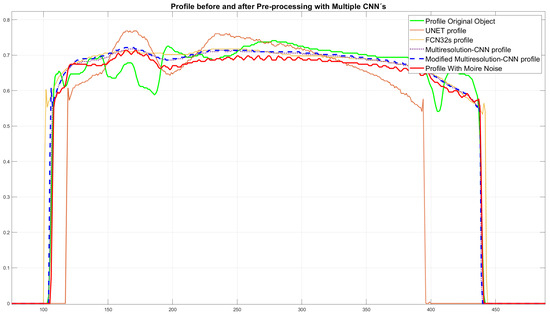
Figure 18.
Profile analysis of the inferred objects using CNNs, original object and object contaminated with quasi/periodic noise.
The metrics obtained in this experiment with equal parameters in the selected CNN models and the proposed CNN model are shown in Table 6.

Table 6.
Training results of proposed CNN model and comparison CNN models.
4. Conclusions
It can be observed from the 3D reconstructions of the object shown in Figure 12, as an example, and which is similar to the human face, that the inference made by the proposed Modified Multiresolution-CNN in experiment 1 is closer to the original object, changing the size of the image to be processed for the model trained and the change to accept a grayscale image. Besides attenuating the quasi/periodic noise present better than the other networks used as a comparison, it is able to better preserve the details of the objects and the whole object. Although it obtained a lower performance in the similarity index metric (SSIM) with the original object, the lower errors obtained both the mean error (IMMSE) of the compared images and the mean error of profile (MSE(Profile)), these indices indicate that the object is more similar to the original object; in addition, the profile analysis shows an inference of the object smoother and closer to the profile of the original 3D object. All this is by performing the training with the best parameters for each CNN model according to how they were originally proposed, and with small changes in order to adapt them to attenuate noise in images. On the other hand, observing the training evolution, it is concluded that the models learn to correctly infer images in the case of the proposed network model and the network model on which it was based, because it produces low training and validation loss values close to what is expected, and can be seen in the graphs, which shows that the ability to erroneously infer 3D objects with the training set provided is low, so that the models fit well to the training.
In experiment 2, the same parameters were used to perform the training in order to equalize conditions; the quantitative results were not favorable in the developed Modified Multiresolution-CNN model; however, it can be observed visually that the inferred object is still superior to the other models, and that even two of the compared models lose object information.
Finally, it is concluded that the lack of data used as a ground truth was not a problem, because was developed an algorithm [25] that preprocesses the images with quasi/periodic noise, and allow us to create a complete database, with sources and ground truth, to train the CNN models. Also, using existing models in the literature for image processing, it is possible to use them as pre-processing of images for 3D object reconstruction from synthetically created images [24], and with a reduced number of them which, however, was not an impediment to perform the training, achieving the objective of attenuating the noise produced during the acquisition of images for reconstruction. Another point to highlight is the time taken for the training of the models being very low in the case of the model that was used as a base and the proposed one producing very similar inferences visually with the real object to be reconstructed, thus this objective was successfully achieved.
Author Contributions
Conceptualization, O.A.E.-B., J.C.P.-O., M.A.A.-F., V.M.M.-S., S.T.-A., J.M.R.-A. and E.G.-H.; methodology, O.A.E.-B.; software, O.A.E.-B.; validation, J.C.P.-O.; formal analysis, J.C.P.-O.; investigation, O.A.E.-B. and V.M.M.-S.; data curation, O.A.E.-B.; writing—original draft preparation, O.A.E.-B.; writing—review and editing, J.C.P.-O., M.A.A.-F., V.M.M.-S., S.T.-A., J.M.R.-A. and E.G.-H.; supervision, J.C.P.-O., M.A.A.-F., V.M.M.-S., S.T.-A., J.M.R.-A. and E.G.-H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
This work was supported in part by the Consejo Nacional de Humanidades, Ciencias y Tecnologías (CONAHCYT), México, in the Postgraduate Faculty of Engineering by the Universidad Autonoma de Querétaro, under Grant CVU 1099050 and CVU 1099400.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- An, H.; Cao, Y.; Zhang, Y.; Li, H. Phase-shifting temporal phase unwrapping algorithm for high-speed fringe projection profilometry. IEEE Trans. Instrum. Meas. 2023, 72, 1–9. [Google Scholar] [CrossRef]
- Zhu, Z.; Li, M.; Zhou, F.; You, D. Stable 3D measurement method for high dynamic range surfaces based on fringe projection profilometry. Opt. Lasers Eng. 2023, 166, 107542. [Google Scholar] [CrossRef]
- Wang, J.; Yang, Y.; Xu, P.; Liu, J. Noise-induced phase error comparison in multi-frequency phase-shifting profilometry based on few fringes. Opt. Laser Technol. 2023, 159, 109034. [Google Scholar] [CrossRef]
- Cai, B.; Tong, C.; Wu, Q.; Chen, X. Gamma error correction algorithm for phase shift profilometry based on polar angle average. Measurement 2023, 217, 113074. [Google Scholar] [CrossRef]
- Chollet, F. Deep Learning with Python; Manning: Shelter Island, NY, USA, 2021. [Google Scholar]
- Otter, D.W.; Medina, J.R.; Kalita, J.K. A survey of the usages of deep learning for natural language processing. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 604–624. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Ji, X.; Ji, W.; Tian, Y.; Zhou, H. CASR: A context-aware residual network for single-image super-resolution. Neural Comput. Appl. 2020, 32, 14533–14548. [Google Scholar] [CrossRef]
- Ismail Fawaz, H.; Forestier, G.; Weber, J.; Idoumghar, L.; Muller, P.A. The title of the cited article. Data Min. Knowl. Discov. 2019, 33, 917–963. [Google Scholar] [CrossRef]
- Liu, Z.; Xu, W.; Feng, J.; Palaiahnakote, S.; Lu, T. Context-aware attention LSTM network for flood prediction. In Proceedings of the 2018 24th International Conference on Pattern Recognition (ICPR), Beijing, China, 20–24 August 2018; pp. 1301–1306. [Google Scholar]
- Naira, C.A.T.; Jos, C. Classification of people who suffer schizophrenia and healthy people by EEG signals using deep learning. Int. J. Adv. Comput. Sci. Appl. 2019, 10. [Google Scholar] [CrossRef]
- Hu, H.; Wang, H.; Bai, Y.; Liu, M. Determination of endometrial carcinoma with gene expression based on optimized Elman neural network. Appl. Math. Comput. 2019, 341, 204–214. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25. Available online: https://proceedings.neurips.cc/paper/2012/hash/c399862d3b9d6b76c8436e924a68c45b-Abstract.html (accessed on 20 May 2024). [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Learning a deep convolutional network for image super-resolution. In Computer Vision—ECCV 2014: 13th European Conference; Springer International Publishing: Zurich, Switzerland, 2014; pp. 184–199. [Google Scholar]
- Gharbi, M.; Chaurasia, G.; Paris, S.; Durand, F. Deep joint demosaicking and denoising. ACM Trans. Graph. (ToG) 2016, 35, 1–12. [Google Scholar] [CrossRef]
- Zhang, K.; Zuo, W.; Gu, S.; Zhang, L. Learning deep CNN denoiser prior for image restoration. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 3929–3938. [Google Scholar]
- Zhang, K.; Zuo, W.; Chen, Y.; Meng, D.; Zhang, L. Beyond a gaussian denoiser: Residual learning of deep cnn for image denoising. IEEE Trans. Image Process. 2017, 26, 3142–3155. [Google Scholar] [CrossRef] [PubMed]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Sun, Y.; Yu, Y.; Wang, W. Moiré photo restoration using multiresolution convolutional neural networks. IEEE Trans. Image Process. 2018, 27, 4160–4172. [Google Scholar] [CrossRef] [PubMed]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In MICCAI 2015: Proceedings of the 18th International Conference, Munich, Germany, 5–9 October 2015; Springer International Publishing: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Martínez-Suárez, V.M.; Pedraza-Ortega, J.C.; Salazar-Colores, S.; Espinosa-Bernal, O.A.; Ramos-Arreguin, J.M. Environment emulation in 3d graphics software for fringe projection profilometry. In International Congress of Telematics and Computing; Springer International Publishing: Cham, Switzerland, 2022; pp. 122–138. [Google Scholar]
- Espinosa-Bernal, O.A.; Pedraza-Ortega, J.C.; Aceves-Fernández, M.A.; Martínez-Suárez, V.M.; Tovar-Arriaga, S. Adaptive Based Frequency Domain Filter for Periodic Noise Reduction in Images Acquired by Projection Fringes. In International Congress of Telematics and Computing; Springer International Publishing: Cham, Switzerland, 2022; pp. 18–32. [Google Scholar]
- Varghese, J. Adaptive threshold based frequency domain filter for periodic noise reduction. AEU-Int. J. Electron. Commun. 2016, 70, 1692–1701. [Google Scholar] [CrossRef]
- Haji, S.H.; Abdulazeez, A.M.; Darrell, T. Comparison of optimization techniques based on gradient descent algorithm: A review. PalArch’s J. Archaeol. Egypt/Egyptol. 2021, 18, 2715–2743. [Google Scholar]
- Elshamy, R.; Abu-Elnasr, O.; Elhoseny, M.; Elmougy, S. Improving the efficiency of RMSProp optimizer by utilizing Nestrove in deep learning. Sci. Rep. 2023, 13, 8814. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Jiang, J.; Bao, S.; Shi, W.; Wei, Z. Improved traffic sign recognition algorithm based on YOLO v3 algorithm. J. Comput. Appl. 2020, 40, 2472. [Google Scholar]
- Gustavo, A.M.J.; Carlos, P.O.J.; Fernández, A.; Antonio, M. Reconstrucción Tridimensional de Objetos Sintéticos Mediante Desplazamiento de Fase. Congreso Nacional de Mecatrónica. Available online: https://www.mecamex.net/revistas/LMEM/revistas/LMEM-V11-N01-03.pdf (accessed on 12 April 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).