Program Equivalence in the Erlang Actor Model
Abstract
1. Introduction
1.1. Our Target Language
1.2. Contributions
- A notion of program equivalence for concurrent Core Erlang, based on bisimulation, that is able to model equivalence between programs that have different communication structures but the same observable behaviour;
- Concurrent program equivalence examples: We show that silent evaluation and process identifier renaming produce equivalent programs, and that transforming lists sequentially is equivalent to doing it concurrently;
- A machine-checked formalisation of the semantics and results concerning it in the Coq proof management system (we establish the link between the code and this paper in Appendix C).
2. Related Work
2.1. Erlang Semantics
2.2. Bisimulation Approaches
2.3. Previous Work
3. Concurrent Formal Semantics
3.1. Language Syntax
3.2. Running Example
3.3. Sequential Semantics
3.4. Process-Local Semantics
- A live process is a quintuple , where K denotes its frame stack, r is the redex currently evaluated, and q is the mailbox. L is the set of linked process identifiers, and b is a metatheoretical boolean value denoting the status of the trap_exit flag.
- A terminated (or dead) process (denoted with T) is a finite map of (linked) process identifiers to values.
- Messages are values that are sent from one process and placed into the mailbox of another process.
- Link signals communicate that two processes should be linked. Links are bidirectional; when one of the processes terminates, it will notify the other process with an exit signal.
- Unlink signals indicate that the link between two processes should be removed.
- Exit signals are used to indicate runtime errors. Terminated processes send them to their links, but they can be created and sent manually (with the ‘exit’/2 BIF) too. Exit signals include a value describing the reason of termination and a boolean flag of whether they have been triggered by a link.
- Signals can be sent, and they can arrive at processes. These actions include the sender’s () and receiver’s () PIDs. Note that signal-passing is not instantaneous; signals reside in “the ether” before their arrival. This behaviour is expressed with the inter-process semantics (we refer to Section 3.5).
- A process can obtain its PID with from the inter-process semantics.
- A process can spawn another process to evaluate a function with . is the PID of the spawned process given by the inter-process semantics, should be a closure value, and should be a (Core) Erlang list of parameters. The flag b denotes whether the spawned process should be linked to its parent (when evaluating spawn_link).
- We use actions to denote reductions of the computational (sequential) layer and some process-local steps for which the system is strongly confluent (formally defined in Theorem 4).
- The local reduction steps are denoted with actions. These steps affect either the mailbox, the set of links, or the process flag (besides the frame stack and the redex) of a process, and they are not confluent with the other actions.
- is used to denote functions of the metatheory.
- denotes metatheoretical false, and denotes metatheoretical true.
- is a higher-order function of the metatheory, transforming all elements of the (metatheoretical) container l (list or set) by applying the (metatheoretical) function f to them.
- is used to transform the metatheoretical (list or boolean) value y to a Core Erlang value (a list or ‘true’ or ‘false’ atoms).
- is used to transform the Core Erlang value v to its metatheoretical counterpart. The result of this function is of option type; it is for unsuccessful conversion, or the metatheoretical counterpart enclosed in .
- denotes the value enclosed in associated with the key k in a finite map M, if it exists. Otherwise, the result is .
- denotes removing the value associated with the key k from the finite map M.
- Rule Msg shows that incoming messages are appended to the list of unseen messages in the mailbox.
- Rules ExitDrop, ExitTerm, and ExitTrap describe the arrival of an exit signal. Based on the set of links L, the state of the trap_exit flag b, the reason value v, and the link flag of the exit signal, and the source and destination PIDs, there are three different behaviours.
- -
- Rule ExitDrop drops the exit signal if its reason was ‘normal’ or it came from an unlinked process and was triggered by a link.
- -
- Rule ExitTerm terminates the process, by transforming it into a dead process which will notify its links with the reason of the termination (each linked PID is associated with this reason value). This rule can be applied in three scenarios: (a) the exit’s reason is ‘kill’ and it was sent manually (in this case, the reason is changed to ‘killed’); (b) exits are not trapped, and a non-‘normal’ exit either came from a linked process or was sent manually with a non-‘kill’ reason; (c) exits are not trapped, and the process terminated itself with an exit signal with ‘normal’ reason.
- -
- Rule ExitTrap “traps” the exit signal by converting it into a message that is appended to the mailbox. This rule can be used if the process traps exits, the incoming signal is either triggered by a link, or its reason is not ‘kill’.
- Rule LinkArr and UnlinkArr describe the arrival of and signals, which modify the set of the linked PIDs.
- Rule Send describes message sending. This BIF reduces to the message value which is also communicated to the inter-process semantics inside the send action.
- Rule Exit describes manual exit signal sending. In this case, the result is ‘true’ while the exit signal is communicated to the inter-process semantics. The link flag of the signal is ff, since it is sent manually.
- Rules Link and Unlink describe sending link and unlink signals. Both evaluate to ‘ok’ while adding or removing a PID from the set of links, and communicating the corresponding action to the inter-process level.
- Rule Dead describes the communication of a dead process. Dead processes send an exit signal to all the linked processes with the given reason value. The flag of the signal is tt, since it is triggered by a link.
- Rule Self reduces to the PID of the current process which is obtained from the inter-process level in the action .
- Rules Spawn and SpawnLink describe process spawning. The spawned process will evaluate the given function applied to the given parameters, which are communicated to it within the action. To be able to evaluate this function application, the parameters of spawn are required to be a closure and a proper Core Erlang list. The result is the PID of the spawned process which is obtained from the inter-process semantics in the action. In the case of rule SpawnLink, the flag in the spawn action is also set, and a link is established to the spawned PID.
- Rule Seq lifts the sequential steps to the process-local level.
- Rule Flag changes the state of the trap_exit flag of the process to the provided boolean value, and its result is the original value of the flag. Rule FlagExc raises an exception, if a non-boolean value was provided.
- Rule Term describes the normal termination. The links are notified with exit signals with ‘normal’ reason.
- Rule TermExc describes the behaviour when an exception terminates the process. Each linked process is notified with an exit signal which includes the exception’s reason.
- Rule Peek checks the first unseen message (if it exists). The result is a value sequence consisting of ‘true’ and the said message.
- Rule PeekFail is used if there are no unseen messages in the mailbox. The result is a value sequence consisting of ‘false’ and an error value (which can be neither observed in the implementations, nor in the generated BEAM code).
- Rule RecvNext moves the first unseen message into the list of seen messages (if it exists).
- Rule RemoveMsg removes the first unseen message from the mailbox and sets all messages as unseen hereafter.
- Rule WaitInf describes the semantics of unblocking. This rule is used if there is an unseen message, otherwise the process is blocked until one arrives. The result ‘false’ indicates that the timeout (‘infinity’) was not reached.
- Rule Wait0 always evaluates to ‘true’, indicating that a timeout was reached. Currently, we have not formalised the timing; thus, only 0 and ‘infinity’ timeouts are modelled; however, we plan to change this in the future.
- Rule WaitExc evaluates to an exception when an invalid timeout value (i.e., non-integer and non-infinity) was used.
3.5. Inter-Process Semantics
- denotes the pool consisting of process p (associated with PID ) and pool .
- updates the ether by binding the pair of PIDs to the list of signals l.
- appends a signal s to the end of the list associated with in the ether . If there is nothing associated with the given source and destination, this function creates a singleton list associated with the given PIDs.
- removes the first signal from the list associated with from . Its result is of option type, if there is a signal to remove, the result is this signal and the modified ether enclosed in , otherwise .
- and denote the PIDs that appear in or , respectively. A PID appears in an ether if it is used as a source or destination of a signal, or if it appears syntactically in one of the signals stored in the ether. Respectively, a PID appears in a pool if there is a process associated with it, or it appears inside a process syntactically.
- notation is taken from [11]; here, we only use it to express beta-reduction of with the parameters . For more details, refer to Appendix A and [11].
- Rule NSend describes signal sending. When a process (associated with ) sends a signal to , this signal is placed into the ether with the source and destination .
- Rule NArrive removes the first signal from the ether (with some source ) to deliver to the process with PID .
- Rule NSpawn describes process creation. When a process reduces with a action, the inter-process semantics assigns a fresh and unobserved PID to the new process which will evaluate the given closure applied to the given parameters of the action. If the flag in the action is set (i.e., spawn_link has been evaluated in the process), a link to the parent process is also established. Whether is a closure and the third parameter of spawn is a proper Core Erlang list of values are checked in the process-local semantics (in rules Spawn and SpawnLink).
- Rule NLocal defines that every other action should be only propagated to the process-local level without modifying the ether, or creating new processes.
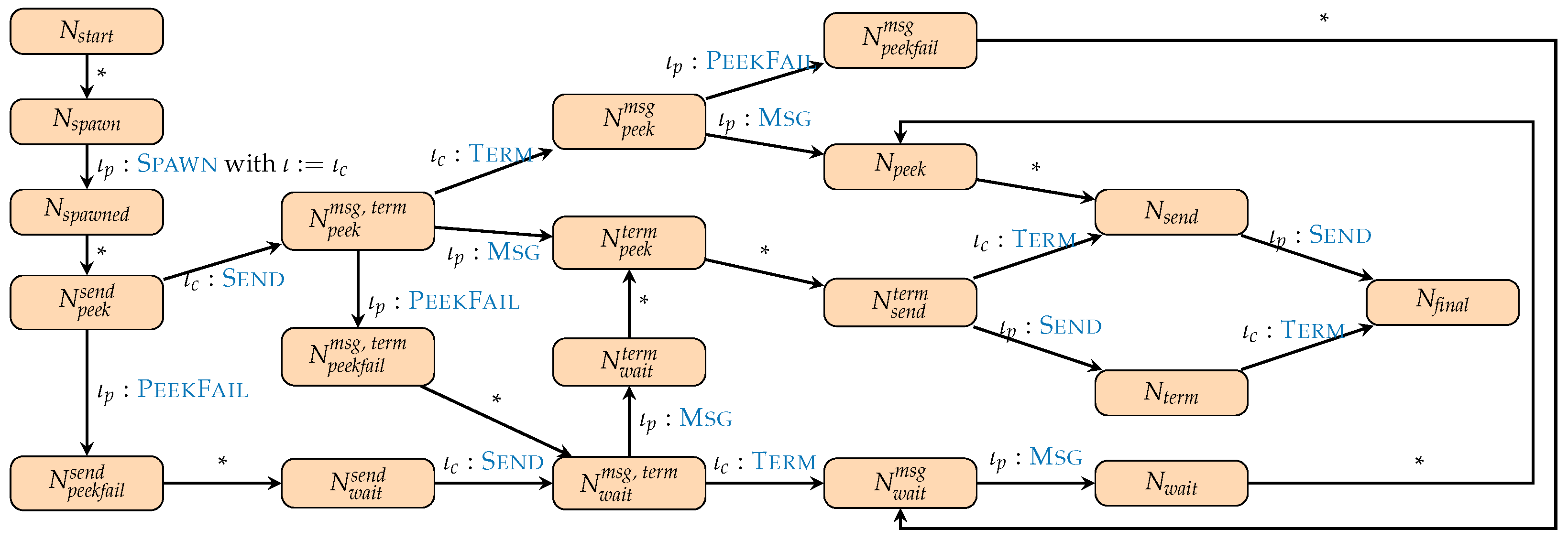
3.6. Example Evaluation
- denotes the expression presented in Figure 4;
- denotes the closure for the spawned process:
- denotes the second subexpression of the do expression from Figure 4, which processes the list suffix sequentially, and receives the result from the child process;
- denote the clauses of the case expression of Figure 3.
- is used for the transformed list [2|[3|[4|[5|[]]]]], and for the transformed prefix [2|[3|[]]].
- = ())
3.7. Semantic Properties
- ;
- ;
- .
- and ; or
- a is an arrive action, there is a node , such that , and either or (in the latter case, the process with PID ι was terminated).
4. Program Equivalence
4.1. Restrictive Notions of Program Equivalence
- For all nodes , actions a, and PIDs ι, if then and ;
- The converse of the previous point for reductions from ;
- and strongly agree on O (note that this property is symmetric).
- For all nodes , actions a, and PIDs ι, if then and ;
- The converse of the previous point for reductions from ;
- and strongly agree on O.
4.2. Alternative Notion for Weak Barbed Bisimulation
- For all nodes , actions a, and PIDs ι, if then and ;
- and and weakly agree on O;
- The converse of the previous points for reductions and observables of .
4.3. Bisimulation Examples
- If NLocal or NArrive was used, then the same step can be made in the updated node (since these actions could not have been taken by terminated processes), and we can use the coinductive hypothesis.
- If NSpawn was used (which could not have been performed by a terminated process), we have to rename the PID of the spawned process to a fresh PID (so that it does not appear anywhere in the modified configuration, nor in the set of PIDs used in l), and we can perform the same reduction step with the fresh PID, since it satisfies the side condition of NSpawn. We finish this case by using the transitivity of barbed bisimulation with Theorem 7 and the coinductive hypothesis.
- In the case of NSend, we can make the same reduction in the updated node, regardless of which process sent the message. Supposing that , we can use the coinductive hypothesis with the list of signals chosen as (or just , if we prove the second part of the theorem).
- If , then .
- If , then .
- If , then there are two options:
- -
- If , i.e., the same step is taken, then and we can choose and use the reflexivity of the bisimulation.
- -
- If , then can only be an arrive action (Theorem 4). Supposing that the arrive action does not terminate the process, it can be postponed after making the reduction with a; thus, there is a node to which and . We choose , which is reachable from based on the first reduction, and prove based on the coinductive hypothesis and the second reduction.
- -
- If , is an arrive action, and it terminates the process, then the process is also if the action arrives in , since silent actions do not modify either of the properties (linked PIDs, source and destination, exit reason, process flag) used in the semantics for arrives (see Figure 8); thus, . We can choose and use the reflexivity of the bisimulation.
- If for some action , PID and node , there is a reduction , then we can use Theorem 3 to derive the existence of a node to which and . We choose , which is reachable from based on the first reduction, and prove based on the coinductive hypothesis and the second reduction.
- .
- The closure value computes a metatheoretical function f, that is, for all values v, we can prove in the sequential layer.
- is a proper Core Erlang list, i.e., it is constructed as , and .
- does not contain any PIDs; moreover, the application of does not introduce any PIDs.
5. Discussion
5.1. Novelty
5.2. Theoretical Challenges
5.3. Formalisation
- We deeply embedded the syntax of Core Erlang into Coq as an inductive definition, so that we can use induction to reason about substitutions, PID renamings, and variable scoping.
- We encoded variables (and function identifiers) of Core Erlang with the nameless variable representation, i.e., all variables are de Bruijn indices. Using a nameless encoding simplifies reasoning about alpha-equivalence to checking equality, and fresh variable generation is simply expressed with addition of natural numbers. This way, the syntax is less readable for the human eye, but it is much simpler to define parallel capture-avoiding substitutions and use them in proofs [31].
- We did not use a similar, nameless encoding for PIDs. While process pools behave like binders, PIDs generally do not behave as variables: PIDs are dynamically created, and we do not apply substitutions for them. Moreover, in some cases, we might need to depend on the exact value of a PID in the program (e.g., for PID comparison). In addition, alpha-equivalence of PIDs cannot be reduced to equality checking with a nameless encoding. Suppose that we have several process spawns that can be executed in any order. After executing all process spawns in all possible orders, the result systems will be alpha-equivalent, but never equal, since the spawned PIDs (as de Bruijn indices) would depend on the particular execution path.
- We expressed all semantic layers as inductive judgements in order so that we could more easily use Coq’s tactics (inversion and constructor) to handle semantic reductions in proofs.
- We formalised process pools, ethers and dead processes as finite maps so that the used PIDs inside such constructs can be collected by a recursive function. Based on the collection result, we can come up with fresh PIDs for spawned processes. If we used functions instead of finite maps, showing that a concrete PID does not appear inside process of a process pool would have required much more complex proofs (potentially based on induction).
- For an implementation of finite maps and freshness, we relied on the Iris project’s stdpp [32] library, which also includes the set_solver tactic that can be used to automatically discharge statements about sets and finite maps.
- The formalisation depends only on one standard axiom; we use functional extensionality for reasoning about parallel substitutions.
- In Theorem 7, we used bisimulation’s symmetry to justify the first clause of Definition 14 for the derivations starting from (i.e., for the node with renamings); however, we are certain that this could be replaced by several analogous helper lemmas, ultimately discharging the potential of invalidity.
- For every other case (including Lemmas 1 and 2), we used bisimulation’s transitivity with Theorem 7 for injective alpha-renaming (based on the soundness results of [33]).
6. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Rules of the Sequential Semantics
- Rules that deconstruct an expression by extracting its first redex while putting the rest of the expression in the frame stack (Figure A1).
- Rules that modify the top frame of the stack by extracting the next redex and putting back the currently evaluated value into this top frame (Figure A2).
- Rules that remove the top frame of the stack and construct the next redex based on this removed frame (Figure A3). We also included rules here which immediately reduce an expression without modifying the stack (e.g., PFun).
- Rules that express concepts of exception creation, handling, or propagation (Figure A4).
- : substitutes names (variables or function identifiers) in the the redex r with the given values . In some cases, we use the same notation () for substituting a list containing name–value pairs in the same way.
- : creates a list of function identifier–closure pairs from the list . Every function definition in the list is mapped to the following pair in the result list: .
- : decides whether a pattern list ps matches pairwise a value list vs (of the same length). A pattern matches a value, when they are constructed from the same elements, while pattern variables match every value.
- : defines the variable-value binding (as a list of pairs) resulted by successfully matching the patterns with the values .
- and , then.
- and v is not a closure, or has an incorrect number of formal parameters, the result is an exception.
- , then .
- , then .
- and n is an even number, thenwhere the result values inside the map are obtained by eliminating duplicate keys and their associated values.
- , then simulates the behaviour of sequential built-in functions of (Core) Erlang.
- , then simulates the behaviour of sequential primitive operations of Core Erlang.

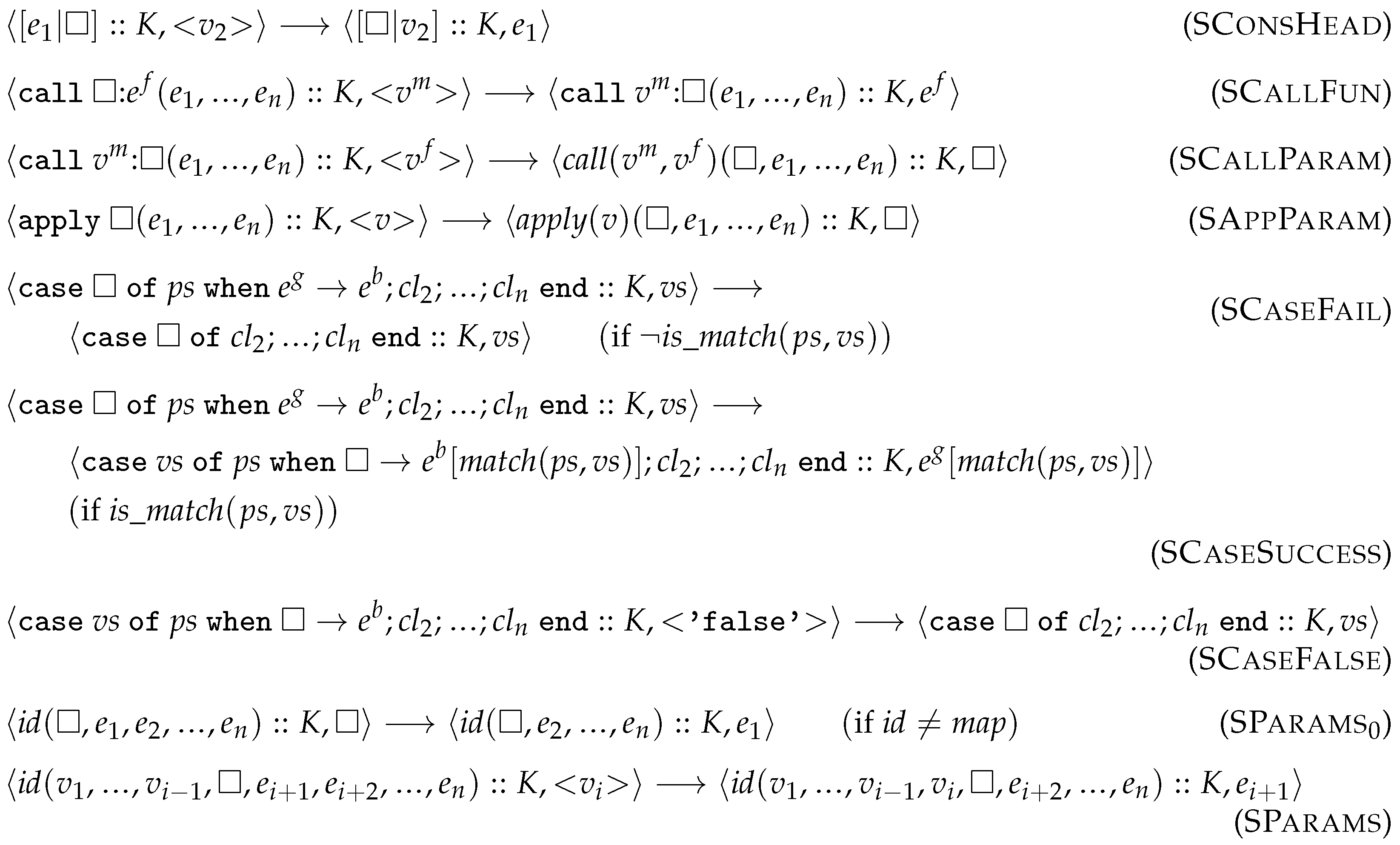

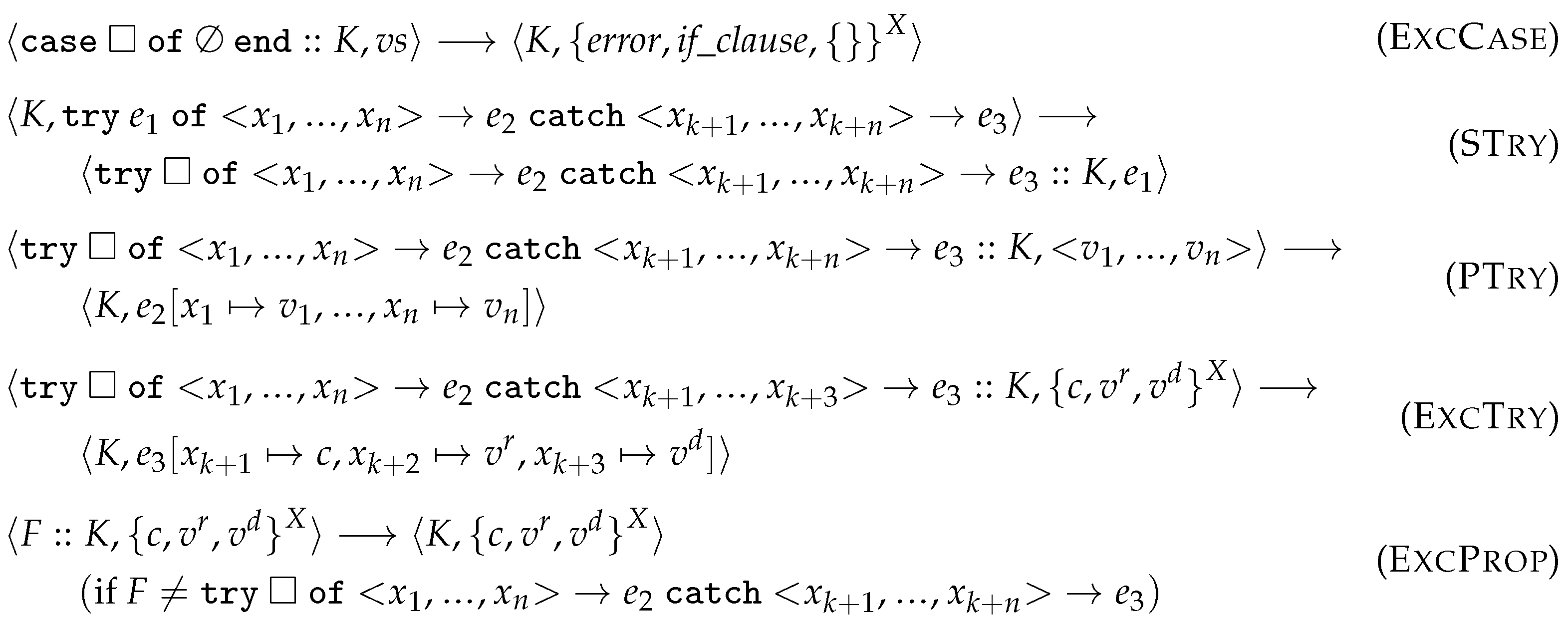
Appendix A.1. Parameter Lists
Appendix A.2. Map Frames
Appendix B. Evaluation of Sequential Map
- .
- The value computes a metatheoretical function f, i.e., for all v values, we can prove in the sequential semantics.
- is a proper Core Erlang list, i.e., it is constructed as , and .
- does not contain any PIDs, moreover, the application of does not introduce any PIDs.
Appendix C. Our Results in the Coq Implementation
| Figure 1 | Syntax.v - Pat, Exp, Val and NonVal |
| Figure 2 | Concurrent/ProcessSemantics.v - EReceive |
| Figure 3 | Concurrent/MapPmap.v - map_clos |
| Figure 4 | Concurrent/MapPmap.v - par_map |
| Figure 5 | Syntax.v - Redex and Frames.v - FrameIdent and Frame |
| Figure 6 | FrameStack/SubstSemantics.v - step |
| Definition 1 | Concurrent/ProcessSemantics.v - Process |
| Figure 7 | Concurrent/ProcessSemantics.v - removeMessage, peekMessage, recvNext, and mailboxPush |
| Definition 2 | Concurrent/ProcessSemantics.v - Signal |
| Definition 3 | Concurrent/ProcessSemantics.v - Action |
| Figure 8, Figure 9, Figure 10 and Figure 11 | Concurrent/ProcessSemantics.v - processLocalStep |
| Definition 4 | Concurrent/NodeSemantics.v - ProcessPool |
| Definition 5 | Concurrent/NodeSemantics.v - Ether |
| Definition 6 | Concurrent/NodeSemantics.v - Node |
| Figure 12 | Concurrent/NodeSemantics.v - interProcessStep |
| Theorem 1 | Concurrent/NodeSemanticsLemmas.v - signal_ordering |
| Example 1 | The paths explored in the example are included in the proof of Concurrent/MapPmap.v - map_pmap_empty_context_bisim |
| Definition 7 | Concurrent/PIDRenaming.v, Concurrent/ProcessSemantics.v, Concurrent/NodeSemanticsLemmas.v - Definitions with renamePID prefixes |
| Definition 8 | Concurrent/BisimRenaming.v - PIDsRespectNode |
| Definition 9 | Concurrent/BisimRenaming.v - PIDsRespectAction |
| Theorem 2 | Concurrent/NodeSemanticsLemmas.v - renamePID_is_preserved |
| Definition 10 | Concurrent/NodeSemanticsLemmas.v - We inline the uses of this definition based on Concurrent/NodeSemanticsLemmas.v - compatiblePIDOf |
| Theorem 3 | Concurrent/NodeSemanticsLemmas.v - confluence |
| Theorem 4 | Concurrent/NodeSemanticsLemmas.v - internal_det |
| Definition 11 | This definition is always inlined in the code |
| Definition 12 | Concurrent/StrongBisim.v - strongBisim |
| Definition 13 | Concurrent/WeakBisim.v - weakBisim |
| Definition 14 | Concurrent/BarbedBisim.v - barbedBisim |
| Theorem 5 | Concurrent/BarbedBisim.v - barbedBisim_refl, barbedBisim_sym, and barbedBisim_trans |
| Theorem 6 | Concurrent/WeakBisim.v - strong_is_weak and Concurrent/BarbedBisim.v - weak_is_barbed |
| Theorem 7 | Concurrent/BisimRenaming.v - rename_bisim |
| Lemma 1 | Concurrent/BisimReductions.v - ether_update_terminated_bisim |
| Lemma 2 | Concurrent/BisimReductions.v - terminated_process_bisim |
| Theorem 8 | Concurrent/BisimReductions.v - silent_steps_bisim |
| Example 2 | Concurrent/MapPmap.v - map_pmap_empty_context_bisim |
References
- Fowler, M. Refactoring: Improving the Design of Existing Code; Addison-Wesley Longman Publishing Co., Inc.: Boston, MA, USA, 1999; ISBN 0201485672. [Google Scholar]
- Kim, M.; Zimmermann, T.; Nagappan, N. A field study of refactoring challenges and benefits. In Proceedings of the ACM SIGSOFT 20th International Symposium on the Foundations of Software Engineering, Cary, NC, USA, 11–16 November 2012. [Google Scholar] [CrossRef]
- Ivers, J.; Nord, R.L.; Ozkaya, I.; Seifried, C.; Timperley, C.S.; Kessentini, M. Industry experiences with large-scale refactoring. In Proceedings of the 30th ACM Joint European Software Engineering Conference and Symposium on the Foundations of Software Engineering, Singapore, 14–18 November 2022; pp. 1544–1554. [Google Scholar] [CrossRef]
- Bagheri, A.; Hegedüs, P. Is refactoring always a good egg? exploring the interconnection between bugs and refactorings. In Proceedings of the 19th International Conference on Mining Software Repositories, Pittsburgh, PA, USA, 23–24 May 2022; 2022; pp. 117–121. [Google Scholar] [CrossRef]
- Erlang/OTP Compiler, Version 24.0. 2021. Available online: https://www.erlang.org/patches/otp-24.0 (accessed on 15 May 2024).
- Carlsson, R.; Gustavsson, B.; Johansson, E.; Lindgren, T.; Nyström, S.O.; Pettersson, M.; Virding, R. Core Erlang 1.0.3 Language Specification. 2004. Available online: https://www.it.uu.se/research/group/hipe/cerl/doc/core_erlang-1.0.3.pdf (accessed on 15 May 2024).
- Brown, C.; Danelutto, M.; Hammond, K.; Kilpatrick, P.; Elliott, A. Cost-Directed Refactoring for Parallel Erlang Programs. Int. J. Parallel Program. 2014, 42, 564–582. [Google Scholar] [CrossRef]
- Agha, G.; Hewitt, C. Concurrent programming using actors: Exploiting large-scale parallelism. In Readings in Distributed Artificial Intelligence; Bond, A.H., Gasser, L., Eds.; Morgan Kaufmann: Burlington, MA, USA, 1988; pp. 398–407. [Google Scholar] [CrossRef]
- Erlang Documentation. Processes. 2024. Available online: https://www.erlang.org/doc/reference_manual/processes.html (accessed on 15 May 2024).
- Bereczky, P.; Horpácsi, D.; Thompson, S. A Formalisation of Core Erlang, a Concurrent Actor Language. Acta Cybern. 2024, 26, 373–404. [Google Scholar] [CrossRef]
- Bereczky, P.; Horpácsi, D.; Thompson, S. A frame stack semantics for sequential Core Erlang. In Proceedings of the 35th Symposium on Implementation and Application of Functional Languages (IFL 2023), Braga, Portugal, 29–31 August 2023. [Google Scholar] [CrossRef]
- Fredlund, L.Å. A Framework for Reasoning About Erlang Code. Ph.D. Thesis, Mikroelektronik och Informationsteknik, Stockholm, Sweden, 2001. [Google Scholar]
- Nishida, N.; Palacios, A.; Vidal, G. A reversible semantics for Erlang. In Proceedings of the International Symposium on Logic-Based Program Synthesis and Transformation, Edinburgh, UK, 6–8 September 2016; Hermenegildo, M.V., Lopez-Garcia, P., Eds.; Springer: Cham, Switzerland, 2017; pp. 259–274. [Google Scholar] [CrossRef]
- Vidal, G. Towards symbolic execution in Erlang. In Proceedings of the International Andrei Ershov Memorial Conference on Perspectives of System Informatics, Petersburg, Russia, 24–27 June 2014; Voronkov, A., Virbitskaite, I., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; pp. 351–360. [Google Scholar] [CrossRef]
- Lanese, I.; Nishida, N.; Palacios, A.; Vidal, G. CauDEr: A causal-consistent reversible debugger for Erlang. In Proceedings of the International Symposium on Functional and Logic Programming, Nagoya, Japan, 9–11 May 2018; Gallagher, J.P., Sulzmann, M., Eds.; Springer: Cham, Switzerland, 2018; pp. 247–263. [Google Scholar] [CrossRef]
- Lanese, I.; Sangiorgi, D.; Zavattaro, G. Playing with bisimulation in Erlang. In Models, Languages, and Tools for Concurrent and Distributed Programming; Boreale, M., Corradini, F., Loreti, M., Pugliese, R., Eds.; Springer: Cham, Switzerland, 2019; pp. 71–91. [Google Scholar] [CrossRef]
- Harrison, J.R. Towards an Isabelle/HOL formalisation of Core Erlang. In Proceedings of the 16th ACM SIGPLAN International Workshop on Erlang, Oxford, UK, 8 September 2017; pp. 55–63. [Google Scholar] [CrossRef]
- Kong Win Chang, A.; Feret, J.; Gössler, G. A semantics of Core Erlang with handling of signals. In Proceedings of the 22nd ACM SIGPLAN International Workshop on Erlang, Seattle, WA, USA, 4 September 2023; pp. 31–38. [Google Scholar] [CrossRef]
- Gustavsson, B. EEP 52: Allow Key and Size Expressions in Map and Binary Matching. 2020. Available online: https://www.erlang.org/eeps/eep-0052 (accessed on 15 October 2024).
- Milner, R.; Parrow, J.; Walker, D. A calculus of mobile processes, I. Inf. Comput. 1992, 100, 1–40. [Google Scholar] [CrossRef]
- Sangiorgi, D.; Milner, R. The problem of “weak bisimulation up to”. In Proceedings of the CONCUR‘92, Stony Brook, NY, USA, 24–27 August 1992; Cleaveland, W., Ed.; Springer: Berlin/Heidelberg, Germany, 1992; pp. 32–46. [Google Scholar]
- Milner, R. Communication and Concurrency; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1989. [Google Scholar]
- Milner, R.; Sangiorgi, D. Barbed bisimulation. In Proceedings of the Automata, Languages and Programming, Wien, Austria, 13–17 July 1992; Kuich, W., Ed.; Springer: Berlin/Heidelberg, Germany, 1992; pp. 685–695. [Google Scholar] [CrossRef]
- Bocchi, L.; Lange, J.; Thompson, S.; Voinea, A.L. A model of actors and grey failures. In Coordination Models and Languages; ter Beek, M.H., Sirjani, M., Eds.; Springer: Cham, Switzerland, 2022; pp. 140–158. [Google Scholar] [CrossRef]
- Plotkin, G.D. A Structural Approach to Operational Semantics; Aarhus University: Aarhus, Denmark, 1981. [Google Scholar]
- Felleisen, M.; Friedman, D.P. Control operators, the SECD-machine, and the λ-calculus. In Proceedings of the Formal Description of Programming Concepts—III: Proceedings of the IFIP TC 2/WG 2.2 Working Conference on Formal Description of Programming Concepts—III, Ebberup, Denmark, 25–28 August 1986; pp. 193–222. [Google Scholar]
- Pitts, A.M.; Stark, I.D. Operational reasoning for functions with local state. In Higher Order Operational Techniques in Semantics; Cambridge University Press: Cambridge, UK, 1998; pp. 227–273. ISBN 9780521631686. [Google Scholar]
- Cesarini, F.; Thompson, S. Erlang Programming, 1st ed.; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2009. [Google Scholar]
- Core Erlang Formalization. 2024. Available online: https://github.com/harp-project/Core-Erlang-Formalization/releases/tag/v1.0.7 (accessed on 4 October 2024).
- Amadio, R.M.; Castellani, I.; Sangiorgi, D. On bisimulations for the asynchronous π-calculus. Theor. Comput. Sci. 1998, 195, 291–324. [Google Scholar] [CrossRef]
- Schäfer, S.; Tebbi, T.; Smolka, G. Autosubst: Reasoning with de Bruijn terms and parallel substitutions. In Proceedings of the Interactive Theorem Proving, Nanjing, China, 24–27 August 2015; Urban, C., Zhang, X., Eds.; Springer: Cham, Switzerland, 2015; pp. 359–374. [Google Scholar] [CrossRef]
- Stdpp: An Extended “Standard Library” for Coq. 2024. Available online: https://gitlab.mpi-sws.org/iris/stdpp (accessed on 1 October 2024).
- Sangiorgi, D. On the proof method for bisimulation. In Proceedings of the Mathematical Foundations of Computer Science 1995, Prague, Czech Republic, 28 August–1 September 1995; Wiedermann, J., Hájek, P., Eds.; Springer: Berlin/Heidelberg, Germany, 1995; pp. 479–488. [Google Scholar]









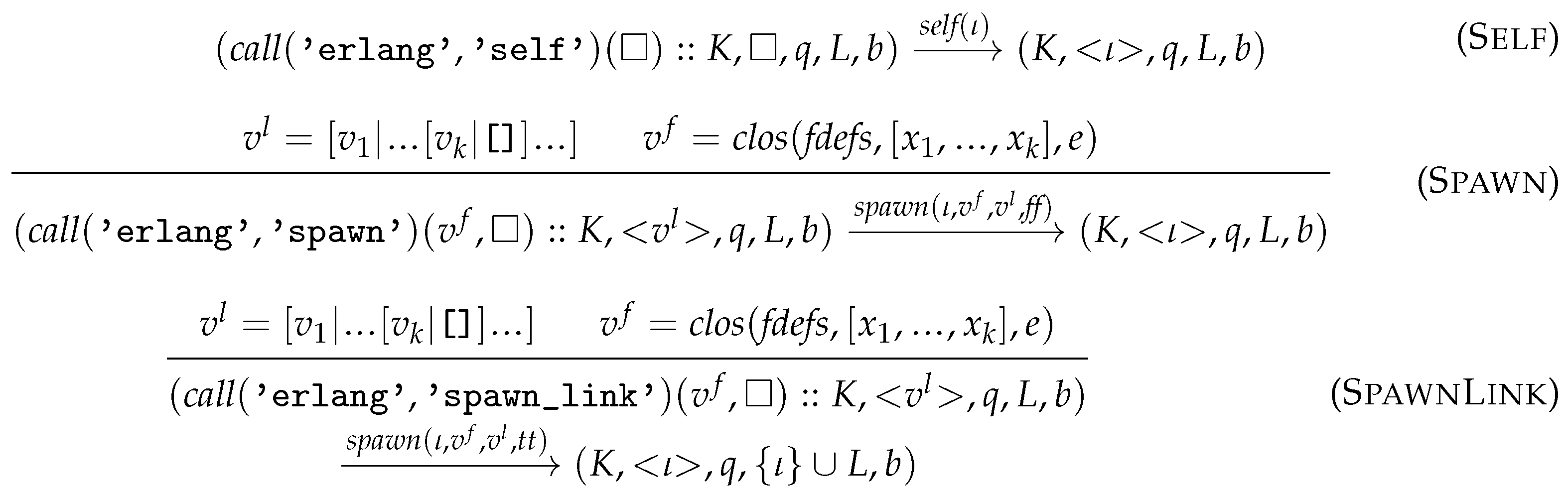
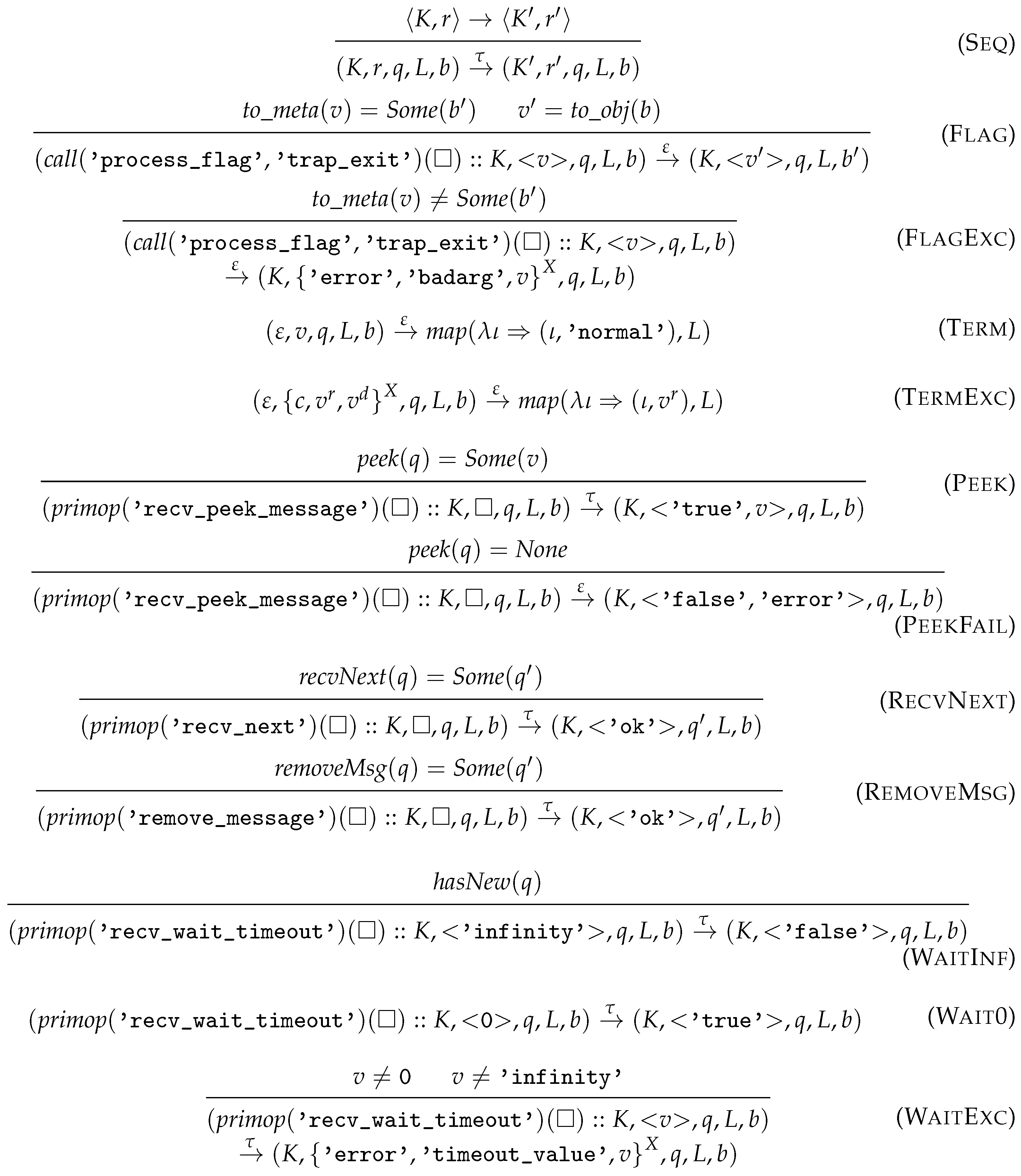

| Layer Name | Notation | Description |
|---|---|---|
| Inter-process (Section 3.5) | System-level reductions | |
| Process-local (Section 3.4) | Process-level reductions | |
| Sequential (Section 3.3) | ⟶ | Computational reductions |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bereczky, P.; Horpácsi, D.; Thompson, S. Program Equivalence in the Erlang Actor Model. Computers 2024, 13, 276. https://doi.org/10.3390/computers13110276
Bereczky P, Horpácsi D, Thompson S. Program Equivalence in the Erlang Actor Model. Computers. 2024; 13(11):276. https://doi.org/10.3390/computers13110276
Chicago/Turabian StyleBereczky, Péter, Dániel Horpácsi, and Simon Thompson. 2024. "Program Equivalence in the Erlang Actor Model" Computers 13, no. 11: 276. https://doi.org/10.3390/computers13110276
APA StyleBereczky, P., Horpácsi, D., & Thompson, S. (2024). Program Equivalence in the Erlang Actor Model. Computers, 13(11), 276. https://doi.org/10.3390/computers13110276





