Algebraic Zero Error Training Method for Neural Networks Achieving Least Upper Bounds on Neurons and Layers

Abstract

In the domain of artificial neural networks, it is important to know what their representation, classification and generalization capabilities are. There is also a need for time and resource-efficient training algorithms. Here, a new zero-error training method is derived for digital computers and single hidden layer networks. This method is the least upper bound on the number of hidden neurons as well. The bound states that if there are N input vectors expressed as rational numbers, a network having N − 1 neurons in the hidden layer and M neurons at the output represents a bounded function F: R^D→R^M for all input vectors. Such a network has massively shared weights calculated by 1 + M regular systems of linear equations. Compared to similar approaches, this new method achieves a theoretical least upper bound, is fast, robust, adapted to floating-point data, and uses few free parameters. This is documented by theoretical analyses and comparative tests. In theory, this method provides a new constructional proof of the least upper bound on the number of hidden neurons, extends the classes of supported activation functions, and relaxes conditions for mapping functions. Practically, it is a non-iterative zero-error training algorithm providing a minimum number of neurons and layers.

1. Introduction

In recent years, artificial neural networks (ANN) have become important tools in many areas of research as well as in industry [1], healthcare [2], finance, media [3], etc. They process all types of data, e.g., pictures, videos, speech, audio, time series, texts, etc. They are particularly important in areas where precise mathematical or physical models are unknown or are difficult to calculate and use and this is because there are several structures of very complex ANNs [4] that can be well adapted to wide range of problems. As ANNs become a part of our lives, it is important to expand our theoretical and practical knowledge about their use.

Since the first application of ANNs, great efforts have been made to analyze their basic abilities from a theoretical and practical point of view [5,6,7], i.e., mainly density and complexity problems. The density aims to determine whether a particular ANN can represent, or at least approximate, a given set of functions. The complexity sets limits on how big or complex such a network must be in order to perform certain representations or approximations. Another major issue is the training process [8], i.e., how to optimally (in terms of accuracy) and efficiently (training times, computational load) set all free ANN parameters with respect to training data. Therefore, a better understanding of theoretical and practical limits can significantly alleviate these problems. There are many useful theorems and measures for evaluating the abilities of various ANNs from different aspects, e.g., approximation, representation, generalization, and related bounds on the number of neurons, layers, free parameters, etc.

This article introduces a new zero-error training/construction process of single hidden layer feed forward networks (SLFN). This method is also the least upper bound on the number of hidden neurons. The presented method and the derived bound differ from the previously published methods mostly by introducing a natural assumption of input samples processed in digital computers, i.e., rational (floating-point) numbers. This allows to derive a new constructional least upper bound achieving zero-error mapping in a fixed number of steps. It defines a network structure with a massive weight sharing, introduces a simple training algorithm that is reduced to solving regular systems of linear equations (upper or lower triangular matrices), relaxes conditions for mapping functions, and extends supported sets of activation functions. Moreover, this process has proved to be fast and robust using only a small number of free parameters compared to similar methods. Finally, this method addresses all three major problems, i.e., density, complexity and training.

2. Related Work

2.1. Approximation Theorems for Single Hidden Layer Networks

In, e.g., [5], it was shown that continuous functions of N variables can be represented by a linear combination of 2N + 1 different nonlinear functions; however, it is not clear what these functions look like. In [6], it was shown that a superposition of sigmoid-like functions can approximate with an arbitrary accuracy any bounded continuous function (Universal Approximation Theorem). This is directly applicable to a standard SLFN; however, it is not known how many neurons are needed. In, e.g., [7], it was further proven that any continuous non-polynomial activation function can be used. There are also several constructional proofs. In, e.g., [9], so-called Fourier neural series were used for approximation. A different approach was presented in [10], where instead of combining many hidden neurons with fixed activation functions, a single neuron and a more general sigmoidal function were used.

2.2. Representation Theorems, Bounds and Construction Methods for Single Hidden Layer Networks

It is possible to construct networks with a zero-error mapping observed on a finite number of input samples. In [11], a proof was derived of an upper bound on the number of hidden neurons in a SLFN that uses signum activation functions. It states that N − 1 neurons are sufficient to perform a mapping of N samples, which is also the least upper bound (LUB). In [12], this result was extended by showing that a SLFN with N hidden neurons can represent N samples implementing any bounded nonlinear activation function that has a limit in −∞ or ∞. Assuming an input sample matrix has at least one row with completely different values, a training approach using N hidden neurons and the rectified linear unit (Relu) was presented in [13]. In [14], weights for N hidden neurons were generated randomly, whereas the biases were calculated with respect to inputs and weights. In, e.g., [15], it was further shown that randomly set weights and biases of N hidden neurons can perform a mapping of N samples using sigmoidal activation functions. In the domain of extreme learning machine (ELM), it was shown in [16] that a network with N hidden neurons can achieve a zero-error approximation with a probability of 1 for all N input samples. It assumes infinitely differentiable activation functions, whereas the weights and biases of hidden neurons can be randomly selected.

2.3. Approximation and Representation Theorems and Bounds for Networks with More Hidden Layers

For networks with more hidden layers, there are several articles proving they can approximate continuous functions. In [17], an approximation power of additional hidden layers was demonstrated, showing that an extra hidden layer can dramatically reduce the number of neurons. An analysis of approximation capabilities for deep ANNs can be found in [18], where the lower bounds are given by the complexity of functions to be approximated and the required accuracy. In [19], an expressive number, i.e., a number of samples that can be expressed by a network, was investigated for a two hidden layer network. Both the lower and upper bounds on the expressive number of networks using Relu activation functions were derived.

2.4. Generalization Theorems and Bounds

There are also several measures related to generalization capabilities, such as the Vapnik–Chervonenkis (VC) dimension [20]. In [21], tighter upper and lower bounds on VC dimensions for deep ANNs with Relu activation functions were presented; however, for special activation functions, even a single hidden layer can have an infinite VC dimension. Another important measure to limit generalization errors is the Rademacher complexity, and there are several articles estimating this measure, e.g., [22]. As a consequence, various regularization techniques [23], often related to these bounds, are used in the training process to increase its generalization capabilities.

3. Construction Method and the Least Upper Bound on Single Hidden Layer Networks

Since the construction process of a zero-error mapping SLFN is the proof of the least upper bound as well, first the mapping theorem is given, followed by its constructional proof.

Theorem 1.

If $F:R^D\to R^M$is a real bounded function defined in a subspace$S\subset R^D$formed by a D dimensional rectangular cuboid of the size $L_1\times L_2\times L_3 \dots \times L_D and \exists k | L_k>0 \wedge L_j<\infty \forall j$, and there is a finite number N of rational samples $\mathit{x}\in S\bigcap Q^D$, then a single hidden layer feed forward network having N − 1 neurons in a hidden layer and M in an output layer is sufficient to realize a mapping defined by$F\left({\mathit{x}}_{\mathit{i}}\right)={\mathit{y}}_{\mathit{i}}, i=1,\dots ,N$. Such a network has D − 1 + M(N − 1) trainable weights and N − 1 + M trainable biases that can be computed by solving 1 + M regular systems of linear equations. The output neurons have identity activation functions and the hidden neurons implement arbitrary activation functions f: R→R satisfying:

$$f\left(x\right)=\langle \begin{array}{c}0, x\le 0\\ R \backslash \left\{0\right\}, x>0 \end{array} or f\left(x\right)=\langle \begin{array}{c}A , x\to \infty \\ B, x\to -\infty \end{array}, A\ne B \wedge A\ne 0$$

3.1. Constructional Proof-Preliminaries

The basic proof is primarily given for Q^D → R mapping, but it can be analogically and easily extended for more outputs, i.e., Q^D → R^M; as shown later in the text. For an exact formulation for how rational and floating-point numbers can be represented, e.g., as given in the IEEE 754 standard, see Appendix A, as this is crucial for the proof. For the proof only, it is assumed that N input samples x_i are sorted in ascending order along all dimensions D, as stated in Appendix B. Finally, it is assumed the space bounding rectangular cuboid originates in the beginning of a Cartesian coordinate system (to make the proof more concise), Δ > 0, 0 < step < Δ, L₁ > 0, and x_i(k) denotes k-th dimension of i-th sample. The proof is divided into several logical steps as follows.

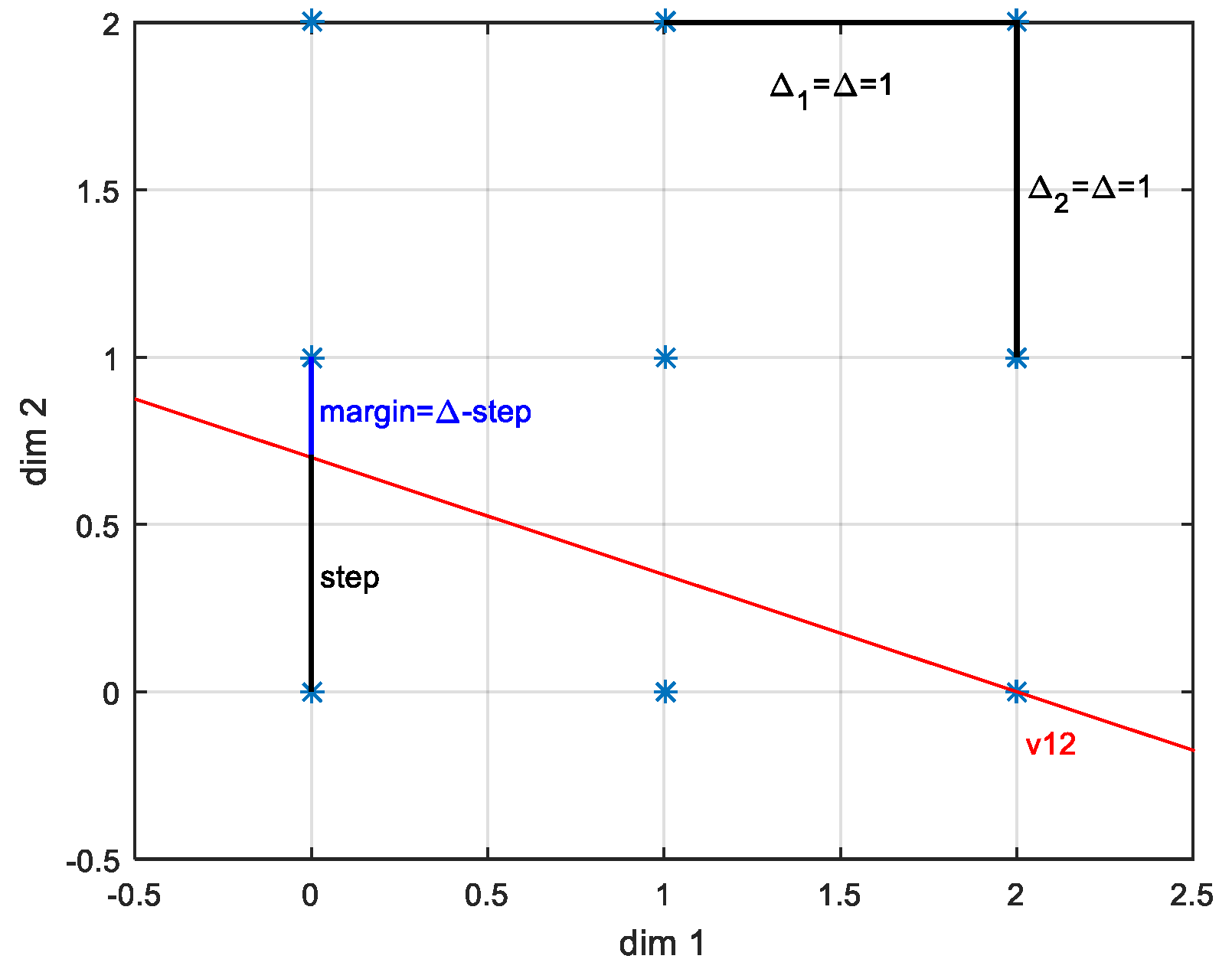
3.2. Separating Affine Hyperplanes

This step is essential for the proof and can be easily and graphically represented in three dimensions (1D and 2D cases are omitted as they can be easily inferred). Then the process will be generalized for a D dimensional case using mathematical induction.

3.2.1. 3D Case

Since the design is geometric, see Figure 1 showing the finite precision grid bounded by a prism of the size 2 × 2 × 1, i.e., L₁ × L₂ × L₃ originating at (0, 0, 0)^T that contains all rational numbers with Δ = 1 (a difference between grid points). The task is to construct affine planes that can gradually separate all grid points (potentially all possible input samples) one by one from the remaining ones. Such a process starts at (0, 0, 0)^T then moves to (1, 0, 0)^T, (2, 0, 0)^T, (0, 1, 0)^T, etc., and ends at the last but one point of the bounding prism, i.e., (1, 2, 1)^T. It is important that once the grid point is separated, it must remain separated by all other planes in the following steps. A grid point separating plane is defined by v₁₂ and v₁₂₃ vectors. v₁₂ with a 3rd dimension equal to 0 that satisfies the property of gradual separation (see Figure 2) can be expressed as follows:

$${\mathit{v}}_{12}={\left(L_1, 0 , 0\right)}^{\mathrm{T}}-{\left(0,step,0\right)}^{\mathrm{T}}={\left(L_1,-step,0\right)}^{\mathrm{T}}$$

(1)

It is clear from Figure 2 that step must be in range (0, Δ) so as not to interfere with other points having 3rd dimension equal to 0. Next, choosing v₁₂₃ as shown in Figure 1 secures the separating plane will not intersect any points in the above parallel plane, i.e., 3rd dimension = Δ. Thus, v₁₂₃ can be expressed as:

$${\mathit{v}}_{123}={\left(L_1, L_2, 0\right)}^{\mathrm{T}}-{\left(0, 0,step\right)}^{\mathrm{T}}={\left(L_1, L_2,-step\right)}^{\mathrm{T}}$$

(2)

It is then possible to calculate a normalized normal vector n ((A4), Appendix C) of such a plane allowing a gradual separation process using (A5) as follows:

$$-\left(\begin{array}{cc}{\mathit{v}}_{12}\left(2\right)& {\mathit{v}}_{12}\left(3\right)\\ {\mathit{v}}_{123}\left(2\right)& {\mathit{v}}_{123}\left(2\right)\end{array}\right)\left(\begin{array}{c}\mathit{n}\left(2\right)\\ \mathit{n}\left(3\right)\end{array}\right)=-\left(\begin{array}{cc}-step& 0\\ L_2& -step\end{array}\right)\left(\begin{array}{c}\mathit{n}\left(2\right)\\ \mathit{n}\left(3\right)\end{array}\right)=\left(\begin{array}{c}{L}_1\\ L_1\end{array}\right)$$

(3)

This forms a lower triangular matrix with non-zero diagonal elements, thus, the solution always exists and can be easily found. Finally, N − 1 separating affine planes w_i sharing the same normal vector n, each intersecting different sample x_i, i = 1, …, N − 1, and multiplied by −1 are defined in (4).

$${\mathit{w}}_{\mathrm{i}}:-{\mathit{x}}^{\mathrm{T}}\mathit{n}-d_i=-{\mathit{x}}^{\mathrm{T}}\left(\begin{array}{c}1\\ \mathit{n}\left(2\right)\\ \mathit{n}\left(3\right)\end{array}\right)+{\mathit{x}}_i^{\mathrm{T}}\left(\begin{array}{c}1\\ \mathit{n}\left(2\right)\\ \mathit{n}\left(3\right)\end{array}\right)=0,\hspace{1em}i=1,\dots ,N-1$$

(4)

For the proof only, it is assumed that N input samples x_i are sorted as stated in (A3). The −1 multiplication is applied only to swap the subspaces each plane creates, i.e., positive to negative and vice versa, which is what is needed when using common forms of activation functions, e.g., Relu, tanh, Heaviside, etc.

3.2.2. D-Dimensional Case

Using mathematical induction, assuming there are already correctly found vectors v₁₂, v₁₂₃,… v_123…m−1 partially defining the separating affine hyperplane (in m − 1 dimensions), a new vector v_123…m is constructed in the same way as before. Thus, it connects the most distant point in m − 1 dimensional subspace, i.e., (L₁, L₂, … L_m−1, 0, …, 0)^T and the “begging” point located in m dimensional subspace, i.e., (0, …, 0, step_m, 0, …, 0)^T, while introducing a proper margin given by step_m (here step_m is used to explicitly indicate that it is in the m-th dimension, otherwise step is regarded to be the same across dimensions), i.e.,

$$\begin{array}{c}{\mathit{v}}_{12\dots m}={\left(L_1,L_2,\dots ,L_{m-1}, 0,\dots , 0\right)}^{\mathrm{T}}-{\left(0, 0,\dots , 0, ste{p}_m,0,\dots , 0\right)}^{\mathrm{T}}=\\ {\left(L_1,L_2,\dots ,L_{m-1},-ste{p}_m,0,\dots , 0\right)}^{\mathrm{T}}\end{array}$$

(5)

Once having v_123…m, it is possible to reach points p_12…m in m dimensional subspace from points p_12…m−1 in m − 1 dimensional subspace simply by adding properly scaled (c) vector v_123…m to p_12…m−1 as:

$$\begin{array}{c}{\mathit{p}}_{12\dots m}={\left({\mathit{p}}_{12\dots m-1}\left(1\right),{\mathit{p}}_{12\dots m-1}\left(2\right),\dots ,{\mathit{p}}_{12\dots m-1}\left(m-1\right), 0,\dots 0\right)}^{\mathrm{T}}+c{\mathit{v}}_{12\dots m}=\\ {\left(k_1\Delta ,k_2\Delta ,\dots ,k_{m-1}\Delta , 0, \dots , 0\right)}^{\mathrm{T}}+c{\mathit{v}}_{12\dots m}=\\ {\left(k_1\Delta +c{L}_1, k_2\Delta +c{L}_2,\dots , k_{m-1}\Delta +c{L}_{m-1}, c\left(-ste{p}_m\right),0,\dots 0\right)}^{\mathrm{T}}\end{array}$$

(6)

Now, to prove the existence of the separation property, it is sufficient to show that any grid point in the m-th dimension closest to the m − 1 subspace (minimal distance = Δ), i.e., (k₁ Δ, k₂ Δ, …, k_m−1 Δ, Δ, 0, …, 0)^T cannot be reached from the m − 1 subspace by v_123…m as given in (6) within the allowable grid limits. Using the assumptions, the finite precision grid limits can be applied to any valid point p_12…m and dimension i < m as:

$$0\le {\mathit{p}}_{12\dots m}\left(i\right)\le L_i\to 0\le k_i\Delta +c{L}_i\le L_i \wedge k_i\in \left[0, \frac{L_i}{\mathsf{\Delta }}\right]$$

(7)

where c is calculated such that when v_123…m is added to any grid point in m − 1 subspace as given in (6), it just intersects Δ (minimal separation distance) in m-th dimension, i.e.,

$$c\left(-ste{p}_m\right)=\mathsf{\Delta } \Rightarrow c=-\frac{\mathsf{\Delta }}{ste{p}_m}$$

(8)

Substituting c into (7) yields:

$$\begin{array}{c}{k}_i\Delta +c{L}_i=\Delta \left(k_i-\frac{L_i}{ste{p}_m}\right)\le \Delta \left(\frac{L_i}{\mathsf{\Delta }}-\frac{L_i}{ste{p}_m}\right)<0\\ \mathrm{as} ste{p}_m<\mathsf{\Delta }\wedge k_i\le \frac{L_i}{\mathsf{\Delta }} \wedge \exists i | L_i>0\end{array}$$

(9)

The inequality in (9) violates the boundary limits for a valid grid point in i-th dimension, i.e., any grid point in dimension i must be in a close interval [0, L_i], whereas (9) states it must be strictly negative for at least one dimension where L_i > 0. Therefore, v_123…m enables the gradual separation process also along the newly incorporated dimension m. By gradually generating vectors as in (5) dimension by dimension, D − 1 base vectors forming the separating affine hyperplane are found. Using (A5), the normalized normal vector n of the separating affine hyperplane is calculated as in (10):

$$\begin{gathered} \left(\begin{array}{cccc}{\mathit{v}}_{12}\left(2\right)& {\mathit{v}}_{12}\left(3\right)& \dots & {\mathit{v}}_{12}\left(D\right)\\ {\mathit{v}}_{123}\left(2\right)& {\mathit{v}}_{123}\left(3\right)& \dots & {\mathit{v}}_{123}\left(D\right)\\ ⋮& ⋮& \ddots & ⋮\\ {\mathit{v}}_{1234\dots D}\left(2\right)& {\mathit{v}}_{1234\dots D}\left(3\right)& \dots & {\mathit{v}}_{1234\dots D}\left(D\right)\end{array}\right)\left(\begin{array}{c}\mathit{n}\left(2\right)\\ \mathit{n}\left(3\right)\\ ⋮\\ \mathit{n}\left(D\right)\end{array}\right)= \\ \left(\begin{array}{ccccc}-step& 0& \dots & 0& 0\\ L_2& -step& 0& \dots & 0\\ L_2& L_3& \ddots & ⋮& ⋮\\ ⋮& ⋮& ⋮& -step& 0\\ L_2& L_3& \dots & L_{D-1}& -step\end{array}\right)\left(\begin{array}{c}\mathit{n}\left(2\right)\\ \mathit{n}\left(3\right)\\ \mathit{n}\left(4\right)\\ ⋮\\ \mathit{n}\left(D\right)\end{array}\right)=-\left(\begin{array}{c}{L}_1\\ L_1\\ L_1\\ ⋮\\ L_1\end{array}\right) \end{gathered}$$

(10)

This is a lower triangular D − 1 × D − 1 matrix with non-zero diagonal elements, thus the solution always exists. Such an affine hyperplane having its normal vector calculated as in (10) is able to gradually separate all points in the finite precision grid and thus N input samples as well. Now this hyperplane is gradually shifted to intersect the first N − 1 sorted samples x_i. This creates N − 1 separating affine hyperplanes as in (11), multiplied by −1 to enable the use of common activation functions:

$${\mathit{w}}_{\mathrm{i}}:-{\mathit{x}}^{\mathrm{T}}\mathit{n}-d_i=-{\mathit{x}}^{\mathrm{T}}\left(\begin{array}{c}1\\ \mathit{n}\left(2\right)\\ ⋮\\ \mathit{n}\left(D\right)\end{array}\right)+{\mathit{x}}_i^{\mathrm{T}}\left(\begin{array}{c}1\\ \mathit{n}\left(2\right)\\ ⋮\\ \mathit{n}\left(D\right)\end{array}\right)=0$$

(11)

3.3. Dot-Product Matrix

Having N − 1 affine hyperplanes (11) (weights and biases of hidden neurons), a dot-product matrix DP can be constructed as in (12). It contains dot products of all input samples (extended by constant 1, i.e., input to a bias term) and vectors (−n^T, −d_i) defining the separating affine hyperplanes w_i, i.e., DP represents the application of weights and biases of hidden neurons to all input vectors x_i:

$$\begin{gathered} \mathit{D}\mathit{P}=-\left(\begin{array}{c}\left({\mathit{x}}_1^{\mathrm{T}}, 1\right)\\ \left({\mathit{x}}_2^{\mathrm{T}}, 1\right)\\ ⋮\\ \left({\mathit{x}}_N^{\mathrm{T}}, 1\right)\end{array}\right)\left(\begin{array}{cccc}\left(\begin{array}{c}\mathit{n}\\ d_1\end{array}\right),& \left(\begin{array}{c}\mathit{n}\\ d_2\end{array}\right),& \dots & , \left(\begin{array}{c}\mathit{n}\\ d_{N-1}\end{array}\right)\end{array}\right)= \\ -\left(\begin{array}{cccc}{\mathit{x}}_1^{\mathrm{T}}\mathit{n}+d_1& {\mathit{x}}_1^{\mathrm{T}}\mathit{n}+d_2& \dots & {\mathit{x}}_1^{\mathrm{T}}\mathit{n}+d_{N-1}\\ {\mathit{x}}_2^{\mathrm{T}}\mathit{n}+d_1& {\mathit{x}}_2^{\mathrm{T}}\mathit{n}+d_2& \dots & {\mathit{x}}_2^{\mathrm{T}}\mathit{n}+d_{N-1}\\ ⋮& ⋮& \ddots & ⋮\\ {\mathit{x}}_N^{\mathrm{T}}\mathit{n}+d_1& {\mathit{x}}_2^{\mathrm{T}}\mathit{n}+d_2& \dots & {\mathit{x}}_N^{\mathrm{T}}\mathit{n}+d_{N-1}\end{array}\right)=\left(\begin{array}{cccc}0& {\epsilon }^{+}& \dots & {\epsilon }^{+}\\ {\epsilon }^{-}& 0& \dots & {\epsilon }^{+}\\ ⋮& ⋮& \ddots & 0\\ {\epsilon }^{-}& {\epsilon }^{-}& \dots & {\epsilon }^{-}\end{array}\right) \end{gathered}$$

(12)

Due to the gradual point by point separation of N sorted samples by N − 1 affine hyperplanes w_i, such a matrix (N × N − 1) has a special structure, i.e., its main diagonal is equal to 0, samples below the diagonal are negative, for simplicity marked as ε⁻, and elements above the diagonal are positive (ε⁺). Next, a sufficiently small positive constant ξ_i is added to each column of DP, so that the diagonal elements become positive, but still securing that the negative elements remain negative. This can be achieved by directly adding such ξ_i to d_i for each affine hyperplane, i.e.,

$$d_i=-\left({\mathit{x}}_i^{\mathrm{T}}\left(\begin{array}{c}1\\ \mathit{n}\left(2\right)\\ \mathit{n}\left(3\right)\end{array}\right)+{\xi }_i\right)$$

(13)

A proper ξ_i can be found for each column by inspecting negative elements located below the main diagonal as in (14):

$$0<{\xi }_i<\underset{j>i}{min}\left|\mathit{D}{\mathit{P}}_{j,i}\right|i=1,\dots ,N-1$$

(14)

Here DP_j,i denotes j-th raw and i-th column of the matrix. A single constant satisfying such requirements can be calculated by parameters of the finite precision grid and the normal vector n, i.e.:

$$0<\xi <min\left\{\left(-\Delta , 0, \dots , 0\right)\mathit{n}, \left(L_1,-\Delta , 0,\dots ,0\right)\mathit{n}, \dots ,\left(L_1,L_2 ,\dots , L_{D-1} ,-\Delta \right)\mathit{n}\right\}$$

(15)

Although (15) is a faster solution, (14) is more suitable for better numerical stability.

3.4. Hidden Output Matrix

In the next step, a proper nonlinear function is applied element-wise to the adjusted DP matrix by ξ_i (14), thus producing a hidden output matrix H. Such a matrix (N × N − 1) contains outputs of all hidden neurons for all input samples x_i. In this case two broad classes of functions can be used. For simplicity, first consider functions satisfying the definition in (16):

$$f\left(x\right)=\langle \begin{array}{c}0,\hspace{1em}x\le 0\\ R \backslash \left\{0\right\}, x>0\end{array}$$

(16)

Such functions, when applied to the adjusted DP matrices, produce upper triangular matrices with non-zero diagonal elements. In the following steps, this ensures the existence of a unique solution, e.g., in the case of the Heaviside function satisfying (16), this results in the hidden output matrix H, as shown in (17):

$$\mathit{H}=Heavisde\left(\left(\begin{array}{cccc}{\xi }_1& {\epsilon }^{+}+{\xi }_2& \dots & {\epsilon }^{+}+{\xi }_{N-1}\\ {\epsilon }^{-}+{\xi }_1& {\xi }_2& \dots & {\epsilon }^{+}+{\xi }_{N-1}\\ ⋮& ⋮& \ddots & {\xi }_{N-1}\\ {\epsilon }^{-}+{\xi }_1& {\epsilon }^{-}+{\xi }_2& \dots & {\epsilon }^{-}+{\xi }_{N-1}\end{array}\right)\right)=\left(\begin{array}{cccc}1& 1& \dots & 1\\ 0& 1& \dots & 1\\ ⋮& ⋮& \ddots & 1\\ 0& 0& \dots & 0\end{array}\right)$$

(17)

3.5. Output Neuron Weights and Biases

First, the hidden output matrix in (17) is extended from the right by a column of units, as shown in (18). This represents a constant input 1 to a bias for each training sample. The output neuron has N − 1 inputs from hidden neurons and the bias term fed by 1 (the last column of the extended matrix H). Thus, the extended matrix H is a square N × N upper triangular matrix with non-zero diagonal elements. Then, N − 1 output weights in w₂₁ and the bias term b₂₁ can be calculated simultaneously using (18):

$$\left(\begin{array}{ccccc}1& 1& \dots & 1& 1\\ 0& 1& \dots & ⋮& 1\\ ⋮& ⋮& \ddots & 1& ⋮\\ 0& 0& \dots & 0& 1\end{array}\right)\left(\begin{array}{c}{\mathit{w}}_{21}\left(1\right)\\ ⋮\\ {\mathit{w}}_{21}\left(N-1\right)\\ b_{21}\end{array}\right)=\left(\begin{array}{c}{\mathit{y}}_1\left(1\right)\\ {\mathit{y}}_2\left(1\right)\\ ⋮\\ {\mathit{y}}_N\left(1\right)\end{array}\right)$$

(18)

where y_i(1) i = 1, …, N, denotes outputs along the first dimension, i.e., output values of the first output neuron for all N inputs samples that realize F(x_i) = y_i, i = 1, …, N. The matrix in (18) is by theory regular [24], thus there are exactly N − 1 weights and the bias of the output neuron realizing the required mapping for all N input samples.

3.6. Comments and Extensions

For the sake of brevity, only the basic proof was provided by introducing some assumptions and limitations that, in fact, are not necessary. Thus, in the following, there are several extensions and implementation comments in the form of remarks to make the proof more general.

Remark 1.

A single hidden layer network having P hidden and M output neurons performing R^D → R^M mapping is described as:

$$\mathit{y}\left(j\right)=f_{2j}\left(b_{2j}+{\displaystyle \sum }_{i=1}^P{\mathit{w}}_{2j}\left(i\right)f_{1i}\left({\mathit{x}}^{\mathrm{T}} {\mathit{w}}_{1i}+b_{1i}\right)\right),\hspace{1em}j=1,\dots ,M$$

Then the weights of hidden neurons, i.e., w_1i i = 1, …, N − 1 are equal to −n as calculated in (10), their biases b_1i are equal to −d_i as derived in (13), output weights w_2j and biases b_2j are calculated as in (18), f_1i satisfy (16) or (19), f_2j are identity functions, and P = N − 1. Such a network has N − 1 neurons in the hidden layer and M neurons in the output one.

Remark 2.

A unique solution always exists if (18) is in the form of an upper triangular matrix with non-zero diagonal elements. Given the form of the hidden output matrix as appeared in (17) and prior to the use of an activation function, it is obvious that this can be easily achieved by all activation functions satisfying (16), i.e., set all negative (under diagonal) elements to 0 and secure the diagonal (positive) elements remain non-zero. Another class of activation functions ensuring the extended matrix H is regular is defined in (19):

$$f\left(x\right)=\langle \begin{array}{c}A, x\to \infty \\ B, x\to -\infty \end{array},\hspace{1em}A\ne B\wedge A\ne 0$$

(19)

By multiplying elements of the DP matrix by a positive constant α and applying f(x) from (19), the extended matrix H, as appeared in (18), can be written as follows:

$$\left(\begin{array}{ccccc}f\left(\alpha {\xi }_1\right)& f\left(\alpha \left({\epsilon }^{+}+{\xi }_2\right)\right)& \dots & f\left(\alpha \left({\epsilon }^{+}+{\xi }_{N-1}\right)\right)& 1\\ f\left(\alpha \left({\epsilon }^{-}+{\xi }_1\right)\right)& f\left(\alpha {\xi }_2\right)& \dots & ⋮& 1\\ ⋮& ⋮& \ddots & f\left(\alpha {\xi }_{N-1}\right)& ⋮\\ f\left(\alpha \left({\epsilon }^{-}+{\xi }_1\right)\right)& f\left(\alpha \left({\epsilon }^{-}+{\xi }_2\right)\right)& \dots & f\left(\alpha \left({\epsilon }^{-}+{\xi }_{N-1}\right)\right)& 1\end{array}\right)\left(\begin{array}{c}{\mathit{w}}_{21}\left(1\right)\\ ⋮\\ {\mathit{w}}_{21}\left(N-1\right)\\ b_{21}\end{array}\right)=\left(\begin{array}{c}{\mathit{y}}_1\left(1\right)\\ {\mathit{y}}_2\left(1\right)\\ ⋮\\ {\mathit{y}}_N\left(1\right)\end{array}\right)$$

This multiplication constant is applied to the normal vector (10) and to biases/shifts d_i (13). Based on Lemma A2 (Appendix D), there exist α for which the rank of H becomes N, i.e., such a matrix is regular and can be used to solve (18). This class of functions comprises sigmoid-type functions that play important theoretical and practical roles in ANNs.

Remark 3.

The multiplication of affine hyperplanes by −1, as applied in (4) and (11), is completed only to allow a direct use of Relu, Heaviside, and sigmoid-type activation functions that are very common. If this is not needed it can be skipped. Then, however, a different class of activation functions must be used. Such a class of function would be redefined to g(x) = f(−x) as given in (16) and (19), and large enough, but still negative constants would have to be added to columns of the dot-product matrix (17). This is to secure negative diagonal and positive below-diagonal elements prior to the application of g(x). This secures H to be regular in the case of (16) or for some positive α in the case of (19).

Remark 4.

The construction of the dot-product matrix required input samples to be sorted across dimensions. It should be noted that this was only to show that such a matrix is upper triangular with non-zero diagonal elements, and therefore must be regular; however, a permutation of rows (samples) as well as columns (hyperplanes) can be realized by elementary matrix operations, and therefore even such an “unordered” matrix is also regular [24]. Thus, this step is not necessary, although it can significantly simplify the computation of (18). In this case, the input sample x_i satisfying:

$${\mathit{x}}_j^{\mathrm{T}}\left(\begin{array}{c}1\\ w_2\\ ⋮\\ w_d\end{array}\right)-{\mathit{x}}_i^{\mathrm{T}}\left(\begin{array}{c}1\\ w_2\\ ⋮\\ w_d\end{array}\right)\le 0, \forall j=1,\dots ,N | i\ne j,$$

is omitted in the construction of N − 1 hidden layer neurons.

Remark 5.

The basic proof primarily addressed Q^D →R mapping. Nevertheless, it can be easily extended to Q^D →R^M mapping. In this case, the construction of separating affine hyperplanes and the hidden output matrix, as appeared in (18), remain unchanged, i.e., the hidden layer as a whole. Now, the network has M output neurons, while the hidden ones remain intact. Thus, only the weights and biases of additional output neurons must be calculated independently of each other, e.g., in the case of Heaviside function by:

$$\left(\begin{array}{cccc}1& 1& \dots & 1\\ 0& 1& \dots & 1\\ ⋮& ⋮& \ddots & 1\\ 0& 0& \dots & 1\end{array}\right)\left(\begin{array}{c}{\mathit{w}}_{2j}\left(1\right)\\ ⋮\\ {\mathit{w}}_{2j}\left(N-1\right)\\ b_{2j}\end{array}\right)=\left(\begin{array}{c}{\mathit{y}}_1\left(j\right)\\ {\mathit{y}}_2\left(j\right)\\ ⋮\\ {\mathit{y}}_N\left(j\right)\end{array}\right),j=2,\dots ,M$$

(20)

where y_i(j) i = 1, …, N, denotes N output values for j-th output neuron (j-th dimension of y). Therefore, a SLFN performing Q^D →R^M mapping of N samples has N − 1 hidden and M output neurons. There are altogether D − 1 + M(N − 1) trainable weights and N − 1 + M trainable biases. To calculate all free parameters, it is enough to solve M systems of linear equations as in (20) and one system given in (10), i.e., all expressed as triangular matrices.

4. Results

This construction method was tested with respect to two aspects, i.e., its practical limitations and in comparison to similar methods. In addition, the performance of back propagation-based (BP) training was evaluated on the test data as well.

4.1. Performance of the Proposed Method

Although Theorem 1 gives an upper bound on the number of hidden neurons, it can be directly used to train SLFNs depending on the precision of the training data and applied arithmetic. To show its abilities, three kinds of random data were generated for each test, i.e., 3000 samples in 2, 50, and 60 dimensions, satisfying Δ = 10⁻⁶ (a sample precision). Both classification and mapping errors were measured, whereas the output values were random samples from the set {0, 1}. Classification errors were calculated after converting ANN outputs to binary classes, i.e., y < 0.5 → {0}, and y ≥ 0.5 → {1}. The mapping errors were evaluated by mean square errors (MSE). All calculations were realized in the Python 3.6.9 environment [25] using double float arithmetic. The results are listed in

Table 1. Performance of the proposed algorithm for different dimensions and activation functions in the case of 3000 training samples; precision Δ = 10⁻⁶, number of tests = 100.

Dimension	Input Sample Bounding Space Size	Number of Grid Points	Activation Function	Number of Trainable Parameters	Ratio of Found Nets (0 Classification Error) [%]	MSE
2	1 × 2	≈2 × 1012	Heaviside	6000	100	0.0
50	1 × 2 × 1 × … × 1	≈2 × 10300	Heaviside	6048	100	0.0
60	1 × 2 × 1 × … × 1	≈2 × 10360	Heaviside	6058	0	-
2	1 × 2	≈2 × 1012	Relu	6000	100	2.37 × 10−18
50	1 × 2 × 1 × … × 1	≈2 × 10300	Relu	6048	100	1.59 × 10−17
60	1 × 2 × 1 × … × 1	≈2 × 10360	Relu	6058	0	-
2	1 × 2	≈2 × 1012	tanh, α = 1	6000	100	4.27 × 10−28
50	1 × 2 × 1 × … × 1	≈2 × 10300	tanh, α = 1	6048	100	0.0
60	1 × 2 × 1 × … × 1	≈2 × 10360	tanh, α = 1	6058	0	-

for the tested activation functions and generated data. As can be seen, for the selected precision (Δ), bounding subspace, double precision arithmetic, and the number of samples, a reasonable limit on the number of dimensions is 50, e.g., for 60 dimensions, no network was found providing error-free classification due to numerical overflows. For a sample precision of Δ = 10⁻¹⁰ (not shown in the table) the allowable number of dimensions dropped to 30, e.g., for 40 dimensions no network was found providing a perfect classification.

4.2. Comparison to Similar Approaches

The proposed method was compared to other similar approaches, i.e., algorithms that theoretically provide zero-error mapping in a fixed number of steps, while minimizing the number of hidden neurons in a SLFN. The comparison was performed in terms of the number of neurons, the number of trainable and free parameters, training times, MSE, and the ratio of successfully found networks, i.e., networks where the maximum mapping error (absolute difference) did not exceed 10⁻⁹. All algorithms were implemented as described in their articles except of [13]. It was found that a bias vector given in [13] (Equation (8)) could not be used because it had a wrong size, i.e., N − 1 and it should be N, when applied in [13] (Equation (9)) so that H can be invertible for all N input samples. Thus, in the present implementation, the correct bias vector was derived in the following form: $b={\left(-{\mathit{X}}_{i1}+k\left({\mathit{X}}_{i1}-{\mathit{X}}_{i2}\right),-{\mathit{X}}_{i2}+k\left({\mathit{X}}_{i2}-{\mathit{X}}_{i3}\right),\dots ,-{\mathit{X}}_{iN-1}+k\left({\mathit{X}}_{iN-1}-{\mathit{X}}_{iN}\right),-{\mathit{X}}_{iN}+1\right)}^{\mathrm{T}}, 0<k<1$. X is an input data matrix having training vectors in its columns and i is the dimension in which all samples are different (requirement of the method). This secures to produce a lower triangular matrix H in [13] (Equation (9)). In [12], the authors did not specify exact hyperparameters x₁, and x₂ that were set to 0 and 5, respectively, securing regular matrices H in all experiments.

All methods were implemented in the Python 3.6.9 environment using a double float precision. In the case of [16], the least mean square method as implemented in Python 3.6.9 was used to solve potentially irregular matrices H. Training vectors were randomly generated from a hypercube with the finite precision of Δ = 10⁻¹⁰ and labels from the closed interval [0, 1]. Results for easy-to-map data, i.e., 100 vectors in 30 dimensions and a challenging case, i.e., 3000 vectors in 2 dimensions, are listed in

Table 2. Comparison of zero-error construction methods for different number of samples and dimensions; input precision Δ = 10⁻¹⁰, bounding space: hypercube of the size 1, number of tests = 100.

Methods	Dimension	Number of Samples	Number of Hidden Neurons	Number of Trainable Parameters	Ratio of Found Nets (Approx. Error ≤10−9) (%)	Average Training Time (ms)	MSE
proposed	30	100	99	228	100	1	3.2 × 10−31
[11]	30	100	99	3169	100	6	1.2 × 10−28
[12]	30	100	100	3070	100	2.5	1.3 × 10−29
[16]	30	100	100	100 3200 *	100	5	1.25 × 10−21
[13] revised	30	100	100	200	93	1	1.67 × 10−21
proposed	2	3000	2999	6000	100	210	1.2 × 10−28
[11]	2	3000	2999	11,997	0	-	-
[12]	2	3000	3000	11,998	100	400	3.8 × 10−27
[16]	2	3000	3000	3000 9000 *	0	-	-
[13] revised	2	3000	3000	6000	0	-	-

* The number of all free parameters; most of which were set randomly from the Normal distribution.

. As can be seen, there were only two algorithms reaching the least upper bound (N − 1 neurons), i.e., the proposed one and that one in [11]. When considering the number of parameters that must be computed, the lowest number was reported in [16]. Nevertheless, when the number of all free parameters was regarded, the method in [13] and the proposed one were more efficient. This is because most of the weights in [16] were set randomly from the Normal distribution. The most robust methods, i.e., methods producing the desired networks in 100% of tests, were the proposed one and the method in [12]; however, when comparing the average training times, the proposed one was approx. two times faster, and together with [13] these were the fastest methods.

4.3. Comparison to Back Propagation-Based Approach

To assess the performance of the proposed method in the context of the ubiquitous BP algorithm, BP-based training was applied to the test data in terms of both classification and mapping tasks. Feed forward networks with one and two hidden layers were implemented and trained in the Keras (version 2.2.4) system run on PC Intel core i7, 3.5 GH, 16 GB RAM, 64 bit Windows 10 professional, i.e., the same platform for all tests. Several optimizers (Adam, SGD, RmsProbs), in combination with loss functions (MSE, cross entropy) and learning rate schemes were tested. Here, the best performing settings (on average) were used, i.e., Adam optimizer, MSE loss, exponential learning decay (0.001–0.0001), maximum number of epochs 1.5 × 10⁴, and Relu activation functions. Training vectors were randomly generated from a hypercube with a finite precision of Δ = 10⁻⁶; no networks were successfully trained for finer precisions, e.g., Δ = 10⁻¹⁰, partly due to numerical limitations. In the case of the classification tests, binary outputs were generated randomly, whereas in the mapping tests the outputs were random float numbers from the interval [0, 1]. The results, i.e., the ratios of networks with zero-classification errors, ratios of networks having mapping errors not greater than 10⁻³, training times for classification and mapping tests, and the number of free parameters, for the different network structures and the tested data are listed in

Table 3. Performance of BP-based training on different data and network structures (number of neurons in hidden layers); input finite precision Δ = 10⁻⁶, max. number of epochs 1.5 × 10⁴, number of tests 20.

Neurons in Hidden Layers	Dimension	Samples	Free Parameters	Found Nets (Zero Classification Error) (%)	Average Training Time (Zero Classification Error) (ms)	Found Nets (Approx. Error ≤10−3) (%)	Average Training Time (Approx. Error ≤10−3) (ms)
[100]	30	100	3201	75	587	0	- *
[1000]	30	100	32,001	85	408	0	-
[3000]	30	100	96,001	95	446	0	-
[5000]	30	100	160,001	90	497	0	-
[100, 10]	30	100	4121	75	603	0	-
[500, 10]	30	100	20,501	85	496	0	-
[1000, 10]	30	100	41,021	80	467	0	-
[3000]	2	3000	12,001	0	-	0	-
[6000]	2	3000	24,001	0	-	0	-
[10,000]	2	3000	40,001	0	-	0	-
[3000, 100]	2	3000	≈3 × 105	0	-	0	-
[6000, 100]	2	3000	≈54 × 105	0	-	0	-

* Training times not provided for networks that did not converge below the pre-set threshold.

. It can be seen that for the challenging case (3000 2D samples) no network having a zero-classification error was found, while networks with one and two hidden layers and a wide range of neurons were tested. The same holds for the mapping tests (max. mapping error ≤ 10⁻³), both for the easy-to-map case (100 30D samples) and the challenging one. The most successful networks for 100 30D samples and the classification task were SLFNs with a number of neurons ranging from 1000 to 5000. In that case the average training time was 450 ms, requiring approx. 54 training epochs (not listed in the table).

5. Discussion

Based on the proofs, analyses and experiments, several findings and comments can be made as follows:

The assumed constrain, i.e., finite number of rational samples located in a finite size space, is very weak and not limiting when using a standard representation of numbers in digital computers (floating points). Thus, this construction and the least upper bound focus directly on data as they appear in digital computers.

The number of neurons increases linearly with the number of training samples. For a fully connected SLFN, the number of free parameters would be N(D + M + 1) − D − 1; however, due to the massive weight sharing in the hidden layer (the same normal vector) and the hyperplane normalization, there are only (N − 1)(M + 1) + D − 1 + M free parameters. Therefore, the sample dependent growth of free parameters is significantly lower, i.e., (N − 1)(M + 1) compared to N(D + M + 1) as in a standard SLFN.

The shared hidden layer weights are given only by the input data format (10).

Several limit testing experiments have shown that this constructional bound can be used directly to train networks on various samples, e.g., it was capable to map 3000 50-dimensional samples expressed to 6 decimal places using Heaviside, Relu and tanh (with α = 1) functions. Such calculations required currently the standard double float precision. The worst MSE was observed for the Relu function, but was still less than 1.6 × 10⁻¹⁷; in the case of Heaviside function the displayed MSE was 0.0, i.e., approx. less than 10⁻³²⁰ as tested in the Python 3.6.9 environment.

In practice, such an approach has its numerical limitations, therefore it cannot be safely used for high dimensional data, e.g., D > 50 with the sample precision of Δ ≤ 10⁻⁶ or D > 30 and Δ ≤ 10⁻¹⁰ using double float arithmetic. These limits can be naturally extended by using, e.g., quadruple or octuple arithmetic.

In the construction process, it is naturally assumed that the precision Δ of input samples is known. If this is not the case for any reason, such a parameter can still be calculated (least common multiple) for each dimension separately, as stated in the proof of Lemma A1. Nevertheless, this can be computationally expensive, but it can still increase numerical stability.

It was not explicitly mentioned, but each hidden neuron can implement a different activation function satisfying (16), as it still secures a triangular matrix in (18).

Compared to other similar approaches (Table 2), the proposed method reaches the least upper bound (N − 1 neurons) as well as the approach in [11]; however, the proposed one is approx. six times faster and uses significantly fewer free parameters, e.g., in case of 100 30D samples it is 228 vs. 3169. Moreover, the proposed method is more robust, i.e., for 3000 2D samples the approach in [11] was not able to realize any random mapping in 100 tests meeting the required precision (10⁻⁹). The proposed method and the method in [12] were the only ones able to find all networks in all experiments, which shows their higher robustness. Nevertheless, the proposed one is faster and uses fewer free parameters, e.g., in case of 100 30D samples it is 228 vs. 3070 and is approx. 2.5 times faster. In terms of the number of trainable parameters, the best method is in [16], which randomly sets most of the free parameters, therefore, it may not always find the exact mapping; however, considering all free parameters, the most efficient method in [13] is followed by the proposed one. Finally, given the training time, the proposed method and that one in [13] are the fastest.

A standard BP-based training was used on the test data to assess the performance of the proposed and other similar approaches. In mapping tests, i.e., where the maximal absolute error is not greater than 10⁻³, no networks having one or two hidden layers and a wide range of neurons were found (max. number of epochs was 1.5 × 10⁴). This shows how challenging it is for BP-based approaches to map such data while meeting this precision. On the other hand, the proposed method and the method in [12] found all networks even with maximal errors not greater than 10⁻⁹. In the classification task, while deploying proper networks and easy-to-classify data (100 30D samples), the BP-based design led in most cases (85–95%) to zero-classification errors; however, such networks required a lot of neurons and a large number of free parameters compared to the proposed and other similar methods. The same findings also apply to training times that were much longer for BP-based methods, i.e., more than 100 times, requiring on average more than 50 training epochs.

Although it is obvious, it should be emphasized that such a training process produces an inconsistent estimator, as it is not aimed at generalizing training data. It is designed to provide the required mapping in a fixed number of steps and to minimize the number of neurons. Instead, BP-based approaches deploying different regularizations, e.g., [23], are vital to achieve a high degree of generalization and robustness when processing noisy or incomplete data. This is undertaken by introducing some redundancy in the form of additional neurons and free parameters; however, such an algebraic training can be used as a quick initialization before the training process that uses additional data and more complex networks (additional neurons).

6. Conclusions

The article presents a new zero-error construction method applicable to feed forward neural networks. In particular, it is focused on the construction of zero-error mapping networks having the minimum possible number of layers and neurons. The design defines the exact structure of the network, the calculation process of free parameters (weights and biases), the classes of supported activation functions, and the conditions for mapping functions that the network can express. The design is unique because it is based on the representation of numbers in digital computers processing floating-point data. Since this construction process has been shown to provide an exact mapping of N samples, this method is also the least upper bound on the number of hidden neurons. Therefore, the presented method addresses three major problems at the same time, i.e., the complexity, density, and training of feed forward networks.

The main theoretical and practical contributions can be summarized as follows:

A new design of a zero-error mapping neural network with the minimal number of neurons and layers. This design and proof are unique because they assume rational numbers (floating-point data).

The resulting structure is very efficient in terms of free parameters because all weights in the hidden layer are shared and do not depend on the input data, i.e., they are given by the data format instead.

The design and its proof constitute the least upper bound on the number of hidden neurons needed for an exact mapping/classification.

Two new and broad sets of supported activation functions, for which the proof holds, were introduced. Moreover, these sets include common functions in the domain of ANN as Relu, sigmoid, tanh, Heaviside, etc.

A very relaxed condition for mapping functions was derived, i.e., it is enough that they are bounded.

A very efficient calculation process was introduced, i.e., for an exact mapping of N samples from the D dimensional space to the M dimensional one it is enough to solve M + 1 regular systems of linear equations. Moreover, all these systems exist in forms of upper or lower triangular matrices, thus the process is very fast and simple.

In comparison to similar methods, the proposed one (as shown in Table 2) achieves the least upper bound (together with [11]), is robust, i.e., it found 100% of networks (together with [12]), is fast (best together with [13]) and uses few free parameters (2nd most efficient).