Metaheuristic Extreme Learning Machine for Improving Performance of Electric Energy Demand Forecasting

Abstract

Electric energy demand forecasting is very important for electric utilities to procure and supply electric energy for consumers sufficiently, safely, reliably, and continuously. Consequently, the processing time and accuracy of the forecast system are essential to consider when applying in real power system operations. Nowadays, the Extreme Learning Machine (ELM) is significant for forecasting as it provides an acceptable value of forecasting and consumes less computation time when compared with the state-of-the-art forecasting models. However, the result of electric energy demand forecasting from the ELM was unstable and its accuracy was increased by reducing overfitting of the ELM model. In this research, metaheuristic optimization combined with the ELM is proposed to increase accuracy and reduce the cause of overfitting of three forecasting models, composed of the Jellyfish Search Extreme Learning Machine (JS-ELM), the Harris Hawk Extreme Learning Machine (HH-ELM), and the Flower Pollination Extreme Learning Machine (FP-ELM). The actual electric energy demand datasets in Thailand were collected from 2018 to 2020 and used to test and compare the performance of the proposed and state-of-the-art forecasting models. The overall results show that the JS-ELM provides the best minimum root mean square error compared with the state-of-the-art forecasting models. Moreover, the JS-ELM consumes the appropriate processing time in this experiment.

1. Introduction

For several decades, electric energy has been essential for living, and it is a basic utility that governments must provide for their people. Indeed, power utilities or electricity providers must procure and supply electric energy to consumers sufficiently, safely, reliably, and continuously [1]. In order to achieve all those factors previously mentioned, forecasting electric energy demand is necessary for utilities. Forecasting is the famous well-known method that learns the historical data and then predicts the expected data [2]. Many works have used various forecasting models [3], such as the dynamic regression model [4], ARIMA model [5], exponential smoothing model [6], neural network model [7], and so on, to generate the trend of future forecasted data and select the best model that is evaluated from its performance and accuracy.

Many researchers have proposed machine learning models to increase the accuracy of electric energy demand forecast. Gholamreza Memarzadeh and Farshid Keynia [8] proposed the new optimal long short-term memory model to predict electric energy demand and price based on Pennsylvania, New Jersey, and Maryland databases. Zongying Liu et al. [9] proposed the novel adaptive method applied with the kernel ELM model called the error-output recurrent two-layer ELM and used the quantum particle swarm optimization to increase the forecast accuracy of the time-series predicted demand. Mikel Larrea et al. [10] proposed the particle swarm optimization algorithm to optimize weight parameters in the ensemble ELM model for forecasting the Spanish time-series electric consumption. Yanhua Chen et al. [11] proposed the empirical mode decomposition to decompose the time-series forecasting data and mixed kernel with radial basis function and UKF to implement on the ELM model. The New South Wales, Victoria, and Queensland electric load databases were used for testing the proposed model. Qifang Chen et al. [12] proposed the novel deep learning model by using the stacked auto-encoder framework applied to the ELM model to improve the capabilities of forecasting. Moreover, the raw time-series data were analyzed by using the empirical mode decomposition method. Shafiul Hasan Rafi et al. [13] proposed the hybrid methodology of deep learning by integrating the convolutional neural network and long short-term memory to improve the forecast accuracy for forecasting the Bangladesh power system dataset. Muhammad Sajjad et al. [14] proposed the hybrid convolutional neural network and gated recurrent units to maximize forecast performance for appliance energy demand and individual household electric power demand. Yusha Hu et al. [15] proposed the optimization methods consisting of the genetic algorithm and particle swarm optimization applied to the backpropagation model to forecast the electric demand dataset. Mohammad-Rasool Kazemzadeh et al. [16] proposed the novel hybrid optimization method, which combines the particle swarm optimization with a machine learning model, to forecast the long-term electricity peak demand and electric energy demand. Ghulam Hafeez et al. [17] proposed the novel hybrid model of modified mutual information, factored condition restricted Boltzmann machine, and genetic wind driven optimization to forecast the hourly load data of FE, Dayton, and EKPC USA power grids.

From the aforementioned works, one of the machine learning models that can learn rapidly and provide acceptable results is the Extreme Learning Machine (ELM) [18]. The concept of this model is to learn the data without iterative tuning in the hidden layer phase and then calculate the output weight parameter with a pseudo-inverse matrix called the Moore–Penrose inverse matrix [19] in the output layer phase. However, the disadvantage of the ELM model [20,21,22] is that it uses the standard randomization of the input weight to compute in the input layer phase that can cause overfitting and has a high probability to fall into local optima.

To improve the performance of the electric energy demand forecasting model, this paper proposes a method to develop the ELM model by using metaheuristic optimization algorithms to adjust the appropriate result of the output weight, which can reduce the cause of overfitting. The Jellyfish Search Optimization (JSO) [23], the Harris Hawk Optimization (HHO) [24], and the Flower Pollination Algorithm (FPA) [25] were selected for adjusting the output weight and reducing the cause of overfitting as mentioned before. The performances of these three proposed forecasting models were evaluated via an experiment that used the seven groups of the electric energy demand datasets in Thailand. The main contributions of this work can be summarized as follows:

• This paper presents the novel hybrid method combining the ELM and metaheuristic optimization consisting of the JSO, the HHO, and the FPA to forecast the electric energy demand. Furthermore, the proposed model is investigated with the real-life dataset of electric energy demand to challenge the forecasting performance in terms of forecasting accuracy and stability.
• To increase the robustness of forecasting in the training and testing processes of the traditional ELM model, the randomization process of the initial weight parameter in the ELM is developed to obtain the optimal weight parameter. The proposed metaheuristic optimization algorithms are not complex to implement, leading to less processing time, low population usage, and fast convergence to the optimal solution. In addition, these three optimization methods can reduce the number of hidden nodes of the ELM model.
• Finally, the presented metaheuristic algorithms (the JSO, the HHO, and the FPA) have the characteristic of being self-adaptive to tune the weight parameter of the ELM without trapping in the local optima. This characteristic can increase the forecasting stability of the traditional model. Furthermore, this method can reduce the cause of sensitivity to outliers, which leads the forecasting process to be more stable, and the standard deviation was used to calculate the forecasting stability of the proposed models.

This paper is organized as follows. Section 2 indicates the basic principles of the algorithms used in this paper. Section 3 indicates the methodology of the datasets’ preparation and the proposed models. Section 4 indicates the overall experimental results using the datasets and the proposed models in Section 3. Lastly, the conclusion and future work of this work are described in Section 5.

2. Basic Principles

This section describes the basic principles and materials used in this research, which consists of forecasting methodology, ELM, JSO, HHO, FPA, a summary of selected metaheuristic optimization, and related works as shown below.

2.1. Forecasting Methodology

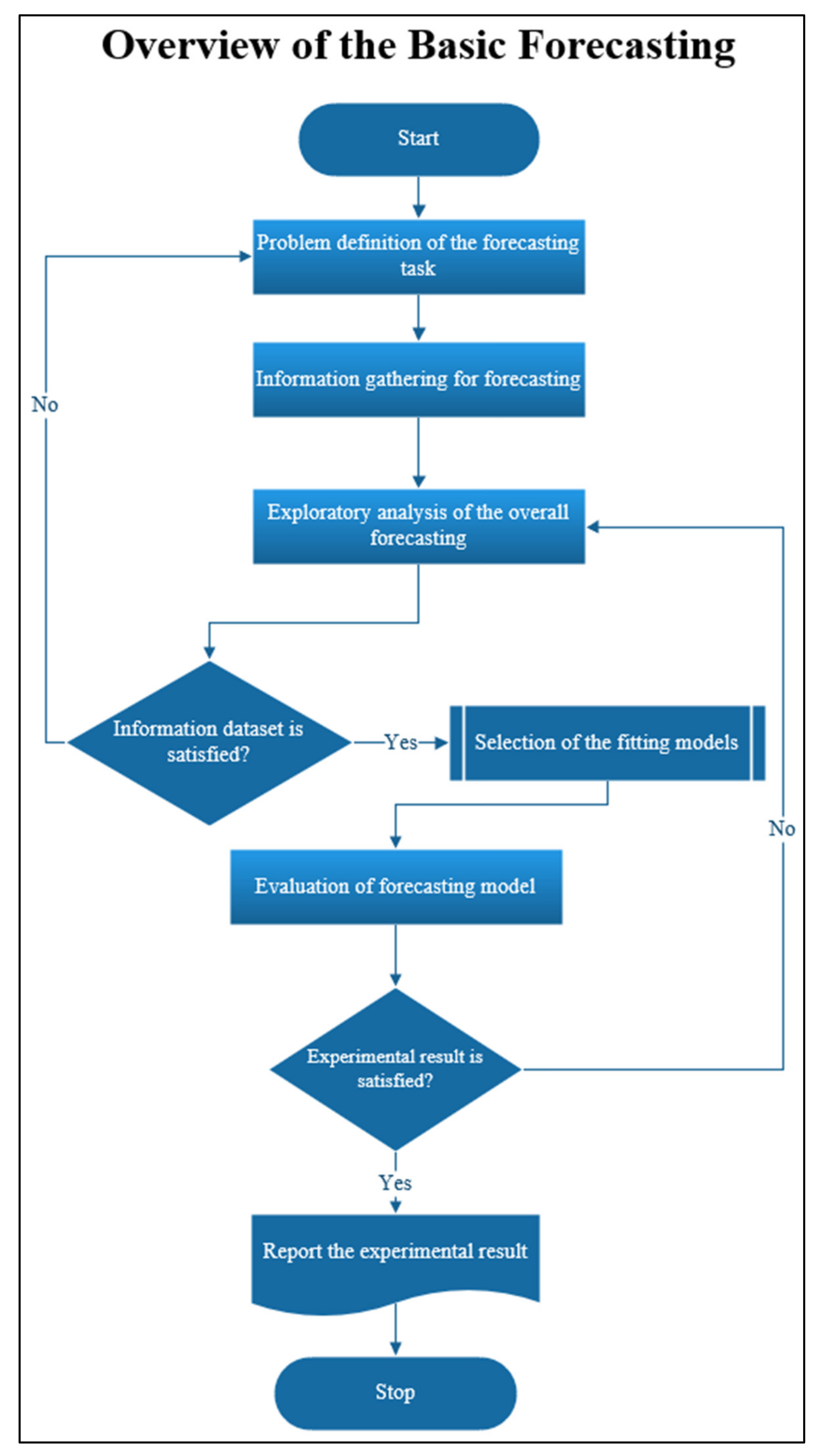
The basic methodology for forecasting (Figure 1) can be described in five steps [26] as follows. Firstly, the forecasting task problem is defined; the aim of this step is to study the problem and factors that can affect the outcome of forecasting. Secondly, the information is gathered for forecasting; the aim of this step is to collect and analyze the significant data needed for forecasting and finding the expected result [27]. Thirdly, the exploratory analysis of the overall forecasting is conducted; the aim of this step is to actively analyze the consistency of data to so that they can be implement without noise or elements missing in the dataset such as the imbalance or inconsistency of data [28], missing values of data [29], and so on. Fourthly, the fitting models are selected; this step is the key of this research, which proposes the new model to increase the performance of the forecasting. Fifthly, the evaluation of the forecasting model is conducted, this step aims to consider and evaluate the experimental results obtained from all models and then select the best model for forecasting. The performances of all models [30] can be compared by considering error metrics such as the Mean Absolute Error (MAE), Mean Absolute Percentage Error (MAPE), Root Mean Square Error (RMSE), and so on.

2.2. Extreme Learning Machine

The Extreme Learning Machine (ELM) was proposed by Guang-Bin Huang et al. [18]. Due to the non-iterative tuning model, the training time of the ELM model was faster than other machine learning models in the hidden layer.

Figure 2 is the architecture of the ELM model. The structure of this model has three layers. The first layer is the input layer, which imports the sample dataset $\left(a_j,t_j\right)$ of input data $\left(a_j={\left[a_{j1},a_{j2},a_{j3},\dots ,a_{jn}\right]}^T\in R^n\right)$ and target data $\left(t_j={\left[t_{j1},t_{j2},t_{j3},\dots ,t_{jm}\right]}^T\in R^m\right)$ where $n$ is the number of instances of data with $j=1,2,\dots ,n$. After the input layer step is completed, the second hidden layer is calculated as shown as in (1).

$${\displaystyle \sum }_{i=1}^L{\beta }_i{g}_i\left(a_j\right)={\displaystyle \sum }_{i=1}^L{\beta }_{i}g\left(w_i·a_j+b_i\right)=e_j$$

(1)

where $w_i$ is the initial weight randomization, ${\beta }_i$ is the connecting weight of hidden nodes and output nodes, $L$ is the random number of hidden nodes, and $g\left(a\right)$ is the activation function. Equation (1) can be revised to a short equation defined as the matrix, as in (2).

$$H\beta =T$$

(2)

where $H=\left[\begin{array}{c}h\left(a_1\right)\\ ⋮\\ h\left(a_N\right)\end{array}\right]={\left[\begin{array}{ccc}G\left(w_1,b_1,a_1\right)& \cdots & G\left(w_L,b_L,a_1\right)\\ ⋮& \ddots & ⋮\\ G\left(w_1,b_1,a_N\right)& \cdots & G\left(w_L,b_L,a_N\right)\end{array}\right]}_{NxL}\beta ={\left[\begin{array}{c}{\beta }_1^T\\ ⋮\\ {\beta }_L^T\end{array}\right]}_{Lxm}$ and $T={\left[\begin{array}{c}{t}_1^T\\ ⋮\\ t_L^T\end{array}\right]}_{Nxm}$.

After the hidden layer step is completed, the aim of the third output layer step is to find the β matrix; Equation (2) is inversed to Equation (3) as shown below.

$$\beta =H^{†}T$$

(3)

where $H^{†}$ is the Moore–Penrose pseudo-inverse [19] of the $H$ matrix.

Due to the problem of overfitting of the ELM model [20], this paper proposes a method to find the optimal weight parameter with the metaheuristic optimization that can reduce the cause of the overfitting.

2.3. Jellyfish Search Optimization

Jellyfish Search Optimization (JSO) was proposed by Jui-Sheng Chou and Dinh-Nhat Truong [23]. The main idea of this optimization was inspired by the nature of jellyfish behavior in the ocean when hunting prey for their food [32]. Figure 3 is the JSO algorithm flowchart that can be described as follows:

• Define the objective function ($f\left(X\right)$) in terms of $X={\left(x_1,\dots ,x_d\right)}^T$, the best location parameter ($X^{\ast }$), the number of search space, the number of population ($N$), the max iteration ($T$), the iteration cycle time starting from 1 to max iteration ($t$). Jellyfish population $\left(X_i\right)$ is initialized with a logistic chaotic map [33].
• Calculate the control time ($c\left(t\right)$) as presented in (4).

  $$c\left(t\right)=\left|\left(1-\frac{1}{T}\right)\times \left(2\times rand\left(0,1\right)-1\right)\right|$$

  (4)

  where $rand\left(0,1\right)$ is the number of randomization from 0 to 1, which changes in every iteration.

If the control time is greater than or equal to 0.5 ($c\left(t\right)\ge 0.5$), then the jellyfish decides to follow the ocean tides as shown in (5). Otherwise, the movement of jellyfish to the swarm is calculated by Equation (7).

$$\stackrel{\rightharpoonup }{trend}=X^{\ast }-\beta \times rand\left(0,1\right)\times \mu$$

(5)

where $\stackrel{\rightharpoonup }{trend}$ is the direction of the ocean tides, $\beta$ is a distribution coefficient that is greater than 0 ($\beta >0),$ and $\mu$ is the mean location of all jellyfishes.

After that, jellyfish live at the new position that can be calculated as shown as in (6).

$$X_i\left(t+1\right)=X_i\left(t\right)+rand\left(0,1\right)\times \left(X^{\ast }-\beta \times rand\left(0,1\right)\right)\times \mu$$

(6)

If $rand\left(0,1\right)$ is greater than $1-c\left(t\right)$, then jellyfish show the passive motions, which can be calculated by Equation (7). Otherwise, jellyfish show the active motions by deciding the direction as shown by Equation (8).

$$X_i\left(t+1\right)=X_i\left(t\right)+\gamma \times rand\left(0,1\right)\times \left(U_b-L_b\right)$$

(7)

where $\gamma$ is the motion coefficients, and $U_b$ and $L_b$ are upper bound and lower bound, respectively.

$$\stackrel{\rightharpoonup }{Step}=X_i\left(t+1\right)-X_i\left(t\right)=rand\left(0,1\right)\times \stackrel{\rightharpoonup }{Direction}$$

(8)

where $\stackrel{\rightharpoonup }{Step}$ is the direction of the movement of jellyfish and $\stackrel{\rightharpoonup }{Direction}$ can be decided by Equation (9).

$$\stackrel{\rightharpoonup }{Direction}=\left\{\begin{array}{c}{X}_j\left(t\right)-X_i\left(t\right)\\ X_i\left(t\right)-X_j\left(t\right)\end{array}\begin{array}{c} if f\left(X_i\right)\ge f\left(X_j\right)\\ if f\left(X_i\right)<f\left(X_j\right)\end{array}\right\}$$

(9)

3.

Update the new position of the jellyfish and the best location parameter.

4.

Repeat step 2 until the iteration reaches the max iteration criterion.

The JSO algorithm is used to optimize the weight parameter in the ELM model that is described in Section 3.3.

2.4. Harris Hawk Optimization

The Harris Hawk Optimization (HHO) was proposed by Ali Asghar Heidari et al. [24]. The main idea of this optimization model came from the cooperative behavior and hunting of prey of Harris Hawk [34]. Figure 4 presents a flowchart of the HHO algorithm that can be described as follows:

• Define the objective function ($f\left(X\right)$) in terms of $X={\left(x_1,\dots ,x_d\right)}^T$, the location of rabbit (best location parameter) ($X^{\ast }$), the number of population ($N$), the max iteration ($T$), the iteration cycle time starting from 1 to max iteration ($t$), and initialize hawk population $\left(X_i\right)$.
• Specify the initial energy $\left(E_0\right)$ as in (10).

  $$E_0=2\times rand\left(0,1\right)-1$$

  (10)
• Specify the initial jump strength ($J$) as in (11).

  $$J=2\times \left(1-rand\left(0,1\right)\right)$$

  (11)
• Adjust the escaping energy of the prey ($E$) as in (12).

  $$E=2E_0\left(1-\frac{t}{T}\right)$$

  (12)
• If $\left|E\right|\ge 1$, then go to the exploration phase as in (13).

  $$\begin{array}{l}\mathrm{If} q\ge 0.5\text{:}\\ X\left(t+1\right)=X_{rand}\left(t\right)-ran{d}_1\left(0,1\right) \left|X_{rand}\left(t\right)-2ran{d}_2\left(0,1\right)X\left(t\right)\right|\\ \mathrm{If} q<0.5:\\ X\left(t+1\right)=\left(X^{\ast }-X_m\left(t\right)\right)-ran{d}_3\left(0,1\right)\left(L_b+ran{d}_4\left(0,1\right)\left(U_b-L_b\right)\right)\end{array}$$

  (13)

  where $X_{rand}\left(t\right)$ is the random position of the currently selected hawk, $X_m\left(t\right)$ is the average position of the current population, and $q$ is random numbers between 0 and 1.
• If $\left|E\right|<1$, then consider with four conditions of the exploitation phase as follows:

  6.1.

  If the instantly randomized number $\left(r\right)$ is greater than or equal to 0.5 $\left(r\ge 0.5\right)$ and $\left|E\right|\ge 0.5$, then go to the soft besiege as in (14).

  $$X\left(t+1\right)=\left(X^{\ast }-X\left(t\right)\right)-E\left|J{X}^{\ast }-X\left(t\right)\right|$$

  (14)

  6.2.

  If $r\ge 0.5$ and $\left|E\right|<0.5$, then go to the hard besiege as in (15).

  $$X\left(t+1\right)=X^{\ast }-E\left|X^{\ast }-X\left(t\right)\right|$$

  (15)

  6.3.

  If $r<0.5$ and $\left|E\right|\ge 0.5$, then go to the soft besiege with progressive rapid dives as in (16).

  $$X\left(t+1\right)=\left\{\begin{array}{ll}Y& if f\left(Y\right)<f\left(X\left(t\right)\right)\\ Z& if f\left(Z\right)<f\left(X\left(t\right)\right)\end{array}\right.$$

  (16)

  where $Y$ is the next movement of the hawk as in (17).

  $$Y=X^{\ast }-E\left|J{X}^{\ast }-X\left(t\right)\right|$$

  (17)

  and Z is the random movement of the hawk with the levy flight concept as in (18).

  $$Z=\left(X^{\ast }-E\left|J{X}^{\ast }-X\left(t\right)\right|\right) S\times LF\left(D\right)$$

  (18)

  where $D$ is the dimension of the problem, $S$ is the $1\times D$ size of random vector and $LF$ is the levy flight function [35] as in (19).

  $$LF=0.01\times \frac{rand\left(0,1\right)\times {\left(\frac{\mathsf{\Gamma }\left(1+\beta \right)\times sin\left(\frac{\pi \beta }{2}\right)}{\mathsf{\Gamma }\left(\frac{1+\beta }{2}\right)\times \beta \times 2^{\left(\frac{\beta -1}{2}\right)}}\right)}^{\frac{1}{\beta }}}{{\left|rand\left(0,1\right)\right|}^{\frac{1}{\beta }}}$$

  (19)

  where $\beta$ is the default constant set to 1.5.

  6.4.

  If $r<0.5$ and $\left|E\right|<0.5$, then go to the hard besiege with progressive rapid dives as in (20).

  $$X\left(t+1\right)=\left\{\begin{array}{ll}Y& if f\left(Y\right)<f\left(X\left(t\right)\right)\\ Z& if f\left(Z\right)<f\left(X\left(t\right)\right)\end{array}\right.$$

  (20)

  where $Y$ is the next movement of the hawk as in (21).

  $$Y=X^{\ast }-E\left|J{X}^{\ast }-X_m\left(t\right)\right|$$

  (21)

  and Z is the random movement of the hawk with levy flight concept as in (22).

  $$Z=\left(X^{\ast }-E\left|J{X}^{\ast }-X_m\left(t\right)\right|\right)S\times LF\left(D\right)$$

  (22)

• Update the new position of the hawk and the location of the rabbit (best location parameter).
• Repeat step 4 until the iteration reaches the max iteration criterion.

The HHO algorithm is used to optimize the weight parameter in the ELM model that is described in Section 3.3.

2.5. Flower Pollination Algorithm

The Flower Pollination Algorithm (FPA) was proposed by Xin-She Yang [25]. The main idea of this optimization model was inspired by the nature of the pollination process of flowers. Figure 5 presents the FPA algorithm flowchart that can be described as follows:

• Define the objective function ($f\left(X\right)$) in terms of $X={\left(x_1,\dots ,x_d\right)}^T$, define the best location parameter ($X^{\ast }$), set the number of population ($N$), set the max iteration ($T$), set the iteration cycle time starting from 1 to max iteration ($t$), and initialize flower population $\left(X_i\right)$ and fixed switch probability set to 0.8 $\left(p=0.8\right)$.
• Define the random number between 0 and 1 and compare it with switch probability. If $rand\left(0,1\right)<p$, then go to the global pollination phase as in (23). Otherwise, go to the local pollination phase as in (24).

  $$X_i\left(t+1\right)=X_i\left(t\right)+LF\left(X_i\left(t\right)-X^{\ast }\right)$$

  (23)

  where LF is the levy flight function [35], which is defined as in (19).

  $$X_i\left(t+1\right)=X_i\left(t\right)+rand\left(0,1\right)\times \left(X_j\left(t\right)-X_k\left(t\right)\right)$$

  (24)

  where $X_j\left(t\right)$ and $X_k\left(t\right)$ are other populations obtained from a random position in terms of $t$.
• Update the new position of flowers and the best location parameter.
• Repeat step 2 until the iteration reaches the max iteration criterion.

The FPA algorithm is used to optimize the weight parameter in the ELM model that is described in Section 3.3.

2.6. Summary of the JSO, the HHO, and the FPA

As aforementioned, the Jellyfish Search Optimization, the Harris Hawk Optimization, and the Flower Pollination Algorithm are the metaheuristic algorithms inspired by animals’ and plants’ behavior in nature [36,37]. According to

Table 1. Benefits and Drawbacks of the JSO, the HHO, and the FPA.

Metaheuristic Algorithms	Benefits	Drawbacks
JSO	Fast calculation. Stability of the processing. Hard to trap in local optima.	There are quite a minor of related works due to the novel metaheuristic model (2020).
HHO	Hard to trap in local optima.	Slow calculation due to the complex steps of the algorithm.
FPA	Fast calculation due to the simple steps of the algorithm	Easy to trap in local optima.

, the benefits and drawbacks of the three metaheuristics are summarized. The benefits of JSO [23] include its fast speed to converge calculation, stability in the processing of the problem, and being hard to trap in local optima. However, the drawback of JSO is that there are quite a minor of related works because this optimization was a novel metaheuristics model in 2020. The benefit of HHO [38] is there are many steps of calculation that are hard to trap in local optima; however, the drawback of HHO is that it is slow to converge calculation. Finally, the benefits of FPA [39] are it is fast to converge calculation because the steps of this optimization are simple and easy to implement; however, the drawback of FPA is that it is easy to trap in local optima.

In conclusion, the three metaheuristic optimizations were merged with the ELM model to optimize the weight parameter, compare the three proposed models with the forecasting dataset, and evaluate the model with the error metrics objective function.

3. Data Preparation and Proposed Models

This section describes the technique of this research work, which consists of an overview of the electric energy demand datasets in Thailand, proposed data, and models used in the experiment to achieve the best result, the experimental setup and hyper-parameter settings for all proposed and state-of-the-art models, and performance evaluation of each model.

3.1. Preparation of Electric Energy Demand Data

Electric energy demand datasets were collected from Provincial Electricity Authority in Thailand (PEA), which can be accessed from references [40,41]. The scope of the electric energy demand datasets in this research was set from 2018 to 2020.

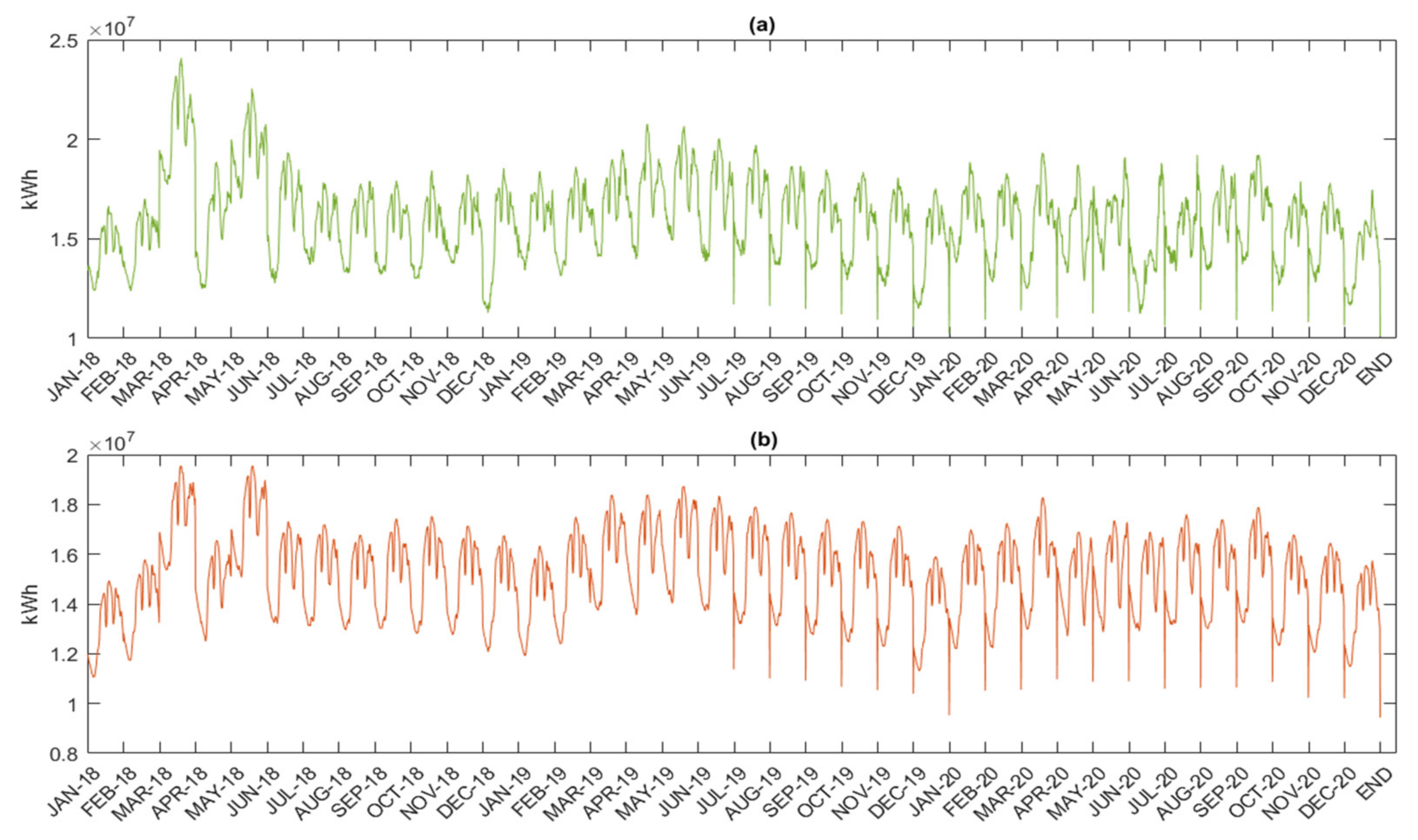
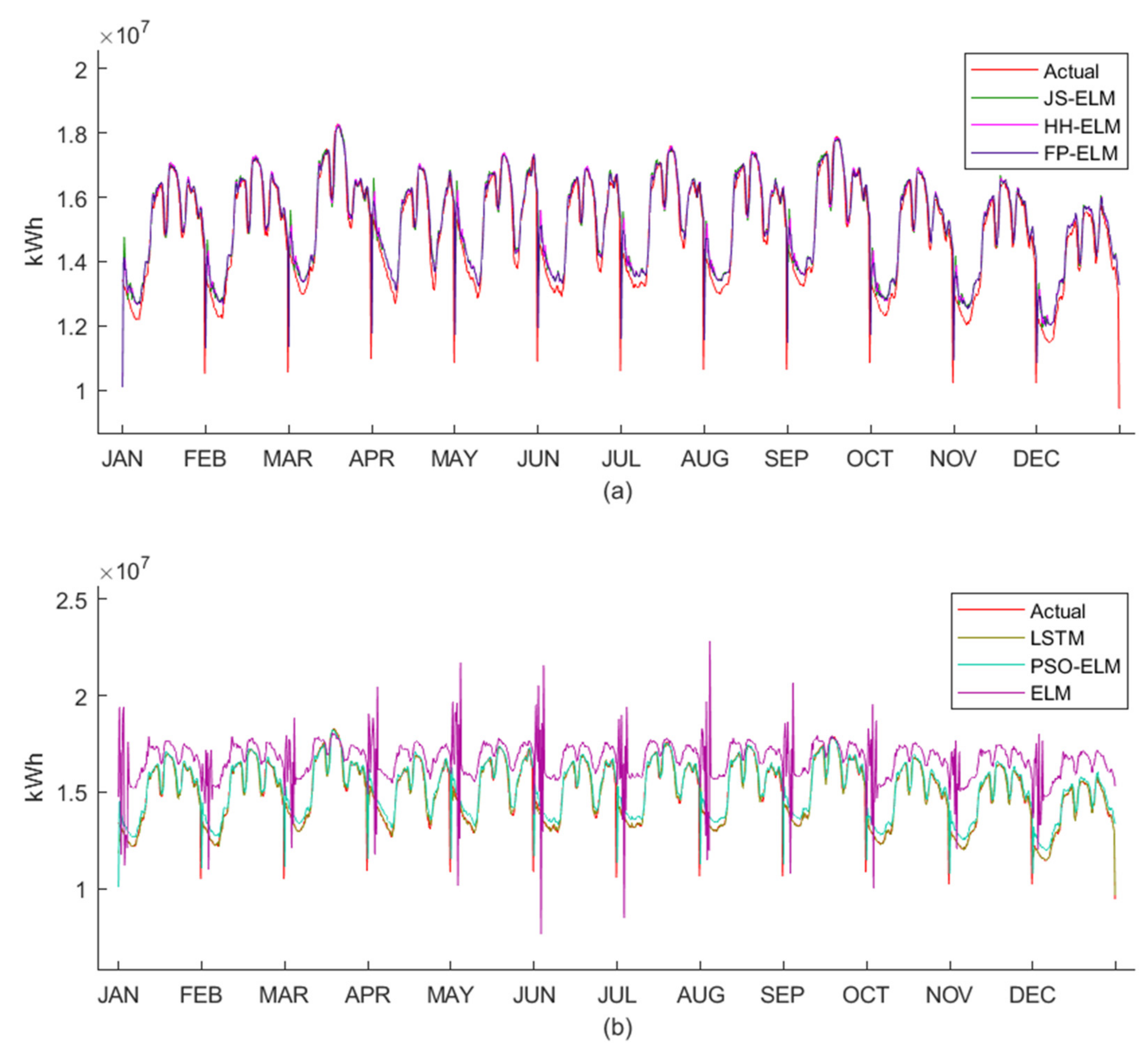
Figure 6a is the pattern of the monthly demand data of electric energy from January 2018 to December 2020 in terms of MegaWatt-Hour (MWh). The minimum electric energy demand is 9909 MWh in February 2018, the maximum electric energy is 12,752 MWh in May 2019, and the average electric energy demands in 2018, 2019, and 2020 are 11,222 MWh, 11,514 MWh, and 11,239 MWh, respectively. Figure 6b is the pattern of the monthly loss data of electric energy in Thailand from January 2018 to December 2020. The minimum loss is 387 MWh in October 2020, the maximum loss is 1036 MWh in March 2020, and the average losses in 2018, 2019, and 2020 are 635 MWh, 653 MWh, and 650 MWh, respectively.

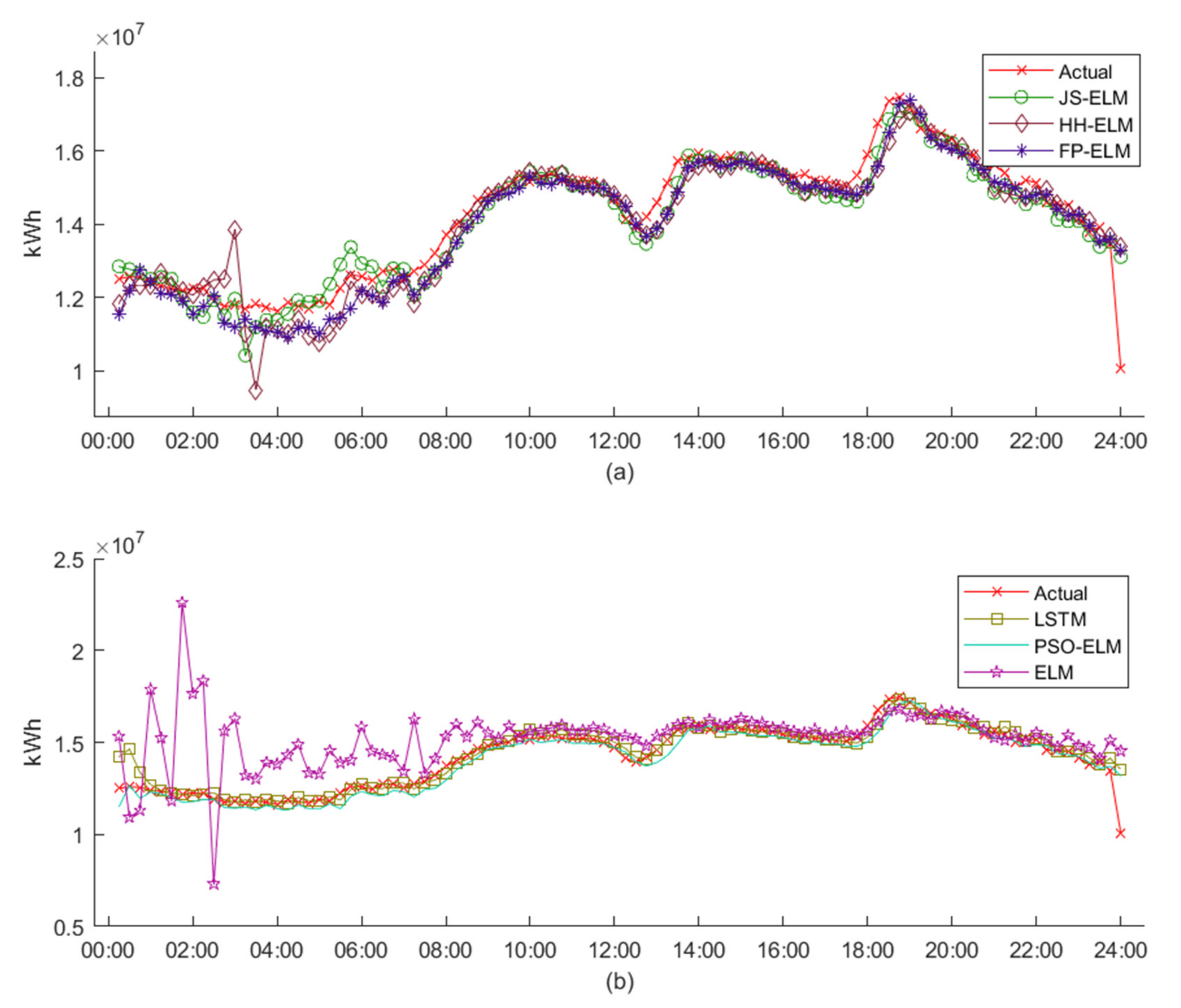
Figure 7a,b are the patterns of the peak demand data of electric energy and the pattern of the workday demand data of electric energy, respectively. Both peak demand data and workday demand data were collected in 15 min intervals from January 2018 to December 2020 in terms of a kiloWatt-Hour (kWh). The peak demand data were collected from the days that use the highest electricity for each month, and the workday demand data were collected from Monday to Friday for each month.

Figure 8 is the group pattern of the peak demand data of electric energy collected in 15 min intervals from January 2018 to December 2020 in terms of kWh. This dataset can be separated into 8 clusters when sorting from the highest total electric energy demand to the lowest total electric energy demand. The 8 clusters consist of Large Business (LB), Large Residential or Residential (L-RES) demand, which consumes energy greater than or equal to 150 kWh per month, Medium Business (MB), Small Business (SB), Small Residential or Residential (S-RES) demand, which consumes energy less than 150 kWh per month, Specific Business (SPB), Water Pumping for Agriculture (WPA), and Nonprofit Organization (NPO).

3.2. Dataset

When the preparation of electric energy demand data was completed, the experimental datasets were built to be tested in proposed models to forecast data with minimum error. In this research, the datasets were classified into seven groups for testing the proposed models.

Table 2. Details of Datasets.

Datasets	Dataset Type	Forecasting Type	Train Data	Test Data
1	Monthly electric energy demand data	Long-term forecasting	JAN 2018–DEC 2019	JAN 2020–DEC 2020
2	Monthly electric energy loss data	Long-term forecasting	JAN 2018–DEC 2019	JAN 2020–DEC 2020
3	Peak day 15 min interval electric energy demand data	Long-term forecasting	JAN 2018–DEC 2019	JAN 2020–DEC 2020
4	Workday 15 min interval electric energy demand data	Long-term forecasting	JAN 2018–DEC 2019	JAN 2020–DEC 2020
5	Peak day 15 min interval electric energy demand data	Short-term forecasting	JAN 2020–NOV 2020	DEC 2020
6	Workday 15 min interval electric energy demand data	Short-term forecasting	JAN 2020–NOV 2020	DEC 2020
7A	Cluster of 15 min interval peak day electric energy demand data—S-RES	Short-term forecasting	JAN 2020–NOV 2020	DEC 2020
7B	Cluster of 15 min interval peak day electric energy demand data—L-RES	Short-term forecasting	JAN 2020–NOV 2020	DEC 2020
7C	Cluster of 15 min interval peak day electric energy demand data—SB	Short-term forecasting	JAN 2020–NOV 2020	DEC 2020
7D	Cluster of 15 min interval peak day electric energy demand data—MB	Short-term forecasting	JAN 2020–NOV 2020	DEC 2020
7E	Cluster of 15 min interval peak day electric energy demand data—LB	Short-term forecasting	JAN 2020–NOV 2020	DEC 2020
7F	Cluster of 15 min interval peak day electric energy demand data—SPB	Short-term forecasting	JAN 2020–NOV 2020	DEC 2020
7G	Cluster of 15 min interval peak day electric energy demand data—NPO	Short-term forecasting	JAN 2020–NOV 2020	DEC 2020
7H	Cluster of 15 min interval peak day electric energy demand data—WPA	Short-term forecasting	JAN 2020–NOV 2020	DEC 2020

describes the detail of each dataset, which is separated in terms of train and test data.

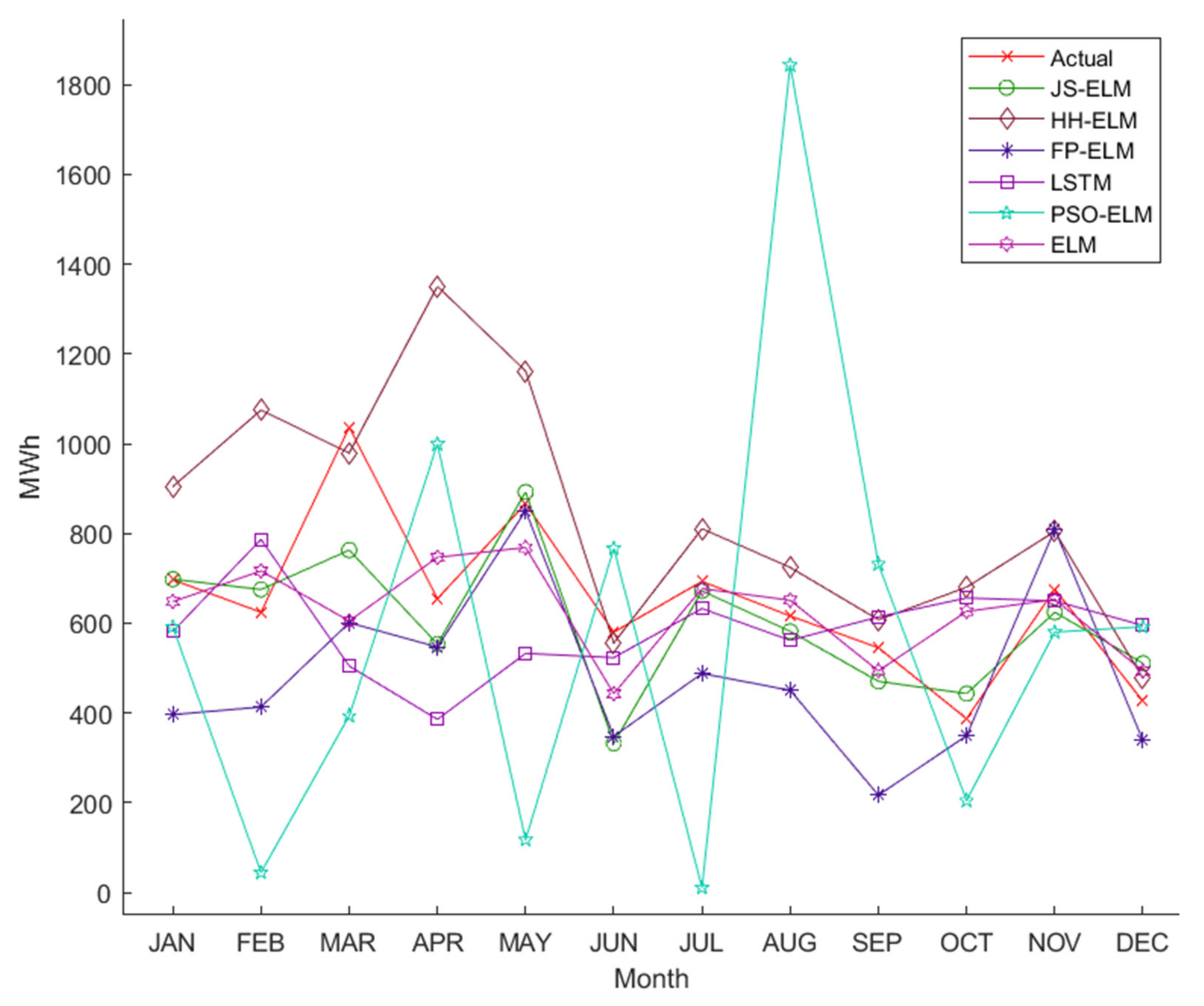
Figure 9 is the electric energy pattern data from dataset 1 to dataset 6, where the blue line is the train data for machine learning, and the red line is the test data for machine learning. Therefore, the detail from dataset 1 to dataset 6 can be described as follows:

Dataset 1 is the monthly electric energy demand data that is separated from January 2018 to December 2019 as train data (24 instances) and from January 2020 to December 2020 as test data (12 instances).

Dataset 2 is the monthly electric energy loss data that is separated from January 2018 to December 2019 as train data (24 instances) and from January 2020 to December 2020 as test data (12 instances).

Dataset 3 is the peak day 15 min interval electric energy demand data that is separated from January 2018 to December 2019 as train data (2304 instances) and from January 2020 to December 2020 as test data (1151 instances).

Dataset 4 is the workday 15 min interval electric energy demand data that is separated from January 2018 to December 2019 as train data (2304 instances) and from January 2020 to December 2020 as test data (1151 instances).

Dataset 5 is the peak day 15 min interval electric energy demand data that is separated from January 2020 to December 2020 as train data (1506 instances) and only December 2020 as test data (96 instances).

Dataset 6 is the workday 15 min interval electric energy demand data that is separated from January 2020 to December 2020 as train data (1506 instances) and only December 2020 as test data (96 instances).

Figure 10 is the electric energy pattern data of dataset 7, where the blue line is the train data for machine learning, and the red line is the test data for machine learning. Therefore, the detail of dataset 7 can be described as follows:

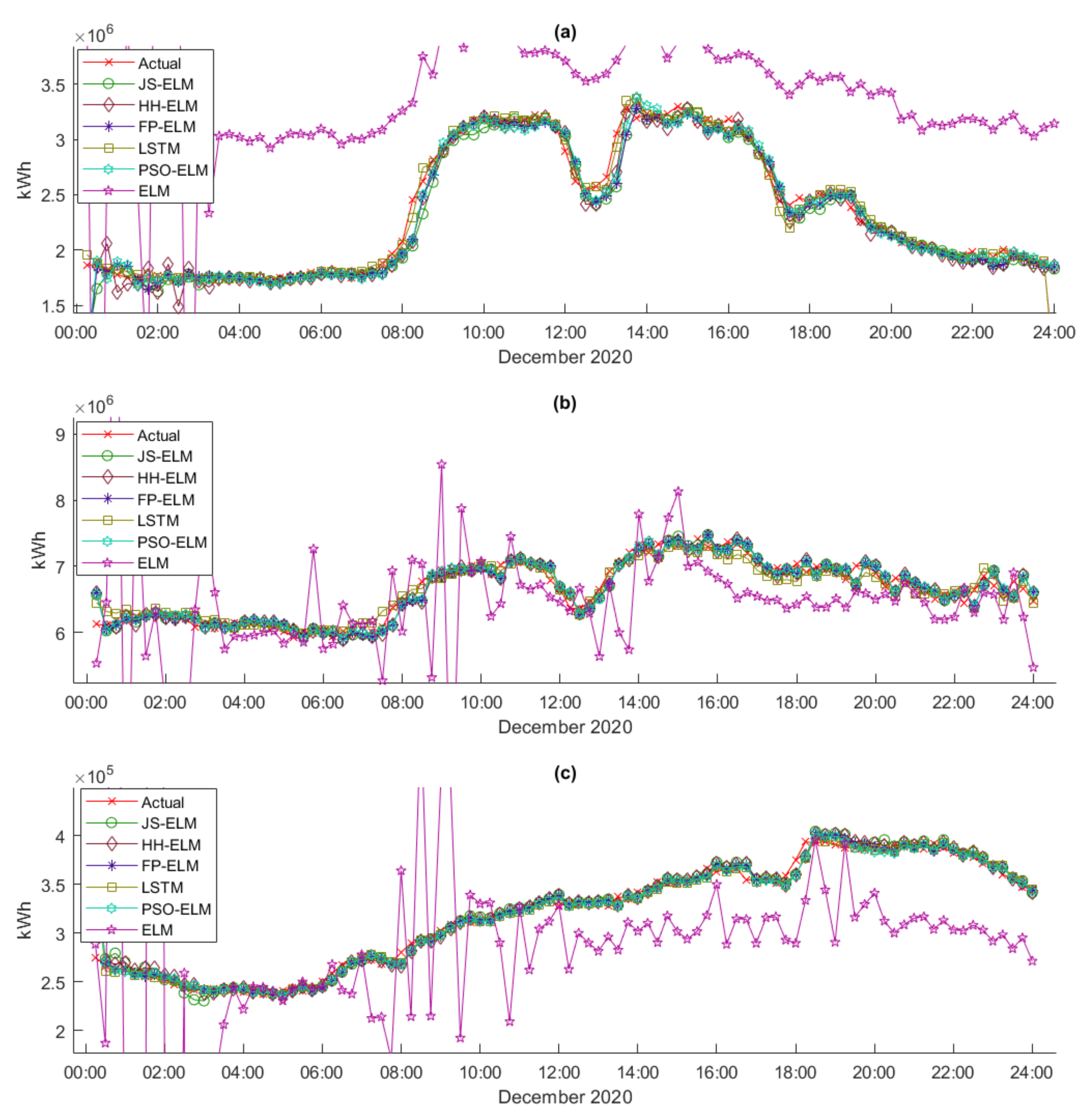
Dataset 7 is the cluster of 15 min interval peak day electric energy demand data that are separated into 8 subcases (7A to 7H). Subcase 7A is the cluster of S-RES electric energy demand data, subcase 7B is the cluster of L-RES electricity demand data, subcase 7C is the cluster of SB electricity demand data, subcase 7D is the cluster of MB electricity demand data, subcase 7E is the cluster of LB electricity demand data, subcase 7F is the cluster of SPB electricity demand data, subcase 7G is the cluster of NPO electricity demand data, and subcase 7H is the cluster of WPA electricity demand data. All subcases are separated from January 2020 to December 2020 as train data (1506 instances) and only December 2020 as test data (96 instances).

3.3. Proposed Models

The concept of the proposed models is using metaheuristic algorithms to optimize the weight parameter to reduce the cause of overfitting. In this research, three metaheuristic algorithms, which consist of JSO, HHO, and FPA, modified the randomization of weight parameter for searching the best weight parameter to improve the performance of the forecasting. The algorithm of the proposed models is described in Algorithm 1.

Algorithm 1. Pseudo-code of the Proposed Models.
1:	Define objective function f(x), ${(x}_i{,t}_i)\in {\mathrm{R}}^{\mathrm{n}}{\times \mathrm{R}}^{\mathrm{m}}$ by $i=1,2,\dots ,N$
2:	Define the initialize n number of population in metaheuristic models (JSO, HHO, or FPA)
3:	Define a switch probability p $\mathsf{ϵ}$ [0,1] (FPA only)
4:	Define the best solution $g_{\ast }$ in the initial population
5:	Define L hidden nodes in ELM
6:	Define $G\left(w_i,b_i,x_i\right)$ Hidden nodes activation function in ELM (sigmoidal function)
7:	Define $\beta$ output weight vector
8:	Define T as the max iteration for metaheuristic models
9:	while (t < T)
10:	for i = 1: n
11:	Adjust $w_i^{t+1}$ as the population with the metaheuristic models (JSO, HHO, or FPA)
12:	Evaluate new solution $w_i^{t+1}$ to ELM
13:	for i = 1:L
14:	for j = 1:N
15:	H(i,j) =$G\left(w_i^{t+1},b_i,x_i\right)\ast \beta$
16:	end
17:	end
18:	$\beta =H^{†}T$
19:	If new solutions are better, update new $g_{\ast }$ in the population
20:	end for
21:	Find the current best solution $g_{\ast }$ & best output weight $\beta$
22:	end while

First of all, based on the ELM model, all setting parameters were defined in the model, which consisted of a number of hidden nodes, input and target data, and initial weight parameter. Secondly, based on metaheuristic models, all setting parameters of each model were defined, which consisted of the number of populations, switch probability for the FPA model, and the best solution of the population. Thirdly, the weight parameter was defined based on metaheuristic models and then evaluated the new weight parameter for calculating in the ELM model. Fourthly, the activation function was calculated in the ELM model to receive the last weight parameter from the hidden layer. All processes were calculated until the iteration reached the max iteration criterion and the best weight parameter was received for calculating in the testing phase.

3.4. Experimental Setup and Hyper-Parameters Setting

The hardware specification of the computer used in this research work was CPU Intel Core i7-7700HQ 2.80 GHz (up to 3.40 GHz), RAM 32 GB, and SSD NVMe. The software was the MATLAB version R2020a. The major hyper-parameters [42,43] of proposed models consisted of the number of hidden nodes and the number of populations and the major hyper-parameters [44] of state-of-the-art models consisting of the number of hidden nodes that were analyzed through the electric energy demand datasets. The objective function to find the best hyper-parameters was the Root Mean Square Error (RMSE).

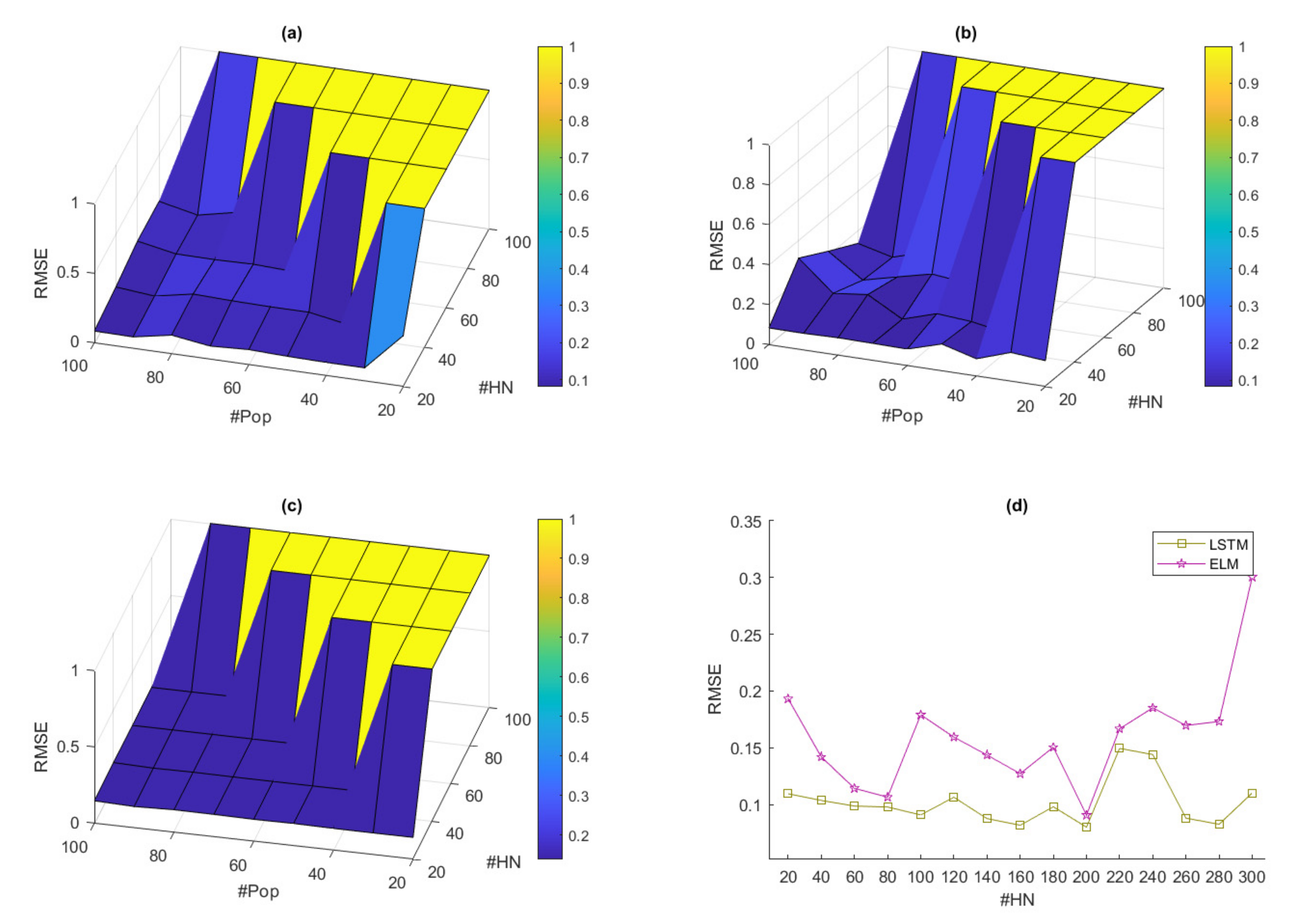
The hyper-parameter tuning [45,46] of the proposed and state-of-the-art models is shown in Figure 11. In this experiment, the average of RMSE from all models was obtained by taking all the datasets (7 datasets) used to find the RMSE value, then averaging RMSE value in terms of the number of hidden nodes and population. In the proposed models, the boundary of hidden nodes was set from 20 to 200 (increasing 20 nodes), the boundary of populations was set from 20 to 100 (increasing 10 populations), and the number of iterations for metaheuristics was set to 100 due to the fast computation. In the state-of-the-art models, the boundary of hidden nodes was set from 20 to 300 (increasing 20 nodes). For fast computing in the long short-term memory (LSTM) model, the fixed setting of hyper-parameters in the LSTM model consisted of 2 hidden layers, 1000 epochs, 64 batch size, and optimizer was set to Adam.

According to Figure 11, the hyper-parameter experiment results show that the best average RMSE of JS-ELM is 0.0838, and the locations of hidden nodes and populations are 40 and 50, respectively. The best average RMSE of HH-ELM is 0.0927, and the locations of hidden nodes and populations are 40 and 50, respectively. The best average RMSE of FP-ELM is 0.1384, and the locations of hidden nodes and populations are 40 and 50, respectively. The best average RMSE of LSTM is 0.0880, and the location of hidden nodes is 200. The best average RMSE of ELM is 0.0907, and the location of hidden nodes is 200.

For comparing with the metaheuristic-based proposed models, the Particle Swarm Optimization Extreme Learning Machine (PSO-ELM) [47,48] model was considered to forecast in electric energy demand datasets. The best hyper-parameters of PSO-ELM model were received from [48], which consist of 150 hidden nodes, 30 populations (swarm size), acceleration coefficients $C_1=1$ and $C_2=2$, and inertia weight was set to 0.9.

To summarize, the best hyper-parameters of JS-ELM, HH-ELM, and FP-ELM are 40 hidden nodes and 50 populations. The best hyper-parameters of LSTM and ELM are 200 hidden nodes. All suitable hyper-parameters were defined as presented in

Table 3. Initial Parameters of All Models.

Models	Number of Hidden Nodes	Number of Populations	Number of Iterations for Metaheuristic Optimization	Number of Global Iterations for Machine Learning Model
JS-ELM	40	50	100	20
HH-ELM	40	50	100	20
FP-ELM	40	50	100	20
LSTM	200	-	-	20
PSO-ELM	150	30	100	20
ELM	200	-	-	20

.

3.5. Performance Evaluation

In this research, all datasets were processed by min–max normalization [49] as calculated in (25).

$$x^{\prime }=\frac{x-\min \left(x\right)}{\max \left(x\right)-\min \left(x\right)}$$

(25)

where $x$ is a data point and $x^{\prime }$ is normalized data.

To evaluate the performance of proposed models, three error metrics, Mean Absolute Error (MAE), Mean Absolute Percentage Error (MAPE), and Root Mean Square Error (RMSE), were used in this experiment as presented in (26)–(28), respectively.

$$MAE\left(t\right)=\frac{1}{n}{\displaystyle \sum }_{i=1}^n\left|e_i-t_i\right|$$

(26)

$$MAPE\left(t\right)=\frac{100}{n}{\displaystyle \sum }_{i=1}^n\left|\frac{e_i-t_i}{t_i}\right|$$

(27)

$$RMSE\left(t\right)=\sqrt{\frac{{{\displaystyle \sum }}_{i=1}^n{\left(e_i-t_i\right)}^2}{n}}$$

(28)

where $i$ is the present time variable, n is the number of input data, $e_i$ is the expected data at the time i, and $t_i$ is the actual data at the time i.

To receive the best solution from the performance evaluation, which is suggested from [50,51], all error metrics were combined to the Cumulative Weighted Error (CWE) for evaluating the final result of the experiment as presented in (29).

$$CWE=\frac{MAE+\left(\frac{MAPE}{100}\right)+RMSE}{3}$$

(29)

After error metrics were completely calculated, the result of error metrics was used to evaluate the performance of the proposed models as discussed in Section 4.

4. Experimental Results

This section describes the experimental results of the proposed models and ELM using electric energy demand datasets. This section is separated into three subsections consisting of the experimental results overview, forecasting time consumption for each model, and the summary of the experimental results.

4.1. Discussion of the Experimental Results

In the experimental results, the datasets mentioned in Section 3.2 were set. The forecasting error of the proposed models was presented and all error metrics as mentioned in Section 3.5 were compared. According to

Table 4. Experimental results of all models (bold text is the best error result).

Datasets	Forecasting Error Metric		Proposed Models			State-of-the-Art Models
			JS-ELM	HH-ELM	FP-ELM	LSTM	PSO-ELM	ELM
1	MAE	$E_{\ast }$	0.1122	0.1491	0.2010	0.1868	0.2277	0.1571
		$\mu$	0.1829	0.2268	0.3039	0.2326	0.2683	0.1740
		$\sigma$	0.0390	0.0387	0.0455	0.0224	0.0277	0.0115
	MAPE	$E_{\ast }$	2.4418	2.6958	4.7795	3.2880	2.6200	3.5355
		$\mu$	3.8853	3.9704	7.9162	3.5178	3.4023	4.7433
		$\sigma$	1.6551	0.7713	2.2491	0.1998	0.4985	0.7377
	RMSE	$E_{\ast }$	0.1717	0.2026	0.2761	0.2307	0.2729	0.2000
		$\mu$	0.2255	0.2712	0.3733	0.2776	0.3181	0.2184
		$\sigma$	0.0408	0.0426	0.0494	0.0237	0.0310	0.0106
	CWE	$E_{\ast }$	0.1028	0.1262	0.1750	0.1501	0.1756	0.1308
		$\mu$	0.1491	0.1792	0.2521	0.1818	0.2068	0.1466
		$\sigma$	0.0321	0.0297	0.0391	0.0160	0.0212	0.0098
2	MAE	$E_{\ast }$	0.1662	0.1845	0.1866	0.3406	0.3014	0.3075
		$\mu$	0.2803	0.2826	0.2657	0.4095	0.3366	0.3192
		$\sigma$	0.0448	0.0399	0.0510	0.0299	0.0308	0.0077
	MAPE	$E_{\ast }$	16.8109	21.8086	20.0015	24.3841	39.6875	17.0482
		$\mu$	101.3614	87.9551	110.2814	32.0613	324.3600	19.8431
		$\sigma$	237.7910	114.8906	167.0535	4.2338	366.7532	2.7022
	RMSE	$E_{\ast }$	0.1918	0.2513	0.2323	0.4140	0.3291	0.3472
		$\mu$	0.3361	0.3346	0.3291	0.4852	0.4008	0.3592
		$\sigma$	0.0456	0.0376	0.0600	0.0329	0.0358	0.0064
	CWE	$E_{\ast }$	0.1754	0.2179	0.2063	0.3328	0.3424	0.2751
		$\mu$	0.5433	0.4989	0.5659	0.4051	1.3269	0.2923
		$\sigma$	0.8228	0.4088	0.5938	0.0350	1.2447	0.0137
3	MAE	$E_{\ast }$	0.0493	0.0496	0.0370	0.0356	0.0441	0.1371
		$\mu$	0.0854	0.0922	0.0524	0.0720	0.0553	0.1644
		$\sigma$	0.0298	0.0332	0.0092	0.0359	0.0532	0.0263
	MAPE	$E_{\ast }$	2.0761	2.2084	2.2287	2.0124	2.2983	6.7634
		$\mu$	2.2080	2.3103	2.2734	2.2679	2.2789	12.5276
		$\sigma$	0.1040	0.0610	0.0811	0.1488	0.0542	6.5947
	RMSE	$E_{\ast }$	0.0832	0.0843	0.0784	0.0688	0.0818	0.1668
		$\mu$	0.1087	0.1141	0.0862	0.0985	0.0945	0.1996
		$\sigma$	0.0225	0.0251	0.0063	0.0301	0.0212	0.0289
	CWE	$E_{\ast }$	0.0511	0.0520	0.0459	0.0415	0.0499	0.1238
		$\mu$	0.0721	0.0765	0.0538	0.0644	0.0678	0.1631
		$\sigma$	0.0178	0.0196	0.0054	0.0225	0.0031	0.0404
4	MAE	$E_{\ast }$	0.0276	0.0262	0.0259	0.0180	0.0298	0.1221
		$\mu$	0.0579	0.0519	0.0294	0.0725	0.0578	0.1555
		$\sigma$	0.0176	0.0220	0.0047	0.0302	0.0019	0.0323
	MAPE	$E_{\ast }$	2.1786	2.2010	2.3628	0.8040	2.4519	7.3798
		$\mu$	2.2888	2.3608	2.4075	0.9159	2.4599	15.2733
		$\sigma$	0.0945	0.0773	0.0391	0.0711	0.9825	4.8535
	RMSE	$E_{\ast }$	0.0639	0.0668	0.0674	0.0503	0.0698	0.1504
		$\mu$	0.0830	0.0812	0.0692	0.0900	0.0782	0.1861
		$\sigma$	0.0120	0.0132	0.0019	0.0271	0.0429	0.0349
	CWE	$E_{\ast }$	0.0377	0.0383	0.0390	0.0254	0.0399	0.1154
		$\mu$	0.0546	0.0522	0.0409	0.0572	0.0569	0.1648
		$\sigma$	0.0102	0.0120	0.0023	0.0193	0.0341	0.0386
5	MAE	$E_{\ast }$	0.0464	0.0596	0.0994	0.0807	0.1078	0.1509
		$\mu$	0.1444	0.1044	0.1103	0.1377	0.1985	0.1955
		$\sigma$	0.0928	0.0234	0.0057	0.0372	0.0231	0.0321
	MAPE	$E_{\ast }$	2.6149	2.7385	2.7791	1.9792	2.8974	7.8708
		$\mu$	7.1240	2.9822	2.8590	3.7442	2.9987	15.5761
		$\sigma$	11.7593	0.1493	0.0493	0.8836	0.1293	6.4519
	RMSE	$E_{\ast }$	0.0706	0.0896	0.1221	0.1308	0.1298	0.2092
		$\mu$	0.1792	0.1235	0.1300	0.1793	0.1984	0.2460
		$\sigma$	0.0924	0.0184	0.0043	0.0313	0.0231	0.0308
	CWE	$E_{\ast }$	0.0477	0.0589	0.0831	0.0771	0.0868	0.1463
		$\mu$	0.1316	0.0859	0.0896	0.1182	0.0981	0.1991
		$\sigma$	0.1009	0.0144	0.0035	0.0258	0.0412	0.0425
6	MAE	$E_{\ast }$	0.0838	0.0828	0.1194	0.1356	0.1427	0.2016
		$\mu$	0.1451	0.1352	0.1383	0.1538	0.1549	0.2878
		$\sigma$	0.0317	0.0189	0.0064	0.0125	0.0542	0.0669
	MAPE	$E_{\ast }$	2.7064	2.6429	2.7679	0.8133	2.9145	9.4805
		$\mu$	3.0684	2.9169	2.8812	1.0700	2.8992	48.6885
		$\sigma$	0.3358	0.2019	0.0497	0.1153	0.0341	57.6711
	RMSE	$E_{\ast }$	0.1068	0.1139	0.1648	0.1767	0.1809	0.2347
		$\mu$	0.1712	0.1631	0.1723	0.1885	0.1874	0.3268
		$\sigma$	0.0286	0.0173	0.0036	0.0087	0.0241	0.0692
	CWE	$E_{\ast }$	0.0726	0.0744	0.1040	0.1068	0.1175	0.1770
		$\mu$	0.1157	0.1092	0.1131	0.1177	0.1237	0.3671
		$\sigma$	0.0212	0.0127	0.0035	0.0075	0.0412	0.2376
7A	MAE	$E_{\ast }$	0.0820	0.0772	0.0741	0.1178	0.0863	0.1682
		$\mu$	0.1153	0.1218	0.1005	0.1652	0.1562	0.2885
		$\sigma$	0.0249	0.0177	0.0146	0.0339	0.0369	0.0791
	MAPE	$E_{\ast }$	10.3068	10.5220	10.5318	17.3387	15.1356	159.3181
		$\mu$	12.4254	11.8836	11.1192	55.7781	15.3368	921.8174
		$\sigma$	1.8623	0.9537	0.3495	66.0648	0.8156	1800.9530
	RMSE	$E_{\ast }$	0.1115	0.1052	0.1022	0.1691	0.1934	0.2211
		$\mu$	0.1427	0.1471	0.1260	0.2181	0.1996	0.3286
		$\sigma$	0.0225	0.0172	0.0133	0.0380	0.058	0.0755
	CWE	$E_{\ast }$	0.0989	0.0959	0.0939	0.1534	0.1867	0.6608
		$\mu$	0.1274	0.1292	0.1126	0.3137	0.1923	3.2784
		$\sigma$	0.0220	0.0148	0.0105	0.2442	0.0265	6.0547
7B	MAE	$E_{\ast }$	0.0704	0.1335	0.1179	0.0571	0.1394	0.1583
		$\mu$	0.1643	0.1804	0.3152	0.1337	0.1557	0.2125
		$\sigma$	0.0577	0.0170	0.0943	0.0381	0.0878	0.0498
	MAPE	$E_{\ast }$	10.6971	10.3719	9.0110	4.1967	9.1245	29.5542
		$\mu$	11.4928	11.6090	13.0535	6.4049	9.6878	77.1914
		$\sigma$	0.7465	0.6466	2.4811	1.4669	5.7795	46.7933
	RMSE	$E_{\ast }$	0.0964	0.1525	0.1368	0.1027	0.1475	0.2282
		$\mu$	0.1830	0.2001	0.3414	0.1594	0.1969	0.2732
		$\sigma$	0.0579	0.0159	0.1032	0.0294	0.0677	0.0451
	CWE	$E_{\ast }$	0.0912	0.1299	0.1149	0.0673	0.1264	0.2273
		$\mu$	0.1541	0.1655	0.2624	0.1191	0.1377	0.4192
		$\sigma$	0.0410	0.0131	0.0741	0.0274	0.0547	0.1876
7C	MAE	$E_{\ast }$	0.0614	0.1533	0.1706	0.0795	0.1677	0.1620
		$\mu$	0.1514	0.1892	0.1811	0.1548	0.1814	0.3231
		$\sigma$	0.0345	0.0520	0.0058	0.0281	0.0611	0.1019
	MAPE	$E_{\ast }$	4.0018	4.3382	4.2618	3.2813	4.4435	20.5478
		$\mu$	4.6888	4.6820	4.4270	7.9141	4.6989	59.7436
		$\sigma$	0.8142	0.2128	0.0764	12.3156	0.0896	62.1757
	RMSE	$E_{\ast }$	0.1025	0.1810	0.1910	0.1308	0.1973	0.2197
		$\mu$	0.1825	0.2136	0.2042	0.1924	0.2137	0.3597
		$\sigma$	0.0274	0.0467	0.0064	0.0243	0.0631	0.0983
	CWE	$E_{\ast }$	0.0680	0.1259	0.1347	0.0810	0.1361	0.1957
		$\mu$	0.1269	0.1499	0.1432	0.1421	0.1468	0.4268
		$\sigma$	0.0233	0.0336	0.0043	0.0585	0.0435	0.2740
7D	MAE	$E_{\ast }$	0.0672	0.0389	0.0317	0.0210	0.0379	0.2040
		$\mu$	0.1192	0.1007	0.0423	0.0623	0.0576	0.2310
		$\sigma$	0.0323	0.0499	0.0157	0.0611	0.0193	0.0241
	MAPE	$E_{\ast }$	3.5799	3.4621	3.7425	1.8334	3.7989	23.2984
		$\mu$	3.9516	4.4777	3.9223	2.3698	3.9155	42.9784
		$\sigma$	0.2343	1.3263	0.1612	0.4682	0.1789	19.6851
	RMSE	$E_{\ast }$	0.0897	0.0712	0.0676	0.0285	0.0797	0.2336
		$\mu$	0.1368	0.1191	0.0734	0.0726	0.0895	0.2838
		$\sigma$	0.0333	0.0438	0.0126	0.0611	0.0567	0.0356
	CWE	$E_{\ast }$	0.0642	0.0482	0.0456	0.0226	0.0489	0.2235
		$\mu$	0.0985	0.0882	0.0516	0.0528	0.0597	0.3149
		$\sigma$	0.0227	0.0357	0.0100	0.0423	0.0935	0.0855
7E	MAE	$E_{\ast }$	0.0612	0.0612	0.0608	0.0591	0.0688	0.2469
		$\mu$	0.0647	0.0642	0.0634	0.0769	0.0712	0.2797
		$\sigma$	0.0035	0.0021	0.0037	0.0119	0.0121	0.0255
	MAPE	$E_{\ast }$	1.3713	1.3617	1.3800	1.4003	1.3966	7.4999
		$\mu$	1.4018	1.3958	1.4350	1.7621	1.4579	17.5561
		$\sigma$	0.0176	0.0217	0.0767	0.2355	0.2899	23.2809
	RMSE	$E_{\ast }$	0.0818	0.0818	0.0817	0.0756	0.0799	0.2915
		$\mu$	0.0859	0.0853	0.0836	0.1019	0.0897	0.3304
		$\sigma$	0.0035	0.0019	0.0031	0.0163	0.0048	0.0291
	CWE	$E_{\ast }$	0.0523	0.0522	0.0521	0.0496	0.0587	0.2045
		$\mu$	0.0549	0.0545	0.0538	0.0655	0.0574	0.2619
		$\sigma$	0.0024	0.0014	0.0025	0.0102	0.0040	0.0958
7F	MAE	$E_{\ast }$	0.0370	0.0364	0.0351	0.0298	0.0389	0.2810
		$\mu$	0.0445	0.0410	0.0384	0.0368	0.0415	0.3115
		$\sigma$	0.0049	0.0050	0.0016	0.0055	0.0063	0.0290
	MAPE	$E_{\ast }$	1.5979	1.518	1.4372	1.3786	1.4889	23.3061
		$\mu$	1.7345	1.6883	1.5431	1.4887	1.7562	34.2174
		$\sigma$	0.1305	0.1385	0.0765	0.1271	0.1015	18.2012
	RMSE	$E_{\ast }$	0.0657	0.0664	0.0659	0.0659	0.0678	0.3297
		$\mu$	0.0718	0.0691	0.0675	0.0686	0.0782	0.3637
		$\sigma$	0.0032	0.0030	0.0009	0.0030	0.0087	0.0312
	CWE	$E_{\ast }$	0.0396	0.0393	0.0384	0.0365	0.0399	0.2813
		$\mu$	0.0445	0.0423	0.0404	0.0401	0.0484	0.3391
		$\sigma$	0.0032	0.0031	0.0011	0.0033	0.0087	0.0807
7G	MAE	$E_{\ast }$	0.0285	0.0281	0.0276	0.0298	0.0379	0.1073
		$\mu$	0.0300	0.0296	0.0297	0.0621	0.0485	0.1729
		$\sigma$	0.0008	0.0009	0.0015	0.0427	0.0042	0.0370
	MAPE	$E_{\ast }$	1.8554	1.8418	1.7774	1.9445	1.7884	13.4419
		$\mu$	1.8964	1.8908	1.8846	4.0213	1.8993	14.7832
		$\sigma$	0.0239	0.0268	0.0934	5.0059	0.0367	0.6157
	RMSE	$E_{\ast }$	0.0380	0.0379	0.0380	0.0461	0.0388	0.1363
		$\mu$	0.0395	0.0393	0.0401	0.0827	0.0399	0.2280
		$\sigma$	0.0008	0.0007	0.0023	0.0558	0.0010	0.0538
	CWE	$E_{\ast }$	0.0284	0.0281	0.0278	0.0318	0.0288	0.1260
		$\mu$	0.0295	0.0293	0.0296	0.0617	0.0298	0.1829
		$\sigma$	0.0005	0.0006	0.0016	0.0495	0.0007	0.0323
7H	MAE	$E_{\ast }$	0.0296	0.0298	0.0293	0.0482	0.0311	0.2217
		$\mu$	0.0352	0.0348	0.0327	0.0934	0.0324	0.2857
		$\sigma$	0.0033	0.0029	0.0021	0.0443	0.0115	0.0465
	MAPE	$E_{\ast }$	3.7510	4.0816	3.9517	6.1304	3.8854	53.3827
		$\mu$	4.4249	4.3978	4.2475	12.0408	4.5691	153.4755
		$\sigma$	0.3165	0.1781	0.1753	8.1731	0.5362	107.6369
	RMSE	$E_{\ast }$	0.0491	0.0498	0.0476	0.0684	0.0562	0.2875
		$\mu$	0.0550	0.0534	0.0513	0.1252	0.0556	0.3252
		$\sigma$	0.0032	0.0023	0.0022	0.0535	0.0135	0.0448
	CWE	$E_{\ast }$	0.0387	0.0401	0.0388	0.0593	0.0398	0.3477
		$\mu$	0.0448	0.0441	0.0421	0.1130	0.0455	0.7152
		$\sigma$	0.0032	0.0023	0.0020	0.0599	0.0068	0.3892

, the detail of the experimental result is described in terms of the dataset with the minimum error, minimum mean error, and standard deviation (S.D.) error result when using the number of global iterations defined in Table 3.

The minimum error was obtained by finding the lowest forecasting error result from the global iterations as presented in (30). The minimum mean error was obtained by averaging all results from the global iterations as presented in (31). The minimum S.D. error was obtained by using the forecasting error result and the minimum mean error result to indicate the standard deviation of the error solution from global iterations as presented in (32).

$$E_{\ast }=\underset{i}{\min }{\left\{E_i\right\}}_{i=1}^N$$

(30)

$$\mu =\frac{1}{N}{\displaystyle \sum }_{i=1}^N{E}_i$$

(31)

$$\sigma =\sqrt{\frac{1}{N-1}{\displaystyle \sum }_{i=1}^N{\left|E_i-\mu \right|}^2}$$

(32)

where $E_{\ast }$ is the minimum error, $\mu$ is the minimum mean error, $\sigma$ is the minimum S.D. error, $i$ is the present time variable, $N$ is the number of global iterations, and $E_i$ is the result of the forecasting error metric for each global iteration.

The minimum forecasting error result of dataset 1 is shown in Figure 12. The result shows that all models provided results near the actual target value. Furthermore, according to the CWE error metric in Table 4, JS-ELM provided the best minimum error result when compared to the other models’ results. However, LSTM, PSO-ELM, and ELM provided higher stability of forecasting when considered on the minimum mean error and minimum S.D. error. HH-ELM provided the minimum error lower than that of the ELM model, but the minimum mean error was higher than that of the ELM model. The overall error metrics of FP-ELM were higher than those of other models.

The minimum forecasting error result of dataset 2 is shown in Figure 13. The result shows that all models provided results near the actual target value. Furthermore, according to the CWE error metric in Table 4, JS-ELM provided the best minimum error result when compared to the other models’ results. However, the minimum mean error and minimum standard deviation of JS-ELM, HH-ELM, FP-ELM, and PSO-ELM were higher than those of the LSTM and ELM models, which means the proposed models could provide the instability of the attempt to dataset 2.

The minimum forecasting error result of dataset 3 s shown in Figure 14. All proposed models and LSTM provided results near the actual target value. The ELM model was already overfitted because the training RMSE result was 0.0207, but the forecasting RMSE result was 0.1668. Furthermore, the minimum mean error and minimum standard deviation of ELM were higher than those of the proposed models, which means the ELM could provide the instability of the attempt to dataset 3.

The minimum forecasting error result of dataset 4 is shown in Figure 15. All proposed models and LSTM provided results near the actual target value. The ELM model was already overfitted because the training RMSE result was 0.0253, but the forecasting RMSE result was 0.1504. Furthermore, the minimum mean error and minimum standard deviation of ELM were higher than those of proposed models, which means the ELM could provide the instability of the attempt to dataset 4.

The minimum forecasting error result of dataset 5 is shown in Figure 16. The result shows that the expected target value of JS-ELM was close to the actual target value. The expected target values of HH-ELM and FP-ELM slightly swung from 02:00 to 04:00 when compared to the actual target value. The expected target values of LSTM slightly swung from 00:00 to 01:00 when compared to the actual target value. The expected target value of ELM was clearly different from the actual target value.

The minimum forecasting error result of dataset 6 is shown in Figure 17. The result shows that all models provided results near the actual target value. However, the ELM model was already overfitted because the training RMSE result was 0.0151, but the forecasting RMSE result was 0.2347. Furthermore, the minimum mean error and minimum standard deviation of ELM were higher than those of the proposed models, which means ELM could provide the instability of the attempt to dataset 6.

The minimum forecasting error results of dataset 7 are shown in Figure 18, Figure 19 and Figure 20. Dataset 7 contained eight sub-datasets to attempt on this experiment, which consists of sub-dataset 7A (the S-RES profile), sub-dataset 7B (the L-RES profile), sub-dataset 7C (the SB profile), sub-dataset 7D (the MB profile), sub-dataset 7E (the LB profile), sub-dataset 7F (the SPB profile), sub-dataset 7G (the NPO profile), and sub-dataset 7H (the WPA profile). The overall results of dataset 7 show that the proposed models provided the results nearest to the actual target value. However, the expected target value of the ELM model was instability, which means the ELM model was already overfitted because the training accuracy between the expected target value and actual target value was overrated, thus, the forecasting result was unacceptable. Furthermore, the minimum mean error and minimum standard deviation of ELM were higher than those of the proposed models, which means the ELM could provide the instability of the attempt to dataset 7.

4.2. Discussion on the Time Consumption

In this research, the training times of each forecasting model were calculated and compared. According to

Table 5. Result of the Training Time Experiment (Bold text is the suitable time processing result).

Datasets	The Training Time of Models (Seconds)
	JS-ELM	HH-ELM	FP-ELM	LSTM	PSO-ELM	ELM
1	11.7813	20.0781	9.5625	43.7802	17.3698	0.0001
2	9.1094	17.2500	8.4844	35.4268	14.2356	0.0001
3	102.8281	228.6250	96.1563	397.0562	135.3756	0.7188
4	89.3438	183.2188	89.6563	393.6320	129.8451	0.5781
5	74.5469	146.0156	70.4844	386.5398	107.6406	0.4844
6	69.6563	137.0156	67.0469	375.6900	108.0342	0.2500
7A	61.0313	124.6563	60.5781	345.5692	109.0312	0.2344
7B	62.1719	126.6250	61.1875	358.3612	108.0781	0.2969
7C	64.2031	132.9688	64.2344	362.5597	107.9843	0.3281
7D	70.8438	138.5625	66.0625	372.6623	106.2031	0.3594
7E	64.2188	138.9375	65.7656	351.1258	108.9218	0.2500
7F	65.5625	132.3281	64.3594	363.6690	106.5625	0.4219
7G	62.6719	127.1406	67.9063	349.9562	108.9531	0.3906
7H	74.6094	145.0469	75.4219	383.3356	104.0156	0.2188

, the result of the training time showed that ELM consumed the least time compared with other models. Due to the metaheuristic calculation, JS-ELM and FP-ELM consumed a lower amount of time to calculate the data and provide the best result. HH-ELM consumed more time than the other models because the number of time steps of the HHO calculation are greater than JSO and FPA. However, the LSTM model consumed more time than all other models in the experiment. The forecasting time was not focused upon because all models consumed a low forecasting time (in milliseconds).

4.3. Summary of the Experimental Results

In this research, three main factors, the minimum error, minimum mean error, and minimum standard deviation, were analyzed by error metrics (MAE, MAPE, RMSE, and CWE) to evaluate the performance of all models that fitted each dataset.

The CWE comparison for all models from datasets 1 to 6 is shown in Figure 21. For datasets 1 and 2, the JS-ELM model was the most suitable in terms of the minimum error result, while the ELM was the most suitable in terms of the minimum mean error and S.D. error. For dataset 3, the FP-ELM model was suitable for all three factors. For dataset 4, the LSTM model was the most suitable in terms of the minimum error result, while the FP-ELM was the most suitable in terms of the minimum mean error and S.D. error. For datasets 5 and 6, the JS-ELM model was the most suitable in terms of the minimum error result, while HH-ELM and FP-ELM were the most suitable in terms of the minimum mean error and S.D. error, respectively.

The CWE comparison of all models for dataset 7 is shown in Figure 22. All proposed models were the most suitable for all three factors, while the ELM model provided the highest CWE rate, which means the ELM model was already overfitted, as referred to in Section 4.1.

According to Section 4.2, the time consumptions of the proposed models were higher than the time consumption of the ELM model because the proposed models were tuned by metaheuristics optimization. Major factors that directly affected the high time consumption of the proposed models consist of the time step calculation for each metaheuristic algorithm, number of populations, iterations of the metaheuristics algorithms, and number of hidden nodes of the ELM model. In conclusion, the proposed models slightly consumed more time in calculation than the time consumption of the ELM model, while the experiment results for all datasets were highly accurate and more stable than the result of the ELM model.

In comparison, the overall error results of the proposed models and LSTM were close. However, according to Table 5, the training time of the proposed models was faster than the LSTM model.

5. Conclusions and Future Work

This research proposed the novel ELM model optimized by metaheuristic algorithms, namely JS-ELM, HH-ELM, and FP-ELM, to forecast the electric energy dataset. The characteristic of the metaheuristic optimizations, namely JSO, HHO, and FPA, is that they are self-adaptive to tune the weight parameter of the ELM model without being trapped in the local optimum. Therefore, the models mentioned earlier were applied to the ELM model by tuning the weight parameter of the ELM model instead of using the traditional randomization of the weight parameter. In addition, these three optimization methods can reduce the number of hidden nodes of the ELM model. To demonstrate the performance of the proposed method, all models were applied to forecast seven real-life electric energy datasets. The dataset of electric energy demand consists of monthly electric energy demand data from 2018 to 2020, monthly electric energy loss data from 2018 to 2020, peak day 15 min interval electric energy demand data from 2018 to 2020, workday 15 min interval electric energy demand data from 2018 to 2020, peak day 15 min interval electric energy demand data in 2020, workday 15 min interval electric energy demand data in 2020, and cluster of 15 min interval peak day electric energy demand data. Consequently, the result showed that the proposed models could improve the forecasting accuracy, provide forecasting stability, and reduce the cause of overfitting from the traditional model.

According to

Table 6. Summary of the Outperformance models (ranking by CWE).

Datasets	Outperformance Models (Ranking by CWE)
	Best	Mean	S.D.
1	JS-ELM	JS-ELM	ELM
2	JS-ELM	ELM	ELM
3	JS-ELM	FP-ELM	FP-ELM
4	LSTM	FP-ELM	FP-ELM
5	JS-ELM	HH-ELM	FP-ELM
6	JS-ELM	HH-ELM	FP-ELM
7A	FP-ELM	FP-ELM	FP-ELM
7B	LSTM	LSTM	LSTM
7C	FP-ELM	JS-ELM	JS-ELM
7D	LSTM	FP-ELM	FP-ELM
7E	LSTM	FP-ELM	HH-ELM
7F	LSTM	FP-ELM	FP-ELM
7G	FP-ELM	HH-ELM	JS-ELM
7H	JS-ELM	FP-ELM	FP-ELM

, the JS-ELM model was the most suitable for the minimum error result. The overall forecasting results of the HH-ELM model were similar to the JS-ELM model results, but the time consumption was higher than the time consumption of other models. The FP-ELM model was the most suitable in terms of the minimum mean error and minimum S.D. The time consumption of the proposed models depended on the number of populations, iterations criterion of metaheuristics algorithms, and the number of hidden nodes of the ELM model. The HH-ELM model used twice the time consumption compared with the time consumptions of the JS-ELM and the FP-ELM models. Furthermore, the time consumptions of the proposed models were lower than the LSTM model, while the overall error results of the proposed models and LSTM were close.

For suggestions for future works, the proposed models can improve the stability of forecasting, for instance, according to Table 6, JS-ELM was the most suitable when considering the minimum error result, and FP-ELM was the most suitable when considering the S.D. result. Therefore, future work may propose a novel model that applies the hybrids of JSO and FPA to the ELM model. Due to the benefits of JSO and FPA, the expected results of the aforementioned novel model can be achieved with a more stable accuracy of forecasting and provide the best forecasting result. Moreover, the time consumption of forecasting is the major topic to discuss. According to Table 5, the time consumption of JS-ELM and FP-ELM were close and less than other models except for ELM. The time consumption of the proposed models and the future novel model can be reduced by using the step of tuning the hyper-parameters with a suitable algorithm and the methodology of an ensemble learning algorithm [52,53,54] that splits the appropriate sub-datasets from the primary dataset, forecasts the sub-datasets, and aggregates the forecasted model results. Finally, due to the variety of metaheuristics algorithms [47] that are continuously being developed, an alternative metaheuristics algorithm can be discussed to implement with the ELM model or other machine learning models to improve the accuracy of the forecasted electric energy demand.