An Applying Colored Petri Net for Computerized Accounting System and Ledger Accounts Instruction
Abstract
:1. Introduction
2. Literature Reviews
3. Background
3.1. Computer-Aided Instruction and Accounting Information Systems
- Point of sale module (POS module): this represents the place where the raw financial transactions takes place. The financial transactions may be posted by hand or automated by an integrated POS module. In the integrated POS module, the account mapping profile is used to map the raw financial transactions into the accounting transactions.
- Chart of account module or COA: A chart of accounts is manipulated at the COA module, on which the accounts in the list are classified into five series: assets, liabilities, equity, revenue, and expenses.
- Accounts receivable module: accounts receivable handles the invoicing and manages the customer payments.
- Accounts payable module: accounts payable handles the recording and tracking of the money owned by a business.
- General ledger module: the general ledger module is responsible for consolidating the accounting information from the point of sale module, accounts receivable module, and accounts payable module. Financial reports are computed from the accounting transactions stored in the general ledger module, and these transactions may be used for auditing purposes.
- Trial balance module: the trial balance module shows a listing of accounts that come along with the net balance of each account. It is useful for an internal checking because a trial balance can disclose the net balance both before adjustment and after adjustment, and it comprises the primary data for creating the balance sheet, income statement and cash flow report.
- Balance sheet module: this details a list of the organization assets, liabilities, and equity. It also be used to create and estimate the clash flow budget.
3.2. Colored Petri Net
4. Designing the Accounting System Using Colored Petri Net
- To demonstrate the accounting system, accounting components and accounting modules in terms of the graphical model advocating the instruction of computerized accounting system;
- To simulate the accounting behaviors and to verify the correctness of the accounting transaction flows.
4.1. Formal Definitions of CPN Model and Accounting System
- P is a set of places representing a state of system.
- T is a set of transitions representing an action of system, P ∩ T = ∅.
- A is a set of arcs connecting between the place and transition, A ⊆ ((P × T) ∪ (T × P)).Σ is finite set of color sets or data types.
- V is a finite set of colored variables, Type(v) ∈ Σ, for all variables v ∈ V.
- fs is a function used to assign a color set to each place, fs: P →Σ.
- fg is a guard-labeling function assigning a guard condition to a transition t ∈ T, fg: T → conditional expression and Type(fg(t)) = Boolean expression.
- fe is a function used to assign an arc expression for an arc a ∈ A, fe: A → arc expression and Type(fe(a)) = fs(p) where p is the target place of arc a. It indicates that the color set of the target place must conform to the output data type of the arc expression. The arc expression may be a list of variables including the conditional expression that come along with a list of variables.
- fi is an initialization function used to assign a marking to each place, fi:
- P → initial expression, Type(fi(p)) = fs(p) for all the places p ∈ P. It indicates that the data type of the initial marking in a place must be conformed to the place’s color.
- Ca is a set of core account types. For ∈ Ca, = (Name, Prefix, Type), where .Name indicates the core account name of described as a string expression. .Prefix indicates the account code prefix of . .Type indicates the account type of . There are five core account types: Asset, Liability, Equity, Revenue, and Expense.
- Aa is a set of accounts. For ∈ Aa, = (Name, Code), where .Name indicates the account name of , and .Code indicates the account code of described as a string expression, and the length of the account code depends on a system configuration.
- Ac is a chart of accounts, which is a list of accounts where (Ac ⊆ Aa).
- Bb is a set of beginning balances. For ∈ Bb, = (Code, Bal, Year), where .Code indicates the account code of , which can be referred to the account code ∈ Aa as well. .Bal means the total balance of at the specific account period (month), and .Year is the year of an account period.
- Jn is a set of journals. For ∈ Jn, = (Date, Src, Vouc), where .Date is the date of journal. .Src determines the data source of the financial transaction used for generating the accounting transactions, and .Vouc indicates the voucher number of journal.
- Jr is a set of accounting transactions in the journal. For ∈ Jr,
- = (Seq, Acc, RefTrx, TType, Amt), where .Seq is an ordering number of . .Acc indicates the account code. .RefTrx indicates the reference number of the financial transaction of , whereas .TType and .Amt indicate the T-account entry type (Dr or Cr) and the T-account amount, respectively.
- Ld is a set of ledgers, Ld ⊆ Aa. For ∈ Ld, = (Name, Code), where .Name is the name of the ledger. .Code is the account code that refers to the account code declared in the chart of accounts (.Code = .Code).
- fAp is a mapping function used to indicate the core account type, fAp: Aa → ca, or fAp: Ld → ca.
- Lr is a set of accounting transactions in the ledger, for ∈ Lr, = (ID, Date, Type, TotalBl), where .ID is an ordering number of ; .Date indicates the transaction date of . .Type is the ledger transaction type composing the Beginning and Accumulating; and .TotalBl indicates the net balance of .
- fLd is a mapping function used to indicate the ledger of the accounting transaction, fLd: Lr → Ld.
- fMax is a function used to retrieve the last number of the accounting transaction in the ledger. fMax: Lr →.
- fList is a binding function used to retrieve the last accounting transactions of all ledgers under a specific core account type, fList:Ca → a list of accounts, where ∈ Lr comes from the last transaction in each ledger.
- fSumTB is a function used to summarize the total balance of all ledgers, grouped by a specific core account type, fSumTB:Ca →≡.
4.2. Modules of CPN Accounting System
- Configuration module
- Journal entries module
- Ledger account module
- Lost/Profit module
- Trial balance module
- Balance sheet module
- Integrated module (all the above modules are integrated to form an integrated module, and it is arranged in hierarchical structure.)
- All the modules can be simulated and verified by using the simulation palate of the CPN tools for checking and tracing the CPN model execution.
- Provide the journal entry scenarios or case studies of the two business domains—a retail system and mortgage loan system—that come along with the accounting case studies for simulating the journal entries. The journal entry scenarios are defined in terms of a set of the token colors. The learners can take them to initiate and simulate to see the accounting system behaviors.
- The learners can use the provided CPN function to collect all the model execution events occurring during a simulation or verification and can export the execution events as a log file if they need.
4.2.1. Configuration Module
- The CPN model parameters (Param-Net) that comprise the configuration of the account period, running number of voucher, validating policies, and the beginning balances of ledger (Begin-Net).
- A chart of accounts (Chart-Net).
- An account mapping profile (Map-Net).
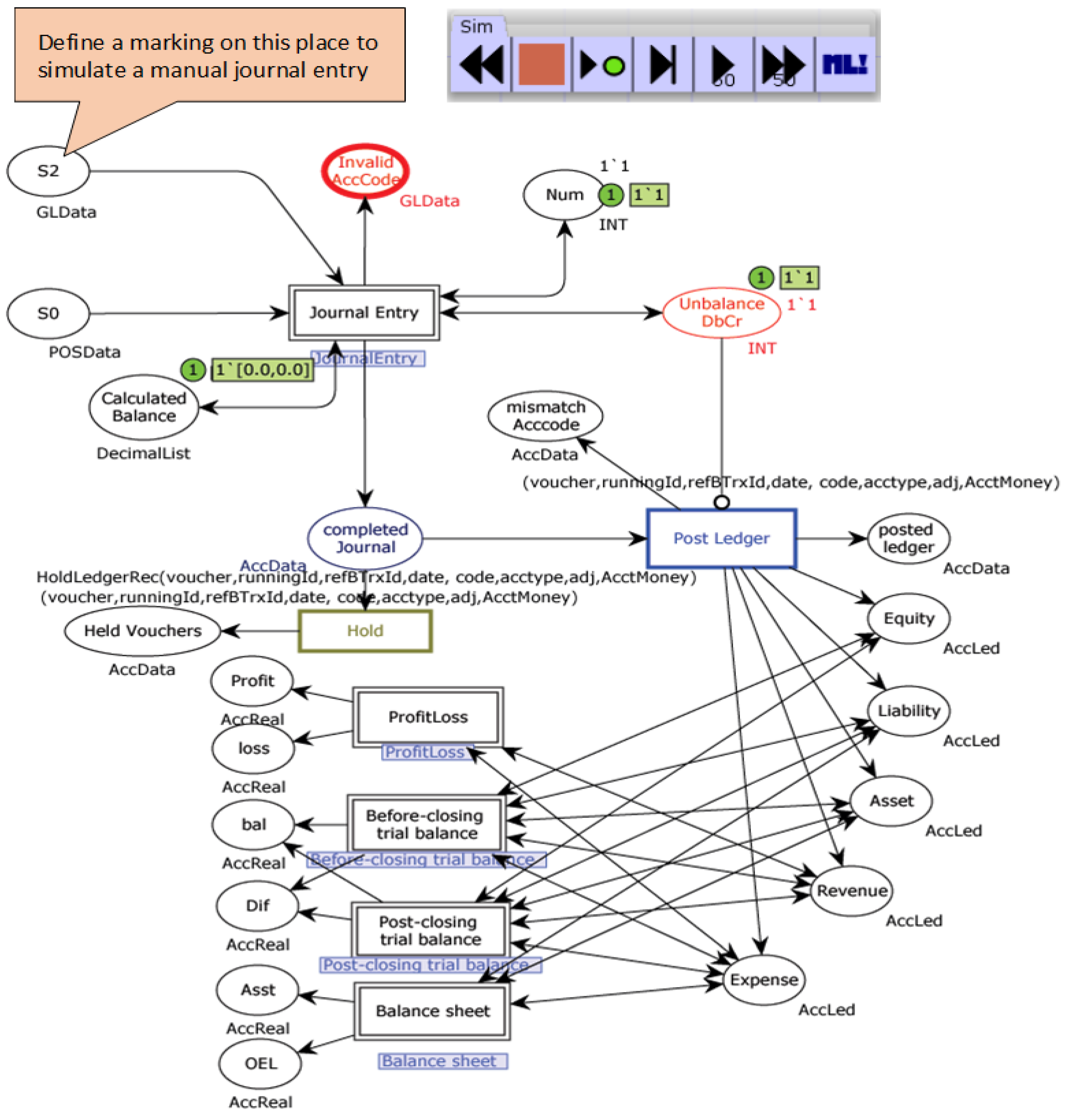
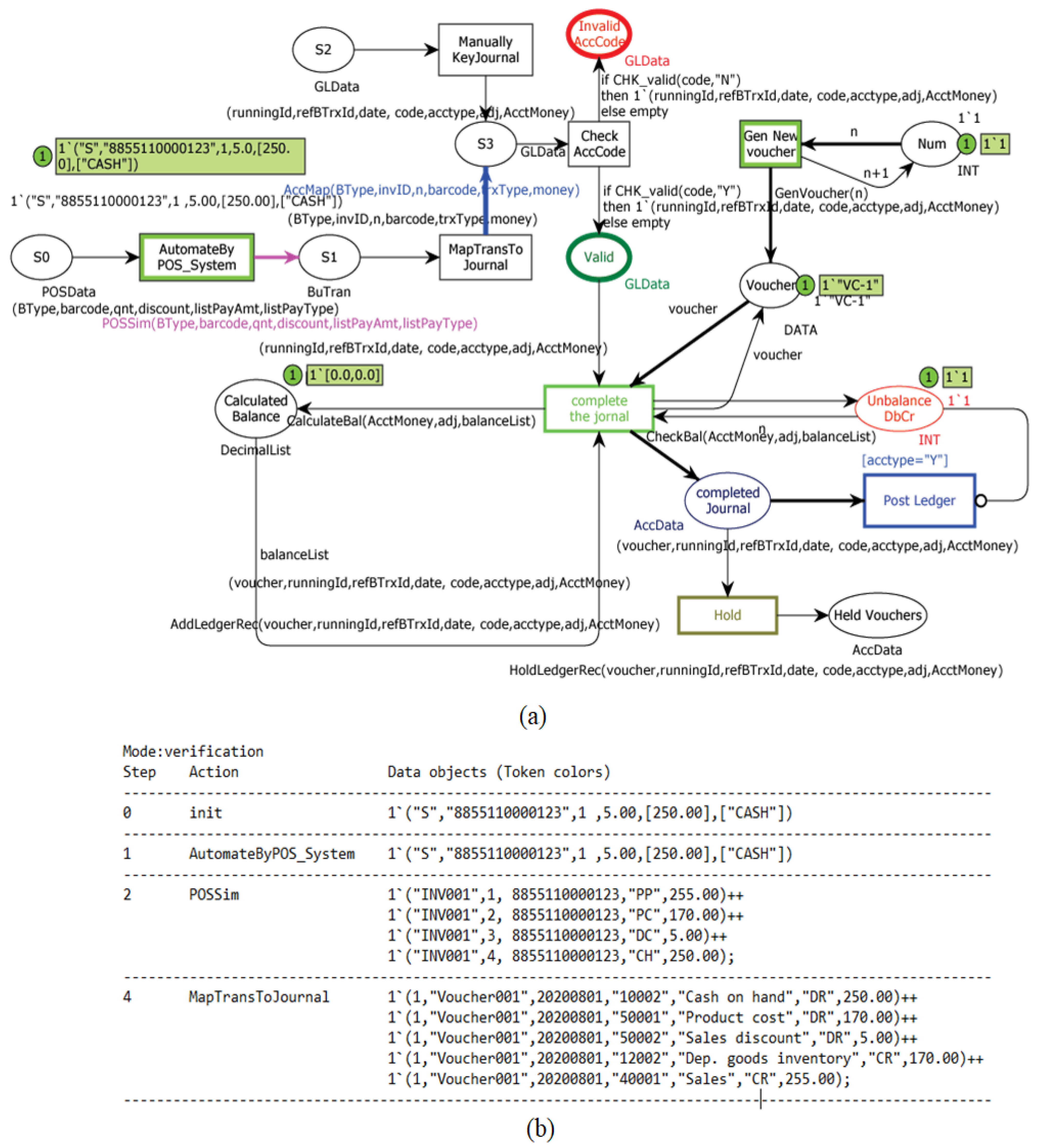
4.2.2. Journal Entries Module
Simulating the Manual Journal Entry
Simulating the Automatic Journal Entry
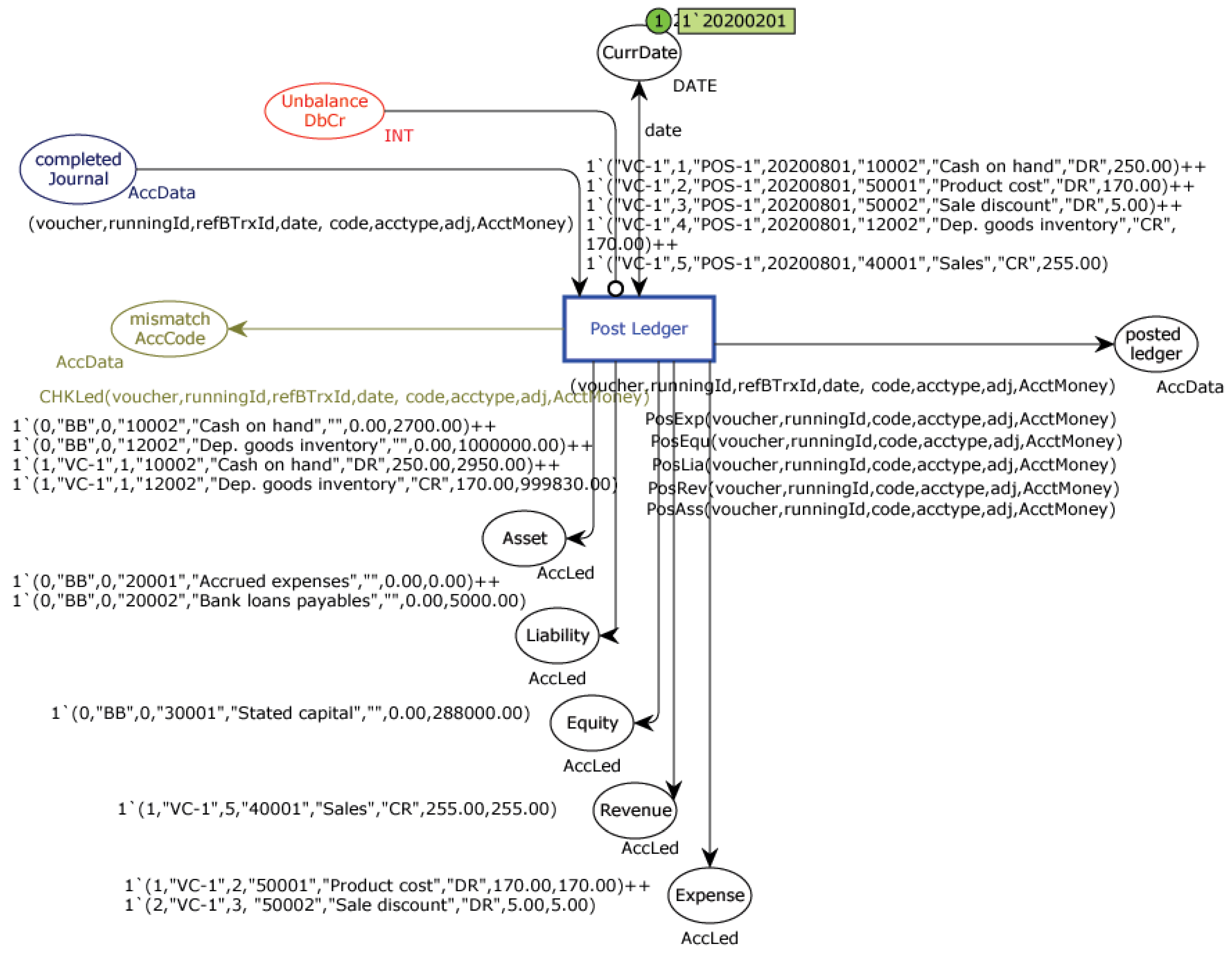
4.2.3. Ledger Posting Module
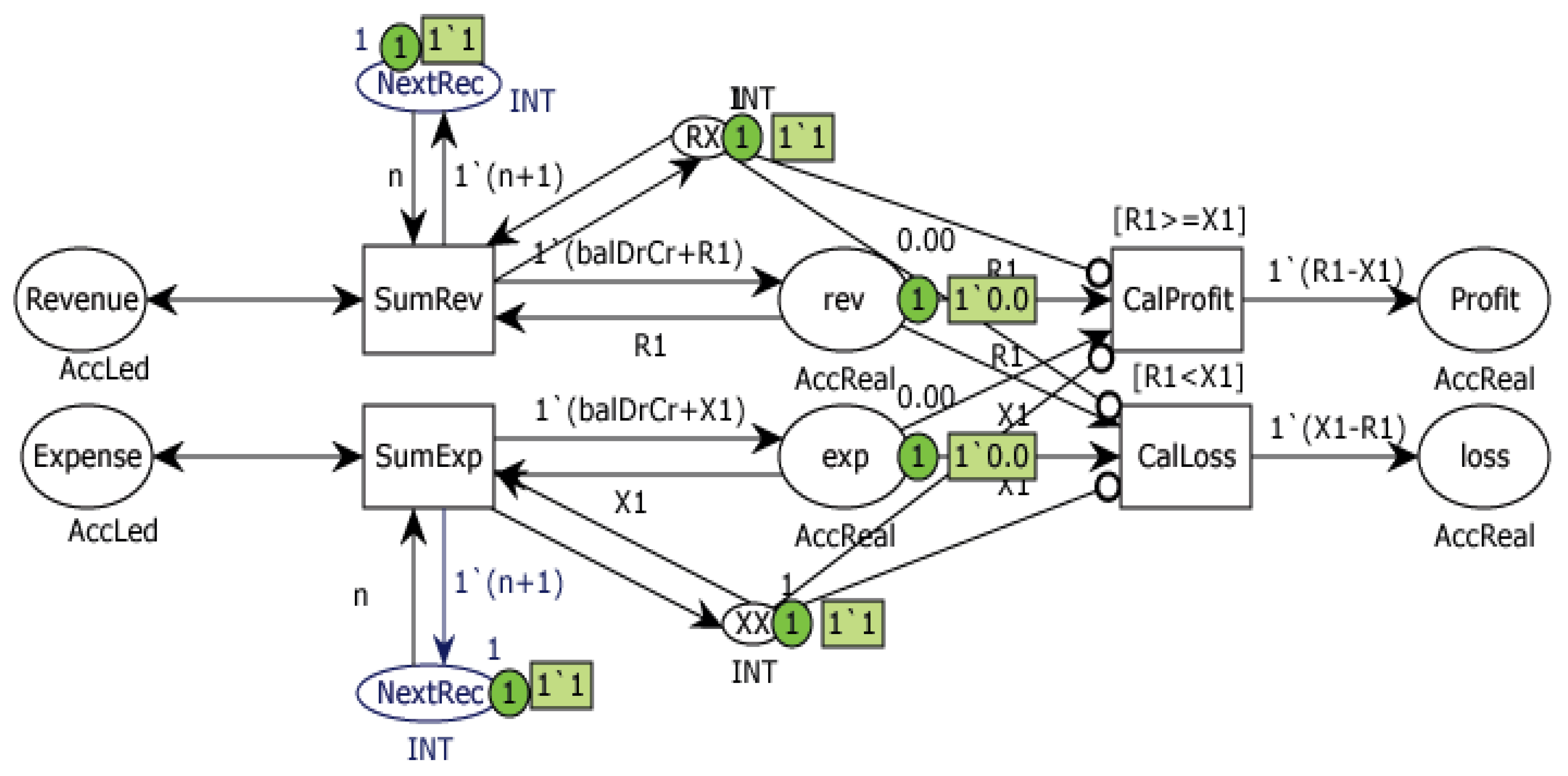
4.2.4. Lost/Profit Module
4.2.5. Trial Balance Module
4.2.6. The Balance Sheet Report
5. Evaluation the CPN Accounting System Model
- To demonstrate the accounting system that advocates the instruction of the accounting system and journal entries, we provided the CPN accounting system model that supports the simulation mode and verification mode. The obtained CPN model represents the accounting transaction flows likely to occur in an actual accounting system. It comes along with 232 cases of the journal entries for the retail system and loan system.
- To simulate and verify the correctness of the accounting transaction flows, we provided the CPN modules that come along with the CPN function that allows the learners to trace the model’s execution as a system log. Furthermore, the learners can configure a chart of accounts, account mapping profile, and the beginning balance, including the simulation of journal entries by using the simulation palate of CPN tools.
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Heiner, M.; Herajy, M.; Liu, F.; Rohr, C.; Schwarick, M. Snoopy—A unifying Petri net tool. In Proceedings of the International Conference on Application and Theory of Petri Nets and Concurrency, Hamburg, Germany, 25–29 June 2012; pp. 398–407. [Google Scholar]
- Jensen, K.; Kristensen, L.M.; Wells, L. Coloured Petri Nets and CPN Tools for modelling and validation of concurrent systems. Int. J. Softw. Tools Technol. Transf. 2007, 9, 213–254. [Google Scholar] [CrossRef]
- Chiola, G.; Franceschinis, G.; Gaeta, R.; Ribaudo, M. GreatSPN 1.7: Graphical editor and analyzer for timed and stochastic Petri nets. Perform. Eval. 1995, 24, 47–68. [Google Scholar] [CrossRef]
- Wolf, K. Petri net model checking with LoLA 2. In Proceedings of the International Conference on Applications and Theory of Petri Nets and Concurrency, Bratislava, Slovakia, 24–29 June2018; pp. 351–362. [Google Scholar]
- Singh, H.; Conrad, M.; Sadeghipour, S. Test case design based on Z and the classification-tree method. In Proceedings of the First IEEE International Conference on Formal Engineering Methods, Hiroshima, Japan, 12–14 November1997; pp. 81–90. [Google Scholar]
- Poolsawasdi, W.; Dechsupa, C. Formal Verification of the Accounting Information Interfaces Using Colored Petri Net. In Proceedings of the 2019 5th International Conference on Engineering, Applied Sciences and Technology (ICEAST), Luang Prabang, Laos, 2–5 July 2019; pp. 362–365. [Google Scholar]
- Kim, R.; Gangolly, J.; Elsas, P. A framework for analytics and simulation of accounting information systems: A Petri net modeling primer. Int. J. Account. Inf. Syst. 2017, 27, 30–54. [Google Scholar] [CrossRef]
- Yingwei, L.; Jiuzhi, M. The research of computerized accounting system of internal control. In Proceedings of the 2011 IEEE 3rd International Conference on Communication Software and Networks, Xi’an, China, 27–29 May 2011; pp. 302–304. [Google Scholar]
- Szpyrka, M.; Szmuc, T. Decision tables in Petri net models. In Proceedings of the International Conference on Rough Sets and Intelligent Systems Paradigms, Warsaw, Poland, 28–30 June 2007; pp. 648–657. [Google Scholar]
- Deesukying, J.; Vatanawood, W. Generating of business rules for Coloured Petri Nets. In Proceedings of the 2016 IEEE/ACIS 15th International Conference on Computer and Information Science (ICIS), Okayama, Japan, 26–29 June 2016; pp. 1–6. [Google Scholar]
- Bredmar, K.; Ask, U.; Frisk, E.; Magnusson, J. Accounting Information Systems implementation and management accounting change. Bus. Syst. Res. J. 2014, 5, 125–138. [Google Scholar] [CrossRef] [Green Version]
- Niu, Y. An empirical analysis of accounting information integration in integrated systems. In Proceedings of the 2010 2nd IEEE International Conference on Information Management and Engineering, Chengdu, China, 16–18 April 2010; pp. 107–110. [Google Scholar]
- Zuama, R.A.; Hudin, J.M.; Puspitasari, D.; Hermaliani, E.H.; Riana, D. Quality dimensions of Delone-McLean model to measure students’ accounting computer satisfaction: An empirical test on accounting system information. In Proceedings of the 2017 5th International Conference on Cyber and IT Service Management (CITSM), Denpasar, Indonesia, 8–10 August 2017; pp. 1–6. [Google Scholar]
- Mauldin, E.G.; Ruchala, L.V. Towards a meta-theory of accounting information systems. Organ. Soc. 1999, 24, 317–331. [Google Scholar] [CrossRef]
- Collins, D.; Deck, A.; McCrickard, M. Computer aided instruction A study of student evaluations and academic performance. J. Coll. Teach. Learn. 2008, 5, 49–58. [Google Scholar] [CrossRef]
- Cooper, J.P.; Pattanayak, S. Chart of Accounts: A Critical Element of the Public Financial Management Framework; Citeseer: Princeton, NJ, USA, 2011. [Google Scholar]
- Bryer, R.A. Double-entry bookkeeping and the birth of capitalism: Accounting for the commercial revolution in medieval northern Italy. Crit. Perspect. Account. 1993, 4, 113–140. [Google Scholar] [CrossRef]
- Baier, C.; Katoen, J.P. Principles of Model Checking; MIT Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Fisher, M. An Introduction to Practical Formal Methods Using Temporal Logic; John Wiley & Sons: Hoboken, NJ, USA, 2011; Volume 82. [Google Scholar]
- Clarke, E.M.; Klieber, W.; Nováček, M.; Zuliani, P. Model checking and the state explosion problem. In LASER Summer School on Software Engineering; Springer: Berlin/Heidelberg, Germany, 2011; pp. 1–30. [Google Scholar]
- Koch, I. Petri nets in systems biology. Softw. Syst. Model. 2015, 14, 703–710. [Google Scholar] [CrossRef]
- Blätke, M.A.; Heiner, M.; Marwan, W. Petri Nets in Systems Biology; Technical Report; Otto von Guericke University Magdeburg: Magdeburg, Germany, 2011. [Google Scholar]
- Pinney, J.W.; Westhead, D.R.; McConkey, G.A. Petri Net representations in systems biology. Biochem. Soc. Trans. 2003, 31, 1513–1515. [Google Scholar] [CrossRef] [PubMed]
- Heiner Monika, D.G.; Donaldson, R. Petri nets for systems and synthetic biology. In Proceedings of the International School on Formal Methods for the Design of Computer, Communication and Software Systems, Bertinoro, Italy, 2–7 June 2008; pp. 215–264. [Google Scholar]
- Liu, F. Colored Petri Nets for Systems Biology. Master’s Thesis, Brandenburg University of Technology, Cottbus, Germany, 2012. [Google Scholar]
- Jorgensen, P.C. Software Testing: A Craftsman’s Approach; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Computer Science Department, Boston University. SNOOPY: Web Animation. 2008. Available online: https://www-dssz.informatik.tu-cottbus.de/web_animation/pn/tram1.spped (accessed on 10 July 2021).







| Accounting Properties and Test Cases | POS | LOAN |
|---|---|---|
| Account codes and ledgers | 57 | 77 |
| Transaction types: (Auto entries) | 6 | 7 |
| Test cases: (Auto entries) | 49 | 57 |
| Transaction types: (Manual entries) | 5 | 8 |
| Test cases: (Manual entries) | 41 | 65 |
| Conditions | Types |
|---|---|
| A0 = bType : XX | Invalid |
| A1 = bType : NS (Normal sale) | Valid |
| A2 = bType : DS (Deposit sale) | Valid |
| A3 = bType : VS (Voided sale) | Valid |
| A4 = bType : VD (Voided deposit sale) | Valid |
| A5 = bType : RS (Returned sale) | Valid |
| A6 = bType : RD (Returned deposit sale) | Valid |
| P0 = Dr ≠ Cr | Valid |
| P1 = Dr = Cr | Valid |
| C0 = Matched code | Invalid |
| C1 = Mismatched code | Valid |
| H0 = Holding journal | Valid |
| H1 = Unholding journal | Valid |
| Condition | Cases | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | ... | 49 | |
| Business transaction type | A0 | A1 | A1 | A1 | A1 | A1 | A1 | A1 | ... | A6 |
| The net balance of Dr and Cr of a voucher | P0-P1 | P0 | P0 | P0 | P0 | P1 | P1 | P1 | ... | P1 |
| Account code matching | C0-C1 | C0 | C0 | C1 | C1 | C0 | C0 | C1 | ... | C1 |
| Journal holding | H0-H1 | H0 | H1 | H0 | H1 | H0 | H1 | H0 | ... | H1 |
| Rule Count | 8 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ... | 1 |
| Action or State(CPN Place ) | ||||||||||
| Generate financial transactions (“S1”) | x | x | x | x | x | x | x | ... | x | |
| Invalid account code (“Invalid AccCode”) | x | x | x | ... | x | |||||
| Valid account code (“Valid”) | x | x | x | x | ||||||
| Dr = Cr (“Calculated Balance”) | x | x | x | ... | x | |||||
| Dr ≠ Cr (“Calculated Balance”) | x | x | x | x | ||||||
| Unbalance (“UnbalanceDrCr”) | x | x | x | x | ||||||
| Held journal (“Hold Vouchers”) | x | x | x | x | ||||||
| Completed journal | x | x | ||||||||
| Post the ledgers | x | x | ||||||||
| Posted ledger | x | x | ||||||||
| The function “POSSIM” throws an error message | x | |||||||||
| Poolsawasdi and Dechsupa [6] | Kim et al. [7] | Our Approach | |
|---|---|---|---|
| Model | |||
| Language | CPN | PT | CPN |
| Creation | Automate form BPMN model | Manual | Manual |
| Simulation | Partial | Yes | Yes |
| Execution log | No | No | Yes |
| Accounting features | |||
| Parameterization | No | No | Yes |
| Ledger system | Partial | No | Yes |
| Journal entry | No | No | Yes |
| Account mapping profile | Partial | No | Yes |
| financial report | No | No | Yes |
| Formal verification | |||
| Level of abstraction | Low | Hight | Low |
| Properties | Correctness | Capacity and performance checking | Correctness |
| Appropriate for instruction | No | No | Yes |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dechsupa, C.; Vatanawood, W.; Poolsawasdi, W.; Thongtak, A. An Applying Colored Petri Net for Computerized Accounting System and Ledger Accounts Instruction. Computers 2021, 10, 169. https://doi.org/10.3390/computers10120169
Dechsupa C, Vatanawood W, Poolsawasdi W, Thongtak A. An Applying Colored Petri Net for Computerized Accounting System and Ledger Accounts Instruction. Computers. 2021; 10(12):169. https://doi.org/10.3390/computers10120169
Chicago/Turabian StyleDechsupa, Chanon, Wiwat Vatanawood, Worawit Poolsawasdi, and Arthit Thongtak. 2021. "An Applying Colored Petri Net for Computerized Accounting System and Ledger Accounts Instruction" Computers 10, no. 12: 169. https://doi.org/10.3390/computers10120169
APA StyleDechsupa, C., Vatanawood, W., Poolsawasdi, W., & Thongtak, A. (2021). An Applying Colored Petri Net for Computerized Accounting System and Ledger Accounts Instruction. Computers, 10(12), 169. https://doi.org/10.3390/computers10120169






