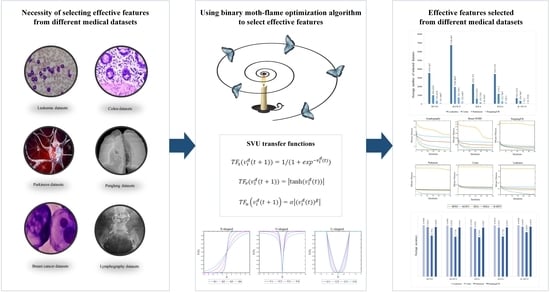
B-MFO: A Binary Moth-Flame Optimization for Feature Selection from Medical Datasets
Abstract
:1. Introduction
2. Related Work
3. The Canonical Moth-Flame Optimization
4. Binary Moth-Flame Optimization (B-MFO)
4.1. Developing Different Variants of B-MFO
4.1.1. B-MFO Using S-Shaped Transfer Function
4.1.2. B-MFO Using V-Shaped Transfer Function
4.1.3. B-MFO Using U-Shaped Transfer Function
4.2. B-MFO for Solving Feature Selection Problem
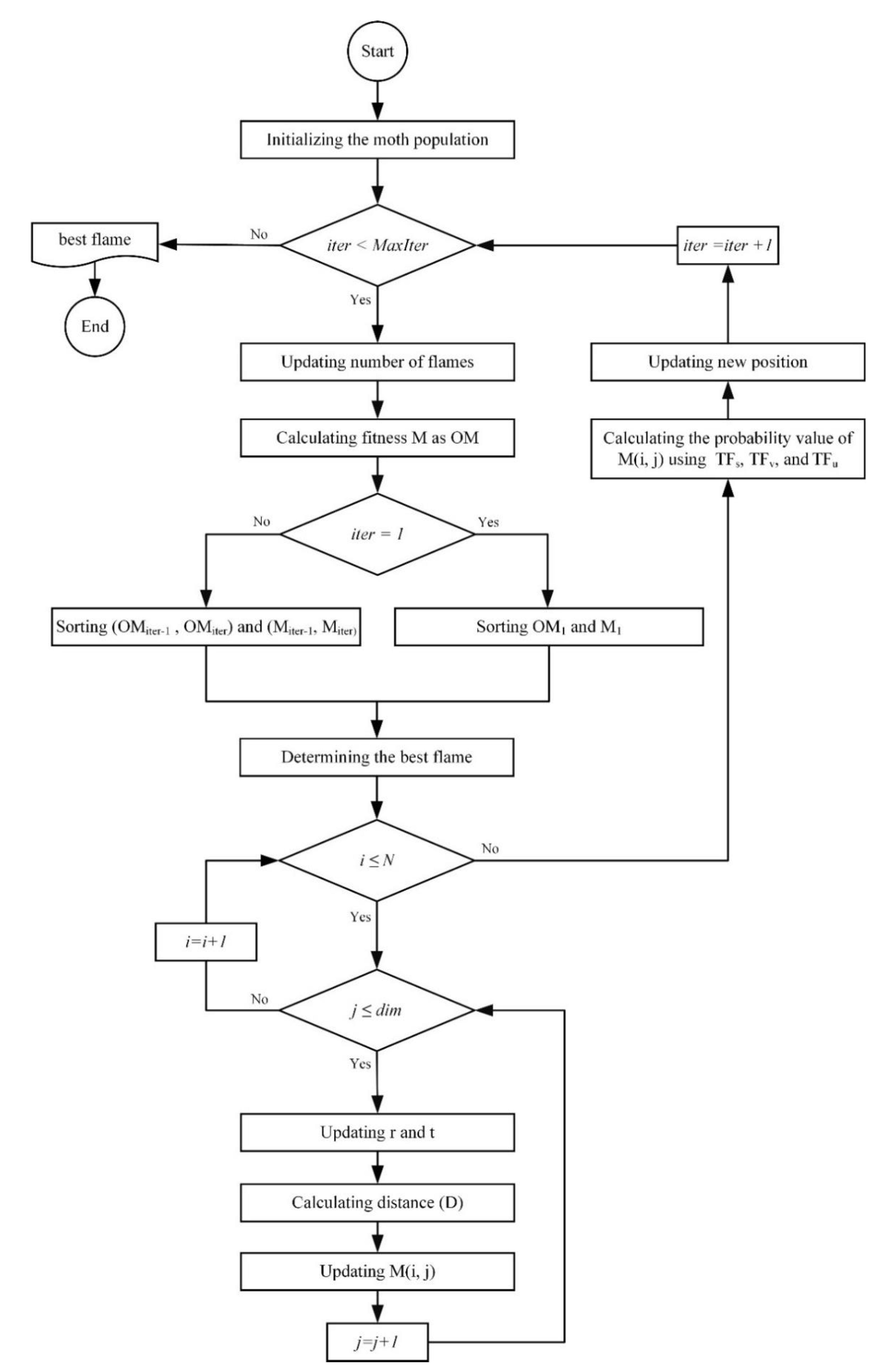
| Algorithm 1. The pseudo-code of B-MFO. | ||
| Algorithm of binary moth-flame optimization (B-MFO) | ||
| Input: N (Population size), MaxIter (Maximum number of iterations), dim (the number of dimensions). | ||
| Output: The global optimum (best flame). | ||
| 1: | Procedure B-MFO | |
| 2: | Initializing the moth population. | |
| 3: | While iter < MaxIter | |
| 4: | Updating number of flames (flameNo) using Equation (4). | |
| 5: | Calculating the fitness function M as OM. | |
| 6: | If iter==1 | |
| 7: | OF = sort (OM1). | |
| 8: | F = sort (M1). | |
| 9: | Else | |
| 10: | OF = sort (OMiter-1, OMiter). | |
| 11: | F = sort (Miter-1, Miter). | |
| 12: | End if | |
| 13: | Determining the best flame. | |
| 14: | For i = 1: N | |
| 15: | For j = 1: dim | |
| 16 | Updating r and t. | |
| 17: | Calculating D using Equation (3). | |
| 18: | Updating M(i, j) using Equation (1) and Equation (2). | |
| 19: | End for | |
| 20: | End for | |
| 21: | Calculating the probability value of M(i, j) using TFs in Equation (5), TFv in Equation (7), and TFu in Equation (9). | |
| 22: | Updating new position using Equation (6), Equation (8), and Equation (10). | |
| 23: | iter = iter +1. | |
| 24: | End while | |
| 25: | Return the global optimum (best flame). | |
| 26: | End Procedure | |
5. Experimental Assessment
5.1. Data Description
5.2. Evaluation Criteria
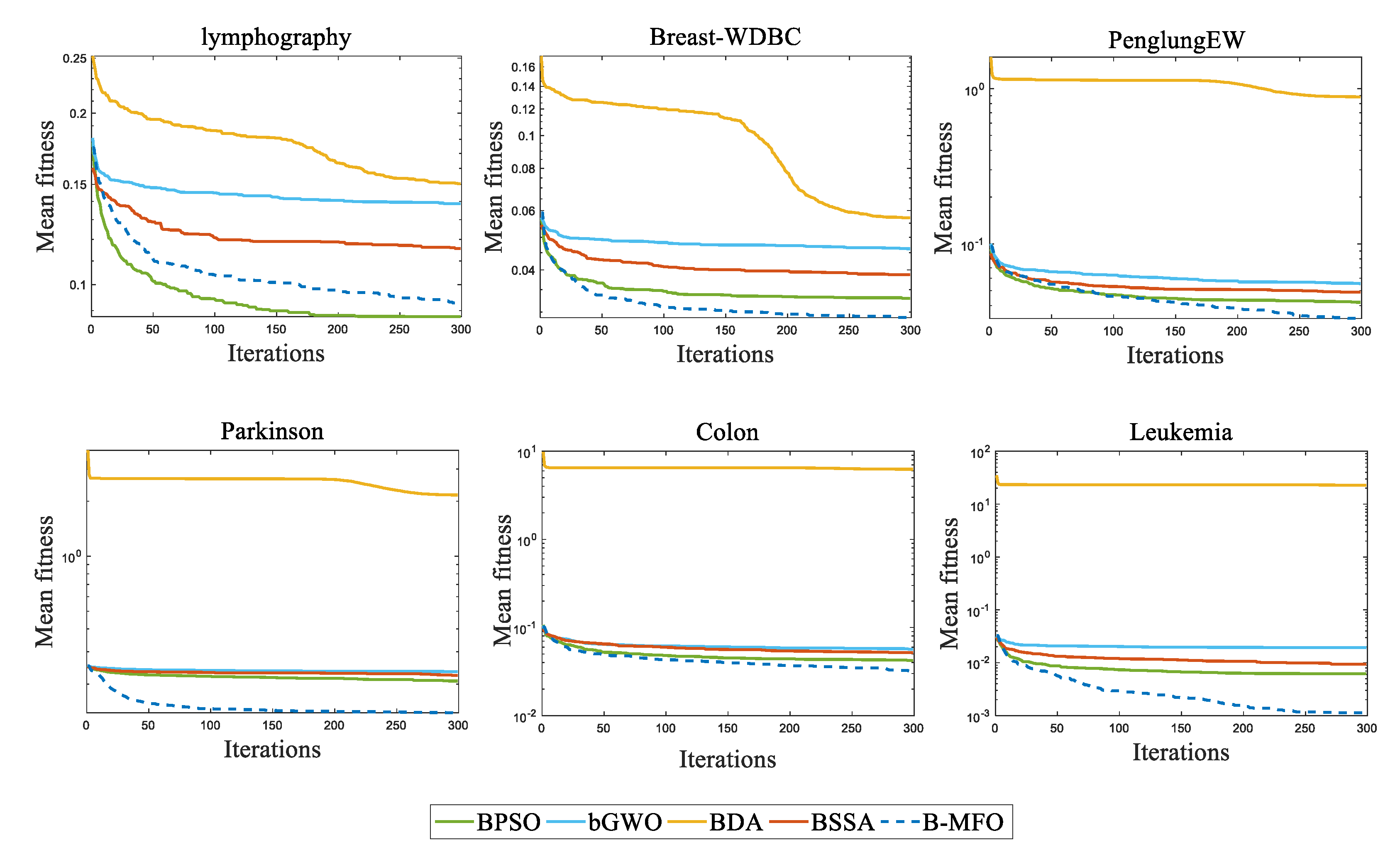
5.3. Discussion of the Results
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sorkhabi, L.B.; Gharehchopogh, F.S.; Shahamfar, J. A systematic approach for pre-processing electronic health records for mining: Case study of heart disease. Int. J. Data Min. Bioinform. 2020, 24, 97. [Google Scholar] [CrossRef]
- Esfandiari, N.; Babavalian, M.R.; Moghadam, A.-M.E.; Tabar, V.K. Knowledge discovery in medicine: Current issue and future trend. Expert Syst. Appl. 2014, 41, 4434–4463. [Google Scholar] [CrossRef]
- Zhang, B.; Cao, P. Classification of high dimensional biomedical data based on feature selection using redundant removal. PLoS ONE 2019, 14, e0214406. [Google Scholar] [CrossRef] [PubMed]
- Arjenaki, H.G.; Nadimi-Shahraki, M.H.; Nourafza, N. A low cost model for diagnosing coronary artery disease based on effective features. IJECCE 2015, 6, 93–97. [Google Scholar]
- Dezfuly, M.; Sajedi, H. Predict Survival of Patients with Lung Cancer Using an Ensemble Feature Selection Algotithm and Classification Methods in Data Mining. J. Inf. 2015, 1, 1–11. [Google Scholar]
- Mohammadzadeh, H.; Gharehchopogh, F.S. Novel Hybrid Whale Optimization Algorithm with Flower Pollination Algorithm for Feature Selection: Case Study Email Spam Detection. Comput. Intell. 2021, 37, 176–209. [Google Scholar] [CrossRef]
- Abualigah, L.M.; Khader, A.T.; Al-Betar, M.A. Unsupervised feature selection technique based on genetic algorithm for improving the Text Clustering. In Proceedings of the 2016 7th International Conference on Computer Science and Information Technology (CSIT), Amman, Jordan, 13–14 July 2016; 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Abualigah, L.M.Q. Feature Selection and Enhanced Krill Herd Algorithm for Text Document Clustering; Springer: Berlin, Germany, 2019. [Google Scholar] [CrossRef]
- Helmi, A.M.; Al-Qaness, M.A.; Dahou, A.; Damaševičius, R.; Krilavičius, T.; Elaziz, M.A. A novel hybrid gradient-based optimizer and grey wolf optimizer feature selection method for human ac-tivity recognition using smartphone sensors. Entropy 2021, 23, 1065. [Google Scholar] [CrossRef] [PubMed]
- Huan, L.; Lei, Y. Toward integrating feature selection algorithms for classification and clustering. IEEE Trans. Knowl. Data Eng. 2005, 17, 491–502. [Google Scholar] [CrossRef] [Green Version]
- Xue, B.; Zhang, M.; Browne, W.N. Particle swarm optimisation for feature selection in classification: Novel initialisation and updating mechanisms. Appl. Soft Comput. 2014, 18, 261–276. [Google Scholar] [CrossRef]
- Guyon, I.; Elisseeff, A. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Pashaei, E.; Aydin, N. Binary black hole algorithm for feature selection and classification on biological data. Appl. Soft Comput. 2017, 56, 94–106. [Google Scholar] [CrossRef]
- de Souza RC, T.; de Macedo, C.A.; dos Santos Coelho, L.; Pierezan, J.; Mariani, V.C. Binary coyote optimization algorithm for feature selection. Pattern Recognit. 2020, 107, 107470. [Google Scholar] [CrossRef]
- Faris, H.; Heidari, A.A.; Al-Zoubi, A.M.; Mafarja, M.; Aljarah, I.; Eshtay, M.; Mirjalili, S. Time-varying hierarchical chains of salps with random weight networks for feature selection. Expert Syst. Appl. 2019, 140, 112898. [Google Scholar] [CrossRef]
- Taghian, S.; Nadimi-Shahraki, M.H. Binary Sine Cosine Algorithms for Feature Selection from Medical Data. Adv. Comput. Int. J. 2019, 10, 1–10. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the MHS’Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl. Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Abualigah, L.; Yousri, D.; Elaziz, M.A.; Ewees, A.A.; Al-Qaness, M.A.; Gandomi, A.H. Aquila Optimizer: A novel meta-heuristic optimization algorithm. Comput. Ind. Eng. 2021, 157, 107250. [Google Scholar] [CrossRef]
- Zamani, H.; Nadimi-Shahraki, M.H.; Gandomi, A. CCSA: Conscious Neighborhood-based Crow Search Algorithm for Solving Global Optimization Problems. Appl. Soft Comput. 2019, 85, 105583. [Google Scholar] [CrossRef]
- Askarzadeh, A. A novel metaheuristic method for solving constrained engineering optimization problems: Crow search al-gorithm. Comput. Struct. 2016, 169, 1–12. [Google Scholar] [CrossRef]
- Shi, Y.; Pun, C.-M.; Hu, H.; Gao, H. An improved artificial bee colony and its application. Knowl. Based Syst. 2016, 107, 14–31. [Google Scholar] [CrossRef]
- Shang, Y. Optimal Control Strategies for Virus Spreading in Inhomogeneous Epidemic Dynamics. Can. Math. Bull. 2013, 56, 621–629. [Google Scholar] [CrossRef]
- Oliva, D.; Abd El Aziz, M.; Hassanien, A.E. Parameter estimation of photovoltaic cells using an improved chaotic whale optimization algorithm. Appl. Energy 2017, 200, 141–154. [Google Scholar] [CrossRef]
- Ewees, A.A.; Abd Elaziz, M.; Houssein, E.H. Improved grasshopper optimization algorithm using opposition-based learning. Expert Syst. Appl. 2018, 112, 156–172. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Taghian, S.; Mirjalili, S. An improved grey wolf optimizer for solving engineering problems. Expert Syst. Appl. 2020, 166, 113917. [Google Scholar] [CrossRef]
- Liu, H.; Ding, G.; Wang, B. Bare-bones particle swarm optimization with disruption operator. Appl. Math. Comput. 2014, 238, 106–122. [Google Scholar] [CrossRef]
- Guo, L.; Wang, G.-G.; Gandomi, A.; Alavi, A.H.; Duan, H. A new improved krill herd algorithm for global numerical optimization. Neurocomputing 2014, 138, 392–402. [Google Scholar] [CrossRef]
- Zaman, H.R.R.; Gharehchopogh, F.S. An improved particle swarm optimization with backtracking search optimization algorithm for solving continuous optimization problems. Eng. Comput. 2021, 1–35. [Google Scholar] [CrossRef]
- Banaie-Dezfouli, M.; Nadimi-Shahraki, M.H.; Beheshti, Z. R-GWO: Representative-based grey wolf optimizer for solving en-gineering problems. Appl. Soft Comput. 2021, 106, 107328. [Google Scholar] [CrossRef]
- Fayyad, U.; Piatetsky-Shapiro, G.; Smyth, P. From data mining to knowledge discovery in databases. AI Mag. 1996, 17, 37. [Google Scholar]
- Taghian, S.; Nadimi-Shahraki, M.H. A binary metaheuristic algorithm for wrapper feature selection. Int. J. Comput. Sci. Eng. 2019, 8, 168–172. [Google Scholar]
- Mafarja, M.; Aljarah, I.; Faris, H.; Hammouri, A.I.; Al-Zoubi, A.M.; Mirjalili, S. Binary grasshopper optimisation algorithm approaches for feature selection problems. Expert Syst. Appl. 2018, 117, 267–286. [Google Scholar] [CrossRef]
- Arora, S.; Anand, P. Binary butterfly optimization approaches for feature selection. Expert Syst. Appl. 2018, 116, 147–160. [Google Scholar] [CrossRef]
- Mohammadzadeh, H.; Gharehchopogh, F.S. Feature Selection with Binary Symbiotic Organisms Search Algorithm for Email Spam Detection. Int. J. Inf. Technol. Decis. Mak. 2021, 20, 469–515. [Google Scholar] [CrossRef]
- Safaldin, M.; Otair, M.; Abualigah, L. Improved binary gray wolf optimizer and SVM for intrusion detection system in wireless sensor networks. J. Ambient. Intell. Humaniz. Comput. 2020, 12, 1559–1576. [Google Scholar] [CrossRef]
- Khurma, R.; Alsawalqah, H.; Aljarah, I.; Elaziz, M.; Damaševičius, R. An Enhanced Evolutionary Software Defect Prediction Method Using Island Moth Flame Optimization. Mathematics 2021, 9, 1722. [Google Scholar] [CrossRef]
- Elsakaan, A.A.; El-Sehiemy, R.A.; Kaddah, S.S.; Elsaid, M.I. An enhanced moth-flame optimizer for solving non-smooth economic dispatch problems with emissions. Energy 2018, 157, 1063–1078. [Google Scholar] [CrossRef]
- Pelusi, D.; Mascella, R.; Tallini, L.; Nayak, J.; Naik, B.; Deng, Y. An Improved Moth-Flame Optimization algorithm with hybrid search phase. Knowl. Based Syst. 2019, 191, 105277. [Google Scholar] [CrossRef]
- Xu, Y.; Chen, H.; Heidari, A.A.; Luo, J.; Zhang, Q.; Zhao, X.; Li, C. An efficient chaotic mutative moth-flame-inspired optimizer for global optimization tasks. Expert Syst. Appl. 2019, 129, 135–155. [Google Scholar] [CrossRef]
- Neshat, M.; Sergiienko, N.; Mirjalili, S.; Nezhad, M.M.; Piras, G.; Garcia, D.A. Multi-Mode Wave Energy Converter Design Optimisation Using an Improved Moth Flame Optimisation Algorithm. Energies 2021, 14, 3737. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. A discrete binary version of the particle swarm algorithm. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics. Computational Cybernetics and Simulation, Orlando, FL, USA, 12–15 October 1997; pp. 4104–4108. [Google Scholar] [CrossRef]
- Emary, E.; Zawbaa, H.M.; Hassanien, A.E. Binary grey wolf optimization approaches for feature selection. Neurocomputing 2016, 172, 371–381. [Google Scholar] [CrossRef]
- Mafarja, M.; Aljarah, I.; Heidari, A.A.; Faris, H.; Fournier-Viger, P.; Li, X.; Mirjalili, S. Binary dragonfly optimization for feature selection using time-varying transfer functions. Knowledge-Based Syst. 2018, 161, 185–204. [Google Scholar] [CrossRef]
- Faris, H.; Mafarja, M.M.; Heidari, A.A.; Aljarah, I.; Al-Zoubi, A.; Mirjalili, S.; Fujita, H. An efficient binary Salp Swarm Algorithm with crossover scheme for feature selection problems. Knowledge-Based Syst. 2018, 154, 43–67. [Google Scholar] [CrossRef]
- El Aziz, M.A.; Hassanien, A.E. Modified cuckoo search algorithm with rough sets for feature selection. Neural Comput. Appl. 2016, 29, 925–934. [Google Scholar] [CrossRef]
- Ibrahim, R.A.; Elaziz, M.A.; Oliva, D.; Cuevas, E.; Lu, S. An opposition-based social spider optimization for feature selection. Soft Comput. 2019, 23, 13547–13567. [Google Scholar] [CrossRef]
- Dezfouli, M.B.; Nadimi-Shahraki, M.H.; Zamani, H. A novel tour planning model using big data. In Proceedings of the 2018 International Conference on Artificial Intelligence and Data Processing, New York, NY, USA, 28–30 September 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Shang, Y.; Bouffanais, R. Consensus reaching in swarms ruled by a hybrid metric-topological distance. Eur. Phys. J. B 2014, 87, 1–7. [Google Scholar] [CrossRef]
- Benyamin, A.; Farhad, S.G.; Saeid, B. Discrete farmland fertility optimization algorithm with metropolis acceptance criterion for traveling salesman problems. Int. J. Intell. Syst. 2020, 36, 1270–1303. [Google Scholar] [CrossRef]
- Talbi, E.-G. Metaheuristics: From Design to Implementation; Wiley Publishing: Hoboken, NJ, USA, 2009. [Google Scholar]
- Hafez, A.I.; Emary, E.; Zawbaa, H.M.; Hassanien, A.E. Sine cosine optimization algorithm for feature selection. In Proceedings of the 2016 International Symposium on INnovations in Intelligent SysTems and Applications, Sinaia, Romania, 2–5 August 2016. [Google Scholar]
- Mafarja, M.; Mirjalili, S. Whale optimization approaches for wrapper feature selection. Appl. Soft Comput. 2018, 62, 441–453. [Google Scholar] [CrossRef]
- Emary, E.; Zawbaa, H.M.; Hassanien, A.E. Binary ant lion approaches for feature selection. Neurocomputing 2016, 213, 54–65. [Google Scholar] [CrossRef]
- Ghimatgar, H.; Kazemi, K.; Helfroush, M.S.; Aarabi, A. An improved feature selection algorithm based on graph clustering and ant colony optimization. Knowledge-Based Syst. 2018, 159, 270–285. [Google Scholar] [CrossRef]
- Mirjalili, S. Dragonfly algorithm: A new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural Comput. Appl. 2015, 27, 1053–1073. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Hashim, F.A.; Houssein, E.H.; Mabrouk, M.S.; Al-Atabany, W.; Mirjalili, S. Henry gas solubility optimization: A novel physics-based algorithm. Futur. Gener. Comput. Syst. 2019, 101, 646–667. [Google Scholar] [CrossRef]
- Shayanfar, H.; Gharehchopogh, F.S. Farmland fertility: A new metaheuristic algorithm for solving continuous optimization problems. Appl. Soft Comput. 2018, 71, 728–746. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Taghian, S.; Mirjalili, S.; Faris, H. MTDE: An effective multi-trial vector-based differential evolution algorithm and its applications for engineering design problems. Appl. Soft Comput. 2020, 97, 106761. [Google Scholar] [CrossRef]
- Zamani, H.; Nadimi-Shahraki, M.H.; Gandomi, A.H. QANA: Quantum-based avian navigation optimizer algorithm. Eng. Appl. Artif. Intell. 2021, 104, 104314. [Google Scholar] [CrossRef]
- Zamani, H.; Nadimi-Shahraki, M.H.; Taghian, S.; Banaie-Dezfouli, M. Enhancement of bernstain-search differential evolution algorithm to solve constrained engineering problems. Int. J. Comput. Sci. Eng. 2020, 386–396. [Google Scholar]
- Ghasemi, M.R.; Varaee, H. Enhanced IGMM optimization algorithm based on vibration for numerical and engineering problems. Eng. Comput. 2017, 34, 91–116. [Google Scholar] [CrossRef]
- Varaee, H.; Hamzehkolaei, N.S.; Safari, M. A Hybrid Generalized Reduced Gradient-Based Particle Swarm Optimizer for Constrained Engineering Optimization Problems. J. Soft Comput. Civil Eng. 2021, 5, 86–119. [Google Scholar] [CrossRef]
- Sayarshad, H.R. Using bees algorithm for material handling equipment planning in manufacturing systems. Int. J. Adv. Manuf. Technol. 2009, 48, 1009–1018. [Google Scholar] [CrossRef]
- Fard, E.S.; Monfaredi, K.; Nadimi-Shahraki, M.H. An Area-Optimized Chip of Ant Colony Algorithm Design in Hardware Platform Using the Address-Based Method. Int. J. Electr. Comput. Eng. 2014, 4, 989. [Google Scholar] [CrossRef]
- Tadi, A.A.; Aghajanloo, Z. Load Balancing in Cloud Computing using Cuckoo Optimization Algorithm. J. Innov. Res. Eng. Sci. 2018, 4, 4. [Google Scholar]
- Zahrani, H.K.; Nadimi-Shahraki, M.H.; Sayarshad, H.R. An intelligent social-based method for rail-car fleet sizing problem. J. Rail Transp. Plan. Manag. 2020, 17, 100231. [Google Scholar] [CrossRef]
- Taghian, S.; Nadimi-Shahraki, M.H.; Zamani, H. Comparative Analysis of Transfer Function-based Binary Metaheuristic Algorithms for Feature Selection. In Proceedings of the International Conference on Artificial Intelligence and Data Processing (IDAP), Malatya, Turkey, 28–30 September 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Aslan, M.; Gunduz, M.; Kiran, M.S. JayaX: Jaya algorithm with xor operator for binary optimization. Appl. Soft Comput. 2019, 82, 105576. [Google Scholar] [CrossRef]
- Jia, D.; Duan, X.; Khan, M.K. Binary Artificial Bee Colony optimization using bitwise operation. Comput. Ind. Eng. 2014, 76, 360–365. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. S-shaped versus V-shaped transfer functions for binary Particle Swarm Optimization. Swarm Evol. Comput. 2013, 9, 1–14. [Google Scholar] [CrossRef]
- Nezamabadi-pour, H.; Rostami-Shahrbabaki, M.; Maghfoori-Farsangi, M. Binary particle swarm optimization: Challenges and new solutions. CSI J Comput Sci Eng 2008, 6, 21–32. [Google Scholar]
- Mirjalili, S.; Zhang, H.; Mirjalili, S.; Chalup, S.; Noman, N. A Novel U-Shaped Transfer Function for Binary Particle Swarm Optimisation. In Soft Computing for Problem Solving 2019; Springer: Singapore, 2019. [Google Scholar]
- Pedrasa, M.A.A.; Spooner, T.D.; MacGill, I.F. Scheduling of Demand Side Resources Using Binary Particle Swarm Optimization. IEEE Trans. Power Syst. 2009, 24, 1173–1181. [Google Scholar] [CrossRef]
- Liao, C.-J.; Tseng, C.-T.; Luarn, P. A discrete version of particle swarm optimization for flowshop scheduling problems. Comput. Oper. Res. 2007, 34, 3099–3111. [Google Scholar] [CrossRef]
- Lin, J.C.-W.; Yang, L.; Fournier-Viger, P.; Hong, T.-P.; Voznak, M. A binary PSO approach to mine high-utility itemsets. Soft Comput. 2016, 21, 5103–5121. [Google Scholar] [CrossRef]
- Yuan, X.; Nie, H.; Su, A.; Wang, L.; Yuan, Y. An improved binary particle swarm optimization for unit commitment problem. Expert Syst. Appl. 2009, 36, 8049–8055. [Google Scholar] [CrossRef]
- Bharti, K.K.; Singh, P.K. Opposition chaotic fitness mutation based adaptive inertia weight BPSO for feature selection in text clustering. Appl. Soft Comput. 2016, 43, 20–34. [Google Scholar] [CrossRef]
- Abualigah, L.; Khader, A.T.; Hanandeh, E.S. A new feature selection method to improve the document clustering using particle swarm optimization algorithm. J. Comput. Sci. 2018, 25, 456–466. [Google Scholar] [CrossRef]
- Lu, Y.; Liang, M.; Ye, Z.; Cao, L. Improved particle swarm optimization algorithm and its application in text feature selection. Appl. Soft Comput. 2015, 35, 629–636. [Google Scholar] [CrossRef]
- Sheikhpour, R.; Sarram, M.A.; Sheikhpour, R. Particle swarm optimization for bandwidth determination and feature selection of kernel density estimation based classifiers in diagnosis of breast cancer. Appl. Soft Comput. 2016, 40, 113–131. [Google Scholar] [CrossRef]
- Gunasundari, S.; Janakiraman, S.; Meenambal, S. Velocity Bounded Boolean Particle Swarm Optimization for improved feature selection in liver and kidney disease diagnosis. Expert Syst. Appl. 2016, 56, 28–47. [Google Scholar] [CrossRef]
- Zamani, H.; Nadimi-Shahraki, M.H. Swarm Intelligence Approach for Breast Cancer Diagnosis. Int. J. Comput. Appl. 2016, 151, 40–44. [Google Scholar] [CrossRef]
- Al-Tashi, Q.; Kadir, S.J.A.; Rais, H.M.; Mirjalili, S.; Alhussian, H. Binary Optimization Using Hybrid Grey Wolf Optimization for Feature Selection. IEEE Access 2019, 7, 39496–39508. [Google Scholar] [CrossRef]
- Panwar, L.K.; Reddy, S.; Verma, A.; Panigrahi, B.K.; Kumar, R. Binary Grey Wolf Optimizer for large scale unit commitment problem. Swarm Evol. Comput. 2018, 38, 251–266. [Google Scholar] [CrossRef]
- Chantar, H.; Mafarja, M.; Alsawalqah, H.; Heidari, A.A.; Aljarah, I.; Faris, H. Feature selection using binary grey wolf optimizer with elite-based crossover for Arabic text classification. Neural Comput. Appl. 2019, 32, 12201–12220. [Google Scholar] [CrossRef]
- Hu, P.; Pan, J.-S.; Chu, S.-C. Improved Binary Grey Wolf Optimizer and Its application for feature selection. Knowledge-Based Syst. 2020, 195, 105746. [Google Scholar] [CrossRef]
- Zamani, H.; Nadimi-Shahraki, M.H. Feature selection based on whale optimization algorithm for diseases diagnosis. Int. J. Comput. Sci. Inf. Secur. 2016, 14, 1243. [Google Scholar]
- Hussien, A.G.; Houssein, E.H.; Hassanien, A.E. A binary whale optimization algorithm with hyperbolic tangent fitness function for feature selection. In Proceedings of the Eighth International Conference on Intelligent Computing and Information Systems, Cairo, Egypt, 5–7 December 2017; pp. 166–172. [Google Scholar] [CrossRef]
- Hussien, A.G.; Hassanien, A.E.; Houssein, E.H.; Bhattacharyya, S.; Amin, M. S-shaped binary whale optimization algorithm for feature selection. In Recent Trends in Signal and Image Processing; Springer: Singapore, 2019; pp. 79–87. [Google Scholar] [CrossRef]
- Reddy, K.S.; Panwar, L.; Panigrahi, B.K.; Kumar, R. Binary whale optimization algorithm: A new metaheuristic approach for profit-based unit commitment problems in competitive electricity markets. Eng. Optim. 2019, 51, 369–389. [Google Scholar] [CrossRef]
- Mafarja, M.M.; Eleyan, D.; Jaber, I.; Hammouri, A.; Mirjalili, S. Binary dragonfly algorithm for feature selection. In Proceedings of the 2017 International Conference on New Trends in Computing Sciences (ICTCS), Amman, Jordan, 11–13 October 2017. [Google Scholar]
- Sawhney, R.; Jain, R. Modified Binary Dragonfly Algorithm for Feature Selection in Human Papillomavirus-Mediated Disease Treatment. In Proceedings of the 2018 International Conference on Communication, Computing and Internet of Things (IC3IoT), Tamil Nadu, India, 15–17 February 2018; pp. 91–95. [Google Scholar] [CrossRef]
- Too, J.; Mirjalili, S. A Hyper Learning Binary Dragonfly Algorithm for Feature Selection: A COVID-19 Case Study. Knowledge-Based Syst. 2020, 212, 106553. [Google Scholar] [CrossRef]
- Ibrahim, R.A.; Ewees, A.; Oliva, D.; Elaziz, M.A.; Lu, S. Improved salp swarm algorithm based on particle swarm optimization for feature selection. J. Ambient. Intell. Humaniz. Comput. 2018, 10, 3155–3169. [Google Scholar] [CrossRef]
- Meraihi, Y.; Ramdane-Cherif, A.; Mahseur, M.; Achelia, D. A Chaotic binary salp swarm algorithm for solving the graph coloring problem. In International Symposium on Modelling and Implementation of Complex Systems; Springer: Cham, Switzerland, 2018; pp. 106–118. [Google Scholar] [CrossRef]
- Geem, Z.W.; Kim, J.H.; Loganathan, G. A New Heuristic Optimization Algorithm: Harmony Search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. BGSA: Binary gravitational search algorithm. Nat. Comput. 2009, 9, 727–745. [Google Scholar] [CrossRef]
- Reddy, S.; Panwar, L.K.; Panigrahi, B.K.; Kumar, R. Solution to Unit Commitment in Power System Operation Planning Using Modified Moth Flame Optimization Algorithm (MMFOA): A Flame Selection Based Computational Technique. J. Comput. Sci. 2017, 25, 298–317. [Google Scholar]
- Ghosh, K.K.; Singh, P.K.; Hong, J.; Geem, Z.W.; Sarkar, R. Binary Social Mimic Optimization Algorithm With X-Shaped Transfer Function for Feature Selection. IEEE Access 2020, 8, 97890–97906. [Google Scholar] [CrossRef]
- Wang, L.; Fu, X.; Menhas, M.I.; Fei, M. A Modified Binary Differential Evolution Algorithm; Springer: Berlin, Germany, 2010; pp. 49–57. [Google Scholar] [CrossRef]
- Michalak, K. Selecting Best Investment Opportunities from Stock Portfolios Optimized by a Multiobjective Evolutionary Al-gorithm. In Proceedings of the 2015 Annual Conference on Genetic and Evolutionary Computation. 2015, Association for Computing Machinery, Madrid, Spain, 11–15 July 2015; pp. 1239–1246. [Google Scholar]
- Daolio, F.; Liefooghe, A.; Verel, S.; Aguirre, H.; Tanaka, K. Global vs local search on multi-objective NK-landscapes: Contrasting the impact of problem features. In Proceedings of the 2015 Annual Conference on Genetic and Evolutionary Computation, Madrid, Spain, 11–15 July 2015; 2015. [Google Scholar]
- Statnikov, A.; Aliferis, C.F.; Tsamardinos, I.; Hardin, D.; Levy, S. A comprehensive evaluation of multicategory classification methods for microarray gene expression cancer diagnosis. Bioinformatics 2004, 21, 631–643. [Google Scholar] [CrossRef] [Green Version]
- Dua, C.G.D. Machine Learning Repository. 2017. Available online: http://archive.ics.uci.edu/ml/index.php (accessed on 18 October 2021).
- Derrac, J.; García, S.; Molina, D.; Herrera, F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]
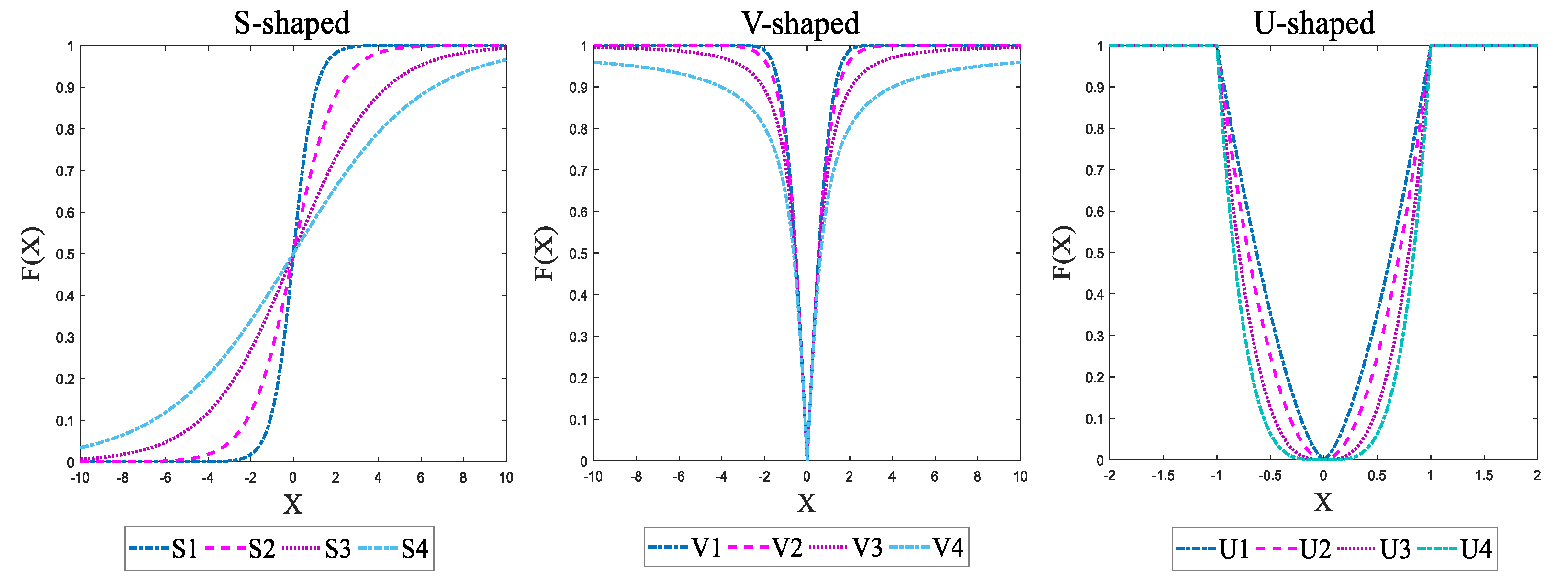


| S-Shaped Transfer Function | V-Shaped Transfer Function | U-Shaped Transfer Function | |||
|---|---|---|---|---|---|
| No. | Transfer Function | No. | Transfer Function | No. | Transfer Function |
| S1 | V1 | U1 | |||
| S2 | V2 | U2 | |||
| S3 | V3 | U3 | |||
| S4 | V4 | U4 | |||
| No. | Medical Datasets | No. Features | No. Samples | Size |
|---|---|---|---|---|
| 1 | Pima | 8 | 768 | Small |
| 2 | Lymphography | 18 | 148 | Small |
| 3 | Breast-WDBC | 30 | 569 | Small |
| 4 | PenglungEW | 325 | 73 | Large |
| 5 | Parkinson | 754 | 756 | Large |
| 6 | Colon | 2000 | 62 | Large |
| 7 | Leukemia | 7129 | 72 | Large |
| Datasets (Winner) | Metrics | BPSO | bGWO | BDA | BSSA | B-MFO |
|---|---|---|---|---|---|---|
| Pima (B-MFO-S1) | Avg accuracy | 0.7922 | 0.7726 | 0.7849 | 0.7798 | 0.7902 |
| Std accuracy | 0.0033 | 0.0063 | 0.0119 | 0.0079 | 0.0046 | |
| Avg no. features | 4.7333 | 7.6000 | 3.2667 | 4.7667 | 5.2667 | |
| Lymphography (B-MFO-V3) | Avg accuracy | 0.9163 | 0.8694 | 0.9041 | 0.8882 | 0.9095 |
| Std accuracy | 0.0099 | 0.0108 | 0.0182 | 0.8882 | 0.0089 | |
| Avg no. features | 8.9333 | 16.9667 | 5.5333 | 9.1000 | 5.3667 | |
| Breast-WDBC (B-MFO-U3) | Avg accuracy | 0.9710 | 0.9626 | 0.9666 | 0.9655 | 0.9719 |
| Std accuracy | 0.0021 | 0.0028 | 0.0078 | 0.0030 | 0.0020 | |
| Avg no. features | 12.8333 | 27.6000 | 2.4000 | 13.8000 | 3.2333 | |
| PenglungEW (B-MFO-U2) | Avg accuracy | 0.9626 | 0.9541 | 0.9507 | 0.9567 | 0.9692 |
| Std accuracy | 0.0040 | 0.0044 | 0.0126 | 0.0058 | 0.0063 | |
| Avg no. features | 161.0667 | 322.6667 | 83.5667 | 199.5000 | 81.5333 | |
| Parkinson (B-MFO-V2) | Avg accuracy | 0.7952 | 0.7736 | 0.7643 | 0.7793 | 0.8603 |
| Std accuracy | 0.0243 | 0.0036 | 0.0056 | 0.0126 | 0.0094 | |
| Avg no. features | 376.4333 | 741.2333 | 192.7333 | 332.7667 | 79.1000 | |
| Colon (B-MFO-U2) | Avg accuracy | 0.9625 | 0.9526 | 0.9296 | 0.9535 | 0.9694 |
| Std accuracy | 0.0056 | 0.0048 | 0.0207 | 0.0051 | 0.0059 | |
| Avg no. features | 999.9333 | 1948.8667 | 618.4333 | 1152.2000 | 350.7667 | |
| Leukemia (B-MFO-U2) | Avg accuracy | 0.9988 | 0.9901 | 0.9703 | 0.9954 | 0.9998 |
| Std accuracy | 0.0013 | 0.0021 | 0.0167 | 0.0023 | 0.0005 | |
| Avg no. features | 3542.0670 | 6746.9670 | 2283.7330 | 3435.2330 | 669.2333 |
| Datasets (Winner) | Metrics | BPSO | bGWO | BDA | BSSA | B-MFO |
|---|---|---|---|---|---|---|
| Pima (B-MFO-S1) | Avg fitness | 0.2117 | 0.2347 | 0.2456 | 0.2240 | 0.2143 |
| Std fitness | 0.0034 | 0.0068 | 0.0052 | 0.0076 | 0.0046 | |
| Lymphography (B-MFO-V3) | Avg fitness | 0.0878 | 0.1387 | 0.1503 | 0.1157 | 0.0925 |
| Std fitness | 0.0095 | 0.0110 | 0.0189 | 0.0106 | 0.0084 | |
| Breast-WDBC (B-MFO-U3) | Avg fitness | 0.0330 | 0.0462 | 0.0571 | 0.0387 | 0.0289 |
| Std fitness | 0.0019 | 0.0027 | 0.0111 | 0.0033 | 0.0021 | |
| PenglungEW (B-MFO-U2) | Avg fitness | 0.0420 | 0.0554 | 0.8845 | 0.0490 | 0.0330 |
| Std fitness | 0.0040 | 0.0043 | 0.1006 | 0.0059 | 0.0061 | |
| Parkinson (B-MFO-V2) | Avg fitness | 0.2078 | 0.2340 | 2.1607 | 0.2229 | 0.1393 |
| Std fitness | 0.0241 | 0.0035 | 0.2104 | 0.0135 | 0.0095 | |
| Colon (B-MFO-U2) | Avg fitness | 0.0421 | 0.0567 | 6.2540 | 0.0518 | 0.0321 |
| Std fitness | 0.0055 | 0.0048 | 0.5740 | 0.0051 | 0.0056 | |
| Leukemia (B-MFO-U2) | Avg fitness | 0.0062 | 0.0192 | 22.8667 | 0.0094 | 0.0011 |
| Std fitness | 0.0013 | 0.0022 | 2.6745 | 0.0023 | 0.0006 |
| Datasets (Winner) | Metrics | BPSO | bGWO | BDA | BSSA | B-MFO |
|---|---|---|---|---|---|---|
| PenglungEW (B-MFO-U2) | Avg specificity | 0.9975 | 1.0000 | 0.9940 | 0.9980 | 0.9945 |
| Avg sensitivity | 0.9722 | 0.9444 | 0.9333 | 0.9500 | 0.9722 | |
| Parkinson (B-MFO-V2) | Avg specificity | 0.9004 | 0.8898 | 0.8876 | 0.8915 | 0.9321 |
| Avg sensitivity | 0.3882 | 0.2913 | 0.3002 | 0.3686 | 0.5510 | |
| Colon (B-MFO-U2) | Avg specificity | 0.9467 | 0.9500 | 0.9392 | 0.9467 | 0.9475 |
| Avg sensitivity | 0.7712 | 0.6970 | 0.6606 | 0.7227 | 0.8227 | |
| Leukemia (B-MFO-U2) | Avg specificity | 1.0000 | 1.0000 | 0.9972 | 0.9957 | 1.0000 |
| Avg sensitivity | 0.9667 | 0.8413 | 0.7800 | 0.9267 | 0.9947 |
| Dataset | BPSO | bGWO | BDA | BSSA | B-MFO |
|---|---|---|---|---|---|
| Pima | 4.27 | 1.47 | 3.17 | 2.33 | 3.77 |
| Lymphography | 3.17 | 7.17 | 2.33 | 8.73 | 3.77 |
| Breast-WDBC | 7.17 | 2.33 | 14.30 | 8.73 | 3.77 |
| PenglungEW | 2.33 | 17.40 | 18.90 | 8.73 | 3.77 |
| Parkinson | 10.10 | 22.40 | 23.90 | 13.70 | 7.10 |
| Colon | 10.10 | 26.50 | 28.60 | 13.90 | 7.10 |
| Leukemia | 10.10 | 27.00 | 29.10 | 13.90 | 7.10 |
| Average rank | 6.76 | 14.90 | 17.20 | 10.00 | 5.20 |
| Overall rank | 2 | 4 | 5 | 3 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nadimi-Shahraki, M.H.; Banaie-Dezfouli, M.; Zamani, H.; Taghian, S.; Mirjalili, S. B-MFO: A Binary Moth-Flame Optimization for Feature Selection from Medical Datasets. Computers 2021, 10, 136. https://doi.org/10.3390/computers10110136
Nadimi-Shahraki MH, Banaie-Dezfouli M, Zamani H, Taghian S, Mirjalili S. B-MFO: A Binary Moth-Flame Optimization for Feature Selection from Medical Datasets. Computers. 2021; 10(11):136. https://doi.org/10.3390/computers10110136
Chicago/Turabian StyleNadimi-Shahraki, Mohammad H., Mahdis Banaie-Dezfouli, Hoda Zamani, Shokooh Taghian, and Seyedali Mirjalili. 2021. "B-MFO: A Binary Moth-Flame Optimization for Feature Selection from Medical Datasets" Computers 10, no. 11: 136. https://doi.org/10.3390/computers10110136
APA StyleNadimi-Shahraki, M. H., Banaie-Dezfouli, M., Zamani, H., Taghian, S., & Mirjalili, S. (2021). B-MFO: A Binary Moth-Flame Optimization for Feature Selection from Medical Datasets. Computers, 10(11), 136. https://doi.org/10.3390/computers10110136