Implementation of an Analytical Model for Leakage Neutron Equivalent Dose in a Proton Radiotherapy Planning System
Abstract
:1. Introduction
2. Methods
2.1. Analytical Model for Neutron Equivalent Dose
2.2. Attenuation of Neutrons Due to Irregular Surfaces and Heterogeneous Tissues
2.3. Implementation of the Analytical H/D Model in a TPS
2.4. Calculation of Equivalent Dose Distributions from Neutrons in a Water Phantom
2.5. Calculation of Neutron Equivalent Dose Distribution in a Patient
2.6. Comparison of Analytical H/D Model against a Monte Carlo H/D Model
3. Results
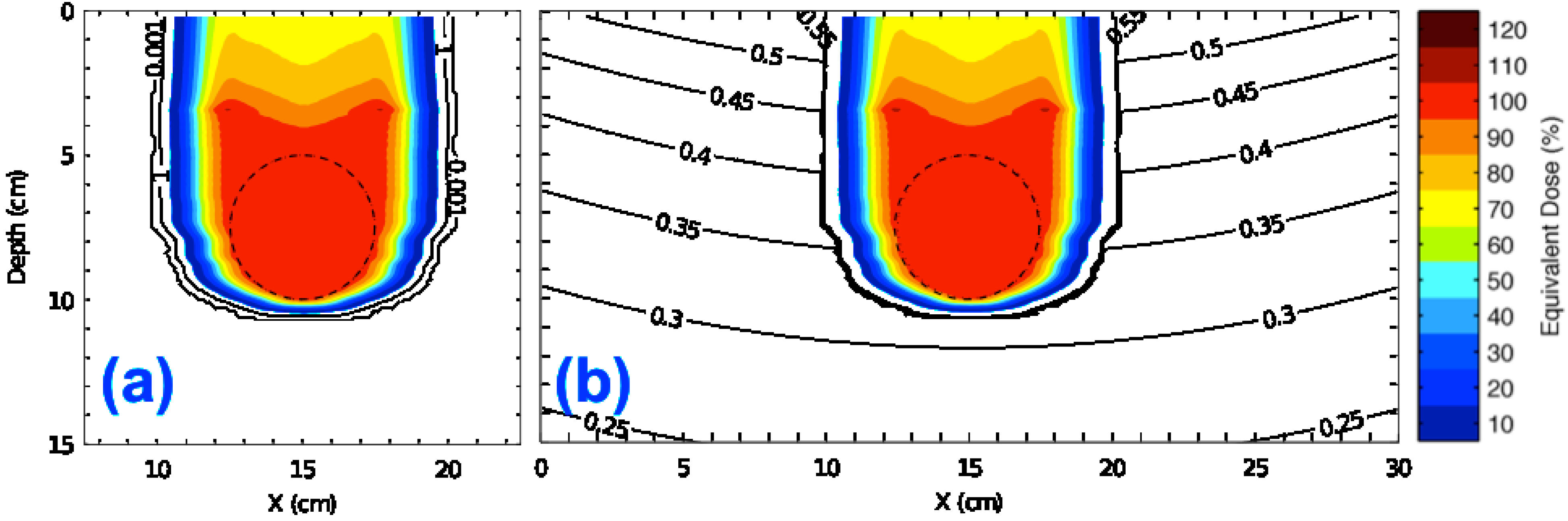
3.1. Equivalent Dose Distributions in a Water-Box Phantom from the Analytical H/D Model
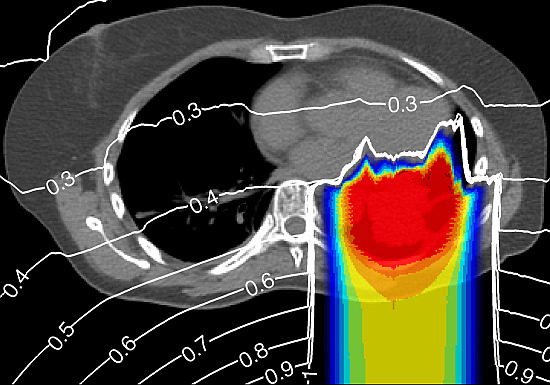
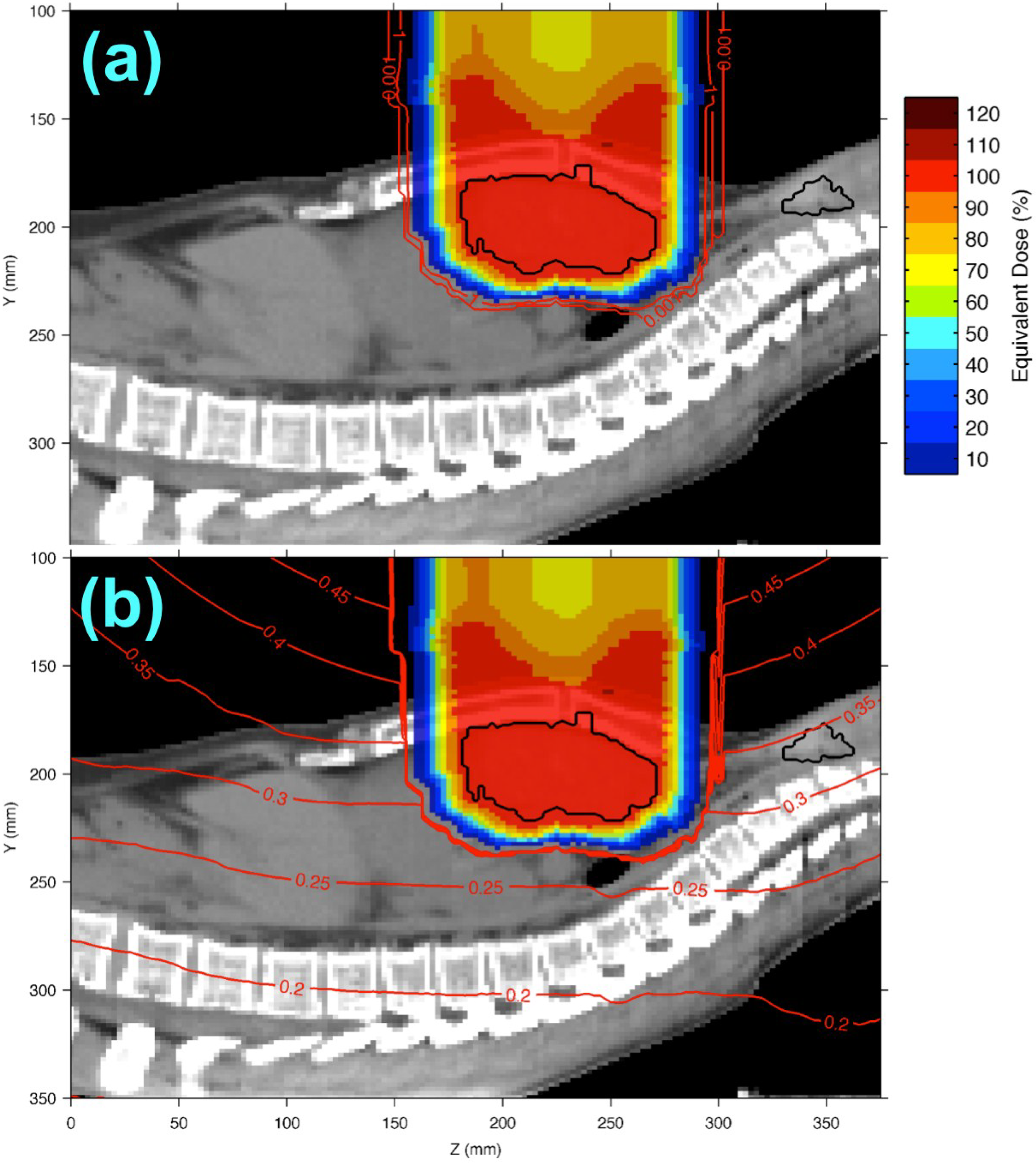
3.2. Equivalent Dose Distributions in a HL Patient from the Analytical H/D Model
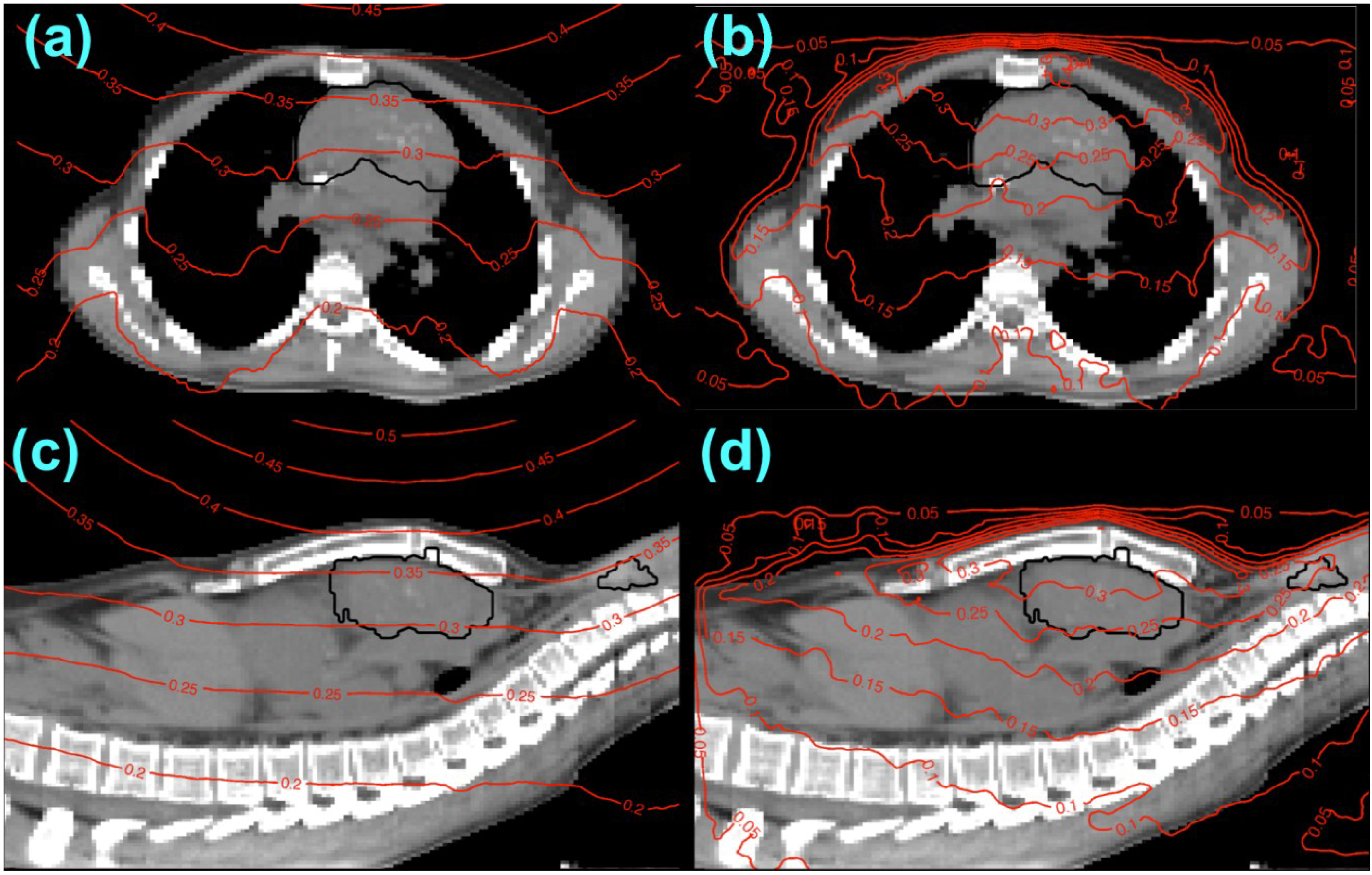
3.3. Dose Calculations Using the Analytical Model and Monte Carlo Simulations
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Howlader, N.; Noone, A.M.; Krapcho, M.; Neyman, N.; Aminou, R.; Altekruse, S.F.; Kosary, C.L.; Ruhl, J.; Tatalovich, Z.; Cho, H.; et al. Seer Cancer Statistics Review, 1975–2009 (Vintage 2009 Populations); National Cancer Institute: Bethesda, MD, USA, 2012. [Google Scholar]
- Ries, L.A.G.; Melbert, D.; Krapcho, M.; Mariotto, A.; Miller, B.A.; Feuer, E.J.; Clegg, L.; Horner, M.J.; Howlader, N.; Eisner, M.P.; et al. Seer Cancer Statistics Review, 1975–2004; National Cancer Instistute: Bethesda, MD, USA, 2007. [Google Scholar]
- Smith, M.A.; Seibel, N.L.; Altekruse, S.F.; Ries, L.A.; Melbert, D.L.; O’Leary, M.; Smith, F.O.; Reaman, G.H. Outcomes for children and adolescents with cancer: Challenges for the twenty-first century. J. Clin. Oncol. 2010, 28, 2625–2634. [Google Scholar] [CrossRef] [PubMed]
- Friedman, D.L.; Whitton, J.; Leisenring, W.; Mertens, A.C.; Hammond, S.; Stovall, M.; Donaldson, S.S.; Meadows, A.T.; Robison, L.L.; Neglia, J.P. Subsequent neoplasms in 5-year survivors of childhood cancer: The childhood cancer survivor study. J. Natl. Cancer Inst. 2010, 102, 1083–1095. [Google Scholar] [CrossRef] [PubMed]
- Newhauser, W.D.; Durante, M. Assessing the risk of second malignancies after modern radiotherapy. Nat. Rev. Cancer 2011, 11, 438–448. [Google Scholar] [CrossRef] [PubMed]
- NCRP. 2010 recommendations of the European Committee on radiation risk: The health effects of exposure to low doses of ionizing radiation-regulators’ edition NCRP report No. 170, secondary primary cancers and cardiovascular disease after radiation therapy. J. Radiol. Prot. 2010, 32, 369–372. [Google Scholar]
- Yan, X.; Titt, U.; Koehler, A.M.; Newhauser, W.D. Measurement of neutron dose equivalent to proton therapy patients outside of the proton radiation field. Nucl. Instrum. Methods Phys. Res. Sec. A 2002, 476, 429–434. [Google Scholar] [CrossRef]
- Schneider, U.; Agosteo, S.; Pedroni, E.; Besserer, J. Secondary neutron dose during proton therapy using spot scanning. Int. J. Radiat. Oncol. Biol. Phys. 2002, 53, 244–251. [Google Scholar] [CrossRef] [PubMed]
- Yonai, S.; Kase, Y.; Matsufuji, N.; Kanai, T.; Nishio, T.; Namba, M.; Yamashita, W. Measurement of absorbed dose, quality factor, and dose equivalent in water phantom outside of the irradiation field in passive carbon-ion and proton radiotherapies. Med. Phys. 2010, 37, 4046–4055. [Google Scholar] [CrossRef] [PubMed]
- Mukherjee, B.; Lambert, J.; Hentschel, R.; Farr, J. Explicit estimation of out-of-field neutron and gamma dose equivalents during proton therapy using thermoluminescence-dosimeters. Radiat. Meas. 2011, 46, 1952–1955. [Google Scholar] [CrossRef]
- Agosteo, S.; Birattari, C.; Caravaggio, M.; Silari, M.; Tosi, G. Secondary neutron and photon dose in proton therapy. Radiother. Oncol. 1998, 48, 293–305. [Google Scholar] [CrossRef] [PubMed]
- Polf, J.C.; Newhauser, W.D. Calculations of neutron dose equivalent exposures from range-modulated proton therapy beams. Phys. Med. Biol. 2005, 50, 3859–3873. [Google Scholar] [CrossRef] [PubMed]
- Polf, J.C.; Newhauser, W.D.; Titt, U. Patient neutron dose equivalent exposures outside of the proton therapy treatment field. Radiat. Prot. Dosim. 2005, 115, 154–158. [Google Scholar] [CrossRef]
- Fontenot, J.D.; Newhauser, W.D.; Titt, U. Design tools for proton therapy nozzles based on the double-scattering foil technique. Radiat. Prot. Dosim. 2005, 116, 211–215. [Google Scholar] [CrossRef]
- Jiang, H.; Wang, B.; Xu, X.G.; Suit, H.D.; Paganetti, H. Simulation of organ-specific patient effective dose due to secondary neutrons in proton radiation treatment. Phys. Med. Biol. 2005, 50, 4337–4353. [Google Scholar] [CrossRef] [PubMed]
- Fontenot, J.D.; Lee, A.K.; Newhauser, W.D. Risk of secondary malignant neoplasms from proton therapy and intensity-modulated x-ray therapy for early-stage prostate cancer. Int. J. Radiat. Oncol. Biol. Phys. 2009, 74, 616–622. [Google Scholar] [CrossRef] [PubMed]
- Newhauser, W.D.; Fontenot, J.D.; Mahajan, A.; Kornguth, D.; Stovall, M.; Zheng, Y.; Taddei, P.J.; Mirkovic, D.; Mohan, R.; Cox, J.D.; et al. The risk of developing a second cancer after receiving craniospinal proton irradiation. Phys. Med. Biol. 2009, 54, 2277–2291. [Google Scholar] [CrossRef] [PubMed]
- Pérez-Andújar, A.; Newhauser, W.D.; Deluca, P.M. Neutron production from beam-modifying devices in a modern double scattering proton therapy beam delivery system. Phys. Med. Biol. 2009, 54, 993–1008. [Google Scholar] [CrossRef] [PubMed]
- Taddei, P.J.; Howell, R.M.; Krishnan, S.; Scarboro, S.B.; Mirkovic, D.; Newhauser, W.D. Risk of second malignant neoplasm following proton versus intensity-modulated photon radiotherapies for hepatocellular carcinoma. Phys. Med. Biol. 2010, 55, 7055–7065. [Google Scholar] [CrossRef] [PubMed]
- Clasie, B.; Wroe, A.; Kooy, H.; Depauw, N.; Flanz, J.; Paganetti, H.; Rosenfeld, A. Assessment of out-of-field absorbed dose and equivalent dose in proton fields. Med. Phys. 2010, 37, 311–321. [Google Scholar] [CrossRef] [PubMed]
- Tayama, R.; Fujita, Y.; Tadokoro, M.; Fujimaki, H.; Sakae, T.; Terunuma, T. Measurement of neutron dose distribution for a passive scattering nozzle at the proton medical research center (PMRC). Nucl. Instrum. Methods Phys. Res. Sec. A 2006, 564, 532–536. [Google Scholar] [CrossRef]
- Herault, J.; Iborra, N.; Serrano, B.; Chauvel, P. Spread-out bragg peak and monitor units calculation with the monte carlo code mcnpx. Med. Phys. 2007, 34, 680–688. [Google Scholar] [CrossRef] [PubMed]
- Titt, U.; Sahoo, N.; Ding, X.; Zheng, Y.; Newhauser, W.D.; Zhu, X.R.; Polf, J.C.; Gillin, M.T.; Mohan, R. Assessment of the accuracy of an mcnpx-based monte carlo simulation model for predicting three-dimensional absorbed dose distributions. Phys. Med. Biol. 2008, 53, 4455–4470. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.S.; Newhauser, W.; Fontenot, J.; Koch, N.; Mohan, R. Monte carlo simulations of stray neutron radiation exposures in proton therapy. J. Nucl. Mater. 2007, 361, 289–297. [Google Scholar] [CrossRef]
- Taddei, P.J.; Mirkovic, D.; Fontenot, J.D.; Giebeler, A.; Zheng, Y.; Kornguth, D.; Mohan, R.; Newhauser, W.D. Stray radiation dose and second cancer risk for a pediatric patient receiving craniospinal irradiation with proton beams. Phys. Med. Biol. 2009, 54, 2259–2275. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Newhauser, W.; Fontenot, J.; Taddei, P.; Mohan, R. Monte carlo study of neutron dose equivalent during passive scattering proton therapy. Phys. Med. Biol. 2007, 52, 4481–4496. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Perez-Andujar, A.; Fontenot, J.D.; Taddei, P.J.; Newhauser, W.D. An analytic model of neutron ambient dose equivalent and equivalent dose for proton radiotherapy. Phys. Med. Biol. 2010, 55, 6975–6985. [Google Scholar] [CrossRef] [PubMed]
- Pérez-Andújar, A.; Zhang, R.; Newhauser, W. Monte carlo and analytical model predictions of leakage neutron exposures from passively scattered proton therapy. Med. Phys. 2013, 40, 121714. [Google Scholar] [CrossRef] [PubMed]
- Anferov, V. Analytic estimates of secondary neutron dose in proton therapy. Phys. Med. Biol. 2010, 55, 7509–7522. [Google Scholar] [CrossRef] [PubMed]
- Siddon, R.L. Fast calculation of the exact radiological path for a three-dimensional CT array. Med. Phys. 1985, 12, 252–255. [Google Scholar] [CrossRef] [PubMed]
- Krämer, M.; Jakel, O.; Haberer, T.; Kraft, G.; Schardt, D.; Weber, U. Treatment planning for heavy-ion radiotherapy: Physical beam model and dose optimization. Phys. Med. Biol. 2000, 45, 3299–3317. [Google Scholar] [CrossRef] [PubMed]
- Bert, C.; Rietzel, E. 4D treatment planning for scanned ion beams. Radiat. Oncol. 2007, 2, 24. [Google Scholar] [CrossRef] [PubMed]
- Bleyer, A.; O’Leary, M.; Barr, R.; Ries, L.A.G. Cancer Epidemiology in Older Adolescents and Young Adults 15 To 29 Years of Age, Including SEER Incidence and Survival: 1975–2000; National Cancer Institute, NIH: Bethesda, MD, USA, 2006. [Google Scholar]
- Armitage, J.O. Early-stage hodgkin’s lymphoma. N. Engl. J. Med. 2010, 363, 653–662. [Google Scholar] [CrossRef] [PubMed]
- Dores, G.M.; Metayer, C.; Curtis, R.E.; Lynch, C.F.; Clarke, E.A.; Glimelius, B.; Storm, H.; Pukkala, E.; van Leeuwen, F.E.; Holowaty, E.J.; et al. Second malignant neoplasms among long-term survivors of hodgkin’s disease: A population-based evaluation over 25 years. J. Clin. Oncol. 2002, 20, 3484–3494. [Google Scholar] [CrossRef] [PubMed]
- Newhauser, W.; Jones, T.; Swerdloff, S.; Cilia, M.; Carver, R.; Halloran, A.; Zhang, R. Anonymization of dicom electronic medical records for radiation therapy. Comput. Biol. Med. 2014, 53, 134–140. [Google Scholar] [CrossRef] [PubMed]
- Hendricks, J.S.; McKinney, G.W.; Durkee, J.W.; Finch, J.P.; Fensin, M.L.; James, M.R.; Johns, R.C.; Pelowitz, D.B.; Waters, L.S.; Gallmeier, F.X. MCNPX, Version 26c; Los Alamos National Laboratory: Los Alamos, NM, USA, 2006. [Google Scholar]
- Newhauser, W.D.; Fontenot, J.D.; Taddei, P.J.; Mirkovic, D.; Giebeler, A.; Zhang, R.; Mahajan, A.; Kornguth, D.; Stovall, M.; Yepes, P.; et al. Contemporary proton therapy systems adequately protect patients from exposure to stray radiation. AIP Conf. Proc. 2009, 1099, 450–455. [Google Scholar] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eley, J.; Newhauser, W.; Homann, K.; Howell, R.; Schneider, C.; Durante, M.; Bert, C. Implementation of an Analytical Model for Leakage Neutron Equivalent Dose in a Proton Radiotherapy Planning System. Cancers 2015, 7, 427-438. https://doi.org/10.3390/cancers7010427
Eley J, Newhauser W, Homann K, Howell R, Schneider C, Durante M, Bert C. Implementation of an Analytical Model for Leakage Neutron Equivalent Dose in a Proton Radiotherapy Planning System. Cancers. 2015; 7(1):427-438. https://doi.org/10.3390/cancers7010427
Chicago/Turabian StyleEley, John, Wayne Newhauser, Kenneth Homann, Rebecca Howell, Christopher Schneider, Marco Durante, and Christoph Bert. 2015. "Implementation of an Analytical Model for Leakage Neutron Equivalent Dose in a Proton Radiotherapy Planning System" Cancers 7, no. 1: 427-438. https://doi.org/10.3390/cancers7010427
APA StyleEley, J., Newhauser, W., Homann, K., Howell, R., Schneider, C., Durante, M., & Bert, C. (2015). Implementation of an Analytical Model for Leakage Neutron Equivalent Dose in a Proton Radiotherapy Planning System. Cancers, 7(1), 427-438. https://doi.org/10.3390/cancers7010427