Isolation of Circulating Tumor Cells by Dielectrophoresis
Abstract
:1. Introduction
2. Dielectrophoretic Principles in the Separation of Cancer from Normal Cells
2.1. Dielectrophoresis
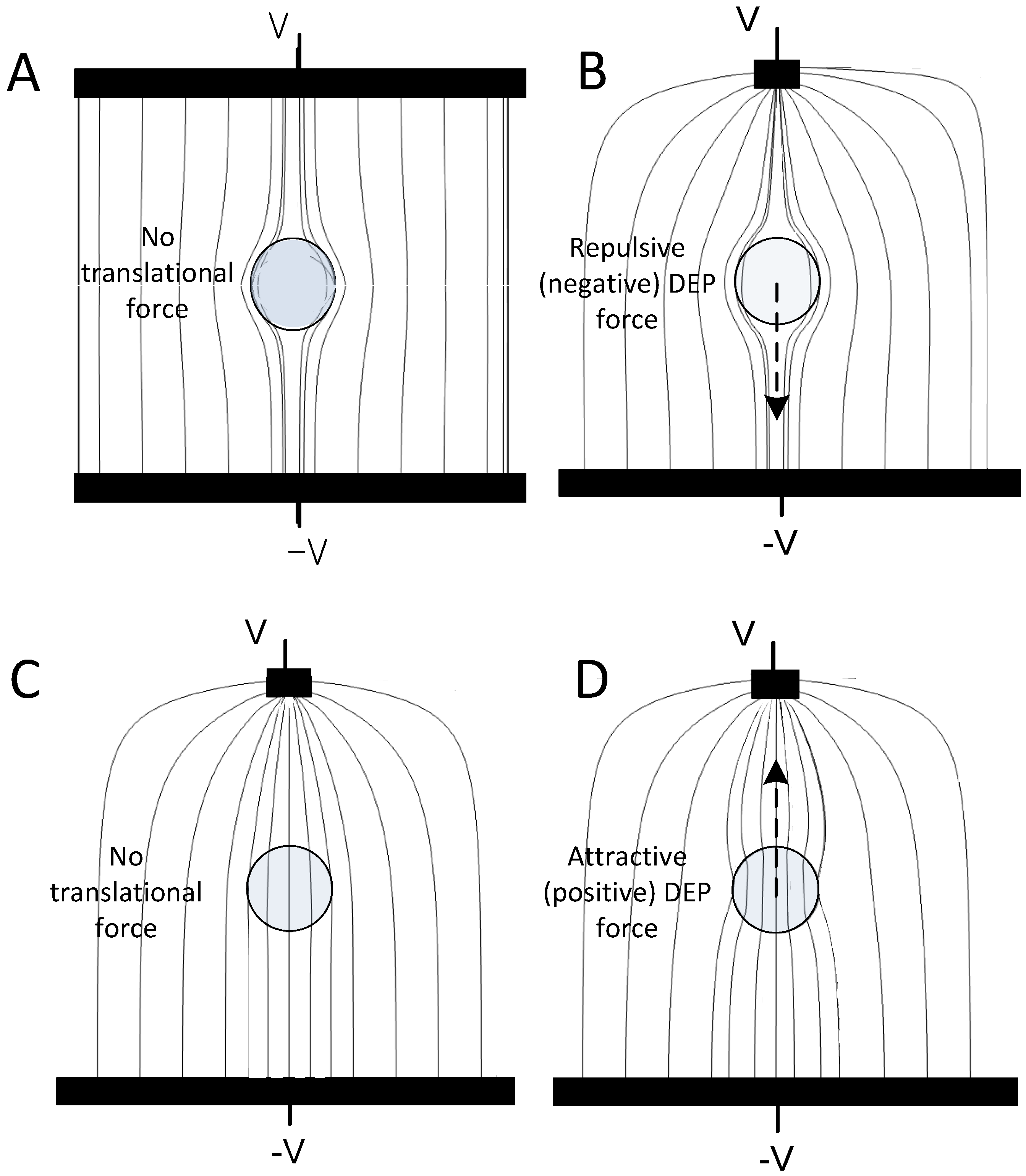
2.2. Cell Membrane Dielectric Properties
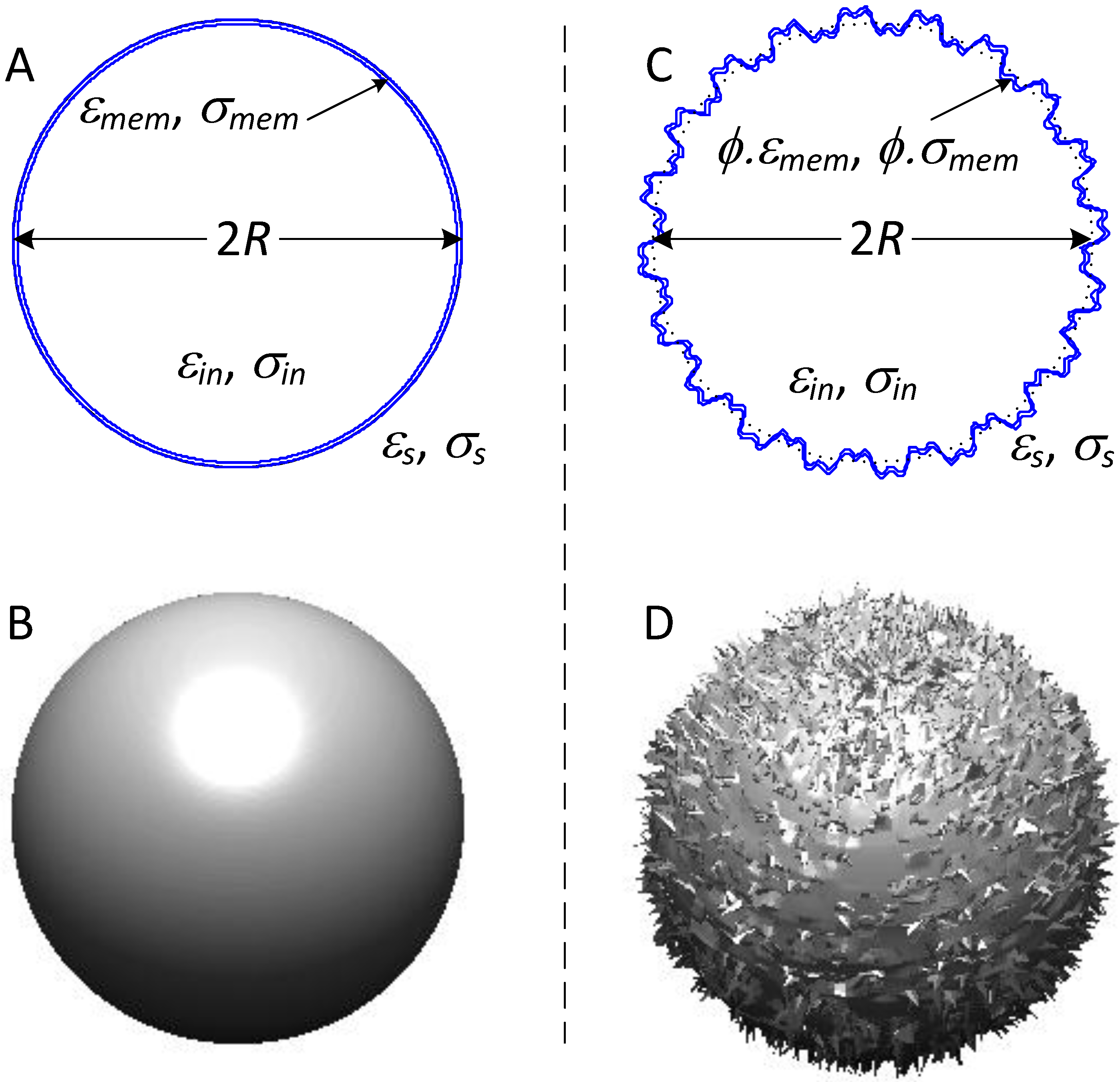
2.3. Cancer Cell Dielectric Properties, Tissue Morphology and Cancer Progression
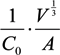 , where V is the volume of the cell and A is its total surface area at its site of origin no matter what shape it assumes in the solid tissue. In principle, V and A can be estimated by examination of the tissue. This relationship provides, for the first time, a means to translate the morphology of cells in solid tissue as viewed by a pathologist to the DEP characteristics those cells will exhibit when they are released as CTCs.
, where V is the volume of the cell and A is its total surface area at its site of origin no matter what shape it assumes in the solid tissue. In principle, V and A can be estimated by examination of the tissue. This relationship provides, for the first time, a means to translate the morphology of cells in solid tissue as viewed by a pathologist to the DEP characteristics those cells will exhibit when they are released as CTCs.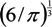 ≈ 1.24. This value, then, is the minimum folding factor possible for cells from well-differentiated, solid tissues. Cells that are not smooth and originate from less well organized tissues will therefore have folding factors, when harvested, in excess of 1.24. In practice we have found from DEP and ROT measurements on cells harvested from tissues that folding factors ϕ can range up to and even above 10. For example [82], perfusion by trypsin solution of the livers of euthanized mice via the hepatic portal vein yielded a harvest of hepatocytes ranging from diploid to 16-ploid having diameters from 15–40 µm and membrane folding factors from 4 to 10.5.
≈ 1.24. This value, then, is the minimum folding factor possible for cells from well-differentiated, solid tissues. Cells that are not smooth and originate from less well organized tissues will therefore have folding factors, when harvested, in excess of 1.24. In practice we have found from DEP and ROT measurements on cells harvested from tissues that folding factors ϕ can range up to and even above 10. For example [82], perfusion by trypsin solution of the livers of euthanized mice via the hepatic portal vein yielded a harvest of hepatocytes ranging from diploid to 16-ploid having diameters from 15–40 µm and membrane folding factors from 4 to 10.5.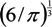 ≈ 1.24; (B) Tumor cells become disorganized as tumor grade increases, leading to increased cell surface area; (C) As tumor cells enter the circulation and round up into spheres, their surfaces wrinkle to accommodate their membrane area (D) leading to a low DEP crossover frequency; (E) Cell membrane area is shed in large vesicles when cancer cells persist in suspension [78]. Nevertheless, the membrane folding factor of the cells still remains high; (F) MDA-MB-231 cells in suspension immediately following harvest showing excess membrane and gross folding. (G) The same cells after being maintained in suspension for 2 h. Despite the loss of large vesicles carrying away cytoplasm and membrane, the cell membranes retain a much higher folding factor than blood cells [78].
≈ 1.24; (B) Tumor cells become disorganized as tumor grade increases, leading to increased cell surface area; (C) As tumor cells enter the circulation and round up into spheres, their surfaces wrinkle to accommodate their membrane area (D) leading to a low DEP crossover frequency; (E) Cell membrane area is shed in large vesicles when cancer cells persist in suspension [78]. Nevertheless, the membrane folding factor of the cells still remains high; (F) MDA-MB-231 cells in suspension immediately following harvest showing excess membrane and gross folding. (G) The same cells after being maintained in suspension for 2 h. Despite the loss of large vesicles carrying away cytoplasm and membrane, the cell membranes retain a much higher folding factor than blood cells [78].
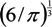 ≈ 1.24; (B) Tumor cells become disorganized as tumor grade increases, leading to increased cell surface area; (C) As tumor cells enter the circulation and round up into spheres, their surfaces wrinkle to accommodate their membrane area (D) leading to a low DEP crossover frequency; (E) Cell membrane area is shed in large vesicles when cancer cells persist in suspension [78]. Nevertheless, the membrane folding factor of the cells still remains high; (F) MDA-MB-231 cells in suspension immediately following harvest showing excess membrane and gross folding. (G) The same cells after being maintained in suspension for 2 h. Despite the loss of large vesicles carrying away cytoplasm and membrane, the cell membranes retain a much higher folding factor than blood cells [78].
≈ 1.24; (B) Tumor cells become disorganized as tumor grade increases, leading to increased cell surface area; (C) As tumor cells enter the circulation and round up into spheres, their surfaces wrinkle to accommodate their membrane area (D) leading to a low DEP crossover frequency; (E) Cell membrane area is shed in large vesicles when cancer cells persist in suspension [78]. Nevertheless, the membrane folding factor of the cells still remains high; (F) MDA-MB-231 cells in suspension immediately following harvest showing excess membrane and gross folding. (G) The same cells after being maintained in suspension for 2 h. Despite the loss of large vesicles carrying away cytoplasm and membrane, the cell membranes retain a much higher folding factor than blood cells [78].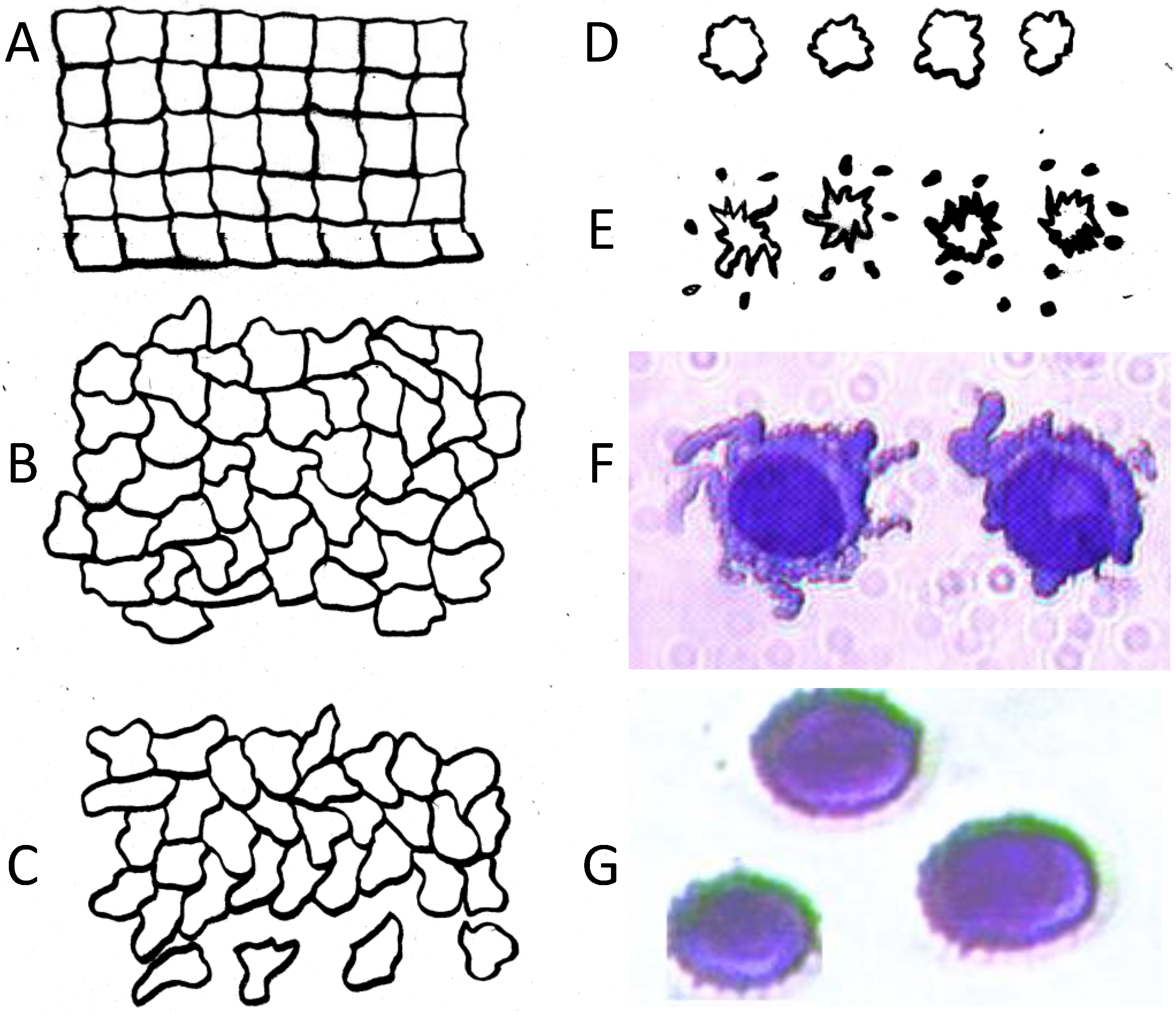
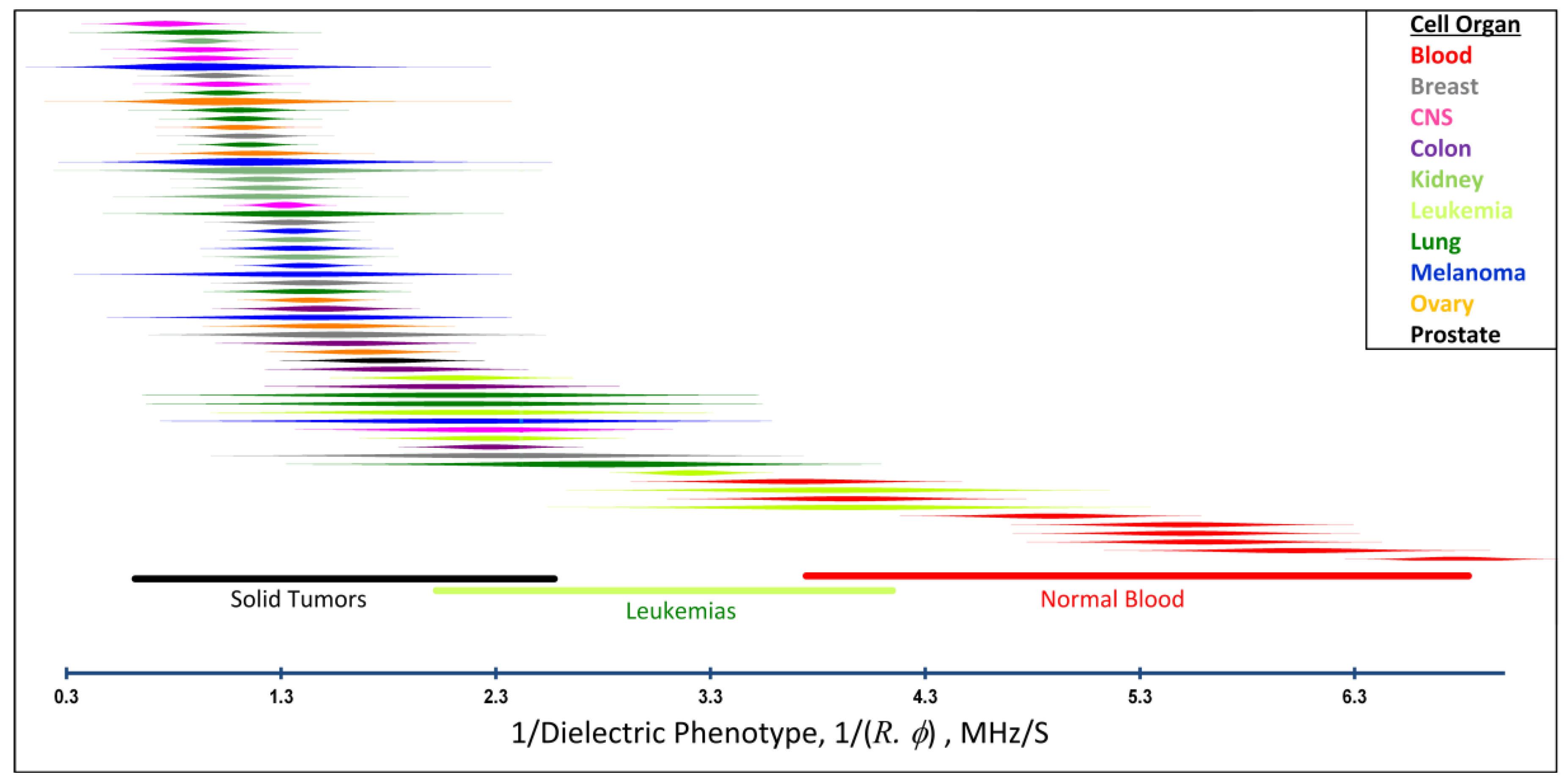
2.4. Distributions of Cancer and Blood Cell Dielectric Properties and Isolation Efficiencies
3. Practical Systems for Separation of Cancer and Normal Cells for Clinical Applications
3.1. Summary of Requirements for DEP Implementations
3.2. Non-Equilibrium Isolation Approaches—DEP Trapping and Deflection by Potential Barriers
3.3. Equilibrium Isolation Methods—DEP-FFF
| Parameter | Practical Requirement | Comments |
|---|---|---|
| Specimen condition | Cells must have intact membrane barrier function | Membrane barrier function must be intact for DEP to discriminate between cells based on their plasma membrane morphology. Also, cells undergo large dielectric changes in early apoptosis, so stressed specimens are undesirable. |
| Specimen volume | 7 to 10 mL | CTCs are so rare that an accepted working volume to allow for meaningful analysis is around 10 mL |
| Processing time | <60 min | It is generally accepted that an instrument to make analysis of CTCs a widespread, routine, clinically-relevant procedure needs to be able to process at least one specimen an hour. |
| Cell throughput | ≥106 cells·min-1 | Even with pre-processing of specimens to remove erythrocytes by lysis or density-gradient separation, a 10 mL specimen contains ~4 × 107 nucleated cells, requiring a high throughput rate to achieve processing of a 10 mL specimen within 60 min. |
| Suspending medium conductivity | <500 mS·m−1 and usually <100 mS·m−1 | To exploit both positive and negative DEP for cell discrimination, the suspending medium must be of much lower conductivity than the cell cytoplasm, which is ~1,400 mS·m−1 due to its physiological ion concentration. The electric current and Joule heating caused by the DEP signal also depends on the suspending medium conductivity. |
| Suspending medium osmolarity | >200 mOs·kg−1 and usually ~300 mOs·kg−1 | Usually DEP is applied in a suspending medium of low ionic conductivity in which physiological osmolarity (~300 mOs·kg−1) is maintained with a non-conductive osmolyte such as sucrose or mannitol. However, osmolarity could be modified substantially to alter cell DEP properties as long as it did not damage the target cancer cell membrane integrity through osmotic stress. |
| DEP frequency | f > 15 kHz | The DEP frequency is chosen to impose differential forces on the cell types to be separated in accordance with the cell crossover frequencies at the chosen suspending medium conductivity. At low frequencies, charge injection from electrodes becomes greater, increasing the production of electrochemical species that can damage cells. At a conductivity of 30 mS·m−1, cells can be protected from such damage for f > 15 kHz by inclusion of catalase in the suspending medium. |
| Electric field strength | <5 × 105 V·m−1 in the highest field regions to which cancer cells are exposed | FDEP increase with the square of the applied voltage making larger voltages desirable for increased cell separation. However, a transmembrane voltage that may be as large as the product of the cell radius and the local field strength is induced in cells undergoing DEP manipulation. If the applied DEP voltage is too high for large cancer cells attracted to high field regions at electrode edges, the transmembrane potential could induce ion leakage, electroporation, or even electrodestruction, leading to their loss. These problems are averted completely at lower voltages that can still provide good cell separation. |
| Cell residency time | <400 s | Once cells are suspended in a low conductivity medium, their internal ions begin to leak out, causing their DEP properties to change with time. Tumor cells tend to be leakier than normal cells and their exposure to high field regions during DEP manipulation can induce still faster ion leakage (see Electric Field above). Cell residency time should be short to avert complications caused by changing cell DEP properties. |
3.4. Collection Purity
3.5. Cancer Cell Isolation Findings
3.6. Post Processing
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix
A1. Dielectrophoresis of Mammalian Cells
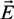 (f) [62,67,122,133], the DEP force FDEP acting on a cell can be written as:
(f) [62,67,122,133], the DEP force FDEP acting on a cell can be written as:
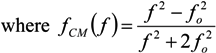
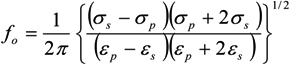
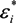 = εi − jσi/(2π f), surrounded by a thin shell of thickness d, representing the membrane of complex permittivity
= εi − jσi/(2π f), surrounded by a thin shell of thickness d, representing the membrane of complex permittivity 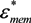 = εmem − jσmem/(2π f). The single shell model gives the complex permittivity of the cell [67,134,135] as:
= εmem − jσmem/(2π f). The single shell model gives the complex permittivity of the cell [67,134,135] as:
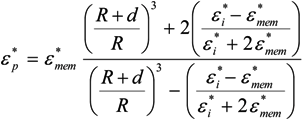
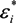 ˃˃
˃˃ 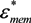 and, for frequencies between approximately 10 kHz and 1 MHz [67,136], this may be approximated as:
and, for frequencies between approximately 10 kHz and 1 MHz [67,136], this may be approximated as:
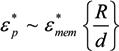
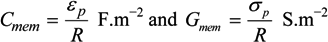
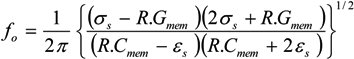
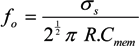
A2. Cell Morphological Considerations
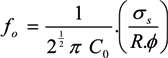
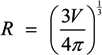
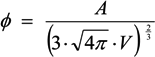
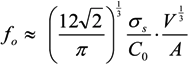
A3. Separability of Cells by DEP Trapping
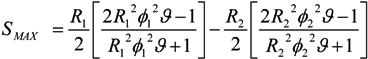
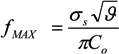
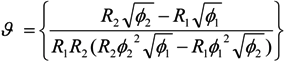
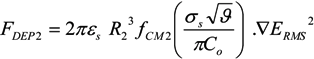
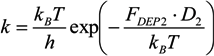
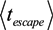 = k−1. In our experiments,
= k−1. In our experiments, 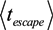 can be as long as thousands of seconds when the trapping is strong or fractions of a second when the trapping is weak [56]. Of course, the trapping may be extended indefinitely by using methods to adhere cells to the DEP trapping sites, if desired [113,138].
can be as long as thousands of seconds when the trapping is strong or fractions of a second when the trapping is weak [56]. Of course, the trapping may be extended indefinitely by using methods to adhere cells to the DEP trapping sites, if desired [113,138].A4. Separation by the Force Equilibrium Methods of DEP-FFF
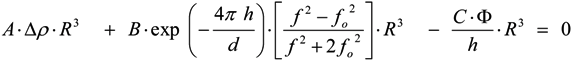
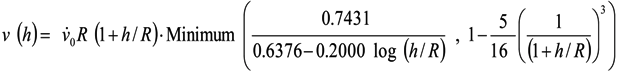
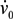 is the shear rate of the eluate flow profile at the chamber floor. Cells elute from the DEP-FFF microelectrode array after a time Telute(h) = L/v(h), where L is the length of array. If the entire DEP-FFF chamber is lined with DEP microelectrodes then L is the length of the DEP-FFF chamber. Thus different cell types starting off together at the front end of the chamber will elute at different times. This is the principle of batch-mode DEP-FFF.
is the shear rate of the eluate flow profile at the chamber floor. Cells elute from the DEP-FFF microelectrode array after a time Telute(h) = L/v(h), where L is the length of array. If the entire DEP-FFF chamber is lined with DEP microelectrodes then L is the length of the DEP-FFF chamber. Thus different cell types starting off together at the front end of the chamber will elute at different times. This is the principle of batch-mode DEP-FFF.References
- Esmaeilsabzali, H.; Beischlag, T.V.; Cox, M.E.; Parameswaran, A.M.; Park, E.J. Detection and isolation of circulating tumor cells: Principles and methods. Biotechnol. Adv. 2013, 31, 1063–1084. [Google Scholar] [CrossRef]
- Millner, L.M.; Linder, M.W.; Valdes, R., Jr. Circulating tumor cells: A review of present methods and the need to identify heterogeneous phenotypes. Ann. Clin. Lab. Sci. 2013, 43, 295–304. [Google Scholar]
- Jin, C.; McFaul, S.M.; Duffy, S.P.; Deng, X.; Tavassoli, P.; Black, P.C.; Ma, H. Technologies for label-free separation of circulating tumor cells: from historical foundations to recent developments. Lab Chip 2014, 14, 32–44. [Google Scholar] [CrossRef]
- Alix-Panabieres, C.; Pantel, K. Circulating tumor cells: Liquid biopsy of cancer. Clin. Chem. 2013, 59, 110–118. [Google Scholar] [CrossRef]
- Parkinson, D.R.; Dracopoli, N.; Petty, B.G.; Compton, C.; Cristofanilli, M.; Deisseroth, A.; Hayes, D.F.; Kapke, G.; Kumar, P.; Lee, J.; et al. Considerations in the development of circulating tumor cell technology for clinical use. J. Transl. Med. 2012, 10. [Google Scholar] [CrossRef]
- Rao, C.G.; Chianese, D.; Doyle, G.V.; Miller, M.C.; Russell, T.; Sanders, R.A., Jr.; Terstappen, L.W. Expression of epithelial cell adhesion molecule in carcinoma cells present in blood and primary and metastatic tumors. Int. J. Oncol. 2005, 27, 49–57. [Google Scholar]
- Coumans, F.A.; Doggen, C.J.; Attard, G.; de Bono, J.S.; Terstappen, L.W. All circulating EpCAM+CK+CD45− objects predict overall survival in castration-resistant prostate cancer. Ann. Oncol. 2010, 21, 1851–1857. [Google Scholar] [CrossRef]
- Criscitiello, C.; Sotiriou, C.; Ignatiadis, M. Circulating tumor cells and emerging blood biomarkers in breast cancer. Curr. Opin. Oncol. 2010, 22, 552–558. [Google Scholar] [CrossRef]
- Patriarca, C.; Macchi, R.M.; Marschner, A.K.; Mellstedt, H. Epithelial cell adhesion molecule expression (CD326) in cancer: A short review. Cancer Treat. Rev. 2012, 38, 68–75. [Google Scholar] [CrossRef]
- Mikolajczyk, S.D.; Millar, L.S.; Tsinberg, P.; Coutts, S.M.; Zomorrodi, M.; Pham, T.; Bischoff, F.Z.; Pircher, T.J. Detection of EpCAM-negative and cytokeratin-negative circulating tumor cells in peripheral blood. J. Oncol. 2011, 2011, e252361. [Google Scholar]
- Konigsberg, R.; Obermayr, E.; Bises, G.; Pfeiler, G.; Gneist, M.; Wrba, F.; de Santis, M.; Zeillinger, R.; Hudec, M.; Dittrich, C. Detection of EpCAM positive and negative circulating tumor cells in metastatic breast cancer patients. Acta Oncol. 2011, 50, 700–710. [Google Scholar]
- Aktas, B.; Tewes, M.; Fehm, T.; Hauch, S.; Kimmig, R.; Kasimir-Bauer, S. Stem cell and epithelial-mesenchymal transition markers are frequently overexpressed in circulating tumor cells of metastatic breast cancer patients. Breast Cancer Res. 2009, 11. [Google Scholar] [CrossRef]
- Vona, G.; Sabile, A.; Louha, M.; Sitruk, V.; Romana, S.; Schutze, K.; Capron, F.; Franco, D.; Pazzagli, M.; Vekemans, M.; et al. Isolation by size of epithelial tumor cells: A new method for the immunomorphological and molecular characterization of circulatingtumor cells. Am. J. Pathol. 2000, 156, 57–63. [Google Scholar] [CrossRef]
- Williams, A.; Balic, M.; Datar, R.; Cote, R. Size-based enrichment technologies for CTC detection and characterization. Recent Results Cancer Res. 2012, 195, 87–95. [Google Scholar] [CrossRef]
- Ma, Y.C.; Wang, L.; Yu, F.L. Recent advances and prospects in the isolation by size of epithelial tumor cells (ISET) methodology. Technol. Cancer Res. Treat. 2013, 12, 295–309. [Google Scholar]
- Park, J.M.; Lee, J.Y.; Lee, J.G.; Jeong, H.; Oh, J.M.; Kim, Y.J.; Park, D.; Kim, M.S.; Lee, H.J.; Oh, J.H.; et al. Highly efficient assay of circulating tumor cells by selective sedimentation with a density gradient medium and microfiltration from whole blood. Anal. Chem. 2012, 84, 7400–7407. [Google Scholar] [CrossRef]
- Rosenberg, R.; Gertler, R.; Friederichs, J.; Fuehrer, K.; Dahm, M.; Phelps, R.; Thorban, S.; Nekarda, H.; Siewert, J.R. Comparison of two density gradient centrifugation systems for the enrichment of disseminated tumor cells in blood. Cytometry 2002, 49, 150–158. [Google Scholar] [CrossRef]
- Gertler, R.; Rosenberg, R.; Fuehrer, K.; Dahm, M.; Nekarda, H.; Siewert, J.R. Detection of circulating tumor cells in blood using an optimized density gradient centrifugation. Recent Results Cancer Res. 2003, 162, 149–155. [Google Scholar] [CrossRef]
- Tanaka, T.; Ishikawa, T.; Numayama-Tsuruta, K.; Imai, Y.; Ueno, H.; Yoshimoto, T.; Matsuki, N.; Yamaguchi, T. Inertial migration of cancer cells in blood flow in microchannels. Biomed. Microdevices 2012, 14, 25–33. [Google Scholar] [CrossRef]
- Bhagat, A.A.; Hou, H.W.; Li, L.D.; Lim, C.T.; Han, J. Pinched flow coupled shear-modulated inertial microfluidics for high-throughput rare blood cell separation. Lab Chip 2011, 11, 1870–1878. [Google Scholar] [CrossRef]
- Hur, S.C.; Henderson-MacLennan, N.K.; McCabe, E.R.; di Carlo, D. Deformability-based cell classification and enrichment using inertial microfluidics. Lab Chip 2011, 11, 912–920. [Google Scholar] [CrossRef]
- Warkiani, M.E.; Guan, G.; Luan, K.B.; Lee, W.C.; Bhagat, A.A.; Kant Chaudhuri, P.; Tan, D.S.; Lim, W.T.; Lee, S.C.; Chen, P.C.; et al. Slanted spiral microfluidics for the ultra-fast, label-free isolation of circulating tumor cells. Lab Chip 2014, 14, 128–137. [Google Scholar] [CrossRef]
- Gascoyne, P.R.; Noshari, J.; Anderson, T.J.; Becker, F.F. Isolation of rare cells from cell mixtures by dielectrophoresis. Electrophoresis 2009, 30, 1388–1398. [Google Scholar] [CrossRef]
- Moon, H.S.; Kwon, K.; Kim, S.I.; Han, H.; Sohn, J.; Lee, S.; Jung, H.I. Continuous separation of breast cancer cells from blood samples using multi-orifice flow fractionation (MOFF) and dielectrophoresis (DEP). Lab Chip 2011, 11, 1118–1125. [Google Scholar] [CrossRef]
- Alazzam, A.; Stiharu, I.; Bhat, R.; Meguerditchian, A.N. Interdigitated comb-like electrodes for continuous separation of malignant cells from blood using dielectrophoresis. Electrophoresis 2011, 32, 1327–1336. [Google Scholar] [CrossRef]
- Sano, M.B.; Henslee, E.A.; Schmelz, E.; Davalos, R.V. Contactless dielectrophoretic spectroscopy: Examination of the dielectric properties of cells found in blood. Electrophoresis 2011, 32, 3164–3171. [Google Scholar] [CrossRef]
- Salmanzadeh, A.; Sano, M.B.; Shafiee, H.; Stremler, M.A.; Davalos, R.V. Isolation of rare cancer cells from blood cells using dielectrophoresis. Conf. Proc. IEEE Eng. Med. Biol. Soc. 2012, 2012, 590–593. [Google Scholar]
- Shim, S.; Stemke-Hale, K.; Noshari, J.; Becker, F.; Gascoyne, P. Dielectrophoresis has broad applicability to marker-free isolation of tumor cells from blood by microfluidic systems. Biomicrofluidics 2013, 7. [Google Scholar] [CrossRef]
- Gascoyne, P.R.; Shim, S.; Noshari, J.; Becker, F.F.; Stemke-Hale, K. Correlations between the dielectric properties and exterior morphology of cells revealed by dielectrophoretic field-flow fractionation. Electrophoresis 2013, 34, 1042–1050. [Google Scholar] [CrossRef]
- Shim, S.; Stemke-Hale, K.; Tsimberidou, A.M.; Noshari, J.; Anderson, T.E.; Gascoyne, P.R.C. Antibody-independent isolation of circulating tumor cells by continuous-flow dielectrophoresis. Biomicrofluidics 2013, 7. [Google Scholar] [CrossRef]
- Gascoyne, P.R.C. “Isolation and Characterization of Cells by Dielectrophoretic Field-Flow Fractionation” in Field-Flow Fractionation in Biopolymer Analysis; Springer-Verlag: Vienna, Austria, 2012. [Google Scholar]
- Pohl, H.A. Dielectrophoresis: The Behavior of Neutral Matter in Nonuniform Electric Fields; Cambridge University Press: Cambridge, UK, 1978. [Google Scholar]
- Pohl, H.A.; Kaler, K. Continuous dielectrophoretic separation of cell mixtures. Cell Biophys. 1979, 1, 15–28. [Google Scholar] [CrossRef]
- Markx, G.H.; Talary, M.S.; Pethig, R. Separation of viable and non-viable yeast using dielectrophoresis. J. Biotechnol. 1994, 32, 29–37. [Google Scholar] [CrossRef]
- Stephens, M.; Talary, M.S.; Pethig, R.; Burnett, A.K.; Mills, K.I. The dielectrophoresis enrichment of CD34+ cells from peripheral blood stem cell harvests. Bone Marrow Transplant. 1996, 18, 777–782. [Google Scholar]
- Pethig, R.; Markx, G.H. Applications of dielectrophoresis in biotechnology. Trends Biotechnol. 1997, 15, 426–432. [Google Scholar] [CrossRef]
- Fatoyinbo, H.O.; Kamchis, D.; Whattingham, R.; Ogin, S.L.; Hughes, M.P. A high-throughput 3-D composite dielectrophoretic separator. IEEE Trans. Biomed. Eng. 2005, 52, 1347–1349. [Google Scholar] [CrossRef]
- Piacentini, N.; Mernier, G.; Tornay, R.; Renaud, P. Separation of platelets from other blood cells in continuous-flow by dielectrophoresis field-flow-fractionation. Biomicrofluidics 2011, 5, 34122–341228. [Google Scholar] [CrossRef]
- Ratanachoo, K.; Gascoyne, P.R.; Ruchirawat, M. Detection of cellular responses to toxicants by dielectrophoresis. Biochim. Biophys. Acta 2002, 1564, 449–458. [Google Scholar] [CrossRef]
- Pui-ock, S.; Ruchirawat, M.; Gascoyne, P. Dielectrophoretic field-flow fractionation system for detection of aquatic toxicants. Anal. Chem. 2008, 80, 7727–7734. [Google Scholar] [CrossRef]
- Pethig, R. Dielectrophoresis: An assessment of its potential to aid the research and practice of drug discovery and delivery. Adv. Drug Deliv. Rev. 2013, 65, 1589–1599. [Google Scholar] [CrossRef]
- Archer, S.; Morgan, H.; Rixon, F.J. Electrorotation studies of baby hamster kidney fibroblasts infected with herpes simplex virus type 1. Biophys. J. 1999, 76, 2833–2842. [Google Scholar] [CrossRef]
- Berardi, V.; Aiello, C.; Bonincontro, A.; Risuleo, G. Alterations of the plasma membrane caused by murine polyomavirus proliferation: An electrorotation study. J. Membr. Biol. 2009, 229, 19–25. [Google Scholar] [CrossRef]
- Gascoyne, P.; Pethig, R.; Satayavivad, J.; Becker, F.F.; Ruchirawat, M. Dielectrophoretic detection of changes in erythrocyte membranes following malarial infection. Biochim. Biophys. Acta 1997, 1323, 240–252. [Google Scholar] [CrossRef]
- Gascoyne, P.; Mahidol, C.; Ruchirawat, M.; Satayavivad, J.; Watcharasit, P.; Becker, F. Microsample preparation by dielectrophoresis: Isolation of malaria. Lab Chip 2002, 2, 70–75. [Google Scholar] [CrossRef]
- Gascoyne, P.; Satayavivad, J.; Ruchirawat, M. Microfluidic approaches to malaria detection. Acta Trop. 2004, 89, 357–369. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, X.B.; Becker, F.F.; Gascoyne, P.R. Membrane changes associated with the temperature-sensitive P85gag-mos-dependent transformation of rat kidney cells as determined by dielectrophoresis and electrorotation. Biochim. Biophys. Acta 1996, 1282, 76–84. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, X.B.; Holzel, R.; Becker, F.F.; Gascoyne, P.R. Electrorotational studies of the cytoplasmic dielectric properties of Friend murine erythroleukaemia cells. Phys. Med. Biol. 1995, 40, 1789–1806. [Google Scholar] [CrossRef]
- Gascoyne, P.R.; Pethig, R.; Burt, J.P.; Becker, F.F. Membrane changes accompanying the induced differentiation of Friend murine erythroleukemia cells studied by dielectrophoresis. Biochim. Biophys. Acta 1993, 1149, 119–126. [Google Scholar] [CrossRef]
- Gascoyne, P.R.; Vykoukal, J. Particle separation by dielectrophoresis. Electrophoresis 2002, 23, 1973–1983. [Google Scholar] [CrossRef]
- Wang, X.B.; Huang, Y.; Gascoyne, P.R.; Becker, F.F.; Holzel, R.; Pethig, R. Changes in friend murine erythroleukaemia cell membranes during induced differentiation determined by electrorotation. Biochim. Biophys. Acta 1994, 1193, 330–344. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, X.B.; Gascoyne, P.R.; Becker, F.F. Membrane dielectric responses of human T-lymphocytes following mitogenic stimulation. Biochim. Biophys. Acta 1999, 1417, 51–62. [Google Scholar] [CrossRef]
- Labeed, F.H.; Coley, H.M.; Hughes, M.P. Differences in the biophysical properties of membrane and cytoplasm of apoptotic cells revealed using dielectrophoresis. Biochim. Biophys. Acta 2006, 1760, 922–929. [Google Scholar] [CrossRef]
- Pethig, R.; Talary, M.S. Dielectrophoretic detection of membrane morphology changes in Jurkat T-cells undergoing etoposide-induced apoptosis. IET Nanobiotechnol. 2007, 1, 2–9. [Google Scholar] [CrossRef]
- Braasch, K.; Nikolic-Jaric, M.; Cabel, T.; Salimi, E.; Bridges, G.E.; Thomson, D.J.; Butler, M. The changing dielectric properties of CHO cells can be used to determine early apoptotic events in a bioprocess. Biotechnol. Bioeng. 2013, 110, 2902–2914. [Google Scholar] [CrossRef]
- Gascoyne, P.R. Dielectrophoretic-field flow fractionation analysis of dielectric, density, and deformability characteristics of cells and particles. Anal. Chem. 2009, 81, 8878–8885. [Google Scholar] [CrossRef]
- Vykoukal, D.M.; Gascoyne, P.R.; Vykoukal, J. Dielectric characterization of complete mononuclear and polymorphonuclear blood cell subpopulations for label-free discrimination. Integr. Biol. 2009, 1, 477–484. [Google Scholar] [CrossRef]
- Sukhorukov, V.L.; Arnold, W.M.; Zimmermann, U. Hypotonically induced changes in the plasma membrane of cultured mammalian cells. J. Membr. Biol. 1993, 132, 27–40. [Google Scholar]
- Sukhorukov, V.L.; Djuzenova, C.S.; Arnold, W.M.; Zimmermann, U. DNA, protein, and plasma-membrane incorporation by arrested mammalian cells. J. Membr. Biol. 1994, 142, 77–92. [Google Scholar]
- Pethig, R. Review article-dielectrophoresis: Status of the theory, technology, and applications. Biomicrofluidics 2010, 4. [Google Scholar] [CrossRef]
- Pethig, R.; Menachery, A.; Pells, S.; de Sousa, P. Dielectrophoresis: A review of applications for stem cell research. J. Biomed. Biotechnol. 2010, 2010, e182581. [Google Scholar]
- Gagnon, Z.R. Cellular dielectrophoresis: Applications to the characterization, manipulation, separation and patterning of cells. Electrophoresis 2011, 32, 2466–2487. [Google Scholar] [CrossRef]
- Voldman, J. Electrical forces for microscale cell manipulation. Annu. Rev. Biomed. Eng. 2006, 8, 425–454. [Google Scholar] [CrossRef]
- Broche, L.M.; Bhadal, N.; Lewis, M.P.; Porter, S.; Hughes, M.P.; Labeed, F.H. Early detection of oral cancer—Is dielectrophoresis the answer? Oral Oncol. 2007, 43, 199–203. [Google Scholar] [CrossRef]
- Gascoyne, P.R.; Vykoukal, J.V. Dielectrophoresis-based sample handling in general-purpose programmable diagnostic instruments. Proc. IEEE Inst. Electr. Electron Eng. 2004, 92, 22–42. [Google Scholar] [CrossRef]
- Irimajiri, A.; Asami, K.; Ichinowatari, T.; Kinoshita, Y. Passive electrical properties of the membrane and cytoplasm of cultured rat basophil leukemia cells. I. Dielectric behavior of cell suspensions in 0.01–500 MHz and its simulation with a single-shell model. Biochim. Biophys. Acta 1987, 896, 203–213. [Google Scholar] [CrossRef]
- Chan, K.L.; Gascoyne, P.R.; Becker, F.F.; Pethig, R. Electrorotation of liposomes: Verification of dielectric multi-shell model for cells. Biochim. Biophys. Acta 1997, 1349, 182–196. [Google Scholar] [CrossRef]
- Wang, X.; Becker, F.F.; Gascoyne, P.R. The fractal dimension of cell membrane correlates with its capacitance: A new fractal single-shell model. Chaos 2011, 20. [Google Scholar] [CrossRef]
- Yang, F.; Yang, X.M.; Jiang, H.; Bulkhaults, P.; Wood, P.; Hrushesky, W.; Wang, G.R. Dielectrophoretic separation of colorectal cancer cells. Biomicrofluidics 2010, 4. [Google Scholar] [CrossRef]
- An, J.; Lee, J.; Lee, S.H.; Park, J.; Kim, B. Separation of malignant human breast cancer epithelial cells from healthy epithelial cells using an advanced dielectrophoresis-activated cell sorter (DACS). Anal. Bioanal. Chem. 2009, 394, 801–809. [Google Scholar] [CrossRef]
- Wu, L.; Lanry Yung, L.-Y.; Lim, K.-M. Dielectrophoretic capture voltage spectrum for measurement of dielectric properties and separation of cancer cells. Biomicrofluidics 2012, 6, 14113:1–14113:10. [Google Scholar]
- Salmanzadeh, A.; Kittur, H.; Sano, M.B.; C Roberts, P.; Schmelz, E.M.; Davalos, R.V. Dielectrophoretic differentiation of mouse ovarian surface epithelial cells, macrophages, and fibroblasts using contactless dielectrophoresis. Biomicrofluidics 2012, 6, e24104. [Google Scholar] [CrossRef]
- Huang, C.; Santana, S.M.; Liu, H.; Bander, N.H.; Hawkins, B.G.; Kirby, B.J. Characterization of a hybrid dielectrophoresis and immunocapture microfluidic system for cancer cell capture. Electrophoresis 2013, 34, 2970–2979. [Google Scholar]
- Chuang, C.H.; Huang, Y.W.; Wu, Y.T. System-level biochip for impedance sensing and programmable manipulation of bladder cancer cells. Sensors 2011, 11, 11021–11035. [Google Scholar] [CrossRef]
- Henslee, E.A.; Sano, M.B.; Rojas, A.D.; Schmelz, E.M.; Davalos, R.V. Selective concentration of human cancer cells using contactless dielectrophoresis. Electrophoresis 2011, 32, 2523–2529. [Google Scholar]
- Mulhall, H.J.; Labeed, F.H.; Kazmi, B.; Costea, D.E.; Hughes, M.P.; Lewis, M.P. Cancer, pre-cancer and normal oral cells distinguished by dielectrophoresis. Anal. Bioanal. Chem. 2011, 401, 2455–2463. [Google Scholar] [CrossRef]
- Gambari, R.; Borgatti, M.; Altomare, L.; Manaresi, N.; Medoro, G.; Romani, A.; Tartagni, M.; Guerrieri, R. Applications to cancer research of “lab-on-a-chip” devices based on dielectrophoresis (DEP). Technol. Cancer Res. Treat. 2003, 2, 31–40. [Google Scholar]
- Shim, S.; Gascoyne, P.; Noshari, J.; Hale, K.S. Dynamic physical properties of dissociated tumor cells revealed by dielectrophoretic field-flow fractionation. Integr. Biol. 2011, 3, 850–862. [Google Scholar] [CrossRef]
- Gascoyne, P.R.; Wang, X.B.; Huang, Y.; Becker, F.F. Dielectrophoretic separation of cancer cells from blood. IEEE Trans. Ind. Appl. 1997, 33, 670–678. [Google Scholar] [CrossRef]
- Becker, F.F.; Wang, X.B.; Huang, Y.; Pethig, R.; Vykoukal, J.; Gascoyne, P.R. Separation of human breast cancer cells from blood by differential dielectric affinity. Proc. Natl. Acad. Sci. USA 1995, 92, 860–864. [Google Scholar] [CrossRef]
- Becker, F.; Wang, X.-B.; Huang, Y.; Pethig, R.; Vykoukal, J.; Gascoyne, P.R.C. The removal of human leukaemia cells from blood by dielectrophoresis. J. Phys. D Appl. Phys. 1994, 27, 2659–2662. [Google Scholar] [CrossRef]
- Stout, D.L.; Becker, F.F.; Wang, X.-B.; Gascoyne, P.R.C.; The University of Texas M.D. Anderson Cancer Center, Houston, TX, USA. Unpublished data. 1998.
- Tarabichi, M.; Antoniou, A.; Saiselet, M.; Pita, J.M.; Andry, G.; Dumont, J.E.; Detours, V.; Maenhaut, C. Systems biology of cancer: Entropy, disorder, and selection-driven evolution to independence, invasion and “swarm intelligence”. Cancer Metastasis Rev. 2013, 32, 403–421. [Google Scholar] [CrossRef]
- Rubin, H. Cancer as a dynamic developmental disorder. Cancer Res. 1985, 45, 2935–2942. [Google Scholar]
- Kayser, K.; Kayser, G.; Metze, K. The concept of structural entropy in tissue-based diagnosis. Anal. Quant. Cytol. Histol. 2007, 29, 296–308. [Google Scholar]
- Van Wieringen, W.N.; van der Vaart, A.W. Statistical analysis of the cancer cell’s molecular entropy using high-throughput data. Bioinformatics 2011, 27, 556–563. [Google Scholar] [CrossRef]
- Duesberg, P.; Li, R.; Fabarius, A.; Hehlmann, R. The chromosomal basis of cancer. Cell. Oncol. 2005, 27, 293–318. [Google Scholar]
- Sato, N.; Mizumoto, K.; Nakamura, M.; Maehara, N.; Minamishima, Y.A.; Nishio, S.; Nagai, E.; Tanaka, M. Correlation between centrosome abnormalities and chromosomal instability in human pancreatic cancer cells. Cancer Genet. Cytogenet. 2001, 126, 13–19. [Google Scholar] [CrossRef]
- De Mello, M.R.; Albuquerque, D.M.; Pereira-Cunha, F.G.; Albanez, K.B.; Pagnano, K.B.; Costa, F.F.; Metze, K.; Lorand-Metze, I. Molecular characteristics and chromatin texture features in acute promyelocytic leukemia. Diagn. Pathol. 2012, 7. [Google Scholar] [CrossRef]
- Gondor, A. Nuclear architecture and chromatin structure on the path to cancer. Semin. Cancer Biol. 2013, 23, 63–64. [Google Scholar] [CrossRef]
- Black, M.M.; Speer, F.D. Nuclear structure in cancer tissues. Surg. Gynecol. Obstet. 1957, 105, 97–102. [Google Scholar]
- Zink, D.; Fischer, A.H.; Nickerson, J.A. Nuclear structure in cancer cells. Nat. Rev. Cancer 2004, 4, 677–687. [Google Scholar] [CrossRef]
- Bocking, A.; Stockhausen, J.; Meyer-Ebrecht, D. Towards a single cell cancer diagnosis. Multimodal and monocellular measurements of markers and morphology (5M). Cell. Oncol. 2004, 26, 73–79. [Google Scholar]
- Sottoriva, A.; Verhoeff, J.J.; Borovski, T.; McWeeney, S.K.; Naumov, L.; Medema, J.P.; Sloot, P.M.; Vermeulen, L. Cancer stem cell tumor model reveals invasive morphology and increased phenotypical heterogeneity. Cancer Res. 2010, 70, 46–56. [Google Scholar] [CrossRef]
- Junker, K.; Langner, K.; Klinke, F.; Bosse, U.; Thomas, M. Grading of tumor regression in non-small cell lung cancer: Morphology and prognosis. Chest 2001, 120, 1584–1591. [Google Scholar] [CrossRef]
- Green, J.; Watson, J.; Roche, M.; Beral, V.; Patnick, J. Stage, grade and morphology of tumours of the colon and rectum recorded in the Oxford Cancer Registry, 1995–2003. Br. J. Cancer 2007, 96, 140–142. [Google Scholar] [CrossRef]
- Lipponen, P.K. The prognostic value of basement membrane morphology, tumour histology and morphometry in superficial bladder cancer. J. Cancer Res. Clin. Oncol. 1993, 119, 295–300. [Google Scholar] [CrossRef]
- Moritani, S.; Ichihara, S.; Hasegawa, M.; Endo, T.; Oiwa, M.; Shiraiwa, M.; Nishida, C.; Morita, T.; Sato, Y.; Hayashi, T.; et al. Topographical, morphological and immunohistochemical characteristics of carcinoma in situ of the breast involving sclerosing adenosis. Two distinct topographical patterns and histological types of carcinoma in situ. Histopathology 2011, 58, 835–846. [Google Scholar] [CrossRef]
- Scarpelli, M.; Bartels, P.H.; Montironi, R.; Galluzzi, C.M.; Thompson, D. Morphometrically assisted grading of astrocytomas. Anal. Quant. Cytol. Histol. 1994, 16, 351–356. [Google Scholar]
- Sommers, C.L.; Byers, S.W.; Thompson, E.W.; Torri, J.A.; Gelmann, E.P. Differentiation state and invasiveness of human breast cancer cell lines. Breast Cancer Res. Treat. 1994, 31, 325–335. [Google Scholar] [CrossRef]
- Lanigan, F.; McKiernan, E.; Brennan, D.J.; Hegarty, S.; Millikan, R.C.; McBryan, J.; Jirstrom, K.; Landberg, G.; Martin, F.; Duffy, M.J.; et al. Increased claudin-4 expression is associated with poor prognosis and high tumour grade in breast cancer. Int. J. Cancer 2009, 124, 2088–2097. [Google Scholar] [CrossRef]
- Sheehan, G.M.; Kallakury, B.V.; Sheehan, C.E.; Fisher, H.A.; Kaufman, R.P., Jr.; Ross, J.S. Loss of claudins-1 and -7 and expression of claudins-3 and -4 correlate with prognostic variables in prostatic adenocarcinomas. Hum. Pathol. 2007, 38, 564–569. [Google Scholar] [CrossRef]
- Spath, C.; Schlegel, F.; Leontyev, S.; Mohr, F.W.; Dhein, S. Inverse relationship between tumor proliferation markers and connexin expression in a malignant cardiac tumor originating from mesenchymal stem cell engineered tissue in a rat in vivo model. Front. Pharmacol. 2013, 4. [Google Scholar] [CrossRef]
- Xing, Y.; Xiao, Y.; Zeng, F.; Zhao, J.; Xiao, C.; Xiong, P.; Feng, W. Altered expression of connexin-43 and impaired capacity of gap junctional intercellular communication in prostate cancer cells. J. Huazhong Univ. Sci. Technolog. Med. Sci. 2007, 27, 291–294. [Google Scholar] [CrossRef]
- Sarrio, D.; Rodriguez-Pinilla, S.M.; Dotor, A.; Calero, F.; Hardisson, D.; Palacios, J. Abnormal ezrin localization is associated with clinicopathological features in invasive breast carcinomas. Breast Cancer Res. Treat. 2006, 98, 71–79. [Google Scholar] [CrossRef]
- Lin, Y.C.; Tsai, P.H.; Lin, C.Y.; Cheng, C.H.; Lin, T.H.; Lee, K.P.; Huang, K.Y.; Chen, S.H.; Hwang, J.J.; Kandaswami, C.C.; et al. Impact of flavonoids on matrix metalloproteinase secretion and invadopodia formation in highly invasive A431-III cancer cells. PLoS One 2013, 8, e71903. [Google Scholar] [CrossRef]
- Wang, S.; Li, E.; Gao, Y.; Wang, Y.; Guo, Z.; He, J.; Zhang, J.; Gao, Z.; Wang, Q. Study on invadopodia formation for lung carcinoma invasion with a microfluidic 3D culture device. PLoS One 2013, 8, e56448. [Google Scholar]
- Yamaguchi, H.; Pixley, F.; Condeelis, J. Invadopodia and podosomes in tumor invasion. Eur. J. Cell Biol. 2006, 85, 213–218. [Google Scholar] [CrossRef]
- Struckhoff, A.P.; Rana, M.K.; Worthylake, R.A. RhoA can lead the way in tumor cell invasion and metastasis. Front. Biosci. 2011, 16, 1915–1926. [Google Scholar] [CrossRef]
- Memmel, S.; Sukhorukov, V.L.; Horing, M.; Westerling, K.; Fiedler, V.; Katzer, A.; Krohne, G.; Flentje, M.; Djuzenova, C.S. Cell surface area and membrane folding in glioblastoma cell lines differing in PTEN and p53 status. PLoS One 2014, 9, e87052. [Google Scholar] [CrossRef]
- Cristofanilli, M.; Krishnamurthy, S.; Das, C.M.; Reuben, J.M.; Spohn, W.; Noshari, J.; Becker, F.; Gascoyne, P.R. Dielectric cell separation of fine needle aspirates from tumor xenografts. J. Sep. Sci. 2008, 31, 3732–3739. [Google Scholar] [CrossRef]
- Das, C.M.; Becker, F.; Vernon, S.; Noshari, J.; Joyce, C.; Gascoyne, P.R. Dielectrophoretic segregation of different human cell types on microscope slides. Anal. Chem. 2005, 77, 2708–2719. [Google Scholar] [CrossRef]
- Wang, X.; Becker, F.F.; Gascoyne, P.R. Membrane dielectric changes indicate induced apoptosis in HL-60 cells more sensitively than surface phosphatidylserine expression or DNA fragmentation. Biochim. Biophys. Acta 2002, 1564, 412–420. [Google Scholar] [CrossRef]
- Yang, J.; Huang, Y.; Wang, X.; Wang, X.B.; Becker, F.F.; Gascoyne, P.R. Dielectric properties of human leukocyte subpopulations determined by electrorotation as a cell separation criterion. Biophys. J. 1999, 76, 3307–3314. [Google Scholar] [CrossRef]
- Wang, X.B.; Huang, Y.; Wang, X.; Becker, F.F.; Gascoyne, P.R. Dielectrophoretic manipulation of cells with spiral electrodes. Biophys. J. 1997, 72, 1887–1899. [Google Scholar] [CrossRef]
- Zhu, J.; Hu, G.; Xuan, X. Electrokinetic particle entry into microchannels. Electrophoresis 2012, 33, 916–922. [Google Scholar] [CrossRef]
- Barrett, L.M.; Skulan, A.J.; Singh, A.K.; Cummings, E.B.; Fiechtner, G.J. Dielectrophoretic manipulation of particles and cells using insulating ridges in faceted prism microchannels. Anal. Chem. 2005, 77, 6798–6804. [Google Scholar] [CrossRef]
- Choi, S.; Park, J.K. Microfluidic system for dielectrophoretic separation based on a trapezoidal electrode array. Lab Chip 2005, 5, 1161–1167. [Google Scholar] [CrossRef]
- Voldman, J.; Braff, R.A.; Toner, M.; Gray, M.L.; Schmidt, M.A. Holding forces of single-particle dielectrophoretic traps. Biophys. J. 2001, 80, 531–541. [Google Scholar] [CrossRef]
- Menachery, A.; Pethig, R. Controlling cell destruction using dielectrophoretic forces. IEE Proc. Nanobiotechnol. 2005, 152, 145–149. [Google Scholar] [CrossRef]
- Wang, X.; Yang, J.; Gascoyne, P.R. Role of peroxide in AC electrical field exposure effects on friend murine erythroleukemia cells during dielectrophoretic manipulations. Biochim. Biophys. Acta 1999, 1426, 53–68. [Google Scholar] [CrossRef]
- Jones, T.B. Electromechanics of Particles; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Washizu, M.; Jones, T.B. Dielectrophoretic interaction of two spherical particles calculated by equivalent multipole-moment method. IEEE Trans. Ind. Appl. 1996, 32, 233–242. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, X.B.; Becker, F.F.; Gascoyne, P.R. Introducing dielectrophoresis as a new force field for field-flow fractionation. Biophys. J. 1997, 73, 1118–1129. [Google Scholar] [CrossRef]
- Wang, X.B.; Vykoukal, J.; Becker, F.F.; Gascoyne, P.R. Separation of polystyrene microbeads using dielectrophoretic/gravitational field-flow-fractionation. Biophys. J. 1998, 74, 2689–2701. [Google Scholar] [CrossRef]
- Lewpiriyawong, N.; Yang, C. Dielectrophoresis field-flow fractionation for continuous-flow separation of particles and cells in microfluidic devices. In Advances in Transport Phenomena 2011; Wang, L., Ed.; Springer International: Cham, Switzerland, 2014; Volume 3, pp. 29–62. [Google Scholar]
- Vykoukal, J.; Vykoukal, D.M.; Freyberg, S.; Alt, E.U.; Gascoyne, P.R. Enrichment of putative stem cells from adipose tissue using dielectrophoretic field-flow fractionation. Lab Chip 2008, 8, 1386–1393. [Google Scholar]
- Park, K.; Suk, H.J.; Akin, D.; Bashir, R. Dielectrophoresis-based cell manipulation using electrodes on a reusable printed circuit board. Lab Chip 2009, 9, 2224–2229. [Google Scholar] [CrossRef]
- Gupta, V.; Jafferji, I.; Garza, M.; Melnikova, V.; Hasegawa, D.; Pethig, R.; Davis, D. ApoStream, a new dielectrophoretic device for antibody independent isolation and recovery of viable cancer cells from blood. Biomicrofluidics 2012, 6. [Google Scholar] [CrossRef]
- Davis, D.; Gupta, V.; Garza, M.; Pace, M.; Wu, W.; Neal, C.; Sukumaran, S.; Woo, J.; Melnikova, V.; Hasegawa, D.K. EpCAM-independent ApoStream™ technology isolates circulating tumor cells from blood of patients with various types of cancer. Mol. Cancer Ther. 2011, 10. [Google Scholar] [CrossRef]
- Varadhachary, G.; Abbruzzese, J.; Shroff, R.; Melnikova, V.; Gupta, V.; Neal, C.; Garza, M.; Hasegawa, D.K.; Anderes, K.L.; Davis, D.; et al. ApoStream, a new dielectrophoretic device for antibody-independent isolation and recovery of circulating tumor cells from blood of patients with metastatic pancreatic adenocarcinoma. Cancer Res. 2013, 73. Abstract No. 1449. [Google Scholar]
- Tran, H.T.; Melnikova, V.O.; Tsao, A.S.; Fossella, F.V.; Johnson, F.M.; Papadimitrakopoulou, V.; Garza, M.; Nea, L.C.; Hasegawa, D.; Kruempel, A.; et al. Characterization and identification of specific EGFR mutations in circulating tumor cells (CTCs) isolated from non-small cell lung cancer patients using antibody independent method, ApoStream. J. Clin. Oncol. 2013, 31. Abstract No. 11044. [Google Scholar]
- Jones, T.B.; Kallio, G.A. Dielectrophoretic levitation of spheres and shells. J. Electrost. 1979, 6, 207–224. [Google Scholar] [CrossRef]
- Green, N.G.; Morgan, H. Dielectrophoretic separation of nano-particles. J. Phys. D Appl. Phys. 1997, 30. [Google Scholar] [CrossRef]
- Irimajiri, A.; Hanai, T.; Inouye, A. A dielectric theory of “multi-stratified shell” model with its application to a lymphoma cell. J. Theor. Biol. 1979, 78, 251–269. [Google Scholar] [CrossRef]
- Wang, X.-B.; Huang, Y.; Holzel, R.; Burt, J.P.; Pethig, R. Theoretical and experimental investigations of the interdependence of the dielectric, dielectrophoretic and electrorotational behaviour of colloidal particles. J. Phys. D Appl. Phys. 1993, 26. [Google Scholar] [CrossRef]
- Pethig, R.; Kell, D.B. The passive electrical properties of biological systems: Their significance in physiology, biophysics and biotechnology. Phys. Med. Biol. 1987, 32, 933–970. [Google Scholar] [CrossRef]
- Huang, C.; Liu, H.; Bander, N.H.; Kirby, B.J. Enrichment of prostate cancer cells from blood cells with a hybrid dielectrophoresis and immunocapture microfluidic system. Biomed. Microdevices 2013, 15, 941–948. [Google Scholar] [CrossRef]
- Hawkins, B.G.; Smith, A.E.; Syed, Y.A.; Kirby, B.J. Continuous-flow particle separation by 3D Insulative dielectrophoresis using coherently shaped, dc-biased, ac electric fields. Anal. Chem. 2007, 79, 7291–7300. [Google Scholar] [CrossRef]
- Hawkins, B.G.; Kirby, B.J. Electrothermal flow effects in insulating (electrodeless) dielectrophoresis systems. Electrophoresis 2010, 31, 3622–3633. [Google Scholar] [CrossRef]
- Wang, X.; Wang, X.-B.; Becker, F.; Gascoyne, P.R. A theoretical method of electrical field analysis for dielectrophoretic electrode arrays using Green’s theorem. J. Phys. D Appl. Phys. 1996, 29. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Gascoyne, P.R.C.; Shim, S. Isolation of Circulating Tumor Cells by Dielectrophoresis. Cancers 2014, 6, 545-579. https://doi.org/10.3390/cancers6010545
Gascoyne PRC, Shim S. Isolation of Circulating Tumor Cells by Dielectrophoresis. Cancers. 2014; 6(1):545-579. https://doi.org/10.3390/cancers6010545
Chicago/Turabian StyleGascoyne, Peter R. C., and Sangjo Shim. 2014. "Isolation of Circulating Tumor Cells by Dielectrophoresis" Cancers 6, no. 1: 545-579. https://doi.org/10.3390/cancers6010545
APA StyleGascoyne, P. R. C., & Shim, S. (2014). Isolation of Circulating Tumor Cells by Dielectrophoresis. Cancers, 6(1), 545-579. https://doi.org/10.3390/cancers6010545




