Deep Vision for Breast Cancer Classification and Segmentation
Abstract
:Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Data, Software, and Hardware
2.2. Training, Validation, and Test Sets
2.3. Image and Label Preprocessing
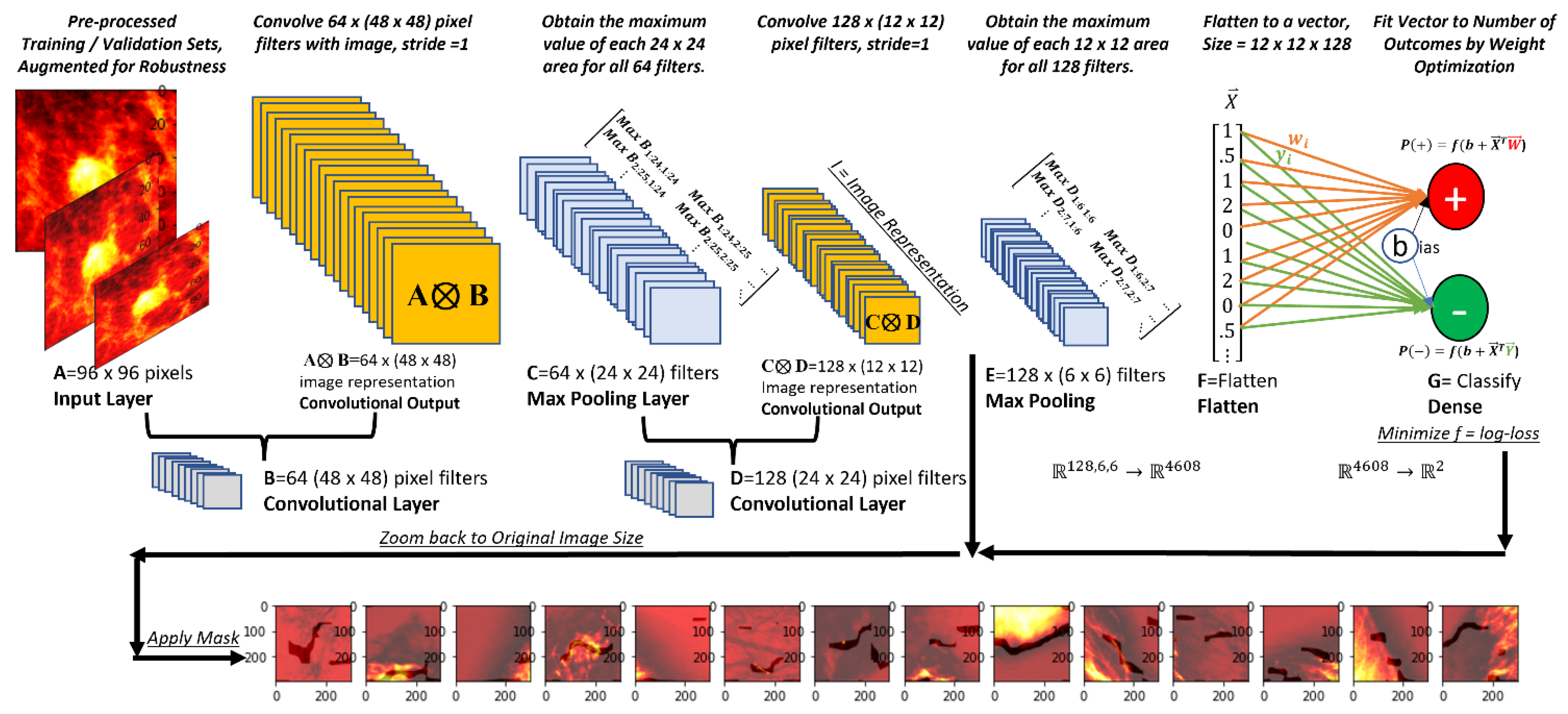
2.4. Architecture
2.5. Deep Vision Basics
2.6. Supervised Classification
2.7. Specific Architecture, Classification Problem
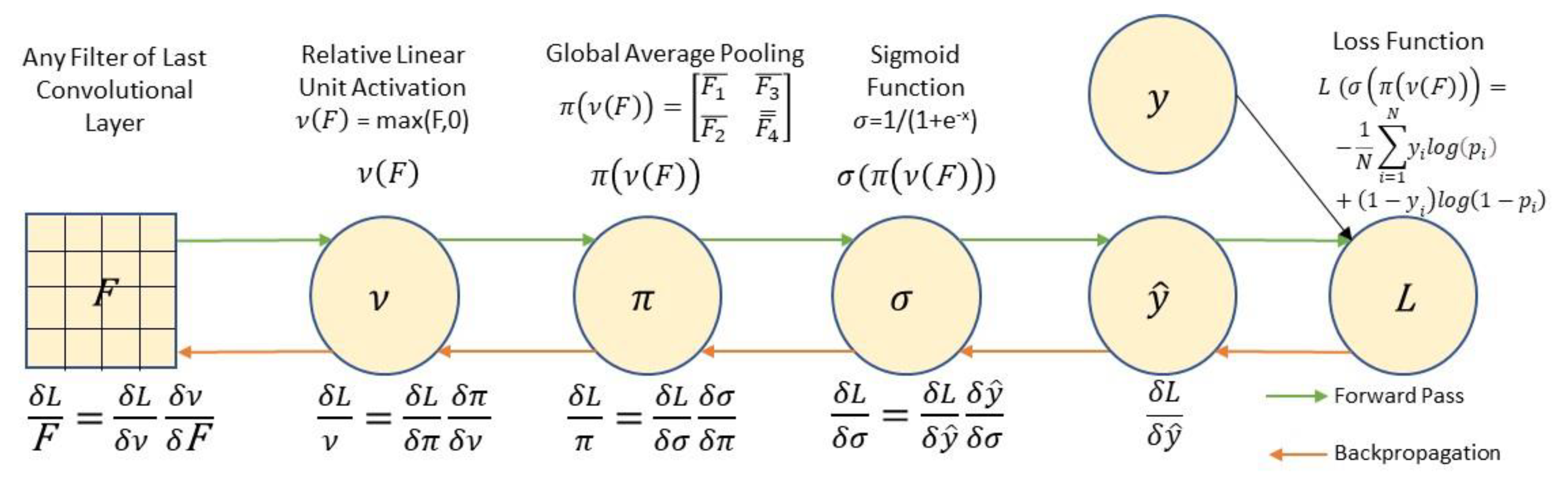
2.8. Unsupervised Region of Interest (ROI) Identification
3. Results
3.1. Descriptive Statistics
3.2. Classification Results
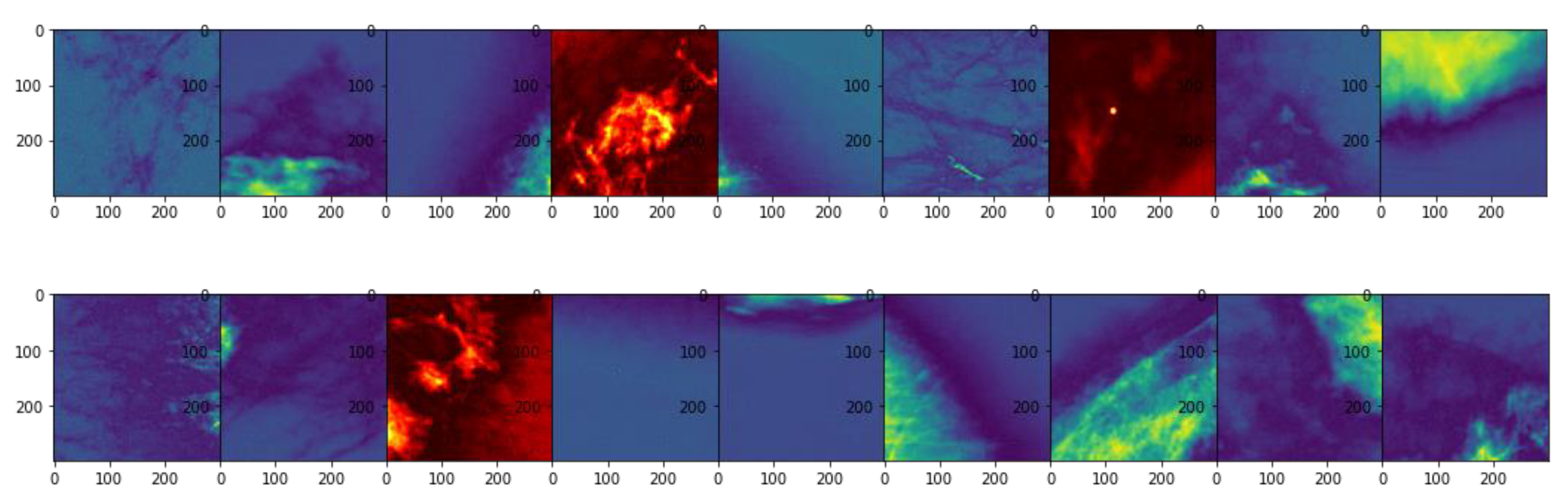
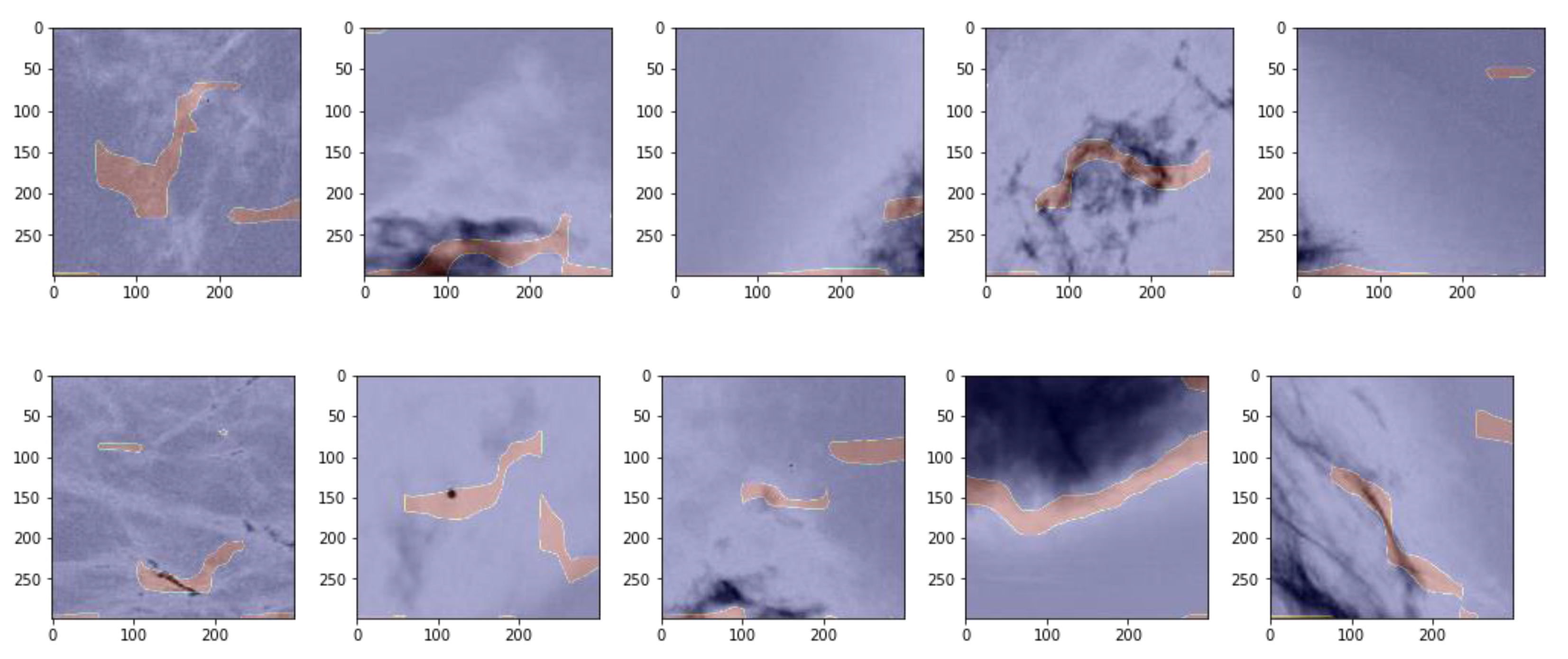
3.3. Unsupervised Gradient Mapping
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sung, H.; Ferlay, J.; Siegel, R.L.; Laversanne, M.; Soerjomataram, I.; Jemal, A.; Bray, F. Global Cancer Statistics 2020: GLOBOCAN Estimates of Incidence and Mortality Worldwide for 36 Cancers in 185 Countries. CA A Cancer J. Clin. 2021, 71, 209–249. [Google Scholar] [CrossRef]
- Siegel, R.L.; Miller, K.D.; Jemal, A. Cancer statistics, 2020. CA A Cancer J. Clin. 2020, 70, 7–30. [Google Scholar] [CrossRef]
- WHO. Breast Cancer. Available online: https://www.who.int/news-room/fact-sheets/detail/breast-cancer (accessed on 18 October 2021).
- CDMRP. Breast Cancer Landscape. Available online: https://cdmrp.army.mil/bcrp/pdfs/Breast%20Cancer%20Landscape2020.pdf (accessed on 1 March 2021).
- Zhu, K.; Devesa, S.S.; Wu, H.; Zahm, S.H.; Jatoi, I.; Anderson, W.F.; Peoples, G.E.; Maxwell, L.G.; Granger, E.; Potter, J.F. Cancer incidence in the US military population: Comparison with rates from the SEER program. Cancer Epidemiol. Prev. Biomark. 2009, 18, 1740–1745. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cancer.org. How Common is Breast Cancer? Available online: https://www.cancer.org/cancer/breast-cancer/about/how-common-is-breast-cancer.html (accessed on 18 October 2021).
- Ross, R.K.; Paganini-Hill, A.; Wan, P.C.; Pike, M.C. Effect of hormone replacement therapy on breast cancer risk: Estrogen versus estrogen plus progestin. J. Natl. Cancer Inst. 2000, 92, 328–332. [Google Scholar] [CrossRef]
- Plasticsurgery.org. National Plastic Surgery Statistics. 2018. Available online: https://www.plasticsurgery.org/documents/News/Statistics/2018/plastic-surgery-statistics-report-2018.pdf (accessed on 18 October 2021).
- Tripodi, D.; Amabile, M.I.; Varanese, M.; D’Andrea, V.; Sorrenti, S.; Cannistrà, C. Large cell anaplastic lymphoma associated with breast implant: A rare case report presentation and discussion of possible management. Gland Surg. 2021, 10, 2076–2080. [Google Scholar] [CrossRef] [PubMed]
- De Jong, W.H.; Panagiotakos, D.; Proykova, A.; Samaras, T.; Clemens, M.W.; De Jong, D.; Hopper, I.; Rakhorst, H.A.; Santanelli di Pompeo, F.; Turner, S.D.; et al. Final opinion on the safety of breast implants in relation to anaplastic large cell lymphoma: Report of the scientific committee on health, emerging and environmental risks (SCHEER). Regul. Toxicol. Pharmacol. 2021, 125, 104982. [Google Scholar] [CrossRef] [PubMed]
- McCarthy, B.D.; Yood, M.U.; MacWilliam, C.H.; Lee, M.J. Screening Mammography Use: The Importance of a Population Perspective. Am. J. Prev. Med. 1996, 12, 91–95. [Google Scholar] [CrossRef]
- Witten, M.; Parker, C.C. Screening mammography: Recommendations and controversies. Surg. Clin. 2018, 98, 667–675. [Google Scholar]
- Duffy, S.W.; Tabár, L.; Yen, A.M.F.; Dean, P.B.; Smith, R.A.; Jonsson, H.; Törnberg, S.; Chen, S.L.S.; Chiu, S.Y.H.; Fann, J.C.Y. Mammography screening reduces rates of advanced and fatal breast cancers: Results in 549,091 women. Cancer 2020, 126, 2971–2979. [Google Scholar] [CrossRef]
- Levinsohn, E.; Altman, M.; Chagpar, A.B. Article Commentary: Controversies Regarding the Diagnosis and Management of Ductal Carcinoma in Situ. Am. Surg. 2018, 84, 1–6. [Google Scholar] [CrossRef]
- Nelson, H.D.; O’Meara, E.S.; Kerlikowske, K.; Balch, S.; Miglioretti, D. Factors associated with rates of false-positive and false-negative results from digital mammography screening: An analysis of registry data. Ann. Intern. Med. 2016, 164, 226–235. [Google Scholar] [CrossRef]
- Liu, X.; Tang, J. Mass Classification in Mammograms Using Selected Geometry and Texture Features, and a New SVM-Based Feature Selection Method. IEEE Syst. J. 2014, 8, 910–920. [Google Scholar] [CrossRef]
- Nishikawa, R.M.; Bae, K.T. Importance of better human-computer interaction in the era of deep learning: Mammography computer-aided diagnosis as a use case. J. Am. Coll. Radiol. 2018, 15, 49–52. [Google Scholar] [CrossRef]
- Saki, F.; Tahmasbi, A.; Soltanian-Zadeh, H.; Shokouhi, S.B. Fast opposite weight learning rules with application in breast cancer diagnosis. Comput. Biol. Med. 2013, 43, 32–41. [Google Scholar] [CrossRef] [PubMed]
- Ertosun, M.G.; Rubin, D.L. Probabilistic visual search for masses within mammography images using deep learning. In Proceedings of the 2015 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Washington, DC, USA, 9–12 November 2015; pp. 1310–1315. [Google Scholar]
- Muramatsu, C.; Higuchi, S.; Morita, T.; Oiwa, M.; Kawasaki, T.; Fujita, H. Retrieval of reference images of breast masses on mammograms by similarity space modeling. In Proceedings of the 14th International Workshop on Breast Imaging (IWBI 2018), Atlanta, GA, USA, 8–11 July 2018; p. 1071809. [Google Scholar]
- Salama, W.M.; Aly, M.H. Deep learning in mammography images segmentation and classification: Automated CNN approach. Alex. Eng. J. 2021, 60, 4701–4709. [Google Scholar] [CrossRef]
- Muhammad, M.; Zeebaree, D.; Brifcani, A.M.A.; Saeed, J.; Zebari, D.A. Region of Interest Segmentation Based on Clustering Techniques for Breast Cancer Ultrasound Images: A Review. J. Appl. Sci. Technol. Trends 2020, 1, 78–91. [Google Scholar] [CrossRef]
- Drukker, K.; Giger, M.L.; Horsch, K.; Kupinski, M.A.; Vyborny, C.J.; Mendelson, E.B. Computerized lesion detection on breast ultrasound. Med. Phys. 2002, 29, 1438–1446. [Google Scholar] [CrossRef]
- Preim, B.; Botha, C.P. Visual Computing for Medicine: Theory, Algorithms, and Applications; Morgan Kaufman (Elsevier): Waltham, MA, USA, 2013. [Google Scholar]
- Huang, Q.-H.; Lee, S.-Y.; Liu, L.-Z.; Lu, M.-H.; Jin, L.-W.; Li, A.-H. A robust graph-based segmentation method for breast tumors in ultrasound images. Ultrasonics 2012, 52, 266–275. [Google Scholar] [CrossRef]
- Çiǧla, C.; Alatan, A.A. Efficient graph-based image segmentation via speeded-up turbo pixels. In Proceedings of the 2010 IEEE International Conference on Image Processing, Piscataway, NJ, USA, 14–19 March 2010; pp. 3013–3016. [Google Scholar]
- Zeiler, M.D.; Fergus, R. Visualizing and understanding convolutional networks. In European Conference on Computer Vision; Springer: Cham, Switzerland, 2014; pp. 818–833. [Google Scholar]
- Springenberg, J.T.; Dosovitskiy, A.; Brox, T.; Riedmiller, M. Striving for simplicity: The all convolutional net. arXiv 2014, arXiv:1412.6806. [Google Scholar]
- Dwaraknath, A.; Menghani, D.; Mongia, M. Fast Unsupervised Object Localization. 2016. Available online: http://vision.stanford.edu/teaching/cs231n/reports/2016/pdfs/285_Report.pdf (accessed on 1 October 2021).
- Heath, M.; Bowyer, K.; Kopans, D.; Moore, R.; Kegelmeyer, W. The digital database for screening mammography. In Proceedings of the Fifth International Workshop on Digital Mammography; Yaffe, M.J., Ed.; Medical Physics Publishing: Madison, WI, USA, 2001; pp. 212–218. [Google Scholar]
- Lee, R.S.; Gimenez, F.; Hoogi, A.; Miyake, K.K.; Gorovoy, M.; Rubin, D.L. A curated mammography data set for use in computer-aided detection and diagnosis research. Sci. Data 2017, 4, 1–9. [Google Scholar] [CrossRef]
- Scuccimara, E. DDSM Mammography. Available online: https://www.kaggle.com/skooch/ddsm-mammography (accessed on 5 October 2021).
- Fulton, L.V. Breast Cancer. Available online: https://github.com/dustoff06/BreastCancers (accessed on 5 October 2021).
- Yue, H.; Liu, J.; Yang, J.; Sun, X.; Nguyen, T.Q.; Wu, F. Ienet: Internal and external patch matching convnet for web image guided denoising. IEEE Trans. Circuits Syst. Video Technol. 2019, 30, 3928–3942. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Lydia, A.; Francis, S. Adagrad—An optimizer for stochastic gradient descent. Int. J. Inf. Comput. Sci. 2019, 6, 566–568. [Google Scholar]
- Adebayo, J.; Gilmer, J.; Muelly, M.; Goodfellow, I.; Hardt, M.; Kim, B. Sanity checks for saliency maps. arXiv 2018, arXiv:1810.03292. [Google Scholar]
- TensorFlow. tf.GradientTape. Available online: https://www.tensorflow.org/api_docs/python/tf/GradientTape (accessed on 5 October 2021).
- Hernández-García, A.; König, P. Further advantages of data augmentation on convolutional neural networks. In Proceedings of the International Conference on Artificial Neural Networks; Springer: Cham, Switzerland, 2018; pp. 95–103. [Google Scholar]
| Metric | Size | Precision | Recall | F1-Score |
|---|---|---|---|---|
| Negative | 13,360 | 0.98 0 | 0.99 * | 0.98 *** |
| Positive | 2004 | 0.93 1 | 0.83 ** | 0.88 *** |
| Weighted Average | 15,364 | 0.97 | 0.97 | 0.97 |
| Actual/Prediction | Negative Prediction | Positive Prediction | Total |
|---|---|---|---|
| Negative | 13,229 | 131 | 13,360 |
| Positive | 334 | 1670 | 2004 |
| Total | 13,563 | 1801 | 15,364 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fulton, L.; McLeod, A.; Dolezel, D.; Bastian, N.; Fulton, C.P. Deep Vision for Breast Cancer Classification and Segmentation. Cancers 2021, 13, 5384. https://doi.org/10.3390/cancers13215384
Fulton L, McLeod A, Dolezel D, Bastian N, Fulton CP. Deep Vision for Breast Cancer Classification and Segmentation. Cancers. 2021; 13(21):5384. https://doi.org/10.3390/cancers13215384
Chicago/Turabian StyleFulton, Lawrence, Alex McLeod, Diane Dolezel, Nathaniel Bastian, and Christopher P. Fulton. 2021. "Deep Vision for Breast Cancer Classification and Segmentation" Cancers 13, no. 21: 5384. https://doi.org/10.3390/cancers13215384
APA StyleFulton, L., McLeod, A., Dolezel, D., Bastian, N., & Fulton, C. P. (2021). Deep Vision for Breast Cancer Classification and Segmentation. Cancers, 13(21), 5384. https://doi.org/10.3390/cancers13215384







