Cell Systems Bioelectricity: How Different Intercellular Gap Junctions Could Regionalize a Multicellular Aggregate
Abstract
Simple Summary
Abstract
1. Introduction
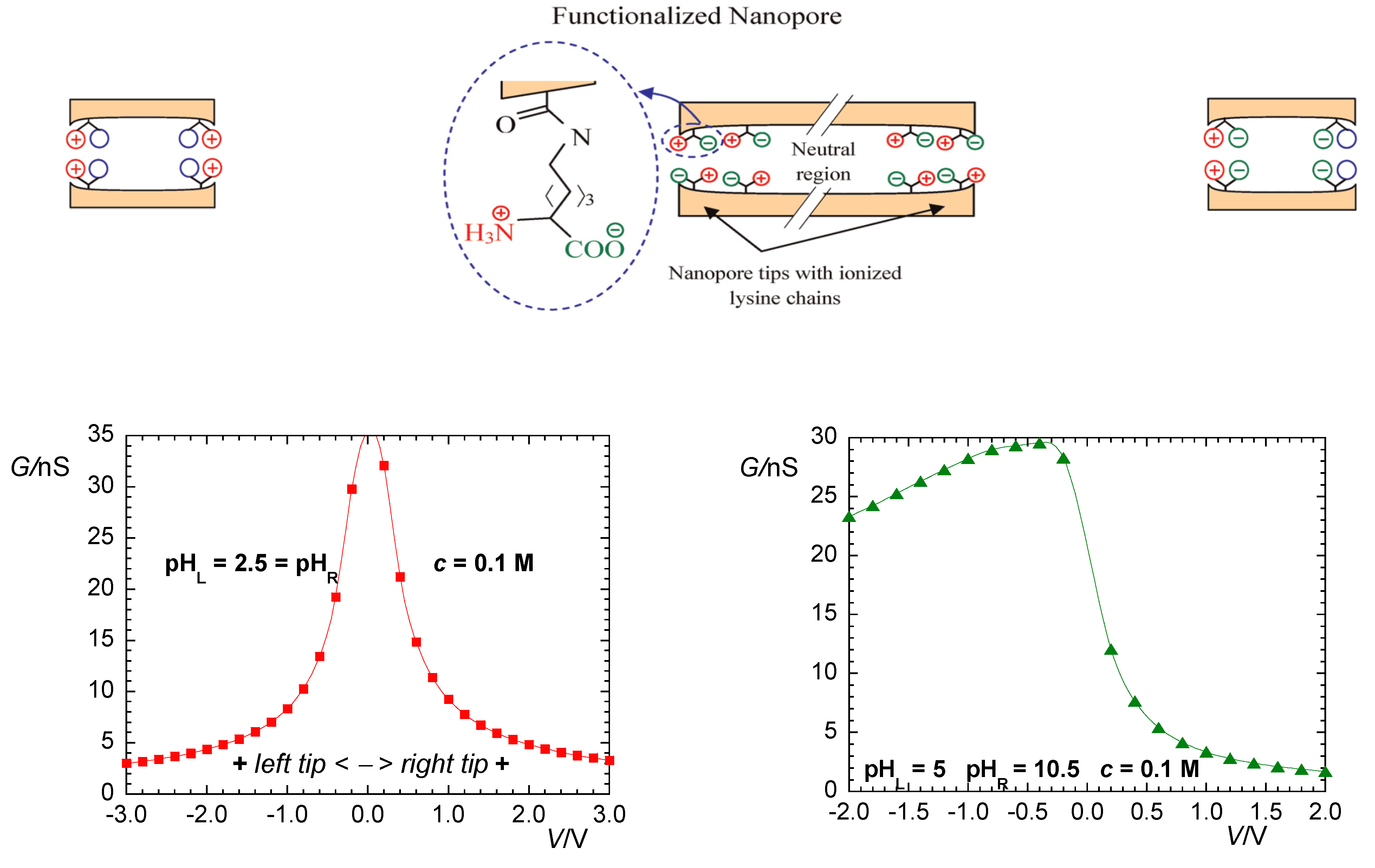
2. Biophysical Model
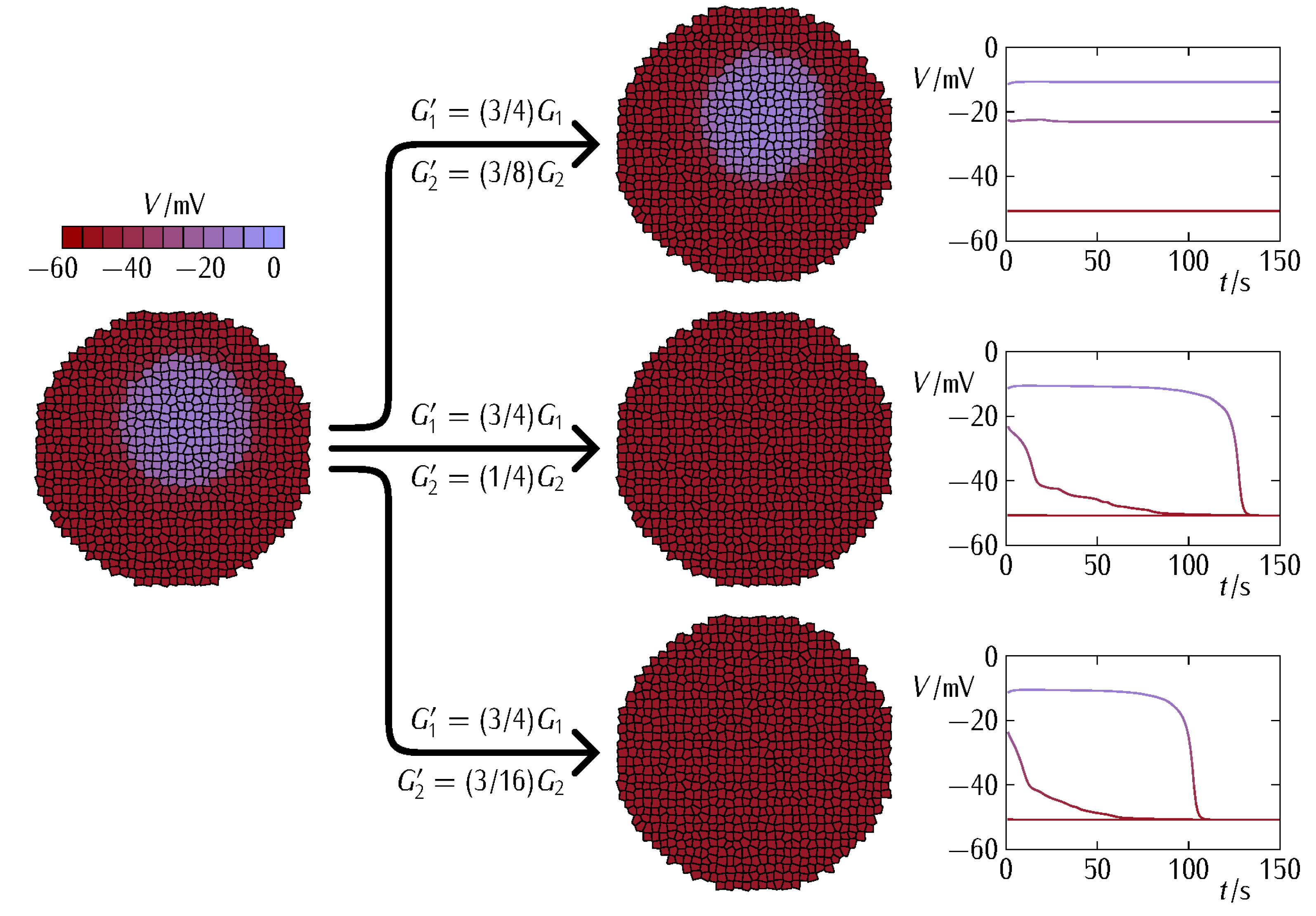
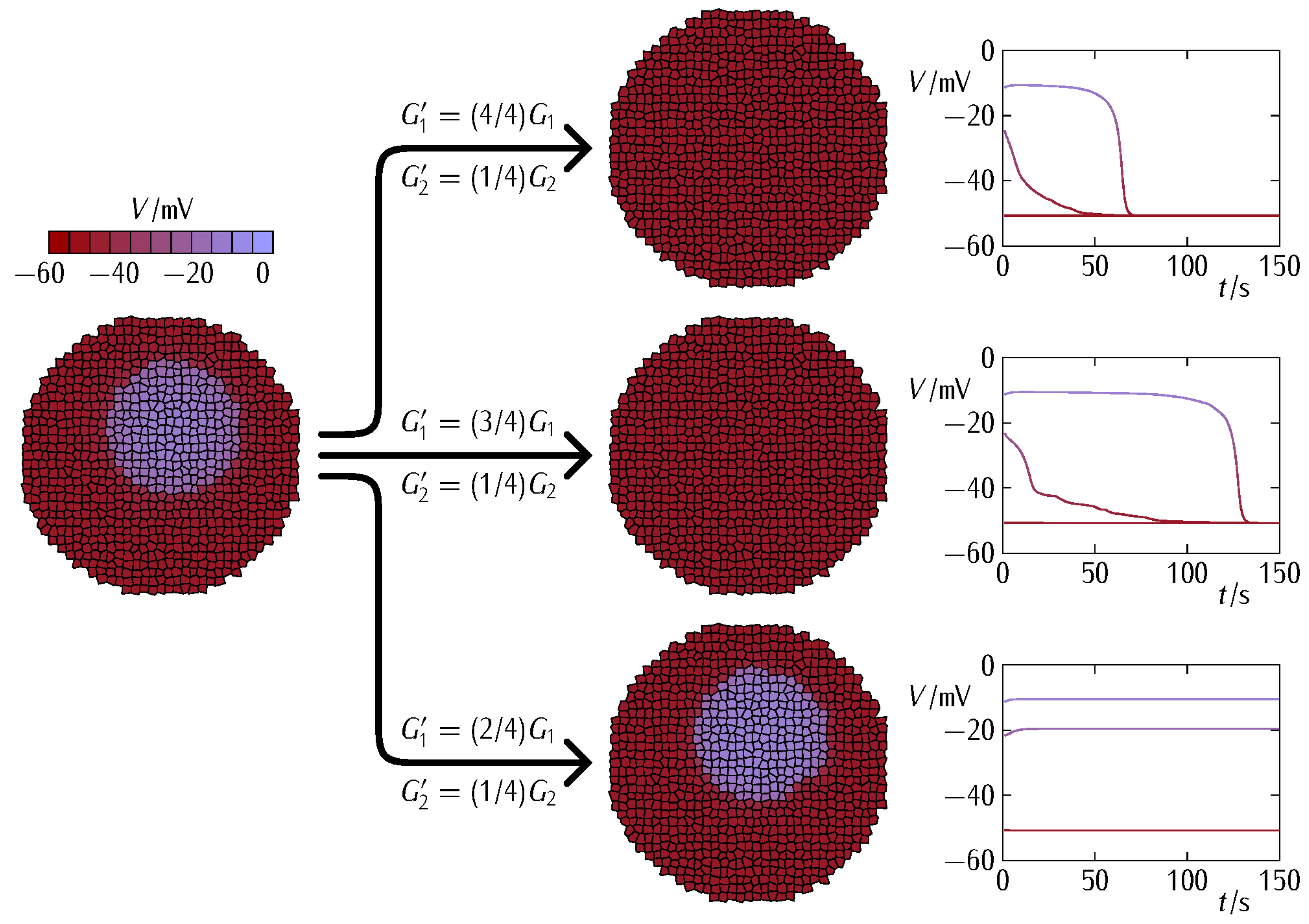
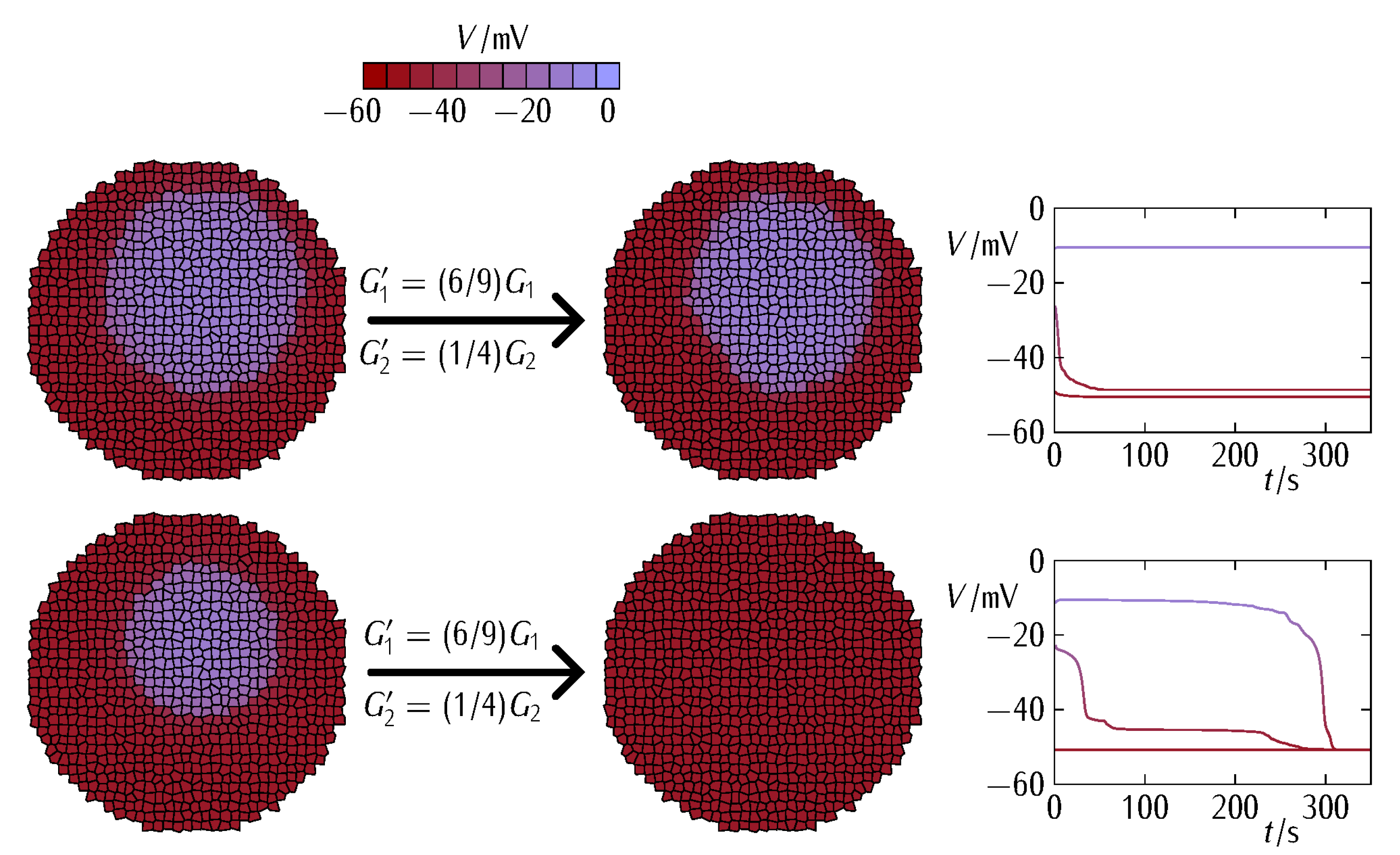
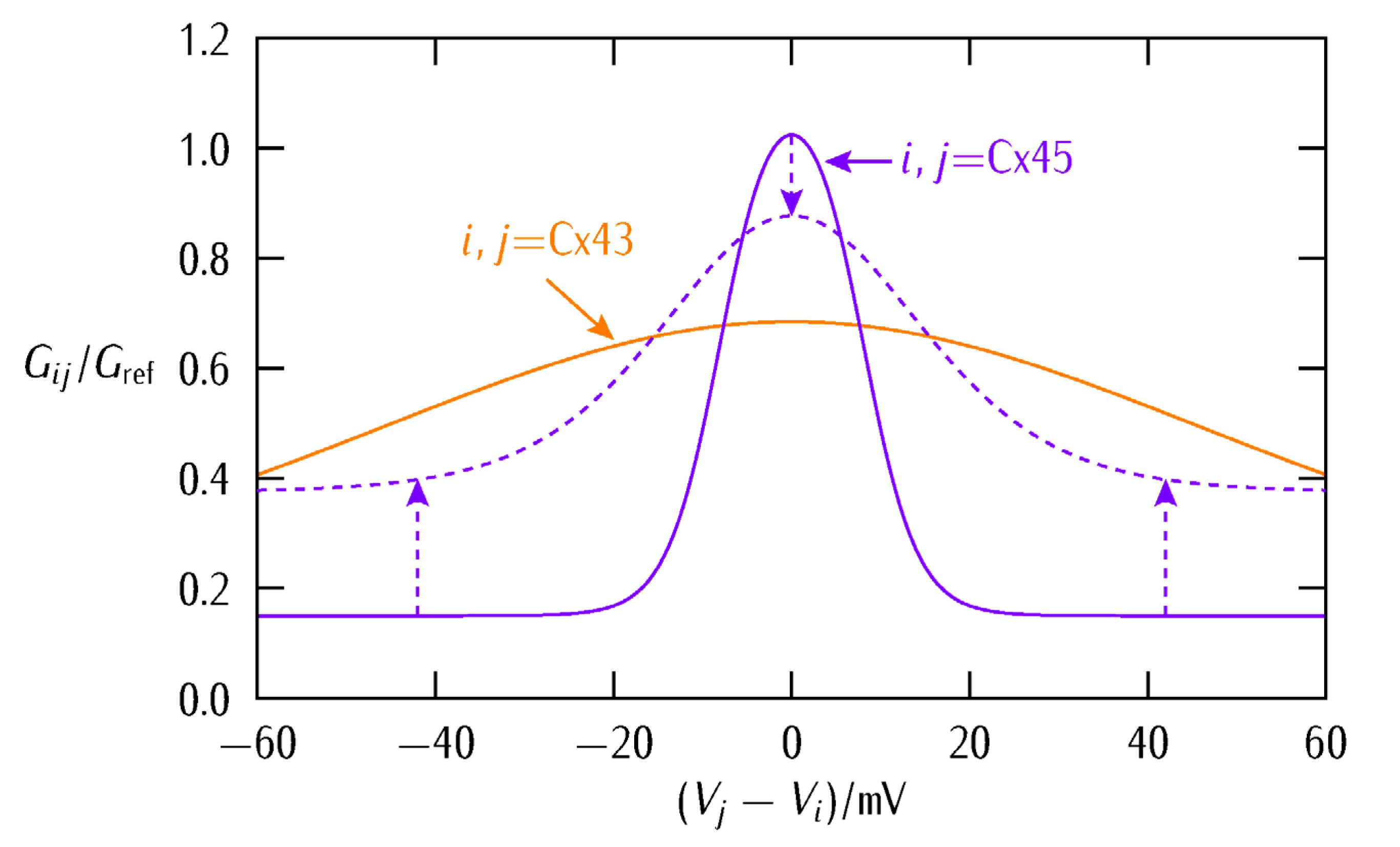
3. Results and Discussion
- (i)
- our approach is bioelectrical and focused only on the junctional effects. Other biochemical effects of connexin proteins are omitted here. For instance, these proteins may exchange specific small molecules between cells as well as between cells and the extracellular space. Thus, the outcomes associated with this exchange will depend not only on the conductive state of the junction but also on the particular signaling permeant being transferred between cells. Additionally, connexins can play non-junctional roles [49], mediating complex intracellular protein–protein interactions;
- (ii)
- although the loss of the intercellular junction communication could be an early event in tumorigenesis, there remains the possibility of gap junction restoration in more advanced tumor stages [35], with partial recovery of the community effect within the patch at later times. Thus, enhancing the intercellular gap junction communication may give different outcomes at distinct tumor time stages;
- (iii)
- gap junctions are also involved in biomechanical effects such as cell detachment and migration that are not accounted for in our bioelectrical model.
4. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Landge, A.N.; Jordan, B.M.; Diego, X.; Müller, P. Pattern formation mechanisms of self-organizing reaction-diffusion systems. Dev. Biol. 2020, 460, 2. [Google Scholar] [CrossRef] [PubMed]
- Leronni, A.; Bardella, L.; Dorfmann, L.; Pietak, A.; Levin, M. On the coupling of mechanics with bioelectricity and its role in morphogenesis. J. R. Soc. Interface 2020, 17, 177. [Google Scholar] [CrossRef]
- Mathews, J.; Levin, M. The body electric 2.0: Recent advances in developmental bioelectricity for regenerative and synthetic bioengineering. Curr. Opin. Biotechnol. 2018, 52, 134. [Google Scholar] [CrossRef] [PubMed]
- Cervera, J.; Pai, V.P.; Levin, M.; Mafe, S. From non-excitable single-cell to multicellular bioelectrical states supported by ion channels and gap junction proteins: Electrical potentials as distributed controllers. Prog. Biophys. Mol. Biol. 2019, 149, 39–53. [Google Scholar] [CrossRef]
- Cervera, J.; Levin, M.; Mafe, S. Bioelectrical Coupling of Single-Cell States in Multicellular Systems. J. Phys. Chem. Lett. 2020, 11, 3234–3241. [Google Scholar] [CrossRef] [PubMed]
- Gatenby, R.A.; Frieden, B.R. Cellular information dynamics through transmembrane flow of Ions. Sci. Rep. 2017, 7, 15075. [Google Scholar] [CrossRef]
- Sousounis, K.; Erdogan, B.; Levin, M.; Whited, J.L. Precise control of ion channel and gap junction expression is required for patterning of the regenerating axolotl limb. Int. J. Dev. Biol. 2020, 64, 485–494. [Google Scholar] [CrossRef]
- Vitali, I.; Fièvre, S.; Telley, L.; Oberst, P.; Bariselli, S.; Frangeul, L.; Baumann, N.; McMahon, J.J.; Klingler, E.; Bocchi, R.; et al. Progenitor Hyperpolarization Regulates the Sequential Generation of Neuronal Subtypes in the Developing Neocortex. Cell 2018, 174, 1264–1276. [Google Scholar] [CrossRef]
- Levin, M.; Pezzulo, G.; Finkelstein, J.M. Endogenous Bioelectric Signaling Networks: Exploiting Voltage Gradients for Control of Growth and Form. Annu. Rev. Biomed. Eng. 2017, 19, 353. [Google Scholar] [CrossRef] [PubMed]
- Mathews, J.; Levin, M. Gap junctional signaling in pattern regulation: Physiological network connectivity instructs growth and form. Dev. Neurobiol. 2017, 77, 643. [Google Scholar] [CrossRef]
- McNamara, H.M.; Zhang, H.; Werley, C.A.; Cohen, A.E. Optically Controlled Oscillators in an Engineered Bioelectric Tissue. Phys. Rev. X 2016, 6, 031001. [Google Scholar] [CrossRef]
- McNamara, H.M.; Salegame, R.; Tanoury, Z.A.; Xu, H.; Begum, S.; Ortiz, G.; Pourquie, O.; Cohen, A.E. Bioelectrical domain walls in homogeneous tissues. Nat. Phys. 2020, 16, 357. [Google Scholar] [CrossRef]
- Shi, W.; Yang, Y.; Gao, M.; Wu, J.; Tao, N.; Wang, S. Optical Imaging of Electrical and Mechanical Couplings between Cells. ACS Sens. 2021, 6, 508–512. [Google Scholar] [CrossRef] [PubMed]
- Hitomi, M.; Deleyrolle, L.P.; Mulkearns-Hubert, E.E.; Jarrar, A.; Li, M.; Sinyuk, M.; Otvos, B.; Brunet, S.; Flavahan, W.A.; Hubert, C.G.; et al. Differential Connexin Function Enhances Self-Renewal in Glioblastoma. Cell Rep. 2015, 11, 1031–1042. [Google Scholar] [CrossRef] [PubMed]
- Pai, V.P.; Cervera, J.; Mafe, S.; Willocq, V.; Lederer, E.K.; Levin, M. HCN2 channel-induced rescue of brain teratogenesis via local and long-range bioelectric repair. Front. Cell. Neurosci. 2020, 14, 136. [Google Scholar] [CrossRef] [PubMed]
- Bates, E. Ion channels in development and cancer. Annu. Rev. Cell Dev. Biol. 2015, 31, 231. [Google Scholar] [CrossRef]
- Levin, M. Bioelectric signaling: Reprogrammable circuits underlying embryogenesis, regeneration, and cancer. Cell 2021, 184, 1971. [Google Scholar] [CrossRef]
- Harris, M.P. Bioelectric signaling as a unique regulator of development and regeneration. Development 2021, 148, dev180794. [Google Scholar] [CrossRef]
- Vandenberg, L.N.; Morrie, R.D.; Adams, D.S. V-ATPase-dependent ectodermal voltage and pH regionalization are required for craniofacial morphogenesis. Dev. Dyn. 2011, 240, 1889. [Google Scholar] [CrossRef]
- Pai, V.P.; Lemire, J.M.; Paré, J.F.; Lin, G.; Chen, Y.; Levin, M. Endogenous gradients of resting potential instructively pattern embryonic neural tissue via Notch signaling and regulation of proliferation. J. Neurosci. 2015, 35, 4366. [Google Scholar] [CrossRef]
- Weiß, I.; Bohrmann, J. Electrochemical patterns during Drosophila oogenesis: Ion-transport mechanisms generate stage-specific gradients of pH and membrane potential in the follicle-cell epithelium. BMC Dev. Biol. 2019, 19, 12. [Google Scholar] [CrossRef]
- Pai, V.P.; Pietak, A.; Willocq, V.; Ye, B.; Shi, N.-Q.; Levin, M. HCN2 Rescues brain defects by enforcing endogenous voltage pre-patterns. Nat. Commun. 2018, 9, 998. [Google Scholar] [CrossRef]
- Durant, F.; Morokuma, J.; Fields, C.; Williams, K.; Adams, D.S.; Levin, M. Long-Term, Stochastic Editing of Regenerative Anatomy via Targeting Endogenous Bioelectric Gradients. Biophys. J. 2017, 112, 2231–2243. [Google Scholar] [CrossRef] [PubMed]
- Morokuma, J.; Blackiston, D.; Adams, D.S.; Seebohm, G.; Trimmer, B.; Levin, M. Modulation of potassium channel function confers a hyperproliferative invasive phenotype on embryonic stem cells. Proc. Natl. Acad. Sci. USA. 2008, 105, 16608–16613. [Google Scholar] [CrossRef] [PubMed]
- Chernet, B.T.; Levin, M. Transmembrane voltage potential is an essential cellular parameter for the detection and control of tumor development in a Xenopus model. Dis. Model. Mech. 2013, 6, 595. [Google Scholar] [CrossRef]
- Sheldon, R.E.; Mashayamombe, C.; Shi, S.-Q.; Garfield, R.E.; Shmygol, A.; Blanks, A.M.; van den Berg, H.A. Alterations in gap junction connexin43/connexin45 ratio mediate a transition from quiescence to excitation in a mathematical model of the myometrium. J. R. Soc. Interface 2014, 11, 20140726. [Google Scholar] [CrossRef] [PubMed]
- Cervera, J.; Manzanares, J.A.; Mafe, S.; Levin, M. Synchronization of Bioelectric Oscillations in Networks of Nonexcitable Cells: From Single-Cell to Multicellular States. J. Phys. Chem. B 2019, 123, 3924–3934. [Google Scholar] [CrossRef] [PubMed]
- Ma, B.; Buckalew, R.; Du, Y.; Kiyoshi, C.M.; Alford, C.C.; Wang, W.; McTigue, D.M.; Enyeart, J.J.; Terman, D.; Zhou, M. Gap Junction Coupling Confers Isopotentiality on Astrocyte Syncytium. Glial 2016, 64, 214–226. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, D. Connexin’s connection in breast cancer growth and progression. Int. J. Cell Biol. 2016, 2016, 9025905. [Google Scholar] [CrossRef]
- Mesnil, M.; Crespin, S.; Avanzo, J.L.; Zaidan-Dagli, M.L. Defective gap junctional intercellular communication in the carcinogenic process. Biochim. Biophys. Acta 2005, 1719, 125–145. [Google Scholar] [CrossRef]
- Capp, J.-P. Stochastic gene expression, disruption of tissue averaging effects and cancer as a disease of development. BioEssays 2005, 27, 1277–1285. [Google Scholar] [CrossRef]
- Aasen, T.; Mesnil, M.; Naus, C.C.; Lampe, P.D.; Laird, D.W. Gap junctions and cancer: Communicating for 50 years. Nat. Rev. Cancer 2016, 16, 775–788. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Liu, C.; Chen, A.; Yao, Z.; Li, W.; Xu, S.; Ma, X. Prognostic and Clinic Pathological Value of Cx43 Expression in Glioma: A Meta-Analysis. Front. Oncol. 2019, 9, 1209. [Google Scholar] [CrossRef]
- Sinyuk, M.; Mulkearns-Hubert, E.E.; Reizes, O.; Lathia, J. Cancer Connectors: Connexins, Gap Junctions, and Communication. Front. Oncol. 2018, 8, 646. [Google Scholar] [CrossRef]
- Phillips, S.L.; Williams, C.B.; Zambrano, J.N.; Williams, C.J.; Yeh, E.S. Connexin 43 in the development and progression of breast cancer: What’s the connection? Int. J. Oncol. 2017, 51, 1005–1013. [Google Scholar] [CrossRef]
- Cervera, J.; Ramirez, P.; Levin, M.; Mafe, S. Community effects allow bioelectrical reprogramming of cell membrane potentials in multicellular aggregates: Model simulations. Phys. Rev. E 2020, 102, 052412. [Google Scholar] [CrossRef] [PubMed]
- Hille, B. Ion Channels of Excitable Membranes; Sinauer Associates Inc.: Sunderland, MA, USA, 1992. [Google Scholar]
- Kirkton, R.D.; Bursac, N. Engineering biosynthetic excitable tissues from unexcitable cells for electrophysiological and cell therapy studies. Nat. Commun. 2011, 2, 300. [Google Scholar] [CrossRef]
- Cervera, J.; Alcaraz, A.; Mafe, S. Bioelectrical signals and ion channels in the modeling of multicellular patterns and caner biophysics. Sci. Rep. 2016, 6, 20403. [Google Scholar] [CrossRef]
- Chen-Izu, Y.; Moreno, A.P.; Spangler, R.A. Opposing gates model for voltage gating of gap junction channels. Am. J. Physiol. Cell Physiol. 2001, 281, C1604–C1613. [Google Scholar] [CrossRef] [PubMed]
- Desplantez, T.; Halliday, D.; Dupont, E.; Weingart, R. Cardiac connexins Cx43 and Cx45: Formation of diverse gap junction channels with diverse electrical properties. Pflugers Arch. 2004, 448, 363–375. [Google Scholar] [CrossRef]
- Ali, M.; Ramirez, P.; Mafe, S.; Neumann, R.; Ensinger, W. A pH-Tunable Nanofluidic Diode with a Broad Range of Rectifying Properties. ACS Nano 2009, 3, 603–608. [Google Scholar] [CrossRef]
- Ali, M.; Ramirez, P.; Nguyen, H.Q.; Nasir, S.; Cervera, J.; Mafe, S.; Ensinger, W. Single cigar-shaped nanopores functionalized with amphoteric amino acid chains: Experimental and theoretical characterization. ACS Nano 2012, 6, 3631–3640. [Google Scholar] [CrossRef] [PubMed]
- Cervera, J.; Meseguer, S.; Mafe, S. The interplay between genetic and bioelectrical signaling permits a spatial regionalisation of membrane potentials in model multicellular ensembles. Sci. Rep. 2016, 6, 35201. [Google Scholar] [CrossRef] [PubMed]
- Glen, C.M.; McDevitt, T.C.; Kemp, M.L. Dynamic intercellular transport modulates the spatial patterning of differentiation during early neural commitment. Nat. Commun. 2018, 9, 4111. [Google Scholar] [CrossRef] [PubMed]
- Glen, C.M.; Kemp, M.L.; Voit, E.O. Agent-based modeling of morphogenetic systems: Advantages and challenges. PLoS Comput. Biol. 2019, 15, e1006577. [Google Scholar] [CrossRef] [PubMed]
- Cervera, J.; Alcaraz, A.; Mafe, S. Membrane potential bi-stability in non-excitable cells as described by inward and outward voltage-gated ion channels. J. Phys. Chem. B 2014, 11, 12444–12450. [Google Scholar] [CrossRef]
- Yang, W.; Lampe, P.D.; Kensel-Hammes, P.; Hesson, J.; Ware, C.B.; Crisa, L.; Cirulli, V. Connexin 43 Functions as a Positive Regulator of Stem Cell Differentiation into Definitive Endoderm and Pancreatic Progenitors. iScience 2019, 19, 450. [Google Scholar] [CrossRef]
- Mulkearns-Hubert, E.E.; Reizes, O.; Lathia, J.D. Connexins in Cancer: Jekyll or Hyde? Biomolecules 2020, 10, 1654. [Google Scholar] [CrossRef] [PubMed]
- Hopperstad, M.G.; Srinivas, M.; Fort, A.; Spray, D.C. Gap junction mutations in human disease. Adv. Mol. Cell Biol. 2004, 32, 161–187. [Google Scholar]
- Tong, J.J.; Liu, X.; Dong, L.; Ebihara, L. Exchange of gating properties between rat cx46 and chicken cx45.6. Biophys. J. 2004, 87, 2397–2406. [Google Scholar] [CrossRef]
- Spray, D.C.; Schemes, E.; Rozental, R.; Dermietzel, R. Cell-Cell Communication: An Overview Emphasizing Gap Junctions. In From Molecules to Networks. An Introduction to Cellular and Molecular Neuroscience; Elsevier: Amsterdam, The Netherlands; Academic Press: Cambridge, MA, USA, 2004. [Google Scholar]
- McNamara, H.M.; Dodson, S.; Huang, Y.L.; Miller, E.W.; Sandstede, B.; Cohen, A.E. Geometry-Dependent Arrhythmias in Electrically Excitable Tissues. Cell Syst. 2018, 7, 359. [Google Scholar] [CrossRef] [PubMed]
- Ebrahimkhani, M.R.; Levin, M. Synthetic living machines: A new window on life. iScience 2021, 24, 102505. [Google Scholar] [CrossRef]
- Acardi, A. Lipids link ion channels and cancer. Membrane voltage connects lipid organization to cell proliferation. Science 2015, 349, 789–790. [Google Scholar]
- Churchill, C.D.M.; Winter, P.; Tuszynski, J.A.; Levin, M. Electroceutical Design Environment: An Ion Channel Database with Small Molecule Modulators and Tissue Expression Information. iScience 2019, 11, 42. [Google Scholar] [CrossRef]
- Soto, A.M.; Sonnenschein, C. The tissue organization field theory of cancer: A testable replacement for the somatic mutation theory. Bioessays 2011, 33, 332–340. [Google Scholar] [CrossRef]
- Aasen, T.; Leithe, E.; Graham, S.V.; Kameritsch, P.; Mayán, M.D.; Mesnil, M.; Pogoda, K.; Tabernero, A. Connexins in cancer: Bridging the gap to the clinic. Oncogene 2019, 38, 4429–4451. [Google Scholar] [CrossRef] [PubMed]
- Yang, M.; Brackenbury, W.J. Membrane potential and cancer progression. Front. Physiol. 2013, 4, 185. [Google Scholar] [CrossRef] [PubMed]
- Blackiston, D.J.; McLaughlin, K.A.; Levin, M. Bioelectric controls of cell proliferation: Ion channels, membrane voltage and the cell cycle. Cell Cycle 2009, 8, 3527–3536. [Google Scholar] [CrossRef]
- Urrego, D.; Tomczak, A.P.; Zahed, F.; Stühmer, W.; Pardo, L.A. Potassium channels in cell cycle and cell proliferation. Phil. Trans. R. Soc. B 2014, 369, 20130094. [Google Scholar] [CrossRef]
- Robinson, A.J.; Jain, A.; Sherman, H.G.; Hague, R.J.M.; Rahman, R.; Sanjuan-Alberte, P.; Rawson, F.J. Toward Hijacking Bioelectricity in Cancer to Develop New Bioelectronic Medicine. Adv. Therap. 2021, 4, 2000248. [Google Scholar] [CrossRef]
- Emmons-Bell, M.; Durant, F.; Hammelman, J.; Bessonov, N.; Volpert, V.; Morokuma, J.; Pinet, K.; Adams, D.S.; Pietak, A.; Lobo, D.; et al. Gap junctional blockade stochastically induces different species-specific head anatomies in genetically wild-type Girardia dorotocephala flatworms. Int. J. Mol. Sci. 2015, 16, 27865–27896. [Google Scholar] [CrossRef]
- Lazzari-Dean, J.R.; Gest, A.M.M.; Miller, E.W. Measuring Absolute Membrane Potential across Space and Time. Annu. Rev. Biophys. 2021, 50, 447–468. [Google Scholar] [CrossRef] [PubMed]
- Cervera, J.; Meseguer, S.; Mafe, S. MicroRNA Intercellular Transfer and Bioelectrical Regulation of Model Multicellular Ensembles by the Gap Junction Connectivity. J. Phys. Chem. B 2017, 121, 7602–7613. [Google Scholar] [CrossRef]
- Ribeiro, M.; Elghajiji, A.; Fraser, S.P.; Burke, Z.D.; Tosh, D.; Djamgoz, M.B.A.; Rocha, P.R.F. Human Breast Cancer Cells Demonstrate Electrical Excitability. Front. Neurosci. 2020, 14, 404. [Google Scholar] [CrossRef] [PubMed]
- Rao, V.R.; Perez-Neut, M.; Kaja, S.; Gentile, S. Voltage-Gated Ion Channels in Cancer Cell Proliferation. Cancers 2015, 7, 849–875. [Google Scholar] [CrossRef] [PubMed]
- Serrano-Novillo, C.; Capera, J.; Colomer-Molera, M.; Condom, E.; Ferreres, J.C.; Felipe, A. Implication of Voltage-Gated Potassium Channels in Neoplastic Cell Proliferation. Cancers 2019, 11, 287. [Google Scholar] [CrossRef]
- Griffin, M.; Khan, R.; Basu, S.; Smith, S. Ion Channels as Therapeutic Targets in High Grade Gliomas. Cancers 2020, 12, 3068. [Google Scholar] [CrossRef] [PubMed]
- Martins-Marques, T.; Ribeiro-Rodrigues, T.; Batista-Almeida, D.; Aasen, T.; Kwak, B.R.; Girao, H. Biological Functions of Connexin43 Beyond Intercellular Communication. Trends Cell Biol. 2019, 29, 835–847. [Google Scholar] [CrossRef]
- Palacios-Prado, N.; Huetteroth, W.; Pereda, A.E. Hemichannel composition and electrical synaptic transmission: Molecular diversity and its implications for electrical rectification. Front. Cell Neurosci. 2014, 8, 324. [Google Scholar] [CrossRef][Green Version]
- Galera-Laporta, L.; Comerci, C.J.; Garcia-Ojalvo, J.; Süel, G.M. IonoBiology: The functional dynamics of the intracellular metallome, with lessons from bacteria. Cell Syst. 2021, 12, 497–508. [Google Scholar] [CrossRef]
- Benninger, R.K.; Zhang, M.; Head, W.S.; Satin, L.S.; Piston, D.W. Gap junction coupling and calcium waves in the pancreatic islet. Biophys. J. 2008, 95, 5048–5061. [Google Scholar] [CrossRef] [PubMed]
- Loewenstein, W.R. Junctional cell-to-cell communication and growth control. Ann. N. Y. Acad. Sci. 1980, 339, 39–45. [Google Scholar] [CrossRef] [PubMed]
- Trosko, J.E. Gap junctional intercellular communication as a biological “Rosetta stone” in understanding, in a systems biological manner, stem cell behavior, mechanisms of epigenetic toxicology, chemoprevention and chemotherapy. J. Membr. Biol. 2007, 218, 93–100. [Google Scholar] [CrossRef]
- Kale, V.P.; Amin, S.G.; Pandey, M.K. Targeting ion channels for cancer therapy by repurposing the approved drugs. Biochim. Biophys. Acta. 2015, 1848, 2747–2755. [Google Scholar] [CrossRef] [PubMed]
- Tuszynski, J.; Tilli, T.M.; Levin, M. Ion Channel and Neurotransmitter Modulators as Electroceutical Approaches to the Control of Cancer. Curr. Pharm. Des. 2017, 23, 4827–4841. [Google Scholar] [CrossRef]
- Tseng, A.S.; Beane, W.S.; Lemire, J.M.; Masi, A.; Levin, M. Induction of vertebrate regeneration by a transient sodium current. J. Neurosci. 2010, 30, 13192–13200. [Google Scholar] [CrossRef] [PubMed]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Riol, A.; Cervera, J.; Levin, M.; Mafe, S. Cell Systems Bioelectricity: How Different Intercellular Gap Junctions Could Regionalize a Multicellular Aggregate. Cancers 2021, 13, 5300. https://doi.org/10.3390/cancers13215300
Riol A, Cervera J, Levin M, Mafe S. Cell Systems Bioelectricity: How Different Intercellular Gap Junctions Could Regionalize a Multicellular Aggregate. Cancers. 2021; 13(21):5300. https://doi.org/10.3390/cancers13215300
Chicago/Turabian StyleRiol, Alejandro, Javier Cervera, Michael Levin, and Salvador Mafe. 2021. "Cell Systems Bioelectricity: How Different Intercellular Gap Junctions Could Regionalize a Multicellular Aggregate" Cancers 13, no. 21: 5300. https://doi.org/10.3390/cancers13215300
APA StyleRiol, A., Cervera, J., Levin, M., & Mafe, S. (2021). Cell Systems Bioelectricity: How Different Intercellular Gap Junctions Could Regionalize a Multicellular Aggregate. Cancers, 13(21), 5300. https://doi.org/10.3390/cancers13215300






