1. Introduction
Rhabdomyosarcoma (RMS) is an aggressive and highly malignant form of sarcoma [
1,
2]. RMS is the most common soft tissue sarcoma in children and adolescents. RMS staging and risk grouping combines: age at diagnosis, size, and localization of the primary tumor, existence of metastatic lymph nodes and/or distant visceral or bone metastasis. Additional risk factors are complete resection and PAX/FOX01 fusion gene status [
3]. The principal treatment includes surgery for complete tumor removal, radiation therapy and systemic chemotherapy because of the high risk of metastasis. The main chemotherapy drugs used to treat patients with intermediate and high risk RMS are vincristine, actinomycin D, ifosfamide, etoposide, irinotecan, and doxorubicin [
4]. In Europe, the most commonly administered combination is ifosfamide, actinomycin D, and vincristine (IVA) [
5,
6]. Ifosfamide is an anti-neoplasic drug which acts by direct interaction on the DNA and inhibits the transcription and replication of the RNA. Principal adverse effects of ifosfamide are renal and urologic toxicity and neutropenia. Vincristine is an anti-mitotic cancer drug which blocks the cancer cell in metaphase and triggers its apoptosis. The principal adverse effect of vincristine is peripheral neuropathy. Actinomycin D is an antibiotic that inhibits the action of topoisomerase II, which is a type of enzyme that controls the changes in DNA structure inhibiting the activity of the cell. This drug inhibits the transcription of the DNA to RNA. The principal adverse effects of actinomycin D are haematological and digestive toxicities. The IVA protocol is administered every 21 days. The IVA protocol is active against a wide range of paediatric tumors, such as RMS and Ewing sarcomas. This treatment induces haematological toxicities, mainly neutropenia and thrombocytopenia. When not directly life-threatening, these toxicities impair the efficacy of the treatment, because they result in either reducing the chemotherapy dose or treatment discontinuation to allow the body to recover from these toxicities.
Building statistical models to describe the dynamics of blood cells upon IVA administration is appealing but challenging. Several modeling-based strategies have been developed over the last two decades to describe the chemotherapy-induced haematological toxicity, including both mathematical modeling [
7,
8,
9] and machine learning (ML). However, these two approaches are two distinct paradigms.
Mathematical modeling of chemotherapy-induced myelosuppression requires full quantitative representation of the main biological processes associated with haematopoiesis, such as the understanding of the chemotherapeutic drugs effects on the bone marrow [
10,
11,
12]. Using a semi-physiologic population pharmacokinetic-pharmacodynamic model to estimate the haematopoietic toxicity of carboplatin, Schmitt et al. proposed an optimal carboplatin target area under the curve as a function of pretreatment or concomitantly administered chemotherapies [
13]. A model proposed by Fornari et al. mimics the neutrophils maturation chain based on five compartments [
14].
On the other hand, machine learning focuses on how computers learn from data while using efficient algorithms—this implies that all relevant information must be included in the dataset. Artificial neural networks were implemented by Pella et al. to predict acute toxicity in organs at risk following prostate radiotherapy [
15]. In their work, Shibahara et al. have developed a machine learning approach to estimate nimustine hydrochloride induced myelosuppression through analysis of patient blood cell counts before treatment [
16]. In another study, Gunčar et al. have built two classifier models that predict haematologic disease while using a machine learning random forest algorithm and based on laboratory blood test results [
17]. Oyaga-Iriarte et al. implemented several machine learning classification algorithms that predict irinotecan toxicity grades in metastatic colorectal cancer while using demographic data, liver function tests, and tumor markers, combined with pharmacokinetic parameters [
18]. Machine learning can also be used for other purposes such as in depth analysis of medical imaging [
19,
20,
21]. In their work, Zacharaki et al. have developed a computer-assisted classification method that is based on support vector machines combining conventional MRI and perfusion MRI for distinguishing different types of brain tumors [
22].
Unlike mathematical modeling, the ML approach does not require in-depth understanding of the modeled phenomenon or process. In addition, a variety of machine learning algorithms are available as open source tools and libraries, such as the scikit-learn library in Python [
23]. For these reasons, the main objective of this work is to develop a machine learning model that would predict patients’ haematological toxicity in time, during an IVA chemotherapy cycle. Predicting the patient’s level of toxicity at the end of a cycle should allow clinicians to adapt the initial chemotherapy dose and avoid treatment delays due to severe neutropenia and/or thrombocytopenia. These models have been integrated in a web-based application, which could be used by clinicians to guide their decisions regarding chemotherapy dose adaptation.
2. Materials and Methods
2.1. Patients and Treatment Protocol
Patients selected in this retrospective study had histologically confirmed rhabdomyosarcoma. They were previously untreated, except for initial surgery/biopsy within eight weeks after the diagnosis. All twenty-four patients that were selected in this study were treated in the Paediatric Haematology and Oncology Department of La Timone Children’s Hospital in Marseille between 1995 and 2019. Selected patients had a minimum, maximum, and median age of 0.4, 15.4, and 5.5 years. They received up to nine cycles of IVA chemotherapy courses, as described in
Table 1, which possesses a non-mandatory part. Indeed, for the two first cycles of chemotherapy, vincristine was also given at day 8 and day 15. All patients from this study have been perfused with ifosfamide with the same protocol schema. Both parents systematically signed an informed consent. The children were also proposed to sign informed consent and would do so depending on their age and will to give consent. The Institutional Ethics Committee from the Marseille Public University Hospital System (Assistance Publique Hôpitaux de Marseille) approved the retrospective study.
2.2. Data Organization
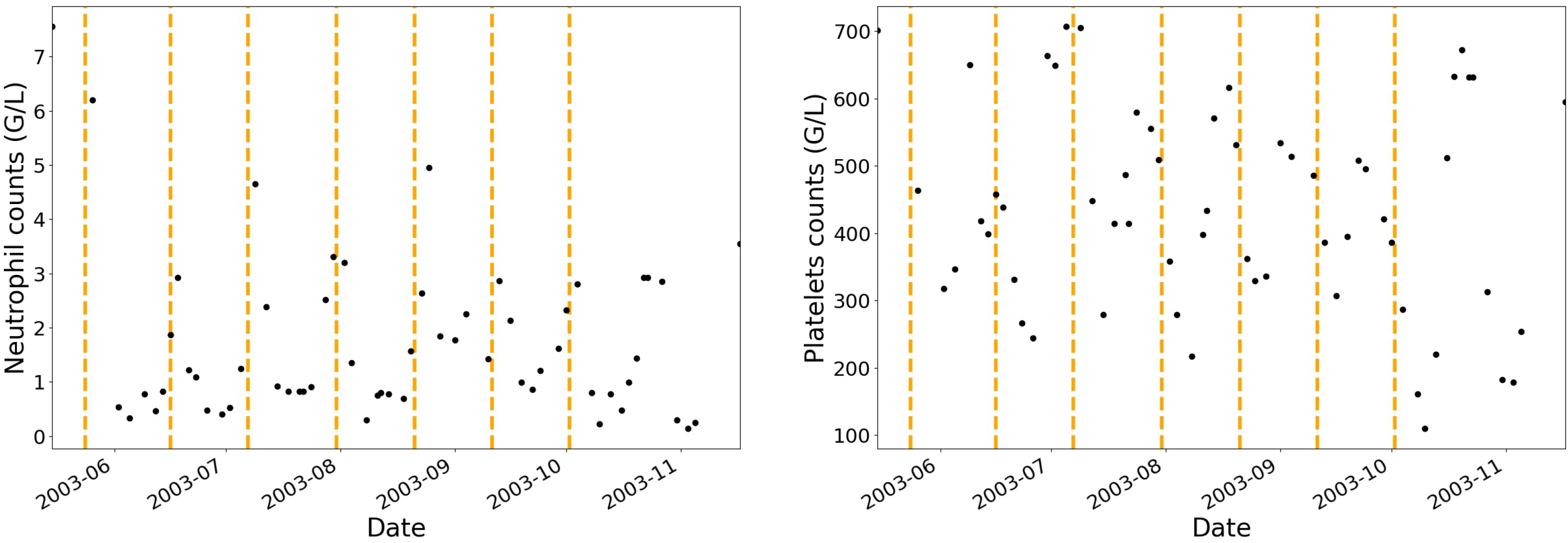
Administration protocols and haematological blood cell counts (i.e., neutrophils, platelets, monocytes, lymphocytes and leucocytes) have been collected for twenty-four patients. None of the patients have been treated with granulocyte-colony stimulating factor. Before and during each IVA cycle, multiple blood cell counts were performed allowing for a dynamic analysis of the haematological toxicities in patients as shown in
Figure 1 where the vertical dashed lines separate each treatment cycle.
The original data have been re-arranged in a tabular data structure with labeled axes for further manipulation, where each row corresponds to the patient’s result of a blood cell count at a particular date of the treatment. Due to multiple blood cell counts in each IVA cycle and the shape of the haematological toxicity profiles, the data have been interpolated at all additional days (dates) of the treatment where no blood tests have been performed in order to provide additional insight into the learning problem for supervised learning models. Common interpolation methods were tested, such as linear, polynomial, spline, and piecewise cubic hermite interpolating polynomial [
24]. The data (observed data plus additional data from interpolation) were finally grouped into individual dataframes, each corresponding to an IVA cycle number. Several information were added in the re-arranged dataset, such as the neutrophils and platelets initial values (measured at the beginning of each cycle), the patient’s weight, the ifosfamide dose normalized to the patient’s weight, and the number of days that has elapsed from the start of the cycle (i.e., cycle elapsed time in days, which is between 1 and 21). The neutrophils and platelets initial values were obtained either directly from the original data or computed at the cycle start date using the interpolation function (sometimes the blood test at the beginning of the cycle was performed one or two days prior to the chemotherapy treatment).
2.3. Regression Algorithms and Training Datasets
Since vincristine has no haematological toxicity and given the low haematological toxicity of actinomycin D in comparison to ifosfamide, only the ifosfamide induced haematological toxicity was modeled. The neutrophils and platelets levels were modeled at any time during a treatment cycle using the following features: initial values of neutrophils and platelets, the initial value of the ifosfamide dose normalized to the patient’s weight and the elapsed time in days in the cycle. To develop these models, we applied a machine learning technique on the interpolation-based resampled training dataset that corresponds to an IVA cycle. There is one training dataset per cycle that groups equivalent patients: the training dataset of cycle c contains all patients who underwent all c successive cycles. For the first four treatment cycles, the number of equivalent patients in the training datasets is 20, 12, 9, and 8, respectively, resulting in 431, 256, 210, and 197 haematological observations or instances after interpolation-based resampling. From the initial 24 patients, only 20 were included in the training dataset for cycle 1, because either a part of the haematological observations or the IVA doses were missing and could not be fully retrieved retrospectively.
In order to build the neutrophils and platelets predictive models, several regression techniques were tried, such as regularized linear models (Lasso, Ridge) and gradient boosted decision trees. Regularization techniques are used to deal with overfitting. Lasso (Ridge) regularization shrinks the regression coefficients by penalizing the regression model with a term called L1-norm (L2-norm), which is the sum of the absolute (squared) coefficients. For both of the methods, the constant that multiplies the penalty term and the maximum number of iterations were optimized using a grid search technique with the mean squared error as the scoring parameter that defines the model evaluation rules. On the other hand, the gradient boosting technique produces a composite model that combines the efforts of multiple weak prediction models (typically decision trees) to make a strong model. Each additional weak model reduces the mean squared error of the overall model. This boosting technique starts with a simple model
that gives an initial approximation of the target
y (e.g., neutrophils level) given the patient’s feature
x (e.g., dose normalized to the patient’s weight) and gradually goes towards the known target
y by adding one or more adjustments
:
The gradient boosting regressor parameters are tree and boosting specific.
Table 2 shows the list of parameters that were optimized while using the same technique as for Lasso and Ridge regressors. The input of each of these cycle-based regressors is a vector composed of the patient’s initial levels of neutrophils and platelets, the ifosfamide dose normalized to the patient’s weight and the cycle elapsed time in days. The output of the regressors is a scalar: neutrophils or platelets count. During the gradient boosting model’s parameters optimization, we applied the special process of early stopping, which monitors the model’s performance on a testing dataset (validation fraction was set to 0.3) and stops the training procedure once the performance on the testing dataset does not improve beyond a certain number of iterations. This technique avoids overfitting by finding the least number of iterations, which is sufficient to build a model that generalizes well to unseen data. Prediction performances (coefficients of determination
) were compared in order to choose between Lasso, Ridge, and gradient boosting regression algorithms.
2.4. Model Validation
To evaluate the performance of neutrophils and platelets estimators on new data, we tested them following a 10-fold cross validation procedure at the observation level. In addition, we performed a leave-one-out cross validation, where the regressor is trained on all od the evaluable data, except one patient, and a prediction is made for that patient. The training datasets are specific to the IVA cycle. Each validation was performed while using a set of optimized regression parameters.
The absolute errors between predicted and true haematological toxicity values were compared. For each patient (left out of the training dataset), the predicted neutrophils and platelets profiles were compared to the true profiles. Prediction intervals (PI) were provided as a way to quantify the accuracy of the predictions:
with
N the number of observables (number of patients in the training dataset) and
being equal to 1.64 and 1.96 for a significance level of 90% and 95%, respectively.
3. Results
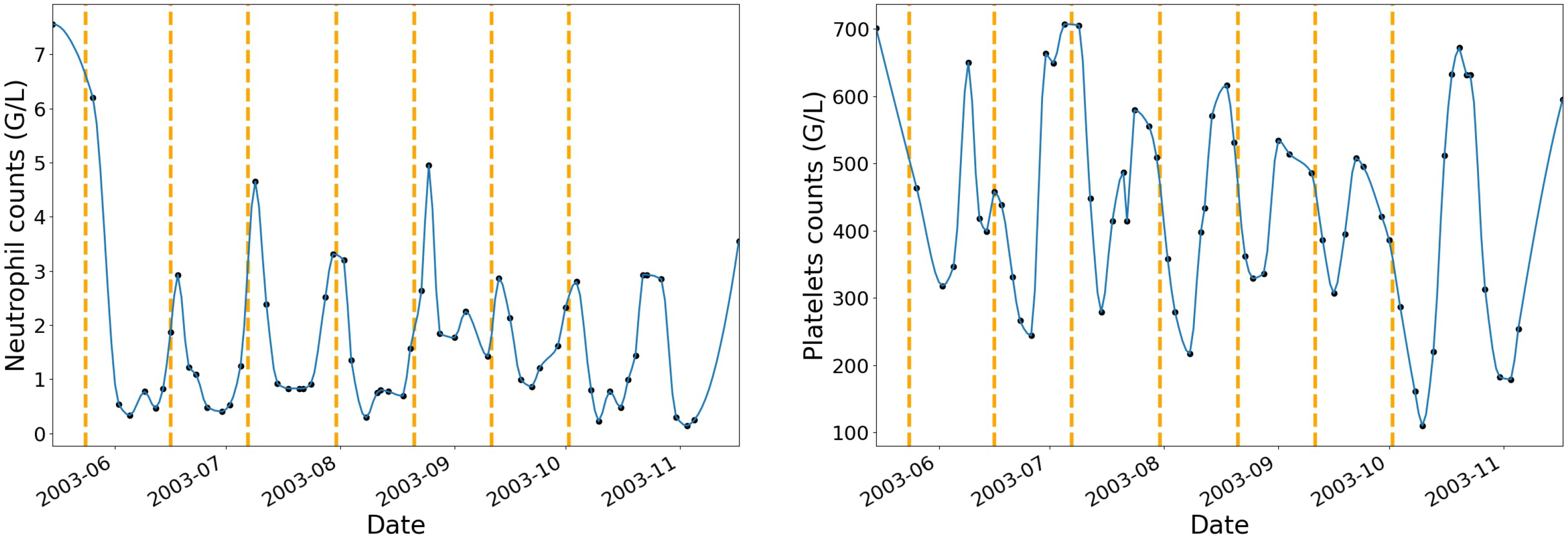
To begin with, neutrophils and platelets data have been interpolated at additional dates where no blood tests have been performed while using a piecewise cubic hermite interpolating polynomial.
Figure 2 shows an example of one patient’s neutrophils and platelets profiles after interpolation with vertical dashed lines that correspond to the beginning of each IVA treatment cycle.
The choice of the interpolating function was based on the review of the haematological toxicity dynamic profiles after interpolation. The piecewise cubic hermite interpolating polynomial (pchip) method gave more natural curves on the interpolated values when compared to linear, polynomial, or spline of order 2 and 3. For each chemotherapy cycle, the pchip interpolation augmentation method allowed for increasing the original dataset by 70%.
Subsequently, regularized linear and gradient boosting regressors were trained on the interpolated resampled data. To avoid overfitting, the number of iterations for each regressor was optimized by finding the least number of iterations, which is sufficient for building a model that generalizes well to unseen data. The performances of Lasso, Ridge, and gradient boosting models are summarized in
Table 3, where the mean prediction performances (
) across the three models are shown along with the difference of
in the training and testing datasets following a 10-fold cross validation procedure at the observation level. For the first four treatment cycles, optimized gradient boosting regressors yielded mean
values that were greater than 0.74 for neutrophils and 0.84 for platelets. The mean differences of
values in the training and testing data were smaller than 0.17 and 0.12 for neutrophils and platelets, respectively. We found that the gradient boosting model was associated to the highest coefficient of determination on randomly split training and testing samples.
Accordingly to this result and for the first four cycles of the IVA treatment, neutrophils and platelets dynamic profiles have been modeled using cycle specific training datasets and optimized gradient boosting regression parameters.
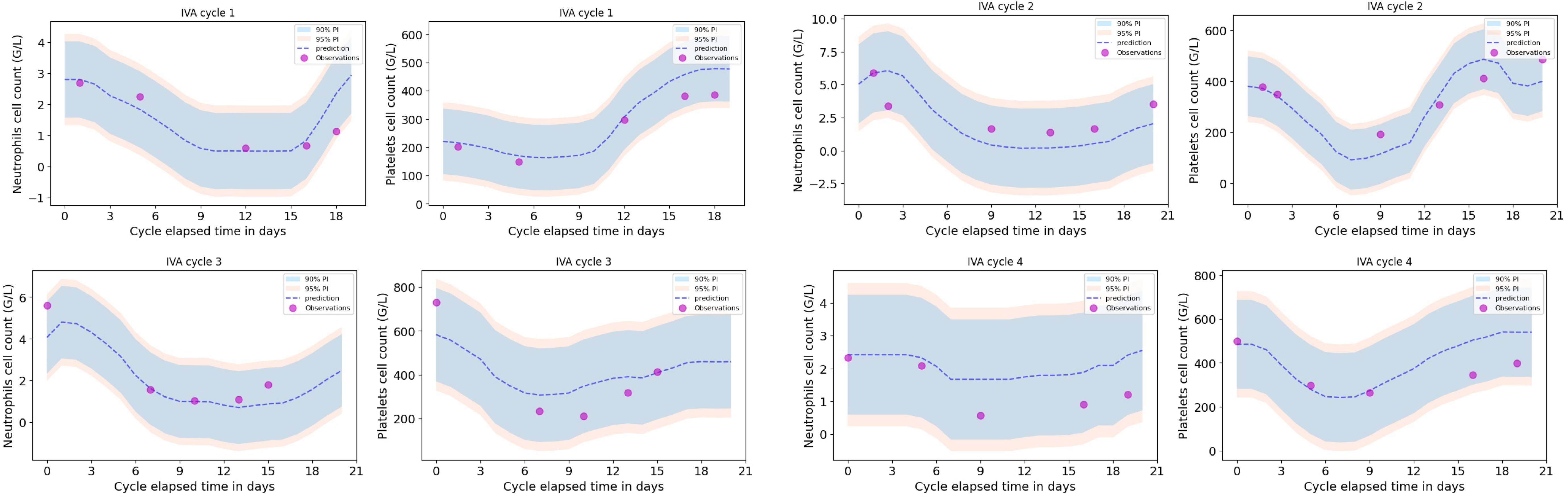
A leave-one-out cross validation was performed, as shown in
Figure 3 for one particular patient (the one removed from the training dataset) for the first four treatment cycles. Neutrophils and platelets dynamic profiles were compared to the predictions for that particular patient together with the 90% and 95% prediction intervals.
Table 4 summarizes all of the results of the leave-one-out cross validation in terms of the median value (over one cycle) together with the interquartile range of the error between predicted and true values of the blood cell counts (
) for each patient that was removed from the dataset on which the regression model was trained. A negative error illustrates that the model under-estimates the toxicity level.
Table 5 shows the mean absolute errors and associated standard deviations for each of the four first treatment cycles, computed from the leave-one-out cross validation results shown in
Table 4. Among all four treatment cycles, the mean errors (in absolute value) between predicted and observed neutrophils and platelets levels are 1.0 and 72.8 G/L, respectively. Assuming that the absolute error between predicted and true haematological toxicity is a reasonable prediction evaluation metric, the magnitude of these errors give an idea of how good the predictions are for new patients. Among the first four cycles, the errors are small from the point of view of an oncologist reviewing neutrophil and platelet levels of patients under chemotherapy.
Web-Based Application
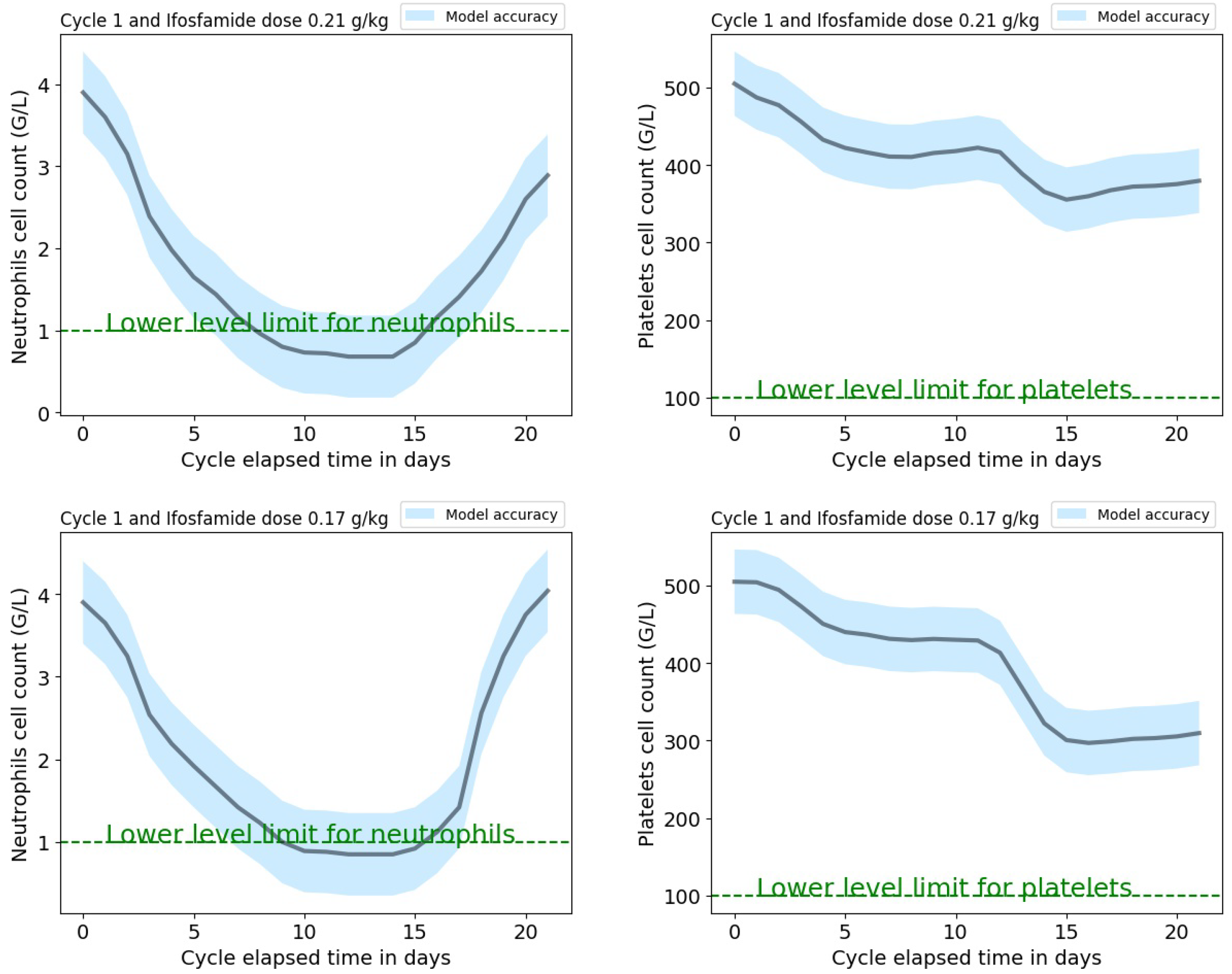
A web-based application has been developed with a Python 3.0 kernel and it will be available on the pythonanywhere platform. The application interface requires the following input parameters: the treatment cycle (between 1 and 4), the initial neutrophils and platelets cell counts, and the ifosfamide dose normalized to the patient’s weight from the protocol. Input parameters values should be within the range that corresponds to these parameters from the cycle-dependent dataset used to train the models. The application provides the predictions of the new patient’s neutrophils and platelets dynamic profiles, as shown in
Figure 4 with the corresponding mean absolute error (which is cycle dependent) extracted from the validation procedure and shown in
Table 5. These predictions could help the clinician to tailor the patient’s protocol by modifying the initial ifosfamide dose normalized to the patient’s weight or administer granulocyte growth factors to avoid unacceptably low levels of neutrophils or platelets at the end of an IVA cycle.
4. Discussion
In the attempt to anticipate chemotherapy induced haematologic toxicity, we have computed a machine learning based model that could accurately predict blood cell count dynamics in individual paediatric patients, with rhabdomyosarcoma receiving the IVA chemotherapy course.
The interpolation augmentation method that was used to resample the original data has some limitations, as it may be dependent on the number of observations per patient. The error on the additional observations where no blood tests have been performed would be larger for patients with less observation points. On average, the number of haematological observations per patient per cycle of 21 days is 6, which corresponds to a blood test every 3.5 days. We believe that the unimodal shape of the neutrophils or platelets profiles (aplasia usually followed by the recovery of normal blood counts) is an advantage for the interpolation procedure.
For consistency, the data used to compute the models were composed of patients who did not skip a cycle of treatment making sure that the haematological toxicity levels were not biased by recovered neutrophils and platelets levels due to a chemotherapy break. The size of the training dataset decreases with the cycle number, leading to larger errors on the toxicities predictions; therefore, both models must be updated and saved as new data are acquired.
A non-ML model, such as the autoregressive integrated moving average (ARIMA), could bring some interesting insights to our problem but is limited to a single time series, unless more complex models are pieced together. Informations about the initial levels of neutrophils or platelets and the ifosfamide dose cannot be easily integrated in an ARIMA model. With ML models, multiple series can be estimated within the same framework providing additional reason for the use of ML in this study. Indeed, seasonal and non-seasonal ARIMA models are powerful, as long as the model’s parameters are well configured.
Our neutrophil models are trained on patients who were not injected with growth factors (i.e., GCSF). The use of these growth factors changes the patient’s neutrophil profile; therefore, neutrophil level predictions for a new patient under GCSF might be under-estimated with our model. Patients demographics, such as age and gender, were not added as features in our models because these informations were not always known for each patient in this retrospective study. On the other hand, patient’s gender does not appear to be involved in the ifosfamide metabolism or toxicity [
25]. In future work with additional data and an investigation to retrieve the missing information from the initial cohort, new covariates will be incorporated in our models, such as age, the use of granulocyte growth factors, and pharmacogenetic markers.
This work is a proof of concept that shows the potential use of neutropenia and thrombocytopenia predictions on ifosfamide dose adjustment for patients with significant reductions in neutrophil or platelet counts, which, if not anticipated, could cause a delay in their subsequent chemotherapy administrations and compromise their treatment outcome. With our ML models—which are available on our online application—neutrophil and platelet counts could be predicted over the course of a chemotherapy cycle based on different ifosfamide doses. This offers the possibility to adjust the ifosfamide dose, which enables personalized treatment of patients undergoing chemotherapy. Indeed, therapy related toxicities have been negatively associated with outcome and survival [
26].
In the near future, we hope to collaborate with more institutions and convince them to provide and gather more data in order to update our predictive models and improve their accuracy. These updated models will be validated while using an independent cohort of patients with intermediate or high risk rhabdomyosarcoma and then tested prospectively through a clinical trial. The web application will greatly facilitate this testing in a multi-center setting. Once, these steps have been completed, the application could be proposed to a collaborative paediatric sarcoma group to test ifosfamide dose adjustment based on the prediction of our models. The models could also be further tested and calibrated on patients with Ewing sarcoma who also receive IVA courses.
Data and Code Availability
The data that support the findings of this study are available on the public repository figshare upon reasonable request. The analysis was developed on a Jupyter notebook with a Python 3.0 kernel. A series of free and open source Python libraries were utilized, such as SciPy for scientific computing, scikit-learn for machine learning, and the multiprocessing module in order to make best use of all CPU cores [
23]. The code for data processing, including interpolation, gradient boosting regression model parameters optimization, and validation, are available on the GitHub platform upon demand.
5. Conclusions
We used a machine learning technique with a gradient boosting regressor to model haematological toxicities in patients with rhabdomyosarcoma treated with several cycles of IVA chemotherapy. Our results show, with a good accuracy, that it is possible to forecast the neutrophils and platelets profiles for a new patient when providing the model with the neutrophils and platelets initial values together with the initial value of the ifosfamide dose normalized to the patient’s weight. This work could be extended to other chemotherapy treatments and/or pathologies.
Author Contributions
Conceptualization, N.A. and V.C.; Methodology, V.C.; Software, V.C.; Validation, V.C.; Formal Analysis, V.C.; Resources, N.A.; Writing—Original Draft Preparation, V.C.; Writing Review and Editing. N.A. and V.C.; Visualization, V.C.; Supervision N.A. and V.C.; Project Administration, N.A.; Funding Acquisition, N.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors would like to thank LN13 La Vie for their support and Sylvie Abed the clinical research associate from La Timone Children’s Hospital who collected all patient data used in this retrospective study. The authors thank Jean Gaudart from the SESSTIM Aix-Marseille University for his advice regarding statistical tests. The authors thank Daniel Orbach from the Institut Curie and Joseph Ciccolini from the Cancer Research Center of Marseille for their rigorous reading of this manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sun, X.; Guo, W.; Shen, J.K.; Mankin, H.J.; Hornicek, F.J.; Duan, Z. Rhabdomyosarcoma: Advances in Molecular and Cellular Biology. Sarcoma 2015, 232010. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Parham, D.M.; Barr, F.G. Classification of rhabdomyosarcoma and its molecular basis. Adv. Anat. Pathol. 2013, 20, 387–397. [Google Scholar] [CrossRef] [PubMed]
- Skapek, S.X.; Anderson, J.; Barr, F.G.; Bridge, J.A.; Gastier-Foster, J.M.; Parham, D.M.; Rudzinski, E.R.; Triche, T.; Hawkins, D.S. PAX-FOXO1 Fusion Status Drives Unfavorable Outcome for Children With Rhabdomyosarcoma: A Children’s Oncology Group Report. Pediatr. Blood Cancer 2013, 60, 1411–1417. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Egas-Bejar, D.; Huh, W.W. Rhabdomyosarcoma in adolescent and young adult patients: Current perspectives. Adolesc. Health Med. Ther. 2014, 5, 115–125. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, C.; Dorado Garcia, H.; Scheer, M.; Henssen, A.G. Current and Future Treatment Strategies for Rhabdomyosarcoma. Front. Oncol. 2019, 9, 1458. [Google Scholar] [CrossRef]
- PDQ® Pediatric Treatment Editorial Board. PDQ Childhood Rhabdomyosarcoma Treatment. National Cancer Institute. Available online: https://www.cancer.gov/types/soft-tissue-sarcoma/hp/rhabdomyosarcoma-treatment-pdq (accessed on 13 October 2019).
- Benzekry, S.; Lamont, C.; Beheshti, A.; Tracz, A.; Ebos, J.M.L.; Hlatky, L.; Hahnfeldt, P. Classical Mathematical Models for Description and Prediction of Experimental Tumor Growth. PLoS Comput. Biol. 2014, 10, e1003800. [Google Scholar] [CrossRef] [Green Version]
- Barbolosi, D.; Ciccolini, J.; Lacarelle, B.; Barlési, F.; André, N. Computational oncology—mathematical modelling of drug regimens for precision medicine. Nat. Rev. Clin. Oncol. 2016, 13, 242–254. [Google Scholar] [CrossRef]
- De Vries Schultink, A.H.M.; Suleiman, A.A.; Schellens, J.H.M.; Beijnen, J.H.; Huitema, A.D.R. Pharmacodynamic modeling of adverse effects of anti-cancer drug treatment. Eur. J. Clin. Pharmacol. 2016, 72, 645–653. [Google Scholar] [CrossRef] [Green Version]
- Meille, C.; Iliadis, A.; Barbolosi, D.; Frances, N.; Freyer, G. An interface model for dosage adjustment connects hematotoxicity to pharmacokinetics. J. Pharmacokinet. Pharmacodyn. 2008, 35, 619–633. [Google Scholar] [CrossRef]
- Friberg, L.E.; Henningsson, A.; Maas, H.; Nguyen, L.; Karlsson, M.O. Model of chemotherapy-induced myelosuppression with parameter consistency across drugs. J. Clin. Oncol. 2002, 20, 4713–4721. [Google Scholar] [CrossRef]
- Netterberg, I.; Nielsen, E.I.; Friberg, L.E.; Karlsson, M.O. Model-based prediction of myelosuppression and recovery based on frequent neutrophil monitoring. Cancer Chemother Pharmacol. 2017, 80, 343–353. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schmitt, A.; Gladieff, L.; Laffont, C.M.; Evrard, A.; Boyer, J.-C.; Lansiaux, A.; Bobin-Dubigeon, C.; Etienne-Grimaldi, M.-C.; Boisdron-Celle, M.; Mousseau, M.; et al. Factors for hematopoietic toxicity of carboplatin: Refining the targeting of carboplatin systemic exposure. J. Clin. Oncol. 2010, 28, 4568–4574. [Google Scholar] [CrossRef] [Green Version]
- Fornari, C.; O’Connor, L.O.; Yates, J.W.T.; Cheung, S.Y.A.; Jodrell, D.I.; Mettetal, J.T.; Collins, T.A. Understanding Hematological Toxicities Using Mathematical Modeling. Clin. Pharmacol. Ther. 2018, 104, 644–654. [Google Scholar] [CrossRef] [PubMed]
- Pella, A.; Cambria, R.; Riboldi, M.; Jereczek-Fossa, B.A.; Fodor, C.; Zerini, D.; Torshabi, A.E.; Cattani, F.; Garibaldi, C.; Pedroli, G.; et al. Use of machine learning methods for prediction of acute toxicity in organs at risk following prostate radiotherapy. Med. Phys. 2011, 138, 2859–2867. [Google Scholar] [CrossRef] [PubMed]
- Shibahara, T.; Ikuta, S.; Muragaki, Y. Machine learning approach for modeling myelosuppression attributed to nimustine hydrochloride. JCO Clin. Cancer Inform. 2018, 2, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Gunčar, G.; Kukar, M.; Notar, M.; Brvar, M.; Černelč, P.; Notar, M.; Notar, M. An application of machine learning to haematological diagnosis. Sci. Rep. 2018, 8, 411. [Google Scholar] [CrossRef]
- Oyaga-Iriarte, E.; Insausti, A.; Sayar, O.; Aldaz, A. Prediction of irinotecan toxicity in metastatic colorectal cancerpatients based on machine learning models with pharmacokineticparameters. J. Pharmacol. Sci. 2019, 140, 20–25. [Google Scholar] [CrossRef]
- Kourou, K.; Exarchos, T.P.; Exarchos, K.P.; Karamouzis, M.V.; Fotiadis, D.I. Machine learning applications in cancer prognosis and prediction. Comput. Struct. Biotechnol. J. 2015, 13, 8–17. [Google Scholar] [CrossRef] [Green Version]
- Esteva, A.; Kuprel, B.; Novoa, R.A.; Ko, J.; Swetter, S.M.; Blau, H.M.; Thrun, S. Dermatologist-level classification of skin cancer with deep neural networks. Nature 2017, 542, 115–118. [Google Scholar] [CrossRef]
- Shen, L.; Margolies, L.R.; Rothstein, J.H.; Fluder, E.; McBride, R.; Sieh, W. Deep Learning to Improve Breast Cancer Detection on Screening Mammography. Sci. Rep. 2019, 9, 12495. [Google Scholar] [CrossRef]
- Zacharaki, E.I.; Wang, S.; Chawla, S.; Yoo, D.S.; Wolf, R.; Melhem, E.R.; Davatzikos, C. Classification of brain tumor type and grade using MRI texture and shape in a machine learning scheme. Magn. Reson. Med. 2009, 62, 1609–1618. [Google Scholar] [CrossRef] [Green Version]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Fritsch, F.N.; Butland, J. A method for constructing local monotone piecewise cubic interpolants. SIAM J. Sci. Comput. 1984, 5, 300–304. [Google Scholar] [CrossRef] [Green Version]
- Boddy, A.V.; Yule, S.M.; Wyllie, R.; Price, L.; Pearson, A.D.; Idle, J.R. Pharmacokinetics and metabolism of ifosfamide administered as a continuous infusion in children. Cancer Res. 1993, 53, 3758–3764. [Google Scholar] [PubMed]
- Gupta, A.A.; Anderson, J.R.; Pappo, A.S.; Spunt, S.L.; Dasgupta, R.; Indelicato, D.J.; Hawkins, D.S. Patterns of chemotherapy-induced toxicities in younger children and adolescents with rhabdomyosarcoma: A report from the Children’s Oncology Group Soft Tissue Sarcoma Committee. Cancer 2012, 118, 1130–1137. [Google Scholar] [CrossRef] [PubMed] [Green Version]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).