Frequency Tuning of Graphene Nanoelectromechanical Resonators via Electrostatic Gating
Abstract
1. Introduction
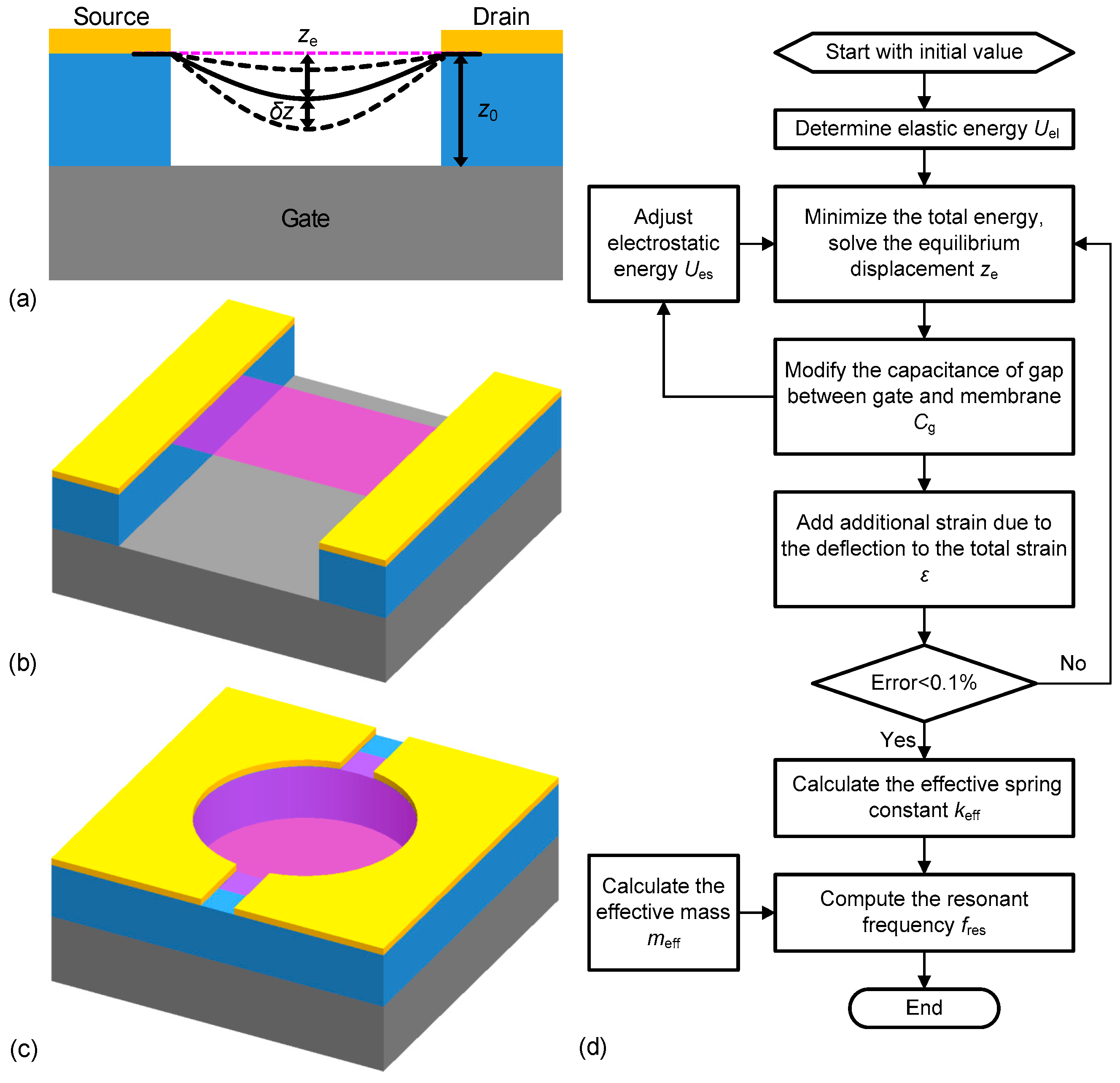
2. Analytical Model and Computational Methods
2.1. Development of Frequency Tuning Model and Analysis Procedure
2.2. Frequency Tuning of Doubly Clamped Graphene Resonator
2.3. Circumference-Clamped Circular Membrane
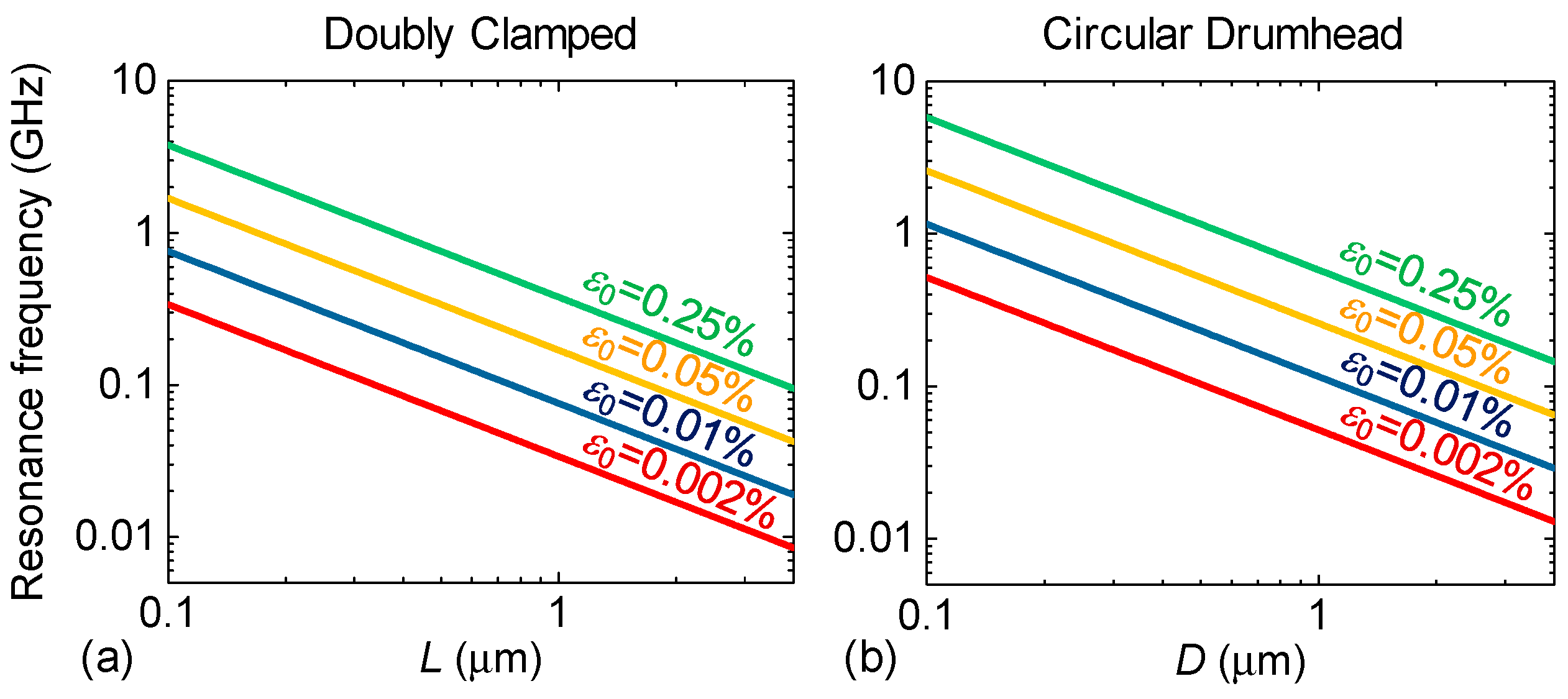
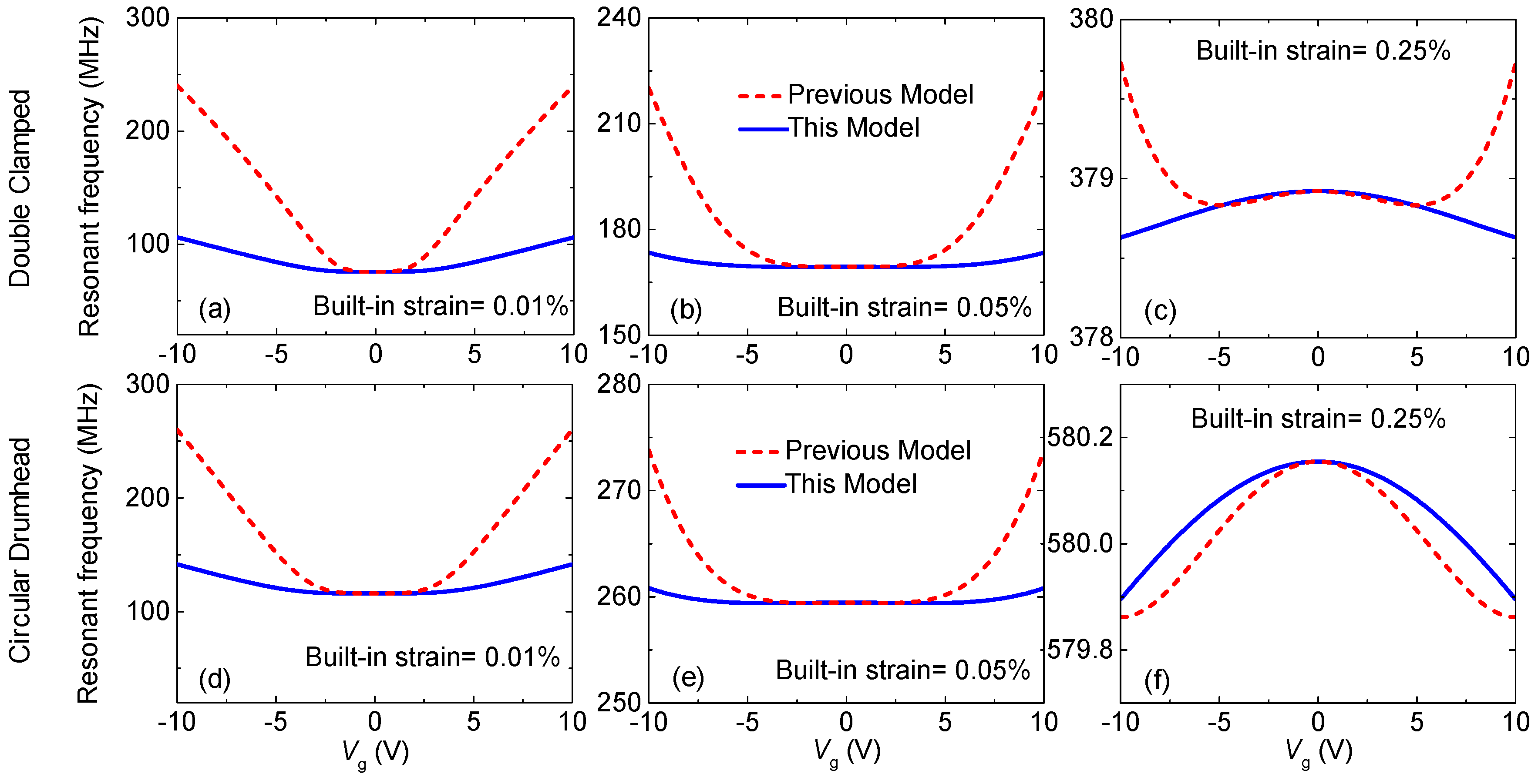
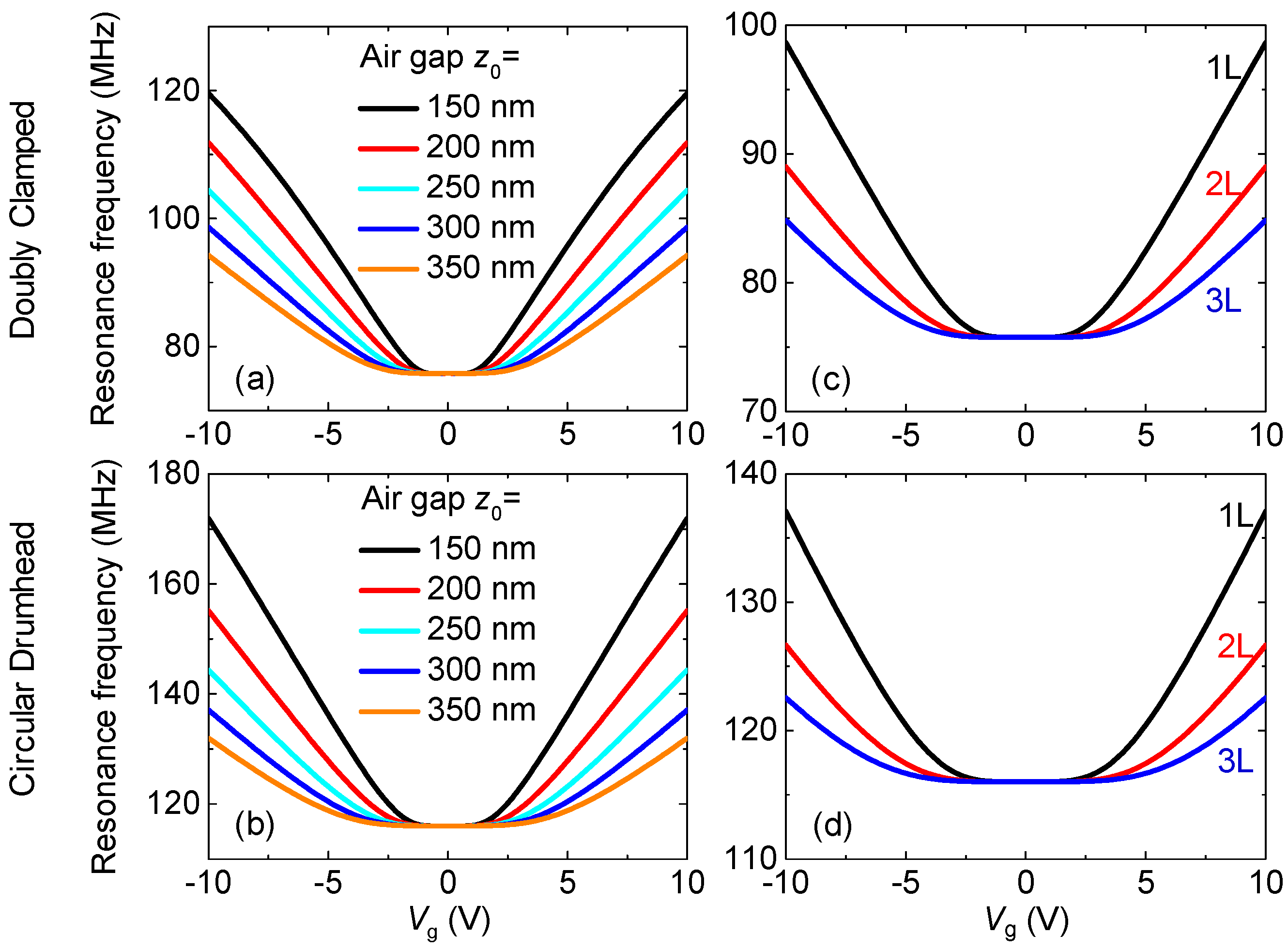
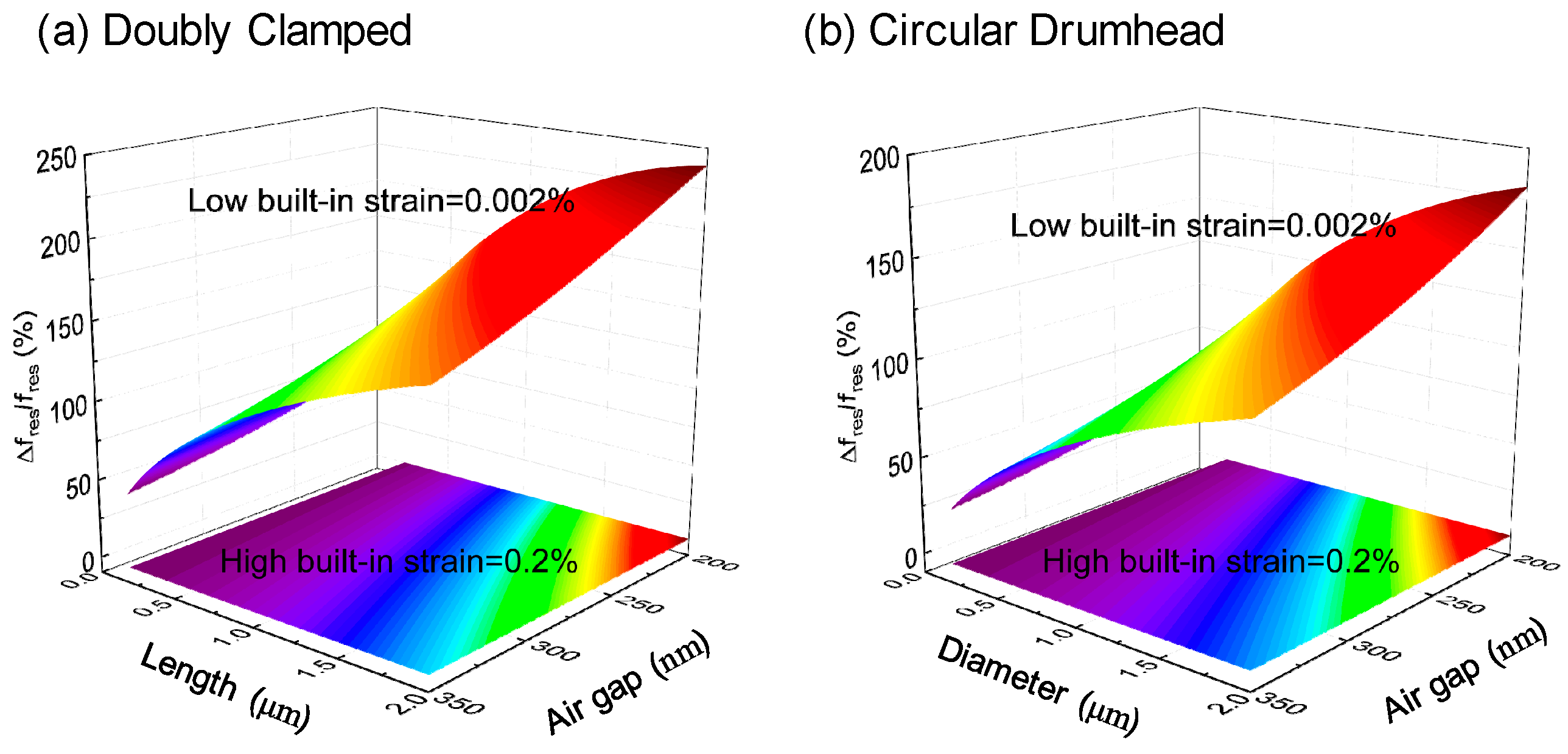
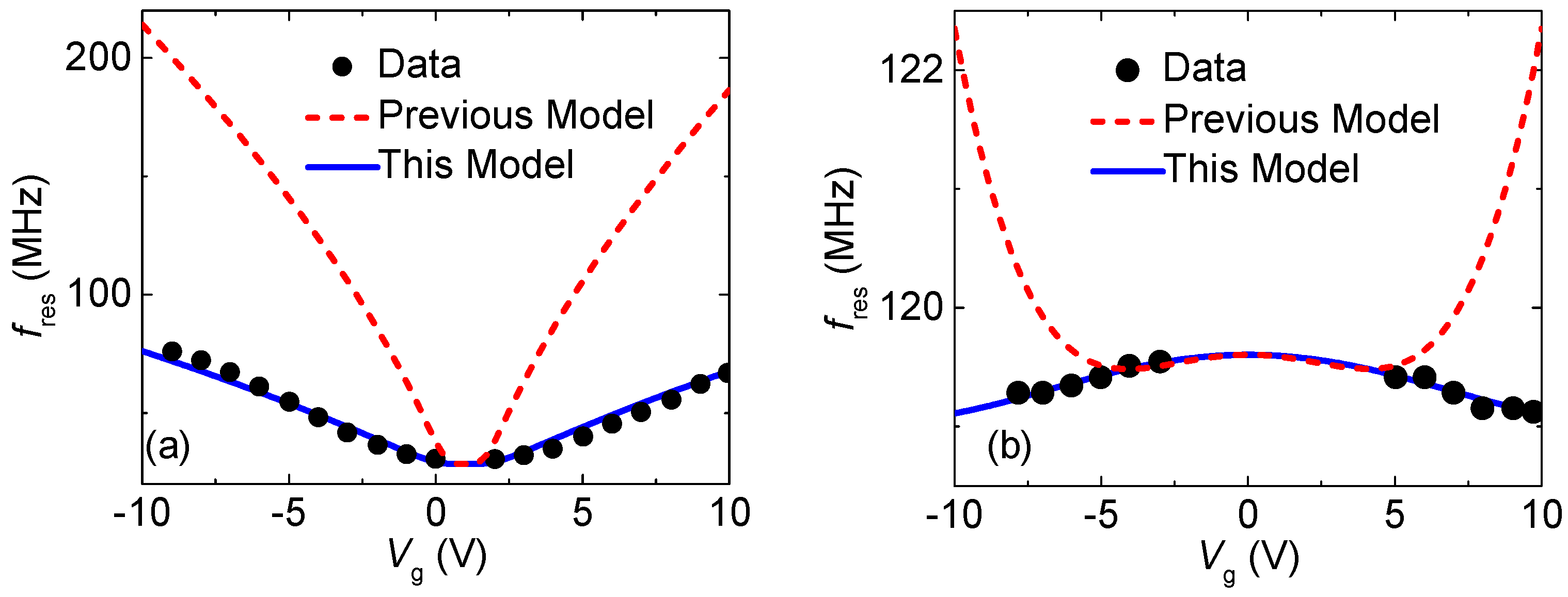
3. Results and Discussions
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Mak, K.F.; Sfeir, M.Y.; Wu, Y.; Lui, C.H.; Misewich, J.A.; Heinz, T.F. Measurement of the optical conductivity of graphene. Phys. Rev. Lett. 2008, 101, 196405. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Meric, I.; Huang, P.Y.; Gao, Q.; Gao, Y.; Tran, H.; Taniguchi, T.; Watanabe, K.; Campos, L.M.; Muller, D.A.; et al. One-dimensional electrical contact to a two-dimensional material. Science 2013, 342, 614–617. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.; Wei, X.; Kysar, J.W.; Hone, J. Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science 2008, 321, 385–388. [Google Scholar] [CrossRef] [PubMed]
- Lee, G.-H.; Cooper, R.C.; An, S.J.; Lee, S.; van der Zande, A.; Petrone, N.; Hammerberg, A.G.; Lee, C.; Crawford, B.; Oliver, W.; et al. High-strength chemical-vapor–deposited graphene and grain boundaries. Science 2013, 340, 1073–1076. [Google Scholar] [CrossRef] [PubMed]
- Bunch, J.S.; van der Zande, A.M.; Verbridge, S.S.; Frank, I.W.; Tanenbaum, D.M.; Parpia, J.M.; Craighead, H.G.; McEuen, P.L. Electromechanical resonators from graphene sheets. Science 2007, 315, 490–493. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.Y.; Rosenblatt, S.; Bolotin, K.I.; Kalb, W.; Kim, P.; Kymissis, I.; Stormer, H.L.; Heinz, T.F.; Hone, J. Performance of monolayer graphene nanomechanical resonators with electrical readout. Nat. Nanotechnol. 2009, 4, 861–867. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.H.; Chen, C.Y.; Deshpande, V.V.; DiRenno, F.A.; Gondarenko, A.; Heinz, D.B.; Liu, S.; Kim, P.; Hone, J. Radio frequency electrical transduction of graphene mechanical resonators. Appl. Phys. Lett. 2010, 97, 243111. [Google Scholar] [CrossRef]
- Singh, V.; Sengupta, S.; Solanki, H.S.; Dhall, R.; Allain, A.; Dhara, S.; Pant, P.; Deshmukh, M.M. Probing thermal expansion of graphene and modal dispersion at low-temperature using graphene nanoelectromechanical systems resonators. Nanotechnology 2010, 21, 165204. [Google Scholar] [CrossRef] [PubMed]
- Weber, P.; Güttinger, J.; Tsioutsios, I.; Chang, D.E.; Bachtold, A. Coupling graphene mechanical resonators to superconducting microwave cavities. Nano Lett. 2014, 14, 2854–2860. [Google Scholar] [CrossRef] [PubMed]
- Miao, T.; Yeom, S.; Wang, P.; Standley, B.; Bockrath, M. Graphene nanoelectromechanical systems as stochastic-frequency oscillators. Nano Lett. 2014, 14, 2982–2987. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Lee, S.; Deshpande, V.V.; Lee, G.-H.; Lekas, M.; Shepard, K.; Hone, J. Graphene mechanical oscillators with tunable frequency. Nat. Nanotechnol. 2013, 8, 923–927. [Google Scholar] [CrossRef] [PubMed]
- Ye, F.; Lee, J.; Feng, P.X.-L. Electrothermally tunable graphene resonators operating at very high temperature up to 1200 K. Nano Lett. 2018, 18, 1678–1685. [Google Scholar] [CrossRef] [PubMed]
- Mathew, J.P.; Patel, R.N.; Borah, A.; Vijay, R.; Deshmukh, M.M. Dynamical strong coupling and parametric amplification of mechanical modes of graphene drums. Nat. Nanotechnol. 2016, 11, 747–751. [Google Scholar] [CrossRef] [PubMed]
- Alba, R.D.; Massel, F.; Storch, I.R.; Abhilash, T.S.; Hui, A.; McEuen, P.L.; Craighead, H.G.; Parpia, J.M. Tunable phonon-cavity coupling in graphene membranes. Nat. Nanotechnol. 2016, 11, 741–746. [Google Scholar] [CrossRef]
- Davidovikj, D.; Alijani, F.; Cartamil-Bueno, S.J.; van der Zant, H.S.J.; Amabili, M.; Steeneken, P.G. Nonlinear dynamic characterization of two-dimensional materials. Nat. Commun. 2017, 8, 1253. [Google Scholar] [CrossRef] [PubMed]
- Güttinger, J.; Noury, A.; Weber, P.; Eriksson, A.M.; Lagoin, C.; Moser, J.; Eichler, C.; Wallraff, A.; Isacsson, A.; Bachtold, A. Energy-dependent path of dissipation in nanomechanical resonators. Nat. Nanotechnol. 2017, 12, 631–636. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Krupcale, M.J.; Feng, P.X.-L. Effects of γ-ray radiation on two-dimensional molybdenum disulfide (MoS2) nanomechanical resonators. Appl. Phys. Lett. 2016, 108, 023106. [Google Scholar] [CrossRef]
- He, R.; Feng, X.L.; Roukes, M.L.; Yang, P. Self-transducing silicon nanowire electromechanical systems at room temperature. Nano Lett. 2008, 8, 1756–1761. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Wang, Z.; He, K.; Yang, R.; Shan, J.; Feng, P.X.-L. Electrically tunable single- and few-layer MoS2 nanoelectromechanical systems with broad dynamic range. Sci. Adv. 2018, 4, eaao6653. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.H.; Li, O.P.; Xu, R.M. Graphene resonant channel transistor. In Proceedings of the IEEE International Wireless Symposium (IWS), Beijing, China, 14–18 April 2013; pp. 1–6. [Google Scholar]
- Lekas, M.; Lee, S.; Cha, W.; Hone, J.; Shepard, K. Noise modeling of graphene resonant channel transistors. IEEE Trans. Electron Devices 2015, 62, 1276–1283. [Google Scholar] [CrossRef]
- Mei, T.D.; Xu, Y.H.; Li, O.P.; Lan, Y.; Wu, Y.Q.; Xu, R.M.; Chen, Y.F.; Li, Y.R. Accurate multi-bias equivalent circuit model for graphene resonant channel transistors. In Proceedings of the IEEE International Microwave Symposium (IMS), San Francisco, CA, USA, 22–27 May 2016; pp. 1–4. [Google Scholar]
- Mei, T.D.; Xu, Y.H.; Lan, Y.; Li, O.P.; Sander, M.R.; Xu, R.M.; Li, Y.R. A high-frequency compact model for graphene resonant channel transistors including mechanical nonlinear effects. IEEE Trans. Microw. Theory Tech. 2017, 65, 4063–4072. [Google Scholar] [CrossRef]
- Chen, C.Y. Graphene nanoElectroMechanical Resonators and Oscillators. Ph.D. Thesis, Columbia University, New York, NY, USA, 2013. [Google Scholar]
- Schomburg, W.K. Introduction to Microsystem Design; Springer: New York, NY, USA, 2011. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mei, T.; Lee, J.; Xu, Y.; Feng, P.X.-L. Frequency Tuning of Graphene Nanoelectromechanical Resonators via Electrostatic Gating. Micromachines 2018, 9, 312. https://doi.org/10.3390/mi9060312
Mei T, Lee J, Xu Y, Feng PX-L. Frequency Tuning of Graphene Nanoelectromechanical Resonators via Electrostatic Gating. Micromachines. 2018; 9(6):312. https://doi.org/10.3390/mi9060312
Chicago/Turabian StyleMei, Tengda, Jaesung Lee, Yuehang Xu, and Philip X.-L. Feng. 2018. "Frequency Tuning of Graphene Nanoelectromechanical Resonators via Electrostatic Gating" Micromachines 9, no. 6: 312. https://doi.org/10.3390/mi9060312
APA StyleMei, T., Lee, J., Xu, Y., & Feng, P. X.-L. (2018). Frequency Tuning of Graphene Nanoelectromechanical Resonators via Electrostatic Gating. Micromachines, 9(6), 312. https://doi.org/10.3390/mi9060312





