An Exact Solution for Power-Law Fluids in a Slit Microchannel with Different Zeta Potentials under Electroosmotic Forces
Abstract
1. Introduction
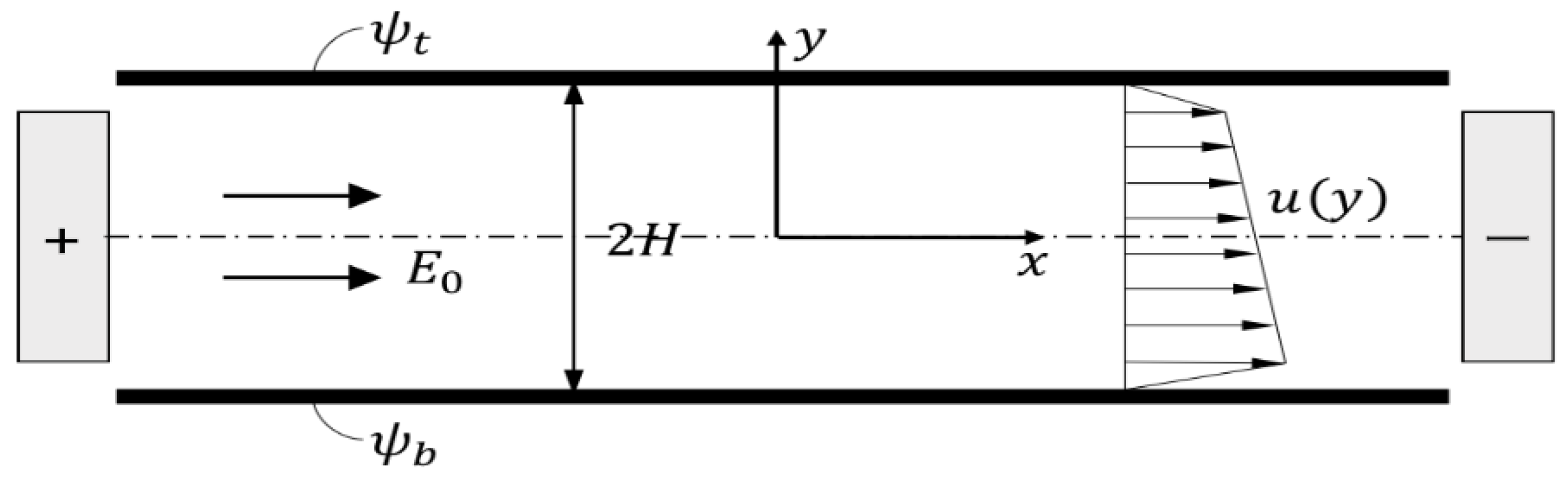
2. Mathematical Formulation
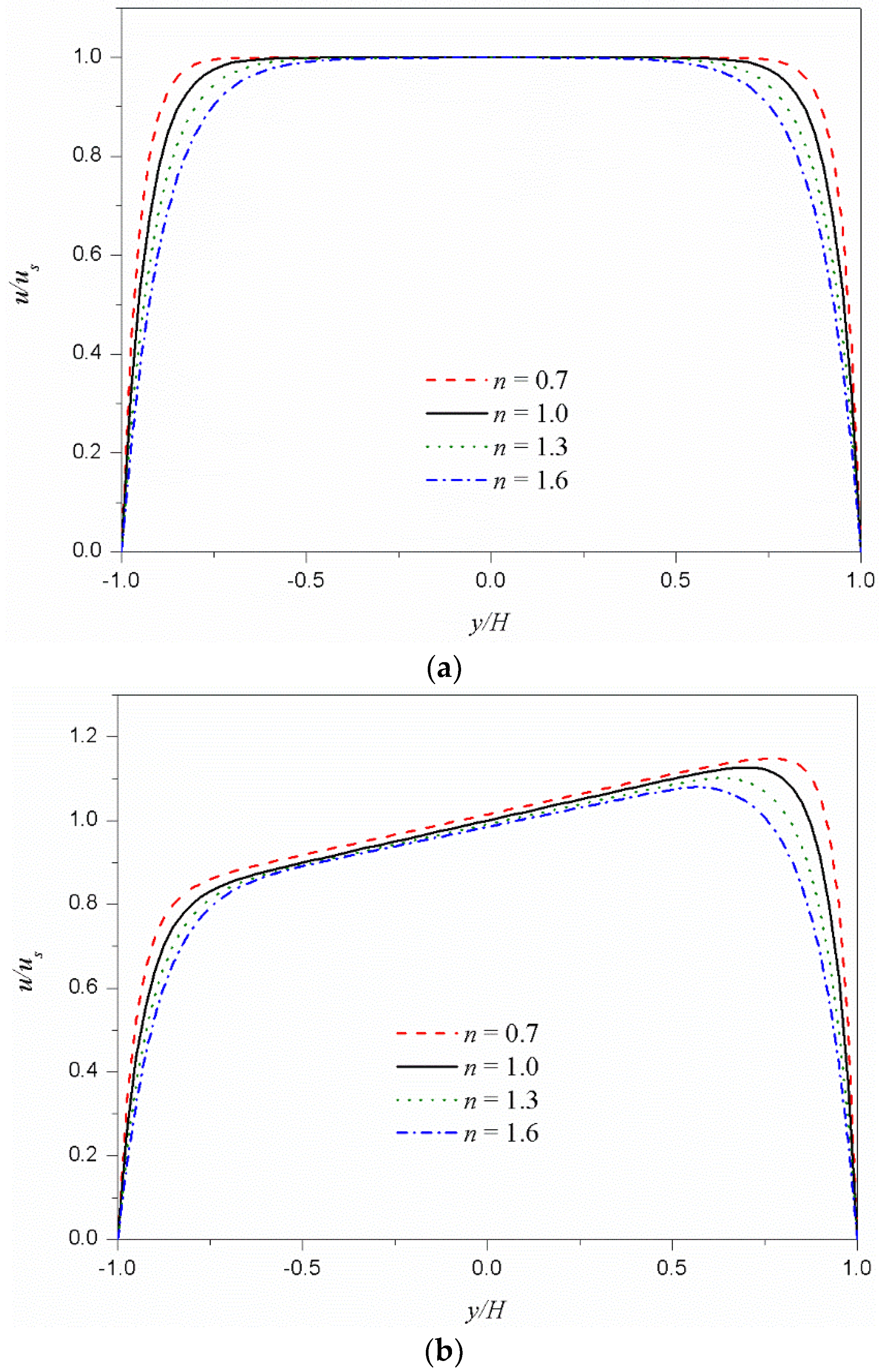
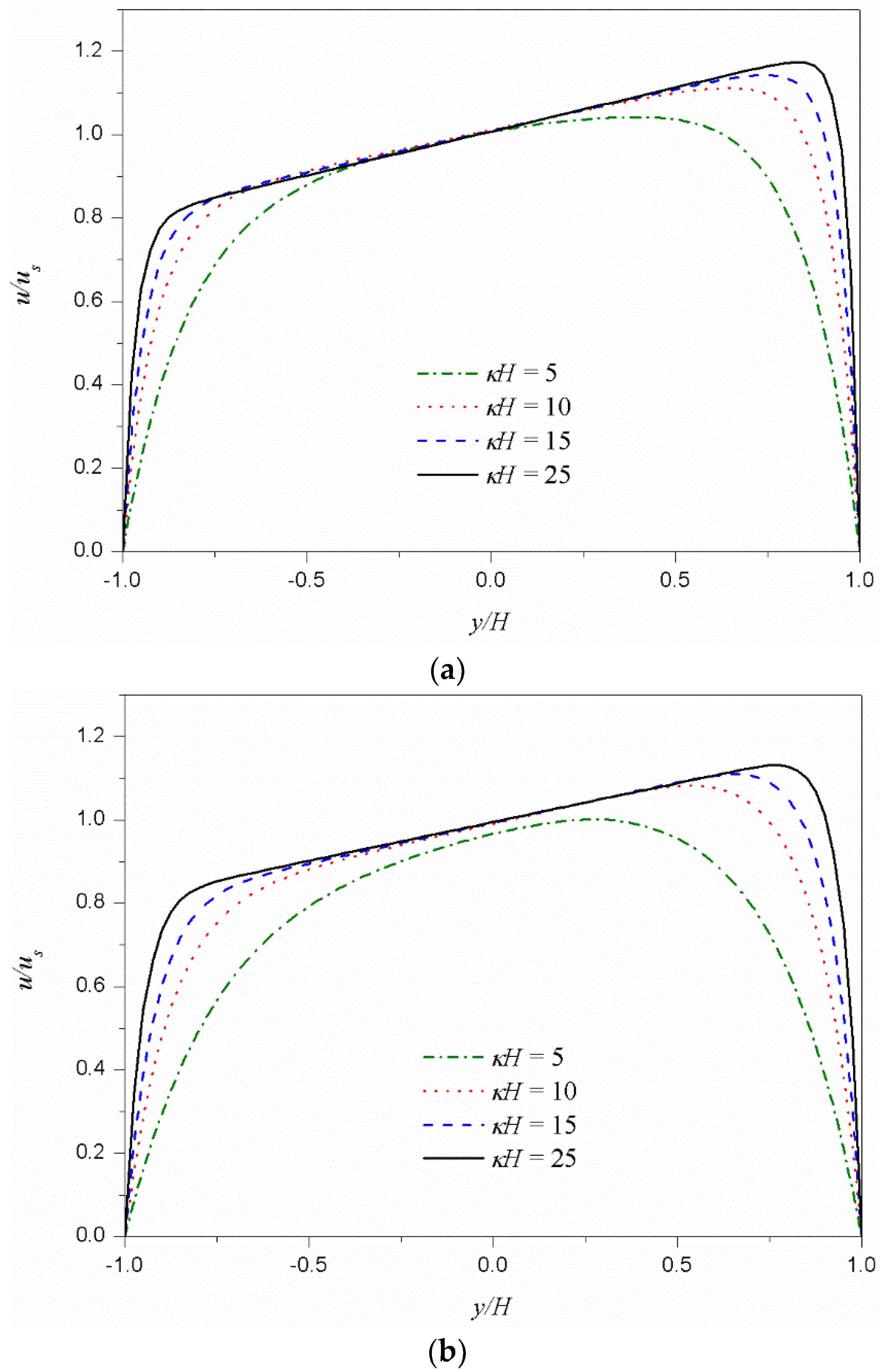
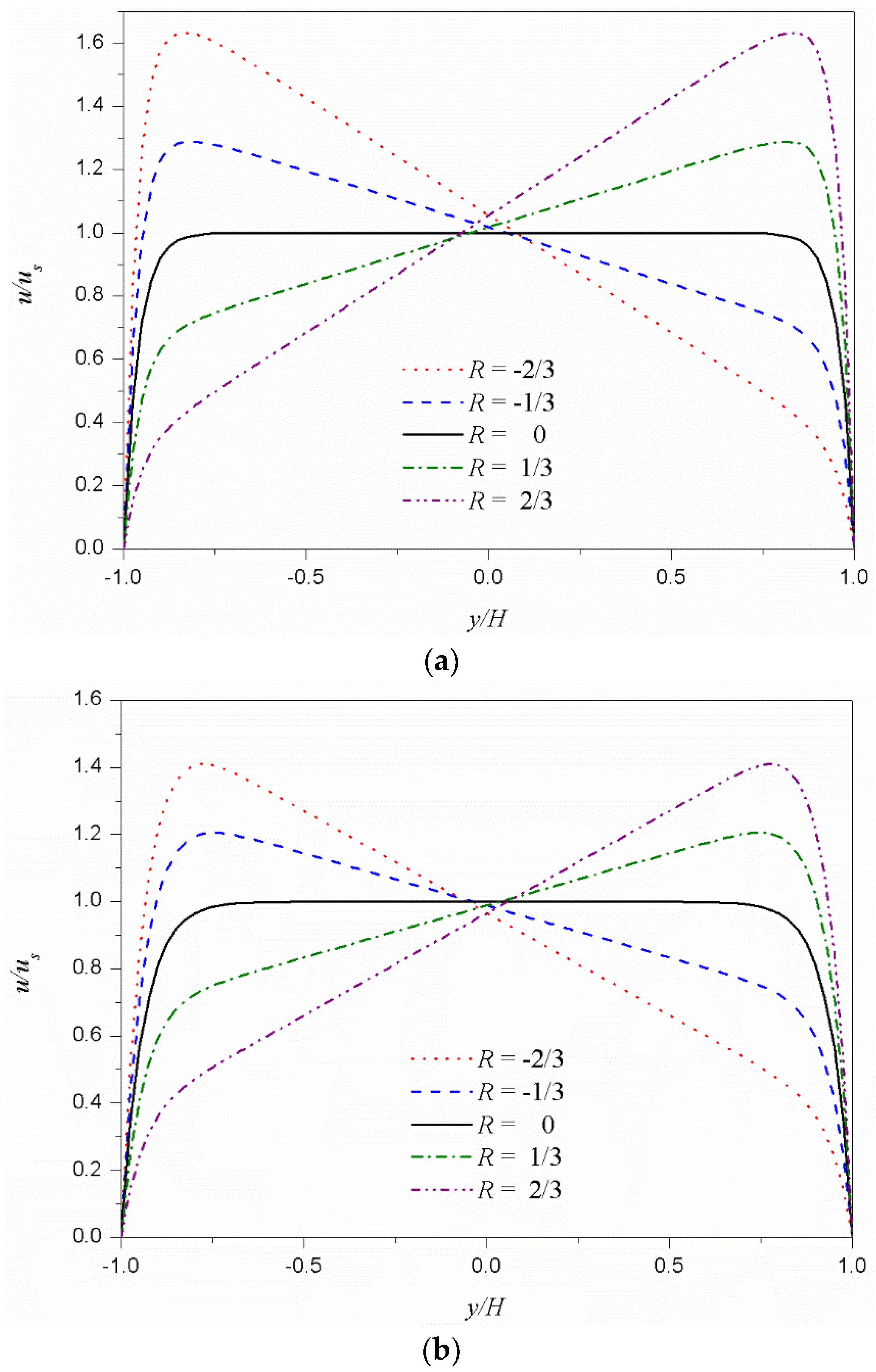
3. Results and Discussions
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Squires, T.M.; Quake, S.R. Microfluidics: Fluid physics at the nanoliter scale. Rev. Mod. Phys. 2005, 77, 977–1026. [Google Scholar] [CrossRef]
- Sackmann, E.K.; Fulton, A.L.; Beebe, D.J. The present and future role of microfluidics in biomedical research. Nature 2014, 507, 181–189. [Google Scholar] [CrossRef] [PubMed]
- Gravesen, P.; Branebjerg, J.; Jensen, O.S. Microfluidics-a review. J. Micromech. Microeng. 1993, 3, 168. [Google Scholar] [CrossRef]
- Akers, A.; Gassman, M.; Smith, R. Hydraulic Power System Analysis; CRC Press: Boca Raton, FL, USA, 2006; ISBN 978-0-8247-9956-4. [Google Scholar]
- Lyklema, J. Fundamentals of Interface and Colloid Science: Solid-Liquid Interfaces, 1st ed.; Academic Press: London, UK, 1995; ISBN 978-0-12-460524-4. [Google Scholar]
- Hunter, R.J. Introduction to Modern Colloid Science, 1st ed.; Oxford University Press: Oxford, NY, USA, 1994; ISBN 978-0-19-855386-1. [Google Scholar]
- Li, D. Electrokinetics in Microfluidics; Academic Press: Cambridge, MA, USA, 2004; ISBN 978-0-08-053074-1. [Google Scholar]
- Das, S.; Chakraborty, S. Analytical solutions for velocity, temperature and concentration distribution in electroosmotic microchannel flows of a non-Newtonian bio-fluid. Anal. Chim. Acta 2006, 559, 15–24. [Google Scholar] [CrossRef]
- Devarakonda, S.B.; Han, J.; Ahn, C.H.; Banerjee, R.K. Bioparticle separation in non-Newtonian fluid using pulsed flow in micro-channels. Microfluid. Nanofluid. 2007, 3, 391–401. [Google Scholar] [CrossRef]
- Kolodner, P. Oscillatory convection in viscoelastic DNA suspensions. J. Non-Newton. Fluid Mech. 1998, 75, 167–192. [Google Scholar] [CrossRef]
- Owens, R.G. A new microstructure-based constitutive model for human blood. J. Non-Newton. Fluid Mech. 2006, 140, 57–70. [Google Scholar] [CrossRef]
- Yilmaz, F.; Gundogdu, M.Y. A critical review on blood flow in large arteries; relevance to blood rheology, viscosity models, and physiologic conditions. Korea-Aust. Rheol. J. 2008, 20, 197–211. [Google Scholar]
- Park, H.M.; Lee, W.M. Helmholtz–Smoluchowski velocity for viscoelastic electroosmotic flows. J. Colloid Int. Sci. 2008, 317, 631–636. [Google Scholar] [CrossRef] [PubMed]
- Olivares, M.L.; Vera-Candioti, L.; Berli, C.L.A. The EOF of polymer solutions. Electrophoresis 2009, 30, 921–928. [Google Scholar] [CrossRef] [PubMed]
- Zhao, C.; Yang, C. Electrokinetics of non-Newtonian fluids: A review. Adv. Colloid Interface Sci. 2013, 201–202, 94–108. [Google Scholar] [CrossRef] [PubMed]
- Zhao, C.; Zholkovskij, E.; Masliyah, J.H.; Yang, C. Analysis of electroosmotic flow of power-law fluids in a slit microchannel. J. Colloid Interface Sci. 2008, 326, 503–510. [Google Scholar] [CrossRef] [PubMed]
- Zhao, C.; Yang, C. Nonlinear Smoluchowski velocity for electroosmosis of power-law fluids over a surface with arbitrary zeta potentials. Electrophoresis 2010, 31, 973–979. [Google Scholar] [CrossRef] [PubMed]
- Zhao, C.; Yang, C. An exact solution for electroosmosis of non-Newtonian fluids in microchannels. J. Non-Newton. Fluid Mech. 2011, 166, 1076–1079. [Google Scholar] [CrossRef]
- Zhao, C.; Yang, C. Electroosmotic flows of non-Newtonian power-law fluids in a cylindrical microchannel. Electrophoresis 2013, 34, 662–667. [Google Scholar] [CrossRef] [PubMed]
- Zhao, C.; Zhang, W.; Yang, C. Dynamic Electroosmotic Flows of Power-Law Fluids in Rectangular Microchannels. Micromachines 2017, 8, 34. [Google Scholar] [CrossRef]
- Tang, G.H.; Li, X.F.; He, Y.L.; Tao, W.Q. Electroosmotic flow of non-Newtonian fluid in microchannels. J. Non-Newton. Fluid Mech. 2009, 157, 133–137. [Google Scholar] [CrossRef]
- Vasu, N.; De, S. Electroosmotic flow of power-law fluids at high zeta potentials. Colloids Surf. A Physicochem. Eng. Asp. 2010, 368, 44–52. [Google Scholar] [CrossRef]
- Babaie, A.; Sadeghi, A.; Saidi, M.H. Combined electroosmotically and pressure driven flow of power-law fluids in a slit microchannel. J. Non-Newton. Fluid Mech. 2011, 166, 792–798. [Google Scholar] [CrossRef]
- Hadigol, M.; Nosrati, R.; Raisee, M. Numerical analysis of mixed electroosmotic/pressure driven flow of power-law fluids in microchannels and micropumps. Colloids Surf. A Physicochem. Eng. Asp. 2011, 374, 142–153. [Google Scholar] [CrossRef]
- Ng, C.-O.; Qi, C. Electroosmotic flow of a power-law fluid in a non-uniform microchannel. J. Non-Newton. Fluid Mech. 2014, 208–209, 118–125. [Google Scholar] [CrossRef]
- Afonso, A.M.; Alves, M.A.; Pinho, F.T. Electroosmotic flow of viscoelastic fluids in microchannels under asymmetric zeta potentials. J. Eng. Math. 2011, 71, 15–30. [Google Scholar] [CrossRef]
- Choi, W.; Joo, S.W.; Lim, G. Electroosmotic flows of viscoelastic fluids with asymmetric electrochemical boundary conditions. J. Non-Newton. Fluid Mech. 2012, 187–188, 1–7. [Google Scholar] [CrossRef]
- Qi, C.; Ng, C.-O. Electroosmotic flow of a power-law fluid through an asymmetrical slit microchannel with gradually varying wall shape and wall potential. Colloids Surf. A Physicochem. Eng. Asp. 2015, 472, 26–37. [Google Scholar] [CrossRef]
- Hadigol, M.; Nosrati, R.; Nourbakhsh, A.; Raisee, M. Numerical study of electroosmotic micromixing of non-Newtonian fluids. J. Non-Newton. Fluid Mech. 2011, 166, 965–971. [Google Scholar] [CrossRef]
- Jiménez, E.; Escandón, J.; Bautista, O.; Méndez, F. Start-up electroosmotic flow of Maxwell fluids in a rectangular microchannel with high zeta potentials. J. Non-Newton. Fluid Mech. 2016, 227, 17–29. [Google Scholar] [CrossRef]
- Peralta, M.; Arcos, J.; Méndez, F.; Bautista, O. Oscillatory electroosmotic flow in a parallel-plate microchannel under asymmetric zeta potentials. Fluid Dyn. Res. 2017, 49, 035514. [Google Scholar] [CrossRef]
- Choi, W.; Yun, S.; Choi, D.-S. Electroosmotic flows of power-law fluids with asymmetric electrochemical boundary conditions in a rectangular microchannel. Micromachines 2017, 8, 165. [Google Scholar] [CrossRef]
- Choi, W.; Yun, S.; Choi, D.-S. Approximate solution for electroosmotic flow of power-law fluids in a planar microchannel with asymmetric electrochemical boundary conditions. Micromachines 2018, 9, 265. [Google Scholar] [CrossRef]
- Kirby, B.J.; Hasselbrink, E.F. Zeta potential of microfluidic substrates: 1. Theory, experimental techniques, and effects on separations. Electrophoresis 2004, 25, 187–202. [Google Scholar] [CrossRef] [PubMed]
- Gallardo-Moreno, A.M.; Vadillo-Rodríguez, V.; Perera-Núñez, J.; Bruque, J.M.; González-Martín, M.L. The zeta potential of extended dielectrics and conductors in terms of streaming potential and streaming current measurements. Phys. Chem. Chem. Phys. 2012, 14, 9758–9767. [Google Scholar] [CrossRef] [PubMed]
- Appell, P. Sur les séries hypergéométriques de deux variables et sur des équations différentielles linéaires aux dérivées partielles. C. R. Hebd. Seances Acad. Sci. 1880, 90, 296–298, 731–735. [Google Scholar]
- Picard, É. Sur une extension aux fonctions de deux variables du problème de Riemann relativ aux fonctions hypergéométriques. Annales Scientifiques de l’École Normale Supérieure Série 2 1881, 10, 305–322. (In French) [Google Scholar] [CrossRef]
- Barnes, E.W. A New Development in the Theory of the Hypergeometric Functions. Proc. Lond. Math. Soc. 1908, 6, 141–177. [Google Scholar] [CrossRef]
- Bailey, W.N. Generalised Hypergeometric Series; Cambridge University Press: Cambridge, UK, 1935; pp. 3–4. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, D.-S.; Yun, S.; Choi, W. An Exact Solution for Power-Law Fluids in a Slit Microchannel with Different Zeta Potentials under Electroosmotic Forces. Micromachines 2018, 9, 504. https://doi.org/10.3390/mi9100504
Choi D-S, Yun S, Choi W. An Exact Solution for Power-Law Fluids in a Slit Microchannel with Different Zeta Potentials under Electroosmotic Forces. Micromachines. 2018; 9(10):504. https://doi.org/10.3390/mi9100504
Chicago/Turabian StyleChoi, Du-Soon, Sungchan Yun, and WooSeok Choi. 2018. "An Exact Solution for Power-Law Fluids in a Slit Microchannel with Different Zeta Potentials under Electroosmotic Forces" Micromachines 9, no. 10: 504. https://doi.org/10.3390/mi9100504
APA StyleChoi, D.-S., Yun, S., & Choi, W. (2018). An Exact Solution for Power-Law Fluids in a Slit Microchannel with Different Zeta Potentials under Electroosmotic Forces. Micromachines, 9(10), 504. https://doi.org/10.3390/mi9100504




