A Review on Lattice Defects in Graphene: Types, Generation, Effects and Regulation
Abstract
:1. Introduction
2. Types of Defects in Graphene
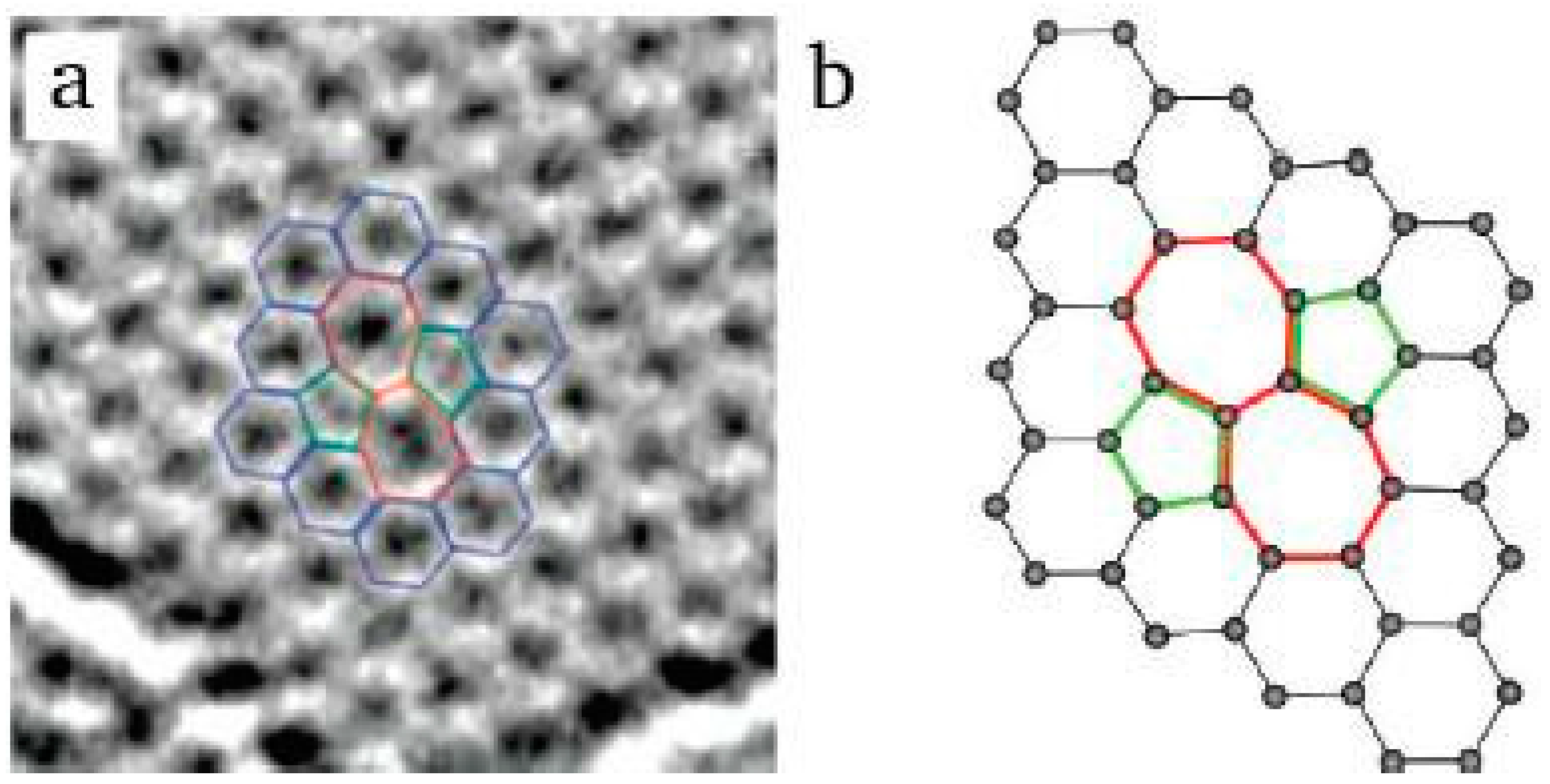
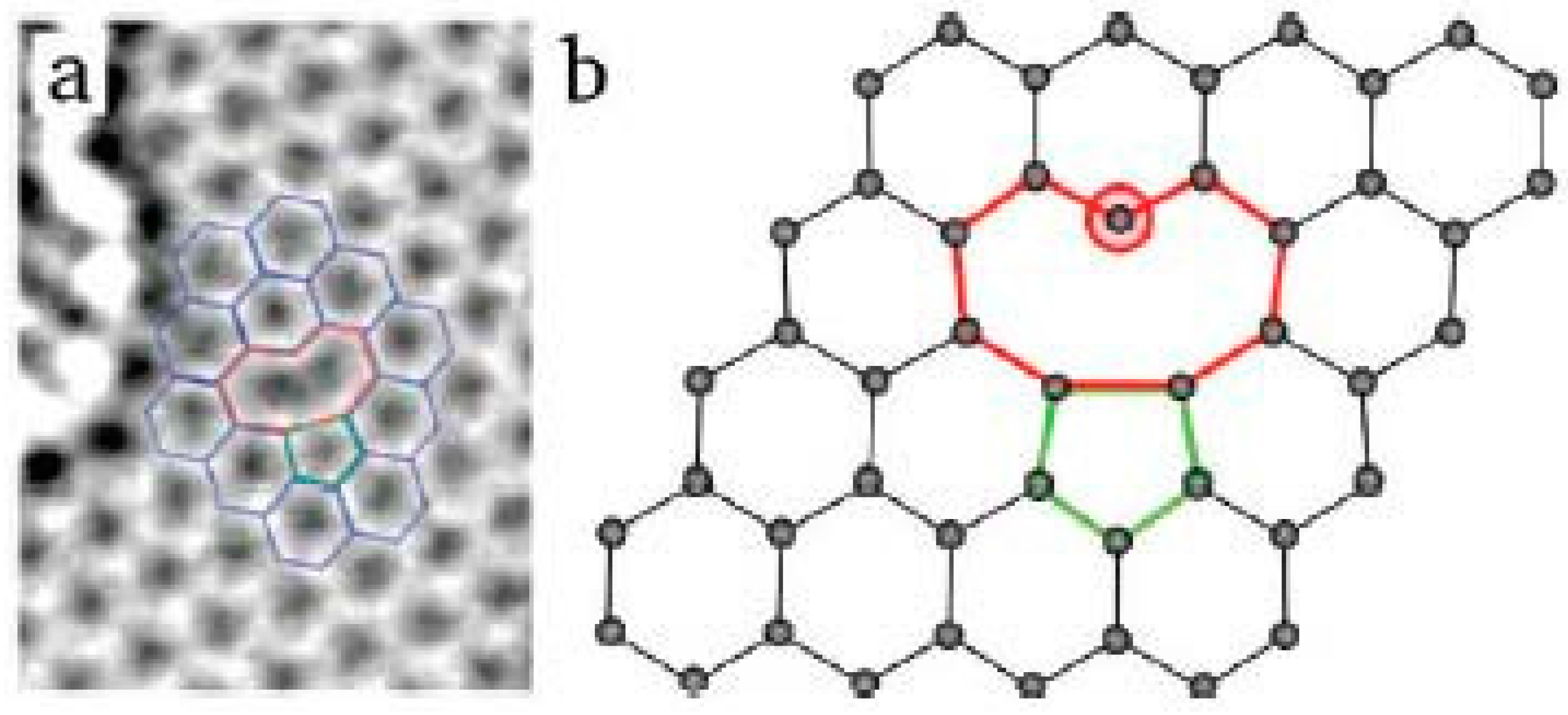
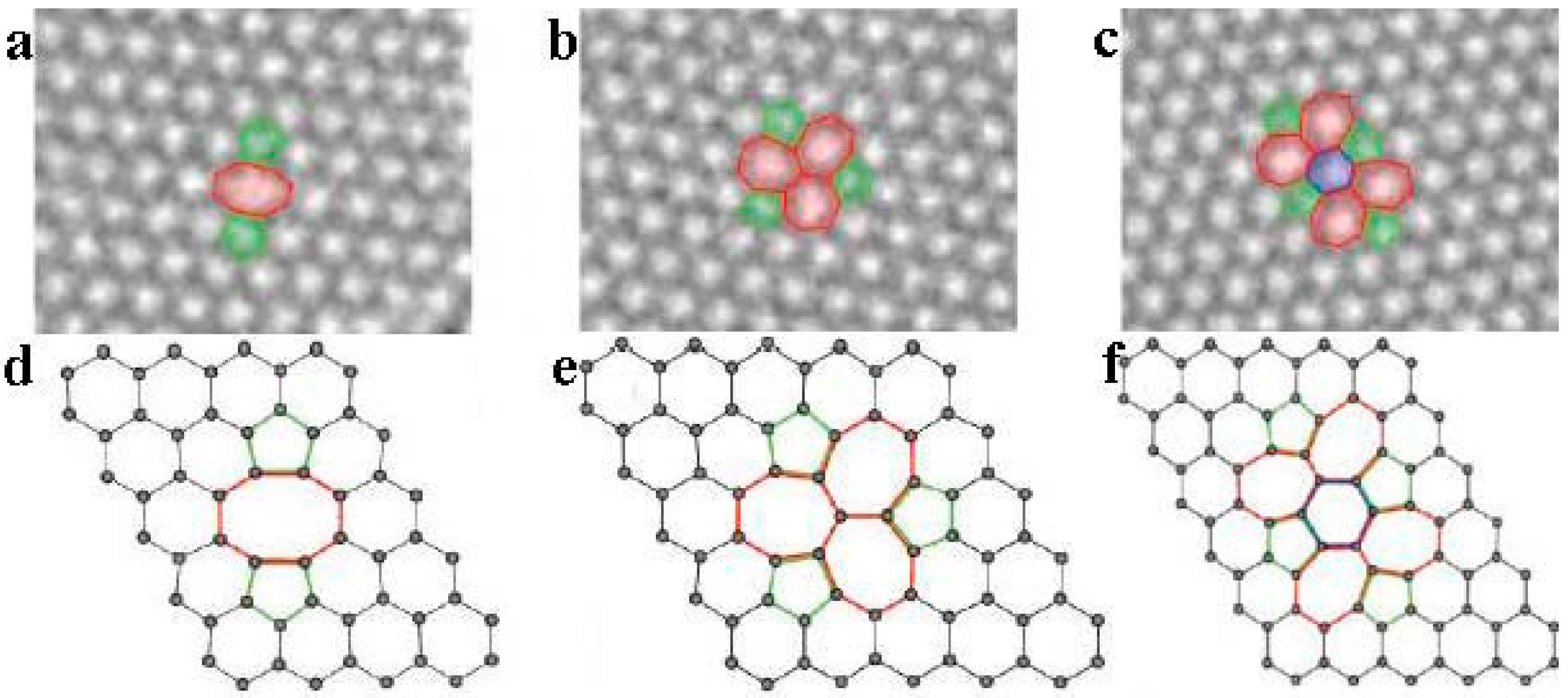
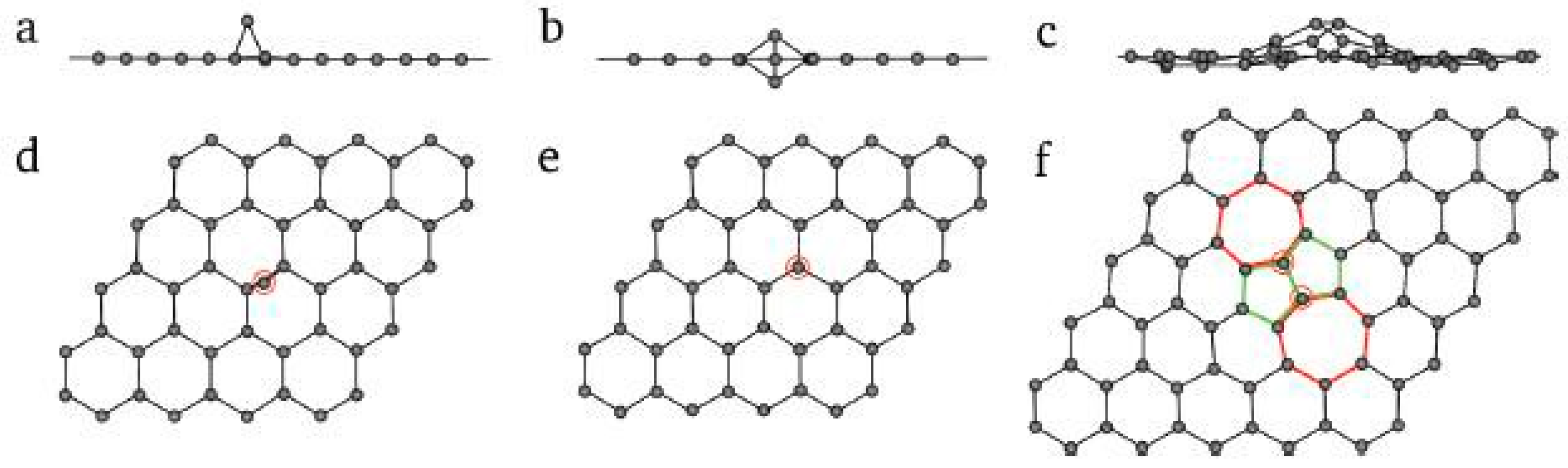
2.1. Intrinsic Defects in Graphene
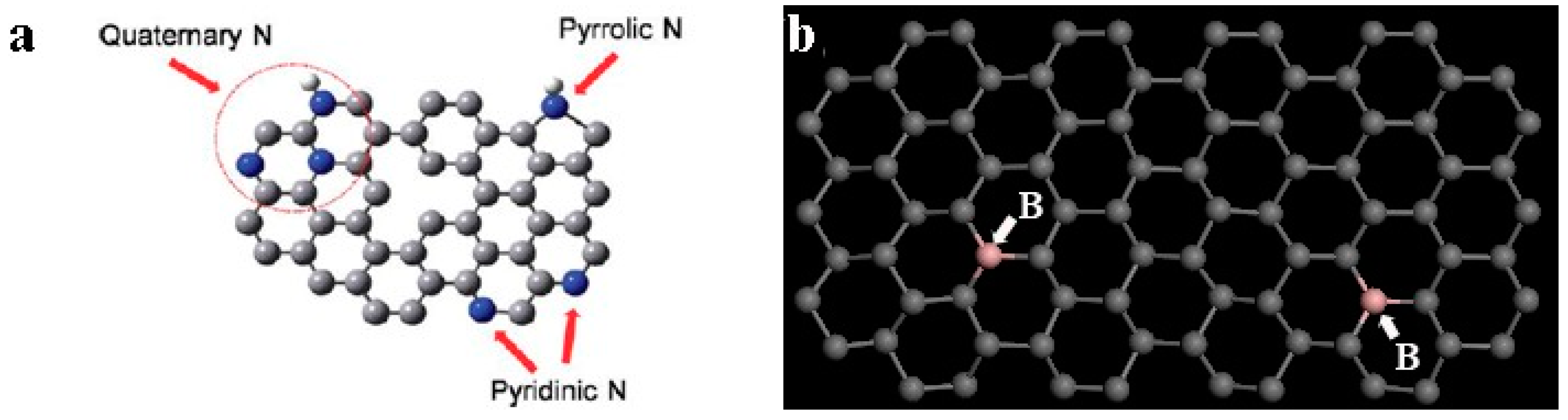
2.2. The Introduction of Defects in Graphene
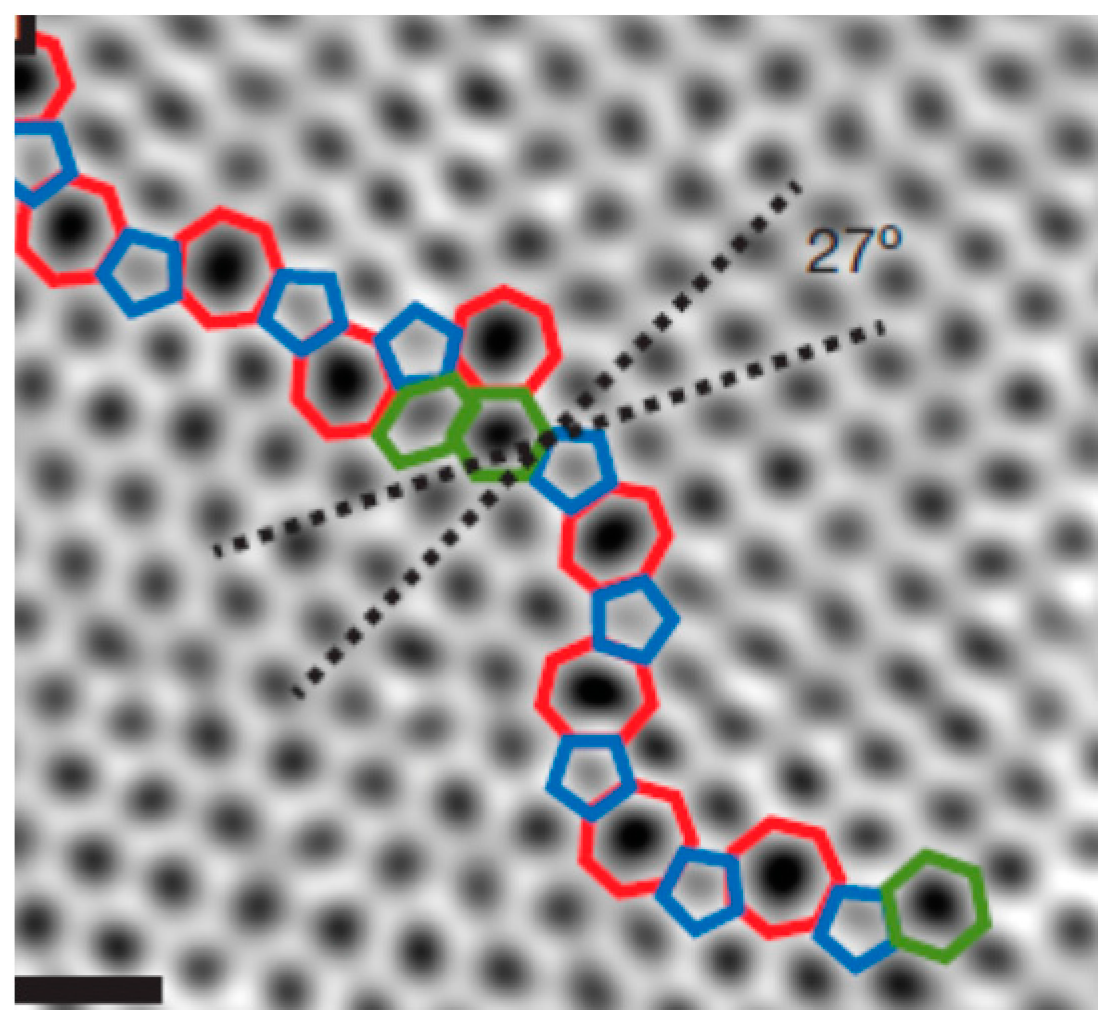
2.3. Double Graphene Structure Defects
3. Preparation of Graphene and Generation of Defects
4. Effect of Defects on Properties of Graphene
4.1. Magnetic Properties
4.2. Electrical Properties
4.3. Mechanical Properties
4.4. Thermal Conductivity Properties
4.5. Chemical Properties
5. Regulation of Graphene Defects
5.1. Defects Manufacturing
5.2. Defects Reduction
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Mermin, N.D. Crystalline order in two dimensions. Phys. Rev. 1968, 176, 250–254. [Google Scholar] [CrossRef]
- Mermin, N.D.; Wagner, H. Absence of anomalous averages in systems of finite nonzero thickness or cross section. Phys. Rev. Lett. 1996, 17, 1307–1311. [Google Scholar] [CrossRef]
- Nelson, D.R.; Peliti, L. Fluctuations in membranes with crystalline and hexatic order. J. Phys. 1987, 48, 1085–1089. [Google Scholar] [CrossRef]
- Le Doussal, P.; Radzihovsky, L. Self-consistent theory of polymerized membranes. Phys. Rev. Lett. 1992, 69, 1209–1211. [Google Scholar] [CrossRef] [PubMed]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56–58. [Google Scholar] [CrossRef]
- Kroto, H.W.; Heath, J.R.; O’Brien, S.C. C60: Buckminsterfullerene. Nature 1985, 318, 162–163. [Google Scholar] [CrossRef]
- Zandiatashbar, A.; Lee, G.H.; An, S.J.; Lee, S.; Mathew, N.; Terroness, M.; Hayashi, T.; Picu, C.R.; Hone, J.; Koratkar, N. Effect of defects on the intrinsic strength and stiffness of graphene. Nat. Commun. 2014, 5, 3186. [Google Scholar] [CrossRef] [PubMed]
- Tian, W.; Zhang, X.Y.; Chen, Z.Q.; Ji, H.Y. A review of graphene on NEMS. Recent Pat. Nanotechnol. 2016, 10, 3–10. [Google Scholar] [CrossRef] [PubMed]
- Novoselov, K.S.; Jiang, Z.; Zhang, Y.; Morozov, S.V.; Stormer, H.L.; Zeitler, U.; Maan, J.C.; Boebinger, G.S.; Kim, P.; Geim, A.K. Room-temperature quantum Hall effect in graphene. Science 2007, 315, 1379. [Google Scholar] [CrossRef] [PubMed]
- Bunch, J.S.; van der Zande, A.M.; Verbridge, S.S.; Frank, I.W.; Tanenbaum, D.M. Electromechanical resonators from graphene sheets. Science 2007, 315, 490–493. [Google Scholar] [CrossRef] [PubMed]
- Xie, S.X.; Jiao, N.D.; Tung, S.; Liu, L.Q. Fabrication of SWCNT-graphene field-effect transistors. Micromachines 2015, 6, 1317–1330. [Google Scholar] [CrossRef]
- Carbone, M.; Gorton, L.; Antiochia, R. An overview of the latest grapheme-based sensors for glucose detection: The effects of graphene defects. Electroanalysis 2015, 27, 16–31. [Google Scholar] [CrossRef]
- Ebrahimi, S.; Montazeri, A.; Rafii-Tabar, H. Molecular dynamics study of the interfacial mechanical properties of the grapheme-collagen biological nanocomposite. Comput. Mater. Sci. 2013, 69, 29–39. [Google Scholar] [CrossRef]
- Terrones, M.; Botello-Méndez, A.R.; Campos-Delgado, J.; López-Urías, F.; Vega-Cantú, Y.I.; Rodríguez-Macías, F.J.; Elias, A.L.; Munoz-Sandoval, E.; Cano-Marquez, A.G.; Charlier, J. Graphene and graphite nanoribbons: Morphology, properties, synthesis, defects and applications. Nano Today 2010, 5, 351–372. [Google Scholar] [CrossRef]
- Araujo, P.T.; Terrones, M.; Dresselhaus, M.S. Defects and impurities in graphene-like materials. Mater. Today 2012, 15, 98–109. [Google Scholar] [CrossRef]
- Berman, D.; Erdemir, A.; Sumant, A.V. Graphene: A new emerging lubricant. Mater. Today 2014, 17, 31–42. [Google Scholar] [CrossRef]
- Kotakoski, J.; Krasheninnikov, A.V.; Nordlund, K. Energetics, structure, and long-range interaction of vacancy-type defects in carbon nanotubes: Atomistic simulations. Phys. Rev. B 2006, 74, 245420. [Google Scholar] [CrossRef]
- Krasheninnikov, A.V.; Lehtinen, P.O.; Foster, A.S.; Nieminen, R.M. Bending the rules: Contrasting vacancy energetics and migration in graphite and carbon nanotubes. Chem. Phys. Lett. 2006, 418, 132–136. [Google Scholar] [CrossRef]
- Lu, A.J.; Pan, B.C. Nature of Single Vacancy in Achiral Carbon Nanotubes. Phys. Rev. Lett. 2004, 92, 105504. [Google Scholar] [CrossRef] [PubMed]
- Miyamoto, Y.; Berber, S.; Yoon, M.; Rubio, A.; Tománek, D. Can photo excitations heal defects in carbon nanotubes? Chem. Phys. Lett. 2004, 392, 209–213. [Google Scholar] [CrossRef]
- Rossato, J.; Baierle, R.J.; Fazzio, A.; Mota, R. Vacancy Formation Process in Carbon Nanotubes: First-Principles Approach. Nano Lett. 2004, 5, 197–200. [Google Scholar] [CrossRef] [PubMed]
- El-Barbary, A.A.; Telling, R.H.; Ewels, C.P.; Heggie, M.I.; Briddon, P.R. Structure and energetics of the vacancy in graphite. Phys. Rev. B 2003, 68, 144107. [Google Scholar] [CrossRef]
- Ewels, C.P.; Telling, R.H.; El-Barbary, A.A.; Heggie, M.I.; Briddon, P.R. Metastable Frenkel Pair Defect in Graphite: Source of Wigner Energy? Phys. Rev. Lett. 2003, 91, 025505. [Google Scholar] [CrossRef] [PubMed]
- Krasheninnikov, A.V.; Elesin, V.F. The effect of interstitial clusters and vacancies on the scanning tunneling microscopy image of graphite. Surf. Sci. 2000, 454–456, 519–524. [Google Scholar] [CrossRef]
- Telling, R.H.; Heggie, M.I. Radiation defects in graphite. Philos. Mag. 2007, 87, 4797–4846. [Google Scholar] [CrossRef]
- Thrower, P.A.; Mayer, R.M. Point defects and self-diffusion in graphite. Phys. Status Solidi (a) 1978, 47, 11–37. [Google Scholar] [CrossRef]
- Hashimoto, A.; Uenaga, K.; Gloter, A.; Urita, K.; Lijima, S. Direct evidence for atomic defects in graphene layers. Nature 2004, 430, 870–873. [Google Scholar] [CrossRef] [PubMed]
- Tapasztó, L.; Dobrik, G.; Nemes-Incze, P.; Vertesy, G.; Lambin, P.; Biró, L.P. Tuning the electronic structure of graphene by ion irradiation. Phys. Rev. B 2008, 78, 233407. [Google Scholar] [CrossRef]
- Wang, S.N.; Wang, R.; Wang, X.W.; Zhang, D.D.; Qiu, X.H. Nanoscale charge distribution and energy band modification in defect-patterned graphene. Nanoscale 2012, 4, 2651–2657. [Google Scholar] [CrossRef] [PubMed]
- Henderson, M.A. Surface perspective on self-diffusion in rutile TiO2. Surf. Sci. 1999, 419, 174–187. [Google Scholar] [CrossRef]
- Janotti, A.; Van de Walle, C.G. Native point defects in ZnO. Phys. Rev. B 2007, 76, 165202. [Google Scholar] [CrossRef]
- Tolchard, J.R.; Islam, M.S.; Slater, P.R. Defect chemistry and oxygen ion migration in the apatite-type materials La9.33Si6O26 and La8Sr2Si6O26. J. Mater. Chem. 2003, 13, 1956–1961. [Google Scholar] [CrossRef]
- Li, L.; Reich, S.; Robertson, J. Defect energies of graphite: Density-functional calculations. Phys. Rev. B 2005, 72, 184109. [Google Scholar] [CrossRef]
- Banhart, F.; Li, J.X.; Krasheninnikov, A.V. Carbon nanotubes under electron irradiation: Stability of the tubes and their action as pipes for atom transport. Phys. Rev. B 2005, 71, 241408. [Google Scholar] [CrossRef]
- Ma, J.; Alfè, D.; Michaelides, A.; Wang, E. Stone-Wales defects in graphene and other planar sp2-bonded materials. Phys. Rev. B 2009, 80, 033407. [Google Scholar] [CrossRef]
- Meyer, J.C.; Kisielowski, C.; Erni, R.; Rossell, M.D.; Crommie, M.F.; Zettl, A. Direct Imaging of Lattice Atoms and Topological Defects in Graphene Membranes. Nano Lett. 2008, 8, 3582–3586. [Google Scholar] [CrossRef] [PubMed]
- Banhart, F.; Kotakoski, J.; Krasheninnikov, A.V. Structural Defects in Graphene. ACS Nano 2011, 5, 26–41. [Google Scholar] [CrossRef] [PubMed]
- Wintterlin, J.; Bocquet, M.L. Graphene on metal surfaces. Surf. Sci. 2009, 603, 1841–1852. [Google Scholar] [CrossRef]
- Huang, P.Y.; Ruiz-Vargas, C.S.; van der Zande, A.M.; Whitney, W.S.; Levendorf, M.P.; Kevek, J.W.; Garg, S.; Alden, J.S.; Hustedt, C.J.; Zhu, Y.; et al. Grains and grain boundaries in single-layer graphene atomic patchwork quilts. Nature 2011, 469, 389–392. [Google Scholar] [CrossRef] [PubMed]
- Coraux, J.; N’Diaye, A.T.; Busse, C.; Michely, T. Structural Coherency of Graphene on Ir (111). Nano Lett. 2008, 8, 565–570. [Google Scholar] [CrossRef] [PubMed]
- Lahiri, J.; Lin, Y.; Bozkurt, P.; Oleynik, I.I.; Batzill, M. An extended defect in graphene as a metallic wire. Nat. Nanotechnol. 2010, 5, 326–329. [Google Scholar] [CrossRef] [PubMed]
- Malola, S.; Häkkinen, H.; Koskinen, P. Structural, chemical, and dynamical trends in graphene grain boundaries. Phys. Rev. B 2010, 81, 165447. [Google Scholar] [CrossRef]
- Yazyev, O.V.; Louie, S.G. Topological defects in graphene: Dislocations and grain boundaries. Phys. Rev. B 2010, 81, 195420. [Google Scholar] [CrossRef]
- Ma, Y. Simulation of interstitial diffusion in graphite. Phys. Rev. B 2007, 76, 075419. [Google Scholar] [CrossRef]
- Tsetseris, L.; Pantelides, S.T. Adatom complexes and self-healing mechanisms on graphene and single-wall carbon nanotubes. Carbon 2009, 47, 901–908. [Google Scholar] [CrossRef]
- Lusk, M.T.; Carr, L.D. Nanoengineering Defect Structures on Graphene. Phys. Rev. Lett. 2008, 100, 175503. [Google Scholar] [CrossRef] [PubMed]
- Lusk, M.T.; Wu, D.T.; Carr, L.D. Graphene nanoengineering and the inverse Stone-Thrower-Wales defect. Phys. Rev. B 2010, 81, 155444. [Google Scholar] [CrossRef]
- Cretu, O.; Krasheninnikov, A.V.; Rodríguez-Manzo, J.A.; Sun, L.; Nieminen, R.M.; Banhart, F. Migration and Localization of Metal Atoms on Strained Graphene. Phys. Rev. Lett. 2010, 105, 196102. [Google Scholar] [CrossRef] [PubMed]
- Chan, K.T.; Neaton, J.B.; Cohen, M.L. First-principles study of metal adatom adsorption on graphene. Phys. Rev. B 2008, 77, 235430. [Google Scholar] [CrossRef]
- Wu, Z.S.; Ren, W.; Gao, L.; Liu, B.; Jiang, C.; Cheng, H.M. Synthesis of high-quality graphene with a pre-determined number of layers. Carbon 2009, 47, 493–499. [Google Scholar] [CrossRef]
- Marcano, D.C.; Kosynkin, D.V.; Berlin, J.M.; Sinitskii, A.; Sun, Z.; Slesarev, A.; Alemany, L.B.; Lu, W.; Tour, J.M. Improved Synthesis of Graphene Oxide. ACS Nano 2010, 4, 4806–4814. [Google Scholar] [CrossRef] [PubMed]
- Cuong, T.V.; Pham, V.H.; Tran, Q.T.; Chuang, J.S.; Shin, E.W.; Kim, J.S.; Kim, E.J. Optoelectronic properties of graphene thin films prepared by thermal reduction of graphene oxide. Mater. Lett. 2010, 64, 765–767. [Google Scholar] [CrossRef]
- Pham, T.A.; Kim, J.S.; Kim, S.; Jeong, Y.T. One-step reduction of graphene oxide with l-glutathione. Colloids Surf. A Phys. Eng. Asp. 2011, 384, 543–548. [Google Scholar] [CrossRef]
- He, H.; Klinowski, J.; Forster, M.; Lerf, A. A new structural model for graphite oxide. Chem. Phys. Lett. 1998, 287, 5356. [Google Scholar] [CrossRef]
- Cheng, M.; Yang, R.; Zhang, L.; Shi, Z.; Yang, W.; Wang, D.; Xie, G.; Shi, D.; Zhang, G. Restoration of graphene from graphene oxide by defect repair. Carbon 2012, 50, 2581–2587. [Google Scholar] [CrossRef]
- Ci, L.; Song, L.; Jin, C.; Jariwala, D.; Wu, D.; Li, Y.; Srivastava, A.; Wang, Z.F.; Storr, K.; Balicas, L.; et al. Atomic layers of hybridized boron nitride and graphene domains. Nat. Mater. 2010, 9, 430–435. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Shao, Y.; Matson, D.W.; Li, J.; Lin, Y. Nitrogen-Doped Graphene and Its Application in Electrochemical Biosensing. ACS Nano 2010, 4, 1790–1798. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.S.; Ren, W.; Xu, L.; Li, F.; Cheng, H.M. Doped Graphene Sheets as Anode Materials with Superhigh Rate and Large Capacity for Lithium Ion Batteries. ACS Nano 2011, 5, 5463–5471. [Google Scholar] [CrossRef] [PubMed]
- Teobaldi, G.; Ohnishi, H.; Tanimura, K.; Tanimura, K.; Shluger, A.L. The effect of van der Waals interactions on the properties of intrinsic defects in graphite. Carbon 2010, 48, 4145–4161. [Google Scholar] [CrossRef]
- Pham, V.P.; Mishra, A.; Yeom, G.Y. The enhancement of hall mobility and conductivity of cvd graphene through radical doping and vacuum annealing. RSC Adv. 2017, 7, 16104–16108. [Google Scholar] [CrossRef]
- McAllister, M.J.; Li, J.-L.; Adamson, D.H.; Schniepp, H.C.; Abdala, A.A.; Liu, L.; Herrera-Alonso, M.; Milius, D.L.; Car, R.; Prud’homme, R.K.; et al. Single sheet functionalized graphene by oxidation and thermal expansion of graphite. Chem. Mater. 2007, 18, 4396. [Google Scholar] [CrossRef]
- Chen, L.; Xu, Z.; Li, J.; Min, C.; Liu, L.; Song, X.; Chen, G.; Meng, X. Reduction and disorder in graphene oxide induced by electron-beam irradiation. Mater. Lett. 2011, 65, 1229–1230. [Google Scholar] [CrossRef]
- Hummers, W.S.; Offeman, R.E. Preparation of Graphitic Oxide. J. Am. Chem. Soc. 1958, 80, 1339. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, L.; Xu, Z.; Li, Y.; Zhou, B.; Shan, M.; Wang, Z.; Guo, Q.; Qian, X. Preparing graphene with notched edges and nanopore defects by γ-ray etching of graphite oxide. Mater. Lett. 2012, 89, 226–228. [Google Scholar] [CrossRef]
- Kim, K.S.; Zhao, Y.; Jang, H.; Lee, S.Y.; Kim, J.M.; Kim, K.S.; Ahn, J.; Kim, P.; Choi, J.; Hong, B.H. Large-scale pattern growth of graphene films for stretchable transparent electrodes. Nature 2009, 457, 706–710. [Google Scholar] [CrossRef] [PubMed]
- Oleg, V.Y. Emergence of magnetism in graphene materials and nanostructures. Rep. Prog. Phys. 2010, 73, 056501. [Google Scholar]
- Wang, Y.; Huang, Y.; Song, Y.; Zhang, X.; Ma, Y.; Liang, J.; Chen, Y. Room-Temperature Ferromagnetism of Graphene. Nano Lett. 2008, 9, 220–224. [Google Scholar] [CrossRef] [PubMed]
- Sun, S.; Wang, C.Y.; Chen, M.M.; Zheng, J. A novel method to control atomic defects in graphene sheets, by selective surface reactions. Appl. Surf. Sci. 2013, 283, 566–570. [Google Scholar] [CrossRef]
- Sepioni, M.; Nair, R.R.; Rablen, S.; Narayanan, J.; Tuna, F.; Winpenny, R.; Geim, A.K.; Grigorieva, I.V. Limits on Intrinsic Magnetism in Graphene. Phys. Rev. Lett. 2010, 105, 207205. [Google Scholar] [CrossRef] [PubMed]
- Hernandez, Y.; Nicolosi, V.; Lotya, M.; Blighe, F.M.; Sun, Z.; De, S.; Mcgovern, I.T.; Holland, B.; Byrne, M.; Gun’ko, Y.K.; et al. High-yield production of graphene by liquid-phase exfoliation of graphite. Nat. Nanotechnol. 2008, 3, 563–568. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Pei, S.; Ren, W.; Gao, L.; Cheng, M. Efficient Preparation of Large-Area Graphene Oxide Sheets for Transparent Conductive Films. ACS Nano 2010, 4, 5245–5252. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Xue, K. Engineering graphene by oxidation: A first-principles study. Nanotechnology 2010, 21, 045704. [Google Scholar] [CrossRef] [PubMed]
- Biel, B.; Blasé, X.; Triozon, F.; Roche, S. Anomalous Doping Effects on Charge Transport in Graphene Nanoribbons. Phys. Rev. Lett. 2009, 102, 096803. [Google Scholar] [CrossRef] [PubMed]
- Hao, F.; Fang, D.; Xu, Z. Mechanical and thermal transport properties of graphene with defects. Appl. Phys. Lett. 2011, 99, 041901. [Google Scholar] [CrossRef]
- Yazyev, O.V. Magnetism in Disordered Graphene and Irradiated Graphite. Phys. Rev. Lett. 2008, 101, 037203. [Google Scholar] [CrossRef] [PubMed]
- Balandin, A.A.; Ghosh, S.; Bao, W.; Calizo, I.; Teweldebrhan, D.; Miao, F.; Lau, C.N. Superior thermal conductivity of single-layer graphene. Nano Lett. 2008, 8, 902–907. [Google Scholar] [CrossRef] [PubMed]
- Reddy, C.D.; Ragendran, S.; Liew, K.M. Equilibrium configuration and continuum elastic properties of finite sized graphene. Nanotechology 2006, 17, 864–870. [Google Scholar] [CrossRef]
- Chien, S.K.; Yang, Y.T.; Chen, C.O.K. Influence of hydrogen functionalization on thermal conductivity of graphene: Nonequilibrium molecular dynamics simulations. Appl. Phys. Lett. 2011, 98, 033107. [Google Scholar] [CrossRef]
- Bo, X.; Li, M.; Han, C.; Guo, L. The influence of boron dopant on the electrochemical properties of graphene as an electrode material and a support for Pt catalysts. Electrochim. Acta 2013, 114, 582–589. [Google Scholar] [CrossRef]
- Yeh, C.C.; Chen, D.H. Ni/reduced graphene oxide nanocomposite as a magnetically recoverable catalyst with near infrared photo thermally enhanced activity. Appl. Catal. B Environ. 2014, 150–151, 298–304. [Google Scholar] [CrossRef]
- Khai, T.V.; Na, H.G.; Kwak, D.S.; Kwon, Y.J.; Ham, H.; Shim, K.B.; Kim, H.W. Comparison study of structural and optical properties of boron-doped and undoped graphene oxide films. Chem. Eng. J. 2012, 211–212, 369–377. [Google Scholar] [CrossRef]
- Verma, S.; Verma, D.; Jain, S.L. Magnetically separable palladium-graphene nanocomposite as heterogeneous catalyst for the synthesis of 2-alkylquinolines via one pot reaction of anilines with alkenyl ethers. Tetrahedron Lett. 2014, 55, 2406–2409. [Google Scholar] [CrossRef]
- Gao, T.; Huang, K.; Qi, X.; Li, H.; Yang, L.; Zhong, J. Free-standing SnO2 nanoparticles graphene hybrid paper for advanced lithium-ion batteries. Ceram. Int. 2014, 40, 6891–6897. [Google Scholar] [CrossRef]
- Li, S.; Wang, B.; Liu, J. In situ one-step synthesis of CoFe2O4/graphene nanocomposites as high-performance anode for lithium-ion batteries. Electrochim. Acta 2014, 129, 33–39. [Google Scholar] [CrossRef]
- Zhang, M.; Yang, X.; Kan, X.; Wang, X.; Ma, L.; Jia, M. Carbon-encapsulated CoFe2O4/graphene nanocomposite as high performance anode for lithium ion batteries. Electrochim. Acta 2013, 112, 727–734. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, Z.; Zhang, H.; Chen, Y.; Cheng, Z.; Zhong, Y.; Ye, Y.; Lei, X. Synthesis of the graphene/nickel oxide composite and its electrochemical performance for supercapacitors. Int. J. Hydrog. Energy 2014, 39, 16171–16178. [Google Scholar] [CrossRef]
- Zhang, F.; Xiao, F.; Dong, Z.H.; Shi, W. Synthesis of polypyrrole wrapped graphene hydrogels composites as supercapacitor electrodes. Electrochim. Acta 2013, 114, 125–132. [Google Scholar] [CrossRef]
- Liu, J.; Cui, L.; Losic, D. Graphene and graphene oxide as new nanocarriers for drug delivery applications. Acta Biomater. 2013, 9, 9243–9257. [Google Scholar] [CrossRef] [PubMed]
- Sevinçli, H.; Topsakal, M.; Durgun, E.; Ciraci, S. Electronic and magnetic properties of 3d transition-metal atom adsorbed graphene and graphene nanoribbons. Phys. Rev. B 2008, 77, 195434. [Google Scholar] [CrossRef]
- Lemme, M.C.; Bell, D.C.; Williams, J.R.; Stern, L.A.; Baugher, B.W.H.; Jarillo-Herrero, P.; Marcus, C.M. Etching of Graphene Devices with a Helium Ion Beam. ACS Nano 2009, 3, 2674–2676. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Cai, W.; An, J.; Kim, S.; Nah, J.; Yang, D.; Piner, R.; Velamakanni, A.; Jung, I.; Tutuc, E.; et al. Large-Area Synthesis of High-Quality and Uniform Graphene Films on Copper Foils. Science 2009, 324, 1312–1314. [Google Scholar] [CrossRef] [PubMed]
- Kalhor, N.; Boden, S.A.; Mizuta, H. Sub-10 nm patterning by focused He-ion beam milling for fabrication of downscaled graphene nano devices. Microelectron. Eng. 2014, 114, 70–77. [Google Scholar] [CrossRef]
- Vaari, J.; Lahtinen, J.; Hautojärvi, P. The adsorption and decomposition of acetylene on clean and K-covered Co(0001). Catal. Lett. 1997, 44, 43–49. [Google Scholar] [CrossRef]
- Vázquez de Parga, A.L.; Calleja, F.; Borca, B.; Passeggi, M.C.G., Jr.; Hinarejos, J.J.; Guinea, F.; Miranda, R. Periodically Rippled Graphene: Growth and Spatially Resolved Electronic Structure. Phys. Rev. Lett. 2008, 100, 056807. [Google Scholar] [CrossRef] [PubMed]
- Ueta, H.; Saida, M.; Nakai, C.; Yamada, Y.; Sasaki, M.; Yamamoto, S. Highly oriented monolayer graphite formation on Pt (111) by a supersonic methane beam. Surf. Sci. 2004, 560, 183–190. [Google Scholar] [CrossRef]
- Starr, D.E.; Pazhetnov, E.M.; Stadnichenko, A.I.; Boronin, A.I.; Shaikhutdinov, S.K. Carbon films grown on Pt (111) as supports for model gold catalysts. Surf. Sci. 2006, 600, 2688–2695. [Google Scholar] [CrossRef]
- Reina, A.; Thiele, S.; Jia, X.; Bhaviripudi, S.; Dresselhaus, M.S.; Schaefer, J.A.; Kong, J. Growth of large-area single- and Bi-layer graphene by controlled carbon precipitation on polycrystalline Ni surfaces. Nano Res. 2009, 2, 509–516. [Google Scholar] [CrossRef]
- Sun, Z.; Yan, Z.; Yao, J.; Beitler, E.; Zhu, Y.; Tour, J.M. Growth of graphene from solid carbon sources. Nature 2010, 468, 549–552. [Google Scholar] [CrossRef] [PubMed]
- Sheng, K.X.; Xu, Y.X.; Li, C.; Shi, G.Q. High-performance self-assembled graphene hydrogels prepared by chemical reduction of graphene oxide. New Carbon Mater. 2011, 26, 9–15. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, W.; Li, W.; Yu, W.; Liu, X. A Review on Lattice Defects in Graphene: Types, Generation, Effects and Regulation. Micromachines 2017, 8, 163. https://doi.org/10.3390/mi8050163
Tian W, Li W, Yu W, Liu X. A Review on Lattice Defects in Graphene: Types, Generation, Effects and Regulation. Micromachines. 2017; 8(5):163. https://doi.org/10.3390/mi8050163
Chicago/Turabian StyleTian, Wenchao, Wenhua Li, Wenbo Yu, and Xiaohan Liu. 2017. "A Review on Lattice Defects in Graphene: Types, Generation, Effects and Regulation" Micromachines 8, no. 5: 163. https://doi.org/10.3390/mi8050163
APA StyleTian, W., Li, W., Yu, W., & Liu, X. (2017). A Review on Lattice Defects in Graphene: Types, Generation, Effects and Regulation. Micromachines, 8(5), 163. https://doi.org/10.3390/mi8050163




