Design and Experiment of a Solder Paste Jetting System Driven by a Piezoelectric Stack
Abstract
:1. Introduction
2. Principle of the Jetting System
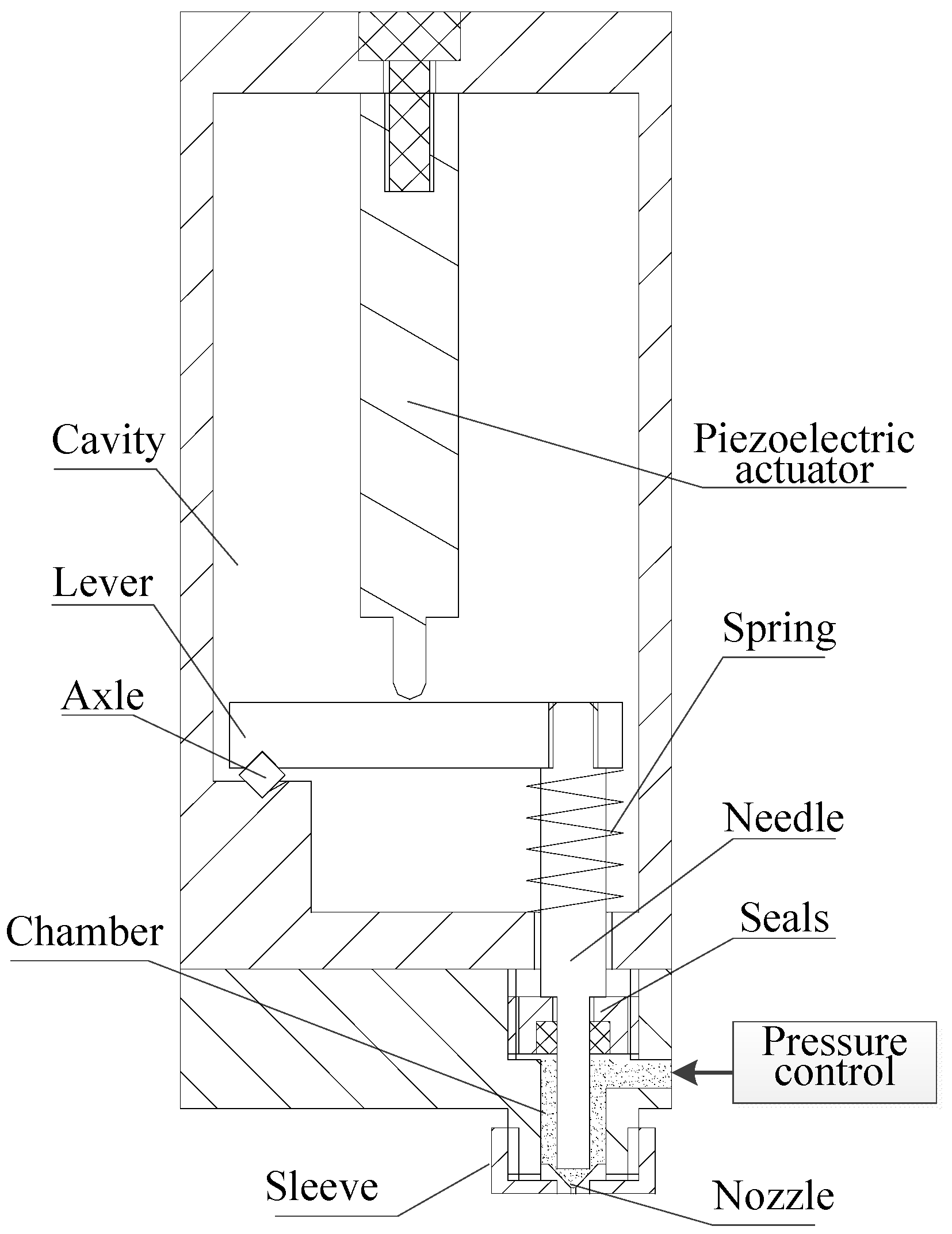
2.1. The Jetting System Structure
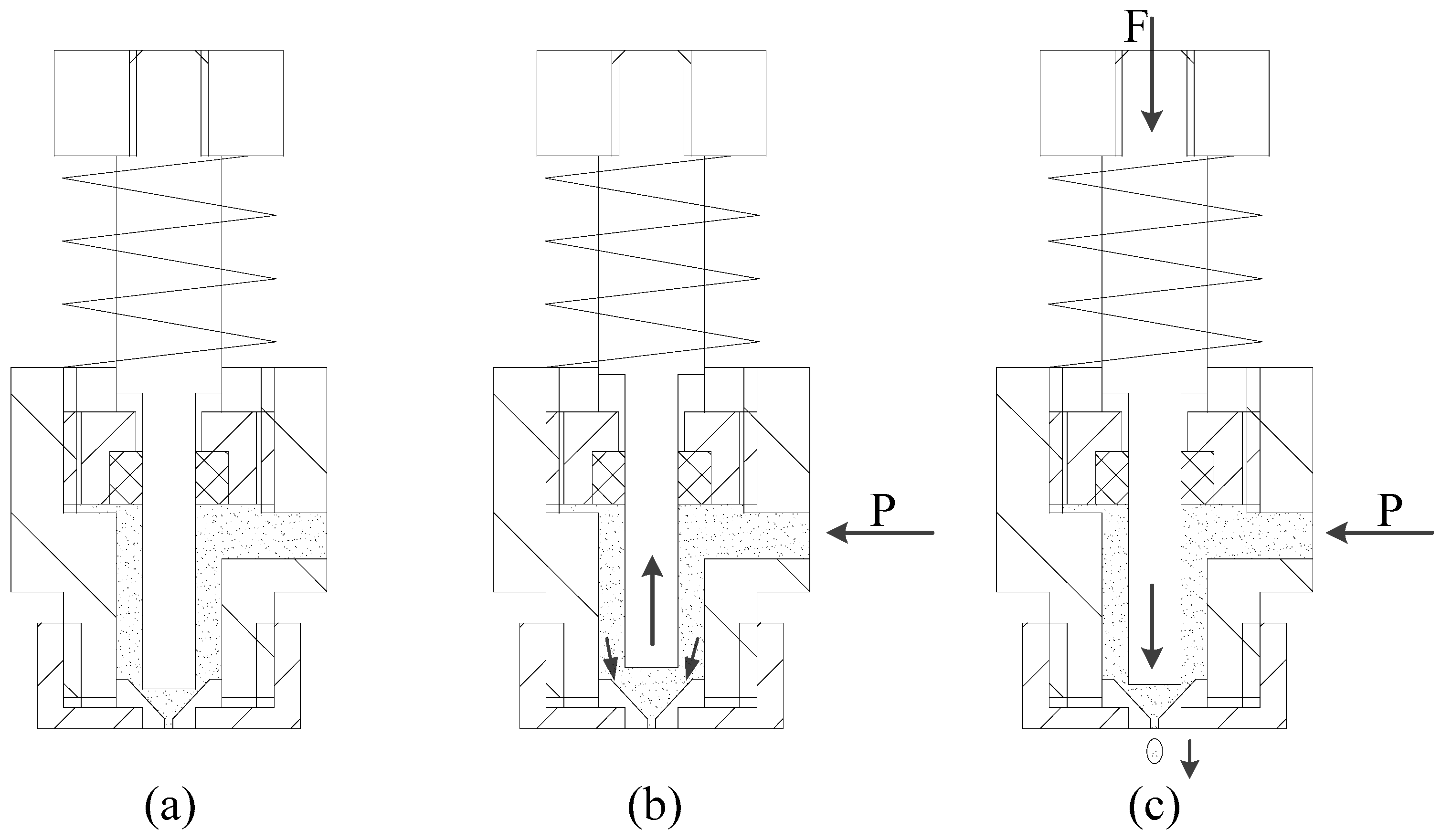
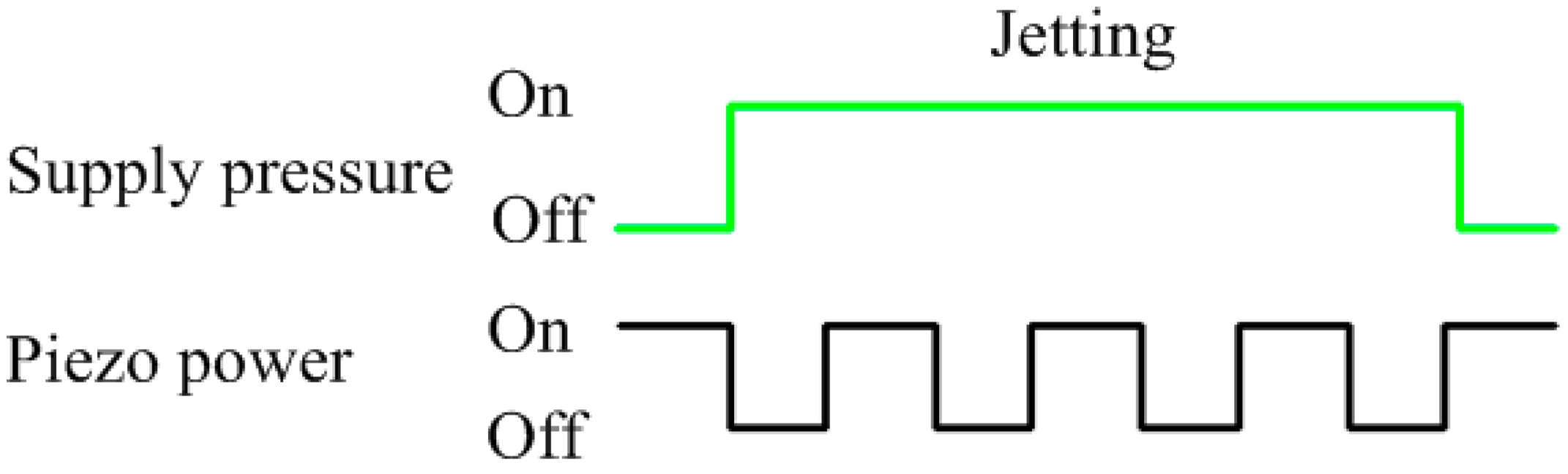
2.2. Theoretical Analysis of Jetting
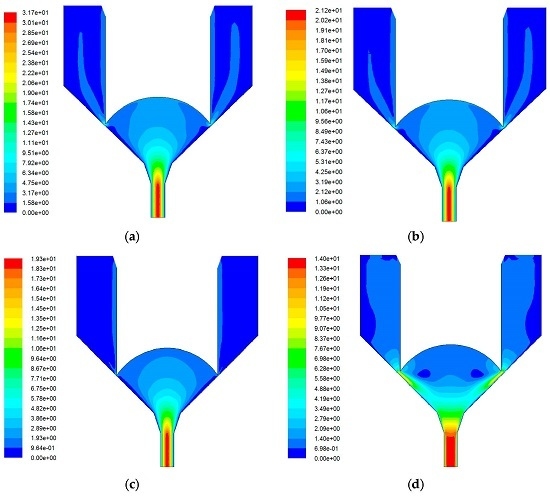
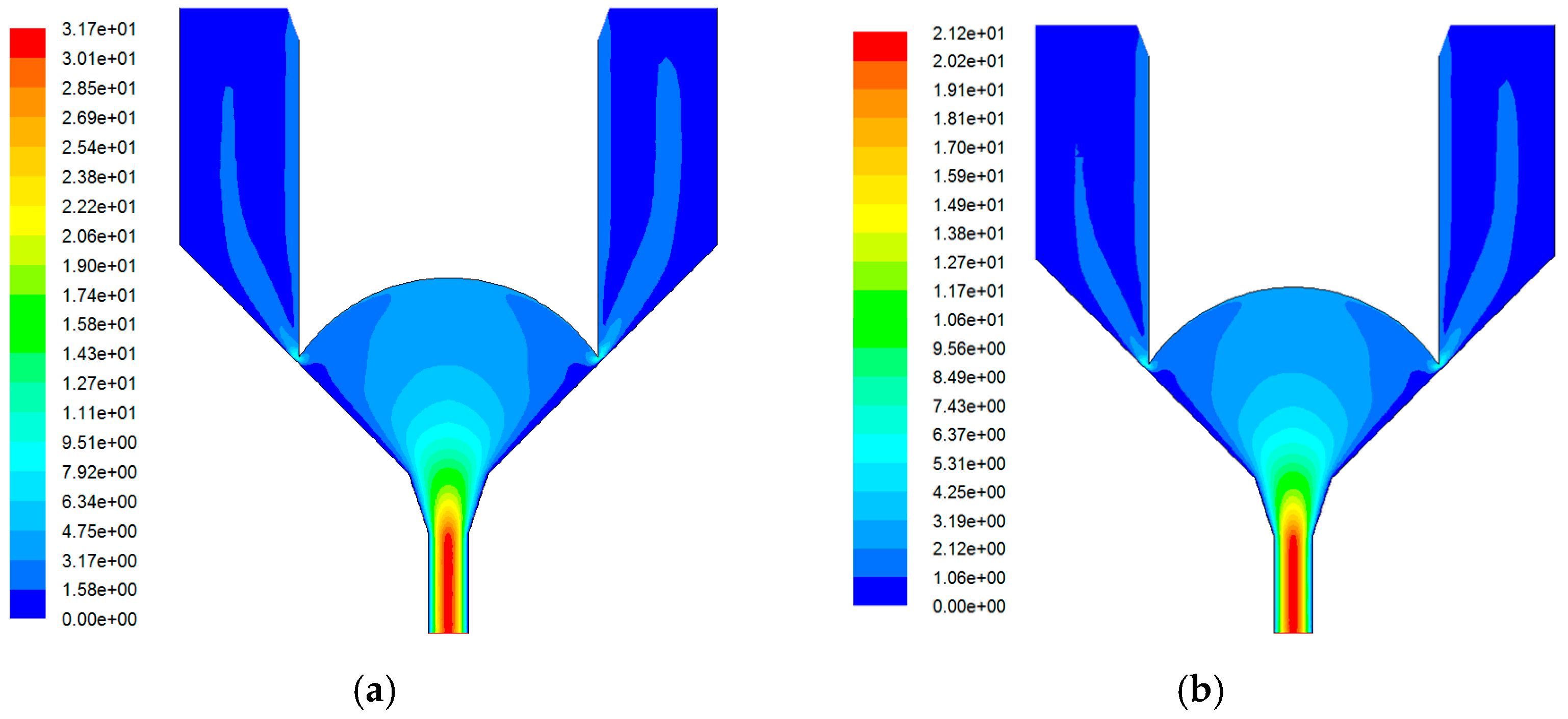
2.3. Flow Field Simulation
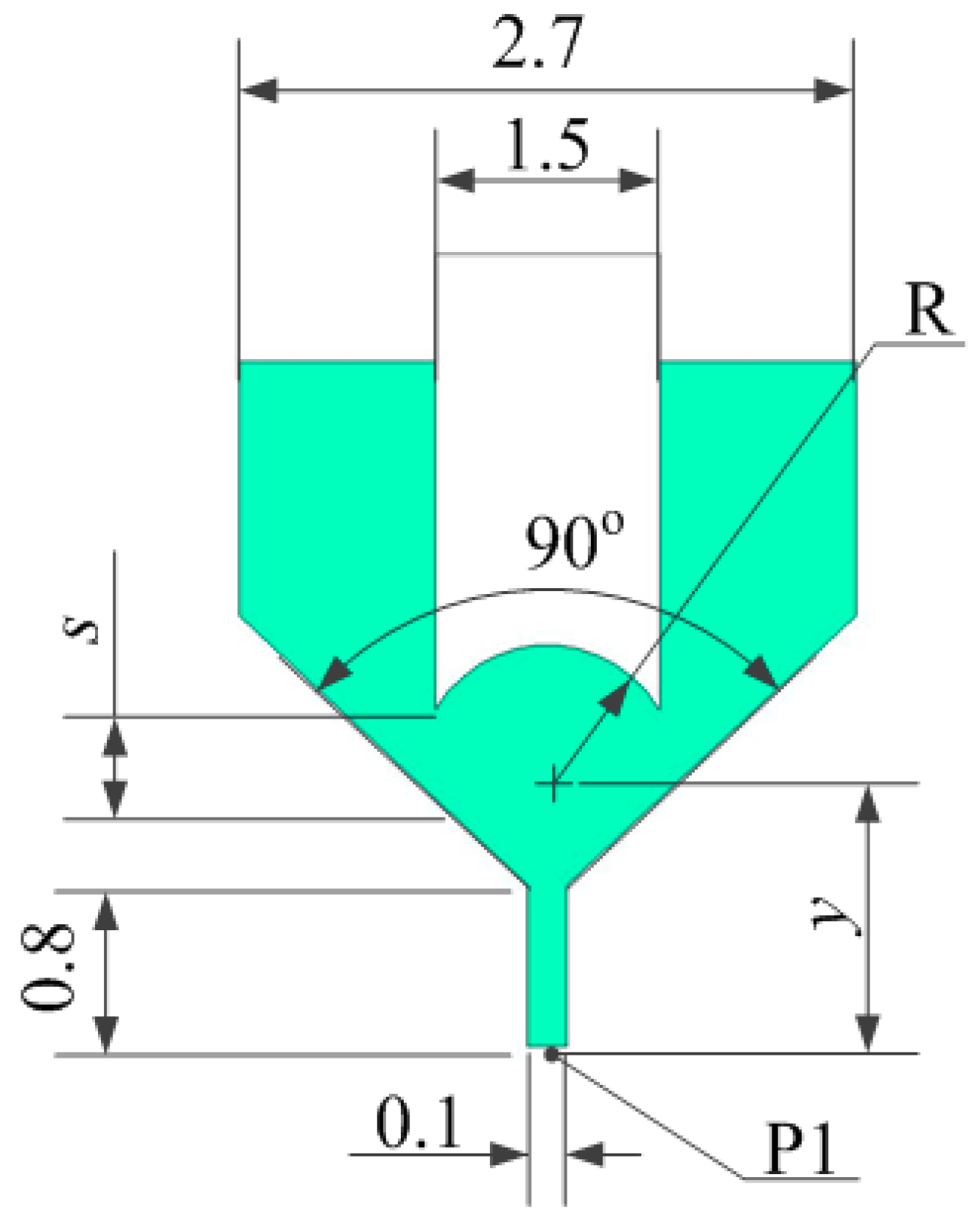
2.3.1. Needle Structure
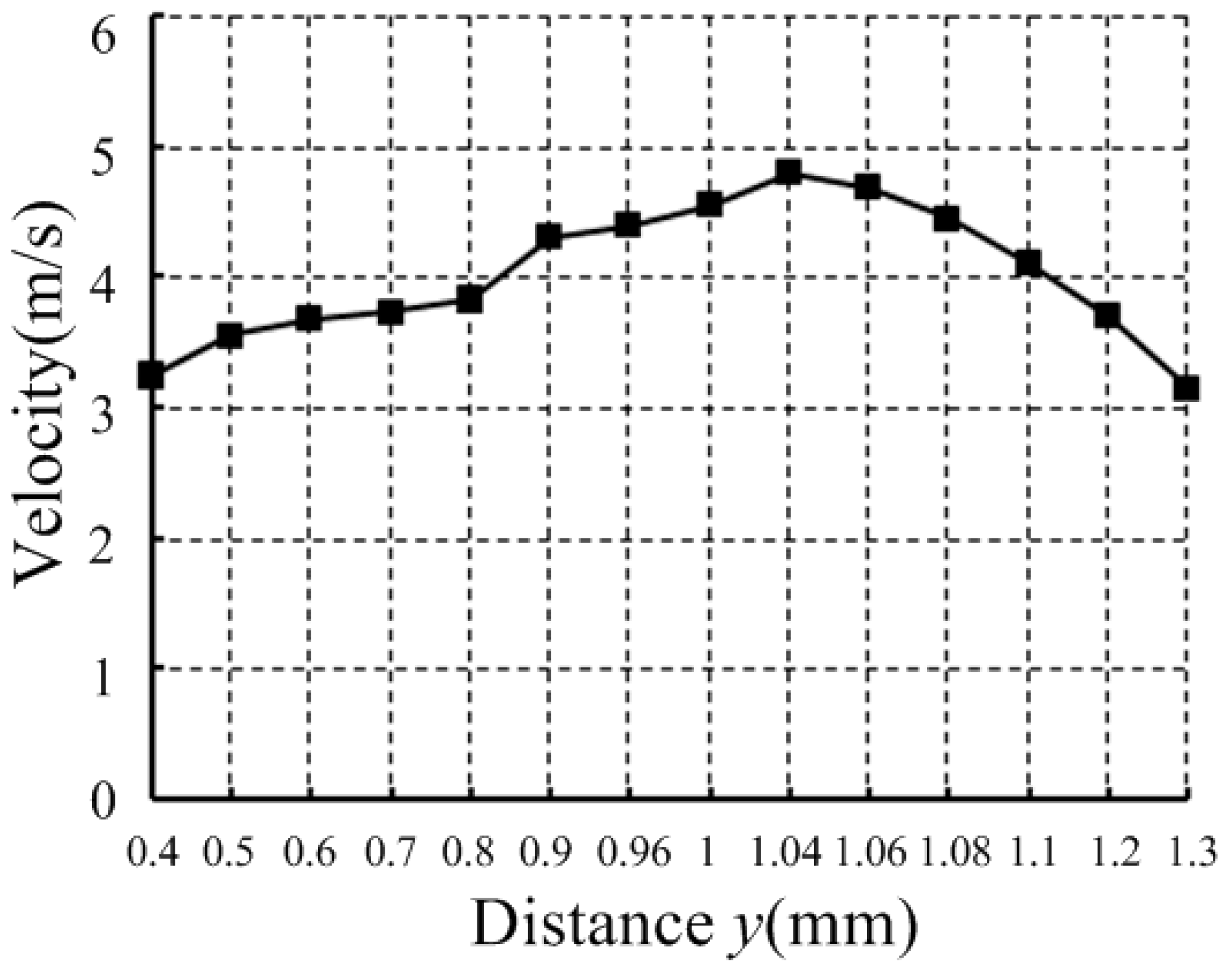
2.3.2. Needle Velocity
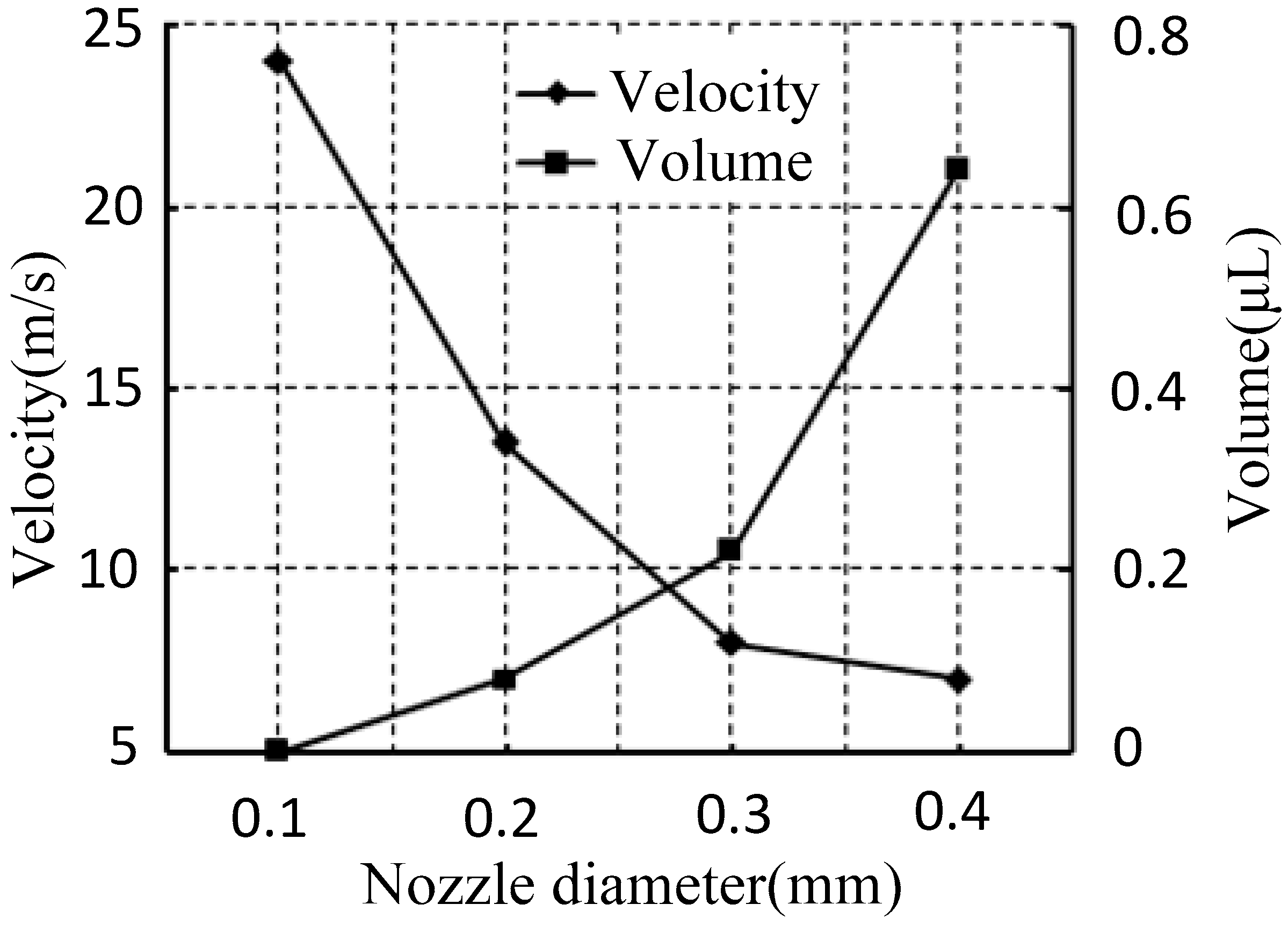
2.3.3. Nozzle Diameter
3. Experiment
3.1. Experimental Set-Up
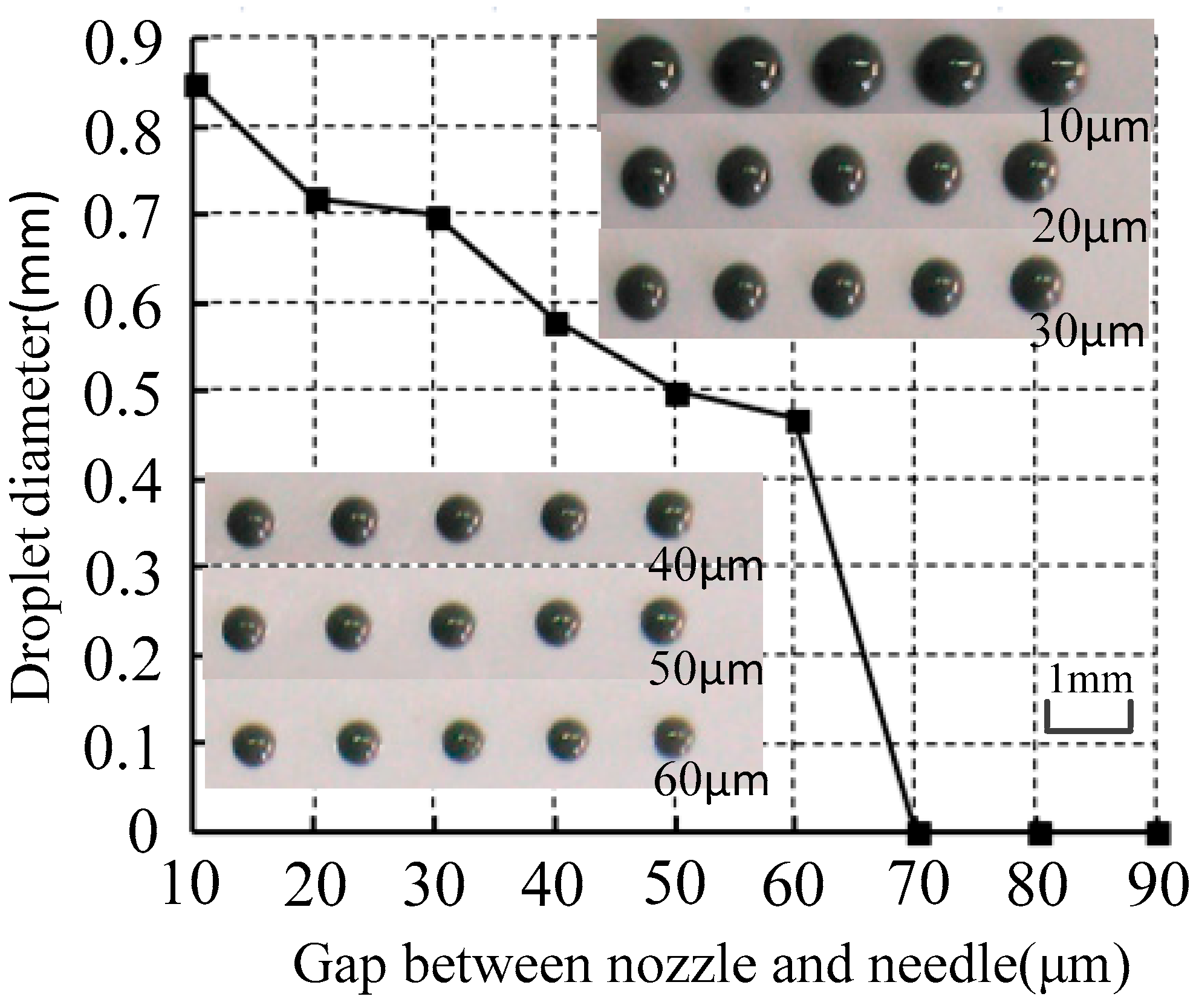
3.2. Gap Between Nozzle and Needle
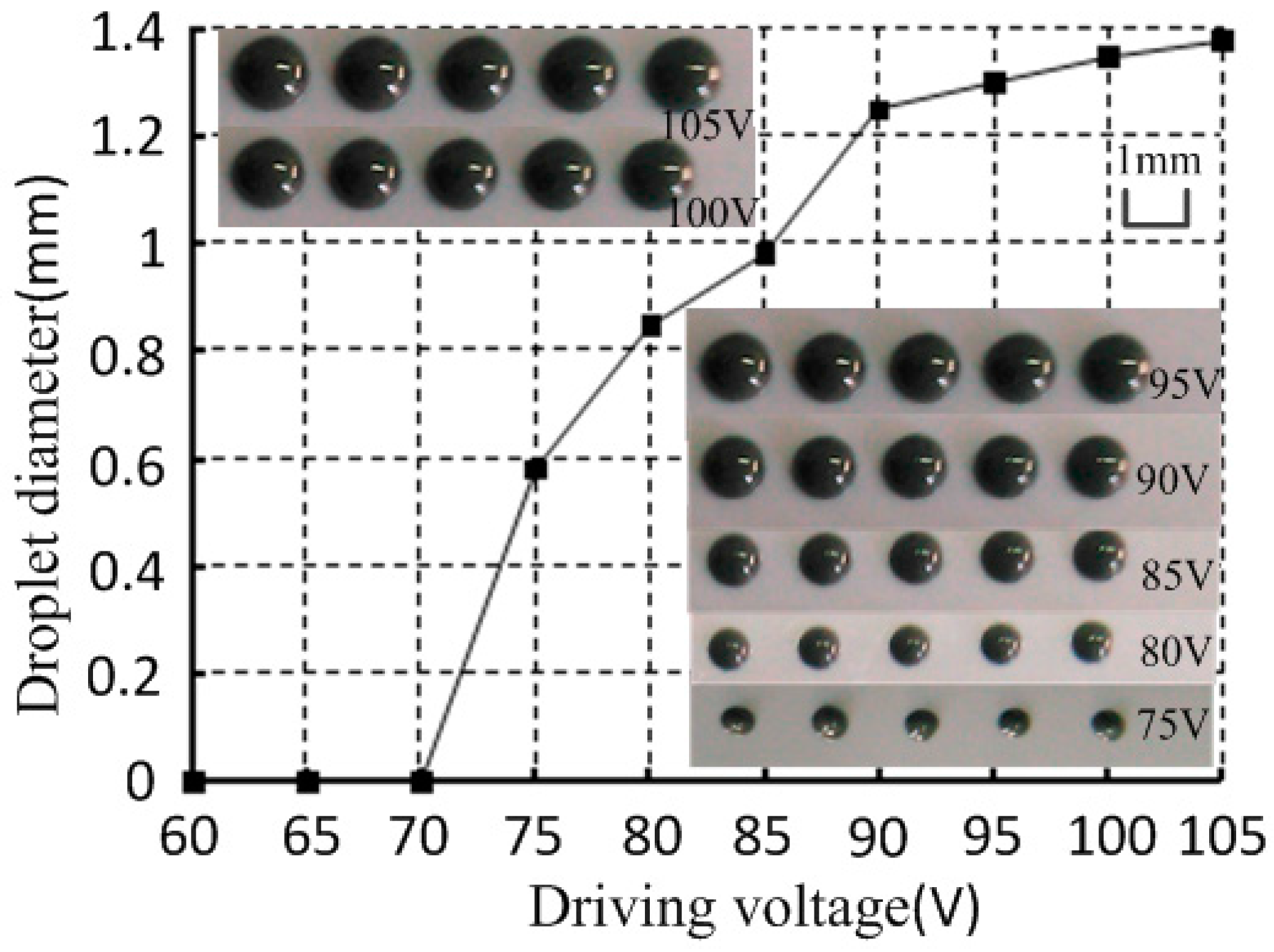
3.3. Driving Voltage
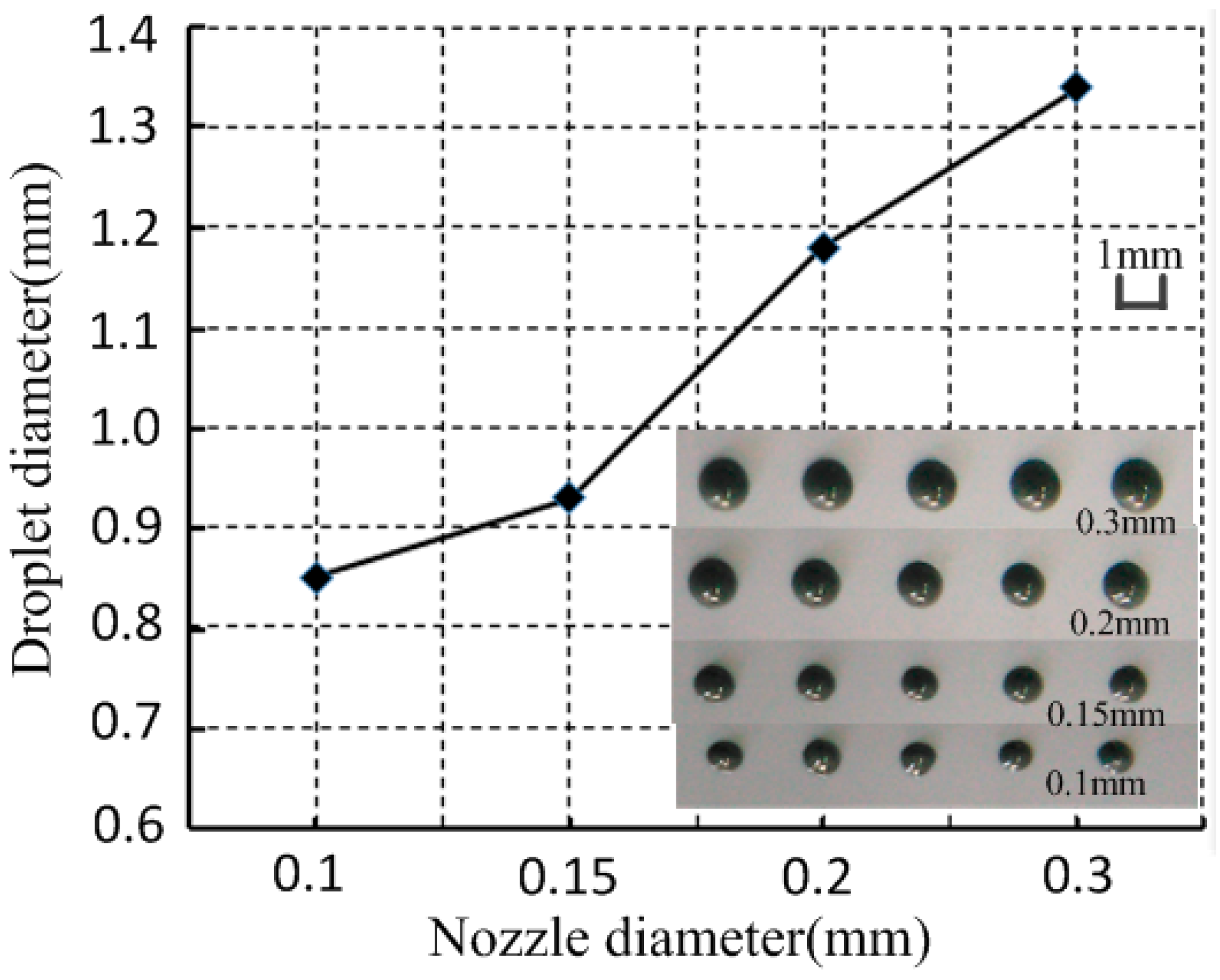
3.4. Nozzle Diameter
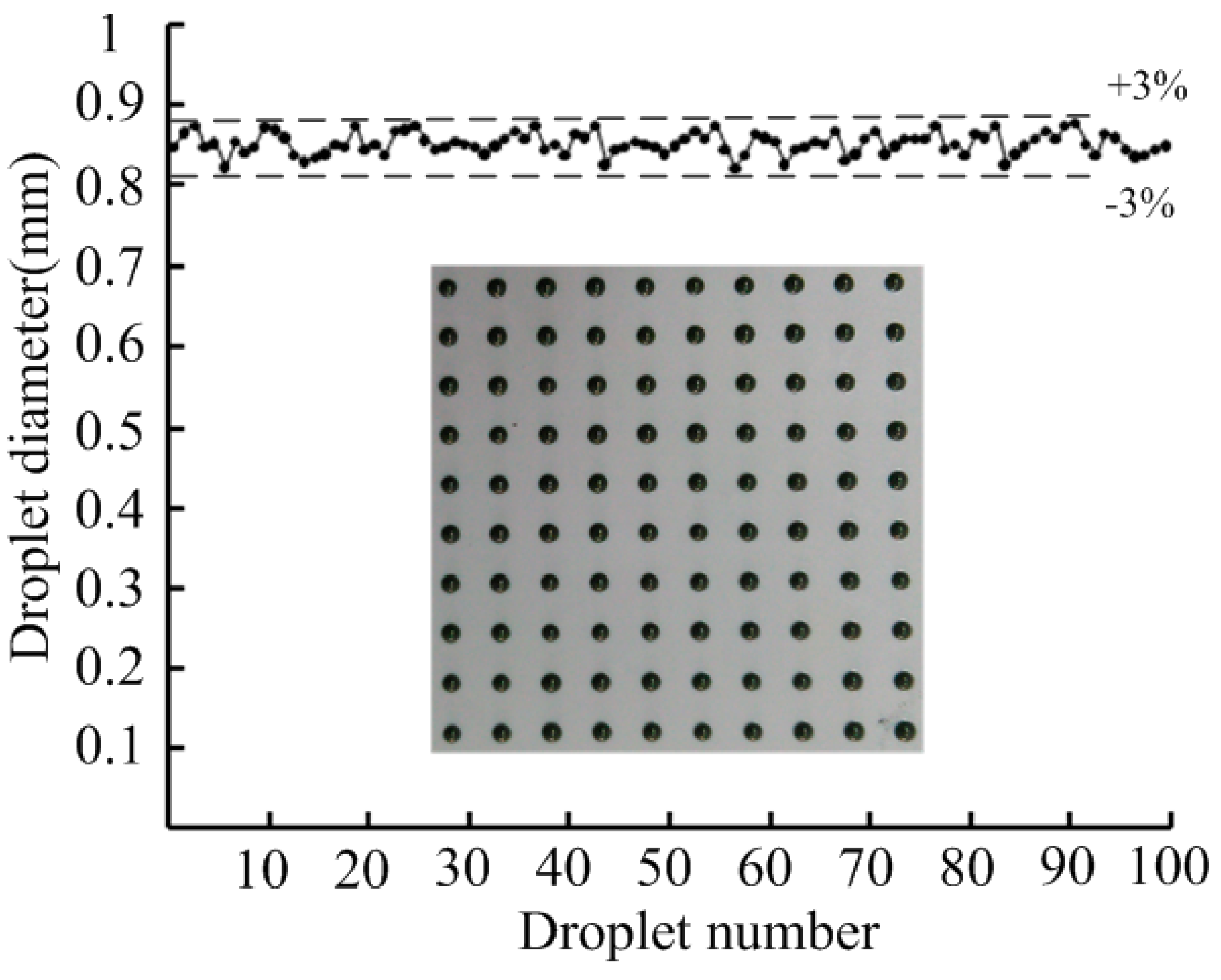
3.5. Consistency Analysis
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Li, M.-H.C.; Al-Refaie, A.; Yang, C.-Y. Dmaic approach to improve the capability of smt solder printing process. IEEE Trans. Electr. Packag. Manuf. 2008, 31, 126–133. [Google Scholar] [CrossRef]
- Becker, K.-F.; Koch, M.; Voges, S.; Thomas, T.; Fliess, M.; Bauer, J.; Braun, T.; Aschenbrenner, R.; Schneider-Ramelow, M.; Lang, K.-D. Precision jetting of solder paste—A versatile tool for small volume production. In Proceedings of the International Symposium on Microelectronics, San Diego, CA, USA, 13–16 October 2014; pp. 000438–000443.
- Chen, C.-P.; Li, H.-X.; Ding, H. Modeling and control of time-pressure dispensing for semiconductor manufacturing. Int. J. Autom. Comput. 2007, 4, 422–427. [Google Scholar] [CrossRef]
- Chen, X.B.; Shoenau, G.; Zhang, W. Modeling of time-pressure fluid dispensing processes. IEEE Trans. Electr. Packag. Manuf. 2000, 23, 300–305. [Google Scholar] [CrossRef]
- Peng, J.; Guiling, D. Numerical simulations of 3d flow in the archimedes pump and analysis of its influence on dispensing quality. In Proceedings of the International Symposium on High Density packaging and Microsystem Integration, HDP’07, Shanghai, China, 26–28 June 2007; pp. 1–5.
- Ashley, D.; Adamson, S.J. Advancements in solder paste dispensing. Smt Surf. Mount Technol. 2008, 22, 10–14. [Google Scholar]
- Hutchings, I.; Tuladhar, T.; Mackley, M.; Vadillo, D.; Hoath, S.; Martin, G. Links between ink rheology, drop-on-demand jet formation, and printability. J. Imag. Sci. Technol. 2009, 53, 41208-1–41208-8. [Google Scholar]
- Meacham, J.; Varady, M.; Degertekin, F.; Fedorov, A. Droplet formation and ejection from a micromachined ultrasonic droplet generator: Visualization and scaling. Phys. Fluids 2005, 17, 100605. [Google Scholar] [CrossRef]
- Lass, N.; Riegger, L.; Zengerle, R.; Koltay, P. Enhanced liquid metal micro droplet generation by pneumatic actuation based on the starjet method. Micromachines 2013, 4, 49–66. [Google Scholar] [CrossRef]
- Maeda, K.; Onoe, H.; Takinoue, M.; Takeuchi, S. Observation and manipulation of a capillary jet in a centrifuge-based droplet shooting device. Micromachines 2015, 6, 1526–1533. [Google Scholar] [CrossRef]
- Jayasinghe, S.N. Advanced jet protocols for directly engineering living cells: A genesis to alternative biohandling approaches for the life sciences. Regen. Med. 2008, 3, 49–61. [Google Scholar] [CrossRef] [PubMed]
- Odenwälder, P.K.; Irvine, S.; McEwan, J.R.; Jayasinghe, S.N. Bio-electrosprays: A novel electrified jetting methodology for the safe handling and deployment of primary living organisms. Biotechnol. J. 2007, 2, 622–630. [Google Scholar] [CrossRef] [PubMed]
- Pierik, A. Advanced Microarray Technologies for Clinical Diagnostics; Technische Universiteit Eindhoven: Eindhoven, The Netherlands, 2011. [Google Scholar]
- Joe Lopes, A.; MacDonald, E.; Wicker, R.B. Integrating stereolithography and direct print technologies for 3d structural electronics fabrication. Rapid Prototyp. J. 2012, 18, 129–143. [Google Scholar] [CrossRef]
- Szczech, J.; Megaridis, C.; Zhang, J.; Gamota, D. Ink jet processing of metallic nanoparticle suspensions for electronic circuitry fabrication. Microscale Thermophys. Eng. 2004, 8, 327–339. [Google Scholar] [CrossRef]
- Nico, C. Jetting solder paste opens up new possibilities in your SMT production. In Proceedings of the ICSR (Soldering and Reliability) Conference Proceedings, Toronto, ON, Canada, 14–17 May 2013; pp. 1–4.
- Mohanty, R. Dispensing-solder paste jetting: A broadband solution. Print. Circuit Des. Fab-Circuits Assem. 2011, 28, 36. [Google Scholar]
- Holm, W.; Nilsson, K.; Berg, J.; Kronstedt, J.; Sandell, H. Jetting Device and Method at a Jetting Device. U.S. Patent 8,215,535, 10 July 2012. [Google Scholar]
- Lu, S.; Jiang, H.; Li, M.; Liu, J.; Gu, S.; Jiao, X.; Liu, X. Nozzle and needle during high viscosity adhesive jetting based on piezoelectric jet dispensing. Smart Mater. Struct. 2015, 24, 105023. [Google Scholar] [CrossRef]
- Nguyen, Q.-H.; Choi, M.-K.; Choi, S.-B. A new type of piezostack-driven jetting dispenser for semiconductor electronic packaging: Modeling and control. Smart Mater. Struct. 2008, 17, 015033. [Google Scholar] [CrossRef]
- Shu, X.; Zhang, H.; Liu, H.; Xie, D.; Xiao, J. Experimental study on high viscosity fluid micro-droplet jetting system. Sci. China Ser. E Technol. Sci. 2010, 53, 182–187. [Google Scholar] [CrossRef]
- Wang, L.; Du, X.; Li, Y.; Luo, Z.; Zheng, G.; Sun, D. Simulation and experiment study on adhesive ejection behavior in jetting dispenser. J. Adhes. Sci. Technol. 2014, 28, 53–64. [Google Scholar] [CrossRef]



| Liquid Density ρ (kg/m−3) | Viscosity μ (Pa·s) | Solid Density (kg/m−3) | Particle Diameter (μm) |
|---|---|---|---|
| 1225 | 40 | 8600 | 20 |
© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, S.; Jiao, X.; Liu, J.; Yang, Z.; Jiang, H.; Lv, Q. Design and Experiment of a Solder Paste Jetting System Driven by a Piezoelectric Stack. Micromachines 2016, 7, 112. https://doi.org/10.3390/mi7070112
Gu S, Jiao X, Liu J, Yang Z, Jiang H, Lv Q. Design and Experiment of a Solder Paste Jetting System Driven by a Piezoelectric Stack. Micromachines. 2016; 7(7):112. https://doi.org/10.3390/mi7070112
Chicago/Turabian StyleGu, Shoudong, Xiaoyang Jiao, Jianfang Liu, Zhigang Yang, Hai Jiang, and Qingqing Lv. 2016. "Design and Experiment of a Solder Paste Jetting System Driven by a Piezoelectric Stack" Micromachines 7, no. 7: 112. https://doi.org/10.3390/mi7070112
APA StyleGu, S., Jiao, X., Liu, J., Yang, Z., Jiang, H., & Lv, Q. (2016). Design and Experiment of a Solder Paste Jetting System Driven by a Piezoelectric Stack. Micromachines, 7(7), 112. https://doi.org/10.3390/mi7070112