A Nonlinear Suspended Energy Harvester for a Tire Pressure Monitoring System
Abstract
:1. Introduction
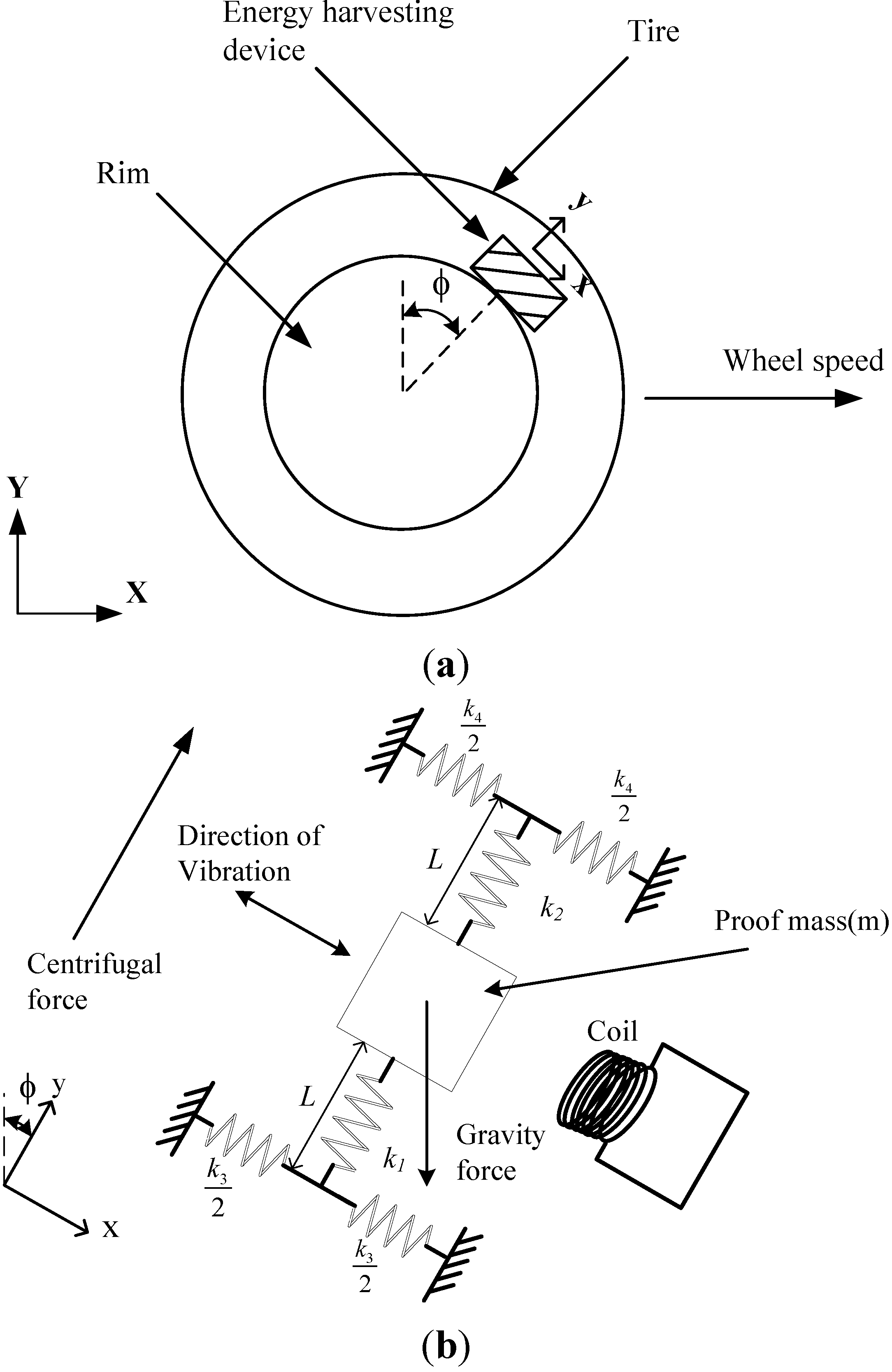
2. Overall Design of the NSEH
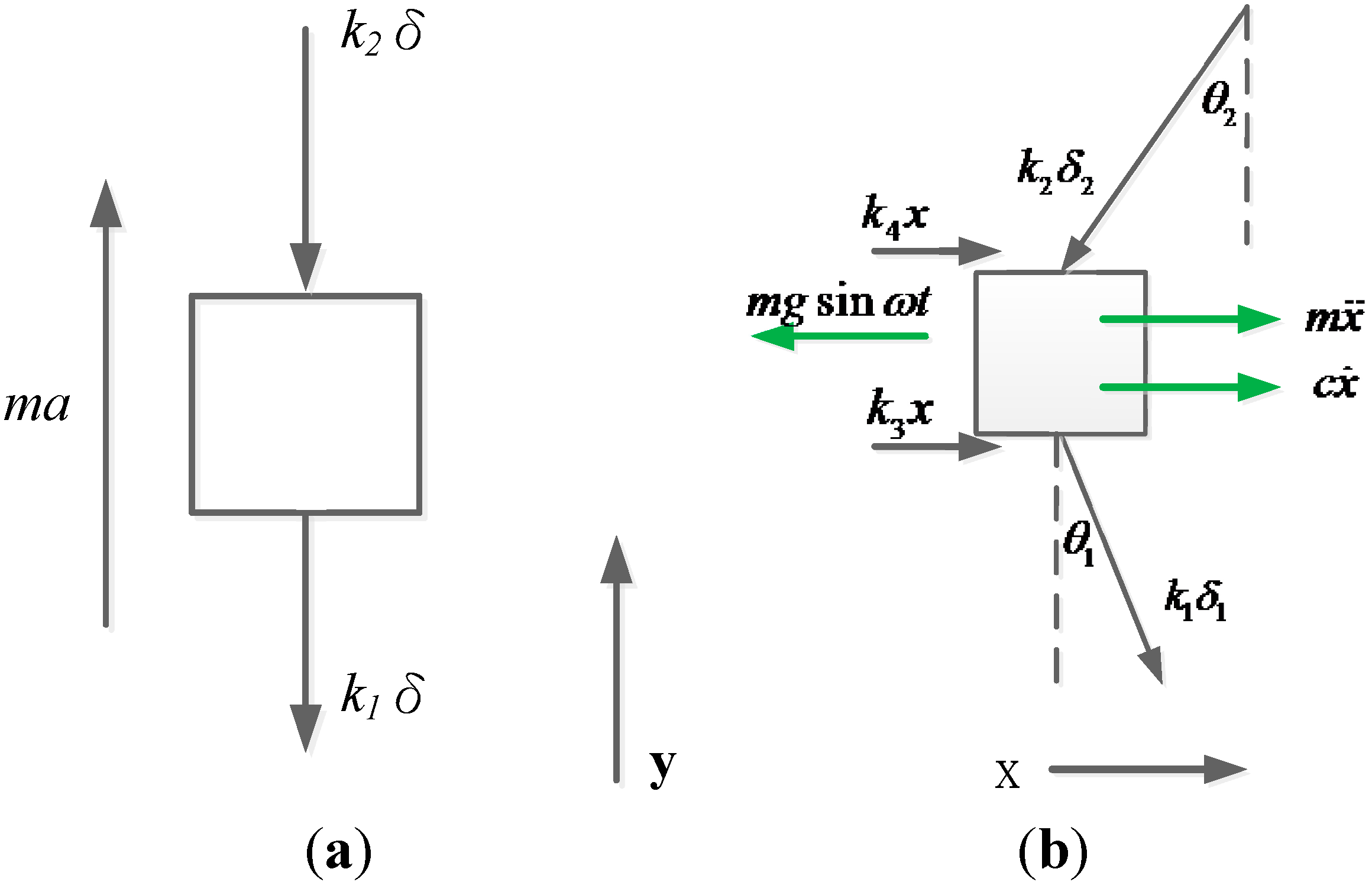
2.1. Kinetic Equations
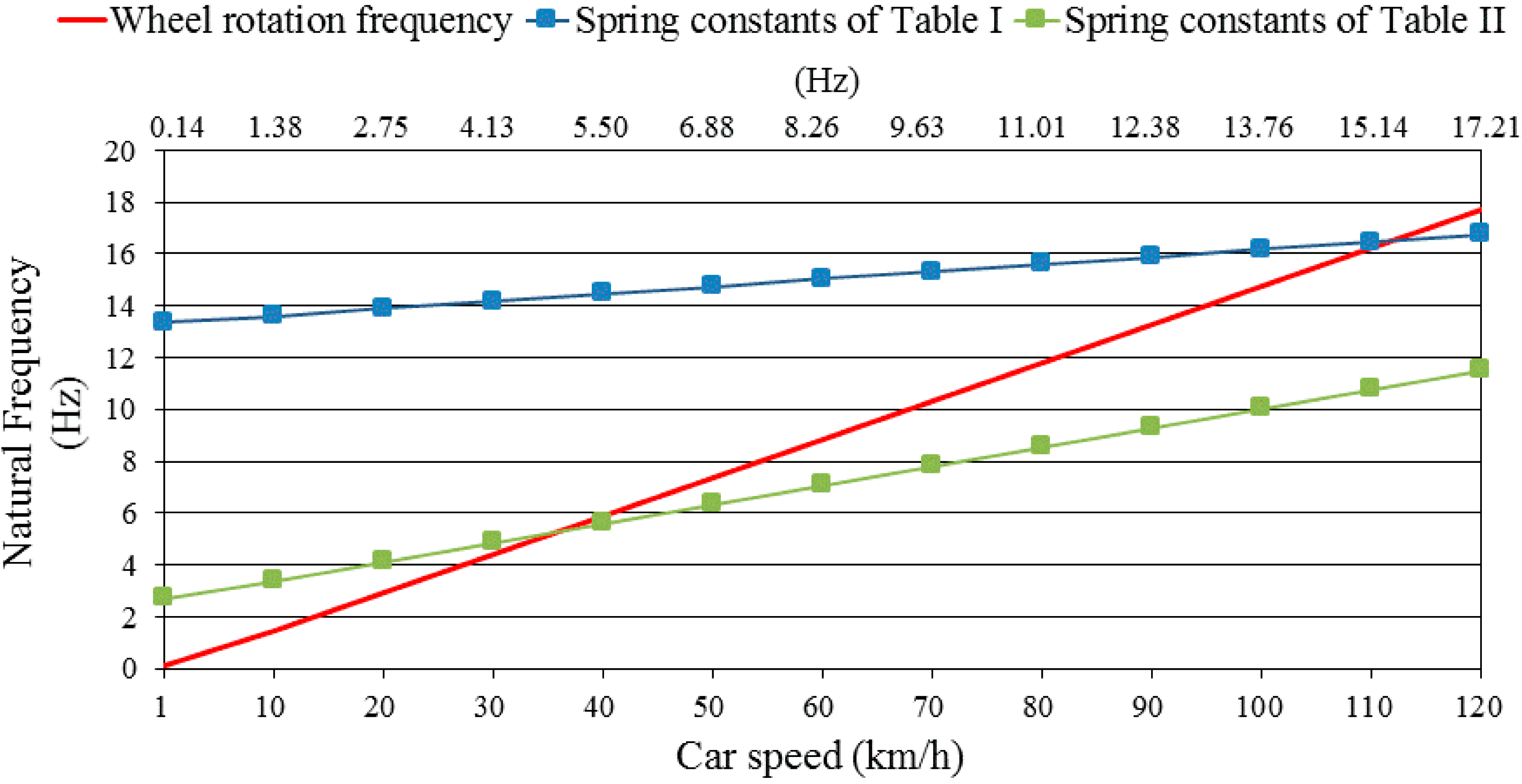
2.2. Natural Frequency of the NSEH
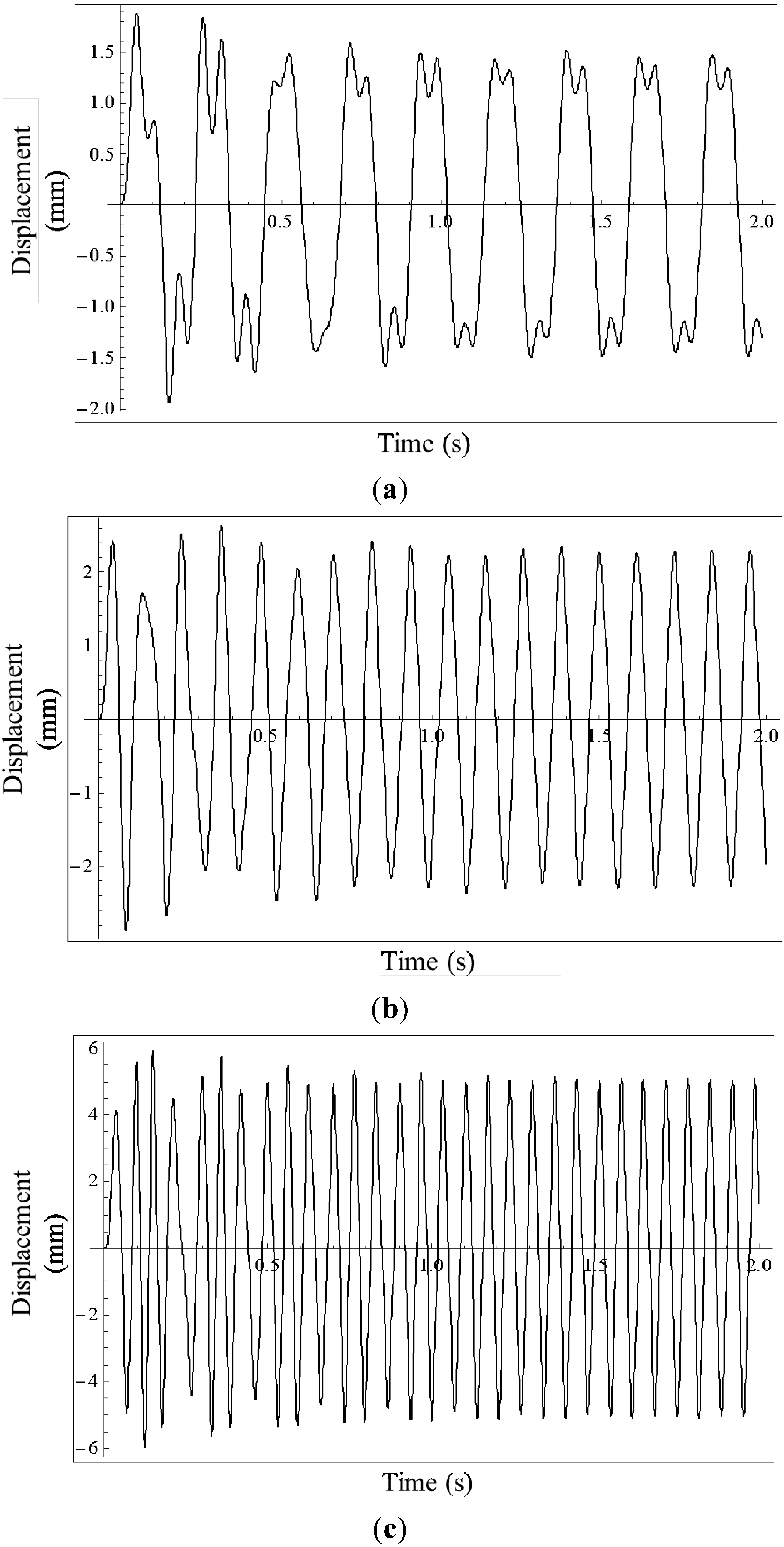
2.3. Numerical Results Obtained Using Analytical Models
| L (m) | k1 (N/m) | k2 (N/m) | k3 (N/m) | k4 (N/m) | m (kg) | r (m) | R (m) | C (N·s/m) |
|---|---|---|---|---|---|---|---|---|
| 0.02 | 4030 | 4000 | 35 | 35 | 0.01 | 0.2 | 0.3 | 0.1 |
| L (m) | k1 (N/m) | k2 (N/m) | k3 (N/m) | k4 (N/m) | m (kg) | r (m) | R (m) | C (N·s/m) |
|---|---|---|---|---|---|---|---|---|
| 0.02 | 1230 | 1170 | 1.4 | 1.4 | 0.01 | 0.2 | 0.3 | 0.1 |
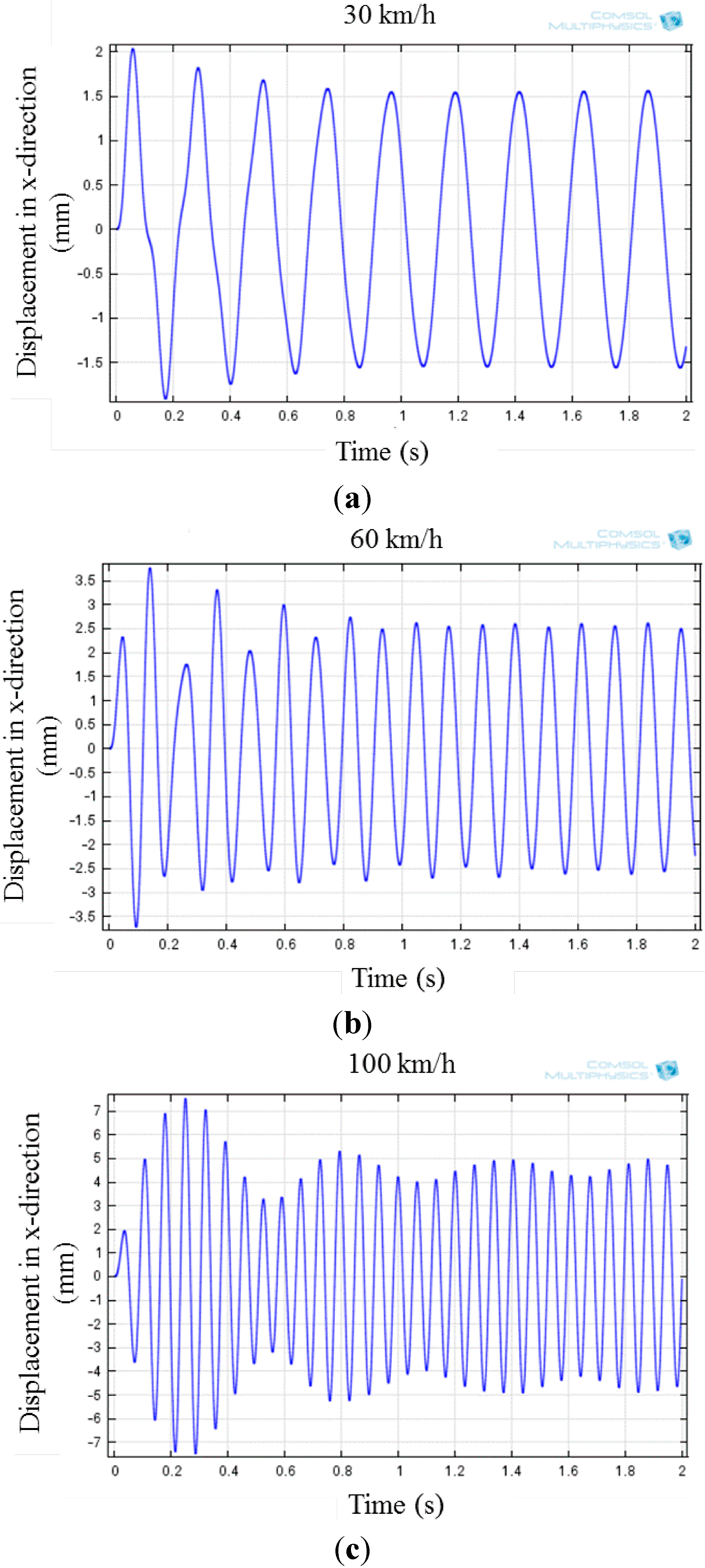
2.4. Numerical Results of the NSEH Obtained Using Finite Element Software
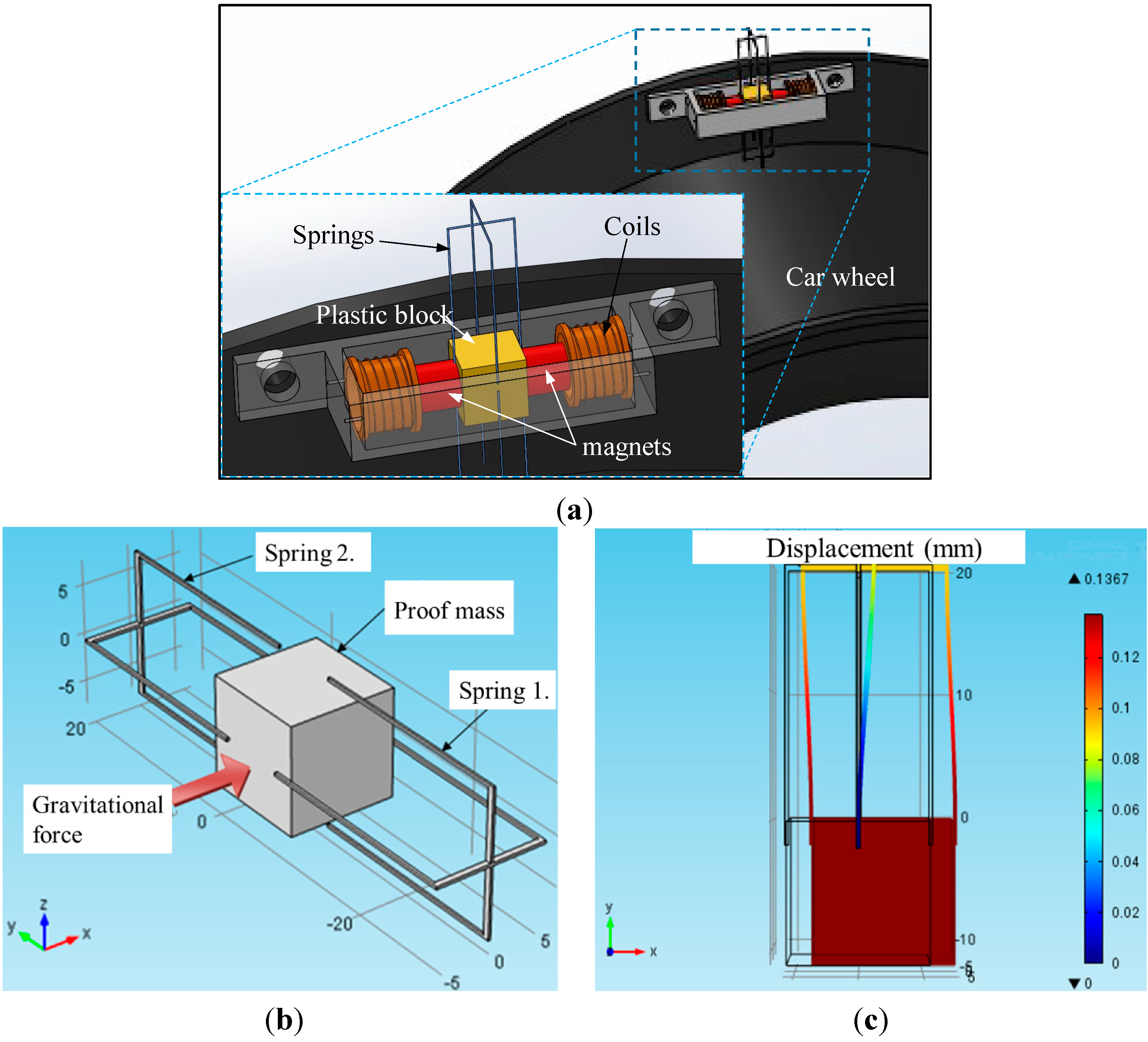
| Item | Length in y direction | Width in x direction | Depth in z direction | Diameter of spring wire | Young’s Modulus |
|---|---|---|---|---|---|
| Upside and downside springs | 22 mm | 11 mm | 15 mm | 0.3 mm | 197 GPa |
| L (m) | k1 (N/m) | k2 (N/m) | k3 (N/m) | k4 (N/m) | m (kg) | r (m) | R (m) | C (N·s/m) |
|---|---|---|---|---|---|---|---|---|
| 0.02 | 4032 | 4000 | 35.1 | 34.9 | 0.01 | 0.2 | 0.3 | 0.1 |
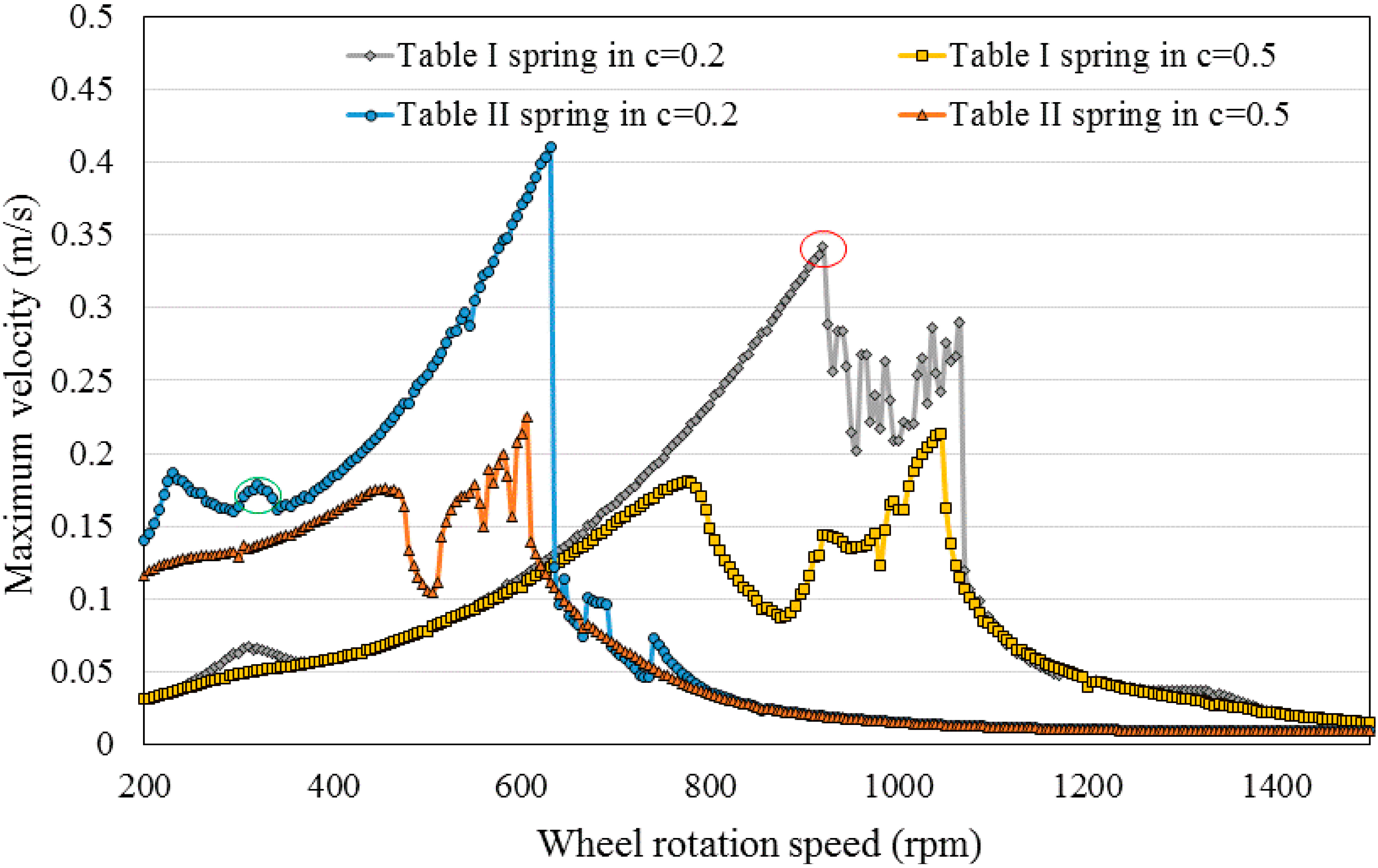
2.5. Frequency Domain Characteristics
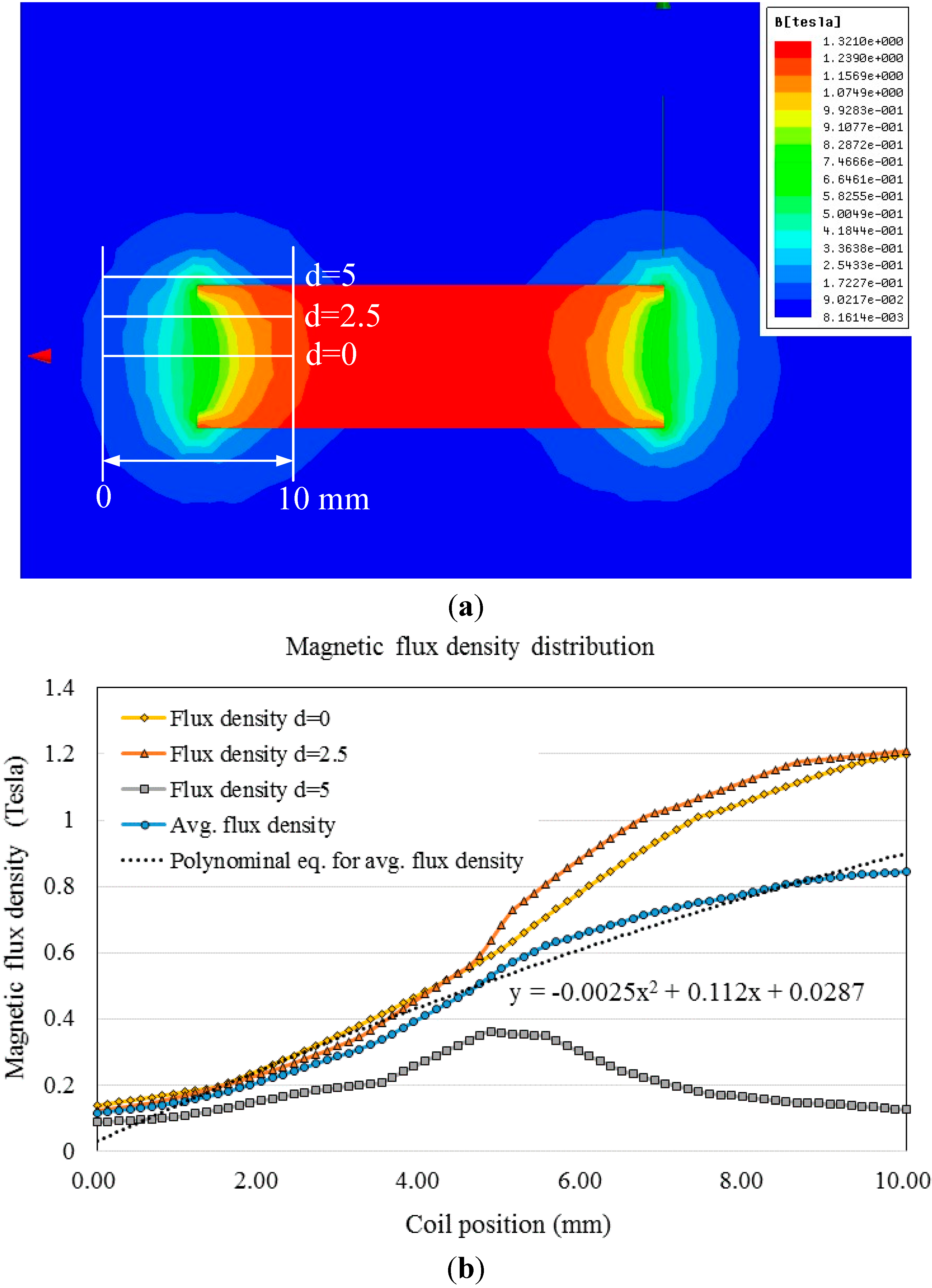
2.6. Output Voltage and Electromagnetic Damping
3. Experimental Results

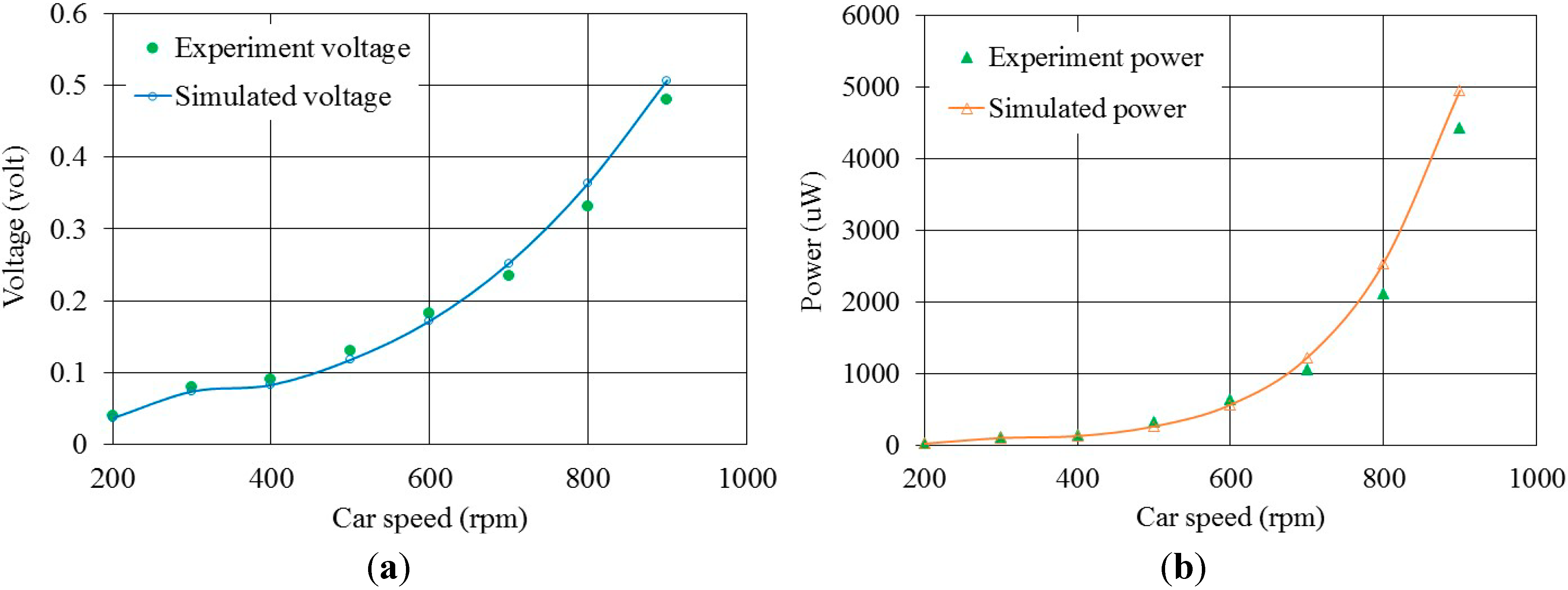
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sodano, H.A.; Inman, D.J. A review of power harvesting from vibration using piezoelectric materials. Shock Vib. Dig. 2004, 36, 197–205. [Google Scholar] [CrossRef]
- Anton, S.R.; Sodano, H.A. A review of power harvesting using piezoelectric materials. Smart Mater. Struct. 2007, 16, R1–R21. [Google Scholar] [CrossRef]
- Roundy, S. On the effectiveness of vibration-based energy harvesting. J. Intell. Mater. Syst. Struct. 2005, 16, 809–823. [Google Scholar] [CrossRef]
- Moon, K.S.; Liang, H.; Yi, J.; Mika, B. Tire tread deformation sensor and energy harvester development for smart tire application. Proc. SPIE 2007, 6529, 65290K. [Google Scholar]
- Karami, M.A.; Inman, D.J. Equivalent damping and frequency change for linear and nonlinear hybrid vibrational energy harvesting systems. J. Sound Vib. 2011, 330, 5583–5597. [Google Scholar] [CrossRef]
- Pan, C.T.; Wu, T.T. Development of a rotary electromagnetic microgenerator. J. Micromech. Microeng. 2007, 17, 120–128. [Google Scholar] [CrossRef]
- Arnold, D.P. Review of microscale magnetic power generation. IEEE Trans. Magn. 2007, 43, 3940–3951. [Google Scholar] [CrossRef]
- Wickenheiser, A.M.; Reissman, T.; Wu, W.J.; Garcia, E. Modeling the effects of electromechanical coupling on energy storage through piezoelectric energy harvesting. IEEE/ASME Trans. Mechatron. 2010, 15, 400–411. [Google Scholar] [CrossRef]
- Leland, E.S.; Wright, P.K. Resonance tuning of piezoelectric vibration energy scavenging generators using compressive axial preload. Smart Mater. Struct. 2006, 15, 1413–1420. [Google Scholar] [CrossRef]
- Platt, S.R.; Farritor, S.; Haider, H. On low-frequency electric power generation with PZT ceramics. IEEE/ASME Trans. Mechatron. 2005, 10, 240–252. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. An experimentally validated bimorph cantilever model for piezoelectric energy harvesting from base excitations. Smart Mater. Struct. 2009, 18, 105019. [Google Scholar] [CrossRef]
- Hobeck, J.D.; Inman, D.J. Artificial piezoelectric grass for energy harvesting from turbulence-induced vibration. Smart Mater. Struct. 2012, 21, 105024. [Google Scholar] [CrossRef]
- Dai, H.L.; Abdelkefi, A.; Wang, L. Theoretical modeling and nonlinear analysis of piezoelectric energy harvesting from vortex-induced vibrations. J. Intell. Mater. Syst. Struct. 2014. [Google Scholar] [CrossRef]
- Marzencki, M.; Defosseux, M.; Basrour, S. MEMS vibration energy harvesting devices with passive resonance frequency adaptation capability. J. Microelectromech. Syst. 2009, 18, 1444–1453. [Google Scholar] [CrossRef]
- Koh, S.J.A.; Keplinger, C.; Li, T.; Bauer, S.; Suo, Z. Dielectric elastomer generators: How much energy can be converted. IEEE/ASME Trans. Mechatron. 2011, 16, 33–41. [Google Scholar] [CrossRef]
- Williams, C.B.; Yates, R.B. Analysis of a micro-electric generator for microsystems. Sens. Actuators A Phys. 1996, 52, 8–11. [Google Scholar] [CrossRef]
- Nguyen, D.S.; Halvorsen, E.; Jensen, G.U.; Vogl, A. Fabrication and characterization of a wideband MEMS energy harvester utilizing nonlinear springs. J. Micromech. Microeng. 2010, 20, 125009. [Google Scholar] [CrossRef]
- Xing, X.; Lou, J.; Yang, G.M.; Obi, O.; Dirscoll, C.; Sun, N.X. Wideband vibration energy harvester with high permeability magnetic material. Appl. Phys. Lett. 2009, 95, 134103. [Google Scholar] [CrossRef]
- Daqaq, M.F. On intentional introduction of stiffness nonlinearities for energy harvesting under white Gaussian excitations. Nonlinear Dyn. 2012, 69, 1063–1079. [Google Scholar] [CrossRef]
- Zheng, R.; Nakano, K.; Hu, H.; Su, D.; Cartmell, M.P. An application of stochastic resonance for energy harvesting in a bistable vibrating system. J. Sound Vib. 2014, 333, 2568–2587. [Google Scholar] [CrossRef]
- Zhu, D.; Robert, S.; Tudor, M.J.; Beeby, S.P. Design and experimental characterization of a tunable vibration-based electromagnetic micro-generator. Sens. Actuators A Phys. 2010, 158, 284–293. [Google Scholar] [CrossRef]
- Wischke, M.; Masur, M.; Goldschmidtboeing, F.; Woias, P. Electromagnetic vibration harvester with piezoelectrically tunable resonance frequency. J. Micromech. Microeng. 2010, 20, 035025. [Google Scholar] [CrossRef]
- Masana, R.; Daqaq, M.F. Electromechanical Modeling and Nonlinear Analysis of Axially Loaded Energy Harvesters. J. Sound Vib. 2011, 133, 011007. [Google Scholar]
- Abdelkefi, A.; Barsallo, N. Comparative modeling of low-frequency piezomagnetoelastic energy harvesters. J. Intell. Mater. Syst. Struct. 2014. [Google Scholar] [CrossRef]
- Ching, N.N.H.; Wong, Y.; Li, W.J.; Leong, P.H.W.; Wen, Z.Y. A laser-micromachined multi-modal resonating power transducer for wireless sensing systems. Sens. Actuators A Phys. 2002, 97–98, 685–690. [Google Scholar]
- Yang, B.; Lee, C.; Xiang, W.; Xie, J.; He, J.H.; Kotlanka, R.K.; Low, S.P.; Feng, H. Electromagnetic energy harvesting from vibrations of multiple frequencies. J. Micromech. Microeng. 2009, 19, 035001. [Google Scholar] [CrossRef]
- Singh, K.B.; Bedekar, V.; Taheri, S.; Priya, S. Piezoelectric vibration energy harvesting system with an adaptive frequency tuning mechanism for intelligent tires. Mechatronics 2012, 27, 970–988. [Google Scholar] [CrossRef]
- Wu, X.; Parmar, M.; Lee, D.W. A Seesaw-Structured Energy Harvester with Superwide Bandwidth for TPMS Application. IEEE/ASME Trans. Mechatron. 2013, 19, 1514–1522. [Google Scholar]
- Lee, J.; Choi, B. Development of a piezoelectric energy harvesting system for implementing wireless sensors on the tires. Energy Convers. Manag. 2014, 78, 32–38. [Google Scholar] [CrossRef]
- Wang, Y.J.; Chen, C.D.; Sung, C.K. System design of a weighted-rotor type electromagnetic generator for harvesting energy from a rotating wheel. IEEE/ASME Trans. Mechatron. 2013, 18, 754–763. [Google Scholar] [CrossRef]
- Wang, Y.J.; Chen, C.D. Design and jump phenomenon analysis of an eccentric ring energy harvester. Smart Mater. Struct. 2013, 22, 105019. [Google Scholar] [CrossRef]
- Wang, Y.J.; Chen, C.D.; Sung, C.K. Design of a frequency-adjusting device for harvesting energy from a rotating wheel. Sens. Actuators A Phys. 2010, 159, 196–203. [Google Scholar] [CrossRef]
- Wang, Y.J.; Chen, C.D.; Sung, C.K.; Li, C. Natural Frequency Self-tuning Energy Harvester using a Circular Halbach Array Magnetic Disk. J. Intell. Mater. Syst. Struct. 2012, 23, 933–943. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.-J.; Chen, C.-D.; Lin, C.-C.; Yu, J.-H. A Nonlinear Suspended Energy Harvester for a Tire Pressure Monitoring System. Micromachines 2015, 6, 312-327. https://doi.org/10.3390/mi6030312
Wang Y-J, Chen C-D, Lin C-C, Yu J-H. A Nonlinear Suspended Energy Harvester for a Tire Pressure Monitoring System. Micromachines. 2015; 6(3):312-327. https://doi.org/10.3390/mi6030312
Chicago/Turabian StyleWang, Yu-Jen, Chung-De Chen, Chung-Chih Lin, and Jui-Hsin Yu. 2015. "A Nonlinear Suspended Energy Harvester for a Tire Pressure Monitoring System" Micromachines 6, no. 3: 312-327. https://doi.org/10.3390/mi6030312
APA StyleWang, Y.-J., Chen, C.-D., Lin, C.-C., & Yu, J.-H. (2015). A Nonlinear Suspended Energy Harvester for a Tire Pressure Monitoring System. Micromachines, 6(3), 312-327. https://doi.org/10.3390/mi6030312