Modeling of Hysteresis in Piezoelectric Actuator Based on Segment Similarity

Abstract

To successfully exploit the full potential of piezoelectric actuators in micro/nano positioning systems, it is essential to model their hysteresis behavior accurately. A novel hysteresis model for piezoelectric actuator is proposed in this paper. Firstly, segment-similarity, which describes the similarity relationship between hysteresis curve segments with different turning points, is proposed. Time-scale similarity, which describes the similarity relationship between hysteresis curves with different rates, is used to solve the problem of dynamic effect. The proposed model is formulated using these similarities. Finally, the experiments are performed with respect to a micro/nano-meter movement platform system. The effectiveness of the proposed model is verified as compared with the Preisach model. The experimental results show that the proposed model is able to precisely predict the hysteresis trajectories of piezoelectric actuators and performs better than the Preisach model.

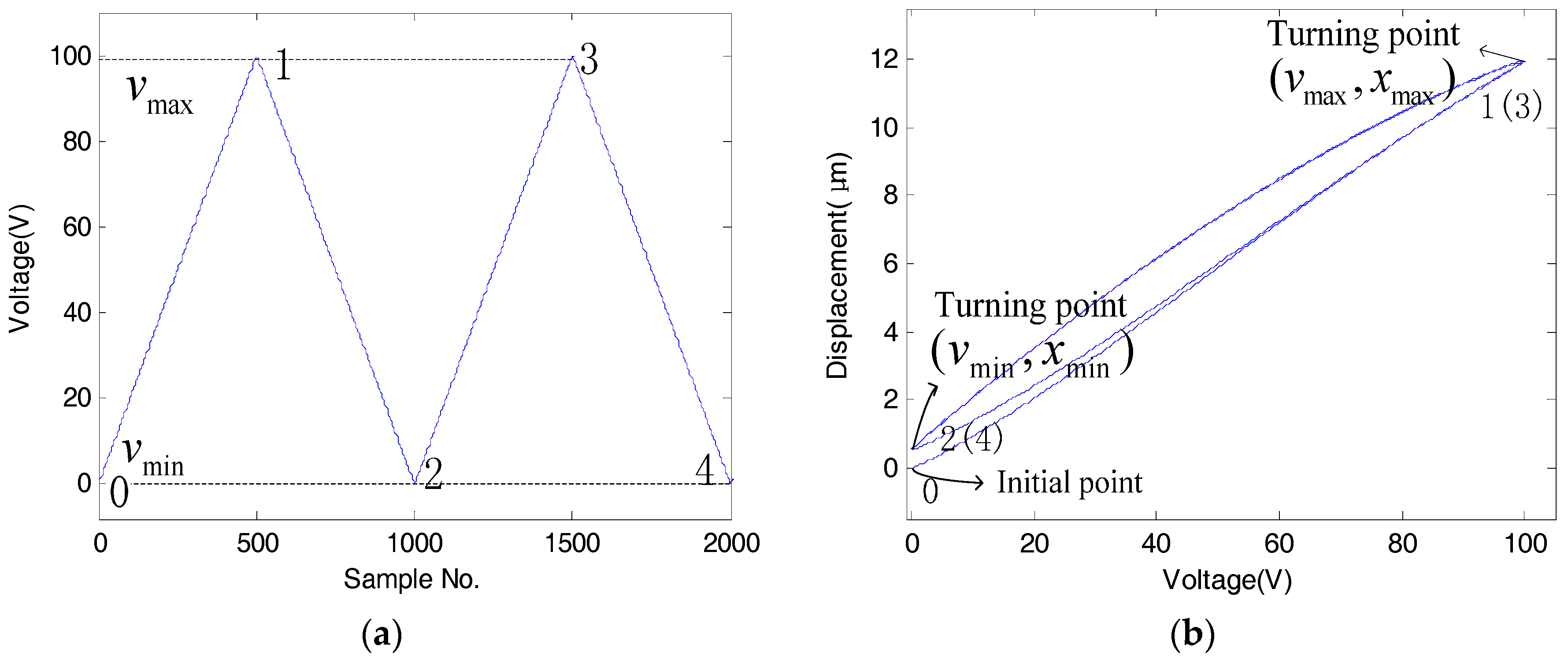
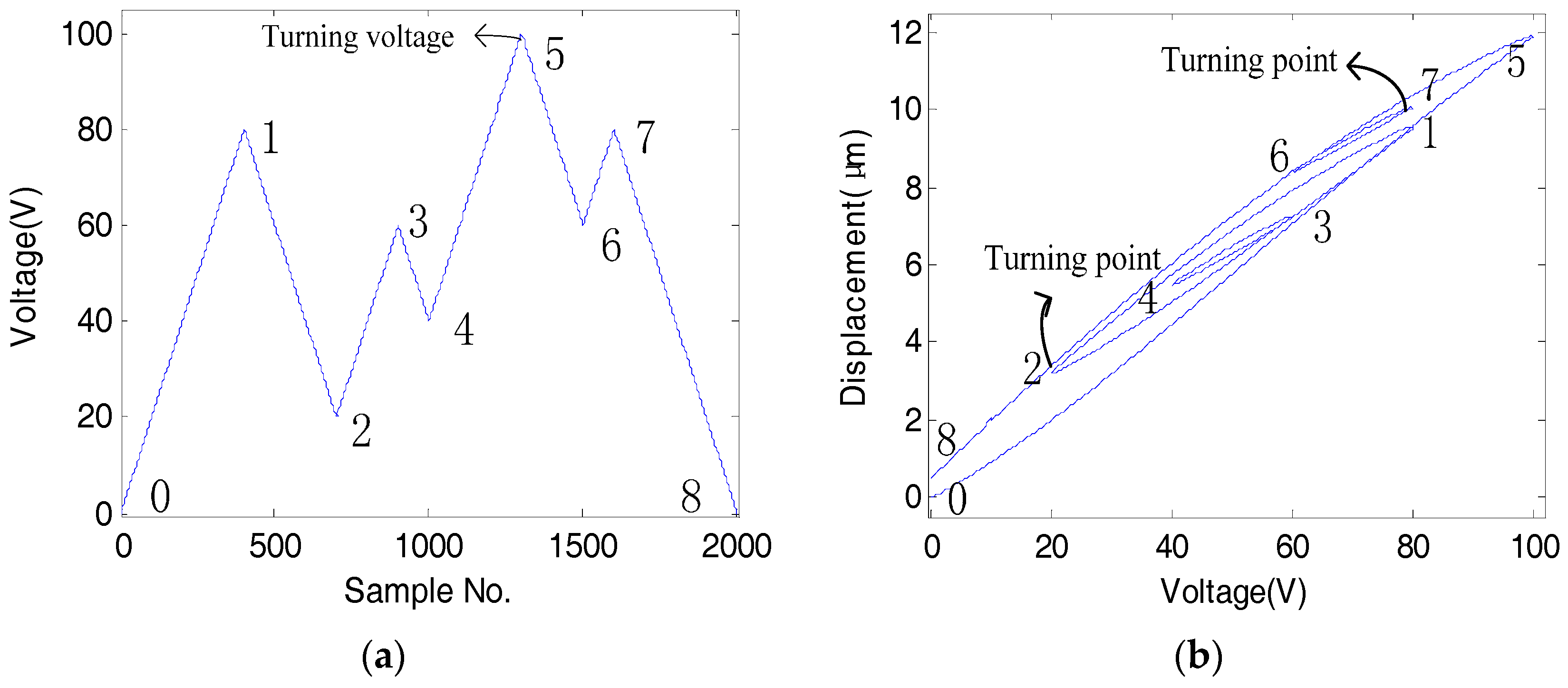
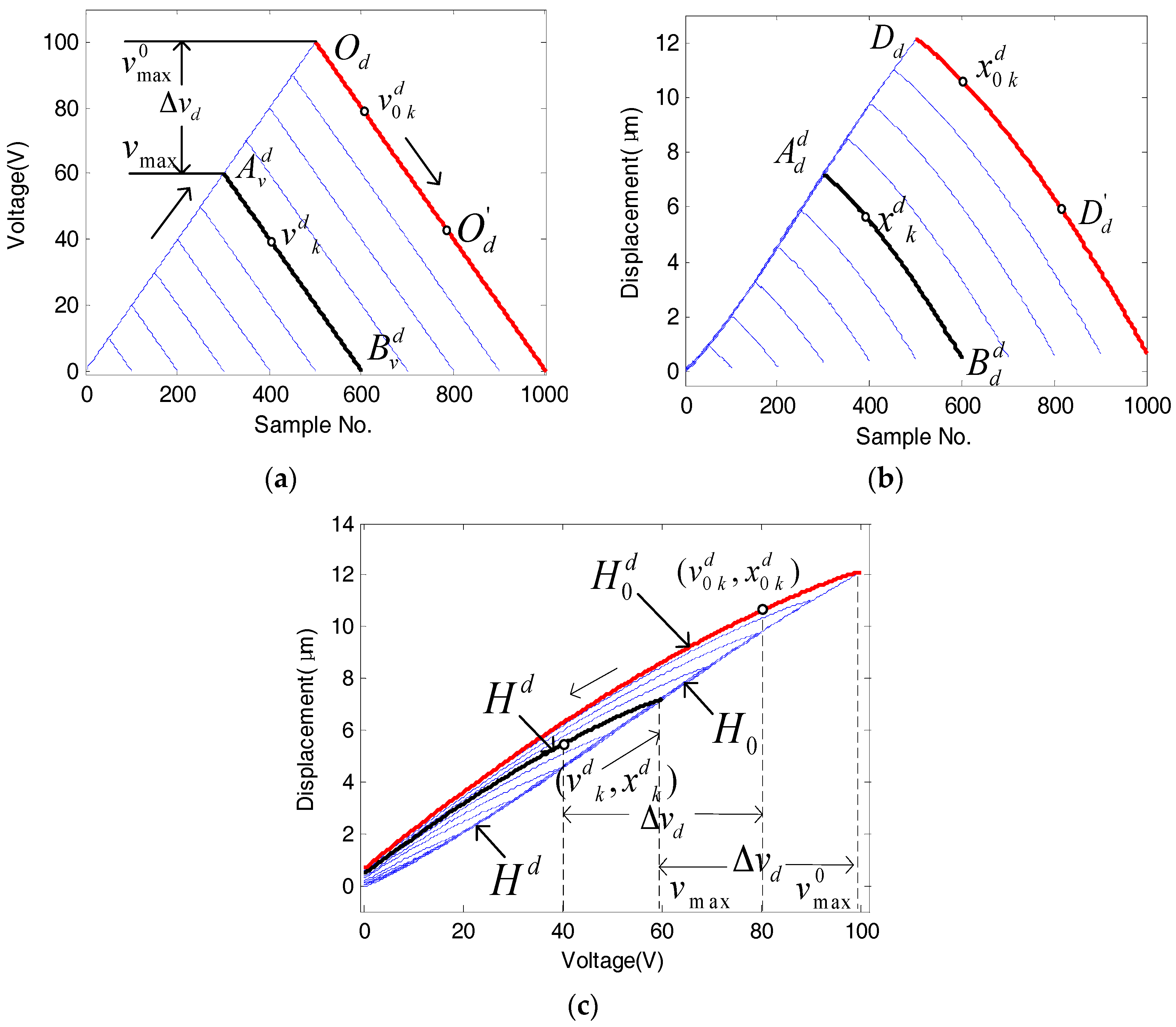
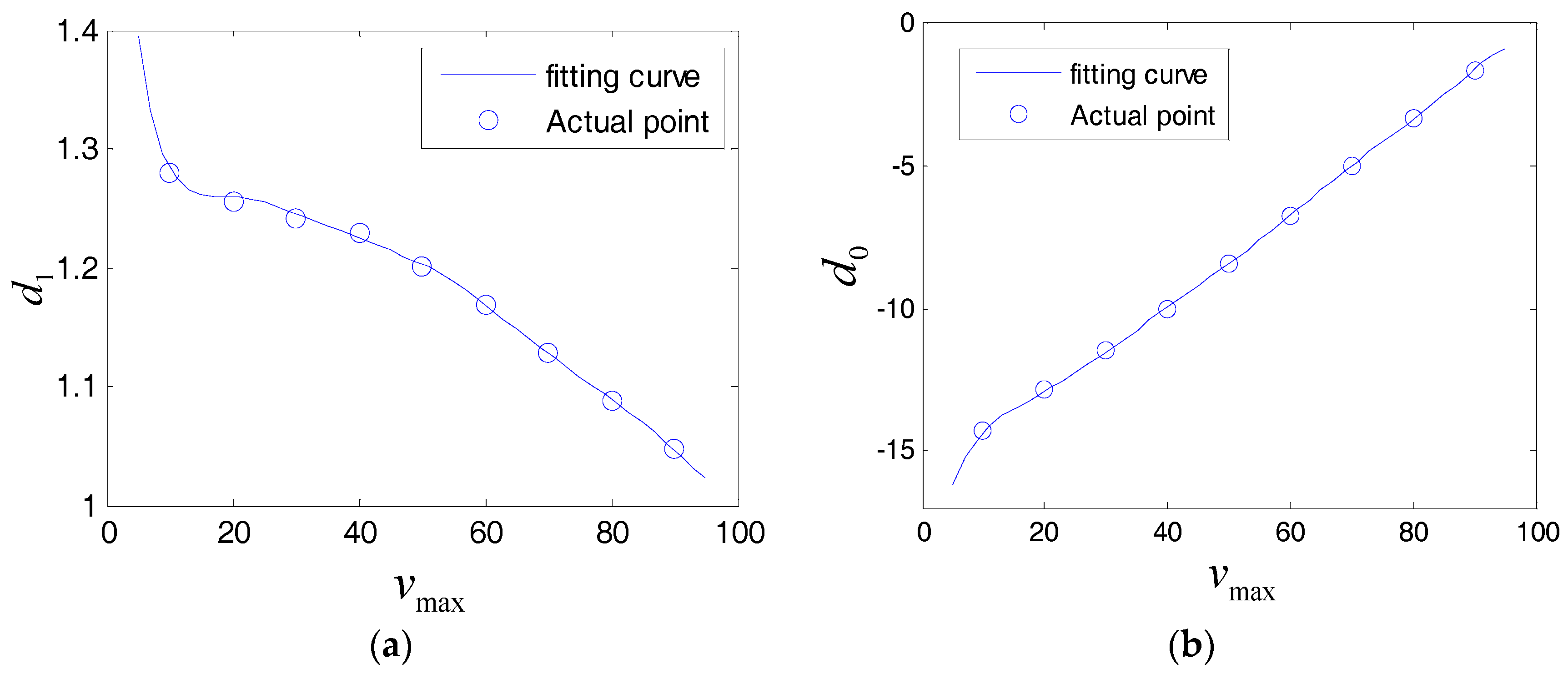
1. Introduction

Since piezoelectric actuators (PZAs) have the advantages of fast response, high displacement resolution, small size, and simple construction, they are widely used in diverse precision positioning applications at the micro/nano scale, such as optical fiber alignment [1], medical micromanipulator [2], micromachining [3,4], and vibration control [5]. However, the hysteresis behavior of PZAs restricts the usefulness of these actuators in precision manipulation applications. Hysteresis is a well-known input/output multi-loop phenomenon that occurs in piezoelectric materials. Its presence is a kind of non-local memory meaning that the response to the input excitation depends not only on the instantaneousness of the input but also its history path [6]. Therefore, accurate modeling and prediction of hysteresis in piezoelectric actuator are fundamental steps to acquire high performance in precision positioning systems.

A number of hysteresis models for PZAs are available in the literature. These models can be divided into two categories: physical and phenomenological model. Physical models try to describe the hysteresis model through internal mechanisms, the relationship of energy, displacement and so on [7,8]. They are based on the physical principles of materials. However, establishing a physical model is difficult since the physical features of a hysteretic system are usually very complicated. Furthermore, the physical model lacks generality. The physical model of one hysteretic system cannot be directly used in another system. Phenomenological models try to describe hysteresis curves by directly using a mathematical model based on experimental data without paying attention to theunderlying physical essence of hysteresis phenomenon. The most widely used phenomenological models are the Preisach model [9,10], Prandtl-Ishlinskii model [11,12] and Bouc-Wen model [13]. However, Preisach models need to store a large number of databases and their calculation is bulky. Prandtl-Ishlinskii models are a subclass of Preisachmodels. Although they have fewer data and analytical properties, their accuracy is limited by their symmetric structure. For the Bouc-Wen model, it is hard to achieve high accuracy because of the rigid structure of its governing equation. These models have rigid structures so that the accuracy is limited. To solve this problem, several phenomenological modeling approaches based on empirical observations have been developed recently. Ru and Sun propose a mathematical model based on the similarities of hysteresis curves and the effects of turning points [14,15]. Bashash and Jalili disclose and demonstrate the underlying intellectual behavior of hysteresis. Based on this, several memory-based constitutive mathematical modeling frameworks have been developed [6,16,17].However, the calculation is bulky. Nguyen and Choi [18] store two discretized first-order datasets of ascending and descending curves in advance and then use congruency property to get high-order hysteretic curves. However, this model needs a lot of memory space to store the datasets. Besides, the above mentioned models do not consider dynamic effect. Little research about dynamic empirical models of piezoelectric actuators have been carried out [19]. In order to solve the problems above, geometric similarity and time-scale similarity of displacement time series were proposed in our previous work [20]. However, geometric similarity is not applicable for predicting high-order hysteresis behavior.

To predict complex dynamic hysteresis behavior, this study proposes a novel hysteresis model to describe the complex dynamic hysteresis behavior of a piezoelectric actuator. The proposed model is formulated based on the segment-similarities of hysteresis nonlinearity. Segment-similarity describes the similarity relationship between hysteresis curves with different turning points. Time-scale similarity, which describes the relationship between hysteresis curves with different rates, is also used to solve the problem of the hysteresis dynamic. Compared to the Preisach model (which is one of the most widely used phenomenological models and is based on the experimental data of first reversal curves), the formulation procedure of the proposed model is simpler and more straightforward and requires less computation. The experimental results show that the proposed model can produce better hysteresis prediction accuracy than the Preisach model.

The rest of the paper is arranged as follows: the experimental platform is shown in Section 2. Section 3 introduces some inherent properties of hysteresis in a PZA. In Section 4, the segment similarity is proposed to describe the similarity relationship between hysteresis curves with different extremes. Time-scale similarity is used to describe the dynamic behavior. Then, a hysteresis model is established based on the similarities in Section 5. In Section 6, the model is tested using different kinds of inputs with multi-amplitude and different rates. The proposed model is also compared with the Preisach model. Finally, the research conclusion is given in Section 7.

2. Experimental Setup

The similarities among hysteresis trajectories are investigated through a set of experimental tests on a piezoelectric actuator-based micro/nano-meter movement platform system as depicted in Figure 1. A digital signal processor (DSP, TMS320LF2407, Texas Instruments, Houston, TX, USA) system is employed to implement controller as shown in Figure 2. The D/A (16-bit AD669, Analog Devices, Norwood, MA, USA) board produces an analogy voltage output which is then amplified by drive power (HPV series) to provide a voltage for driving PZA (MPT-1JRL/I002, Physik Instrumente, Shanghai, China). The output voltages of the power amplifier range from 0 to 150 V, and the resolution is 5 mV. Output displacements of PZA are measured by a resistance strain gauge sensor which is installed within the platform as a micrometer and then are converted into digital signals by A/D (16-bit AD976, Analog Devices, Norwood, MA, USA) board. A serial port is used to pass the data from the DSP to the computer. The devices are shown in Figure 3. The withstand-voltage range of PZA is −30–120 V. The input voltages of the PZA are limited to the range of 0–100 V, considering the safety margin and the driving ability of the power amplifier.

Figure 1. The piezoelectric actuator-based experimental system.

Figure 1. The piezoelectric actuator-based experimental system.

Figure 2. The controller system.

Figure 2. The controller system.

Figure 3. The PZA experiment devices.

Figure 3. The PZA experiment devices.

3. Hysteresis Properties of PZA

The hysteresis nonlinear relationship between input signal and output displacement is a memory effect of PZAs, which depends not only on the instantaneousness of the input but also the history of its operation [6,16,17]. Although the hysteresis trajectories are complicated, they are not random. In fact, hysteresis responses follow certain laws relying on the inherent characteristics of the piezoelectric materials. Some properties of hysteresis in PZA can be seen via experiments and have been proposed and validated in previous studies [6,16,17,18]. In this section, these properties are presented and explained in the following subsections. Triangular signals that have the same voltage difference between adjacent sample points are used to drive the PZA in this paper. The sampling period remains the same.

3.1. Loop Closing between Two Turning Points

Figure 4a shows a triangular input voltage excitation. The displacement response of the PZA versus the input voltage excitation is shown in Figure 4b. Points 1–4 in Figure 4b correspond to the extremes of the input voltage and output displacement. These points are called the turning point. The hysteresis trajectory starts increasing from the initial state 0 to extreme 1. If the direction of input changes immediately after reaching its maximum value, the hysteresis trajectory changes its path and decreases from turning point 1 to 2. After targeting the turning point 2, it increases on the second ascending curve to point 3, coinciding with turning point 1. In other words, this is a property of loop closing between two turning points as illustrated in ref. [18], the curve of output displacement is closed between two consecutive turning points, 1(3) and 2. It should be noted that all the descending trajectories originated from the first ascending curve that originate from initial state do not target the initial point but converge to a single point on the third region of the hysteresis plane [17].

Figure 4. The hysteresis response. (a) The input triangular signals; (b) the corresponding hysteresis response.

Figure 4. The hysteresis response. (a) The input triangular signals; (b) the corresponding hysteresis response.

3.2. Wiping-Out Property and Curve Alignment

As demonstrated in [16,17], the wiping-out effect is another important inherent property of hysteresis in PZAs. If the input voltage value is larger than some history maximums or lower than some history minimums which have yet to be wiped out, these hysteresis extremes are wiped out and the output trajectory associated with these maximums are wiped out and will no longer affect the following output response. The wiped out turning points are no longer affect the future hysteresis responses. For instance, when the input voltage moves on the ascending curve from point 4 to 5 and passes the point with the same magnitude as the extreme point 3 in Figure 5a, turning points with turning points 3 and 4 in Figure 5b are wiped out and the minor loop associated with turning points 3 and 4 is no longer useful for the remaining hysteresis. Similarly, turning points 2 and 1 are wiped out when the input voltage continues to increase to point 5, while turning points 6 and 7 are wiped out when the input voltage moves downward from point 6 to 8. Once the wiping out occurs, the hysteresis trajectory follows the path of the previously broken curve. This property is called curve alignment [17]. In Figure 5b, the hysteresis curve segment 4–3 is associated with turning point 4. Point 4 is called the dominant extreme for curve 4–3. After wiping out of points 3 and 4, trajectory 3–1 slightly bends and aligns to previous broken curve 2–3 that departs from turning point 2. At this time, point 2 is the dominant extreme for curve 3–1. Likewise, the dominant extremes of curve segments 1–5 and 6–8 are extremes 0 and 5, respectively. We conclude that if the direction of input changes before hitting a turning point, the dominant extreme will be different from that after hitting the turning point.

Figure 5. Wiping out effect of hysteresis. (a) The input voltage to the PZA; (b) the output displacement versus the input voltage.

Figure 5. Wiping out effect of hysteresis. (a) The input voltage to the PZA; (b) the output displacement versus the input voltage.

3.3. Congruency

Congruency is when the minor loops with the same consecutive maximum and minimum input voltages are congruent with each other [18]. As shown in Figure 6, loops 1 and 2 with the same maximum and minimum values $v_{\text{min}}$ and $v_{\text{max}}$ are congruent with each other.

Figure 6. Congruency property of the hysteresis.

Figure 6. Congruency property of the hysteresis.

It is can be observed that loop closing between two consecutive turning points, wipe-out and congruency are three important properties of hysteresis in PZA. However, these properties are not adequate to precisely predict hysteresis behavior. Therefore, segment similarity of hysteresis in PZA is proposed in the following section.

4. Segment-Similarity of Hysteresis in PZA

Madelung [21] proposed that any hysteresis curve originating from a turning point of the input-output graph is uniquely determined by the coordinates of this turning point. Therefore what we study here is how the turning point determines the hysteresis curve. In this section, the segment-similarity, which describes the similarity relationship between hysteresis curve segments emanating from different turning points, is investigated.

4.1. Segment-Similarity of Descending Hysteresis Curves

First, we raise the input voltage from initial state (0 V) to its maximum value and then decreasing it to zero. Figure 7a shows 10 sets of driving input signals with the same minimum voltages (0 V) but different maximum voltages. Figure 7b shows the corresponding output displacements of PZA. The displacement responses versus the input excitations are shown in Figure 7c. As seen from Figure 7b,c, all ascending curves departing from initial state have an identical path, and all the descending curves branching from different positions have a similar shape. Therefore, what we study is the similarity of these descending curve segments.

Figure 7. Similarity for descending hysteresis curves. (a) 10 sets of input signals with different maximums; (b) the descending output displacement responses; (c) the hysteresis responses.

Figure 7. Similarity for descending hysteresis curves. (a) 10 sets of input signals with different maximums; (b) the descending output displacement responses; (c) the hysteresis responses.

$\{v_{0k}^d\}$ and {$v_k^d$} are used to describe the sample voltage sequences of voltage curve segments ${\text{O}}_d{\text{O}}_d^{\prime }$ and $A_v^d{B}_v^d$ respectively. $v_{0k}^d$ and $v_{ k}^d$ are expressed as:

$${v_0^d}_k=v_{\max }^0-k\cdot v_{\delta },k=1,\cdots ,n$$

(1)

$${v^d}_k=v_{\max }-k\cdot v_{\delta },k=1,\cdots ,n$$

(2)

where, $v_{\text{max}}^0$, $v_{\text{max}}$ are the maximums of $O_d{O}_{d }^{\prime }$ and $A_v^d{B}_v^d$ respectively, $n$ is the number of sample points $v_{\delta }$ is the voltage difference between adjacent sample points. In this research, $v_{\text{δ}}$ = 0.2 V. And $O_d{O}_d^{\prime }$ and $A_v^d{B}_v^d$ have the same number of sample points.

In Figure 7b, displacement curve segments $D_d{D}_d^{\prime }$ and $A_d^d{B}_d^d$ are the corresponding displacement responses to $O_d{O}_d^{\prime }$ and $A_v^d{B}_v^d$ respectively.

$x_{0k}^{d }$ and $x_{ k}^d$ are the sequences of output displacement corresponding to $v_{0k}^d$ and $v_{ k}^d$ respectively. Suppose the displacement sequences of the curve segments $D_d{D}_d^{\prime }$ and $A_d^d{B}_d^d$ satisfy the similarity relationship:

$${x^d}_k=d_1\cdot {x_0^d}_k+d_0$$

(3)

where, $d_1$, $d_0$ are called similarity factors, which can be identified through a least square error minimization. The identification results are shown in Table 1. Root mean square error (RMSE) is expressed as

$$\mathrm{RMSE}=\sqrt{\frac{1}{n}{\displaystyle \sum _{k=1}^n{(d_1\cdot {x_0^d}_k+d_0-{x^d}_k)}^2}}$$

(4)

Obviously, Table 1 demonstrates that the two displacement curve segment sequences satisfy Equation (3). Therefore the curve segment $O_d{O}_d^{\prime }$ is absolutely similar to $A_v^d{B}_v^d$. It is also shown that the similarity factors $d_1$, $d_0$ change with the turning voltage $v_{\text{max}}$ of descending curve $A_v^d{B}_v^d$. The relationship between similarity factors and $v_{\text{max}}$ can be fitted in polynomial form as follows:

$$d_1(v_{\max })={\displaystyle \sum _{i=0}^8{b}_i\cdot {(v_{\max })}^i}$$

(5)

$$d_0(v_{\max })={\displaystyle \sum _{i=0}^8{c}_i}\cdot {(v_{\max })}^i$$

(6)

where, $b_i$, $c_i$ are the coefficients of polynomials as shown in Table 2. The relationships between $d_1$, $d_0$ and $v_{\text{max}}$ that are expressed by Equations (5) and (6) are shown in Figure 8.

Table 1. The identification results of Equation (1) ($v_{\text{max}}^0$ = 100 V).

$v_{max}$ (V)	$d_1$	$d_0$	RMSE (μm)
10	1.2799	−14.2921	0.0106
20	1.2563	−12.8797	0.0090
30	1.2412	−11.4593	0.0080
40	1.2285	−10.0320	0.0094
50	1.2004	−8.3894	0.0070
60	1.1688	−6.7518	0.0081
70	1.1290	−5.0202	0.0085
80	1.0878	−3.3352	0.0094
90	1.0472	−1.6255	0.0076

Table 1. The identification results of Equation (1) ($v_{\text{max}}^0$ = 100 V).

$v_{max}$ (V)	$d_1$	$d_0$	RMSE (μm)
10	1.2799	−14.2921	0.0106
20	1.2563	−12.8797	0.0090
30	1.2412	−11.4593	0.0080
40	1.2285	−10.0320	0.0094
50	1.2004	−8.3894	0.0070
60	1.1688	−6.7518	0.0081
70	1.1290	−5.0202	0.0085
80	1.0878	−3.3352	0.0094
90	1.0472	−1.6255	0.0076

Table 2. The coefficients of polynomials for Equations (5) and (6).

$i$	$b_i$	$c_i$
0	1.7488	−20.9781
1	−0.1114	1.4668
2	0.0104	−0.1301
3	−5.1226 × 10−4	0.0066
4	1.4642 × 10−5	−1.9458 × 10−4
5	−2.5086 × 10−7	3.4300 × 10−6
6	2.5350 × 10−9	−3.5688 × 10−8
7	−1.3912 × 10−11	2.0174 × 10−10
8	3.1946 × 10−14	−4.7719 × 10−13

Table 2. The coefficients of polynomials for Equations (5) and (6).

$i$	$b_i$	$c_i$
0	1.7488	−20.9781
1	−0.1114	1.4668
2	0.0104	−0.1301
3	−5.1226 × 10−4	0.0066
4	1.4642 × 10−5	−1.9458 × 10−4
5	−2.5086 × 10−7	3.4300 × 10−6
6	2.5350 × 10−9	−3.5688 × 10−8
7	−1.3912 × 10−11	2.0174 × 10−10
8	3.1946 × 10−14	−4.7719 × 10−13

The voltage sequence {$v_{0k}^d$} and the corresponding displacement sequence {$x_{0k}^d$} can constitute the reference hysteresis curve $H_0^d$ in Figure 7c. Similarly, {$v_{0k}^d$} and {$x_{0k}^d$} constitute the descending hysteresis curve $H^d$. Thus, we have $x_{0k}^d=H_0^d(v_{0k}^d)$, $x_{ k}^d=H^d(v_{ k}^d)$. According to Equation (3), the hysteresis curve segment with voltage interval of $[v_{\text{max}}^0-v_{\text{max}},v_{\text{max}}^0]$ on curve $H_0^d$ is absolutely similar to the hysteresis curve segment with voltage interval of $[0,v_{\text{max}}]$ on the curve $H^d$.

Figure 8. The relationship between similarity factors and maximum (a) The relationship between $v_{\text{max}}$ and $d_1$ (b) The relationship between $v_{\text{max}}$ and $d_0$.

Figure 8. The relationship between similarity factors and maximum (a) The relationship between $v_{\text{max}}$ and $d_1$ (b) The relationship between $v_{\text{max}}$ and $d_0$.

As $△v_d=v_{\text{max}}^0-v_{\text{max}}=v_{0k}^d-v_{ k}^d$, the similarity relationship between descending hysteresis curve segments $D_d{D}_d^{\prime }$ and $A_d^d{B}_{vd}^d$ is described by:

$$x=H^d(v)=d_1(v_{\max })\cdot H_0^d(v+\mathrm{\Delta }{v}_d)+d_0(v_{\max }),0\le v\le v_{\max }$$

(7)

where, v is the instantaneousness of input voltage, x is the corresponding displacement of $D_d{D}_d^{\prime }$ when the turning voltage is $v_{\text{max}}$.

4.2. Segment-Similarity of Ascending Hysteresis Curves

For the case of input signals decreasing from the same maximum voltage (100 V) and then increasing from different minimums in Figure 9a, the corresponding output displacement responses of PZA are shown in Figure 9b. We can see that the ascending curves also have similar characteristics to the descending curves.

In Figure 9a, {$v_{0k}^a$} and {$v_{ k}^a$} are the sample voltage sequences of voltage curve segments $O_a{O}_a^{\prime }$ and $A_v^a{B}_v^a$ respectively. $v_{0k}^a$ and $v_{ k}^a$ are expressed as:

$${v_0^a}_k=v_{\min }^0+k\cdot v_{\delta },k=1,\cdots ,n$$

(8)

$${v^a}_k=v_{\min }+k\cdot v_{\delta },k=1,\cdots ,n$$

(9)

where, $v_{\text{min}}^0$, $v_{\text{min}}$ are the minimums of $O_a{O}_a^{\prime }$ and $A_v^a{B}_v^a$ respectively. The curve segments responses to $O_a{O}_a^{\prime }$ and $A_v^a{B}_v^a$ are $D_a{D}_a^{\prime }$ and $A_d^a{B}_d^a$ respectively. $x_{0k}^a$ and $v_{ k}^a$ are the displacement responses to $v_{0k}^a$ and $v_{ k}^a$ respectively. Suppose the two sequences of displacement curve segments $D_a{D}_a^{\prime }$ and $A_d^a{B}_d^a$ satisfy the similarity relationship:

$${x^a}_k=a_1\cdot {x_0^a}_k+a_0$$

(10)

where, $a_1$, $a_0$ are the similarity factors for ascending curve segments.

The identification results of parameters $a_1$, $a_0$ are shown in Table 3. RMSE is expressed as

$$\mathrm{RMSE}=\sqrt{\frac{1}{n}{\displaystyle \sum _{k=1}^n{(a_1\cdot {x_0^d}_k+a_0-{x^d}_k)}^2}}$$

(11)

Obviously, the two sequences of displacement curve segments $D_a{D}_a^{\prime }$ and $A_d^a{B}_d^a$ are absolutely similar. $a_1$, $a_0$ change with the minimum voltage $v_{\text{min}}$. The relationship between similarity factors and $v_{\text{min}}$ is expressed as follows:

$$a_1(v_{\max })={\displaystyle \sum _{i=0}^8{g}_i}\cdot {(v_{\max })}^i$$

(12)

$$a_0(v_{\max })={\displaystyle \sum _{i=0}^4{h}_i}\cdot {(v_{\max })}^i$$

(13)

where, $g_i$, $h_i$ are the coefficients of Equations (12) and (13) respectively. The specific values are shown in Table 4.

Figure 9. Similarity for ascending hysteresis curves. (a) 10 sets of input signals with different minimums; (b) the ascending output displacement responses; (c) the hysteresis responses.

Figure 9. Similarity for ascending hysteresis curves. (a) 10 sets of input signals with different minimums; (b) the ascending output displacement responses; (c) the hysteresis responses.

Table 3. The identification of Equation (3). ($v_{\text{min}}^0$ = 0 V).

$v_{min}$(v)	$a_1$	$a_0$	RMSE (μm)
10	0.9582	1.5769	0.0250
20	0.9177	3.0870	0.0361
30	0.8840	4.4753	0.0387
40	0.8576	5.7537	0.0331
50	0.8358	6. 9430	0.0310
60	0.8256	8.0133	0.0184
70	0.8241	8.9876	0.0129
80	0.7978	9.9819	0.0283
90	0.8056	11.1362	0.0109

Table 3. The identification of Equation (3). ($v_{\text{min}}^0$ = 0 V).

$v_{min}$(v)	$a_1$	$a_0$	RMSE (μm)
10	0.9582	1.5769	0.0250
20	0.9177	3.0870	0.0361
30	0.8840	4.4753	0.0387
40	0.8576	5.7537	0.0331
50	0.8358	6. 9430	0.0310
60	0.8256	8.0133	0.0184
70	0.8241	8.9876	0.0129
80	0.7978	9.9819	0.0283
90	0.8056	11.1362	0.0109

Table 4. The coefficients of polynomials for Equations (12) and (13).

$i$	$g_i$	$h_i$
0	0.9723	−0.0687
1	0.0070	0.1759
2	−0.0016	−9.8262 × 10−4
3	1.0155 × 10−4	6.8658 × 10−6
4	−3.5080 × 10−6	−3.0867 × 10−8
5	6.9492 × 10−8	-
6	−7.8583 × 10−10	-
7	4.7006 × 10−12	-
8	−1.1504 × 10−14	-

Table 4. The coefficients of polynomials for Equations (12) and (13).

$i$	$g_i$	$h_i$
0	0.9723	−0.0687
1	0.0070	0.1759
2	−0.0016	−9.8262 × 10−4
3	1.0155 × 10−4	6.8658 × 10−6
4	−3.5080 × 10−6	−3.0867 × 10−8
5	6.9492 × 10−8	-
6	−7.8583 × 10−10	-
7	4.7006 × 10−12	-
8	−1.1504 × 10−14	-

The relationships between similarity factors $a_1$, $a_0$ and $v_{\text{min}}$ that are expressed by Equations (12) and (13) are shown in Figure 10.

Figure 10. The relationship between similarity factors and minimum. (a) The relationship between $v_{\text{min}}$ and $a_1$ (b) The relationship between $v_{\text{min}}$ and $a_0$.

Figure 10. The relationship between similarity factors and minimum. (a) The relationship between $v_{\text{min}}$ and $a_1$ (b) The relationship between $v_{\text{min}}$ and $a_0$.

As shown in Figure 9c, the voltage sequence {$v_{0k}^a$} and the corresponding displacements sequence {$x_{0k}^a$} can constitute the reference hysteresis curve $H_0^a$. Similarly, {$v_{0k}^a$} and {$x_{0k}^a$} constitute the ascending hysteresis curve $H^a$. Thus, we have $x_{0k}^a=H_0^a(v_{0k}^a)$, $x_{ k}^a=H^a(v_{ k}^a)$. According to Equation (10), the hysteresis curve segment with voltage interval of $[v_{\text{min}},100]$ on the curve $H^a$ is absolutely similar to the hysteresis curve segment with voltage interval of $[v_{\text{min}}^0,v_{\text{min}}^0+100-v_{\text{min}}]$ on the curve $H_0^a$.

As $△v_{\text{a}}=v_{\text{min}}-v_{\text{min}}^0=v_{ k}^a-v_{0k}^a$, the ascending hysteresis trajectories $H^a$ with turning voltage $v_{\text{min}}$ can be obtained from curve segment $H_0^a$ through Equation (14):

$$x=H^a(v)=a_1(v_{\min })\cdot H_0^a(v-\mathrm{\Delta }{v}_a)+a_0(v_{\min }),v_{\min }\le v\le 100$$

(14)

where, v is the instantaneousness of input voltage, and x is the corresponding output displacement of $H^a$ when the turning voltage is $v_{\text{min}}$.

4.3. The Modification of Segment-Similarity

If we get the hysteresis curves corresponding to the triangular input excitation with maximum of 100 V and minimum of 0 V in advance ($H_0$ is the first ascending curve starting from initial state; $H_0^{d }$ is the first descending curve $H_0^a$ is the second ascending curve), other hysteresis curves can be derived by employing the segment-similarity relationship proposed in Section 4.1 and Section 4.2. However, these segment-similarity relationships only consider the case in which the hysteresis curve segments whose turning points are on the curves $H_0$ and $H_0^{d }$ (points A, B, C, D in Figure 11). For the hysteresis curve segments whose turning points are not on $H_0$ and $H_0^{d }$ (E, F in Figure 11), inaccurate hysteresis prediction will be produced by directly using Equations (7) and (14). In this case, we need modify the segment-similarity to guarantee modeling accuracy.

Figure 11. The general view ofturning points.

Figure 11. The general view ofturning points.

According to congruency, the hysteresis curve segments are proposed to be congruent with the one that emanates from the same turning voltage. As shown in Figure 12a, $H_m^{a }$ is proposed to be congruent with $H^a$ (whose turning point is on the curve $H_0^{d }$) which departs from the same turning voltage $v_{\text{min}}$. $H_m^{d }$ in Figure 12b is congruent with $H^d$ (whose turning point is on the curve $H_0$) which departs from the same turning voltage $v_{\text{max}}$. Then we have

$$H_m^a(v)-H^a(v)=x_{\min }-H^a(v_{\min })$$

(15)

$$H_m^d(v)-H^d(v)=x_{\max }-H^a(v_{\max })$$

(16)

where $H_m^a$ is the ascending hysteresis curve segment that departs from turning point $(v_{\text{min}},x_{\text{min}})$. $x_{\text{min}}$ is the displacement value corresponding to turning point $(v_{\text{min}},x_{\text{min}})$. $H^a$, whose turning point is on the curve $H_0^{d }$, is the ascending hysteresis curve segment with turning voltage $v_{\text{min}}$. $H_m^{d }$ is the descending hysteresis curve segment that departing from turning point $(v_{\text{max}},x_{\text{max}})$. $x_{\text{max}}$ is the vertical coordinate value of turning point $x_{\text{max}}$. $H^d$, whose turning point is on the curve $H_0$, is the ascending hysteresis curve segment with turning voltage $v_{\text{max}}$ Hysteresis curve segments $H^a$ and $H^d$ are obtained via Equations (7) and (14) respectively.

Figure 12. Hysteresis response. (a) The case of ascending voltage; (b) the case of descending voltage.

Figure 12. Hysteresis response. (a) The case of ascending voltage; (b) the case of descending voltage.

Therefore, the ascending and descending hysteresis curve segments are obtained by the modified relationships:

$$H_m^a(v)=H^a(v)+x_{\min }-H^a(v_{\min })$$

(17)

$$H_m^d(v)=H^d(v)+x_{\max }-H^d(v_{\max })$$

(18)

Equations (17) and (18) reflect how the coordinates of turning point determine the hysteresis curves. It is noted that the extremes $(v_{\text{min}},x_{\text{min}})$, $(v_{\text{max}},x_{\text{max}})$ are the dominant extremes of the curve segments $H_m^{a }$ and $H_m^{d }$ because of the memory effect of hysteresis.

4.4. Time-Scale Similarity of Hysteresis Nonlinearity

By applying input signals with the same amplitude but different rates (Figure 13a), the corresponding output displacement signals and hysteresis loops are depicted in Figure 13b,c respectively. Their sampling points in one period are the same. The voltage sequence in Figure 13a is expressed as {$v_{\text{k}}$}. From Figure 13c, one can observe that the hysteresis responses also rely on the input rate. Thus in order to obtain a dynamic performance, the rate-dependence characteristic should be taken into account.

In order to compare these displacement sequences, the horizontal axis is labeled by the sample number as shown in Figure 14. It is equivalent to a time-scale amplification that makes the output displacement curve sequences with different rates have the same period. These displacement curves do not coincide. In this section, the similarity relationship between hysteresis responses with different rates is investigated.

The displacement sequence $\left\{x_{ k}^r\right\}$ corresponding to input voltage sequences with rate ${\dot{v}}_0$ (10) V/s is defined as the reference displacement. $\left\{x_k\right\}$ is the displacement sequence obtained by input voltage sequences with rate $\dot{v}$$\left(\dot{v}\ge {\dot{v}}_0\right)$. Suppose the two sequences of displacement curve segments satisfy the similarity relationship:

$$x_{k+l}={\text{λ}}_1{x^r}_k+{\text{λ}}_0$$

(19)

where ${\text{λ}}_1$, ${\text{λ}}_0$ are the time-scale similarity factors, l is the phase-shift, which moves the curves in horizontal axis direction.

Figure 13. The rate-dependence of hysteresis in PZA (a) input voltage signals with different rates; (b) output displacement; (c) hysteresis loops.

Figure 13. The rate-dependence of hysteresis in PZA (a) input voltage signals with different rates; (b) output displacement; (c) hysteresis loops.

Figure 14. Displacement sequences after time-scale transformation.

Figure 14. Displacement sequences after time-scale transformation.

The identification results of time-scale similarity factors ${\text{λ}}_1$, ${\text{λ}}_0$, l are shown in Table 5. RMSE is defined as

$$\mathrm{RMSE}=\sqrt{\frac{1}{n}{\displaystyle \sum _{k=1}^n{({\text{λ}}_1{x^r}_k+{\text{λ}}_0-x_{k+l})}^2}}$$

(20)

Table 5. The identification of Equation (19). (${\dot{v}}_0$ = 10 V/s).

$\dot{v}$	${\text{λ}}_1$	${\text{λ}}_0$	l	RMSE(μm)
50	0.9847	0.0507	0	0.0293
100	0.9761	0.0424	0	0.0300
500	0.9650	0.0681	0	0.0626
1000	0.9624	0.0768	1	0.0714
5000	0.9544	0.0864	2	0.0654
10000	0.9484	0.1071	4	0.0616

Table 5. The identification of Equation (19). (${\dot{v}}_0$ = 10 V/s).

$\dot{v}$	${\text{λ}}_1$	${\text{λ}}_0$	l	RMSE(μm)
50	0.9847	0.0507	0	0.0293
100	0.9761	0.0424	0	0.0300
500	0.9650	0.0681	0	0.0626
1000	0.9624	0.0768	1	0.0714
5000	0.9544	0.0864	2	0.0654
10000	0.9484	0.1071	4	0.0616

Equations (21) and (22) are used to represent the relationships between ${\text{λ}}_1$, ${\text{λ}}_0$ and $\dot{v}$ respectively.

$${\text{λ}}_1({\log }_{10}^{\dot{v}/{\dot{v}}_0})={\displaystyle \sum _{i=0}^5{p}_i}{({\log }_{10}^{\dot{v}/{\dot{v}}_0})}^i$$

(21)

$${\text{λ}}_0({\log }_{10}^{\dot{v}/{\dot{v}}_0})={\displaystyle \sum _{i=0}^5{q}_i}{({\log }_{10}^{\dot{v}/{\dot{v}}_0})}^i$$

(22)

where, $p_i$, $q_i$ are the coefficients of Equations (21) and (22) as shown in Table 6. The relationships between ${\text{λ}}_1$, ${\text{λ}}_0$ and $\dot{v}$ that are expressed by Equations (21) and (22) are shown in Figure 15.

Table 6. The coefficients of polynomials for Equations (21) and (22).

$i$	$p_i$	$q_i$
0	1.0531	−0.3171
1	−0.2194	1.6998
2	0.2667	−2.9957
3	−0.1662	2.5448
4	0.0490	−1.1074
5	−0.0055	0.2381
6	-	−0.0200

Table 6. The coefficients of polynomials for Equations (21) and (22).

$i$	$p_i$	$q_i$
0	1.0531	−0.3171
1	−0.2194	1.6998
2	0.2667	−2.9957
3	−0.1662	2.5448
4	0.0490	−1.1074
5	−0.0055	0.2381
6	-	−0.0200

Figure 15. The relationship between similarity factors and frequency. (a) The relationship between ${\text{λ}}_1$ and $\dot{v}$. (b) The relationship between ${\text{λ}}_0$ and $\dot{v}$.

Figure 15. The relationship between similarity factors and frequency. (a) The relationship between ${\text{λ}}_1$ and $\dot{v}$. (b) The relationship between ${\text{λ}}_0$ and $\dot{v}$.

5. Hysteresis Model Formulation

Based on the similarity proposed in Section 4, the hysteresis model of PZA is formulated in this section. Before implementing the model, the triangular input voltage sequence $\left\{v_k\right\}$ (the reference voltage sequence) with the rate of ${\dot{v}}_0$ (that is 10 V/s in this paper), the minimum of $v_{\text{min}}^0$ (that is 0 V in this paper), the maximum of $v_{\text{max}}^0$ (that is 100 V in this paper), and the corresponding output displacement sequence $\left\{x_{ k}^r\right\}$ (the reference displacement sequence) need to be identified through experiment in advance. When giving PZA an input excitatio $\text{v}\left(\text{t}\right)$ in any waveforms with a rate of $\dot{v}$, the output displacement x(t) can be obtained through this proposed model. The procedure for modeling is as follows:

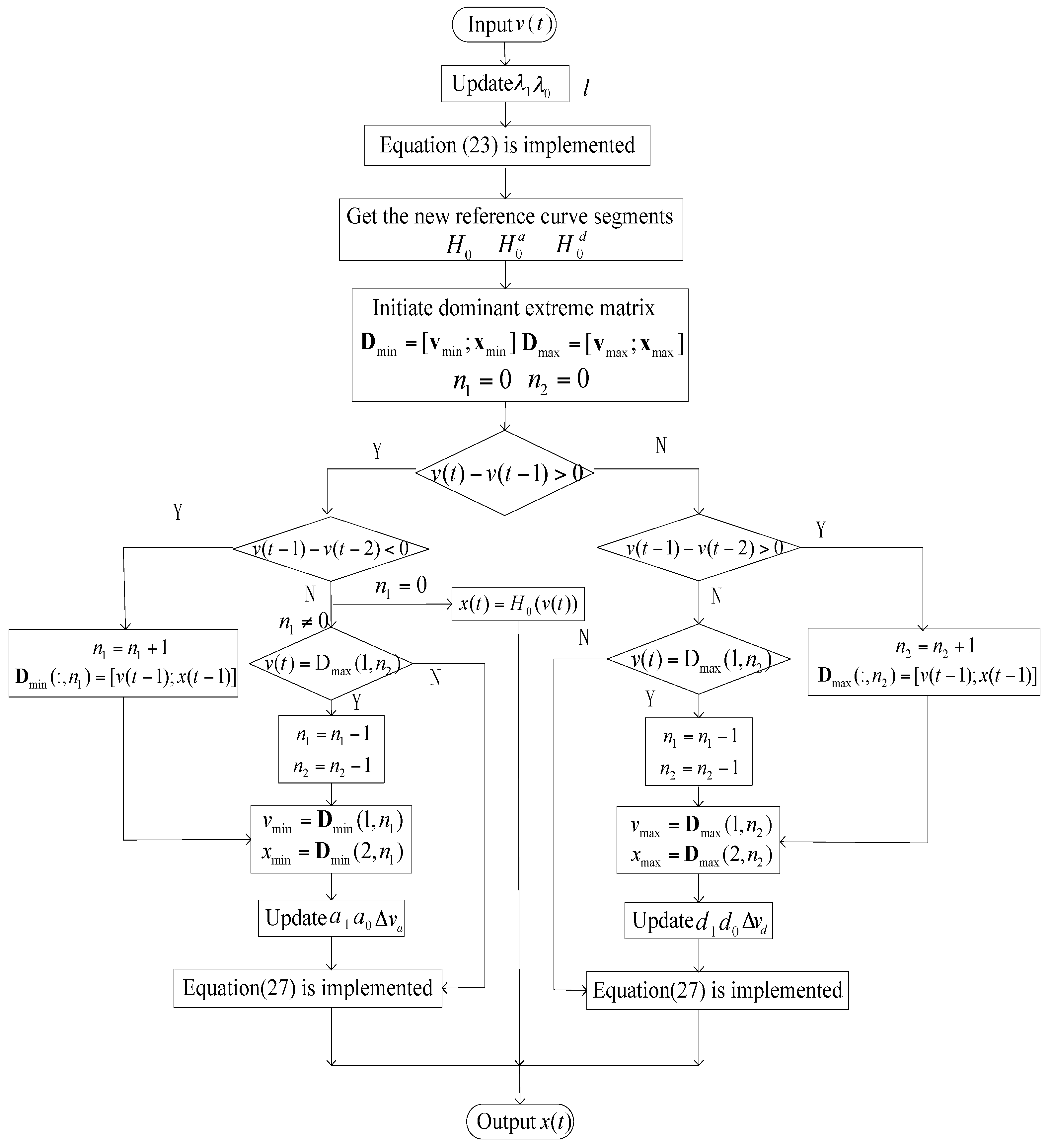
Step1: First, calculate the rate of input voltage according to the amplitude and frequency. The time-scale similarity Equation (23) is implemented to achieve a new reference displacement $\left\{x_k\right\}$ sequence with rate of $\dot{v}$. If ${\dot{v}}_0\ne \dot{v}$, updating the similarity factors ${\text{λ}}_1$, ${\text{λ}}_0$ through Equations (21) and (22). Otherwise, ${\text{λ}}_1=1$, ${\text{ λ}}_0=0$.

$$x_{k+l}={\text{λ}}_1({\log }_{10}^{\dot{v}/{\dot{v}}_0})\cdot {x^r}_k+{\text{λ}}_0({\log }_{10}^{\dot{v}/{\dot{v}}_0})$$

(23)

Step 2: The new reference curve segments constituted by the input voltage sequence $\left\{v_k\right\}$ and new displacement sequence $\left\{x_k\right\}$ are curve-fitted in polynomial forms:

$$H_0(v)={\displaystyle \sum _i^n{\mathrm{\alpha }}_i{v}^i}$$

(24)

$$H_0^a(v)={\displaystyle \sum _i^n{\mathrm{\beta }}_i{v}^i}$$

(25)

$$H_0^a(v)={\displaystyle \sum _i^n{\mathrm{\gamma }}_i{v}^i}$$

(26)

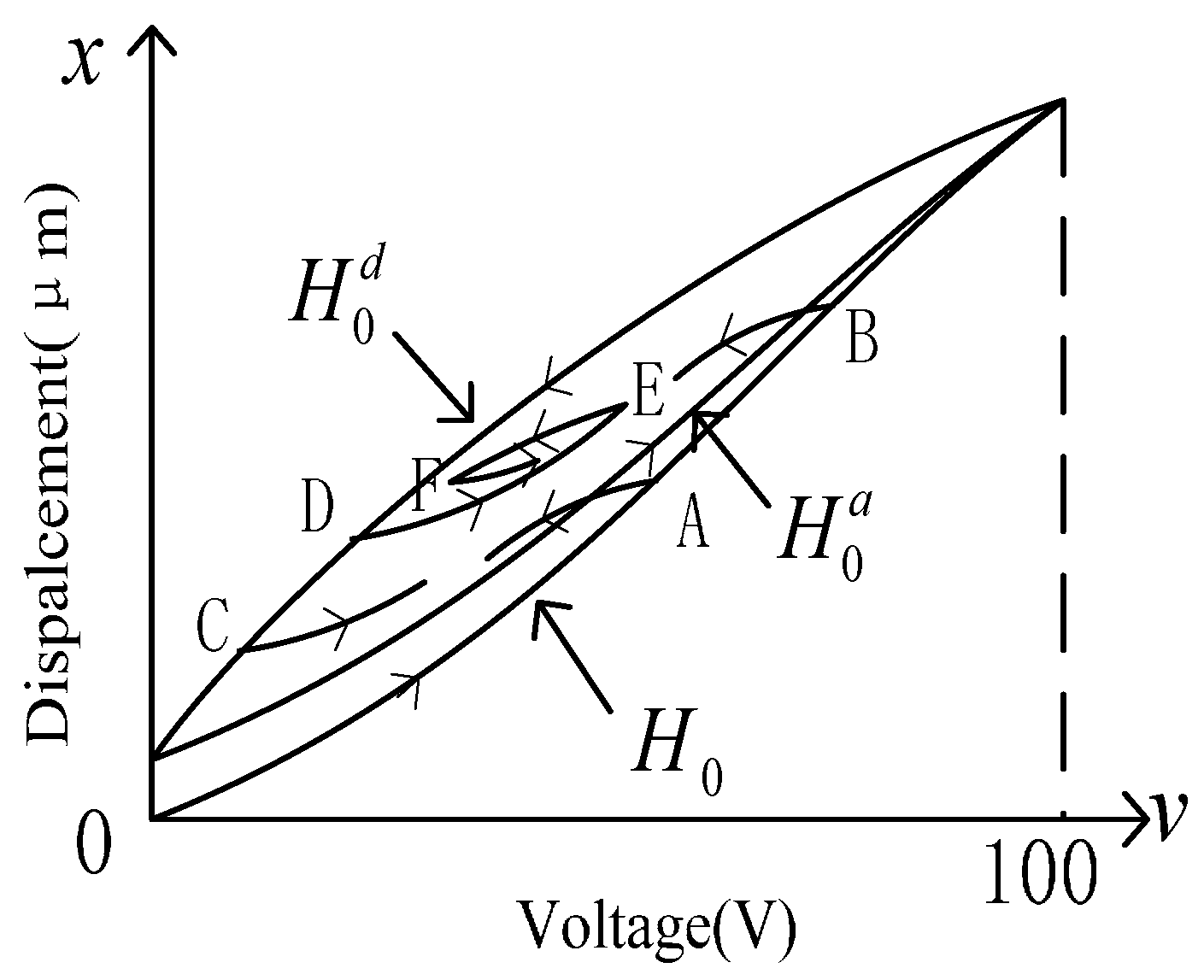
where, $H_0$ is the first reference ascending hysteresis curve segment that departs from the initial state. $H_0^{a }$ is the second reference ascending hysteresis curve segment that departs from the lower turning point. $H_0^{d }$ is the first reference descending hysteresis curve segment that departs from the upper turning point. ${\text{α}}_i, {\text{β}}_i, {\text{γ}}_i$ are the coefficients of polynomials.

Step 3: Updating similarity factors $a_1,a_0,d_1,d_0$ according to the current dominant extreme. If $v_{\text{min}}=v_{\text{min}}^0$, $a_1=1,a_0=0$. If $v_{\text{max}}=v_{\text{max}}^0$, $d_1=1,d_0=0$. Alternatively, these similarity factors are updated by Equations (5), (6), (12) and (13), respectively. The output displacement x(t) corresponding to input excitation v(t) is obtained through Equation (27).

$$\{\begin{array}{l}x(t)=H^a(v(t))=a_1(v_{\min })\cdot H_0^a(v-\mathrm{\Delta }{v}_a)+a_0(v_{\min })+x_{\min }-H^a(v_{\min }),\text{\hspace{0.17em}ascending}\\ x(t)=H^d(v(t))=d_1(v_{\max })\cdot H_0^d(v+\mathrm{\Delta }{v}_d)+d_0(v_{\max })+x_{\max }-H^d(v_{\max }),\text{\hspace{0.17em}descending}\end{array}$$

(27)

where $H^a$ is the ascending hysteresis curve segment whose dominant extreme is $(v_{\text{min}},x_{\text{min}})$. $H^d$ is the descending hysteresis curve segment whose dominant extreme is $(v_{\text{max}},x_{\text{max}})$.

The schematic diagram of the modeling is shown in Figure 16.

Figure 16. The schematic diagram of the modeling.

Figure 16. The schematic diagram of the modeling.

6. Experiments and Discussions

In this section, some experiments with two kinds of input waveforms (Figure 17) at different rates are undertaken to prove the effectiveness of the proposed model. For comparison, the input excitations are also applied to the numerical Preisach model that is based on first reversal curves and is built according to Equation (26) [9].

$$\{\begin{array}{l}f(t)={\displaystyle \sum _{k=1}^{n=1}[F({\mathrm{\alpha }}_k,{\mathrm{\beta }}_{k-1})-F({\mathrm{\alpha }}_k,{\mathrm{\beta }}_k)]}+F(v(t),{\mathrm{\beta }}_k)+c\begin{array}{cc}& \end{array}\begin{array}{cc}& \end{array}\begin{array}{cc}& \end{array}\begin{array}{cc}& \text{ascending}\end{array}\\ f(t)={\displaystyle \sum _{k=1}^{n=1}[F({\mathrm{\alpha }}_k,{\mathrm{\beta }}_{k-1})-F({\mathrm{\alpha }}_k,{\mathrm{\beta }}_k)]}+[F({\mathrm{\alpha }}_n,{\mathrm{\beta }}_{n-1})-F({\mathrm{\alpha }}_n,v(t))]+c\begin{array}{cc}& \begin{array}{cc}\text{descending}& \end{array}\end{array}\end{array}$$

(28)

where f(t) is the output displacement of the system; v(t) is the input voltage. $F\left(\text{α},\text{β}\right)$ is the elongation of the first reversal curve and $F\left(\text{α},\text{β}\right)=f_{\text{α}}-f_{\text{β}}$. $f_{\text{α}}$ stands for the output of the first-order hysteresis curves when $v\left(t\right)=\text{α}$. $f_{\text{αβ}}$ is the output of the first-order hysteresis curves when the input $v\left(t\right)$ decrease to $\text{β }$ from $\text{α}$ c is the bias of the Preisach model. A triangle database of $F\left(\text{α},\text{β}\right)$ with a grid resolution of 5 V and arange of $0\le \text{α}\le 100\text{ V}$ $0\le \text{β}\le 100\text{ V}$ is obtained to prepare for the experiment in this work.

Figure 17. The input excitations. (a) Triangular signals; (b) sinusoidal signals.

Figure 17. The input excitations. (a) Triangular signals; (b) sinusoidal signals.

When implementing the proposed model, only the reference voltage sequence and the reference displacement sequence first need to be stored. While using the Preisach model, a limiting triangle database of the first-order reversal curve elongation, which is difficult to realize and record, needs to be stored in advance through experiments. Storing the database of the reference sequences is much easier than the one for first-order reversal curve elongation. When implementing the proposed model, the current displacement is obtained by only calculating several polynomials, which disclose the rules of hysteresis trajectories and take less computation time. However, the displacement in the Preisach model is obtained by calculating the summation of the weighted effective areas in the limiting triangle database, which is much more complex [18].

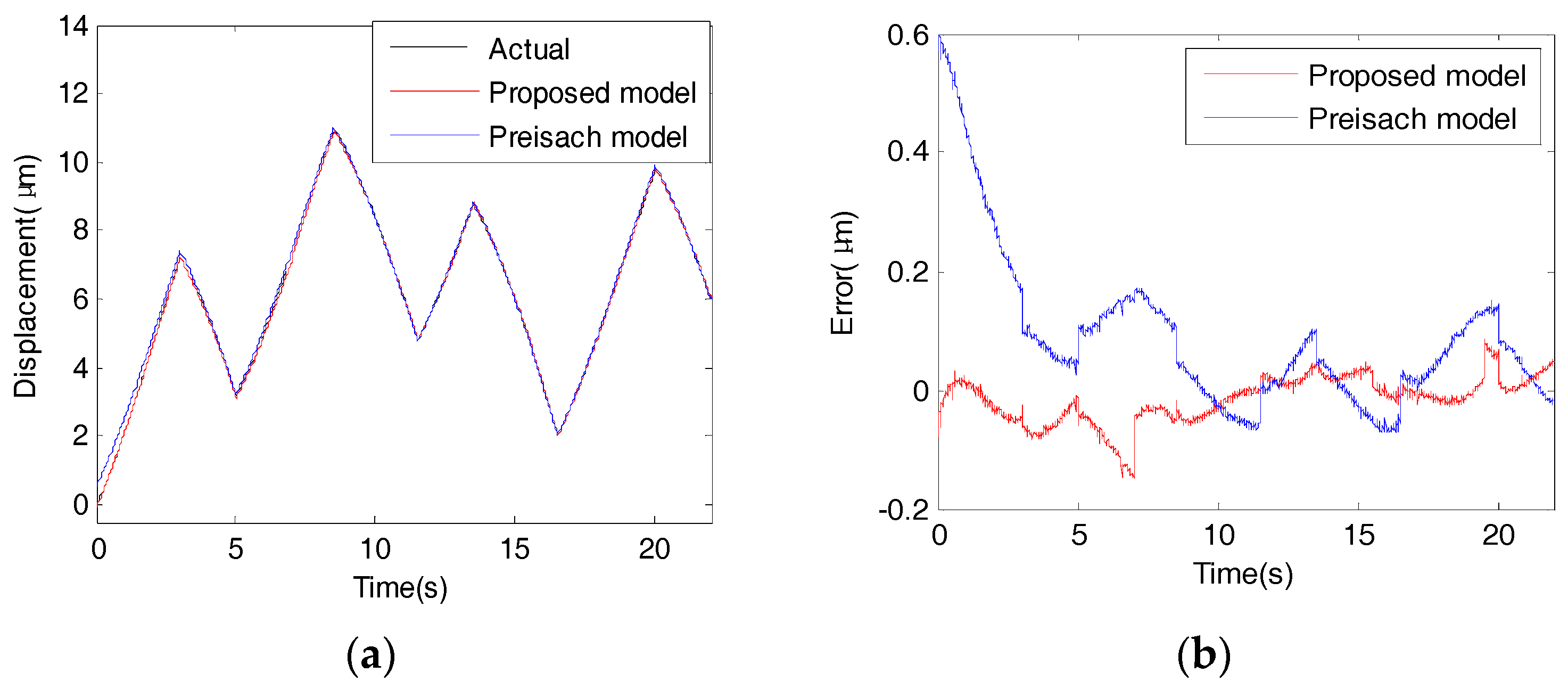
Figure 18 and Figure 19 show the modeling performances of the proposed model and the Preisach model under the triangular input excitation (Figure 17a) at low rate and high rate, respectively. Table 7 gives the specific data of mean absolute errors (MAE) and root mean square error (RMSE). It is observed that when triangular input excitation with a low rate (20 V/s) is applied, the proposed model produces a MAE of 0.0319 μm and a RMSE of 0.0421 μm, which accounts for 0.2924% and 0.3851% of the motion range, respectively. While using the Preisach model, the corresponding MAE and RMSE are 0.1067 μm and 0.1627 μm, which account for 0.9780% and 1.4913% respectively. In the case of high rate (2000 V/s), using the proposed model, the MAE and MSE are 0.0644 μm and 0.0854 μm, which are equivalent to 0.6153% and 0.8159% of the overall motion range, respectively. The Preisach model produces a MAE of 0.2475 μm and a RMSE of 0.3108 μm, i.e., 2.3646% and 2.9694% of the overall motion range. The experimental results show that the proposed modeling method achieves high accuracy.

Table 7. The modeling errors with sinusoidal excitations.

Input Signal		Model	MAE (μm)	RMSE (μm)
Low rate	Triangular	Proposed model	0.0319	0.0421
		Preisach model	0.1067	0.1627
	sinusoidal	Proposed model	0.0523	0.0615
		Preisach model	0.1352	0.1896
High rate	Triangular	Proposed model	0.0644	0.0854
		Preisach model	0.2475	0.3108
	sinusoidal	Proposed model	0.0727	0.0911
		Preisach model	0.2445	0.3087

Table 7. The modeling errors with sinusoidal excitations.

Input Signal		Model	MAE (μm)	RMSE (μm)
Low rate	Triangular	Proposed model	0.0319	0.0421
		Preisach model	0.1067	0.1627
	sinusoidal	Proposed model	0.0523	0.0615
		Preisach model	0.1352	0.1896
High rate	Triangular	Proposed model	0.0644	0.0854
		Preisach model	0.2475	0.3108
	sinusoidal	Proposed model	0.0727	0.0911
		Preisach model	0.2445	0.3087

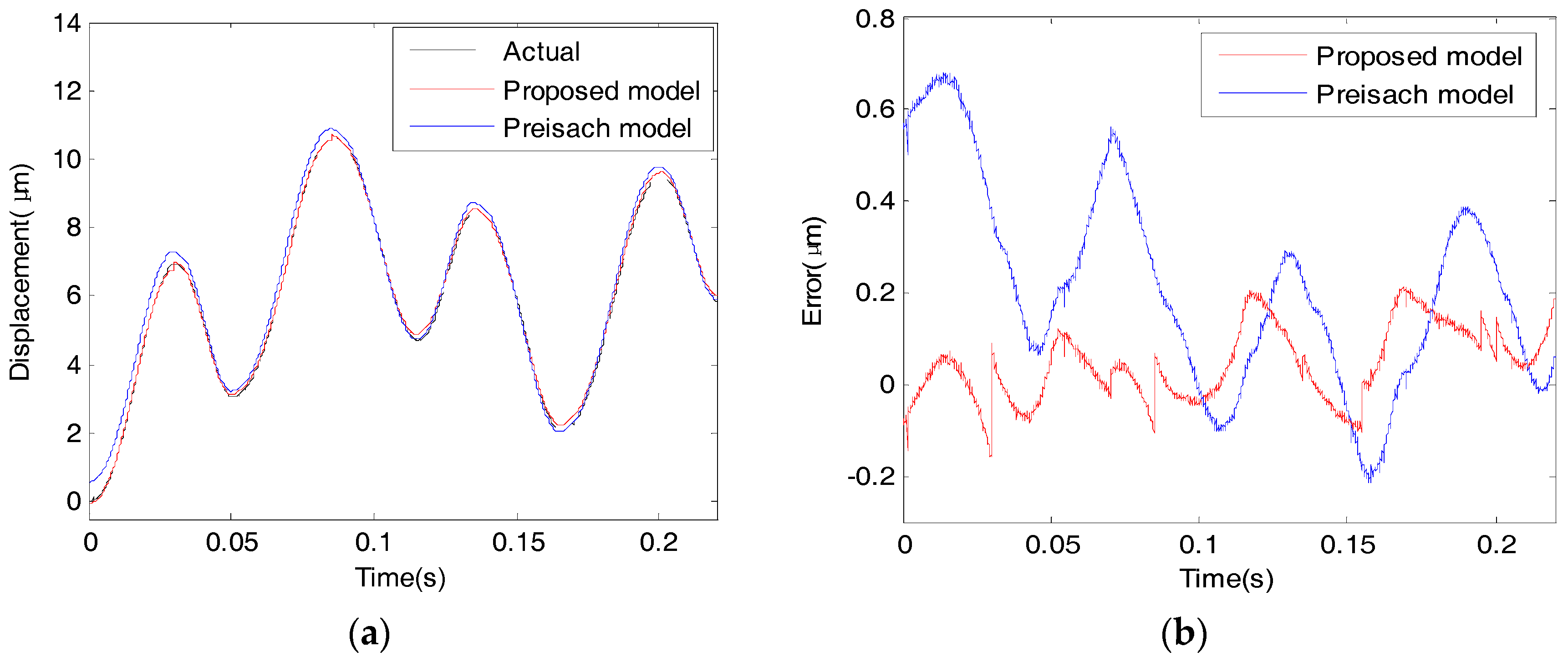
Figure 20 and Figure 21 show the modeling performances of the proposed model and the Preisach model under the sinusoidal input excitation (Figure 17b) at low rate and high rate, respectively. Table 7 gives the specific data of MAE and RMSE. When applying sinusoidal input excitation with low rate, the proposed model produce a MAE of 0.0532 μm and a RMSE of 0.0615 μm, i.e., 0.4716% and 0.5546% of the motion range, respectively. While using the Preisach model, the MAE and RMSE are 0.1352 μm and 0.1896 μm, i.e., 1.2191% and 1.171% of the overall motion range, respectively. When applying sinusoidal signals with a high rate, the MAE and MSE of the proposed model are 0.0727 μm and 0.0911 μm, i.e., 0.6946% and 0.8704% of the overall motion range, respectively. The Preisach model produces a MAE of 0.2445 μm and a RMSE of 0.3087 μm, i.e., 2.3360% and 2.9494% of the motion range.

Figure 18. The responses triangular excitation with a low rate. (a) The output displacement curves; (b) error curves.

Figure 18. The responses triangular excitation with a low rate. (a) The output displacement curves; (b) error curves.

Figure 19. The responses to the random triangular excitation with high rate. (a) The output displacement curves; (b) error curves.

Figure 19. The responses to the random triangular excitation with high rate. (a) The output displacement curves; (b) error curves.

Figure 20. The responses to sinusoidal excitation with a low rate. (a) The output displacement curves; (b) error curves.

Figure 20. The responses to sinusoidal excitation with a low rate. (a) The output displacement curves; (b) error curves.

Figure 21. The responses to sinusoidal excitation with high rate. (a) Output displacement curves; (b) error curves.

Figure 21. The responses to sinusoidal excitation with high rate. (a) Output displacement curves; (b) error curves.

From the experimental results, it is observed that although the similarity relationships are obtained by using the triangular input voltage excitation, the model is also effective when giving other input waveforms. This proposed model can achieve good performance at both low rate and high rate. The modeling ability of the proposed model is better than that of the Preisach model.

7. Conclusions

In this paper, a novel modeling method using segment-similarity of hysteresis nonlinearity in a piezoelectric actuator is proposed. First, the segment-similarity of the hysteresis curves has been presented by using triangular input excitations with different extremes. Segment similarity describes the similarity relationship between hysteresis curve segments with the same voltage interval that depart from different turning points. However, the similarity is only suitable for the hysteresis curve segments that have turning points on the reference curve. For others, large errors may be produced. Therefore, based on the inherent hysteresis properties of a PZA, a modified segment-similarity relationship is proposed to disclose how the coordinates of turning points determine the hysteresis curve. Time-scale similarity is used to obtain a dynamic model. It is remarked that the proposed model is easily established and is more straightforward and simpler and takes less computation time than the Preisach model.

Experiments with different input excitations were carried out. The experimental results demonstrate that the proposed model has good performance in hysteresis trajectory prediction and performs better than the Preisach model. Moreover, although the similarity relationship is concluded from the triangular sequences, the proposed model is suitable for other waveforms. It is expected that the proposed method can be also effectively applied in accurate hysteresis prediction for other smart materials that have similar properties. In future work, the proposed model-based hysteresis compensator will be designed to reduce or eliminate the hysteresis effect in high-precision control systems.