Optimization Design of the Two-Stage Reduction Micro-Drive Mechanism Based on Particle Swarm Algorithm †
Abstract
1. Introduction
2. Optimization Design
2.1. Design of Mechanism
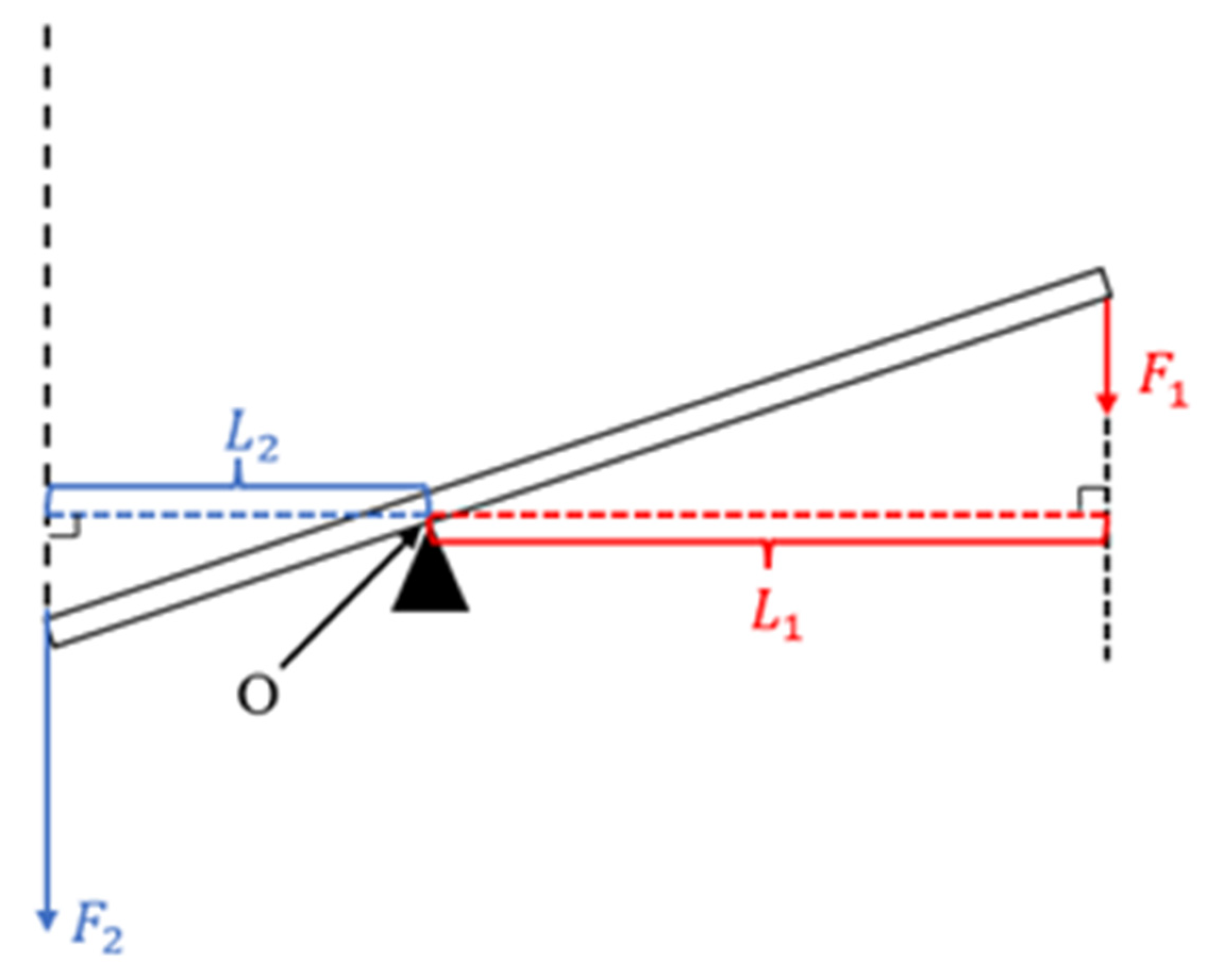
2.1.1. Lever Principle
2.1.2. Principle of Balanced Additional Force
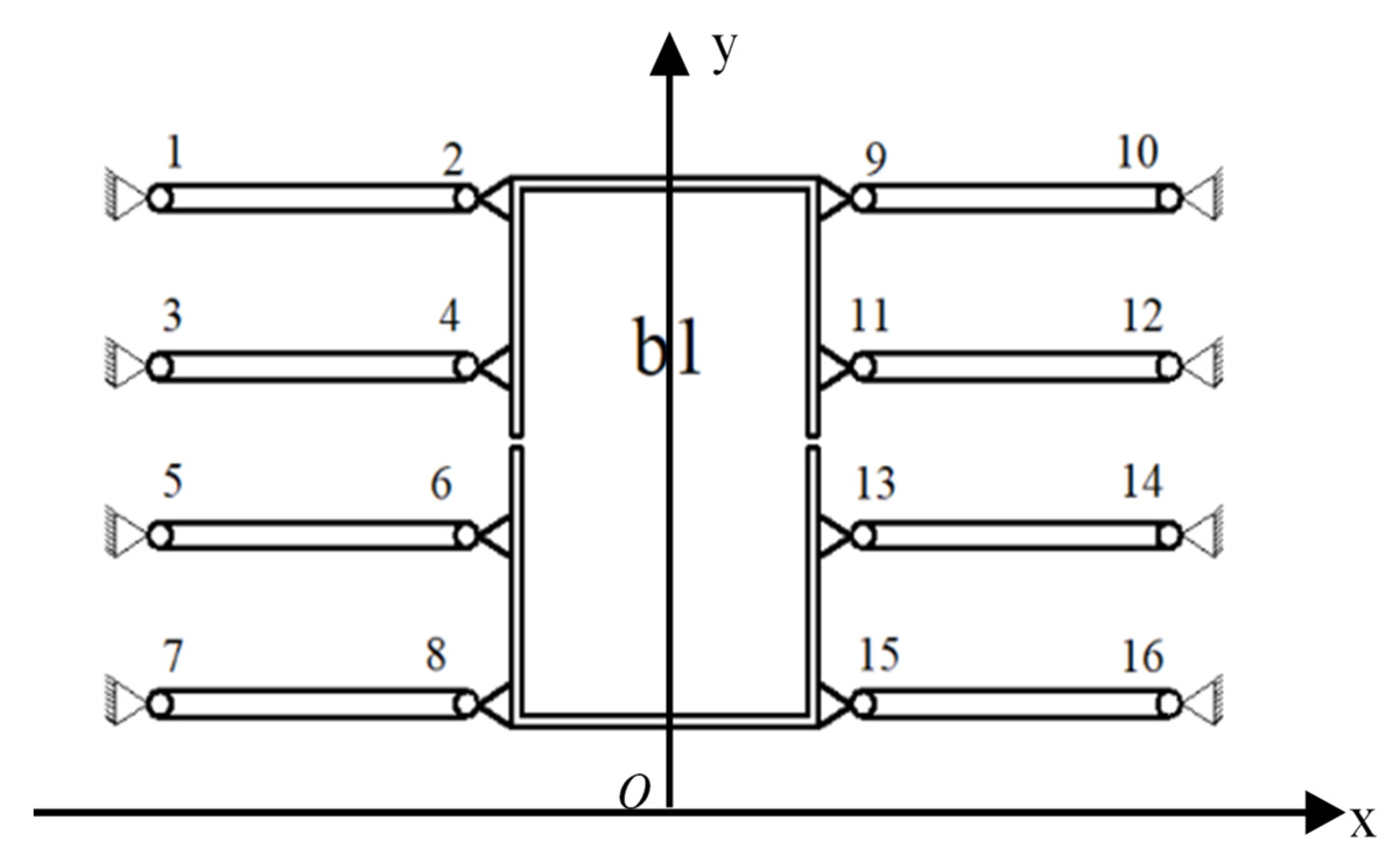
2.1.3. Initial Mechanism Design
2.2. Reduction Ratio Calculation
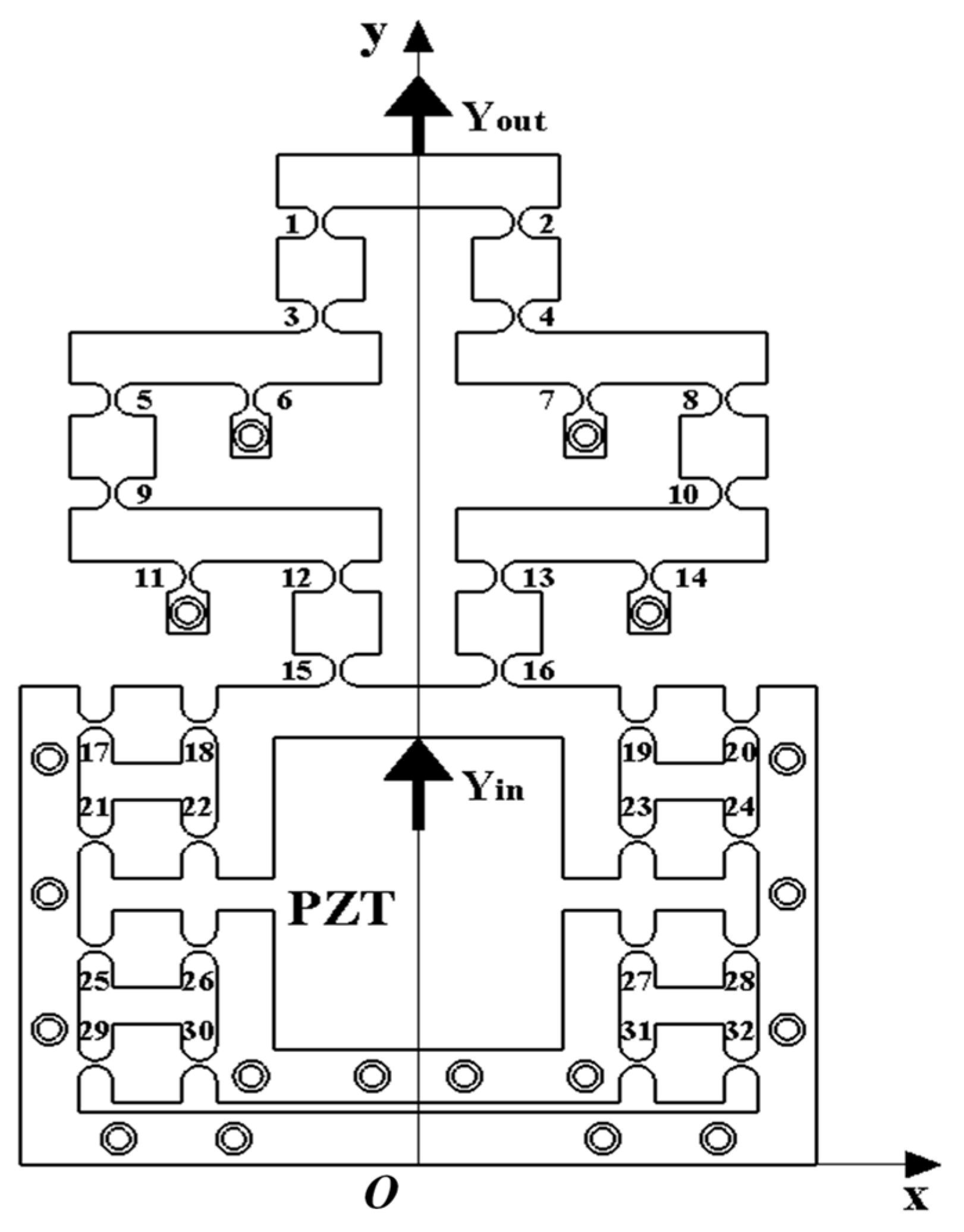
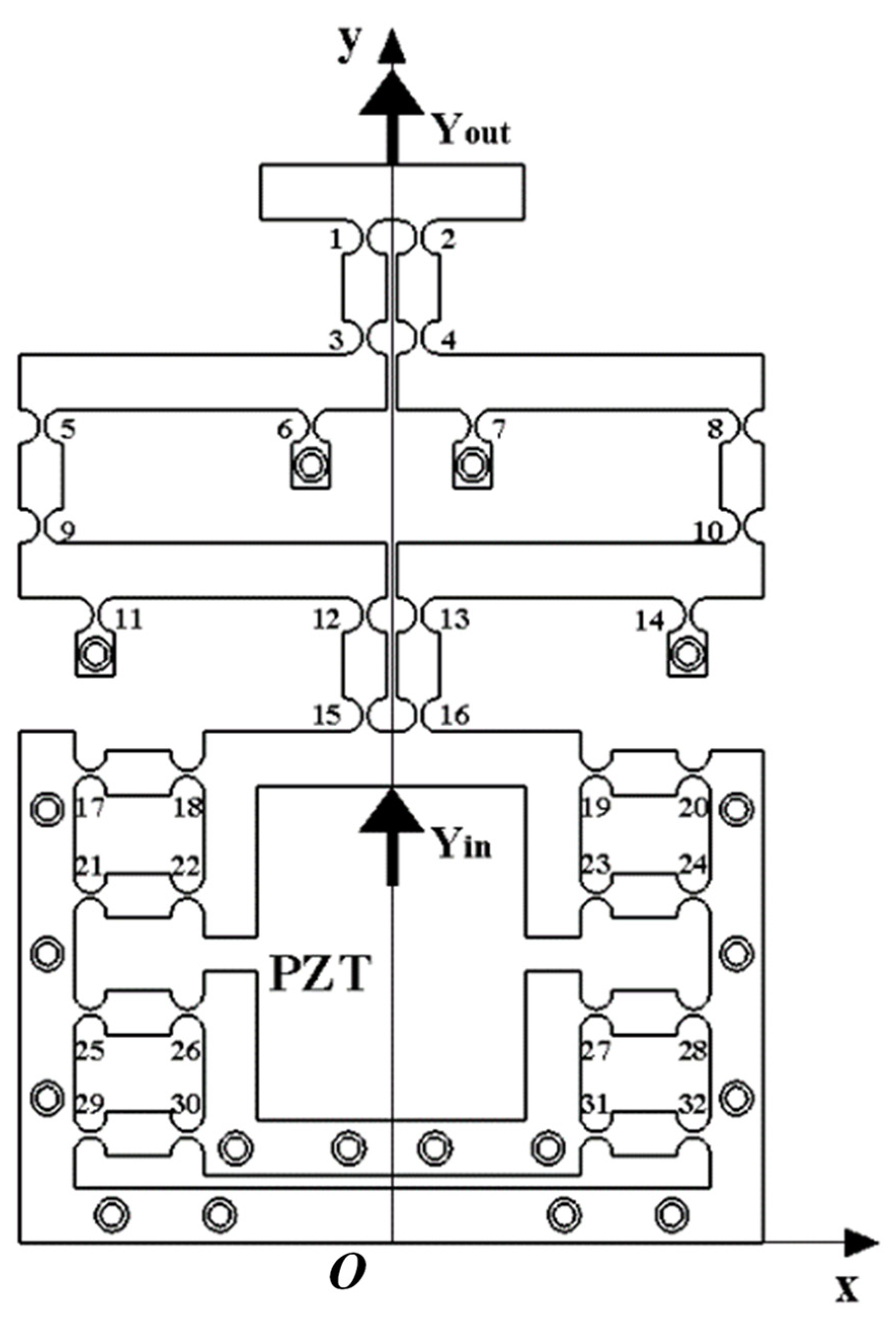
2.3. Structural Optimization
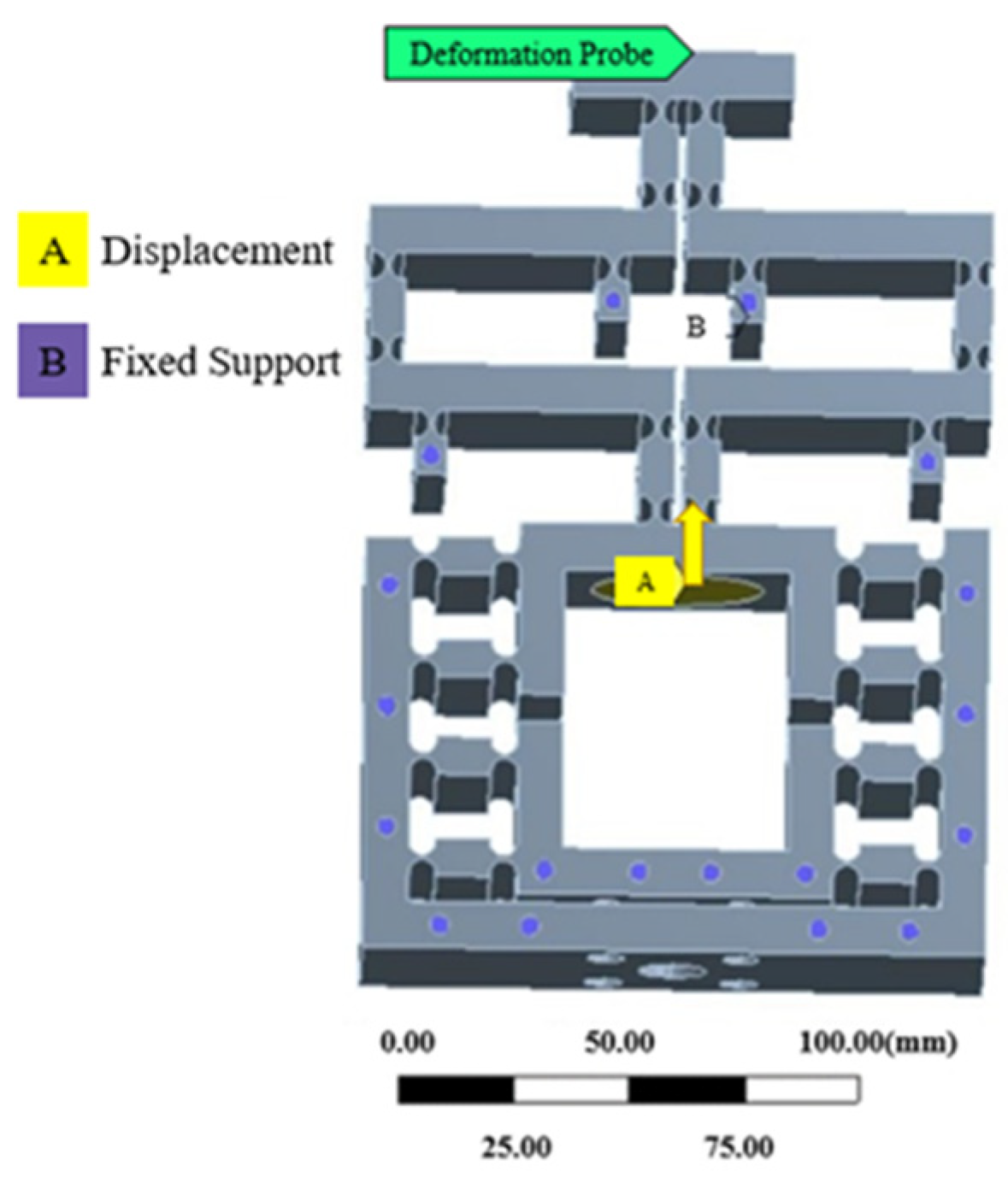
3. Performance Analysis
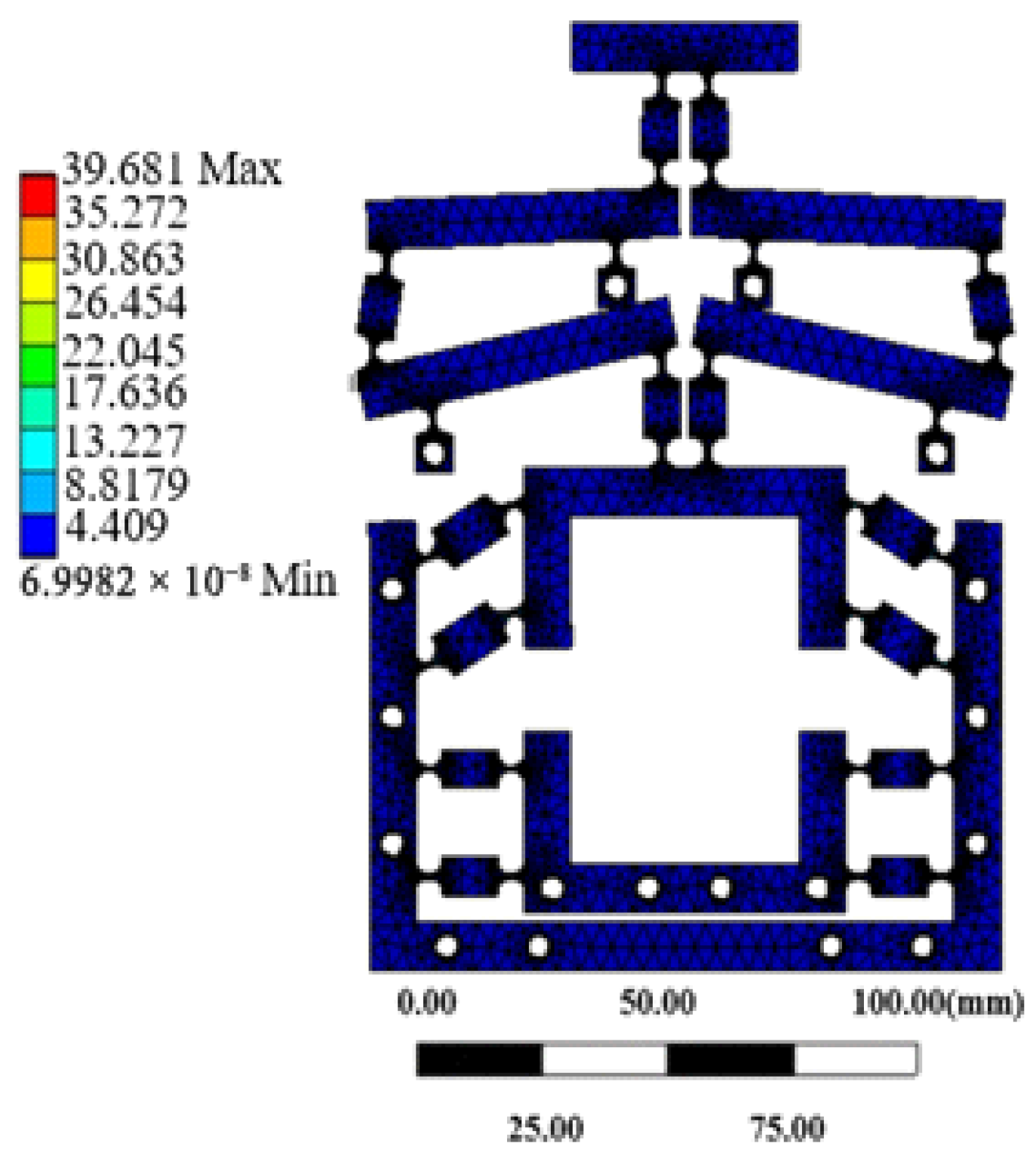
3.1. Strength Analysis
3.2. Dynamic Performance
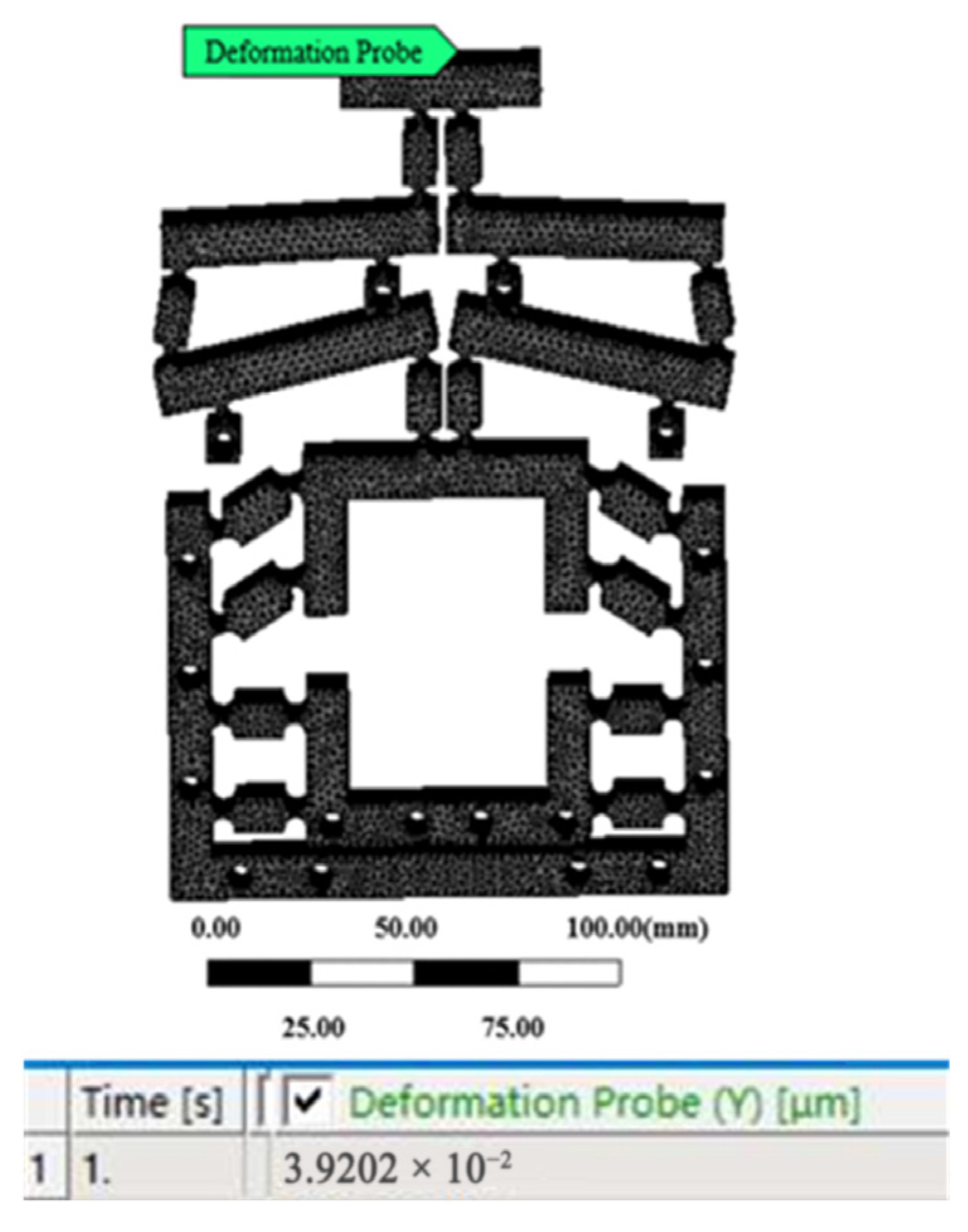
3.3. Motion Performance
4. Experiment and Discussion
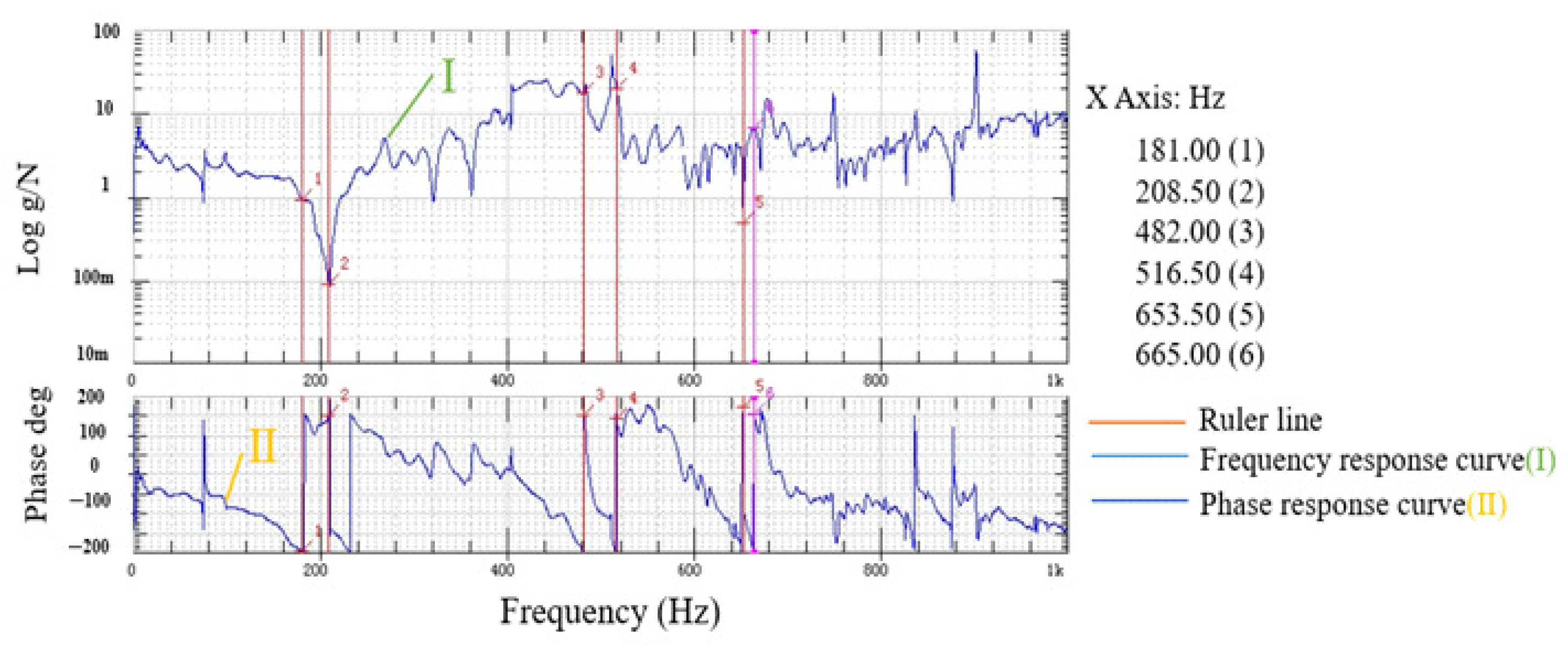
4.1. Dynamic Performance Test
4.2. Motion Performance Test
4.3. Discussion
4.3.1. Dynamic Performance Analysis
- (1)
- The finite element and experimental analysis results were consistent and the maximum error was 8.14%, indicating that the analysis results were accurate and reliable.
- (2)
- The reduction micro-drive mechanism was driven by P235.1s piezoelectric ceramic actuator, whose maximum frequency is 300 Hz and natural frequency was not resonant with the reduction fretting mechanism, and the two-stage reduction micro-drive mechanism has good dynamic performance.
4.3.2. Motion Performance Analysis
- (1)
- Reduction ratio analysis
- (2)
- Error Analysis
5. Conclusions
- (1)
- The micro-drive mechanism designed in this paper incorporates a hinge structure, which effectively eliminates parasitic motion and non-motion direction forces through the application of a balanced additional force function.
- (2)
- Utilizing particle swarm optimization, the structure of the two-stage reduction micro-drive mechanism was optimized to achieve the minimum reduction ratio. After optimization, finite element and experimental analyses revealed that the maximum simulated stress of the mechanism was 39.681 MPa, significantly lower than the allowable stress of the material.
- (3)
- The first six natural frequencies of the mechanism were found to be non-overlapping with the motion frequency of the micro-driver, guaranteeing the absence of resonance during mechanism operation. Therefore, the strength performance and dynamic performance of the mechanism were excellent and met the design and use requirements.
- (4)
- The two-stage reduction micro-drive mechanism achieved a minimum reduction ratio of 24.73:1, representing a reduction of 518.25% compared to the original design. The motion error of this mechanism was determined to be 9.02%, with a maximum motion error of 0.0267 μm, while the minimum motion linearity reached 0.99952. Consequently, this mechanism possesses characteristics such as a small reduction ratio, high motion accuracy, and superior motion linearity.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, Z.; Dai, Y.; Guan, C.; Lai, T.; Sun, Z.; Li, H. An on-machine measurement technique with sub-micron accuracy on a low-precision grinding machine tool. J. Manuf. Process. 2024, 119, 520–530. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, X.; Zhang, J.; Luo, H.; Li, F.; Huang, X.; Jing, F. Automatic phase-locked control of grating tiling. Opt. Lasers Eng. 2012, 50, 262–267. [Google Scholar] [CrossRef]
- Sun, W.; Shan, F.; Zong, N.; Dong, H.; Jing, T. Grain selection and growth orientation of prior-β phase for Ti-6-4 during additive manufacturing: Insights from a modeling perspective. China Foundry 2021, 18, 83–93. [Google Scholar] [CrossRef]
- Gao, Z.; Yuan, Y.; Cao, T.; Yang, J.; Gao, Z.; Yu, Y. Melt structure of NiCrW superalloy near liquidus studied by experiment and molecular dynamics simulation. Mater. Lett. 2025, 389, 138405. [Google Scholar] [CrossRef]
- Luo, Y.; Wang, M.; Tu, J.; Jiang, Y.; Jiao, S. Reduction of residual stress in porous Ti6Al4V by in situ double scanning during laser additive manufacturing. Int. J. Miner. Metall. Mater. 2021, 28, 1844–1853. [Google Scholar] [CrossRef]
- Pérez-Ruiz, J.D.; de Lacalle, L.N.L.; Velilla-Díaz, W.; Mesa, J.A.; Gómez, G.; Maury, H.; Urbikain, G.; Gonzalez, H. Evaluating the feasibility of using crystalline patterns induced by PBF-LB to predict strength enhancing orientations. Mater. Des. 2025, 254, 114006. [Google Scholar] [CrossRef]
- Huang, W.W.; Wang, X.; Meng, Y.; Li, L.; Zhang, X.; Ren, M.; Zhu, L.M. Design, modeling and control of high-bandwidth nano-positioning stages for ultra-precise measurement and manufacturing: A survey. Int. J. Extrem. Manuf. 2024, 6, 062007. [Google Scholar] [CrossRef]
- Liu, R.; Wen, Z.; Cao, T.; Lu, C.; Wang, B.; Wu, D.; Li, X. A precision positioning rotary stage driven by multilayer piezoelectric stacks. Precis. Eng. 2022, 76, 226–236. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Q.; Li, S. Modeling and Prediction of Inter-System Bias for GPS/BDS-2/BDS-3 Combined Precision Point Positioning. Comput. Model. Eng. Sci. 2022, 132, 823–843. [Google Scholar] [CrossRef]
- Díaz-Tena, E.; Ugalde, U.; López de Lacalle, L.N.; De la Iglesia, A.; Calleja, A.; Campa, F.J. Propagation of assembly errors in multitasking machines by the homogenous matrix method. Int. J. Adv. Manuf. Technol. 2013, 68, 149–164. [Google Scholar] [CrossRef]
- Hooijschuur, R.; Saikumar, N.; HosseinNia, S.H.; van Ostayen, R.A. Air-Based Contactless Wafer Precision Positioning System. Appl. Sci. 2021, 11, 7588. [Google Scholar] [CrossRef]
- Jin, T.; Han, X. Robotic arms in precision agriculture: A comprehensive review of the technologies, applications, challenges, and future prospects. Comput. Electron. Agric. 2024, 221, 108938. [Google Scholar] [CrossRef]
- Li, C.; Li, W. Optimization Analysis of Vibration Characteristics for Precision Positioning Stage. J. Phys. Conf. Ser. 2021, 1939, 012072. [Google Scholar] [CrossRef]
- Zhang, X.; Zhong, B.; Liu, B.; Jin, Z.; Wang, Z.; Sun, L. A Small Bipedal Trans-Scale Precision Positioning Stage Based on Inertial Stick-Slip Driving. Int. J. Precis. Eng. Manuf. 2021, 22, 473–482. [Google Scholar] [CrossRef]
- Adizue, U.L.; Tura, A.D.; Isaya, E.O.; Farkas, B.Z.; Takács, M. Surface quality prediction by machine learning methods and process parameter optimization in ultra-precision machining of AISI D2 using CBN tool. Int. J. Adv. Manuf. Technol. 2023, 129, 1375–1394. [Google Scholar] [CrossRef]
- Niu, Z.; Cheng, K. An experimental investigation on surface generation in ultraprecision machining of particle reinforced metal matrix composites. Int. J. Adv. Manuf. Technol. 2019, 105, 4499–4507. [Google Scholar] [CrossRef]
- Li, J.; Wei, W.; Huang, X.; Liu, P. Study on dynamic characteristics of ultraprecision machining and its effect on medium-frequency waviness error. Int. J. Adv. Manuf. Technol. 2020, 108, 2895–2906. [Google Scholar] [CrossRef]
- Yang, M.; Wei, K.; Zhang, C.; Liu, D.; Yang, Y.; Han, F.; Zhao, S. Optimization design of two-stage amplification micro-drive system without additional motion based on particle swarm optimization algorithm. Vis. Comput. Ind. Biomed. Art 2022, 5, 28. [Google Scholar] [CrossRef] [PubMed]
- Yang, M.; Zhang, X.; Zhang, C.; Wu, H.; Yang, Y. Design and performance research of a precision micro-drive reduction system without additional motion. Micromachines 2022, 13, 1636. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Wu, E.G.; Uluşan, H.; Zhao, E.T.; Phillips, A.J.; Kling, A.; Melosh, N.A. Direct-Print 3D Electrodes for Large-Scale, High-Density, and Customizable Neural Interfaces. Adv. Sci. 2025, 12, 2408602. [Google Scholar] [CrossRef] [PubMed]
- Shen, J.; Fang, X.; Liu, J.; Liu, L.; Lu, H.; Lou, J. Design, manufacture, and two-step calibration of a piezoelectric parallel microrobot at the millimeter scale for micromanipulation. Mech. Mach. Theory 2025, 206, 105928. [Google Scholar] [CrossRef]
- Yang, M.; Lv, Z.; Zhang, C.; Yang, Y.; Jing, G.; Guo, W.; Lu, Z.; Huang, Y.; Wei, K.; Li, L.; et al. Positioning Performance of a Sub-Arc-Second Micro-Drive Rotary System. Micromachines 2021, 12, 1063. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.; Leng, J.; Ju, B. Digital twins-based smart design and control of ultra-precision machining: A review. Symmetry 2021, 13, 1717. [Google Scholar] [CrossRef]
- Xu, Q.; Li, Y. Analytical modeling, optimization and testing of a compound bridge-type compliant displacement amplifier. Mech. Mach. Theory 2011, 46, 183–200. [Google Scholar] [CrossRef]
- Kim, M.; Lee, D.W.; Lee, S.; Kim, Y.; Jung, Y. Effects of hinge design of horizontal-swing fast tool servo (HFTS) for micro-patterning on a roll. Int. J. Adv. Manuf. Technol. 2018, 95, 233–241. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, X. A planar 3-DOF nanopositioning platform with large magnification. Precis. Eng. 2016, 46, 221–231. [Google Scholar] [CrossRef]
- Tanikawa, T.; Ukiana, M.; Morita, K.; Koseki, Y.; Ohba, K.; Fujii, K.; Arai, T. Design of 3-DOF parallel mechanism with thin plate for micro finger module in micro manipulation. IEEE 2002, 2, 1778–1783. [Google Scholar]
- Panin, F. A new displacement reduction mechanism for fine positioning. ESA J. 1992, 16, 23–34. [Google Scholar]
- Lin, R.; Li, Y.; Zhang, Y.; Wang, T.; Wang, Z.; Song, Z.; Dou, Z.; Qian, J. Design of A flexure-based mixed-kinematic XY high-precision positioning platform with large range. Mech. Mach. Theory 2019, 142, 103609. [Google Scholar] [CrossRef]
- Sakuma, S.; Arai, F. Cellular force measurement using a nanometric-probe-integrated microfluidic chip with a displacement reduction mechanism. J. Robot. Mechatron. 2013, 25, 277–284. [Google Scholar] [CrossRef]
- Cui, F.; Li, Y.; Qian, J. Development of a 3-DOF flexible micro-motion platform based on a new compound lever amplification mechanism. Micromachines 2021, 12, 686. [Google Scholar] [CrossRef] [PubMed]
- Jiménez Morales, O.L.; Tristán Rodríguez, D.; Garrido, R.; Mezura-Montes, E. Optimal Tuning of an Active Disturbance Rejection Controller Using a Particle Swarm Optimization Algorithm. In Hybrid Intelligent Systems Based on Extensions of Fuzzy Logic, Neural Networks and Metaheuristics; Springer Nature: Cham, Switzerland, 2023; pp. 165–186. [Google Scholar]
- Chen, F.; Zhang, Q.; Dong, W.; Sun, L. Design and test of a compact large-stroke dual-drive linear-motion system. Mech. Syst. Signal Process. 2022, 180, 109438. [Google Scholar] [CrossRef]
- Huang, S.C.; Dao, T.P. Design computational optimization of a flexure-based XYpositioning platform using FEA-based response surface methodology. Int. J. Precis. Eng. Manuf. 2016, 17, 1035–1048. [Google Scholar] [CrossRef]
- Van der Werff, K.; Jonker, J.B. Dynamics of flexible mechanisms. In Computer Aided Analysis and Optimization of Mechanical System Dynamics; Springer: Berlin/Heidelberg, Germany, 1984; pp. 381–400. [Google Scholar]
- Latchoumi, T.P.; Balamurugan, K.; Dinesh, K.; Ezhilarasi, T. Particle swarm optimization approach for waterjet cavitation peening. Measurement 2019, 141, 184–189. [Google Scholar] [CrossRef]
- Yang, W.; Zhou, X.; Luo, Y. Simultaneously optimizing inertia weight and acceleration coefficients via introducing new functions into PSO algorithm. J. Phys. Conf. Ser. 2021, 1754, 012195. [Google Scholar] [CrossRef]
- Zou, D.; Li, S.; Li, Z.; Kong, X. A new global particle s-warm optimization for the economic emission dispatch with or without transmission losses. Energy Convers. Manag. 2017, 139, 45–70. [Google Scholar] [CrossRef]
- Chen, Y.; Lai, L. Design, Modeling, Testing, and Control of a Novel Fully Flexure-Based Displacement Reduction Mechanism Driven by Voice Coil Motor. Actuators 2022, 11, 228. [Google Scholar] [CrossRef]
- Wang, G.; Wang, Y.; Lv, B.; Ma, R.; Liu, L. Research on a new type of rigid-flexible coupling 3-DOF micro-positioning platform. Micromachines 2020, 11, 1015. [Google Scholar] [CrossRef] [PubMed]



| Material Name | Young’s Modulus (MPa) | Limit of Yielding (MPa) | Tensile Strength (MPa) | Poisson’s Ratio | Density (g/cm3) |
|---|---|---|---|---|---|
| 60Si2Mn | 2.06 × 105 | 1176 | 1274 | 0.26 | 7.85 |
| x1 | x2 | x3 | x4 | x5 | x6 |
|---|---|---|---|---|---|
| 14 | 40 | 53 | 53 | 29 | 17 |
| Modal Order | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Natural frequency value (Hz) | 167.62 | 196.99 | 520.44 | 562.27 | 705.14 |
| Order | Natural Frequency Value of Finite Element Analysis (Hz) | Experimental Natural Frequency Value (Hz) | Relative Error (%) |
|---|---|---|---|
| 1 | 167.62 | 181.00 | 7.98% |
| 2 | 196.99 | 208.50 | 5.84% |
| 3 | 520.44 | 482.00 | 7.38% |
| 4 | 562.27 | 516.50 | 8.14% |
| 5 | 705.14 | 653.50 | 7.32% |
| 6 | 712.98 | 665.00 | 6.72% |
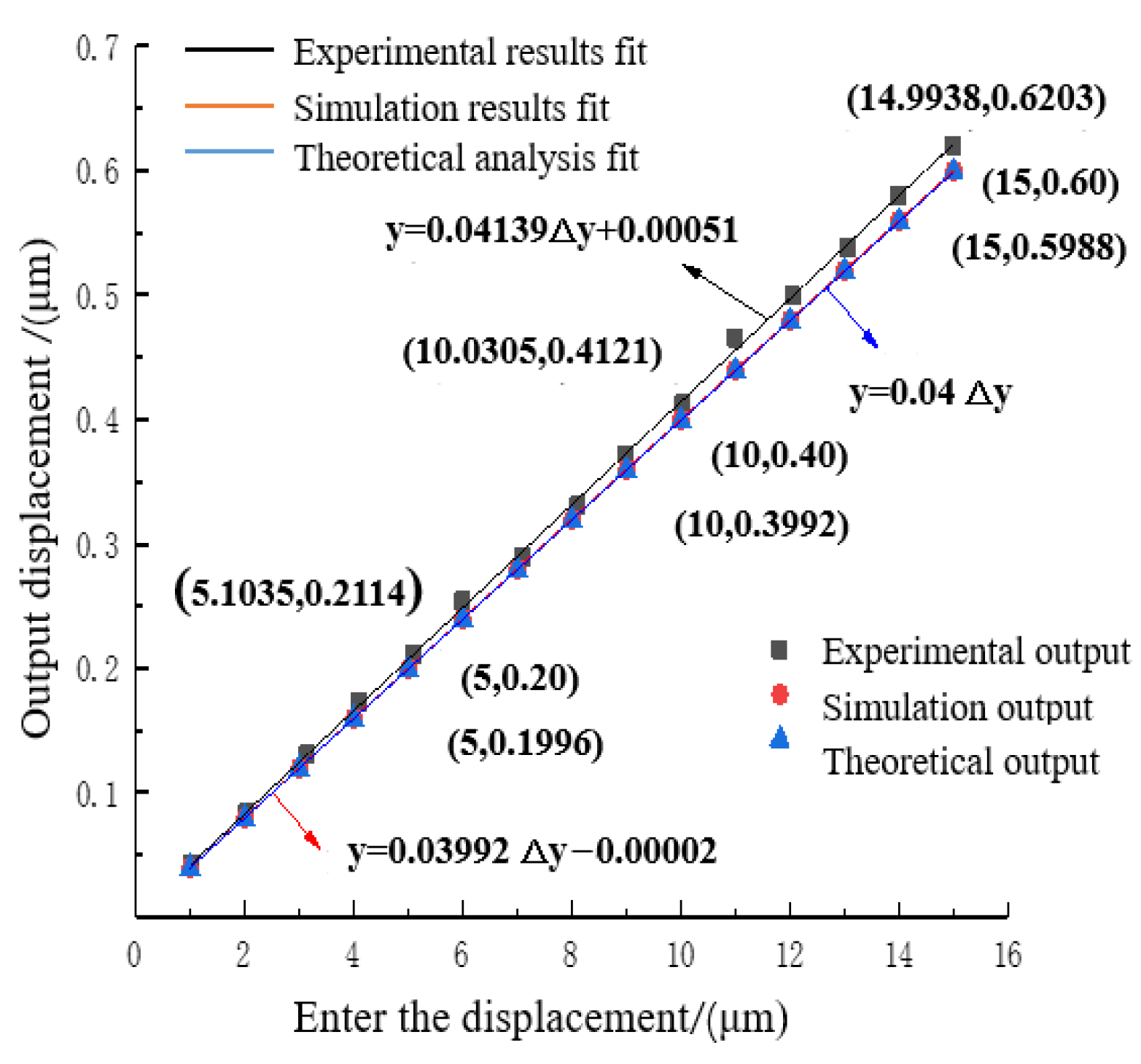
| Enter the Displacement (µm) | Theoretical Output Displacement (µm) | Finite Element Analysis of Output Displacement | Enter the Displacement (µm) |
|---|---|---|---|
| 1.0000 | 0.0400 | 0.0392 | 0.0426 |
| 2.0000 | 0.0800 | 0.0798 | 0.0835 |
| 3.0000 | 0.1200 | 0.1198 | 0.1306 |
| 4.0000 | 0.1600 | 0.1597 | 0.1725 |
| 5.0000 | 0.2000 | 0.1996 | 0.2114 |
| 6.0000 | 0.2400 | 0.2395 | 0.2541 |
| 7.0000 | 0.2800 | 0.2794 | 0.2896 |
| 8.0000 | 0.3200 | 0.3193 | 0.3305 |
| 9.0000 | 0.3600 | 0.3593 | 0.3716 |
| 10.0000 | 0.4000 | 0.3992 | 0.4121 |
| 11.0000 | 0.4400 | 0.4391 | 0.4658 |
| 12.0000 | 0.4800 | 0.4791 | 0.4993 |
| 13.0000 | 0.5200 | 0.5190 | 0.5387 |
| 14.0000 | 0.5600 | 0.5589 | 0.5797 |
| 15.0000 | 0.6000 | 0.5988 | 0.6203 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, N.; Wang, D.; Li, K.; Wei, K.; Ge, H.; Yang, M. Optimization Design of the Two-Stage Reduction Micro-Drive Mechanism Based on Particle Swarm Algorithm. Micromachines 2025, 16, 826. https://doi.org/10.3390/mi16070826
Zhang N, Wang D, Li K, Wei K, Ge H, Yang M. Optimization Design of the Two-Stage Reduction Micro-Drive Mechanism Based on Particle Swarm Algorithm. Micromachines. 2025; 16(7):826. https://doi.org/10.3390/mi16070826
Chicago/Turabian StyleZhang, Na, Dongmei Wang, Kai Li, Kaiyang Wei, Hongyu Ge, and Manzhi Yang. 2025. "Optimization Design of the Two-Stage Reduction Micro-Drive Mechanism Based on Particle Swarm Algorithm" Micromachines 16, no. 7: 826. https://doi.org/10.3390/mi16070826
APA StyleZhang, N., Wang, D., Li, K., Wei, K., Ge, H., & Yang, M. (2025). Optimization Design of the Two-Stage Reduction Micro-Drive Mechanism Based on Particle Swarm Algorithm. Micromachines, 16(7), 826. https://doi.org/10.3390/mi16070826






