A Review of Three-Dimensional Electric Field Sensors
Abstract
1. Introduction
2. Field Mill 3D DC EFSs
2.1. Working Principle
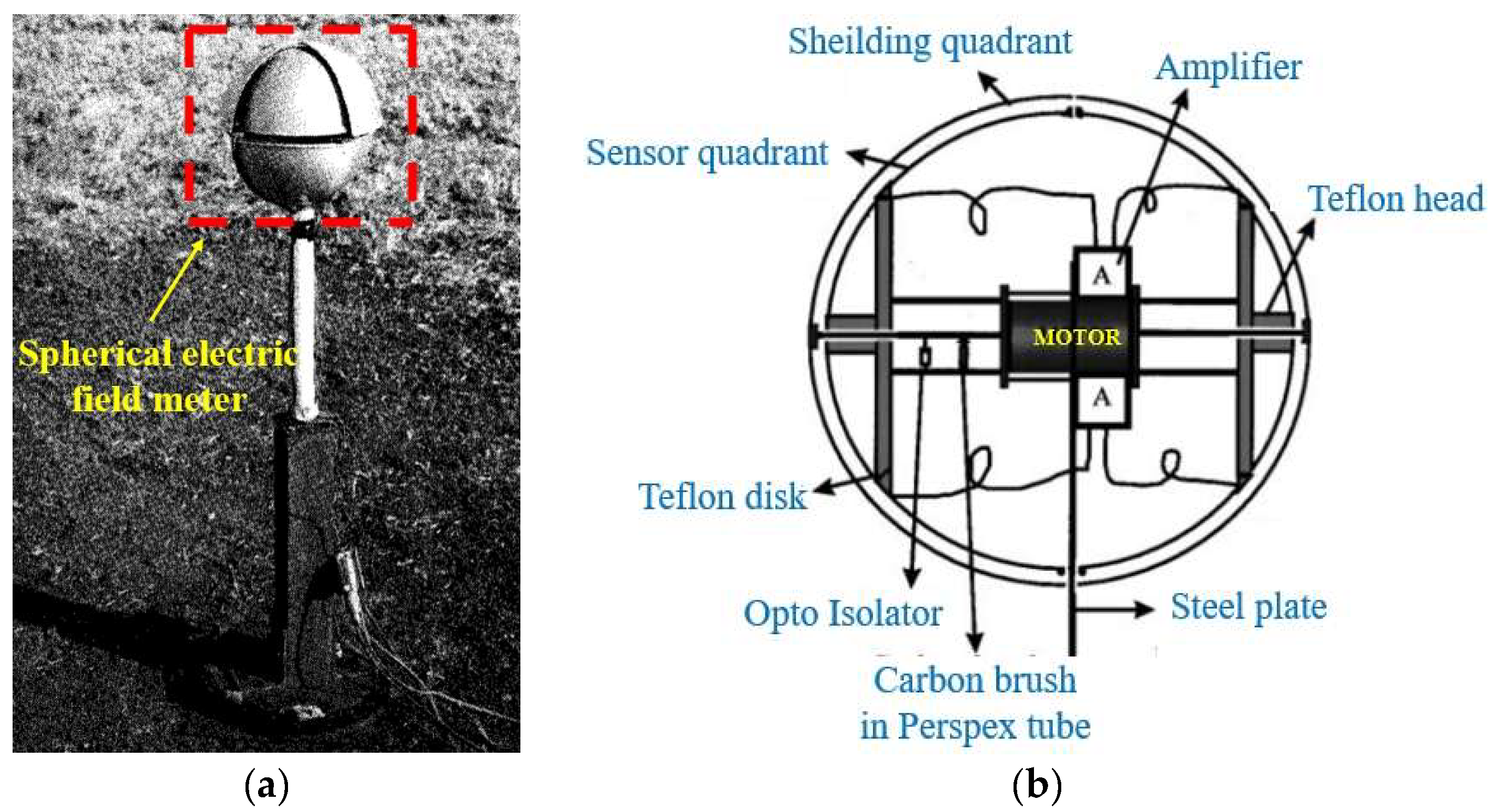
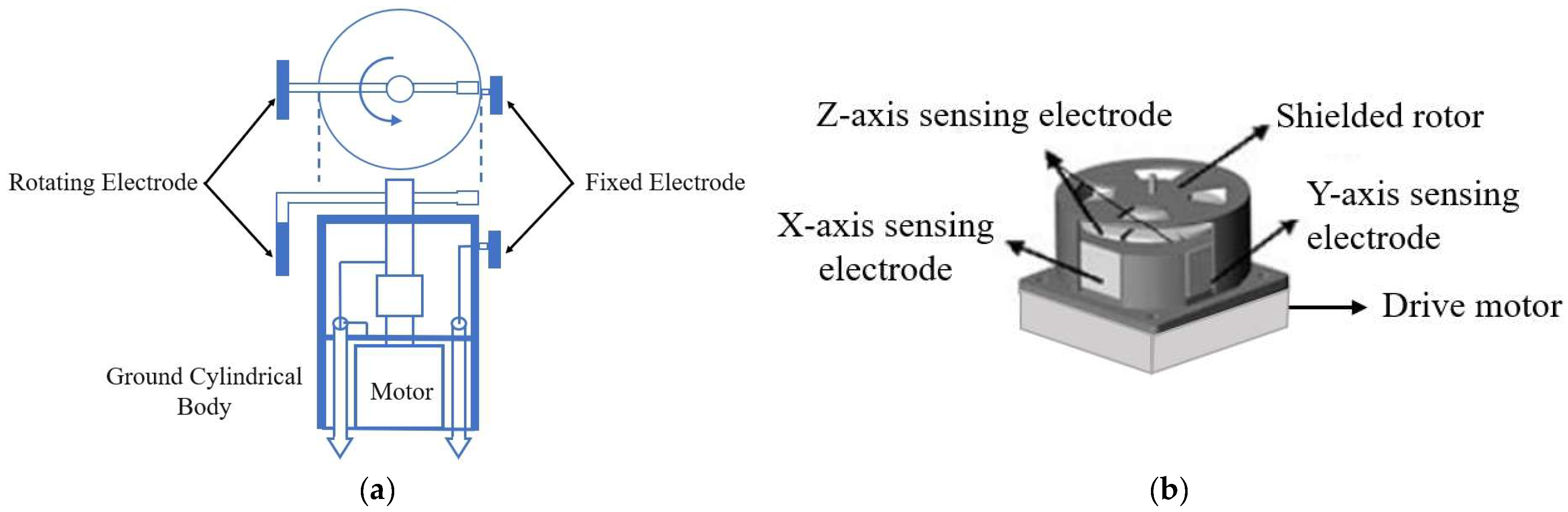
2.2. Prototype Instantiation for Field Mill 3D DC EFSs
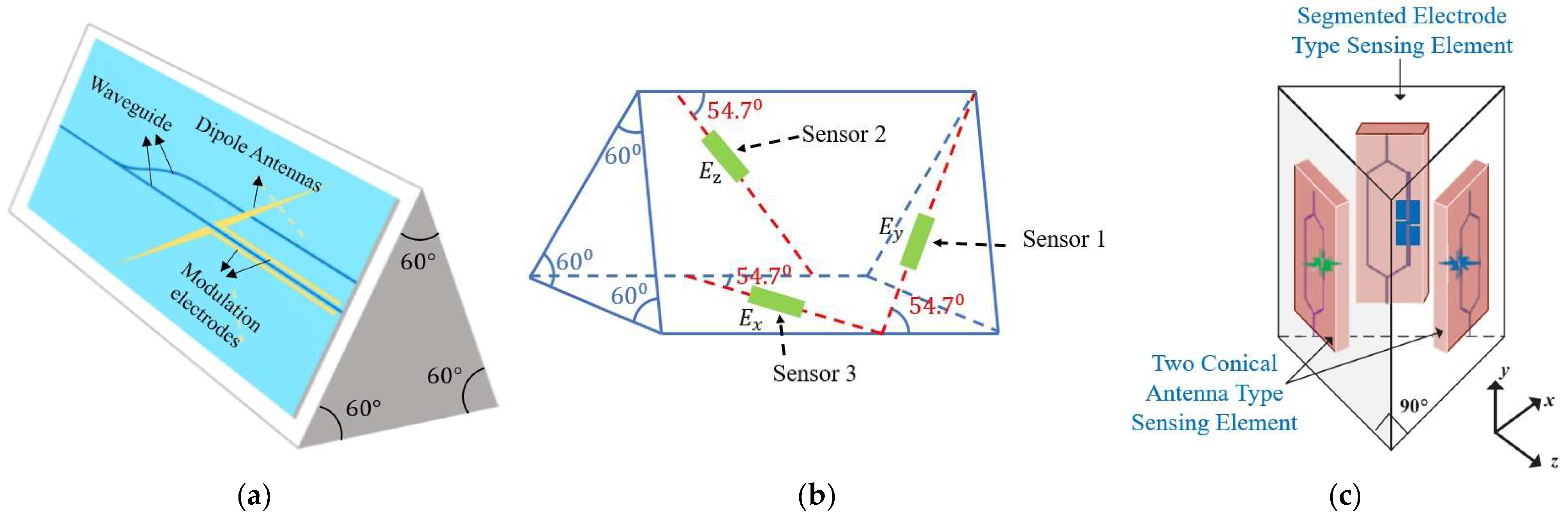
3. 3D Optical EFSs
3.1. Working Principle
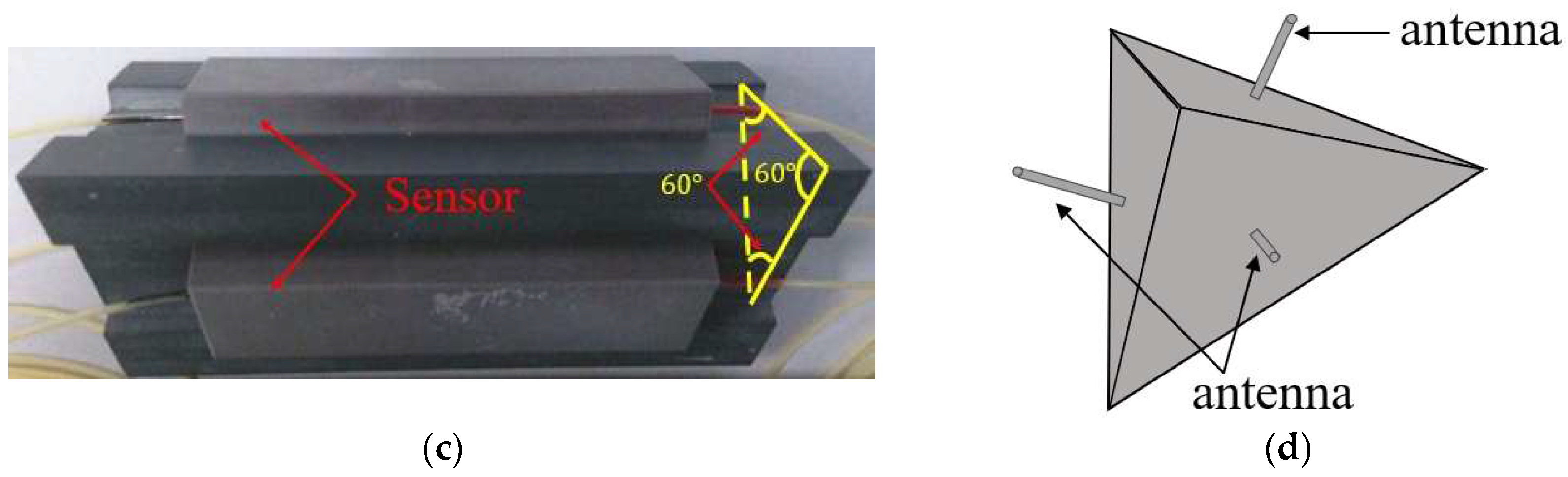
3.2. Prototype Instantiation for 3D Optical EFSs
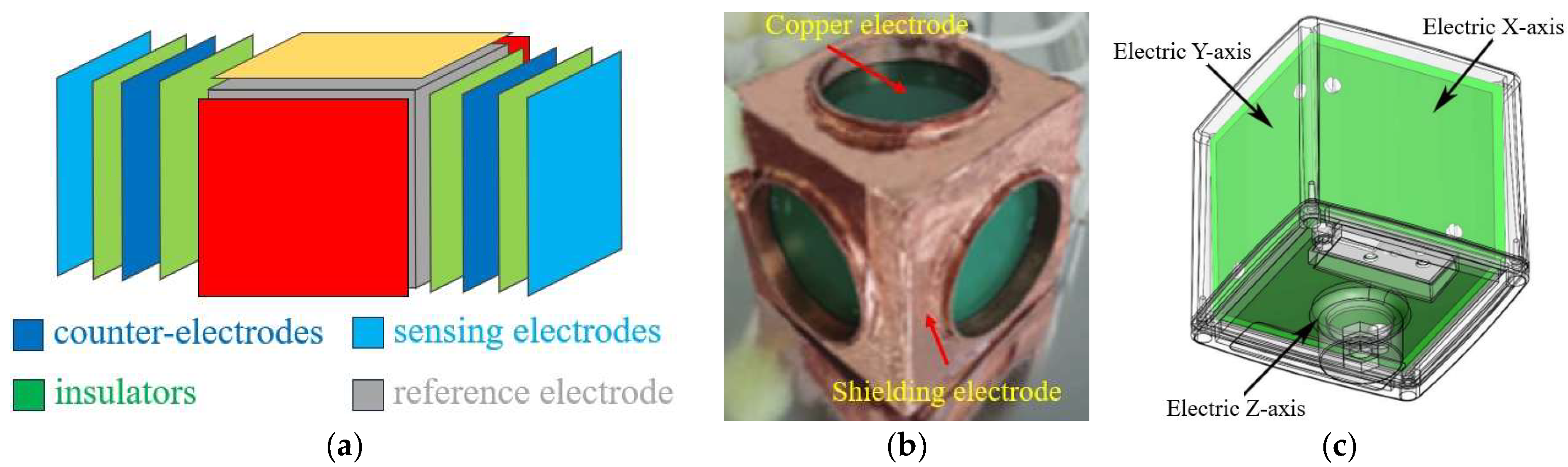
4. 3D Capacitive EFSs
4.1. Working Principle
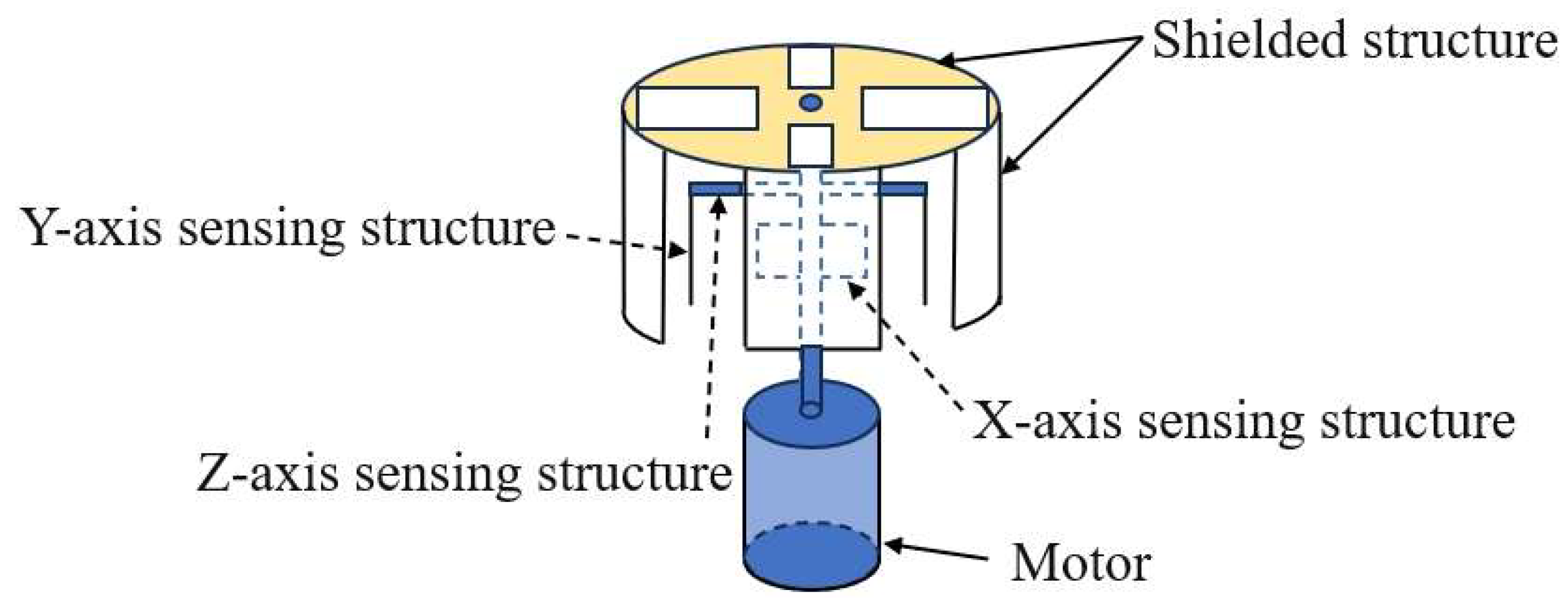
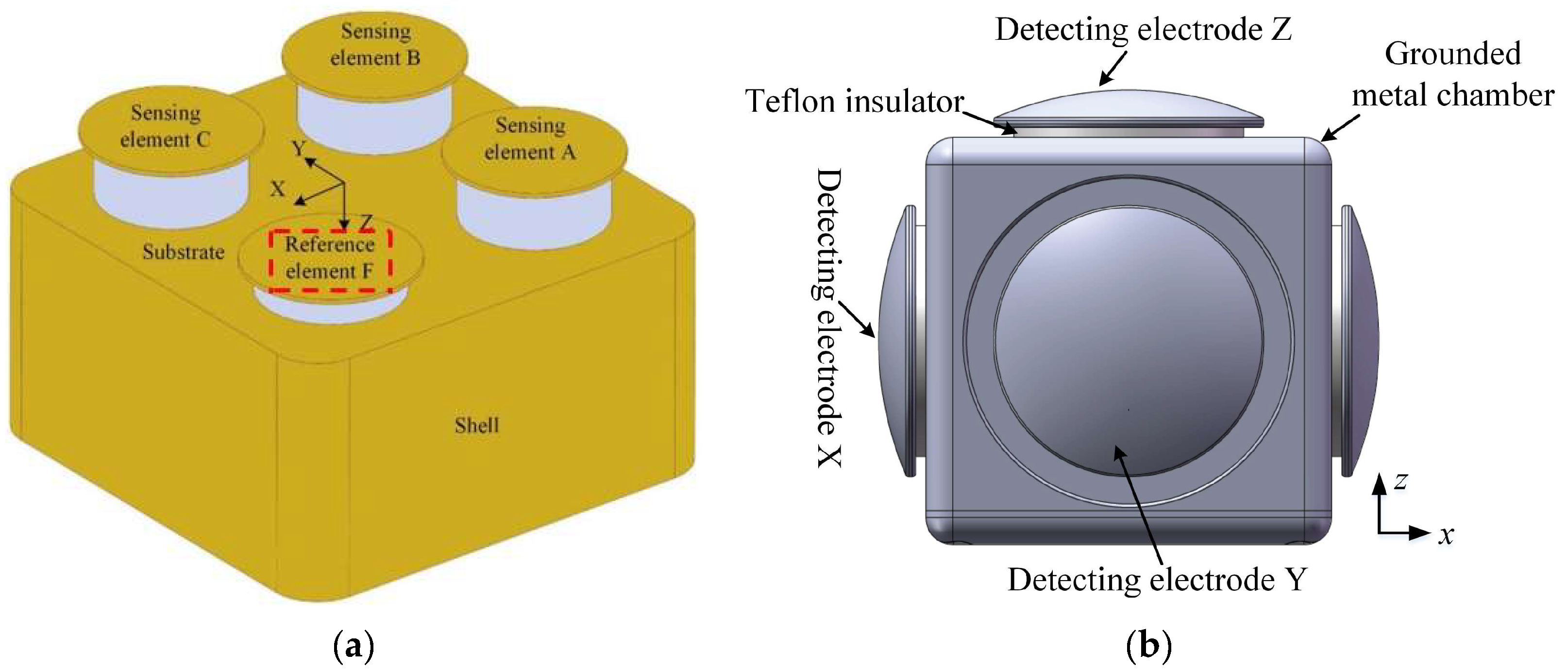
4.2. Prototype Instantiation for 3D Capacitive EFSs
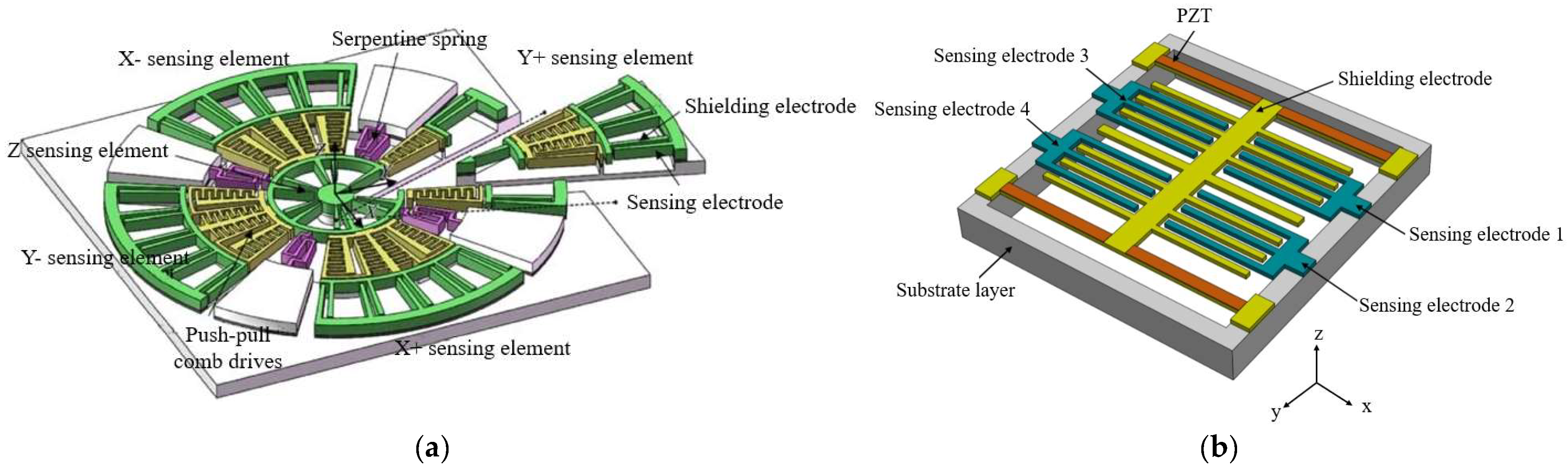
5. MEMS 3D EFSs
5.1. Working Principle and Classification
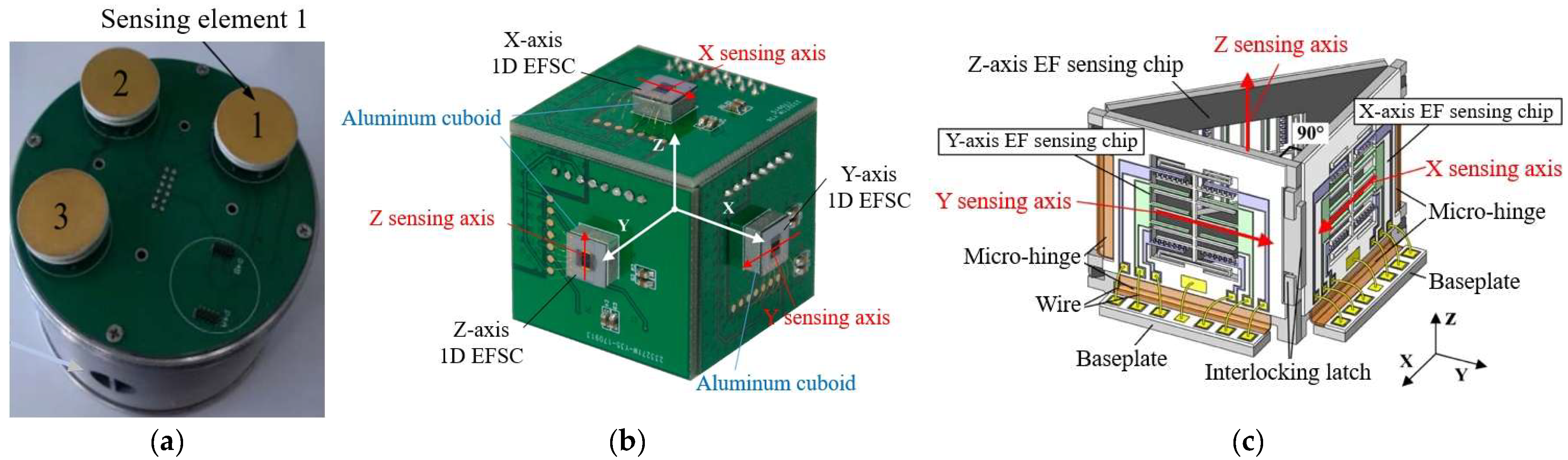
5.2. Prototype Instantiation for MEMS 3D EFSs
5.2.1. Single-Chip 3D MEMS EFSs
5.2.2. Assembled 3D MEMS EFSs
5.3. System-Level Integration and Application
6. Decoupling Calibration Method
6.1. Decoupled Calibration Matrix
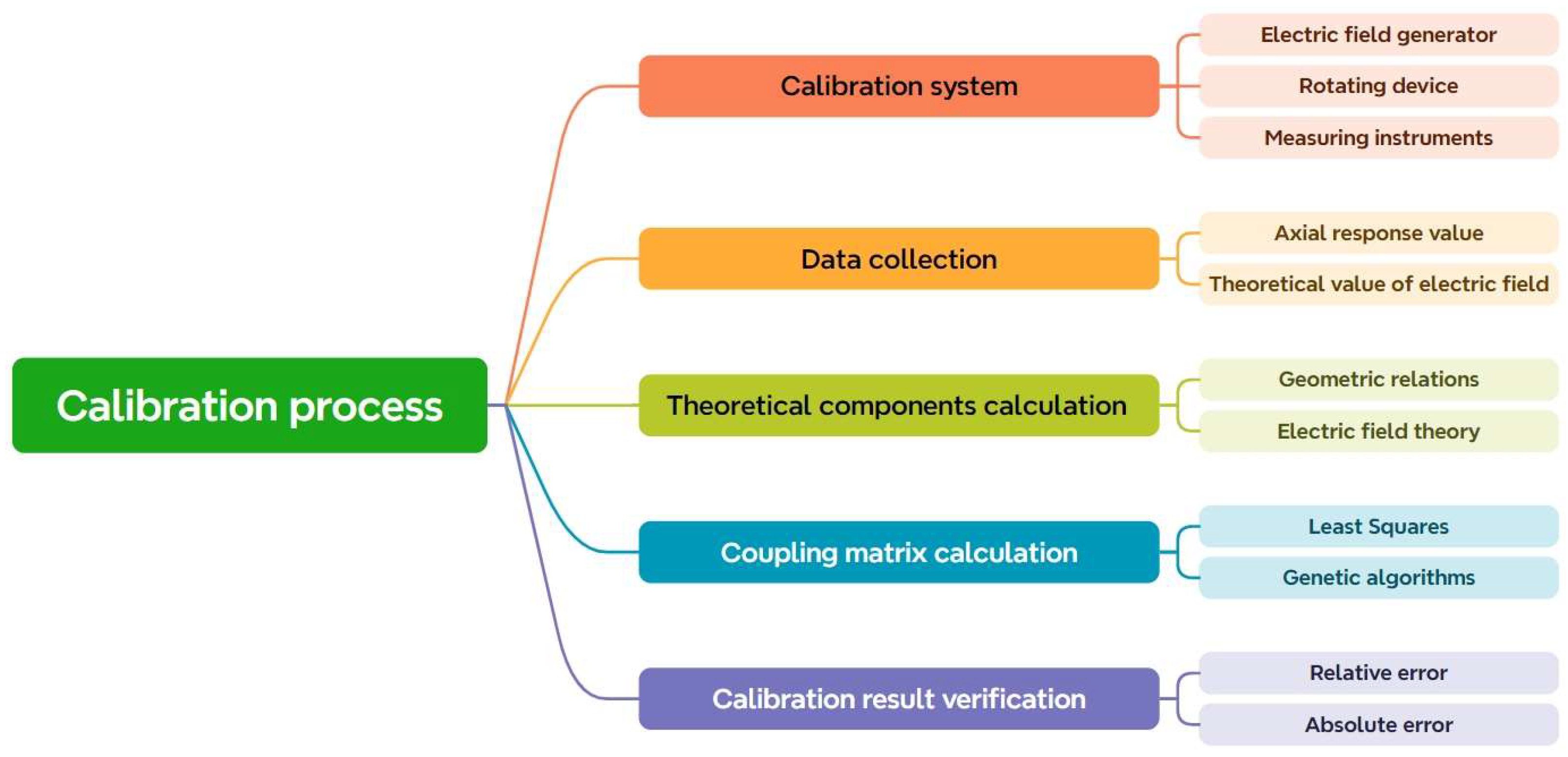
6.2. Calibration Method
- Calibration system construction: Construct a calibration system that can precisely regulate the direction and intensity of the electric field. This generally comprises a device that produces a uniform electric field and a rotating mechanism capable of firmly affixing and accurately rotating the sensor. The rotating apparatus often includes one or more orthogonal axes of rotation, enabling the sensor to be calibrated from various perspectives.
- Data collection: Install the sensor within the calibration system and document the output data of the sensor under varying electric field orientations and intensities. It is imperative to maintain the consistency and stability of the electric field, together with the precise positioning and orientation of the sensor, during the data collection process.
- Calculation of theoretical components: The theoretical components of the electric field in the sensor’s local coordinate system are computed based on the rotation angle and electric field strength, utilizing geometric relationships and electric field theory. These theoretical components will provide the foundation for comparison and calibration throughout the process.
- Coupling matrix calculation: The gathered sensor output data and the computed theoretical electric field components are utilized to determine the coupling matrix via mathematical techniques, including the least squares method, genetic algorithm [78], and differential evolution algorithm [79]. The calculation of the coupling matrix constitutes an optimization problem aimed at identifying a matrix that minimizes the discrepancy between the sensor output, as transformed by the matrix, and the theoretical electric field components.
- Calibration result verification: The coupling matrix derived from calibration is used to execute an inverse computation on the sensor’s output under alternative known conditions, thus acquiring the computed value of the electric field. The computed value is subsequently compared with the actual applied electric field value. The precision of the calibration outcome is assessed by computing the error (e.g., relative error, absolute error, etc.).
6.3. Calibration Applications and Limitations
- Environmental parameter drift: (a) Mechanical vibration interference: Motor vibrations induce irregular rotor motion, which disrupts the periodic shielding of the shielding structure and sensing plate, hence impacting the calibration of the decoupling matrix [38]. (b) Temperature drift: The Pockels effect in lithium niobate is influenced by temperature, although this is not dynamically corrected within the matrix, hence impacting calibration [49]. (c) Effects of humidity: Variations in environmental humidity induce drift in the dielectric constant, modifying capacitance values and leading to alterations in the sensitivity matrix. (d) Ground potential fluctuations: Conventional wired transmission induces variations in the ground potential of the signal conditioning circuit, hence impacting the precision of matrix calibration.
- Calibration system errors: (a) Non-uniformity of the electric field: Edge effects in parallel plate calibration devices induce distortions in field strength, hence impacting matrix calibration.
7. Discussion
7.1. Current Advancements and Applications
7.2. Challenges and Limitations
- Sensitivity and resolution: Current 3D EFSs generally exhibit limited sensitivity and fail to satisfy the stringent detection demands for weak electric fields in domains such as biomedical imaging and nanoelectronics. Investigating novel sensing materials, refining sensor architectures, augmenting signal processing technologies, and further elevating sensitivity and resolution will be essential avenues for the future advancement of 3D EFSs.
- Miniaturization and integration: Despite the advancements in MEMS technology facilitating the downsizing of 3D EFSs, numerous technical obstacles persist. The completed structure remains cumbersome due to the necessity of incorporating three electric field-sensitive chips, whereas single-chip packaging can modify the electric field distribution. Consequently, no viable solution has been established thus far. Attaining downsizing while maintaining sensor performance and reliability is a primary focus of contemporary research.
- Inter-axis coupling interference: The output signal of each measurement axis in a 3D EFS is often affected by the electric field components from the other two orthogonal axes. This inter-axis coupling effect significantly impacts measurement accuracy. Although some studies have explored methods such as decoupling matrices and symmetrical structures combined with differential circuits to reduce coupling interference, these approaches still cannot fully eliminate the issue.
- Space charge interference: In practical settings, space charge can result in charge accumulation on the sensor surface, hence impacting the precision of electric field measurements. While certain studies have suggested techniques, such as differential computations, to alleviate the effects of charge accumulation, investigations into the processes of space charge interference and related remedies are still scarce.
7.3. Future Research Directions
- AI-augmented signal processing: Deep learning algorithms, including convolutional neural networks [88,89] and long short-term memory networks [90], can be developed to denoise, identify patterns, and extract features from raw electric field signals, thereby enhancing the detection sensitivity and precision of weak electric field signals. AI models can be trained to identify anomalous signals in real time by learning to detect nonlinear disturbances in electric fields within intricate surroundings.
- Multi-source sensor fusion: The integration of 3D EFSs with environmental sensors, including temperature, humidity, and barometric pressure, alongside the application of fusion algorithms for the collaborative processing of multi-source data [91], effectively mitigates the interference caused by fluctuations in environmental parameters on electric field measurements. This enhances the system’s robustness and adaptability, making it particularly applicable for meteorological monitoring, disaster warning, and related domains.
- Smart medical/environmental system-level integration applications: Three-dimensional EFSs can be integrated with wearable devices or implantable biosensors for the detection of human electrophysiological signals [92], such as cerebral or cardiac electric fields, thereby facilitating epilepsy prediction [93] and arrhythmia diagnosis. In environmental contexts, these sensors can be incorporated into edge AI devices [94] to enable intelligent monitoring and response to electromagnetic pollution, thunderstorm risks, and other environmental hazards.
- 3D EFS productization/standardization: The productization and standardization of 3D EFSs necessitate the assistance of standardization efforts for their minimization and integration. This necessitates a robust emphasis on the authoritative function of international standards. Applicable standards, including IEEE 1309 [80], IEC 61786 [64], and the IEC 61000 series [95], offer essential rules and frameworks for the accurate calibration, performance assessment, electromagnetic compatibility validation, and final productization and standardization of sensors. Complying with and citing these standards is crucial for improving the environmental adaptability and market competitiveness of 3D EFSs.
8. Conclusions
Funding
Conflicts of Interest
References
- Lee, S.B.; Stone, G.C.; Antonino-Daviu, J.; Gyftakis, K.N.; Strangas, E.G.; Maussion, P.; Platero, C.A. Condition Monitoring of Industrial Electric Machines: State of the Art and Future Challenges. IEEE Ind. Electron. Mag. 2020, 14, 158–167. [Google Scholar] [CrossRef]
- Yang, P.; Wen, X.; Lv, Y.; Chu, Z.; Peng, C.; Liu, Y.; Wu, S. Improved Microsensor-Based Fieldmeter for Ground-Level Atmospheric Electric Field Measurements. IEEE Trans. Instrum. Meas. 2022, 71, 2001510. [Google Scholar] [CrossRef]
- Tsurudome, C.; Flaquiere, A.H.; Mochizuki, K.; Teuff, Y.L.; Sakai, R.; Tuffenis, J.; Suzuki, Y.; Cohen, D.; Fujiwara, H.; Inazaki, K.; et al. Measurement of the atmospheric electric field inside the nonthunderstorm clouds on 2012 BEXUS campaign. J. Atmos. Electr. 2013, 33, 77–80. [Google Scholar] [CrossRef]
- Sun, H.; Cui, X.; Du, L. Electromagnetic Interference Prediction of ±800 kV UHVDC Converter Station. IEEE Trans. Magn. 2016, 52, 9400404. [Google Scholar] [CrossRef]
- Rehman, M.; Nallagownden, P.; Bhayo, M.; Baharudin, Z.; Baba, M. Design of a Field Mill Device for Measuring the High Voltage DC Fields. In Proceedings of the 2020 8th International Conference on Intelligent and Advanced Systems (ICIAS), Kuching, Malaysia, 13–15 July 2021; pp. 1–6. [Google Scholar]
- Song, B.; Zhou, R.; Yang, X.; Zhang, S.; Yang, N.; Fang, J.; Song, F.; Zhang, G. Surface electrostatic discharge of charged typical space materials induced by strong electromagnetic interference. J. Phys. D Appl. Phys. 2021, 54, 275002. [Google Scholar] [CrossRef]
- Williams, K.R.; De Bruyker, D.P.H.; Limb, S.J.; Amendt, E.M.; Overland, D.A. Vacuum steered-electron electric-field sensor. J. Microelectromech. Syst. 2014, 23, 157–167. [Google Scholar] [CrossRef]
- Luo, M.; Yang, Q.; Dong, F.; Chen, N.; Liao, W. Miniature Micro-Ring Resonator Sensor with Electro-Optic Polymer Cladding for Wide-Band Electric Field Measurement. J. Light. Technol. 2021, 40, 2577–2584. [Google Scholar] [CrossRef]
- Liyanage, S.; Shafai, C.; Chen, T.; Rajapakse, A. Torsional Moving Electric Field Sensor with Modulated Sensitivity and Without Reference Ground. Proceedings 2017, 1, 350. [Google Scholar] [CrossRef]
- Andreas, K.; Harald, S.; Johannes, S.; Artur, J.; Franz, K.; Michael, S.; Roman, B.; Franz, K.; Wilfried, H. Distortion-free Measurement of Electric Field Strength with a MEMS Sensor. Nat. Electron. 2018, 1, 68–73. [Google Scholar]
- Elnaz, A.; Tao, C.; Yu, Z.; Gayan, W.; Lot, S.; Cyrus, S. Study of the Shielding Effect of a Vertical Moving Shutter Micromachined Field Mill for Measuring Dc Electric Field. Meas. Sci. Technol. 2020, 31, 105105. [Google Scholar]
- Yang, P.; Peng, C.; Zhang, H.; Liu, S.; Fang, D.; Xia, S. A high sensitivity SOI electric-field sensor with novel comb-shaped microelectrodes. In Proceedings of the 2011 16th International Solid-State Sensors, Actuators and Microsystems Conference, Beijing, China, 5–9 June 2011; pp. 1034–1037. [Google Scholar]
- Chu, Z.; Peng, C.; Zheng, F.; Xia, S. An Electric Field Microsensor with Metal-Silicon Structure. In Proceedings of the 2017 IEEE 12th International Conference on Nano/Micro Engineered and Molecular Systems (NEMS), Los Angeles, CA, USA, 9–12 April 2017; pp. 562–565. [Google Scholar]
- Chu, Z.; Peng, C.; Ren, R.; Ling, B.; Zhang, Z.; Xia, S. A MEMS-based electric field sensor with torsional resonance. Trans. Microsyst. Technol. 2019, 38, 83–85,88. [Google Scholar]
- Liu, X.; Wang, Z.; Wu, Z.; Gao, Y.; Peng, S.; Ren, R.; Zheng, F.; Lv, Y.; Yang, P.; Wen, X.; et al. Enhanced Sensitivity and Stability of a Novel Resonant MEMS Electric Field Sensor Based on Closed-Loop Feedback. IEEE Sens. J. 2021, 21, 22536–22543. [Google Scholar] [CrossRef]
- Huang, J.; Wu, X.; Wang, X.; Yan, X.; Lin, L. A Novel High-Sensitivity Electrostatic Biased Electric Field Sensor. J. Micromech. Microeng. 2015, 25, 095008. [Google Scholar] [CrossRef]
- Ma, Q.; Huang, K.; Yu, Z.; Wang, Z. A MEMS-Based Electric Field Sensor for Measurement of High-Voltage DC Synthetic Fields in Air. IEEE Sens. J. 2017, 17, 7866–7876. [Google Scholar] [CrossRef]
- Xue, F.; Hu, J.; Guo, Y.; Han, G.; Ouyang, Y.; Wang, S.X.; He, J. Piezoelectric–Piezoresistive Coupling MEMS Sensors for Measurement of Electric Fields of Broad Bandwidth and Large Dynamic Range. IEEE Trans. Ind. Electron. 2019, 67, 551–559. [Google Scholar] [CrossRef]
- Han, Z.; Xue, F.; Yang, G.; Yu, Z.; Hu, J.; He, J. Micro-Cantilever Capacitive Sensor for High-Resolution Measurement of Electric Fields. IEEE Sens. J. 2020, 21, 4317–4324. [Google Scholar] [CrossRef]
- Fang, Y.; Peng, C.; Yang, P.; Fang, D.; Xia, S. Electric Field and Induced Charges Distribution Model for MEMS Strip-Type Sensing Electrodes. Microsyst. Technol. 2015, 23, 143–150. [Google Scholar] [CrossRef]
- Han, Z.; Hu, J.; Li, L.; He, J. Micro-Cantilever Electric Field Sensor Driven by Electrostatic Force. Engineering 2023, 24, 184–191. [Google Scholar] [CrossRef]
- Bai, M.; Zhao, Y.; Jiao, B.; Zhai, X.; Geng, Y. A Novel Easy-Driving and Easy-Signal-processing Electrostatic Field Sensor Based on a Piezoresistance and Polyethylene Terephthalate Lever. J. Micromech. Microeng. 2017, 27, 035002. [Google Scholar] [CrossRef]
- Yang, P.; Wen, X.; Chu, Z.; Ni, X.; Peng, C. AC/DC Fields Demodulation Methods of Resonant Electric Field Microsensor. Micromachines 2020, 11, 511. [Google Scholar] [CrossRef]
- Yan, Z.; Liang, J.; Hao, Y.; Chang, H. A Micro Resonant DC Electric Field Sensor Based on Mode Localization Phenomenon. In Proceedings of the 2019 IEEE 32nd International Conference on Micro Electro Mechanical Systems (MEMS), Seoul, Republic of Korea, 27–31 January 2019; pp. 849–852. [Google Scholar]
- Lei, H.; Xia, S.; Peng, C.; Wu, Z.; Zhang, Z.; Liu, J.; Peng, S.; Liu, X.; Gao, Y. Research on MEMS Electric Field Sensor with Low Driving Voltage Based on Lead Zirconate Titanate. J. Electron. Inf. Technol. 2023, 45, 150–157. [Google Scholar]
- Ke, K.; Yang, Q.; Zhou, J.; Qiu, Z.; Yao, Z.; Chen, N.; Liao, W. Piezoelectric PZT Film-Driven Resonant Torsional MEMS Electric Field Sensor. IEEE Sens. J. 2024, 24, 31921–31931. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, D.; Feng, K.; Ren, R.; Chen, B.; Peng, C.; Xia, S. A Novel Micro Electric Field Sensor with X–Y Dual Axis Sensitive Differential Structure. Sens. Actuators A Phys. 2015, 229, 1–7. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, D.; Chen, B.; Peng, C.; Xia, S. Monolithic two-dimensional electric field sensor based on rotary resonant structure. Trans. Microsyst. Technol. 2016, 35, 103–105, 112. [Google Scholar]
- Rajasekar, R.; Robinson, S. Nano-electric Field Sensor Based on Two Dimensional Photonic Crystal Resonator. Opt. Mater. 2018, 85, 474–482. [Google Scholar] [CrossRef]
- López, J.; Pérez, E.; Herrera, J.; Aranguren, D.; Porras, L. Thunderstorm warning alarms methodology using electric field mills and lightning location networks in mountainous regions. In Proceedings of the 2012 International Conference on Lightning Protection (ICLP), Vienna, Austria, 2–7 September 2012; pp. 1–6. [Google Scholar]
- Zhen, Y.; Cui, X.; Lu, T.; Liu, Y.; Li, X.; Li, L.; Zhang, W. Ion Flow Field Analysis Considering the Finite Conductivity of the Building Near HVDC Transmission Lines. IEEE Trans. Magn. 2015, 51, 7202704. [Google Scholar] [CrossRef]
- Kamra, A.K. Spherical field meter for measurement of the electric field vector. Rev. Sci. Instrum. 1983, 54, 1401–1406. [Google Scholar] [CrossRef]
- Ravichandran, M.; Kamra, A.K. Spherical Field Meter to Measure the Electric Field Vector—Measurements in Fair Weather and Inside A Dust Devil. Rev. Sci. Instrum. 1999, 70, 2140–2149. [Google Scholar] [CrossRef]
- Tantisattayakul, T.; Masugata, K.; Kitamura, I.; Kontani, K. Development of the Hybrid Electric Field Meter for Simultaneous Measuring of Vertical and Horizontal Electric Fields of the Thundercloud. IEEE Trans. Electromagn. Compat. 2006, 48, 435–438. [Google Scholar] [CrossRef]
- Zheng, F.; Xia, S.; Chen, X. Simulation Optimization and Performance Test of Three Dimensional Electric Field Sensor. Chin. J. Sens. Actuat. 2008, 21, 946–950. [Google Scholar]
- Xing, H.; He, G.; Ji, X. Analysis on Electric Field Based on Three Dimensional Atmospheric Electric Field Apparatus. J. Electr. Eng. Technol. 2018, 13, 1696–1703. [Google Scholar]
- Lou, H.; Xing, X.; Wang, S.; Shi, C.; Li, H. A field grinding three-dimensional atmospheric electric field sensor. Electr. Meas. Technol. 2024, 47, 32–37. [Google Scholar]
- Liu, C.; Yuan, H.; Lv, J.; Zhao, P.; Li, J.; Xu, H. A sensor for 3-D component measurement of synthetic electric field vector in HVDC transmission lines using unidirectional motion. IEEE Trans. Instrum. Meas. 2022, 72, 1500110. [Google Scholar] [CrossRef]
- Kim, J.H.; Jeon, J.C.; Yoo, J.G. The Measurement for the Underwater Electric Field Using a Underwater 3-Axis Electric Potential Sensor. In Proceedings of the International Conference on Grid and Distributed Computing, Jeju Island, Republic of Korea, 8–10 December 2011; pp. 408–414. [Google Scholar]
- Kim, J.; Lee, I.; Lee, M.; Bae, K.; Yu, S. Analysis of Electrode Configuration of Underwater Electric Field Sensor on Electric-Field-based Localization for Underwater Robots. In Proceedings of the 22nd International Conference on Control, Automation and Systems (ICCAS), BEXCO, Busan, Republic of Korea, 27 November–1 December 2022; pp. 59–63. [Google Scholar]
- Kim, J.; Lee, I.; Yang, C.S.; Park, G.W.; Yu, S.C. Precision 3D Underwater Electric Field Measurement Method for Accurate Marine Localization. IEEE Access 2024, 12, 152798–152811. [Google Scholar] [CrossRef]
- Zeng, R.; Wang, B.; Yu, Z.; Chen, W. Design and Application of an Integrated Electro-Optic Sensor for Intensive Electric Field Measurement. IEEE Trans. Dielectr. Electr. Insul. 2011, 18, 312–319. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, F.; Sun, B.; Li, C. A Novel Bias Angle Control System for LiNbO3 Photonic Sensor Using Wavelength Tuning. IEEE Photonics Technol. Lett. 2013, 25, 1993–1995. [Google Scholar] [CrossRef]
- Tajima, K.; Kobayashi, R.; Kuwabara, N.; Tokuda, M. Development of Optical Isotropic E-Field Sensor Operating More than 10 GHz Using Mach-Zehnder Interferometers. IEICE Trans. Electron. 2002, E85-C, 961–968. [Google Scholar]
- Garzarella, A.; Wu, D.H.; Crim, J.B. An All-Dielectric, 3-Axis Electric Field Sensor Using Quasi-Longitudinally Configured Electro-Optic Crystals. In Proceedings of the SENSORS, 2010 IEEE, Waikoloa, HI, USA, 1–4 November 2010; pp. 983–986. [Google Scholar]
- Si, R.; Shi, L.; Chen, R.; Li, Y. Three-dimensional electric-field sensor for spherical fiber transmission. High Power Laser Part. Beams 2012, 24, 2930–2934. [Google Scholar]
- Zhang, J.; Chen, F.; Sun, B.; Chen, K.; Li, C. 3D Integrated Optical E-Field Sensor for Lightning Electromagnetic Impulse Measurement. IEEE Photonics Technol. Lett. 2014, 26, 2353–2356. [Google Scholar] [CrossRef]
- Yan, X.; Zhu, C. Three-Dimensional Pulse Electric Field Test System with Optical Fiber. In Proceedings of the 2017 International Conference on Computer Technology, Electronics and Communication (ICCTEC), Dalian, China, 19–21 December 2017; pp. 994–997. [Google Scholar]
- Liu, Z.; Qiu, L.; Zhao, L.; Luo, L.; Du, W.; Zhang, L.; Sun, B.; Zhang, Z.; Zhang, S.; Liu, Y. Three-Dimensional Broadband Electric Field Sensor Based on Integrated Lithium Niobate on Insulator. Appl. Sci. 2023, 13, 873. [Google Scholar] [CrossRef]
- Zhu, S.; Fu, Z.; Gao, X.; Li, C.; Chen, Z.; Wang, Y.; Chen, X.; Hu, H. Nanoscale electric field sensing using a levitated nano-resonator with net charge. Photonics Res. 2023, 11, 279–289. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, Z.; Lei, H. 3D power frequency intensive electric field sensor based on a lithium niobate electro-optic crystal. Appl. Opt. 2024, 63, 1761–1768. [Google Scholar] [CrossRef]
- Long, Z.; Li, W.; Fan, J.; Yao, G.; Xi, Y.; Li, X. Development of a Three-Dimensional Optical Waveguide Sensor for Pulsed Electric Field Measurement. In Proceedings of the 2024 IEEE 7th International Electrical and Energy Conference (CIEEC), Harbin, China, 10–12 May 2024; pp. 2734–2740. [Google Scholar]
- Zhou, F.; Chai, Z.; Diao, Y.; Long, Z. Research on Measurement Techniques for Integrated Optical Waveguide-Based Electric Field Sensors. IEEE Access 2025, 13, 90983–90990. [Google Scholar] [CrossRef]
- IEC 61000-4-5; Electromagnetic Compatibility (EMC)—Part 4-5: Testing and Measurement Techniques—Surge Immunity Test. IEC: Geneva, Switzerland, 2014.
- Misakian, M.; Fulcomer, P.M. Measurement of nonuniform power frequency electric fields. IEEE Trans. Electr. Insul. 1983, 18, 657–661. [Google Scholar] [CrossRef]
- Xu, Y.; Gao, C.; Li, Y.; Chang, Y.; Zhou, B. Calculation and experimental validation of 3-D parallel plate sensor for transient electric field measurement. In Proceedings of the 2007 International Symposium on Microwave, Antenna, Propagation and EMC Technologies for Wireless Communications, Hangzhou, China, 16–17 August 2007; pp. 1267–1271. [Google Scholar]
- Zhang, Z.; Li, L.; Xie, X.; Xiao, D.; He, W. Optimization Design and Research Character of the Passive Electric Field Sensor. IEEE Sens. J. 2014, 14, 508–513. [Google Scholar] [CrossRef]
- Jiang, Z.; Jia, S.; Huo, L.; Qiu, S. An integrated three-dimensional sensor for the electric field changes produced by lightning discharges. In Proceedings of the 2015 7th Asia-Pacific Conference on Environmental Electromagnetics (CEEM), Hangzhou, China, 4–7 November 2015; pp. 432–435. [Google Scholar]
- Rumyantseva, E.V.; Biryukov, S.V.; Lyutarevich, A.G.; Dolinger, S.Y. Development of spherical sensor electric field strength measuring method. In Proceedings of the 2016 International Siberian Conference on Control and Communications (SIBCON), Moscow, Russia, 12–14 May 2016; pp. 1–4. [Google Scholar]
- Suo, C.; Wei, R.; Zhang, W.; Li, Y. Research on the Three-Dimensional Power Frequency Electric Field Measurement System. J. Sens. 2021, 2021, 8859022. [Google Scholar] [CrossRef]
- Roblin, M.; Robbes, D.; Allegre, G.; Mareschal, O.; Denoual, M. Spatial distribution of electric field measurement system: Straight characterization of one or more original electric field sources in association with a new triaxial sensor. Meas. Sci. Technol. 2023, 34, 095114. [Google Scholar] [CrossRef]
- Zhao, Z.; Li, Y.; Yang, X.; Luo, C. Three-dimensional electric field sensor with low inter-axis coupling. J. Meas. Sci. Instrum. 2024, 15, 95–104. [Google Scholar] [CrossRef]
- EN 61326-1; Electrical Equipment for Measurement, Control and Laboratory Use—EMC Requirements—Part 1: General Requirements. CENELEC: Brussels, Belgium, 2013.
- IEC 61786-2; Measurement of DC Magnetic, AC Magnetic and AC Electric Fields from 1 Hz to 100 kHz with Regard to Exposure of Human Beings—Part 2: Basic Standard for Measurements. IEC: Geneva, Switzerland, 2014.
- Pullano, S.A.; Fiorillo, A.S.; Barile, G.; Stornelli, V.; Ferri, G. A Second-Generation Voltage-Conveyor-Based Interface for Ultrasonic PVDF Sensors. Micromachines 2021, 12, 99. [Google Scholar] [CrossRef]
- Ling, B.; Wang, Y.; Peng, C.; Li, B.; Chu, Z.; Li, B.; Xia, S. Single-chip 3D Electric Field Microsensor. Front. Mech. Eng. 2017, 12, 581–590. [Google Scholar] [CrossRef]
- Ling, B.; Wang, Y.; Peng, C.; Li, B.; Chu, Z.; Li, B.; Xia, S. Design, Fabrication and Characterization of a Single-Chip Three-Dimensional Electric Field Microsensor. In Proceedings of the 2017 IEEE 12th International Conference on Nano/Micro Engineered and Molecular Systems (NEMS), Los Angeles, CA, USA, 9–12 April 2017; pp. 307–310. [Google Scholar]
- Peng, S.; Zhang, Z.; Liu, X.; Gao, Y.; Zhang, W.; Xing, X.; Liu, Y.; Peng, C.; Xia, S. A Single-Chip 3-D Electric Field Microsensor with Piezoelectric Excitation. IEEE Trans. Electron Devices 2023, 70, 4359–4365. [Google Scholar] [CrossRef]
- Wen, X.; Fang, D.; Peng, C.; Yang, P.; Zheng, F.; Xia, S. Three dimensional electric field measurement method based on coplanar decoupling structure. In Proceedings of the SENSORS, 2014 IEEE, Valencia, Spain, 2–5 November 2014; pp. 582–585. [Google Scholar]
- Ling, B.; Peng, C.; Ren, R.; Chu, Z.; Zhang, Z.; Lei, H.; Xia, S. Design, Fabrication and Characterization of a MEMS-Based Three-Dimensional Electric Field Sensor with Low Cross-Axis Coupling Interference. Sensors 2018, 18, 870. [Google Scholar] [CrossRef]
- Ling, B.; Peng, C.; Ren, R.; Zheng, F.; Chu, Z.; Zhang, Z.; Lei, H.; Xia, S. A Microassembled Triangular-Prism-Shape Three-Dimensional Electric Field Sensor. In Proceedings of the 2019 20th International Conference on Solid-State Sensors, Actuators and Microsystems & Eurosensors XXXIII (TRANSDUCERS & EUROSENSORS XXXIII), Berlin, Germany, 23–27 June 2019; pp. 222–225. [Google Scholar]
- Zhang, W.; Xia, S.; Peng, C. An Anti-Charge-Interference Three-Dimensional Electric Field Sensor. Meas. Sci. Technol. 2024, 35, 055124. [Google Scholar] [CrossRef]
- Yang, P.; Wen, X.; Chu, Z.; Peng, C. Highly Sensitive and Moisture-Resistant 3D DC Electric Field Meter Based on Microsensors. In Proceedings of the 2024 IEEE SENSORS, Kobe, Japan, 20–23 October 2024; pp. 1–4. [Google Scholar]
- Rajendran, S.; Porwal, A.; Anjali, K.; Anvaya; Anuradha, R.J. Portable IoT Devices in Healthcare for Health Monitoring and Diagnostics. In Internet of Things in Bioelectronics: Emerging Technologies and Applications; Wiley-Scrivener: Beverly, MA, USA, 2024; pp. 263–296. [Google Scholar]
- Pullano, S.A.; Oliva, G.; Presta, P.; Carullo, N.; Musolino, M.; Andreucci, M.; Bolignano, D.; Fiorillo, A.S.; Coppolino, G. A portable easy-to-use triboelectric sensor for arteriovenous fistula monitoring in dialysis patients. Sens. Int. 2025, 6, 100309. [Google Scholar] [CrossRef]
- Xiao, D.; Ma, Q.; Xie, Y.; Zheng, Q.; Zhang, Z. A Power-Frequency Electric Field Sensor for Portable Measurement. Sensors 2018, 18, 1053. [Google Scholar] [CrossRef] [PubMed]
- Menniti, M.; Lagana, F.; Oliva, G.; Bianco, M.; Fiorillo, A.S.; Pullano, S.A. Development of Non-Invasive Ventilator for Homecare and Patient Monitoring System. Electronics 2024, 13, 790. [Google Scholar] [CrossRef]
- Li, B.; Peng, C.; Zheng, F.; Ling, B.; Chen, B.; Xia, S. A Decoupling Calibration Method Based on Genetic Algorithm for Three Dimensional Electric Field Sensor. In Proceedings of the 2016 IEEE SENSORS, Orlando, FL, USA, 30 October–3 November 2016; pp. 1–3. [Google Scholar]
- Wu, G.; Cui, Y.; Liu, H.; Zhang, L. Decoupling Calibration Method of 3D Electric Field Sensor Based on Differential Evolution Algorithm. Trans. China Electrotech. Soc. 2021, 36, 3993–4001. [Google Scholar]
- Narang, N.; Dubey, S.K.; Negi, P.S.; Ojha, V.N. Accurate and precise E-field measurement for 2G and 3G networks based on IEEE Std. 1309-2013. Microwave Opt. Technol. Lett. 2015, 57, 1645–1649. [Google Scholar] [CrossRef]
- Alassi, A.; Banales, S.; Ellabban, O.; Adam, G.; MacIver, C. HVDC Transmission: Technology Review, Market Trends and Future Outlook. Renew. Sustain. Energy Rev. 2019, 112, 530–554. [Google Scholar] [CrossRef]
- Barnes, M.; Van Hertem, D.; Teeuwsen, S.P.; Callavik, M. HVDC Systems in Smart Grids. Proc. IEEE 2017, 105, 2082–2098. [Google Scholar] [CrossRef]
- Cui, Y.; Wang, Q.; Yuan, H.; Song, X.; Hu, X.; Zhao, L. Relative Localization in Wireless Sensor Networks for Measurement of Electric Fields under HVDC Transmission Lines. Sensors 2015, 15, 3540–3564. [Google Scholar] [CrossRef]
- Ye, H.; Fechner, T.; Lei, X.; Luo, Y.; Zhou, M.; Han, Z.; Wang, H.; Zhuang, Q.; Xu, R.; Li, D. Review on HVDC Cable Terminations. High Volt. 2018, 3, 79–89. [Google Scholar] [CrossRef]
- Wang, W.; Li, G.; Guo, J. Large-Scale Renewable Energy Transmission by HVDC: Challenges and Proposals. Engineering 2022, 19, 252–267. [Google Scholar] [CrossRef]
- Tamayo Vegas, S.; Lafdi, K. A Literature Review of Non-Contact Tools and Methods in Structural Health Monitoring. Eng. Technol. Open Access J. 2021, 4, 555626. [Google Scholar]
- Loader, B.; Alexander, M.; Osawa, R. Development of Optical Electric Field Sensors for EMC Measurement. In Proceedings of the 2014 International Symposium on Electromagnetic Compatibility, Tokyo, Japan, 12–16 May 2014; pp. 658–661. [Google Scholar]
- Wang, C.; Zhang, X.; Yang, H.; Guo, J.; Xu, J.; Sun, Z. Application research of convolutional neural network and its optimization in lightning electric field waveform recognition. Sci. Rep. 2025, 15, 1883. [Google Scholar] [CrossRef]
- Buongiorno, D.; Cascarano, G.D.; Feudis, I.D.; Brunetti, A.; Carnimeo, L.; Dimauro, G.; Bevilacqua, V. Deep learning for processing electromyographic signals: A taxonomy-based survey. Neurocomputing 2021, 452, 549–565. [Google Scholar] [CrossRef]
- Fukawa, M.; Deng, X.; Imai, S.; Horiguchi, T.; Ono, R.; Rachi, I.; Sihan, A.; Shinomura, K.; Niwa, S.; Kudo, T.; et al. A Novel Method for Lightning Prediction by Direct Electric Field Measurements at the Ground Using Recurrent Neural Network. IEICE Trans. Inf. Syst. 2022, E105-D, 1624–1628. [Google Scholar] [CrossRef]
- Liu, G.; Liu, J.; Wei, R.; Wang, J. Multi-source Data Fusion Technology for Power Wearable System. In Proceedings of the 2018 IEEE International Conference on Computer and Communication Engineering Technology, Beijing, China, 18–20 August 2018; pp. 118–122. [Google Scholar]
- Gray, M.; Meehan, J.; Ward, C.; Langdon, S.P.; Kunkler, I.H.; Murray, A.; Argyle, D. Implantable biosensors and their contribution to the future of precision medicine. Vet. J. 2018, 239, 21–29. [Google Scholar] [CrossRef]
- van Mierlo, P.; Papadopoulou, M.; Carrette, E.; Boon, P.; Vandenberghe, S.; Vonck, K.; Marinazzo, D. Functional brain connectivity from EEG in epilepsy: Seizure prediction and epileptogenic focus localization. Prog. Neurobiol. 2014, 121, 19–35. [Google Scholar] [CrossRef]
- Merenda, M.; Porcaro, C.; Iero, D. Edge Machine Learning for AI-Enabled IoT Devices: A Review. Sensors 2020, 20, 2533. [Google Scholar] [CrossRef]
- IEC 61000-2-5; Electromagnetic Compatibility (EMC), Part 2: Environment—Section 5: Classification of Electromagnetic Environments. Basic EMC Publication; IEC: Geneva, Switzerland, 1995.





| 3D EFSs | Sensitivity/Cross-Axis Sensitivity | Measurement Range | Ref. | Advantages and Disadvantages |
|---|---|---|---|---|
| DC field mill | 2 V/m | / | [32] | Advantages: High stability, strong anti-interference ability. Disadvantage: Narrow frequency band, mechanical wear, High power consumption. |
| 50 V/m | ±30 kV/m | [35] | ||
| 10 V/m | / | [37] | ||
| Optical | / | [45] | Advantages: Non-contact measurement, strong anti-electromagnetic interference capability. Disadvantage: High cost, susceptible to temperature. | |
| X: 1.1 mV/kV/m Y: 1.7 mV/kV/m Z: 1.4 mV/kV/m | 15–370 kV/m | [47] | ||
| Maximum up to 6.5 MV/m | [50] | |||
| X: 0.908 mV/kV/m Y: 1.043 mV/kV/m Z: 0.781 mV/kV/m | X: 3.71 kV/m–388 kV/m Y: 2.78 kV/m–403 kV/m Z: 4.50 kV/m–375 kV/m | [51] | ||
| / | 8–60 kV/m | [52] | ||
| 0.0291 mV/(kV/m) | 5 kV/m–50 kV/m | [53] | ||
| Capacitive | 3.03 mV/kV/m | <12 kV/m | [57] | Advantages: Broadband measurements, AC measurements. Disadvantage: Limited measuring range, weak anti-interference ability. |
| 19.10 mV/(kV · m−1) | 1 kV/m–200 kV/m | [60] | ||
| 0.1 mV/m 1 mV/m | 5 mV/m–1 kV/m 500 mV/m–100 kV/m | / | ||
| MEMS | 0–50 kV/m | [66] | Advantages: Miniaturization, high sensitivity, low power consumption. Disadvantage: High manufacturing costs. | |
| X: 0.2315 mV/kV/m Y: 0.3727 mV/kV/m Z: 2.187 mV/kV/m | 0–50 kV/m | [68] | ||
| 5.48% | 0–120 kV/m | [70] | ||
| 19.54% | 0–120 kV/m | [71] | ||
| 14.78 mV · kV−1 | / | [73] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Gu, Y.; Li, Z.; He, Z.; Yang, P.; Peng, C. A Review of Three-Dimensional Electric Field Sensors. Micromachines 2025, 16, 737. https://doi.org/10.3390/mi16070737
Li X, Gu Y, Li Z, He Z, Yang P, Peng C. A Review of Three-Dimensional Electric Field Sensors. Micromachines. 2025; 16(7):737. https://doi.org/10.3390/mi16070737
Chicago/Turabian StyleLi, Xiaonan, Yu Gu, Zehao Li, Zijian He, Pengfei Yang, and Chunrong Peng. 2025. "A Review of Three-Dimensional Electric Field Sensors" Micromachines 16, no. 7: 737. https://doi.org/10.3390/mi16070737
APA StyleLi, X., Gu, Y., Li, Z., He, Z., Yang, P., & Peng, C. (2025). A Review of Three-Dimensional Electric Field Sensors. Micromachines, 16(7), 737. https://doi.org/10.3390/mi16070737