2.5-Dimensional Structure Approach for Miniaturizing Flapping-Wing Air Vehicles
Abstract
1. Introduction
1.1. General Background
1.2. Miniaturization of Air Vehicles
1.3. Flapping Mechanisms and Systems
1.4. Constraints Due to Fabrication Techniques
1.5. Previous Studies
1.6. Objective in This Study
2. Two-Point-Five-Dimensional Structure Approach for Insect-Mimetic FWAVs
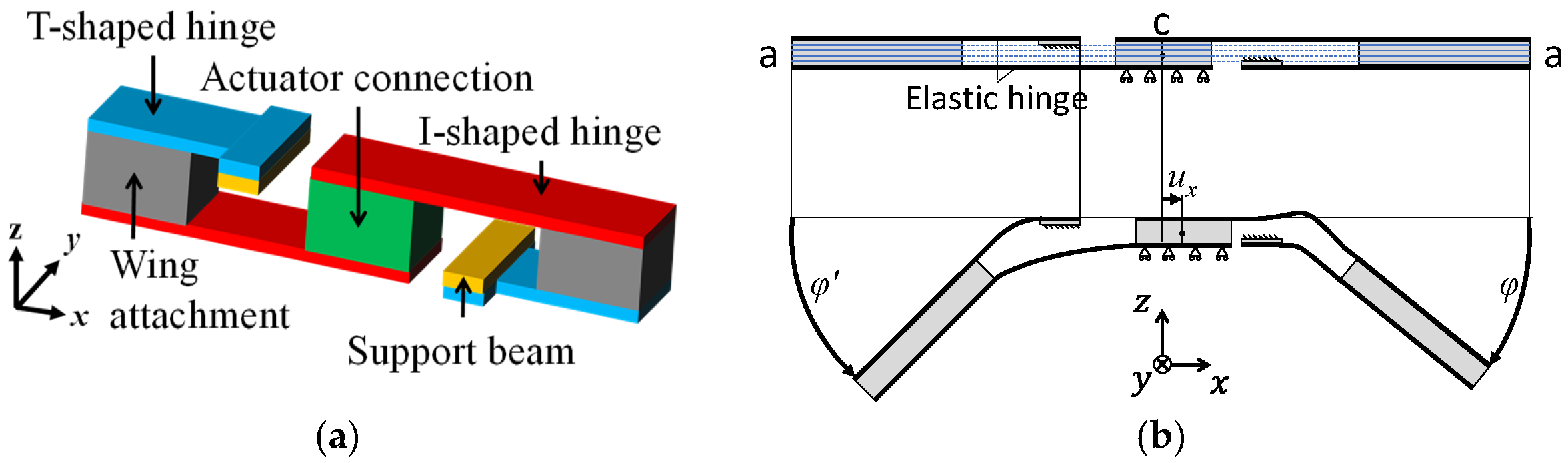
2.1. Concept and Basic Design
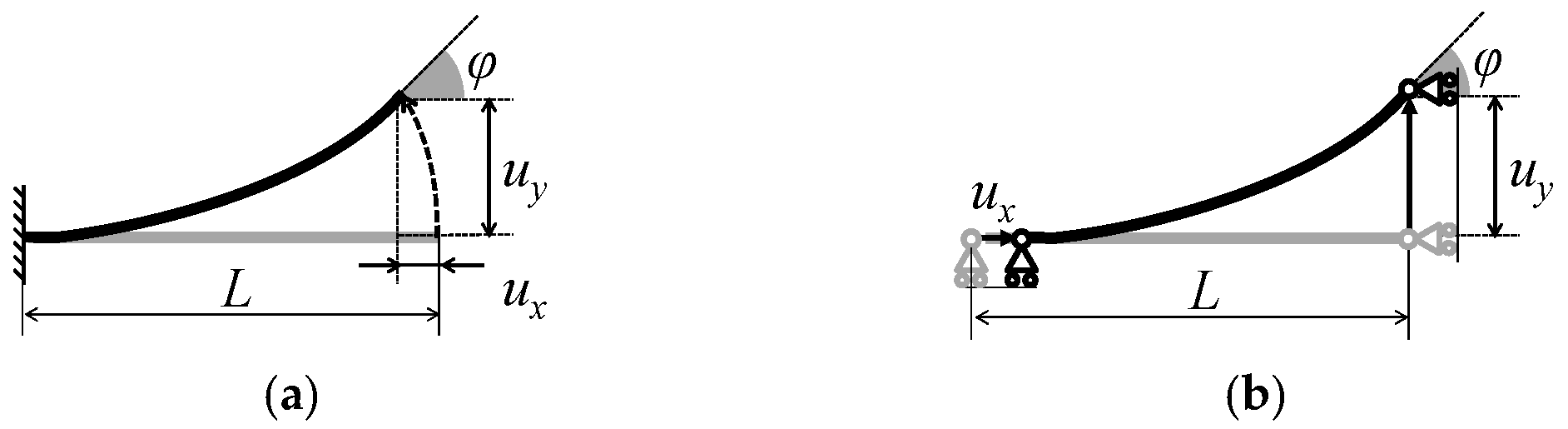
2.1.1. Concept of 2.5-D Structure Approach
2.1.2. Transmission Using Geometrical Nonlinearity
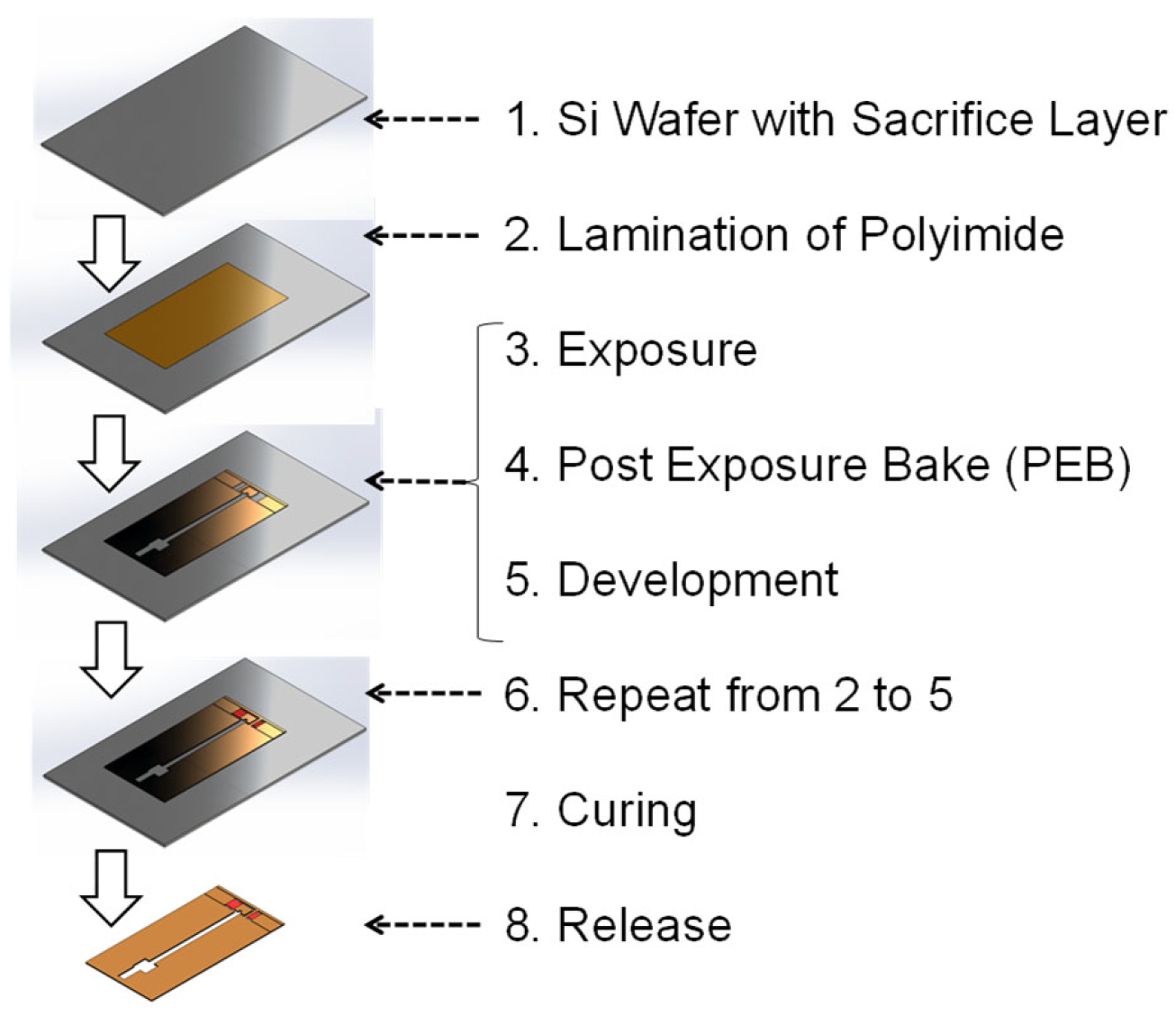
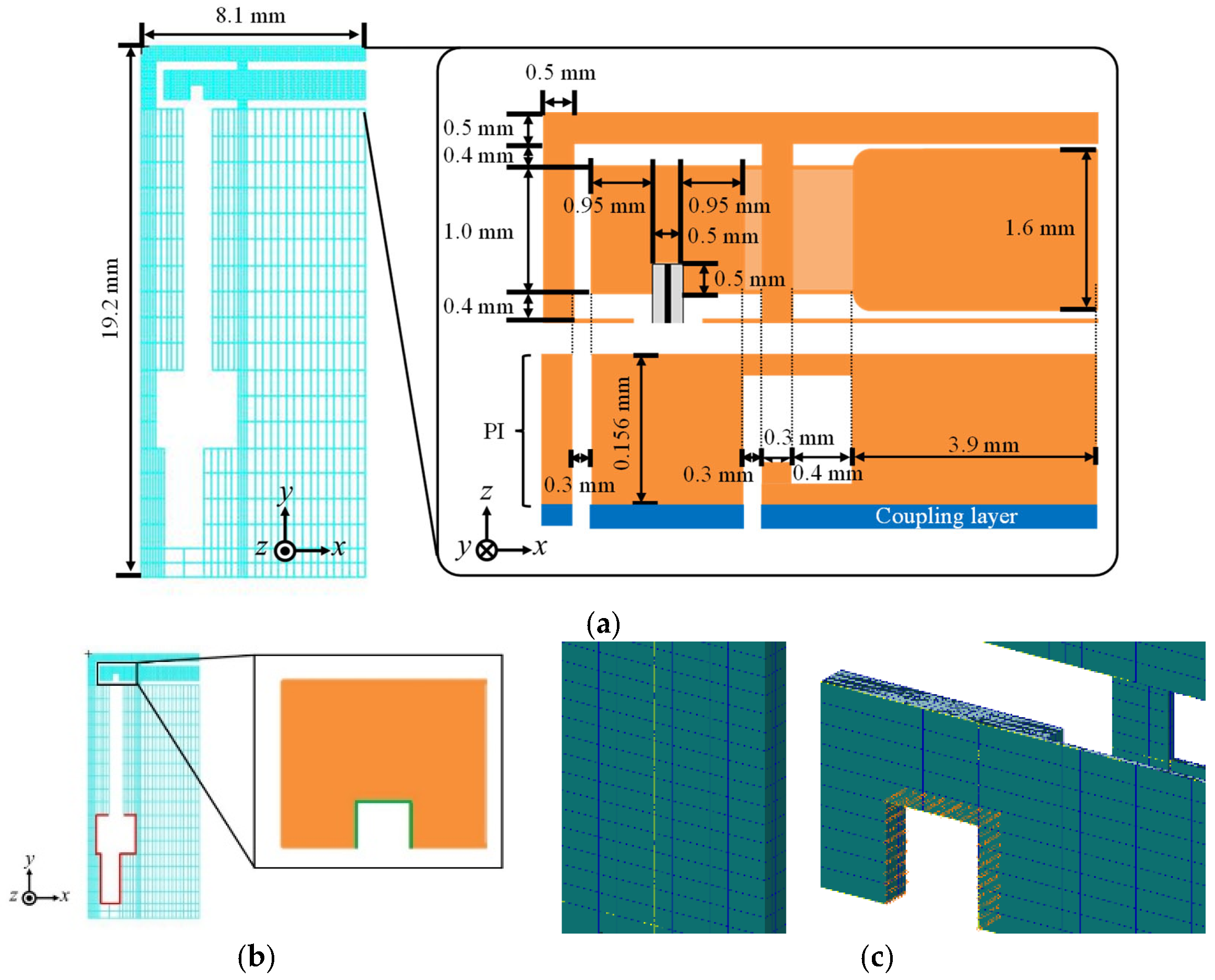
2.2. Fabrication Process of Polymer MEMS Micromachining
2.3. Shape Design for Fabricability
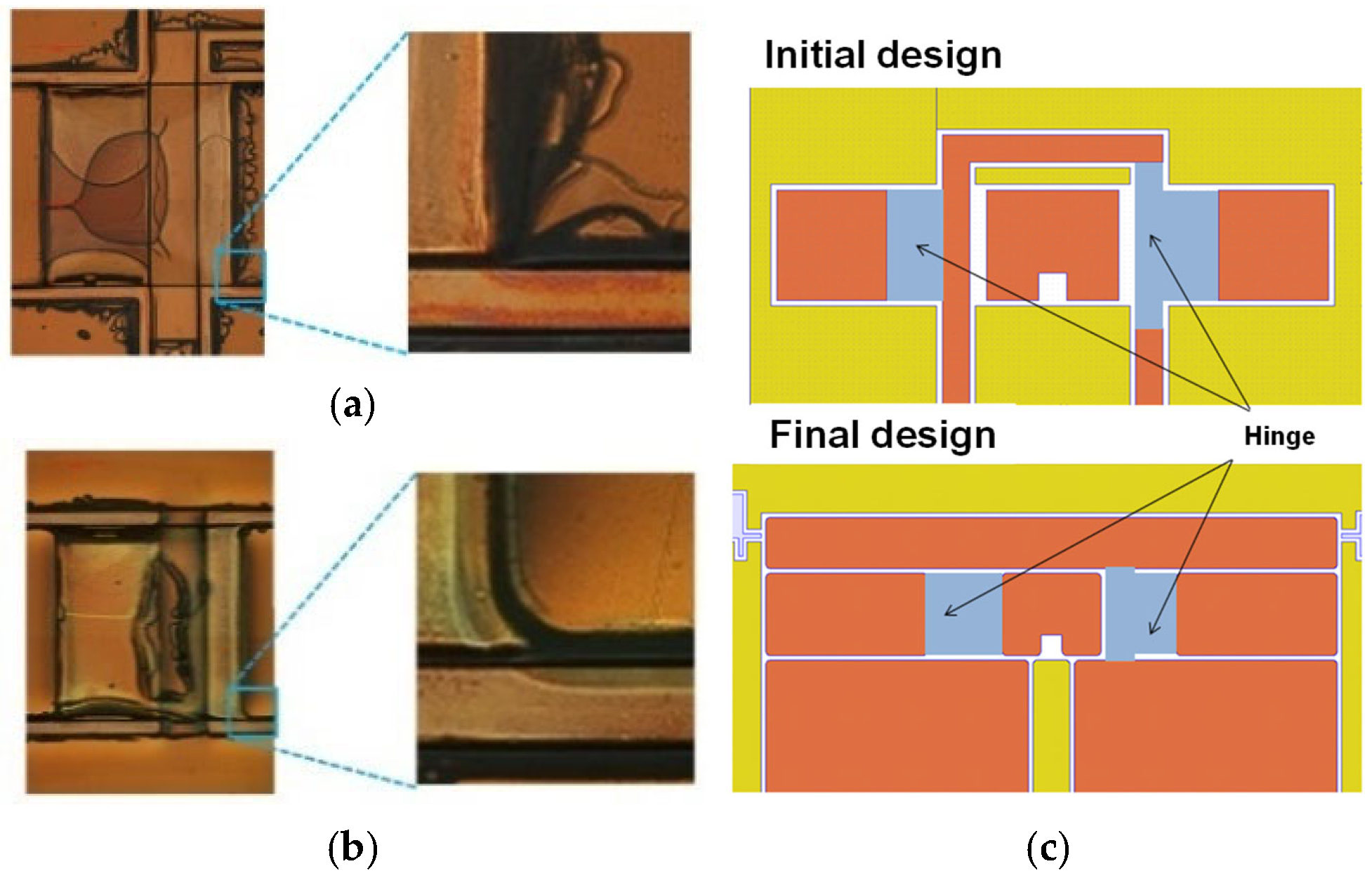
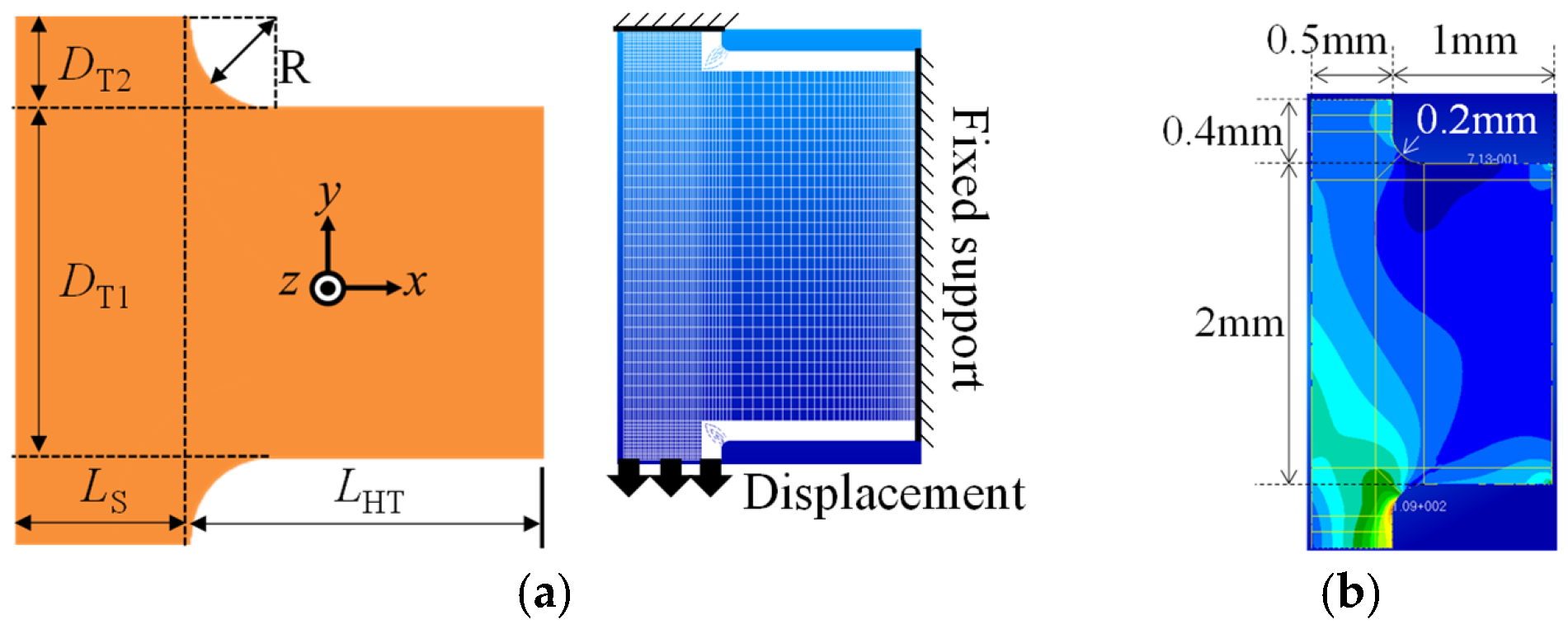
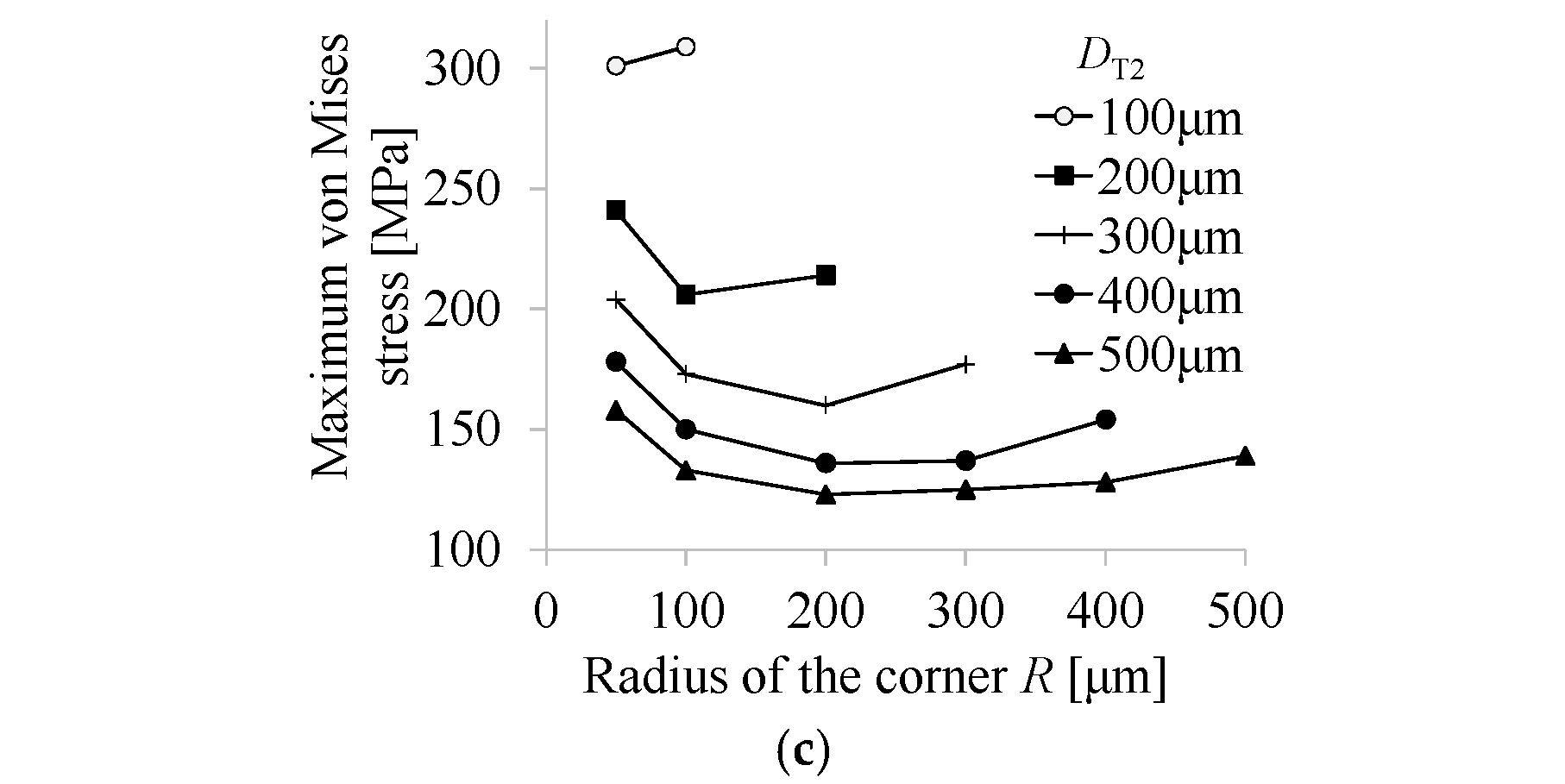
2.3.1. Rounding of Concave Corners
2.3.2. Rounding of and Reduction in Number of Convex Corners
2.3.3. Support Domain for Each Layer in Lamination Process
3. Structural Design for Size Reduction
3.1. Design Problem and Method
3.1.1. Design Problem
3.1.2. Structural Design Method
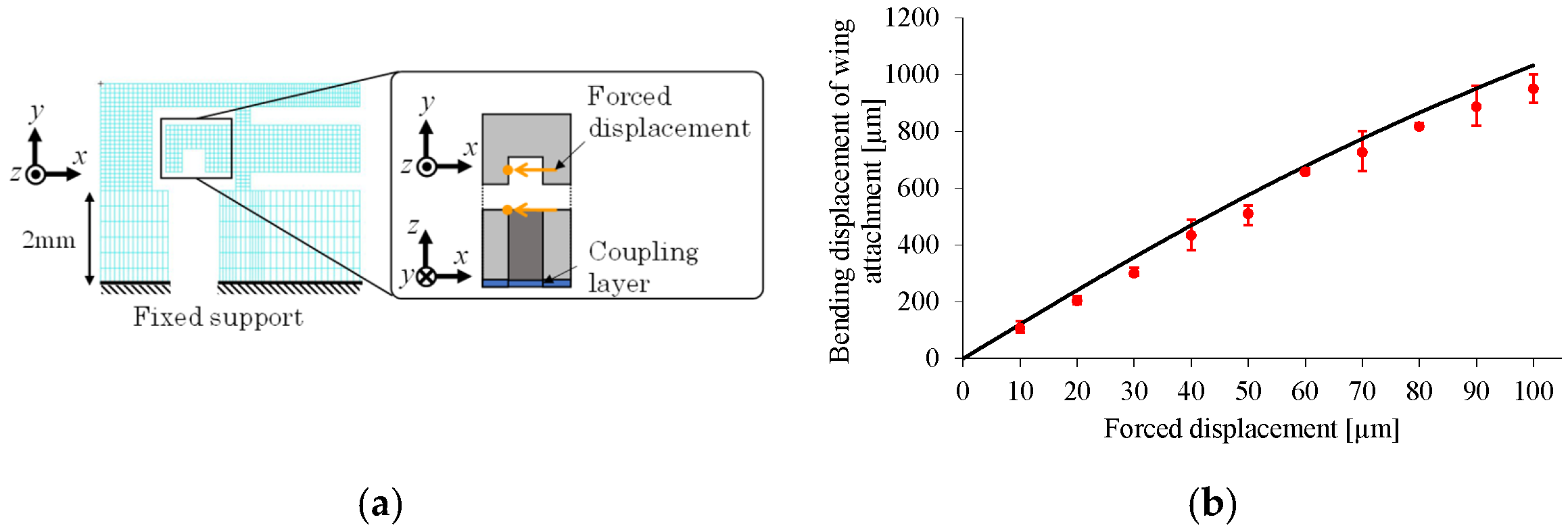
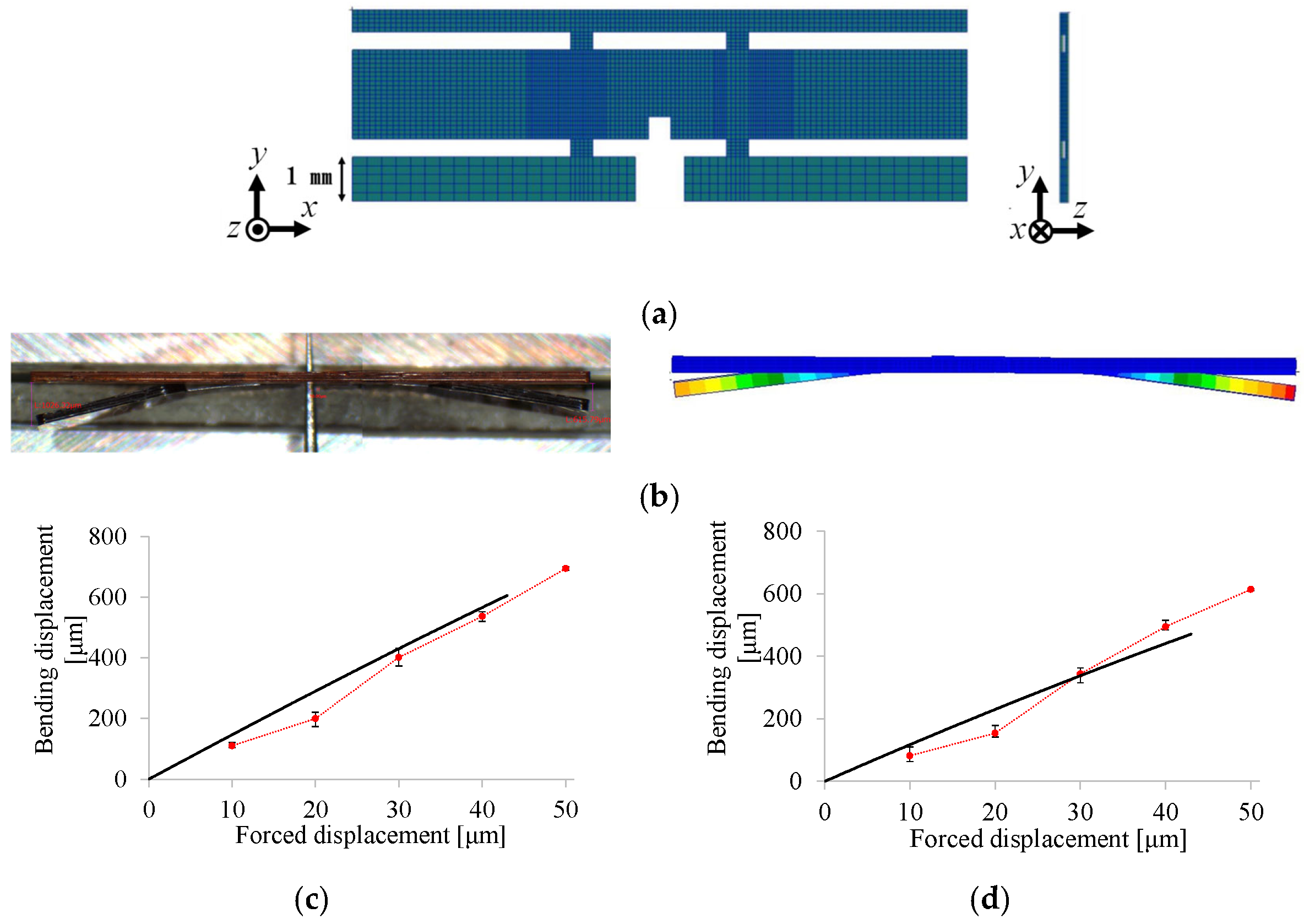
3.1.3. Two-Dimensional Beam Model for Coupling of Transmission and Piezoelectric Bimorph
3.2. Basic Design Results
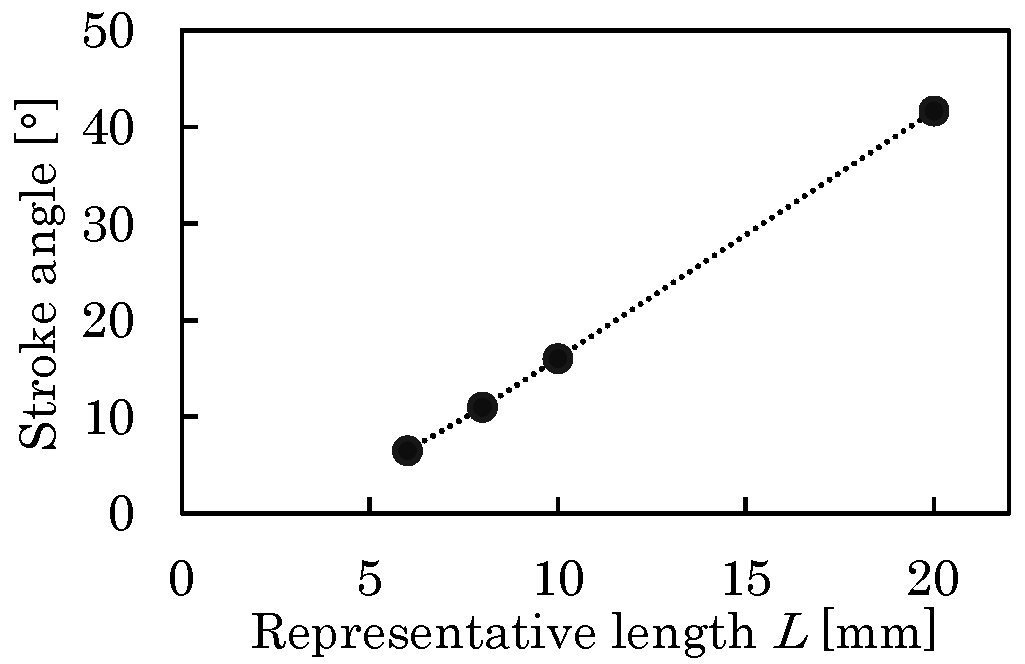
3.2.1. Representative Length of Flapping System
3.2.2. Elastic Hinge Lengths
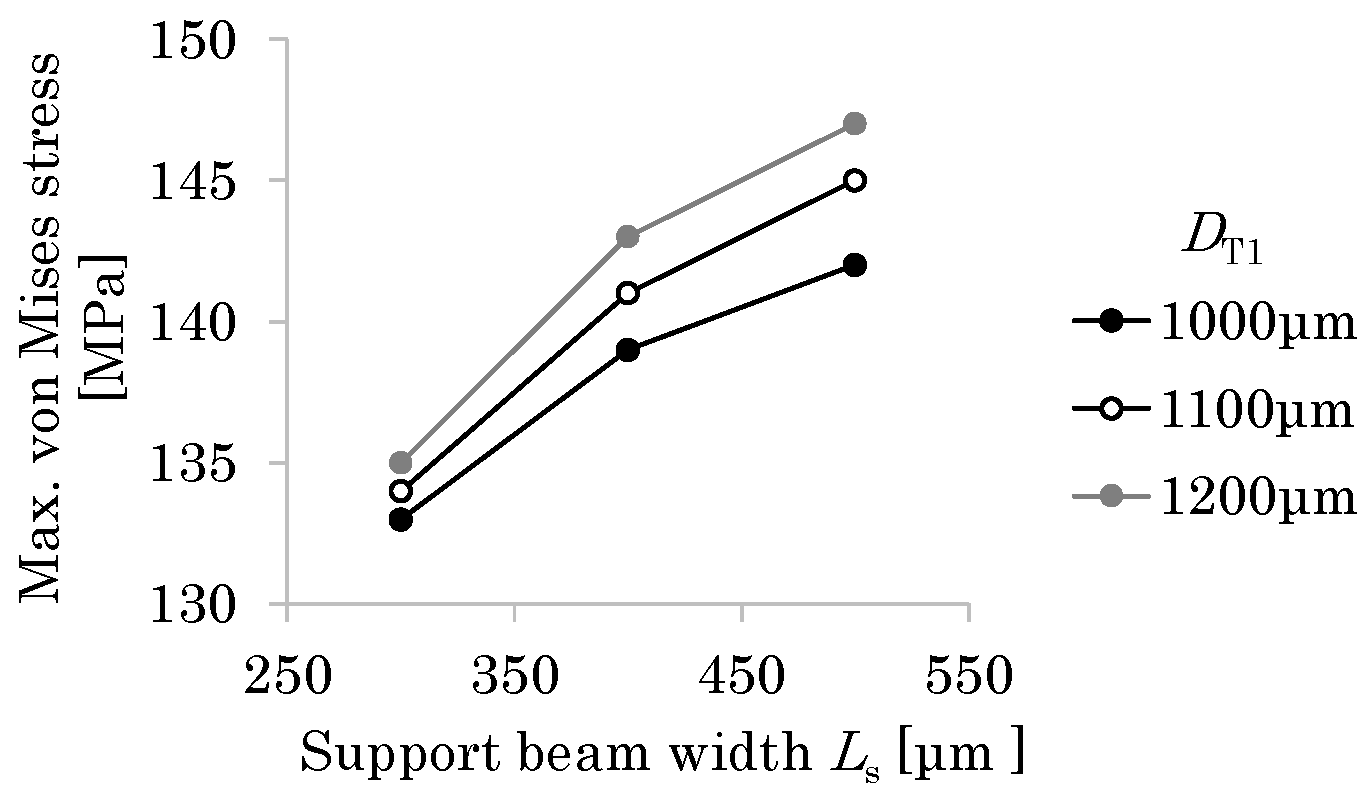
3.2.3. Gap Between T- and I-Shaped Hinges
3.2.4. Stress Reduction in Curing Process
3.3. Detailed Design Results
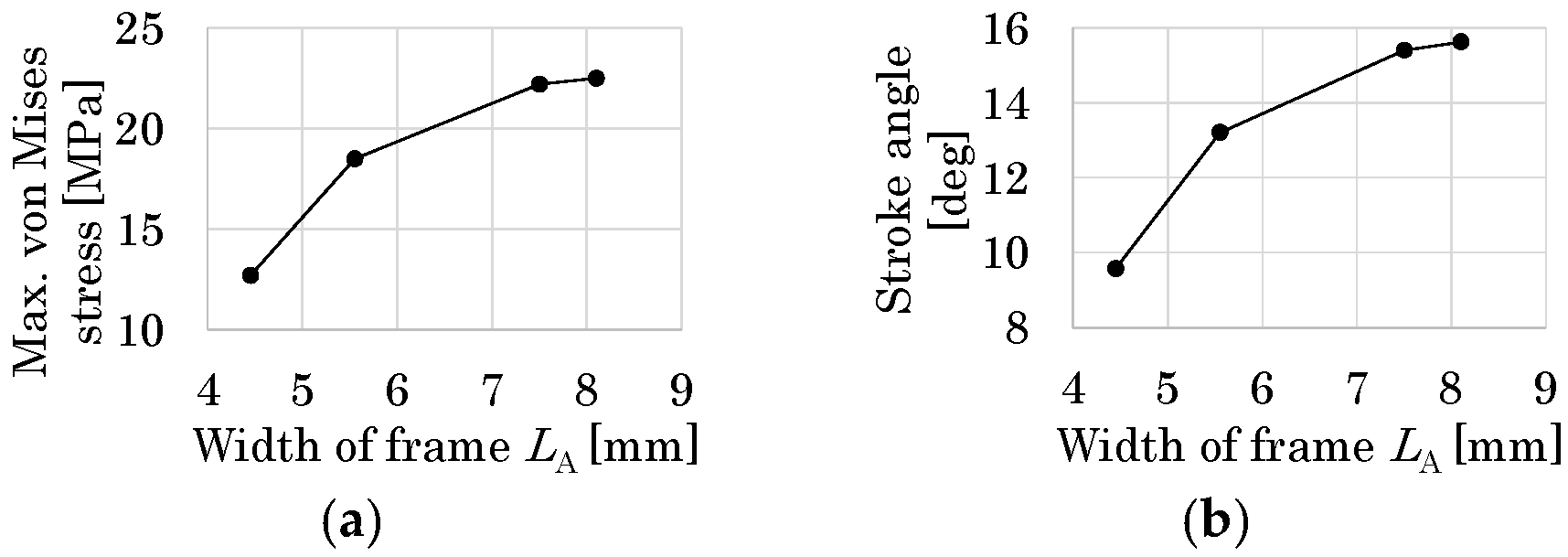
3.3.1. Supporting Frame
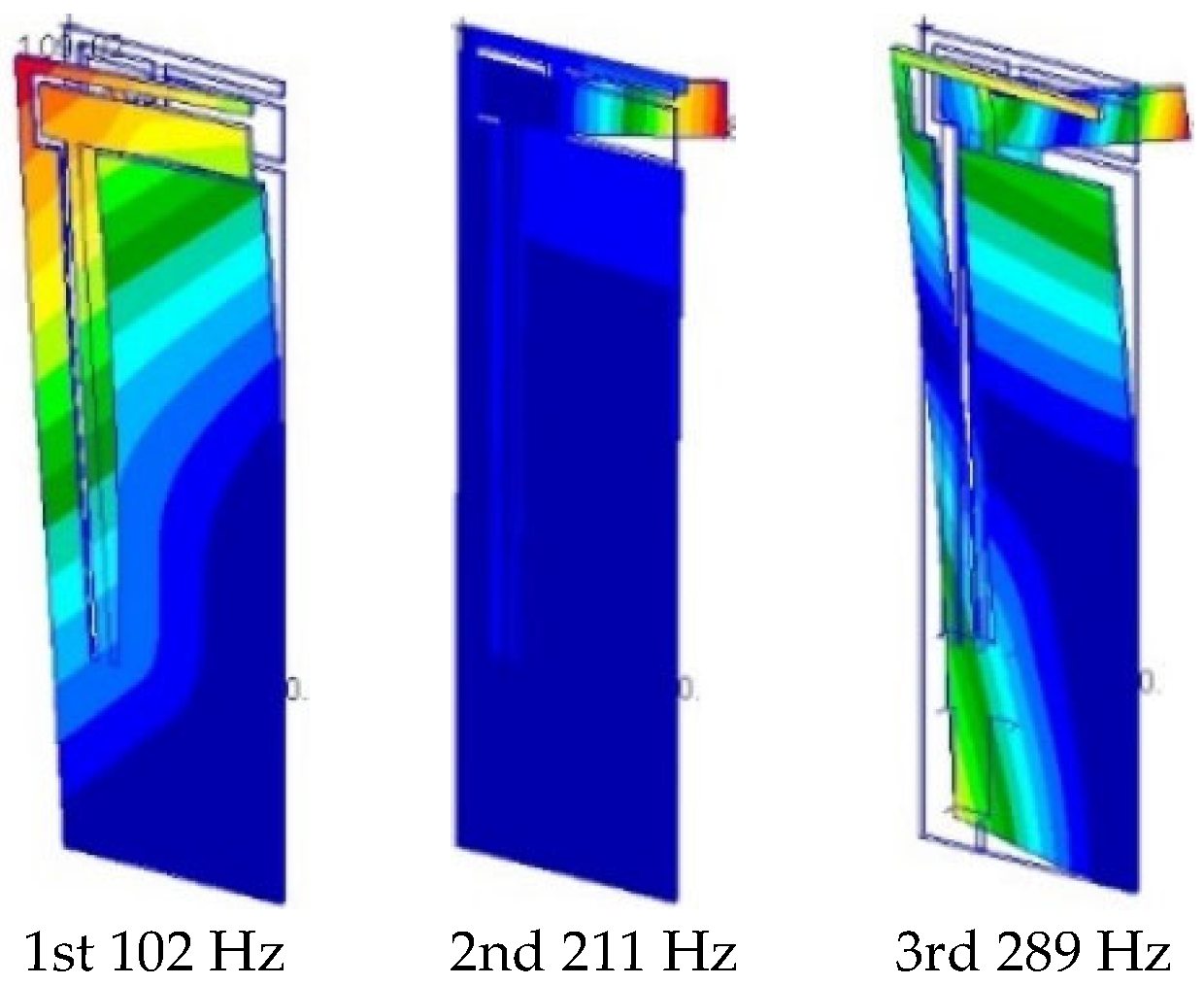
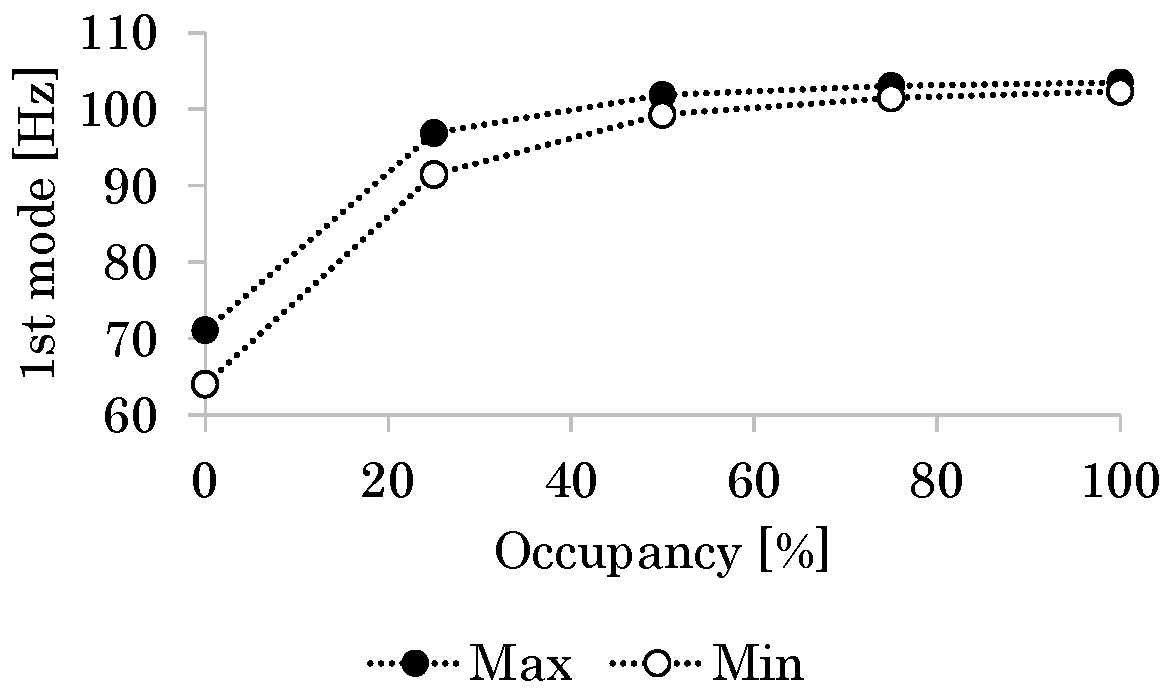
3.3.2. Vibration Modes and Natural Frequencies
4. Micromachining and Testing of Flapping Systems
4.1. Occurrence of Cracks and Failures in Fabrication and Their Prevention
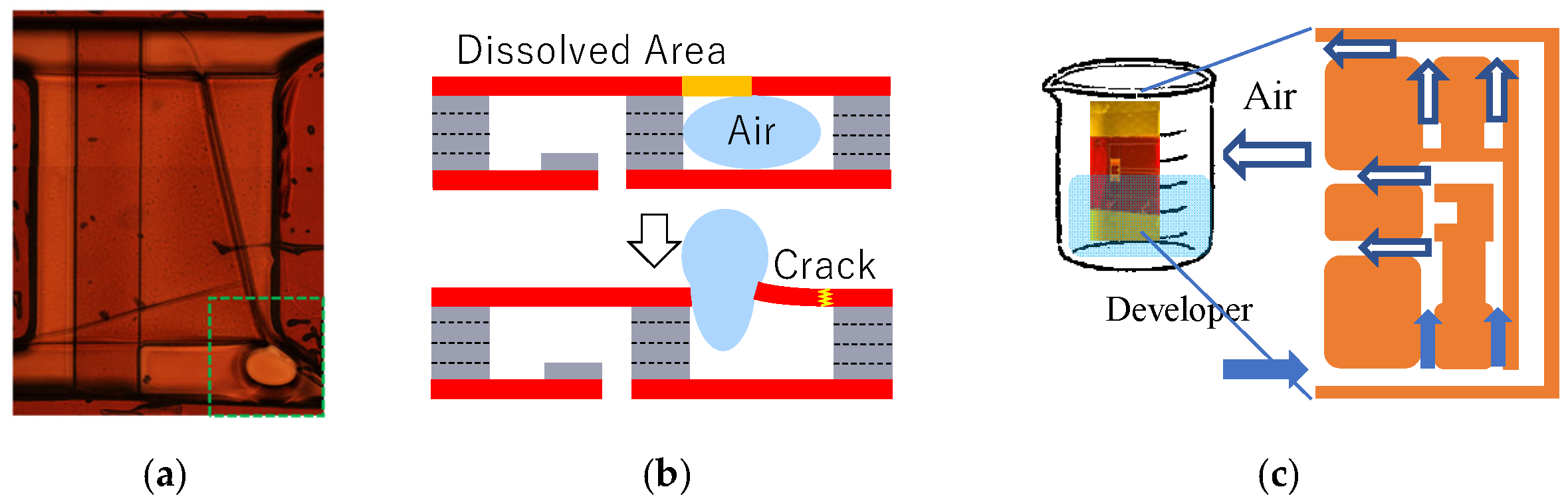
4.1.1. Bubble Control in Development Process
4.1.2. Release Progress Control
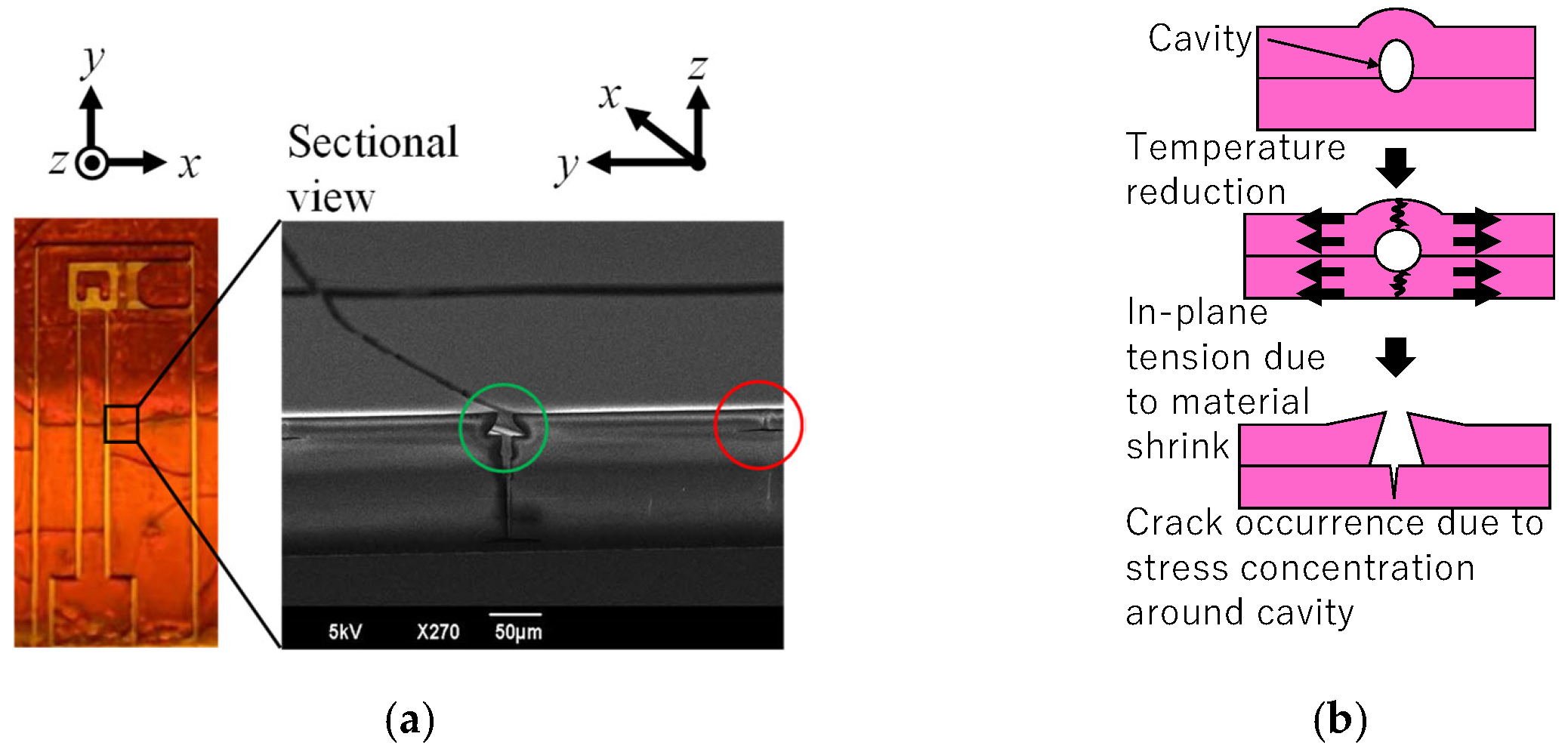
4.1.3. Cooling Process After Post-Exposure Baking
4.2. Size Reduction in Drivetrain
4.3. Fabrication of Complex Drivetrain
4.4. Dynamic Test for Wing Flapping with Sufficient Stroke Angle
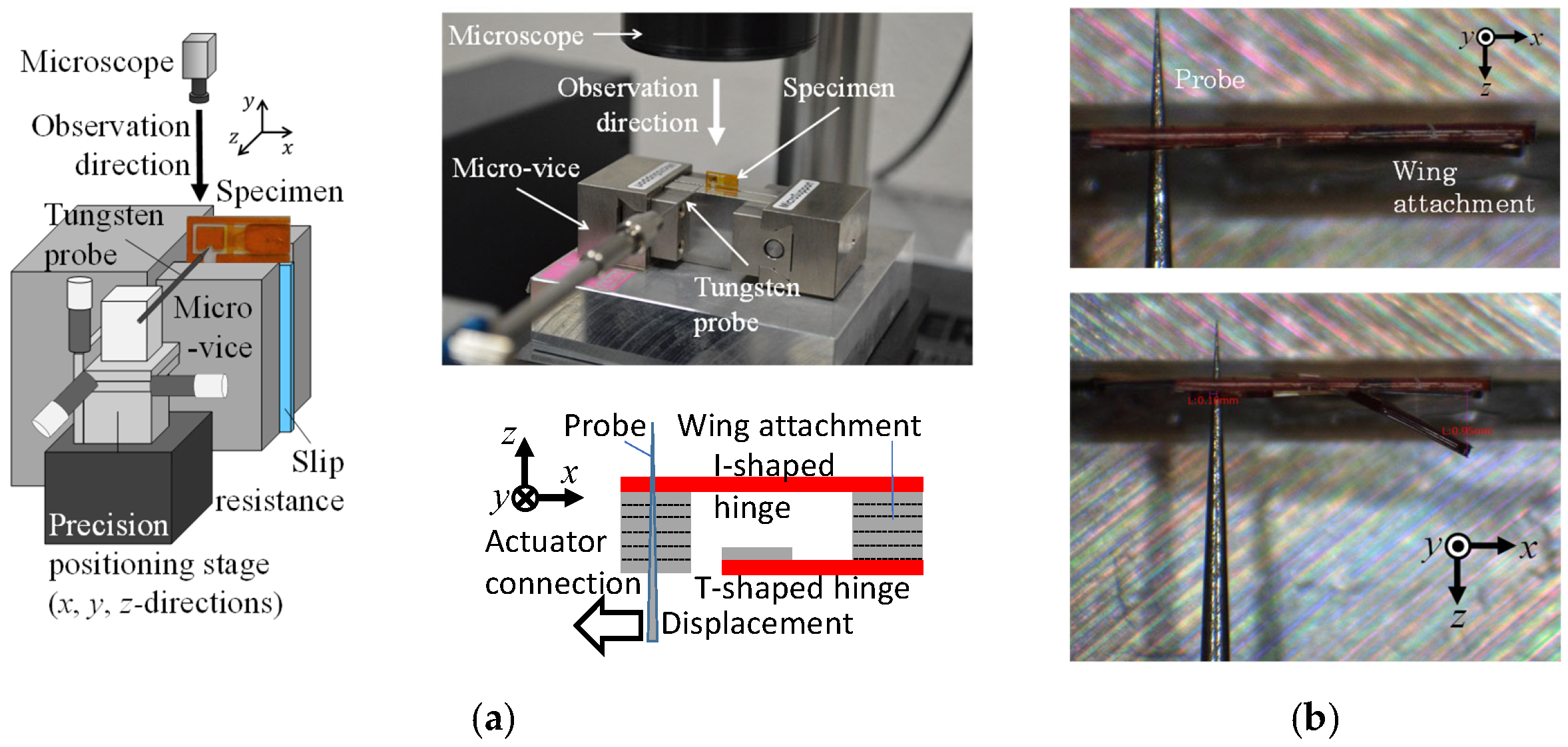
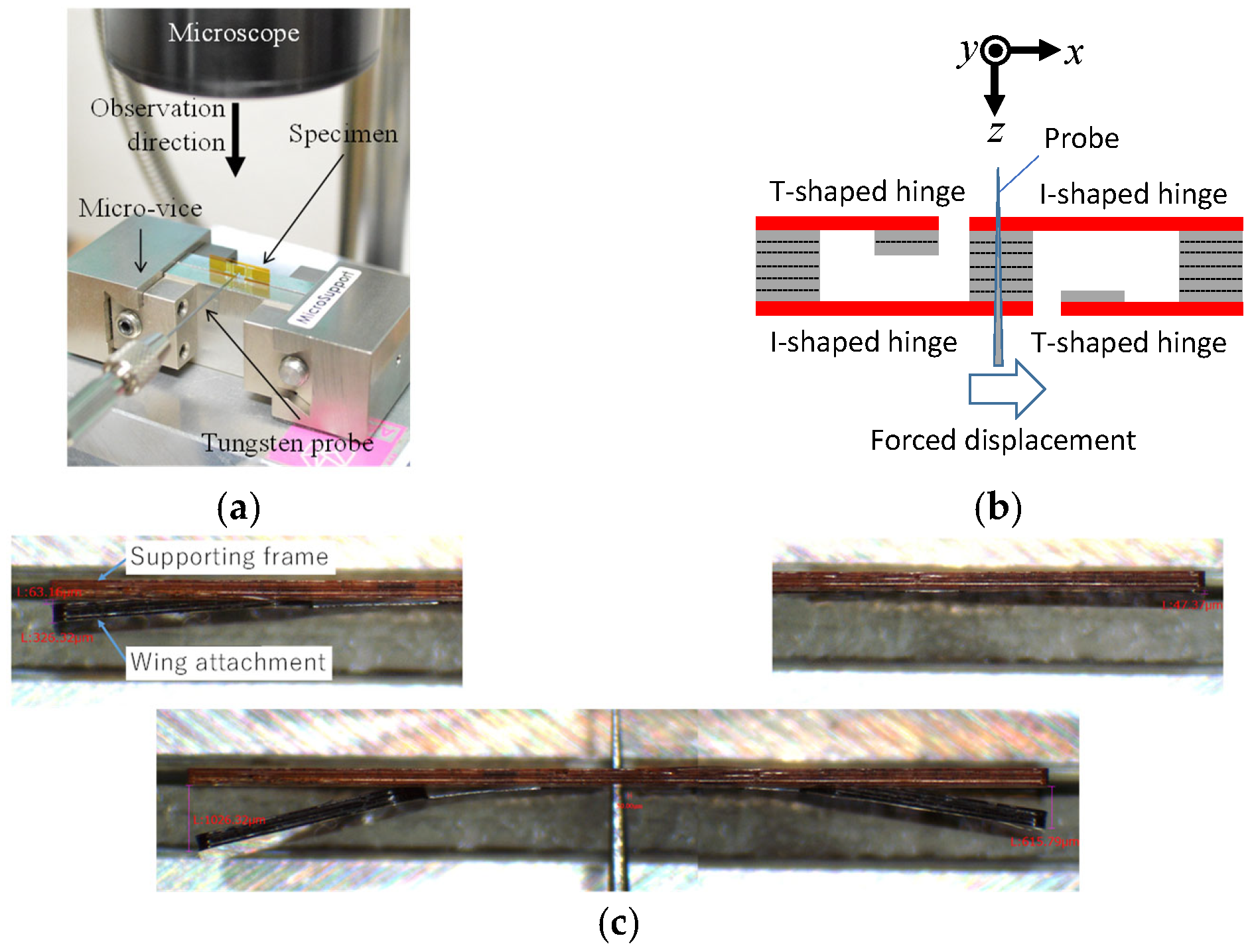
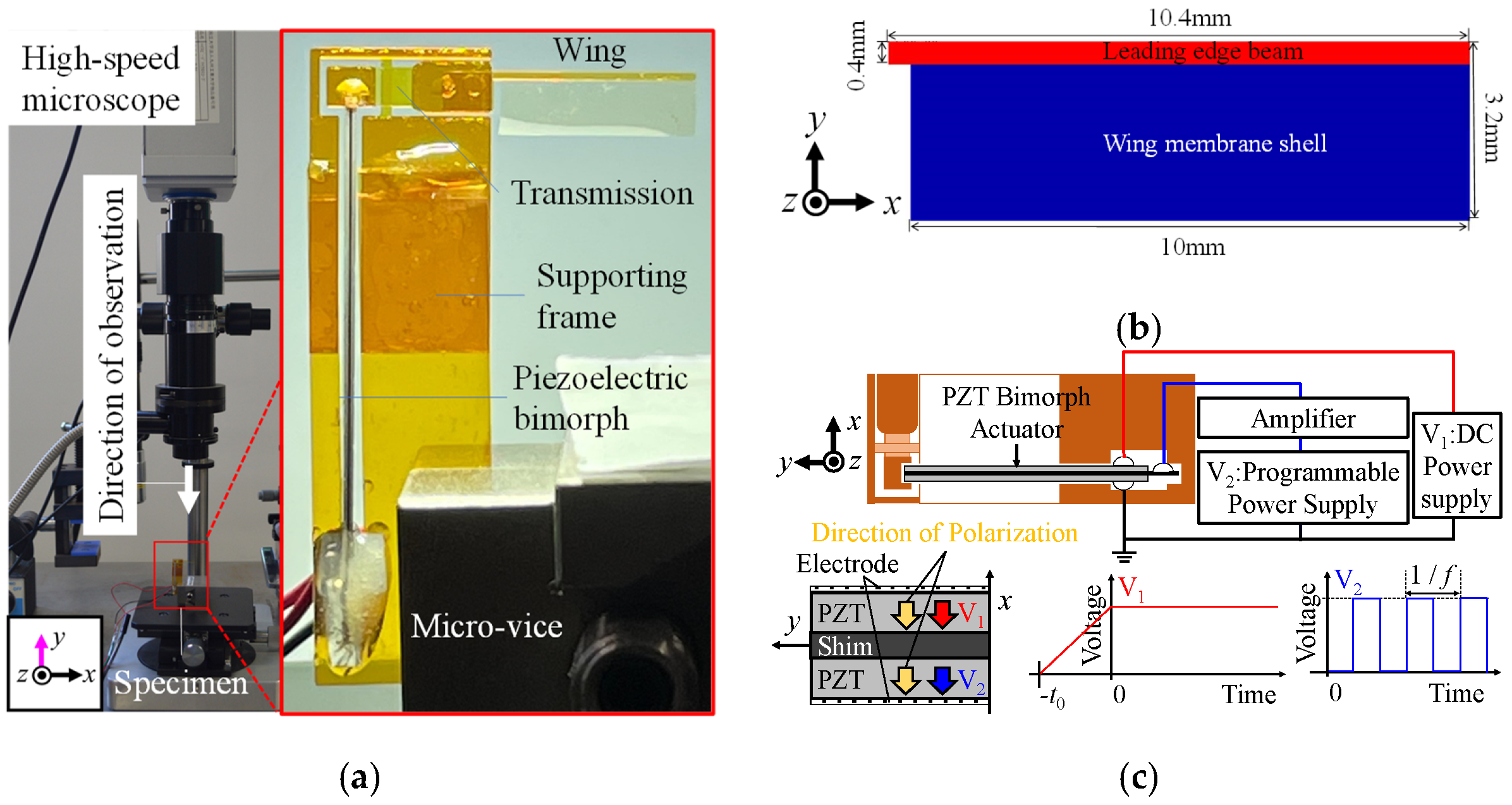
4.4.1. Experimental Setup
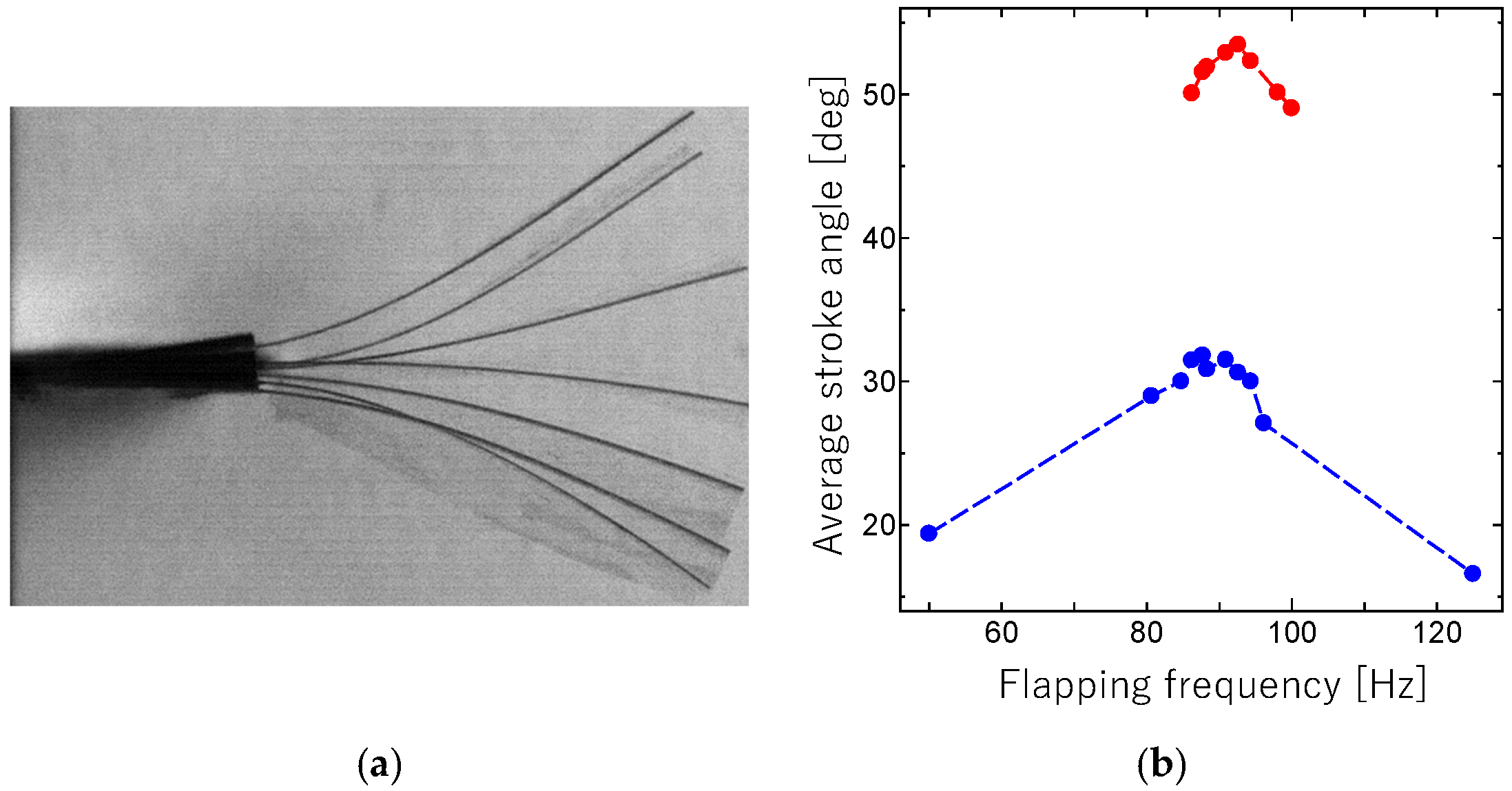
4.4.2. Results and Discussion
5. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ellington, C.P. The Aerodynamics of Hovering Insect Flight. III. Kinematics. Phil. Trans. R. Soc. Lond. B 1984, 305, 41–78. [Google Scholar]
- Sane, S.P. The aerodynamics of insect flight. J. Exp. Biol. 2003, 206, 4191–4208. [Google Scholar] [CrossRef]
- Brodsky, A.K. The Evolution of Insect Flight; Oxford Science Publication: Oxford, UK, 1994. [Google Scholar]
- Wood, R.J. The first takeoff of a biologically inspired at-scale robotic insect. IEEE Trans. Robot. 2008, 24, 341–347. [Google Scholar] [CrossRef]
- Bayiz, Y.; Ghanaatpishe, M.; Fathy, H.; Cheng, B. Hovering efficiency comparison of rotary and flapping flight for rigid rectangular wings via dimensionless multi-objective optimization. Bioinspir. Biomim. 2018, 13, 046002. [Google Scholar] [CrossRef]
- Hilton, T.; Martin, C.; Tun, R.; Castelli, V. The DARPA Nano Air Vehicle Program. In Proceedings of the 50th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Nashville, TN, USA, 9–12 January 2012. [Google Scholar]
- Shyy, W.; Lian, Y.; Tang, J.; Liu, H.; Trizila, P.; Stanford, B.; Bernal, L.; Cesnik, C.; Friedmann, P.; Ifju, P. Computational aerodynamics of low Reynolds number plunging, pitching and flexible wings for MAV applications. Acta Mech. Sin. 2008, 24, 351–373. [Google Scholar] [CrossRef]
- Wood, R.J.; Finio, B.; Karpelson, M.; Ma, K.; Perez-Arancibia, N.O.; Sreetharan, P.S.; Tanaka, H.; Whitney, J.P. Progress on ‘pico’ air vehicles. Int. J. Robot. Res. 2012, 31, 1292–1302. [Google Scholar] [CrossRef]
- Hines, L.; Campolo, D.; Sitti, M. Liftoff of a motor-driven flapping-wing micro aerial vehicle capable of resonance. IEEE Trans. Robot. 2013, 30, 220–232. [Google Scholar] [CrossRef]
- Ozaki, T.; Hamaguchi, K. Bioinspired flapping-wing robot with direct-driven piezoelectric actuation and its takeoff demonstration. IEEE Robot. Autom. Lett. 2018, 3, 4217–4224. [Google Scholar] [CrossRef]
- Jafferies, N.T.; Helbing, E.F.; Karpelson, M.; Wood, R.J. Untethered flight of an insect-inspired sized flapping-wing microscale aerial vehicle. Nature 2019, 570, 491–495. [Google Scholar] [CrossRef] [PubMed]
- Ozaki, T.; Ohta, N.; Jimbo, T.; Hamaguchi, K. Takeoff of a 2.1 g fully untethered tailless flapping-wing micro aerial vehicle with integrated battery. IEEE Robot. Autom. Lett. 2023, 8, 3574–3580. [Google Scholar] [CrossRef]
- Dargent, T.; Bao, X.Q.; Grondel, S.; Le Brun, G.; Paquet, J.B.; Soyer, C.; Cattan, E. Micromachining of an SU-8 flapping-wing flying micro-electro-mechanical system. J. Micromech. Microeng. 2009, 19, 085028. [Google Scholar] [CrossRef]
- Bontemps, A.; Vanneste, T.; Paquet, J.-B.; Dietsch, T.; Grondel, S.; Cattan, E. Design and performance of an insect-inspired nano air vehicle. Smart Mater. Struct. 2013, 22, 014008. [Google Scholar] [CrossRef]
- Meng, K.; Zhang, W.; Chen, W.; Li, H.; Chi, P.; Zou, C.; Wu, X.; Cui, F.; Liu, W.; Chen, J. The design and micromachining of an electromagnetic MEMS flapping-wing micro air vehicle. Microsyst. Technol. 2012, 18, 127–136. [Google Scholar] [CrossRef]
- Zou, Y.; Zhang, W.P.; Zhang, Z. Liftoff of an electromagnetically driven insect-inspired flapping-wing robot. IEEE Trans. Robot. 2016, 32, 1285–1289. [Google Scholar] [CrossRef]
- Liu, Z.; Yan, X.; Qi, M.; Zhang, X.; Lin, L. Low-voltage electromagnetic actuators for flapping-wing micro aerial vehicles. Sens. Actuators A 2017, 265, 1–9. [Google Scholar] [CrossRef]
- Liu, Z.; Yan, X.; Qi, M.; Zhu, Y.; Huang, D.; Zhang, X.; Lin, L. Design of flexible hinges in electromagnetically driven artificial flapping-wing insects for improved lift force. J. Micromech. Microeng. 2019, 29, 015011. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, W.; Zou, Y.; Meng, R.; Zhao, J.; Wei, M. A Sub-100 mg electromagnetically driven insect-inspired flapping-wing micro robot capable of liftoff and control torques modulation. J. Bionic Eng. 2020, 17, 1085–1095. [Google Scholar] [CrossRef]
- Lau, G.K.; Lim, H.T.; Teo, J.Y.; Chin, Y.W. Lightweight mechanical amplifiers for rolled dielectric elastomer actuators and their integration with bio-inspired wing flappers. Smart Mater. Struct. 2014, 23, 025021. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, H.; Mao, J.; Chirarattananon, P.; Helbling, E.F.; Hyun, N.S.P.; Clarke, D.R.; Wood, R.J. Controlled flight of a microrobot powered by soft artificial muscles. Nature 2019, 575, 324–329. [Google Scholar] [CrossRef]
- Liu, Z.; Yan, X.; Qi, M.; Huang, D.; Zhang, X.; Lin, L. Electrostatic flapping-wing actuator with improved lift force by the pivot-spar bracket design. Sens. Actuators A 2018, 280, 295–302. [Google Scholar] [CrossRef]
- Kornbluh, R.; Pelrine, R.; Pei, Q.; Heydt, R.; Stanford, S.; Oh, S.; Eckerle, J. Electro elastomers: Applications of dielectric elastomer transducers for actuation, generation, and smart structures. In Proceedings of the SPIE’s 9th Annual International Symposium on Smart Structures and Materials, San Diego, CA, USA, 17–21 March 2002; pp. 254–271. [Google Scholar]
- Steltz, E.; Fearing, R.S. Dynamometer power output measurements of piezoelectric actuators. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, San Diego, CA, USA, 29 October—2 November 2007; pp. 3980–3986. [Google Scholar]
- Sun, M.; Wu, J.H. Aerodynamic force generation and power requirements in forward flight in a fruit fly with modeled wing motion. J. Exp. Biol. 2003, 206, 3065–3083. [Google Scholar] [CrossRef]
- Mamiya, Y. Applications of piezoelectric actuator. NEC Tech. J. 2006, 1, 81–86. [Google Scholar]
- Zhou, X.; Wu, S.; Wang, X.; Wang, Z.; Zhu, Q.; Sun, J.; Huang, P.; Wang, X.; Huang, W.; Lu, Q. Review on piezoelectric actuators: Materials, classifications, applications, and recent trends. Front. Mech. Eng. 2024, 19, 6. [Google Scholar] [CrossRef]
- Howell, L.L. Compliant Mechanisms; John Wiley & Sons: Edison, NJ, USA, 2001. [Google Scholar]
- Zhang, C.; Rossi, C. A review of compliant transmission mechanisms for bio-inspired flapping-wing micro air vehicles. Bioinspir. Biomim. 2017, 12, 025005. [Google Scholar] [CrossRef]
- Ellington, C.P.; Van den Berg, C.; Willmott, A.P.; Thomas, A.L.R. Leading-edge vortices in insect flight. Nature 1996, 384, 626–630. [Google Scholar] [CrossRef]
- Dickinson, M.H.; Lehmann, F.-O.; Sane, S.P. Wing rotation and the aerodynamic basis of insect flight. Science 1999, 284, 1954–1960. [Google Scholar] [CrossRef] [PubMed]
- Ennos, A.R. A comparative study of the flight mechanism of Diptera. J. Exp. Biol. 1987, 127, 355–372. [Google Scholar] [CrossRef]
- Ishihara, D.; Horie, T.; Denda, M. A two-dimensional computational study on the fluid-structure interaction cause of wing pitch changes in dipteran flapping flight. J. Exp. Biol. 2009, 212, 1–10. [Google Scholar] [CrossRef]
- Kim, B.J.; Meng, E. Review of polymer MEMS micromachining. J. Micromech. Microeng. 2016, 26, 013001. [Google Scholar] [CrossRef]
- Ishihara, D. Computational approach for the fluid-structure interaction design of insect-inspired micro flapping wings. Fluids 2022, 7, 26. [Google Scholar] [CrossRef]
- Wang, Q.M.; Cross, L.E. Performance analysis of piezoelectric cantilever bending actuator. Ferroelectrics 1998, 215, 187–213. [Google Scholar] [CrossRef]
- Jankauski, M.A. Measuring the frequency response of the honeybee thorax. Bioinspir. Biomim. 2020, 15, 046002. [Google Scholar] [CrossRef]




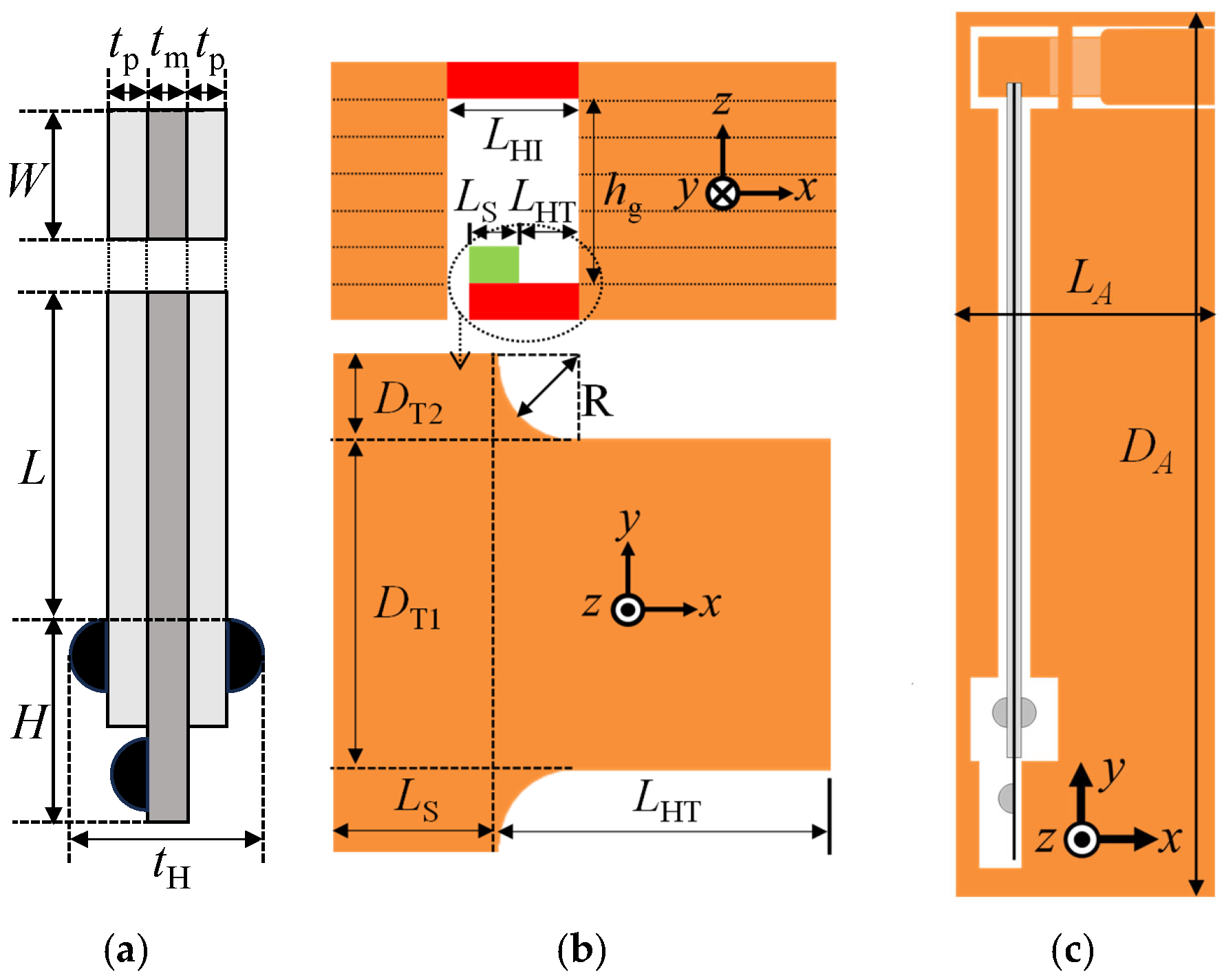









| Parameter | Large | Small |
|---|---|---|
| L [mm] | 20 | 10 |
| LA [mm] | 8.9 | 5.55 |
| DA [mm] | 30.2 | 19.2 |
| W [mm] | 3 | 2 |
| tp [mm] | 0.2 | 0.2 |
| tm [mm] | 0.1 | 0.1 |
| H [mm] | 6.5 | 6.5 |
| tH [mm] | 2.5 | 2.5 |
| Ls [μm] | 500 | 300 |
| LHT [μm] | 1000 | 400 |
| LHI [μm] | 1800 | 1000 |
| hg [μm] | 200 (240) 1 | 104 (146) 2 |
| DT1 [μm] | 2000 | 1000 |
| DT2 [μm] | 400 | 400 |
| R [μm] | 200 | 200 |
| Property | PI | PZT | Shim | Epoxy Resin |
|---|---|---|---|---|
| Young’s modulus [GPa] | 2.5 | 61.0 | 140 | 3.0–6.0 |
| Poisson’s ratio | 0.289 | 0.31 | 0.36 | 0.30 |
| Mass density [kg/m3] | 1420 | 7820 | 8730 | 1100–1400 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ishihara, D.; Kimura, M.; Suetsugu, R.; Ueo, J.; Ohira, N.; Takagi, M.; Ishiba, K.; Shirakawa, N.; Nishinohara, R.; Kimura, M. 2.5-Dimensional Structure Approach for Miniaturizing Flapping-Wing Air Vehicles. Micromachines 2025, 16, 1242. https://doi.org/10.3390/mi16111242
Ishihara D, Kimura M, Suetsugu R, Ueo J, Ohira N, Takagi M, Ishiba K, Shirakawa N, Nishinohara R, Kimura M. 2.5-Dimensional Structure Approach for Miniaturizing Flapping-Wing Air Vehicles. Micromachines. 2025; 16(11):1242. https://doi.org/10.3390/mi16111242
Chicago/Turabian StyleIshihara, Daisuke, Motonobu Kimura, Ryotaro Suetsugu, Jyunpei Ueo, Naoto Ohira, Masakatsu Takagi, Kazuya Ishiba, Nagi Shirakawa, Ryusei Nishinohara, and Masaaki Kimura. 2025. "2.5-Dimensional Structure Approach for Miniaturizing Flapping-Wing Air Vehicles" Micromachines 16, no. 11: 1242. https://doi.org/10.3390/mi16111242
APA StyleIshihara, D., Kimura, M., Suetsugu, R., Ueo, J., Ohira, N., Takagi, M., Ishiba, K., Shirakawa, N., Nishinohara, R., & Kimura, M. (2025). 2.5-Dimensional Structure Approach for Miniaturizing Flapping-Wing Air Vehicles. Micromachines, 16(11), 1242. https://doi.org/10.3390/mi16111242







