A Numerical and Experimental Study on the Enrichment Performance of a Novel Multi-Physics Coupling Microchannel
Abstract
1. Introduction
2. Theory and Mathematical Formulation
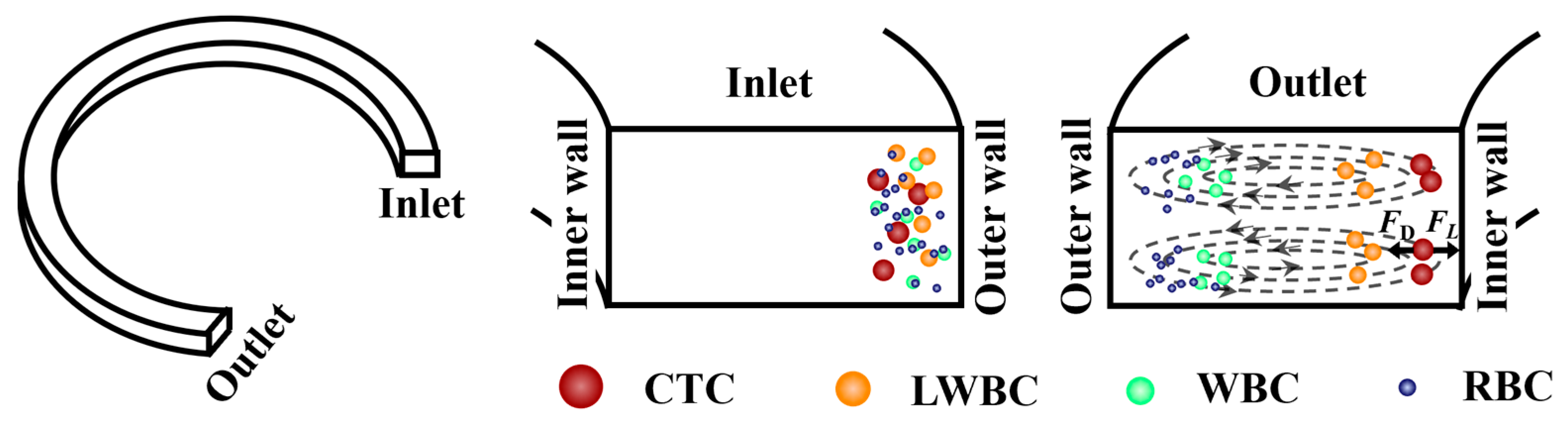
2.1. Principle of Operation
2.2. Principle of Simulation Settings
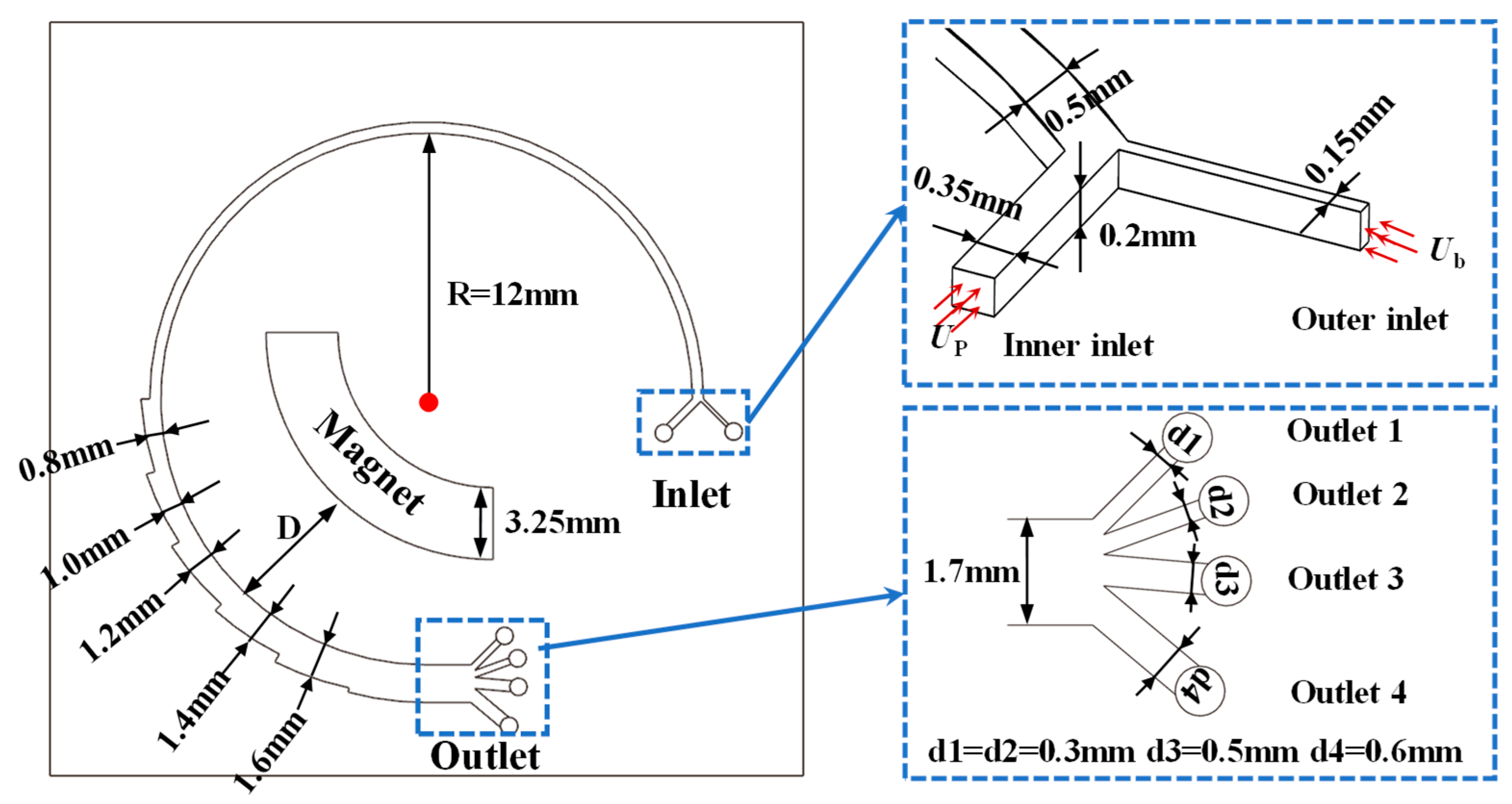
2.2.1. Design of Biochip
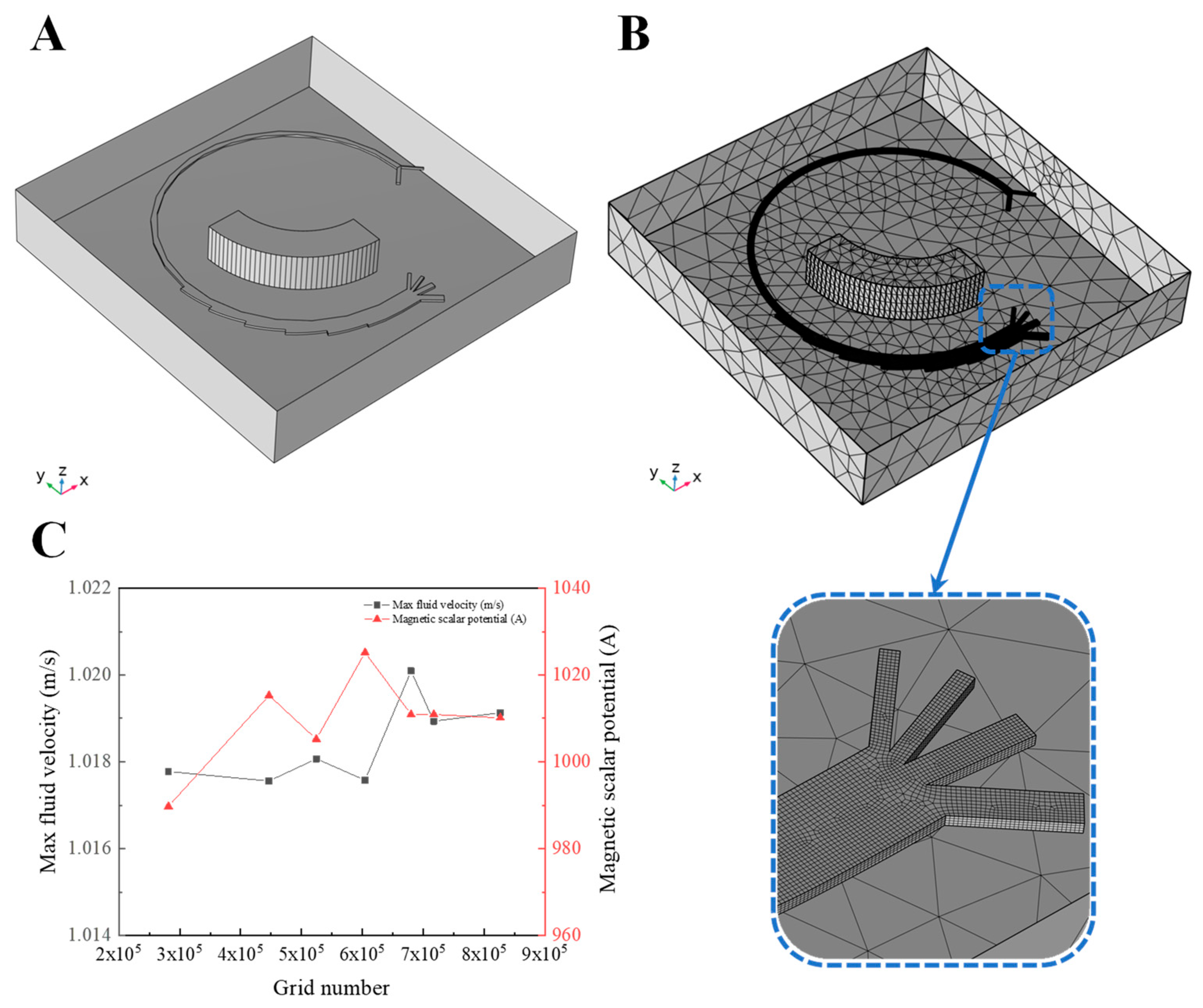
2.2.2. Design of Simulation Settings
3. Numerical Simulation and Results
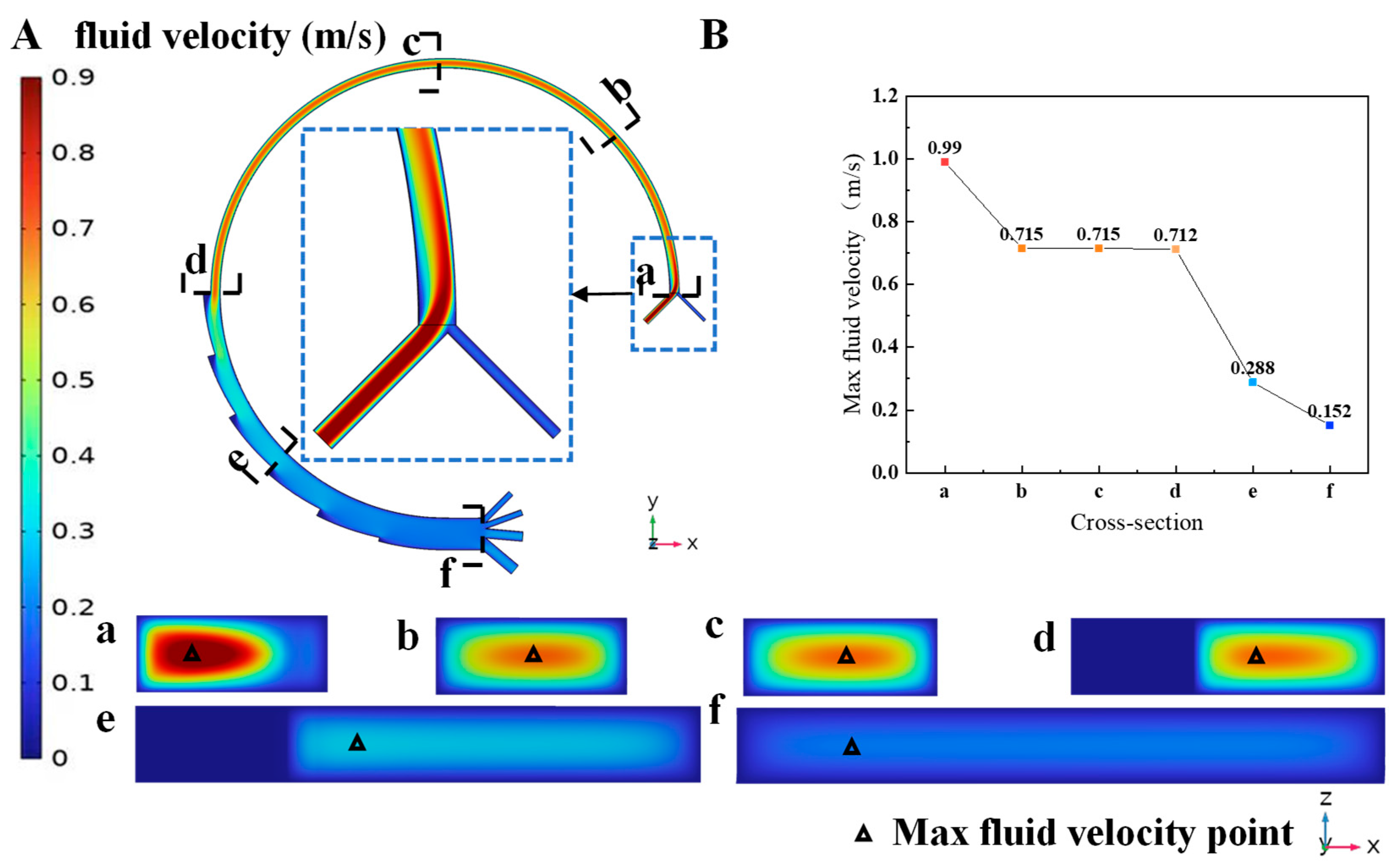
3.1. Simulation of Fluid Flow in Magnetic Field
Flow Field Analysis
3.2. Particle Motion in Multi-Physics Coupling Field
3.3. Analysis of Parameter Effects on Cell Motion
3.3.1. Fluid Velocity
3.3.2. Magnetic Field
3.3.3. Particle Properties
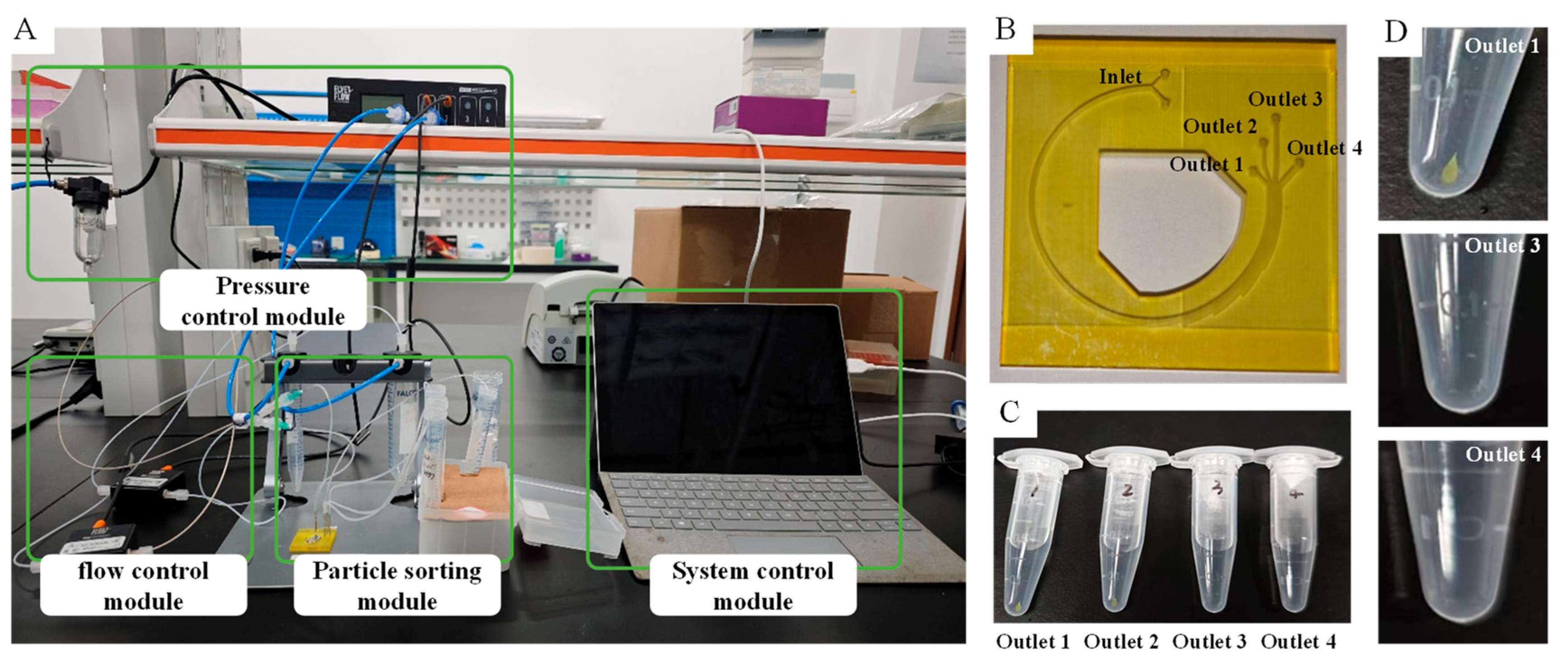
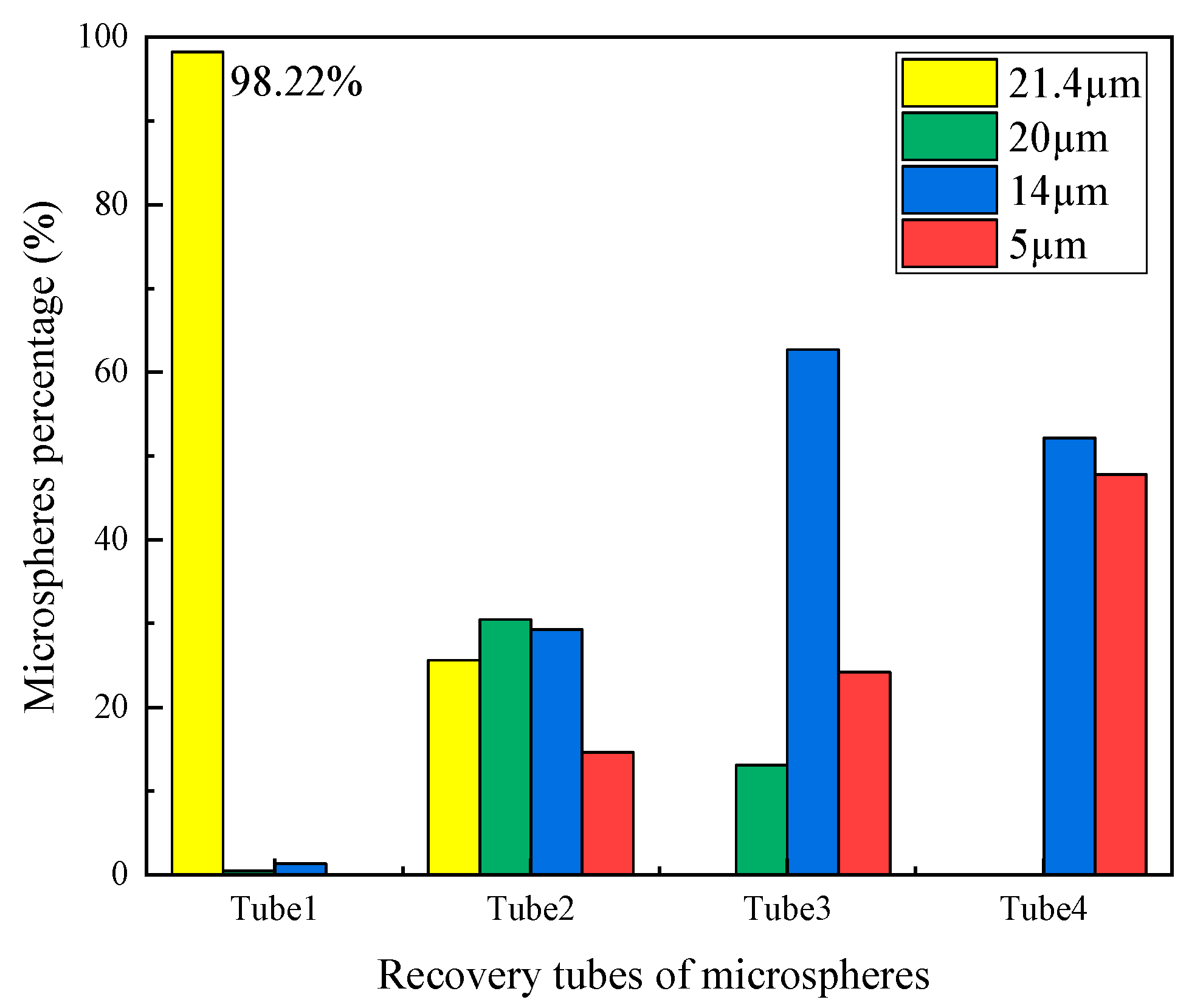
4. Experiment and Results
5. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xia, C.; Dong, X.; Li, H.; Cao, M.; Sun, D.; He, S.; Yang, F.; Yan, X.; Zhang, S.; Li, N.; et al. Cancer statistics in China and United States, 2022: Profiles, trends, and determinants. Chin. Med. J. 2022, 135, 584–590. [Google Scholar] [CrossRef]
- Shiriny, A.; Bayareh, M. Inertial focusing of CTCs in a novel spiral microchannel. Chem. Eng. Sci. 2021, 229, 116102. [Google Scholar] [CrossRef]
- Abdulla, A.; Liu, W.; Gholamipour-Shirazi, A.; Sun, J.; Ding, X. High-throughput isolation of circulating tumor cells using cascaded inertial focusing microfluidic channel. Anal. Chem. 2018, 90, 4397–4405. [Google Scholar] [CrossRef]
- Syed, M.S.; Rafeie, M.; Vandamme, D.; Asadnia, M.; Henderson, R.; Taylor, R.A.; Warkiani, M.E. Selective separation of microalgae cells using inertial microfluidics. Bioresour. Technol. 2018, 252, 91–99. [Google Scholar] [CrossRef]
- Ozbey, A.; Karimzadehkhouei, M.; Kocaturk, N.M.; Bilir, S.E.; Kutlu, O.; Gozuacik, D.; Kosar, A. Inertial focusing of cancer cell lines in curvilinear microchannels. Micro Nano Eng. 2019, 2, 53–63. [Google Scholar] [CrossRef]
- Zhou, Y.; Ma, Z.; Ai, Y. Sheathless inertial cell focusing and sorting with serial reverse wavy channel structures. Microsyst. Nanoeng. 2018, 4, 5. [Google Scholar] [CrossRef] [PubMed]
- Pore, A.A.; Bithi, S.S.; Zeinali, M.; Navaid, H.B.; Nagrath, S.; Layeequr Rahman, R.; Vanapalli, S.A. Phenotyping of rare circulating cells in the blood of non-metastatic breast cancer patients using microfluidic Labyrinth technology. Biomicrofluidics 2022, 16, 064107. [Google Scholar] [CrossRef]
- Volovetsky, A.B.; Novikova, V.A.; Boloban, A.; Rzhevskiy, A.S.; Kapitannikova, A.; Ovchinnikova, E.G.; Klejmentjeva, T.P.; Grishin, V.A.; Pigareva, Y.; Zvyagin, A.V.; et al. Prognostic Value of the Number of Circulating Tumor Cells in Patients with Metastatic Non-Small Cell Lung Cancer. Micromachines 2025, 16, 470. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Li, J.; Sun, Y. Microfluidic approaches for cancer cell detection, characterization, and separation. Lab A Chip 2012, 12, 1753–1767. [Google Scholar] [CrossRef] [PubMed]
- Kulrattanarak, T.; Van Der Sman, R.; Schroën, C.; Boom, R. Classification and evaluation of microfluidic devices for continuous suspension fractionation. Adv. Colloid Interface Sci. 2008, 142, 53–66. [Google Scholar] [CrossRef]
- Manz, A.; Graber, N.; Widmer, H. Miniaturized total chemical analysis systems: A novel concept for chemical sensing. Sens. Actuators B Chem. 1990, 1, 244–248. [Google Scholar] [CrossRef]
- Volpe, A.; Gaudiuso, C.; Ancona, A. Sorting of Particles Using Inertial Focusing and Laminar Vortex Technology: A Review. Micromachines 2019, 10, 594. [Google Scholar] [CrossRef]
- Dalili, A.; Samiei, E.; Hoorfar, M. A review of sorting, separation and isolation of cells and microbeads for biomedical applications: Microfluidic approaches. Analyst 2019, 144, 87–113. [Google Scholar] [CrossRef]
- Martel, J.M.; Toner, M. Inertial focusing in microfluidics. Annu. Rev. Biomed. Eng. 2014, 16, 371–396. [Google Scholar] [CrossRef]
- Warkiani, M.E.; Khoo, B.L.; Wu, L.; Tay, A.K.P.; Bhagat, A.A.S.; Han, J.; Lim, C.T. Ultra-fast, label-free isolation of circulating tumor cells from blood using spiral microfluidics. Nat. Protoc. 2016, 11, 134–148. [Google Scholar] [CrossRef]
- Knapp, M.; Kadić, S.; Lux, A.; Paust, N.; Zengerle, R.; Hoffmann, J. Highly efficient isolation and multistep analysis of tumor cells from whole blood. Lab A Chip 2025, 25, 1938–1946. [Google Scholar] [CrossRef]
- Kim, J.-A.; Kommajosula, A.; Choi, Y.-H.; Lee, J.-R.; Jeon, E.-C.; Ganapathysubramanian, B.; Lee, W. Inertial focusing in triangular microchannels with various apex angles. Biomicrofluidics 2020, 14, 024105. [Google Scholar] [CrossRef]
- Mohammadali, R.; Bayareh, M. Deformability-based isolation of circulating tumor cells in spiral microchannels. Micromachines 2023, 14, 2111. [Google Scholar] [CrossRef] [PubMed]
- Mansor, M.A.; Jamrus, M.A.; Lok, C.K.; Ahmad, M.R.; Petrů, M.; Koloor, S.S.R. Microfluidic device for both active and passive cell separation techniques: A review. Sens. Actuators Rep. 2025, 9, 100277. [Google Scholar] [CrossRef]
- Rzhevskiy, A.S.; Bazaz, S.R.; Ding, L.; Kapitannikova, A.; Zvyagin, A.V. Rapid and Label-Free Isolation of Tumour Cells from the Urine of Patients with Localised Prostate Cancer Using Inertial Microfluidics. Cancers 2019, 12, 81. [Google Scholar] [CrossRef] [PubMed]
- Al-Halhouli, A.A.; Albagdady, A.; Dietzel, A. Sheath-less high throughput inertial separation of small microparticles in spiral microchannels with trapezoidal cross-section. RSC Adv. 2019, 9, 41970–41976. [Google Scholar] [CrossRef]
- Moloudi, R.; Oh, S.; Yang, C.; Teo, K.L.; Lam, A.T.L.; Warkiani, M.E.; Naing, M.W. Scaled-Up Inertial Microfluidics: Retention System for Microcarrier-Based Suspension Cultures. Biotechnol. J. 2019, 14, 1800674. [Google Scholar] [CrossRef] [PubMed]
- Cruz, J.; Graells, T.; Walldén, M.; Hjort, K. Inertial focusing with sub-micron resolution for separation of bacteria. Lab A Chip 2019, 19, 1257–1266. [Google Scholar] [CrossRef]
- Zhu, Z.; Ren, H.; Wu, D.; Ni, Z.; Xiang, N. High-throughput and simultaneous inertial separation of tumor cells and clusters from malignant effusions using spiral-contraction-expansion channels. Microsyst. Nanoeng. 2024, 10, 36. [Google Scholar] [CrossRef] [PubMed]
- Magalhães, V.; Pinto, V.; Sousa, P.; Gonçalves, L.; Fernández, E.; Minas, G. Spiral inertial microfluidics for separation and concentration of phytoplankton. Algal Res. 2023, 76, 103317. [Google Scholar] [CrossRef]
- Ngum, L.F.; Matsushita, Y.; El-Mashtoly, S.F.; Fath El-Bab, A.M.; Abdel-Mawgood, A.L. Separation of microalgae from bacterial contaminants using spiral microchannel in the presence of a chemoattractant. Bioresour. Bioprocess. 2024, 11, 36. [Google Scholar] [CrossRef]
- Emmerich, M.E.; Sinnigen, A.-S.; Neubauer, P.; Birkholz, M. Dielectrophoretic separation of blood cells. Biomed. Microdevices 2022, 24, 30. [Google Scholar] [CrossRef]
- Nasiri, R.; Shamloo, A.; Akbari, J. Design of a Hybrid Inertial and Magnetophoretic Microfluidic Device for CTCs Separation from Blood. Micromachines 2021, 12, 877. [Google Scholar] [CrossRef]
- Jeon, H.; Kwon, T.; Yoon, J.; Han, J. Engineering a deformation-free plastic spiral inertial microfluidic system for CHO cell clarification in biomanufacturing. Lab A Chip 2022, 22, 272–285. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Gao, M.; Niu, Y.; Wang, J.; Shen, S. Flow-rate and particle-size insensitive inertial focusing in dimension-confined ultra-low aspect ratio spiral microchannel. Sens. Actuators B Chem. 2022, 369, 132284. [Google Scholar] [CrossRef]
- Kye, H.G.; Park, B.S.; Lee, J.M.; Song, M.G.; Song, H.G.; Ahrberg, C.D.; Chung, B.G. Dual-neodymium magnet-based microfluidic separation device. Sci. Rep. 2019, 9, 9502. [Google Scholar] [CrossRef] [PubMed]
- Bhagat, A.A.S.; Kuntaegowdanahalli, S.S.; Papautsky, I. Continuous particle separation in spiral microchannels using dean flows and differential migration. Lab A Chip 2008, 8, 1906–1914. [Google Scholar] [CrossRef] [PubMed]
- Di Carlo, D.; Irimia, D.; Tompkins, R.G.; Toner, M. Continuous inertial focusing, ordering, and separation of particles in microchannels. Proc. Natl. Acad. Sci. USA 2007, 104, 18892–18897. [Google Scholar] [CrossRef] [PubMed]
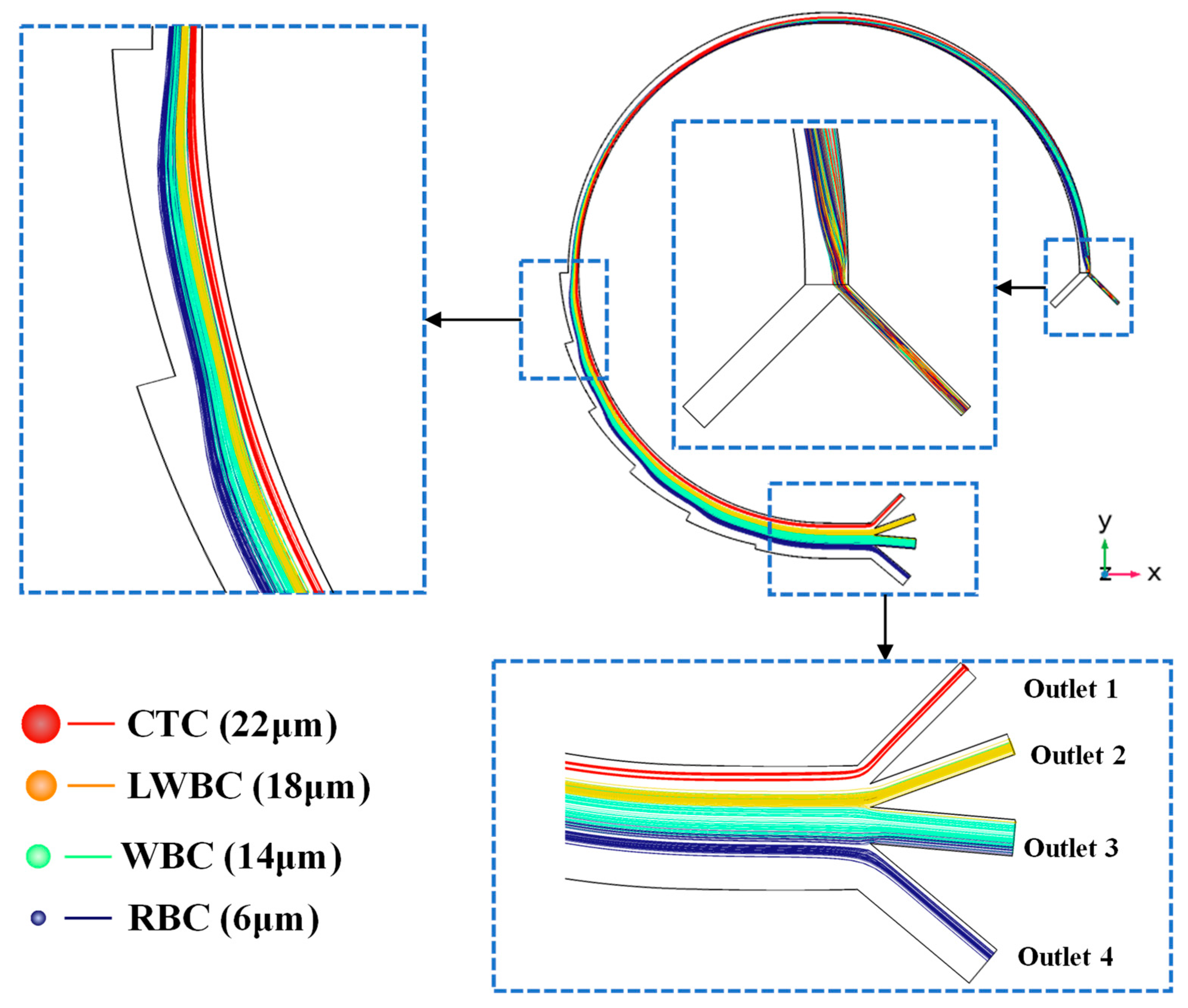
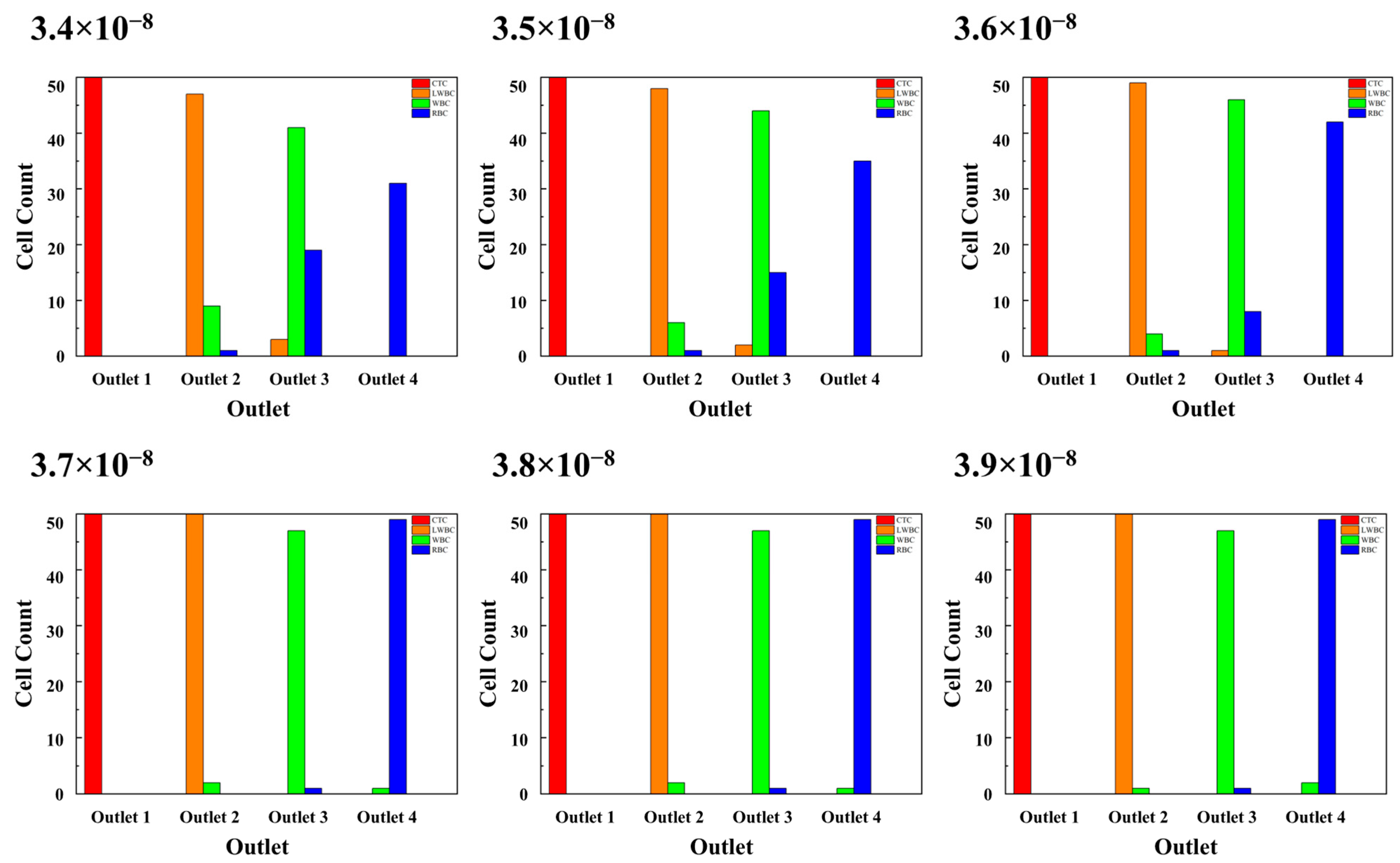
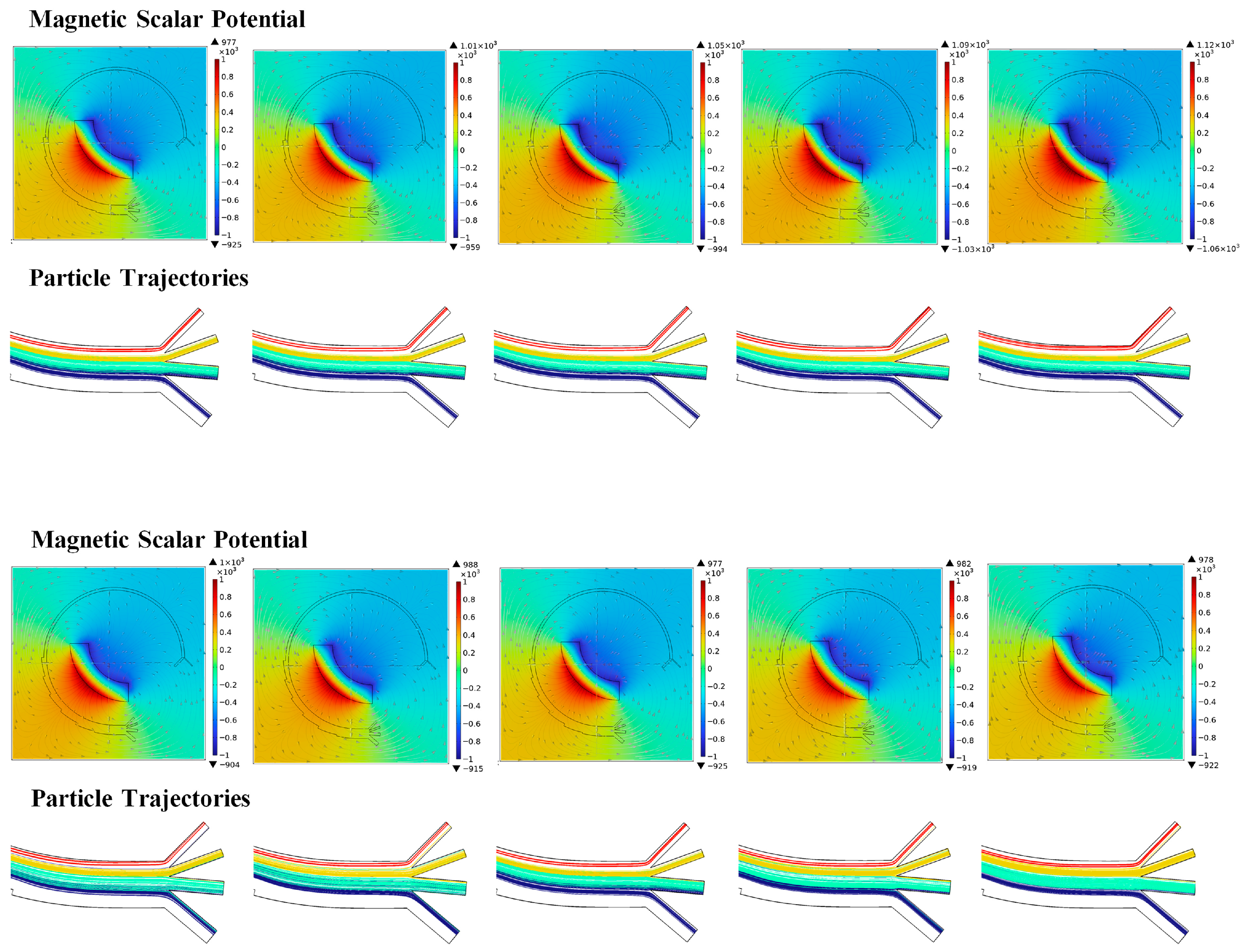
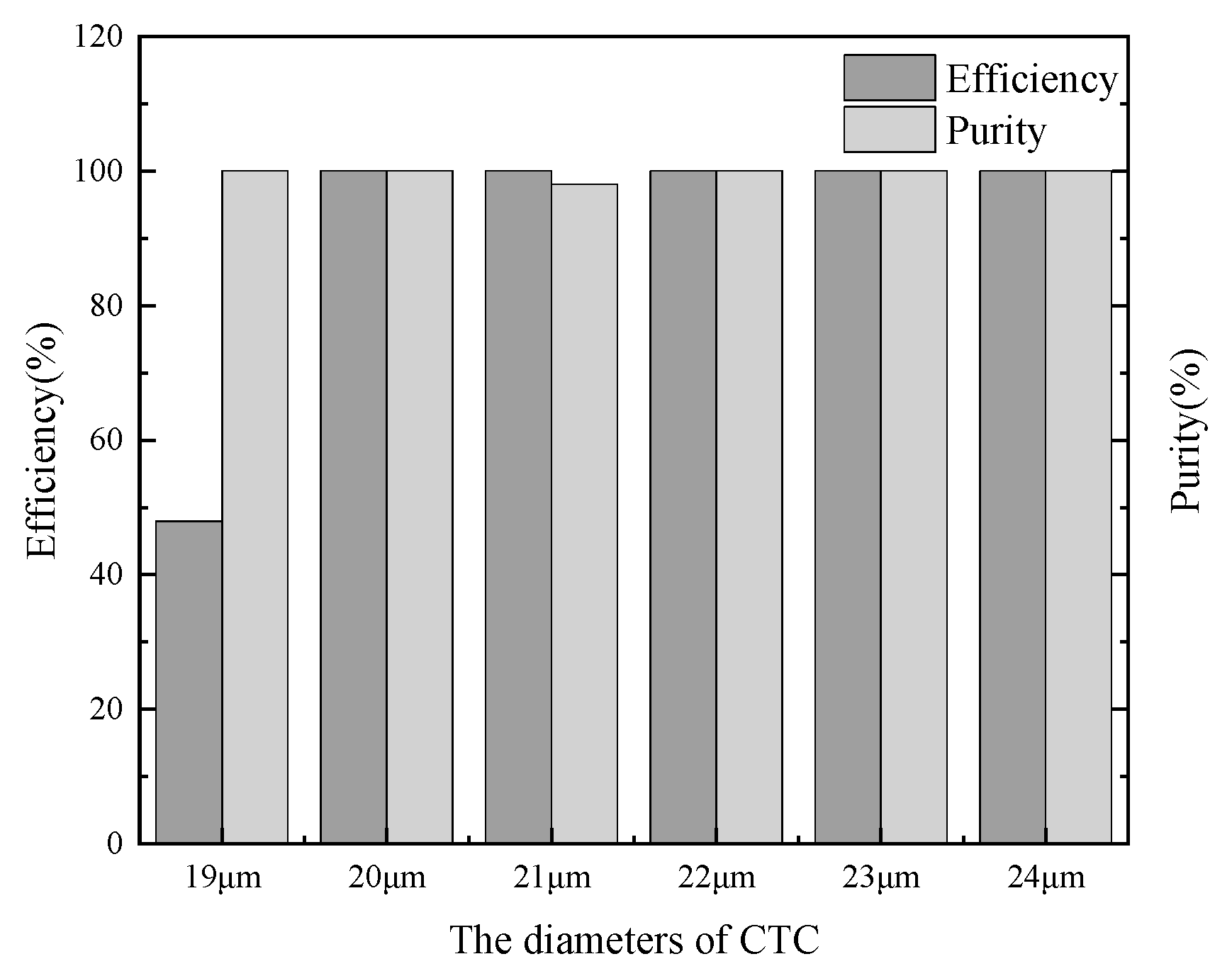
| Parameters | Value | Unit | |
|---|---|---|---|
| Fluid velocity | Up | 3.4 × 10−8, 3.5 × 10−8, 3.6 × 10−8, 3.7 × 10−8, 3.8 × 10−8, 3.9 × 10−8 | m3/s |
| Magnetic field | D | 2.50, 2.75, 3.00, 3.25, 3.50, 3.75 | mm |
| Remanent flux density | 1.08, 1.12, 1.16, 1.20, 1.24, 1.28 | T | |
| Particle properties | dp (CTC) | 19, 20, 21, 22, 23, 24 | μm |
| Physics Interfaces | Major Parameters | Value | Unit | |
|---|---|---|---|---|
| SPF | Fluid properties | Default discretization | P2 + P2 | - |
| Density | 1000 | kg/m3 | ||
| Dynamic viscosity | 1 × 10−3 | Pa × s | ||
| Flow channel parameters | Hydraulic diameter | 2.86 × 10−4 | m | |
| Reynolds number | 40–200 | - | ||
| Dean number | 5–25 | - | ||
| Boundary condition | wall | No slip | - | |
| Inner inlet flow rate | 3.4 × 10−8–3.9 × 10−8 | m3/s | ||
| Outer inlet flow rate | 2.217 × 10−9 | m3/s | ||
| Outlet pressure | 0 | N | ||
| MFNC | Relative permittivity | 1 | 1 | |
| Remanent flux density | 1.08–1.28 | T | ||
| Position of magnet | 2.5–3.75 | mm | ||
| Magnetic flux density | B = μ0μrH + Br | T | ||
| FPT | Wall conditions | Adhesion | ||
| Particle properties | Density | 1050 | kg/m3 | |
| Diameter | 6, 14, 18, 19/20/21/22/23/24 | μm | ||
| Particle number | 50 | - | ||
| Drag force | From SPF of simulation | - | ||
| Lift force | From SPF of simulation | - | ||
| Magnetophoretic force | Particle relative permeability | 1.08 | - | |
| Forces | Parameters/Formula | Value | Unit | |
|---|---|---|---|---|
| FD | Diameter | 6 μm | 1.5 × 10−10–3.18 × 10−9 | N |
| 24 μm | 6.0 × 10−9–1.27 × 10−8 | N | ||
| FL | Diameter | 6 μm | 7.39 × 10−13–3.13 × 10−11 | N |
| 24 μm | 1.89 × 10−10–8.02 × 10−9 | N | ||
| Magnetic force () | From FPT of simulation | N | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Q.; Shi, R.; Gu, T. A Numerical and Experimental Study on the Enrichment Performance of a Novel Multi-Physics Coupling Microchannel. Micromachines 2025, 16, 1146. https://doi.org/10.3390/mi16101146
Liu Q, Shi R, Gu T. A Numerical and Experimental Study on the Enrichment Performance of a Novel Multi-Physics Coupling Microchannel. Micromachines. 2025; 16(10):1146. https://doi.org/10.3390/mi16101146
Chicago/Turabian StyleLiu, Qiao, Ruiju Shi, and Tongxu Gu. 2025. "A Numerical and Experimental Study on the Enrichment Performance of a Novel Multi-Physics Coupling Microchannel" Micromachines 16, no. 10: 1146. https://doi.org/10.3390/mi16101146
APA StyleLiu, Q., Shi, R., & Gu, T. (2025). A Numerical and Experimental Study on the Enrichment Performance of a Novel Multi-Physics Coupling Microchannel. Micromachines, 16(10), 1146. https://doi.org/10.3390/mi16101146






