Zonotope-Based State Estimation for Boost Converter System with Markov Jump Process
Abstract
1. Introduction
2. Model Descriptions and Preliminaries
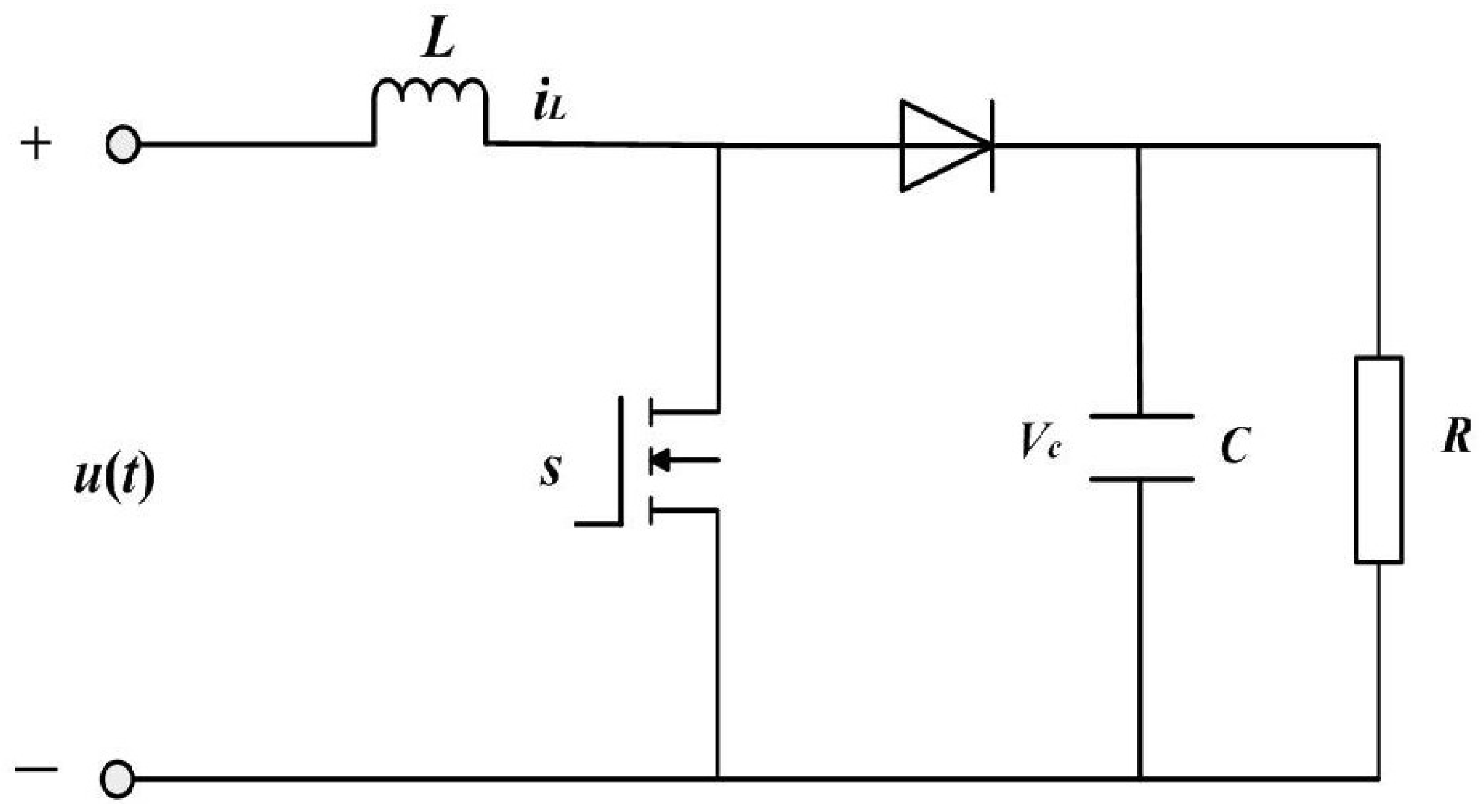
2.1. Boost Converter System
2.2. Generalized Mathematical Description
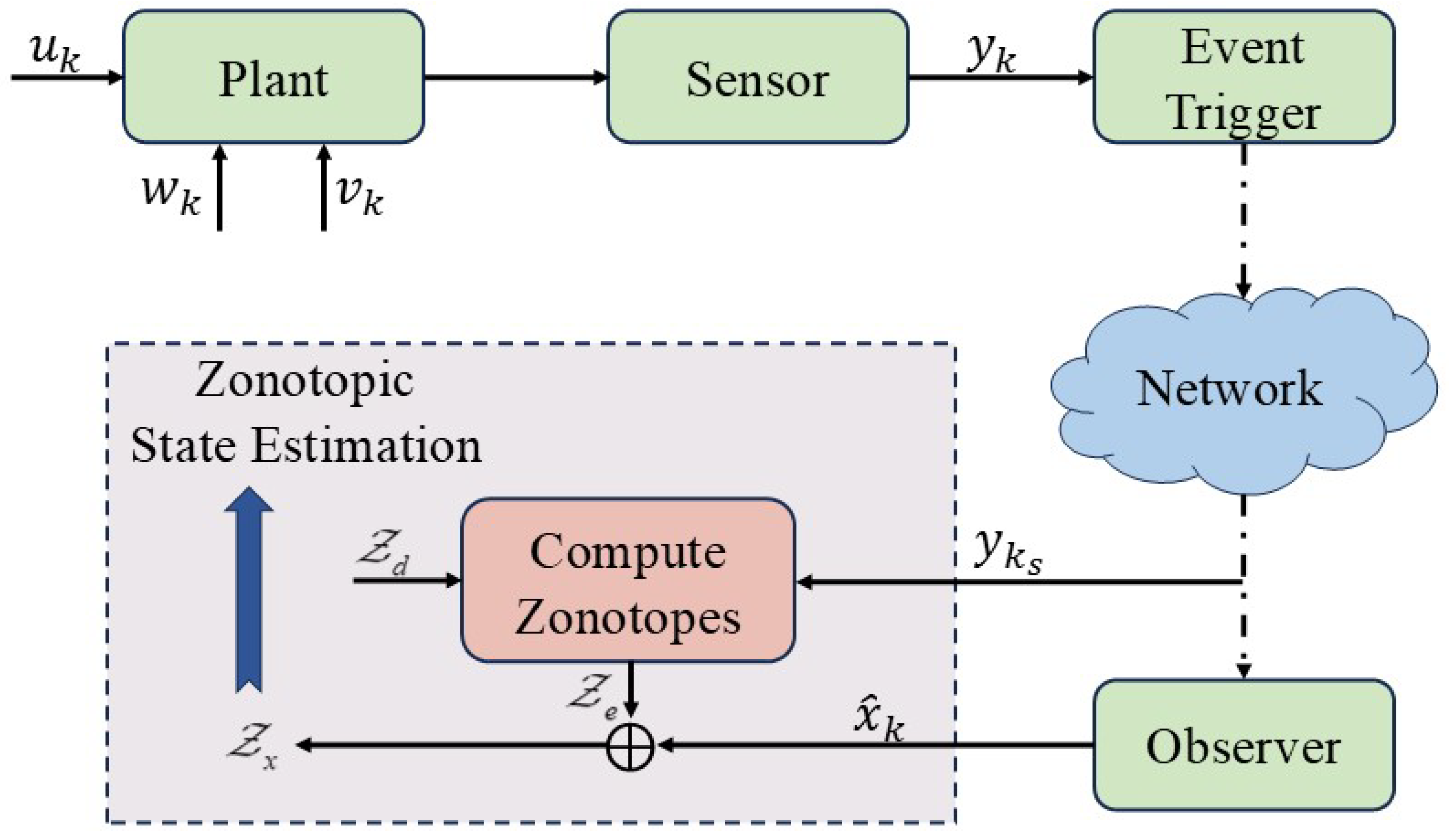
2.3. Adaptive Event-Triggered Observer
3. Zonotope-Based State Estimation
3.1. Observer Design
3.2. Zonotopic Set-Valued Estimation
| Algorithm 1: Order reduction procedure |
Input: generator matrix and ideal order r Process: If , set else if
|
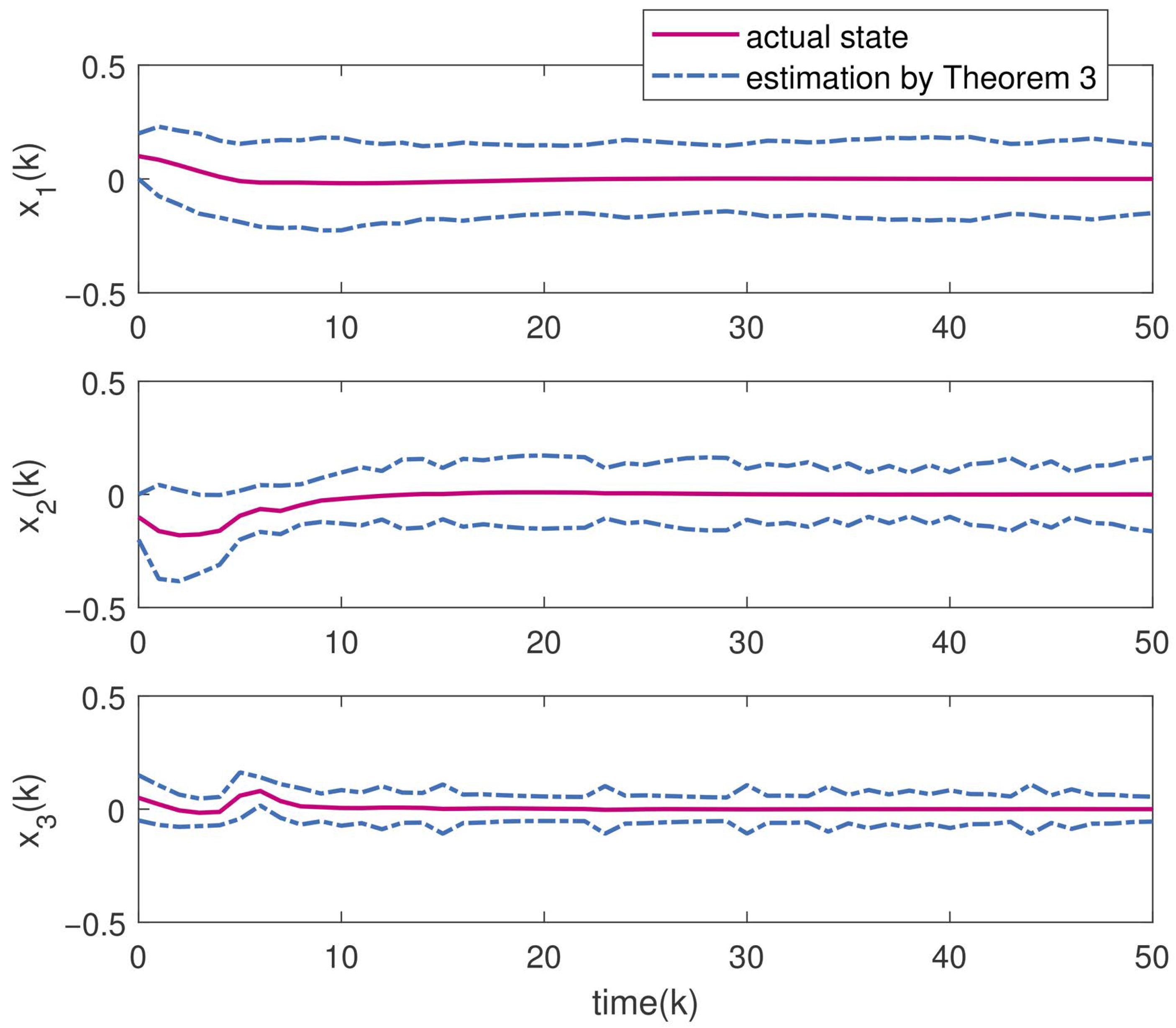
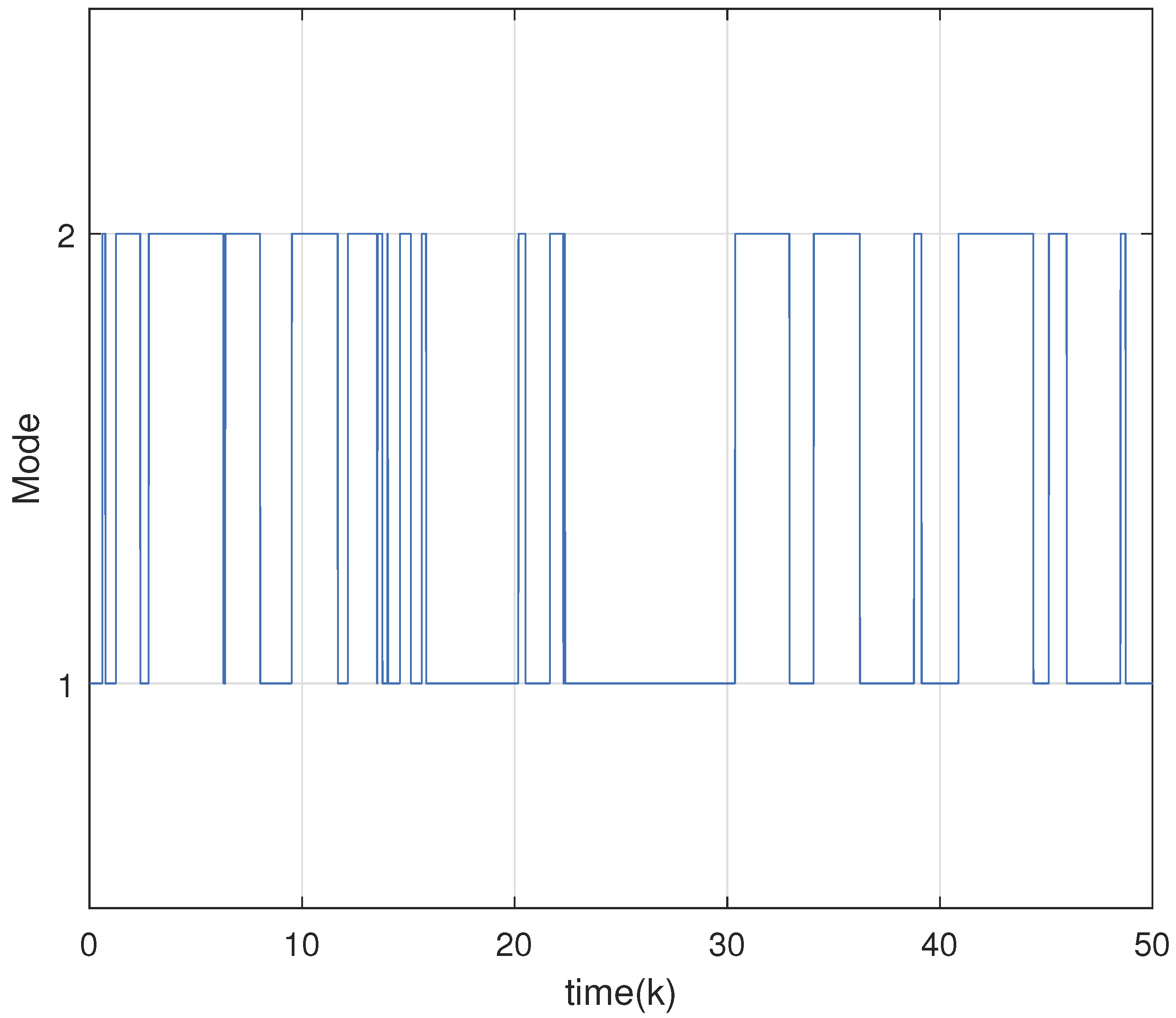
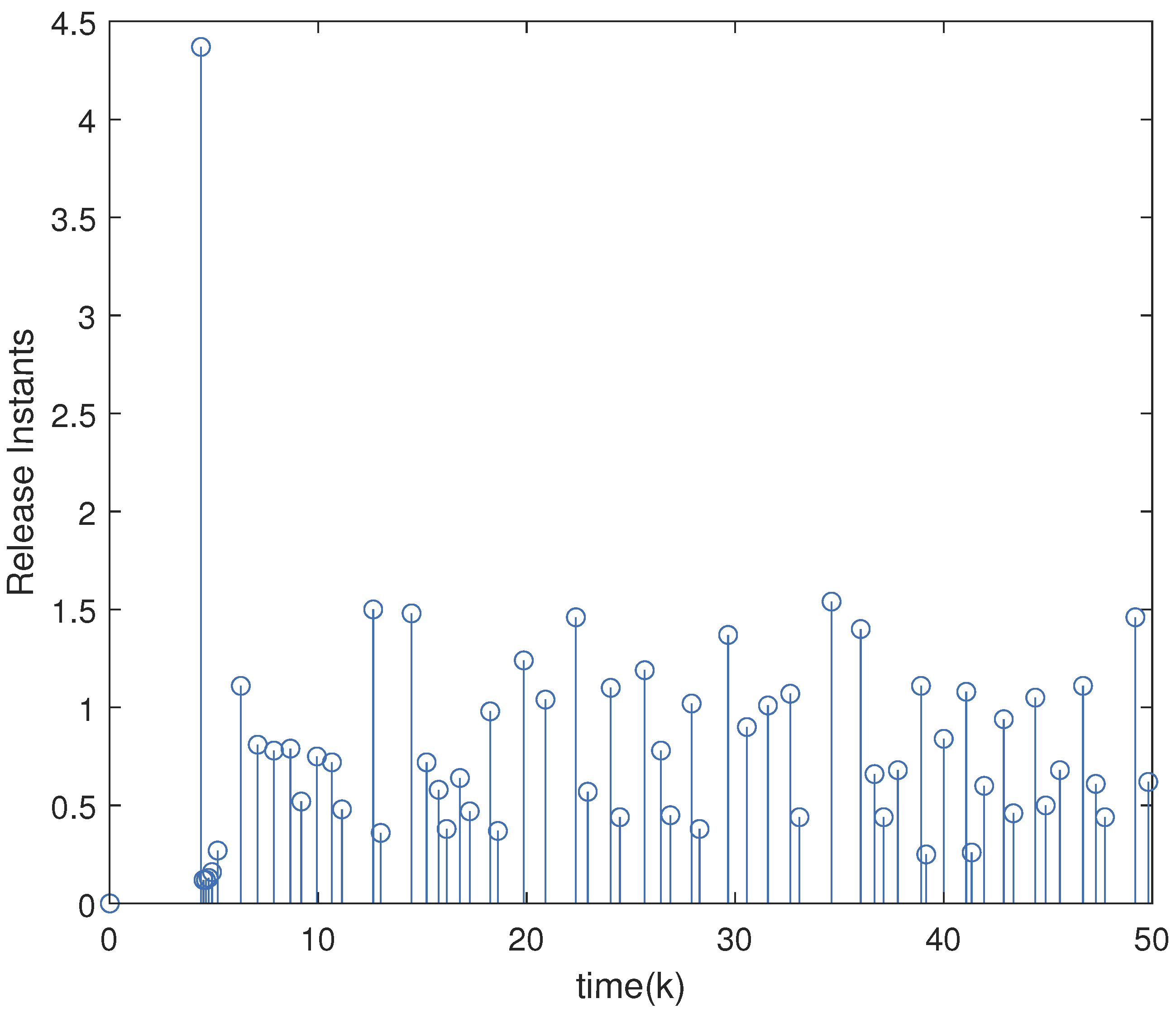
4. Numerical Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Salim, K.; Asif, M.; Ali, F.; Armghan, A.; Ullah, N.; Mohammad, A.S.; Al Ahmadi, A.A. Low-stress and optimum design of boost converter for renewable energy systems. Micromachines 2022, 13, 1085. [Google Scholar] [CrossRef]
- Talebi, P.; Packnezhad, M.; Farzanehfard, H. Single-switch high step-up Y-source-boost converter for renewable energy applications. IEEE Trans. Ind. Electron. 2024, 71, 14067–14074. [Google Scholar] [CrossRef]
- Qin, L.; Qian, T.; Soon, J.L.; Hassan, W.; Liu, Y.; Mao, J. Interleaved split-switched-capacitor boost converter with continuous output current for electric vehicle standalone photovoltaic charging systems. IEEE Trans. Power Electron. 2023, 38, 16165–16179. [Google Scholar] [CrossRef]
- Beltran, C.A.; Diaz-Saldierna, L.H.; Langarica-Cordoba, D.; Martinez-Rodriguez, P.R. Passivity-based control for output voltage regulation in a fuel cell/boost converter system. Micromachines 2023, 14, 187. [Google Scholar] [CrossRef] [PubMed]
- Naresh, S.V.K.; Shareef, H.; Kumar, B.; Peddapati, S. Family of capacitor-diode network extended high gain quadratic boost converters for microgrid applications. IEEE Trans. Power Electron. 2025, 40, 1418–1430. [Google Scholar] [CrossRef]
- Zhang, H.; Li, H.; Mao, J.; Pan, C.; Luan, Z. Model-free control of single-phase boost AC/DC converters. IEEE Trans. Power Electron. 2022, 37, 11828–11838. [Google Scholar] [CrossRef]
- Kalim, M.I.; Ali, A. Maximum sensitivity constrained graphical controller tuning for a DC-DC boost converter loaded with a CPL. IEEE Trans. Ind. Electron. 2024, 71, 2933–2941. [Google Scholar] [CrossRef]
- Cao, M.; Li, S.; Yang, J.; Zhang, K. Mismatched disturbance compensation enhanced robust H∞ control for the DC-DC boost converter feeding constant power loads. IEEE Trans. Energy Convers. 2023, 38, 1300–1310. [Google Scholar] [CrossRef]
- Lambe, A.; Sharma, S.N.; Patel, H.G. Carleman linearization approach for state estimation of stochastic boost converter with constant power load. In Proceedings of the 7th International Conference on Advances in Control and Optimization of Dynamical Systems (ACODS), Assam, India, 22–25 February 2022; pp. 807–812. [Google Scholar]
- Cao, C.; Zhao, Y. Distributed heterogenous multi-sensor fusion based on labeled random finite set for multi-target state estimation using information geometry. Signal Process. 2026, 238, 110135. [Google Scholar] [CrossRef]
- Jovicic, A.; Jereminov, M.; Pileggi, L.; Hug, G. Enhanced modelling framework for equivalent circuit-based power system state estimation. IEEE Trans. Power Electron. 2020, 35, 3790–3799. [Google Scholar] [CrossRef]
- Esfetanaj, N.N.; Wang, H.; Blaabjerg, F.; Davari, P. Differential mode noise estimation and filter design for interleaved boost power factor correction converters. Appl. Sci. 2021, 11, 2716. [Google Scholar] [CrossRef]
- Fei, Z.; Yang, L.; Sun, X.; Ren, S. Zonotopic set-membership state estimation for switched systems with restricted switching. IEEE Trans. Autom. Control 2022, 67, 6127–6134. [Google Scholar] [CrossRef]
- Tang, W.; Zhang, Q.; Wang, Z.; Shen, Y. Set-membership estimation based on ellipsoid bundles for discrete-time LPV descriptor systems. Automatica 2022, 145, 110580. [Google Scholar] [CrossRef]
- Fei, Z.; Chen, W.; Zhao, X. Interval estimation for asynchronously switched positive systems. Automatica 2022, 143, 110427. [Google Scholar] [CrossRef]
- Tang, W.; Wang, Z.; Wang, Y.; Raissi, T.; Shen, Y. Interval estimation methods for discrete-time linear time-invariant systems. IEEE Trans. Autom. Control 2019, 64, 4717–4724. [Google Scholar] [CrossRef]
- Zhu, Y.; Fang, X.; Li, C. Multi-sensor information fusion for mobile robot indoor-outdoor localization: A zonotopic set-membership estimation approach. Electronics 2025, 14, 867. [Google Scholar] [CrossRef]
- Li, Q.; Zhi, Y.; Tan, H.; Sheng, W. Protocol-based zonotopic state and fault estimation for communication-constrained industrial cyber-physical systems. Inf. Sci. 2023, 634, 730–743. [Google Scholar] [CrossRef]
- Li, J.; Liu, Y.; Jiang, Y.; Wang, Z.; Li, Y. Fault detection for autonomous underwater vehicles based on zonotopic set-membership estimation. IEEE Trans. Ind. Inform. 2025. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, Z.; Zou, L.; Chen, Y.; Sheng, W. Zonotopic non-fragile set-membership fusion estimation for nonlinear systems under sensor resolution effects: Boundedness and monotonicity. Inf. Fusion 2024, 105, 102232. [Google Scholar] [CrossRef]
- Li, J.; Wang, Y.; Liu, X.; Yao, F.; Zhang, M. Zonotopic resilient state estimation for unmanned surface vehicles subject to integrity attacks. Ocean Eng. 2023, 273, 113934. [Google Scholar] [CrossRef]
- Zhou, M.; Wu, Y.; Wang, J.; Xue, T.; Raissi, T. Zonotopic state estimation and sensor fault detection for a wastewater treatment bioprocess. Int. J. Robust Nonlinear Control 2024, 34, 9298–9315. [Google Scholar] [CrossRef]
- Luo, W.; Chen, H.; Zong, G.; Zhao, X.; Wang, W. Probabilistic event-triggered H∞ control of Markov jump cyber-physical systems under hybrid cyber-attacks. Nonlinear Dyn. 2025, 113, 18381–18397. [Google Scholar] [CrossRef]
- Sun, W.; Zhou, J.; Sun, B.; Zhou, Y.; Jiang, Y. Markov transition field enhanced deep domain adaptation network for milling tool condition monitoring. Micromachines 2022, 13, 873. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Ni, Z.; Wang, J.; Park, J.H.; Shen, H. Asynchronous reduced-order filtering for Markov jump systems and its application in PWM circuits. IEEE Trans. Circuits Syst. II Exp. Briefs 2025, 72, 598–602. [Google Scholar] [CrossRef]
- Bueno, J.N.A.D.; Marcos, L.B.; Rocha, K.D.T.; Terra, M.H. Regulation of uncertain Markov jump linear systems with application on automotive powertrain control. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 5019–5031. [Google Scholar] [CrossRef]
- Song, X.; Sun, P.; Song, S.; Stojanovic, V. Saturated-threshold event-triggered adaptive global prescribed performance control for nonlinear Markov jumping systems and application to a chemical reactor model. Expert Syst. Appl. 2024, 249, 123490. [Google Scholar] [CrossRef]
- Jiang, B.; Karimi, H.R.; Yang, S.; Gao, C.; Kao, Y. Observer-based adaptive sliding mode control for nonlinear stochastic Markov jump systems via T-S fuzzy modeling: Applications to robot arm model. IEEE Trans. Ind. Electron. 2021, 68, 466–477. [Google Scholar] [CrossRef]
- Shiau, J.K.; Ma, C.W. Li-ion battery charging with a buck-boost power converter for a solar powered battery management system. Energies 2013, 6, 1669–1699. [Google Scholar] [CrossRef]
- Qi, W.; Zong, G.; Zheng, W.X. Adaptive event-triggered SMC for stochastic switching systems with semi-Markov process and application to boost converter circuit model. IEEE Trans. Circuits Syst. I Reg. Papers 2021, 68, 786–796. [Google Scholar] [CrossRef]
- Shen, H.; Wu, J.; Wang, Y.; Wang, J. Reinforcement learning-based robust tracking control for unknown Markov jump systems and its application. IEEE Trans. Circuits Syst. II Exp. Briefs 2024, 71, 1211–1215. [Google Scholar] [CrossRef]
- Alamo, T.; Bravo, J.M.; Camacho, E.F. Guaranteed state estimation by zonotopes. Automatica 2005, 41, 1035–1043. [Google Scholar] [CrossRef]
- Sakthivel, R.; Nithya, V.; Suveetha, V.T. Resilient finite-time fault detection dissipative-based filter for semi-Markovian jump systems with incomplete measurements. Int. J. Robust Nonlinear Control 2022, 36, 1216–1230. [Google Scholar] [CrossRef]
- Efimov, D.; Raissi, T. Design of interval observers for uncertain dynamical systems. Autom. Remote Control 2016, 77, 191–225. [Google Scholar] [CrossRef]
| Symbols | Meanings |
|---|---|
| Euclidean norm of matrix X | |
| Transpose of matrix X | |
| Matrix X is positive (negative) definite | |
| * | Wntry induced by symmetric matrix |
| ⊕ | Minkowski sum |
| ⊙ | Linear image operator |
| Mathematical expectation operator | |
| Block diagonal matrix | |
| Positive integer set |
| Methods | Widths |
|---|---|
| by Theorem 3 | |
| by [34] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guan, C.; Li, Y.; Wang, Z.; Chen, W. Zonotope-Based State Estimation for Boost Converter System with Markov Jump Process. Micromachines 2025, 16, 1099. https://doi.org/10.3390/mi16101099
Guan C, Li Y, Wang Z, Chen W. Zonotope-Based State Estimation for Boost Converter System with Markov Jump Process. Micromachines. 2025; 16(10):1099. https://doi.org/10.3390/mi16101099
Chicago/Turabian StyleGuan, Chaoxu, You Li, Zhenyu Wang, and Weizhong Chen. 2025. "Zonotope-Based State Estimation for Boost Converter System with Markov Jump Process" Micromachines 16, no. 10: 1099. https://doi.org/10.3390/mi16101099
APA StyleGuan, C., Li, Y., Wang, Z., & Chen, W. (2025). Zonotope-Based State Estimation for Boost Converter System with Markov Jump Process. Micromachines, 16(10), 1099. https://doi.org/10.3390/mi16101099






