Optimal Design and Analysis of Wide-Band Near-Infrared Hybrid Dielectric Gratings with High Transmission Efficiency
Abstract
1. Introduction
2. Optimal Multilayer Dielectric Design in Grating Grooves
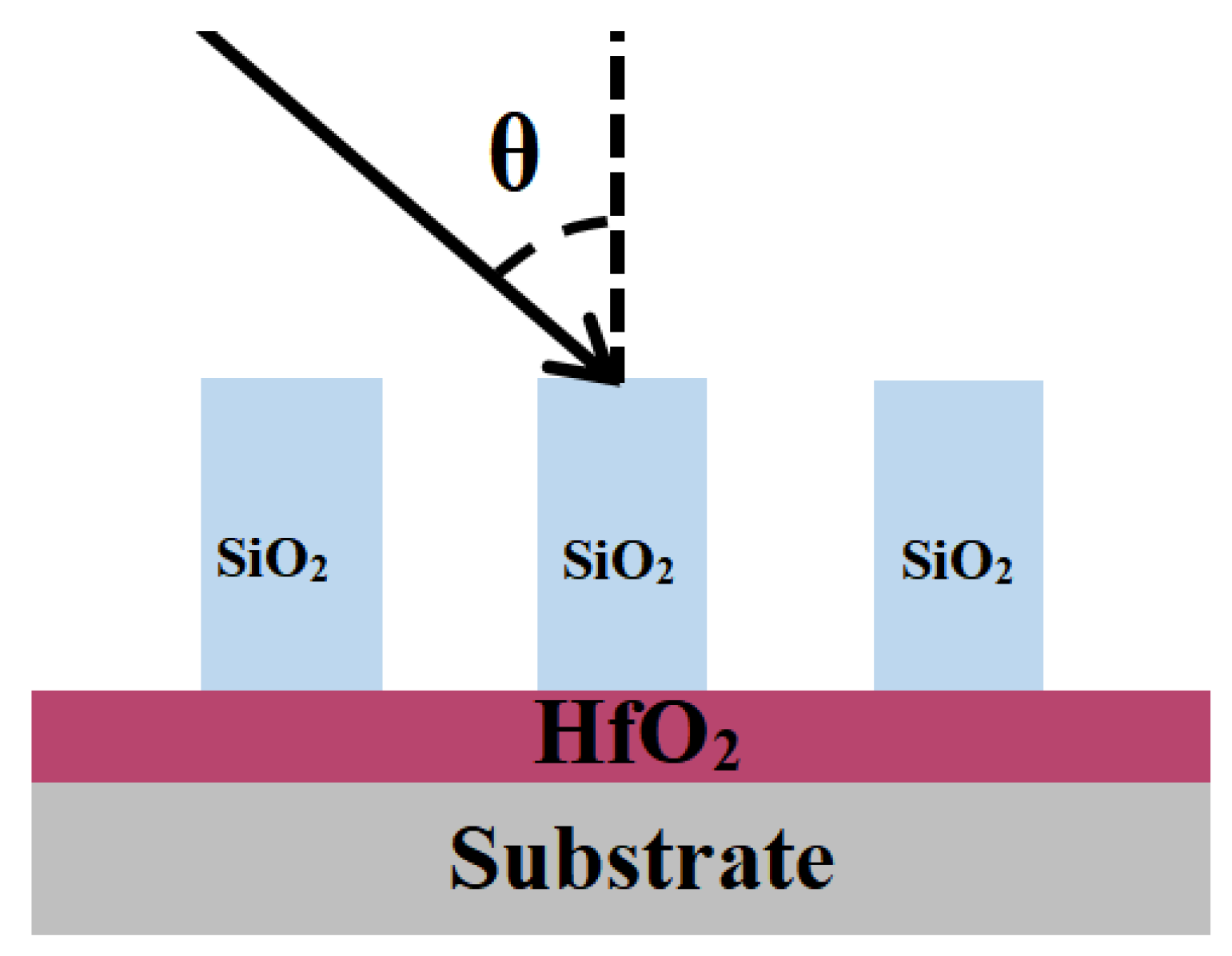
2.1. Transmission Grating Based on Pure Fused Silica and Si3N4 Grating
2.2. Using HfO2 Filled Instead of Pure SiO2 for the Grating
2.2.1. The Effect of Groove Depth
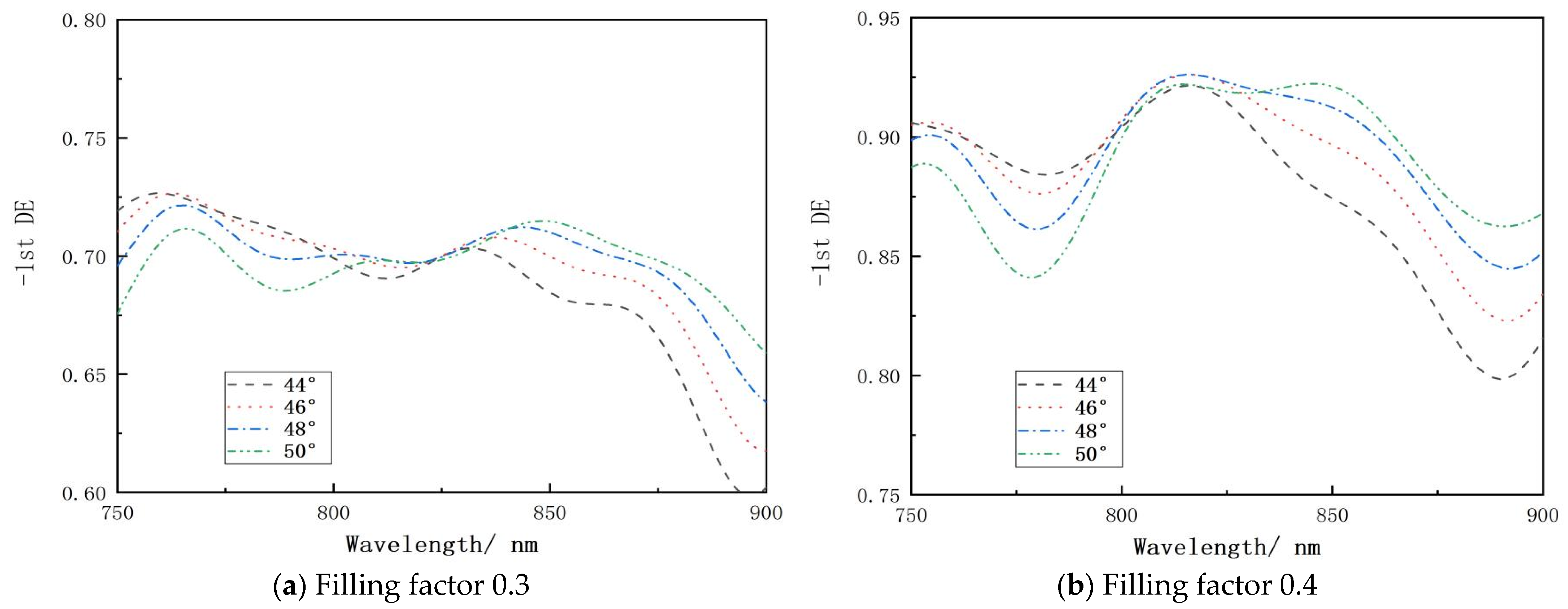
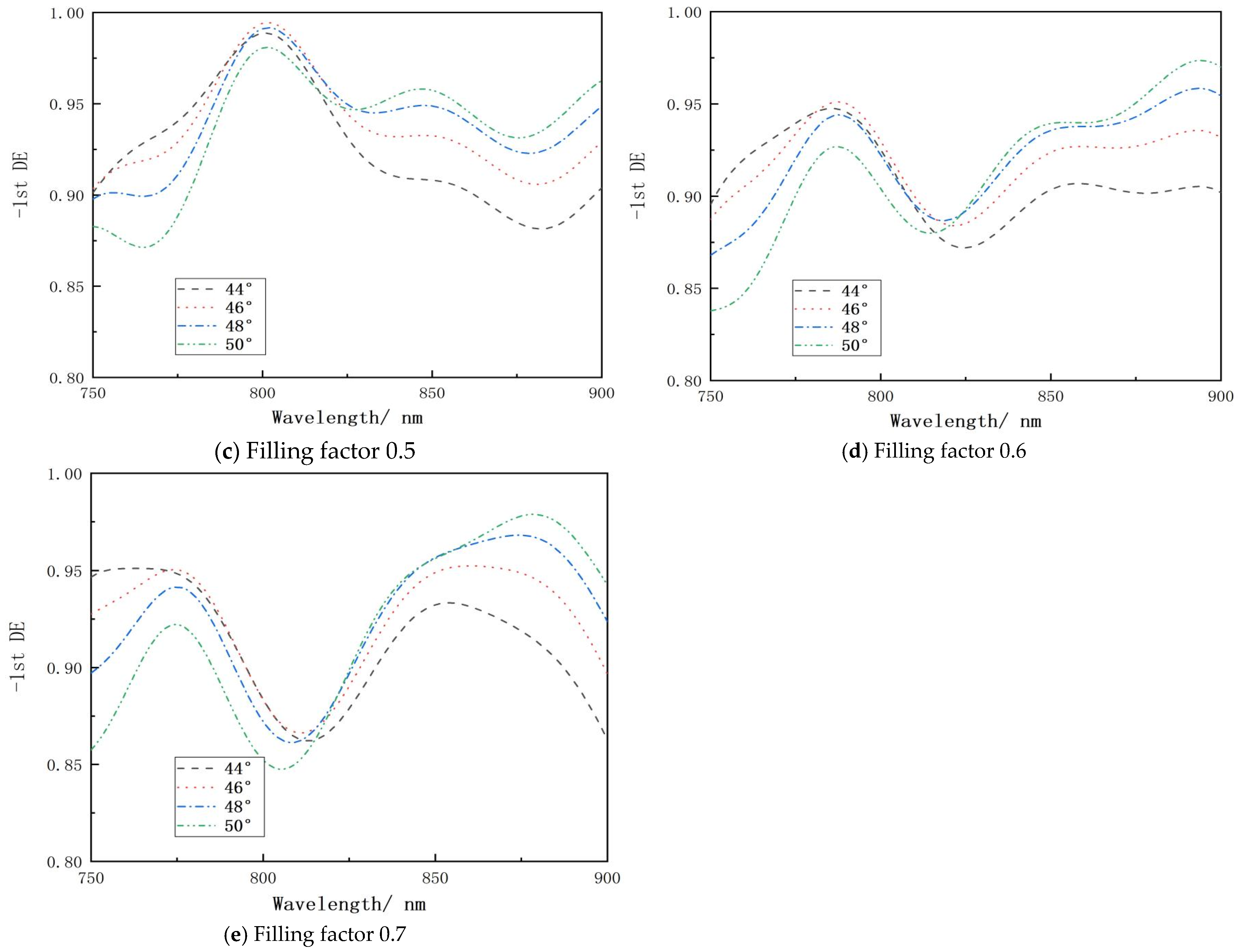
2.2.2. The Effect of Incidence Angle
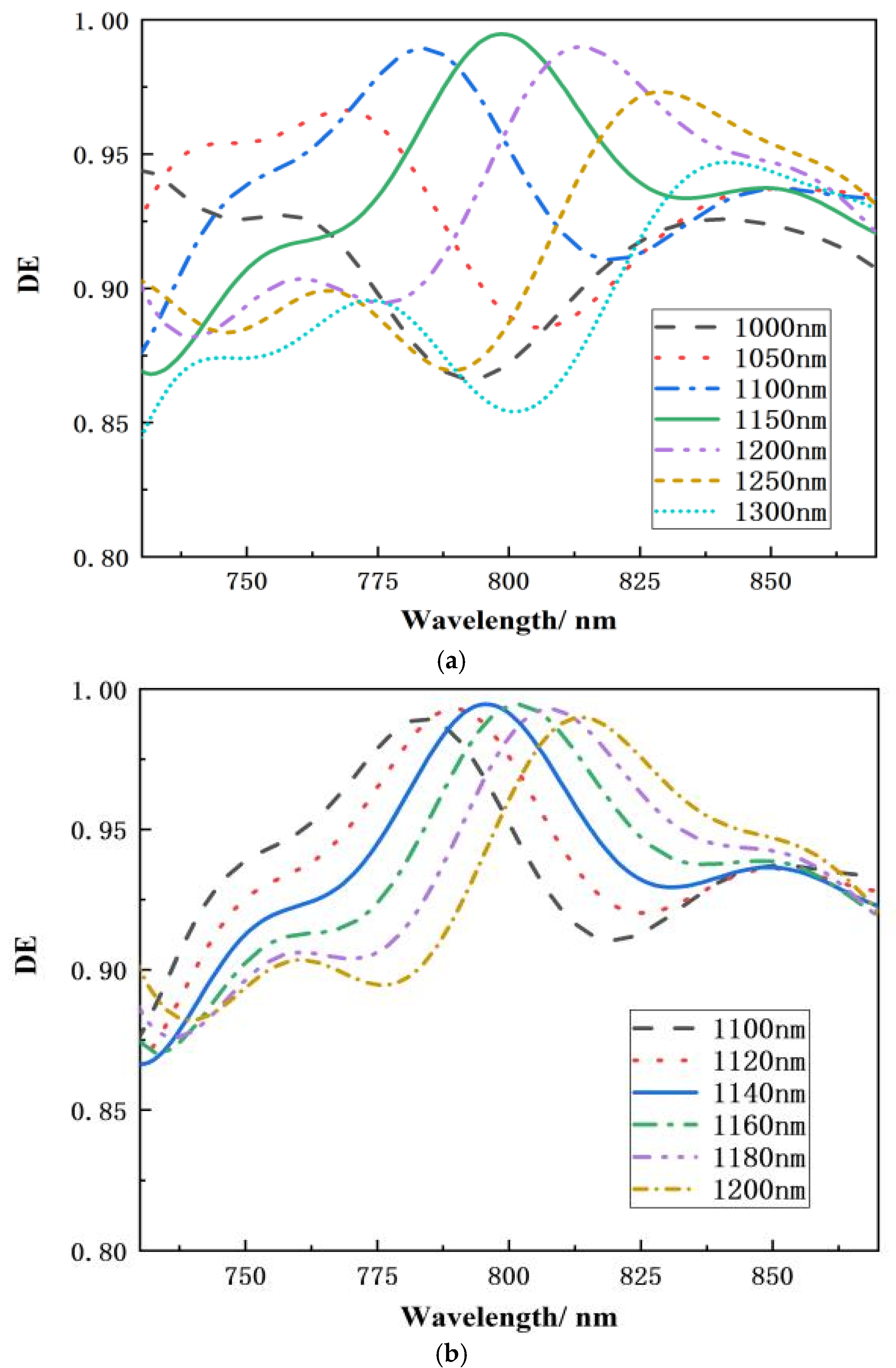
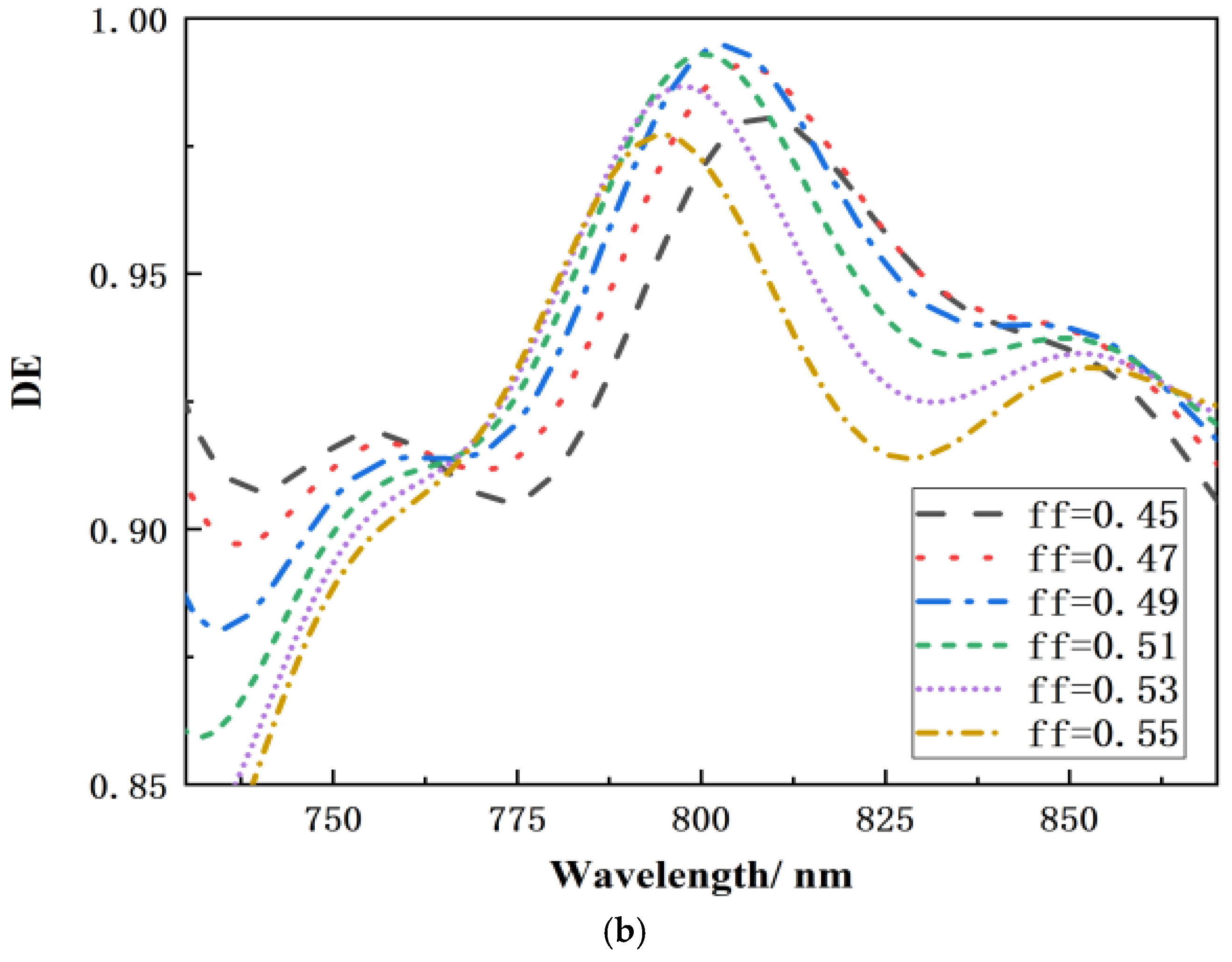
2.2.3. The Effect of Duty Cycle
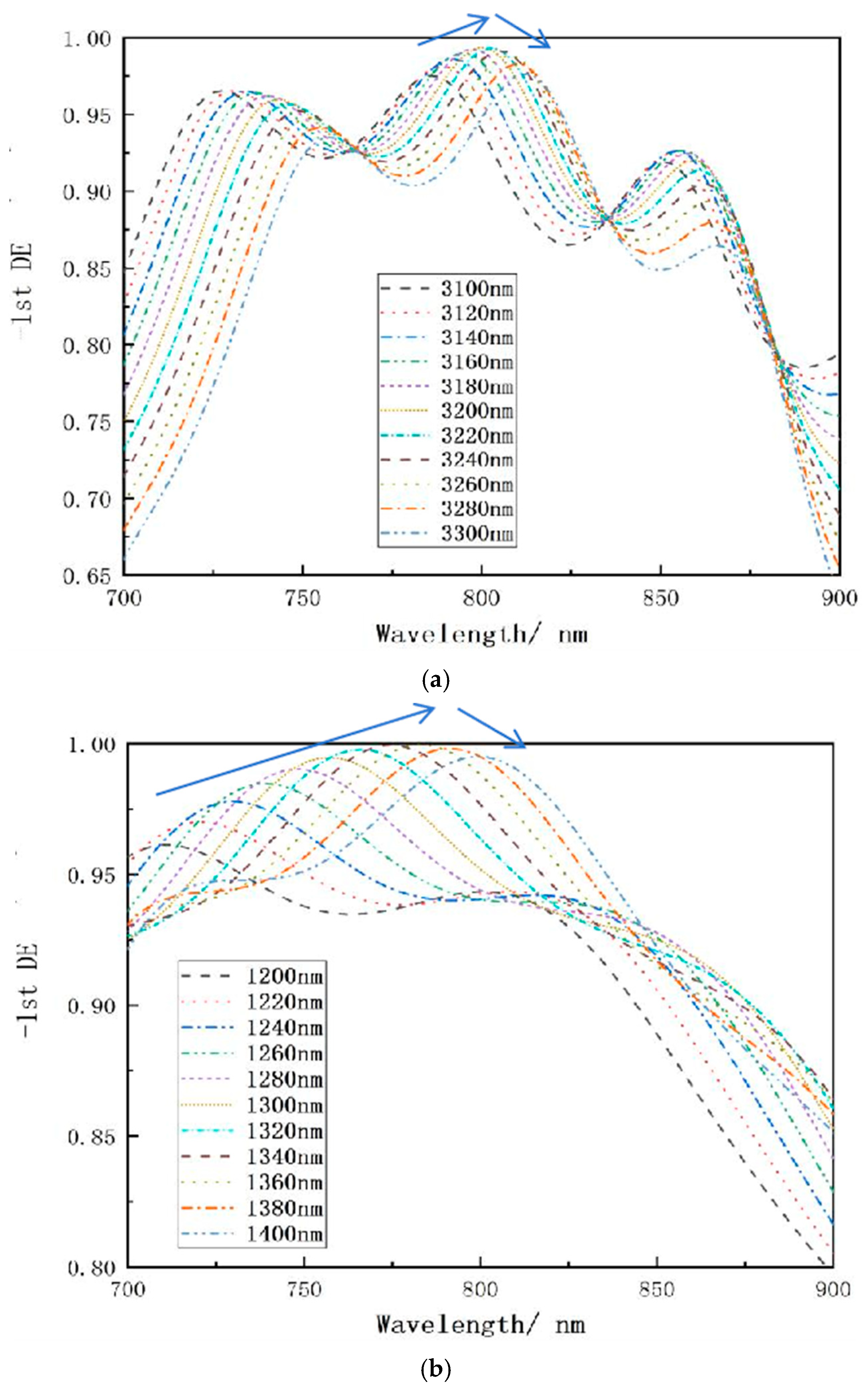
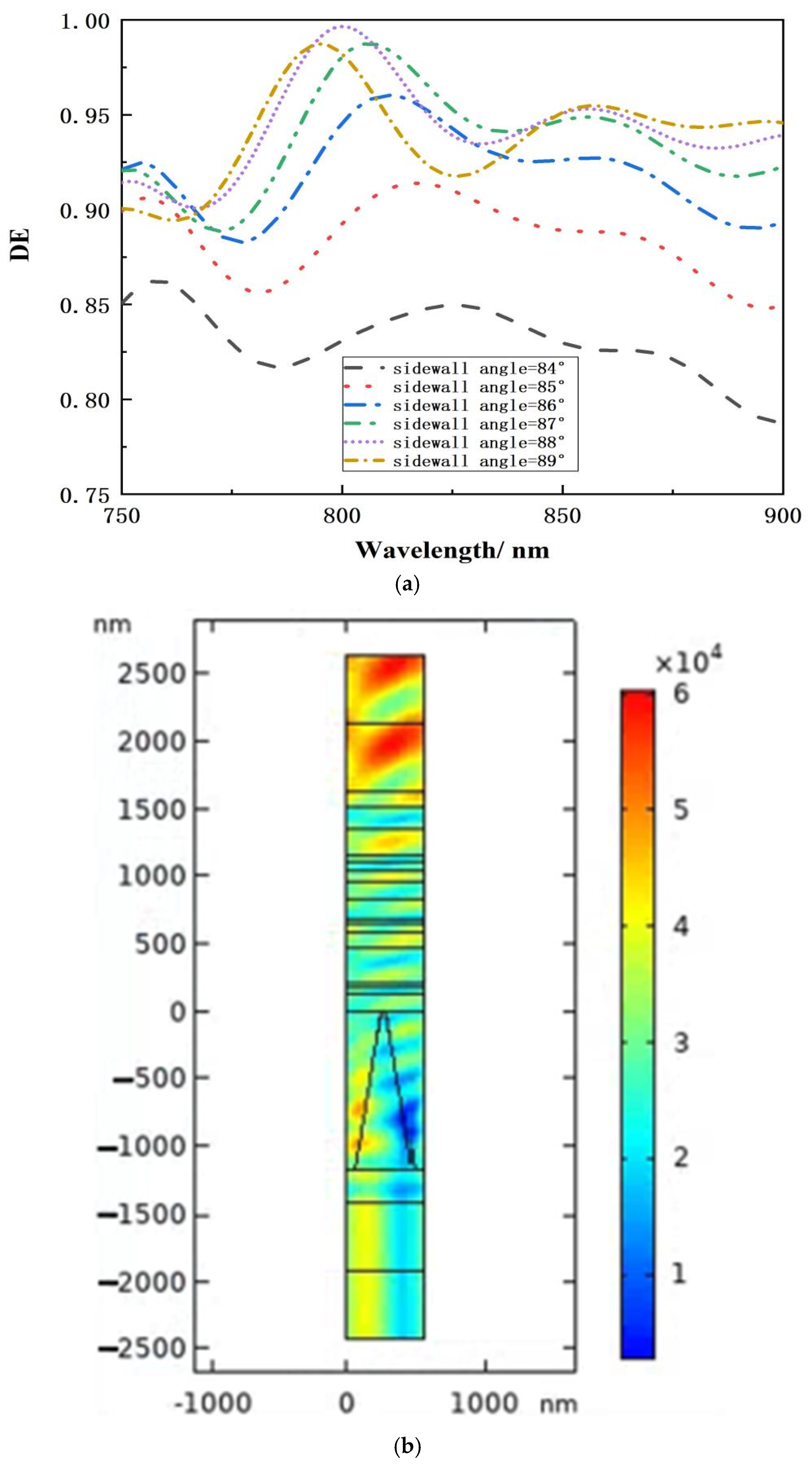
2.2.4. The Effect of Sidewall Inclination
2.3. Anti-Reflective Coating Design
3. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Niu, S.; Aierken, P.; Ababaike, M.; Wang, S.; Yusufu, T. Widely tunable, high-energy, mid-infrared (2.2–4.8 m) laser based on a multi-grating MgO: PPLN optical parametric oscillator. Infrared Phys. Technol. 2020, 104, 103121. [Google Scholar] [CrossRef]
- Zhang, J.; Peng, H.; Wang, J.; Zhang, J.; Qin, L.; Ning, Y.; Wang, L. Dense spectral beam combining of quantum cascade lasers by multiplexing a pair of blazed gratings. Opt. Express 2022, 30, 966. [Google Scholar] [CrossRef] [PubMed]
- Gu, Z.; Zhang, J.; Zhai, S.; Zhuo, N.; Liu, S.; Liu, J.; Wang, L.; Liu, F.; Wang, Z. Spectral beam combining of discrete quantum cascade lasers. Opt. Quantum Electron. 2021, 53, 584. [Google Scholar] [CrossRef]
- Gallais, L.; Mangote, B.; Zerrad, M.; Commandré, M.; Melninkaitis, A.; Mirauskas, J.; Jeskevic, M.; Sirutkaitis, V. Laser-induced damage of hafnia coatings as a function of pulse duration in the femtosecond to nanosecond range. Appl. Opt. 2011, 50, C178–C187. [Google Scholar] [CrossRef] [PubMed]
- Available online: www.gitterwerk.com (accessed on 28 May 2024).
- Canova, F.; Uteza, O.; Chambaret, J.-P.; Flury, M.; Tonchev, S.; Fechner, R.; Parriaux, O. High-efficiency, broad band, high-damage threshold high-index gratings for femtosecond pulse compression. Opt. Express 2007, 15, 15324–15334. [Google Scholar] [CrossRef] [PubMed]
- Guan, H.; Jin, Y.; Liu, S.; Kong, F.; Du, Y.; He, K.; Yi, K.; Shao, J. Broadband trapeziform multilayer dielectric grating for femtosecond pulse compressor: Design, fabrication, and analysis. Laser Phys. 2013, 23, 115301. [Google Scholar] [CrossRef]
- Proust, J.; Fehrembach, A.-L.; Bedu, F.; Ozerov, I.; Bonod, N. Optimized 2D array of thin silicon pillars for efficient antireflective coatings in the visible spectrum. Sci. Rep. 2016, 6, 24947. [Google Scholar] [CrossRef] [PubMed]
- Michine, Y.; Yoneda, H. Ultra high damage threshold optics for high power lasers. Commun. Phys. 2020, 3, 24. [Google Scholar] [CrossRef]
- Lohithakshan, L.C.; Kannan, P. Realisation of optical filters using multi-layered thin film coatings by transfer matrix model simulations. Mater. Today Proc. 2022, 66, 1671–1677. [Google Scholar] [CrossRef]
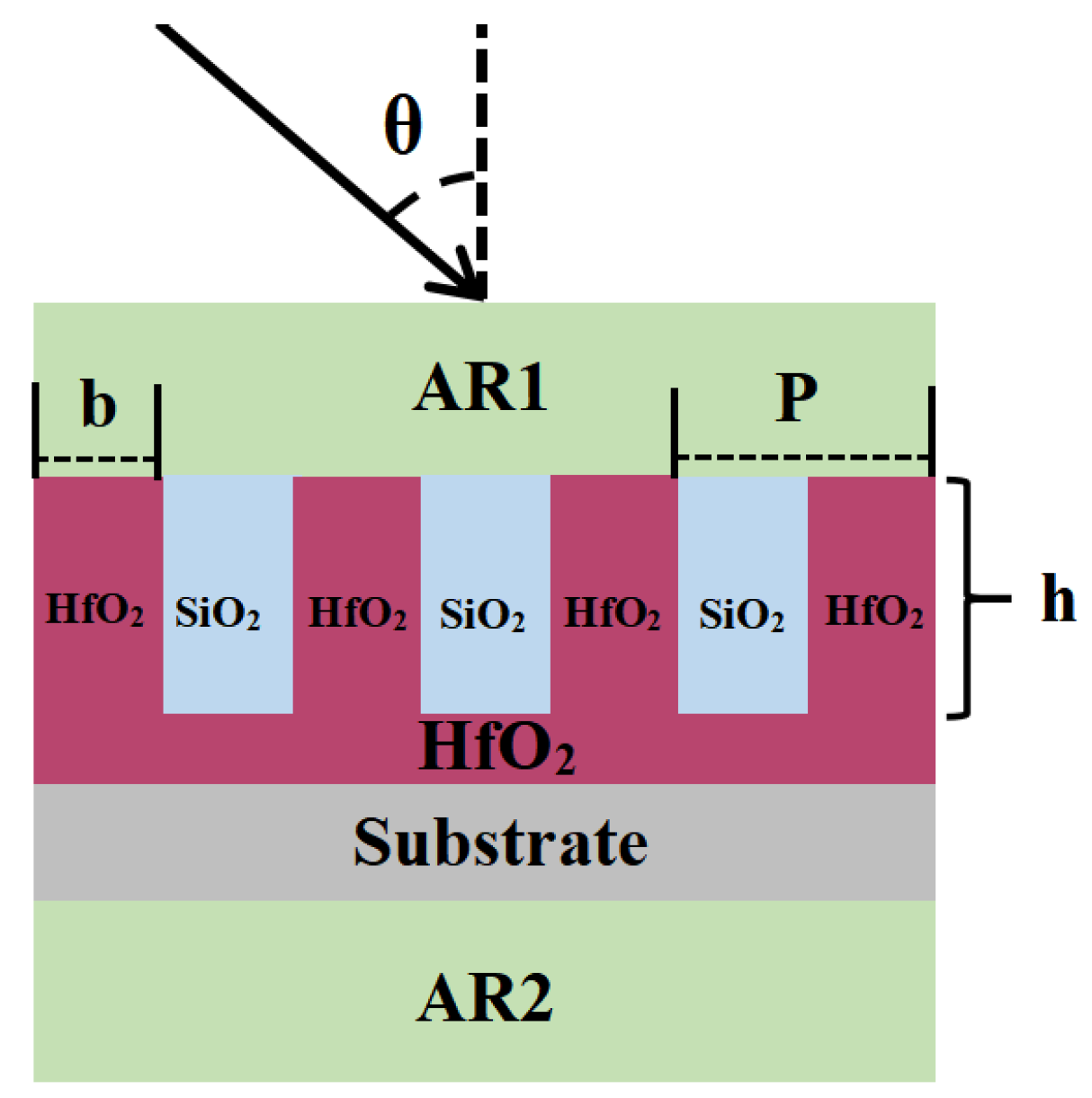

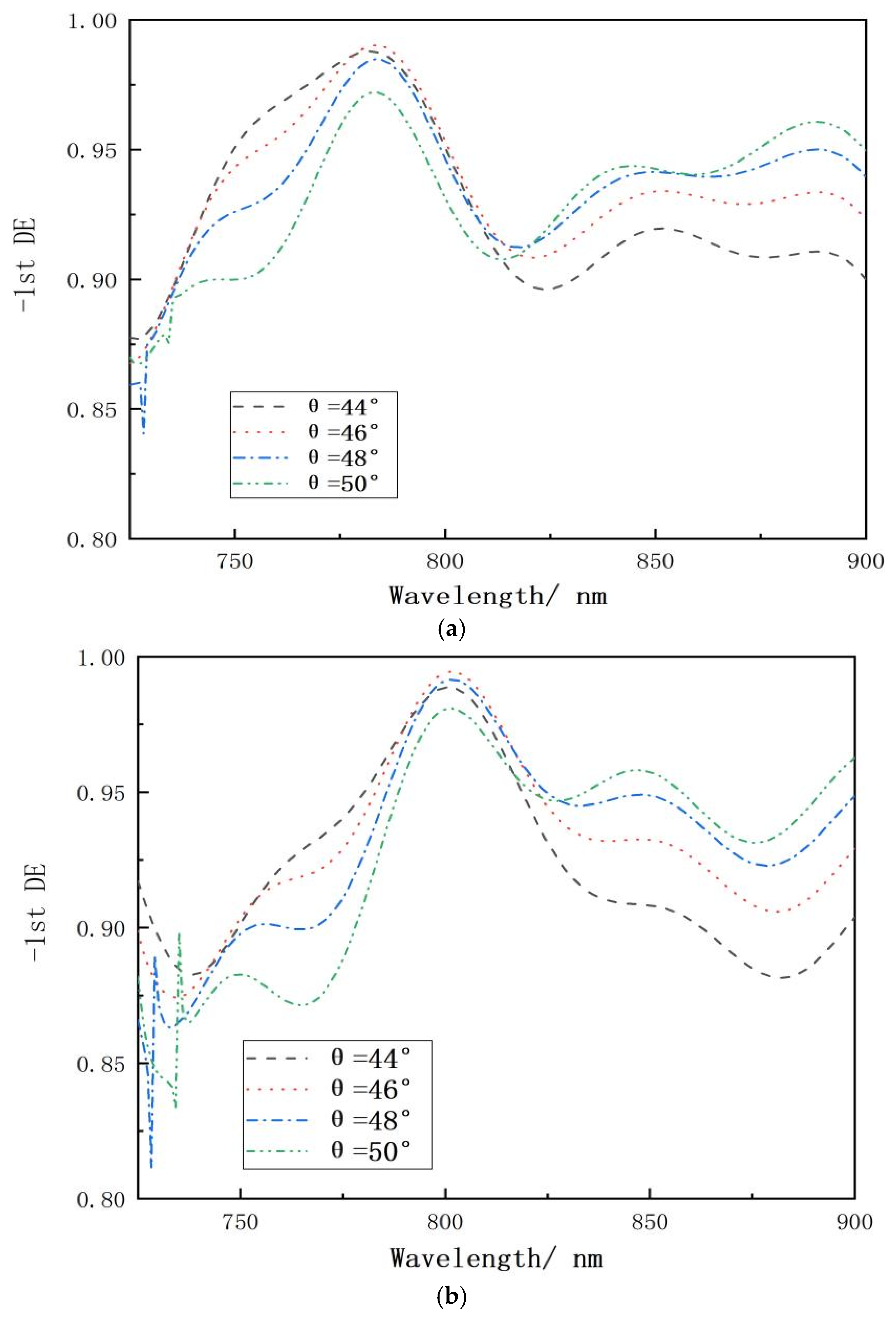
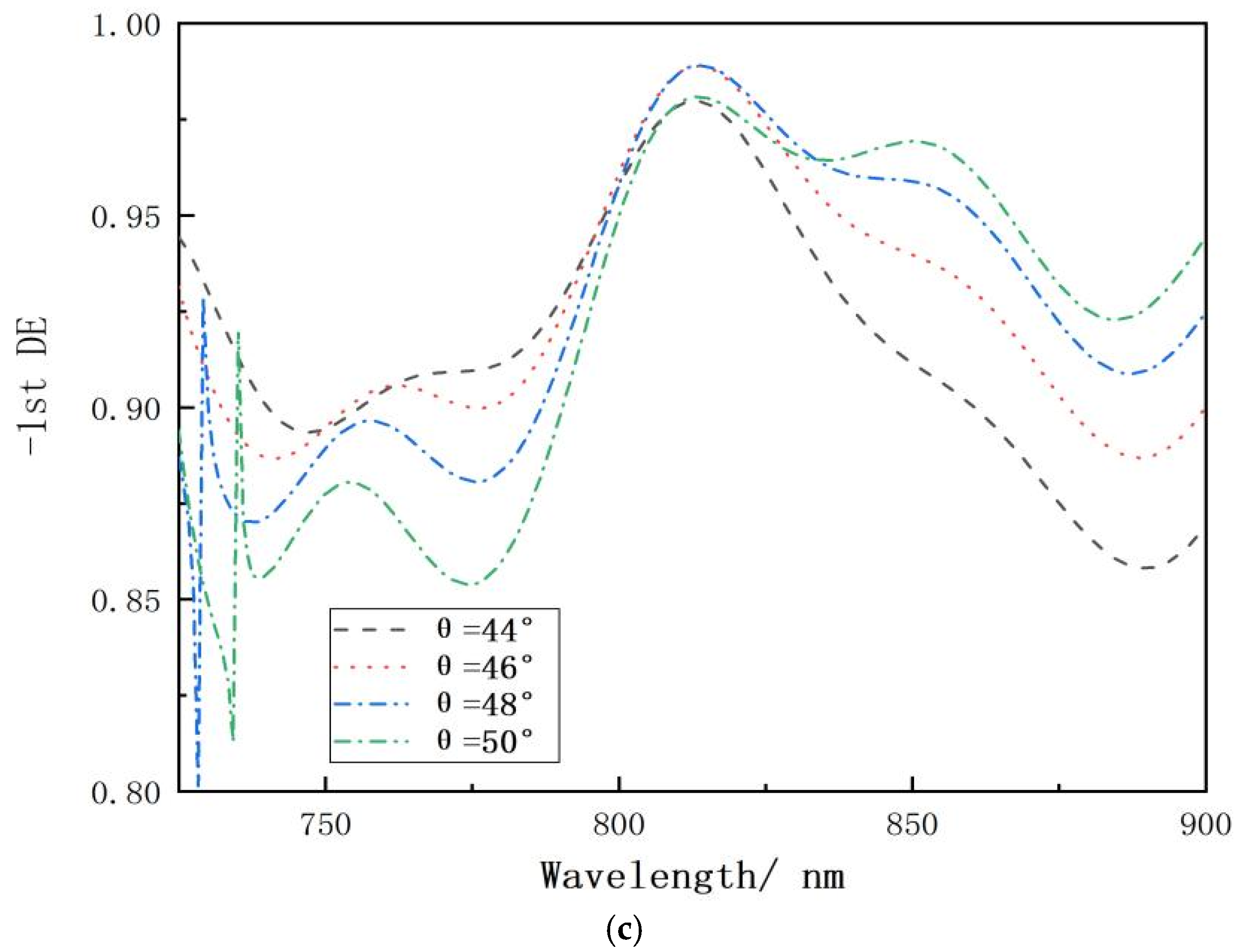

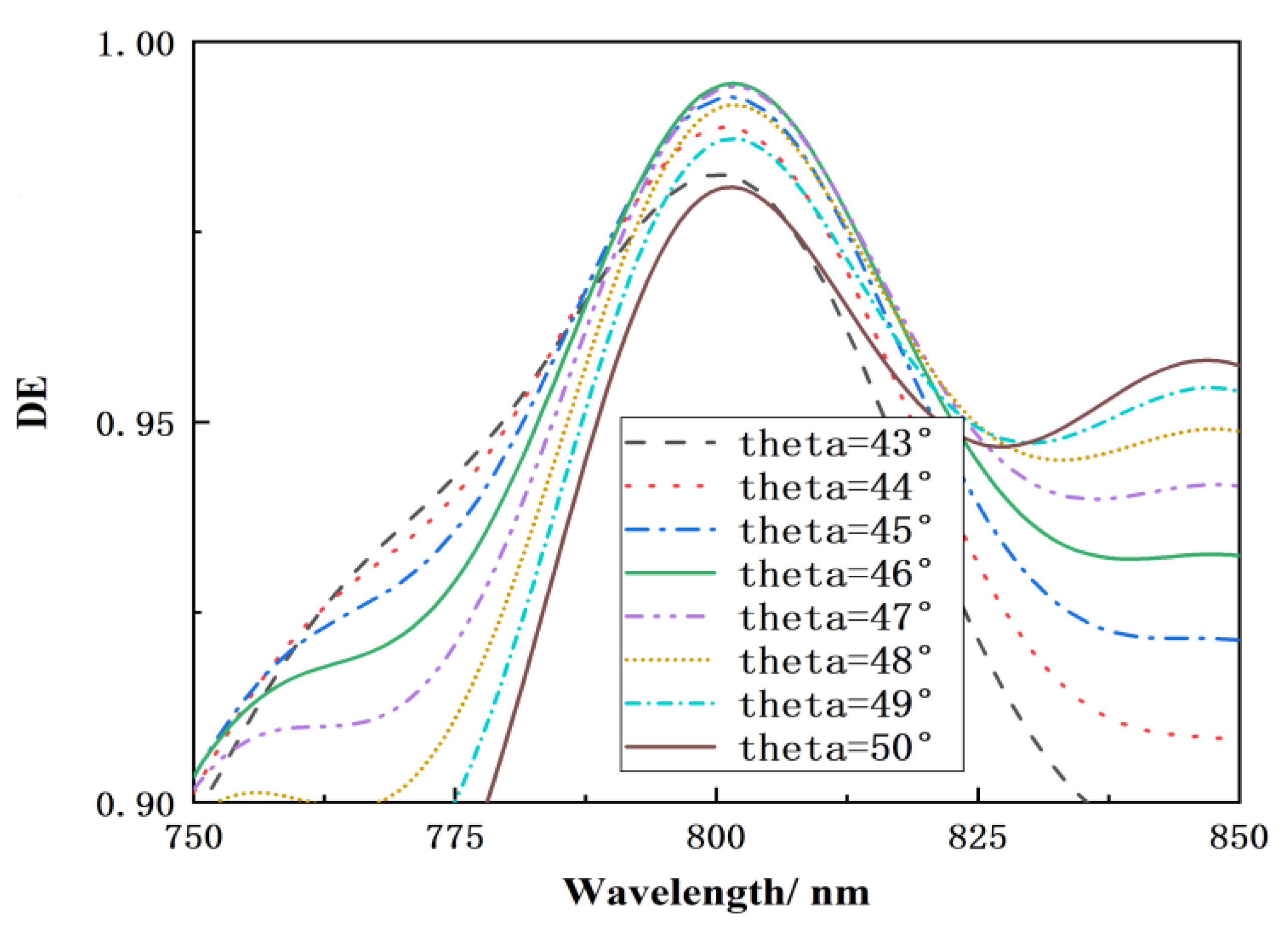
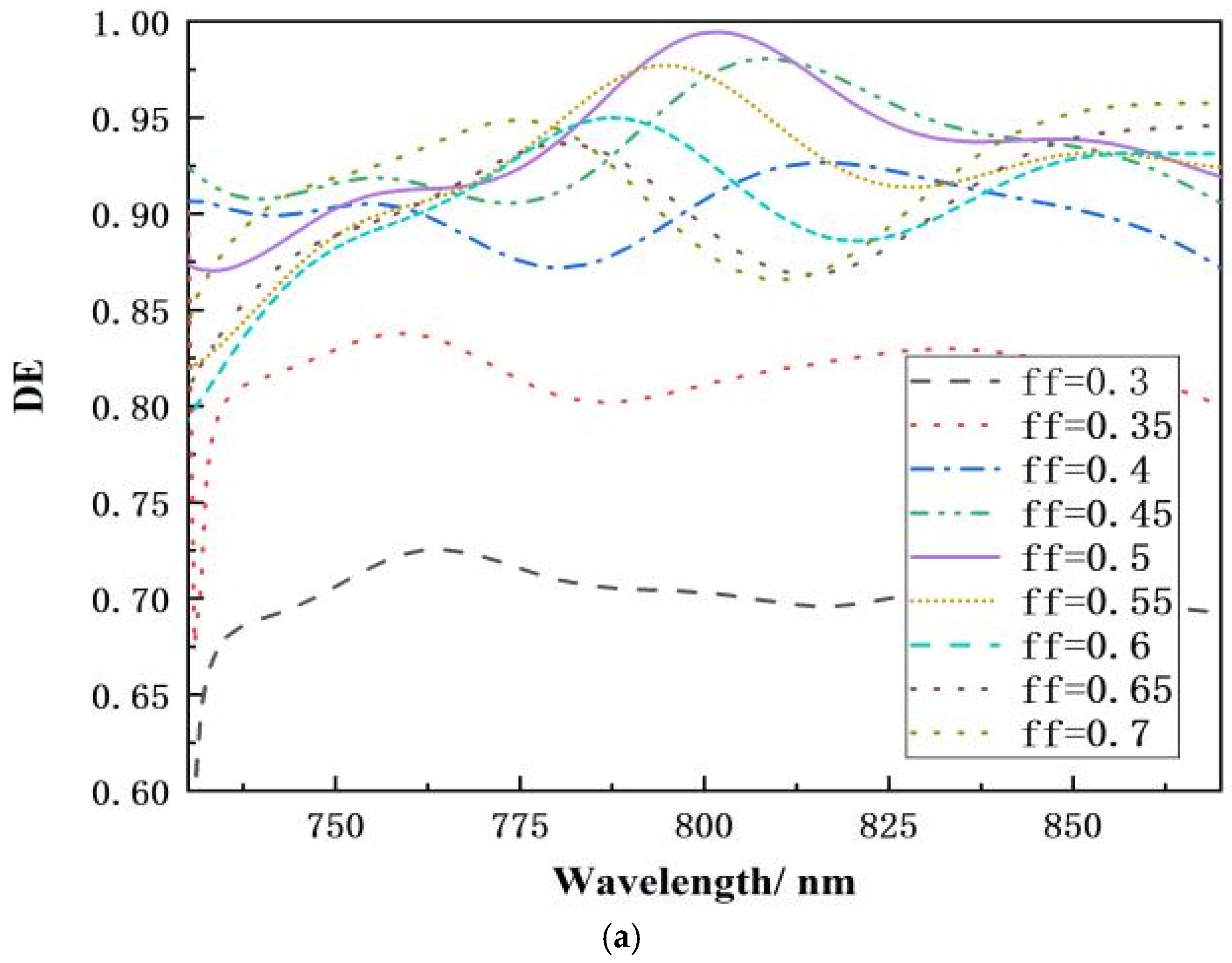
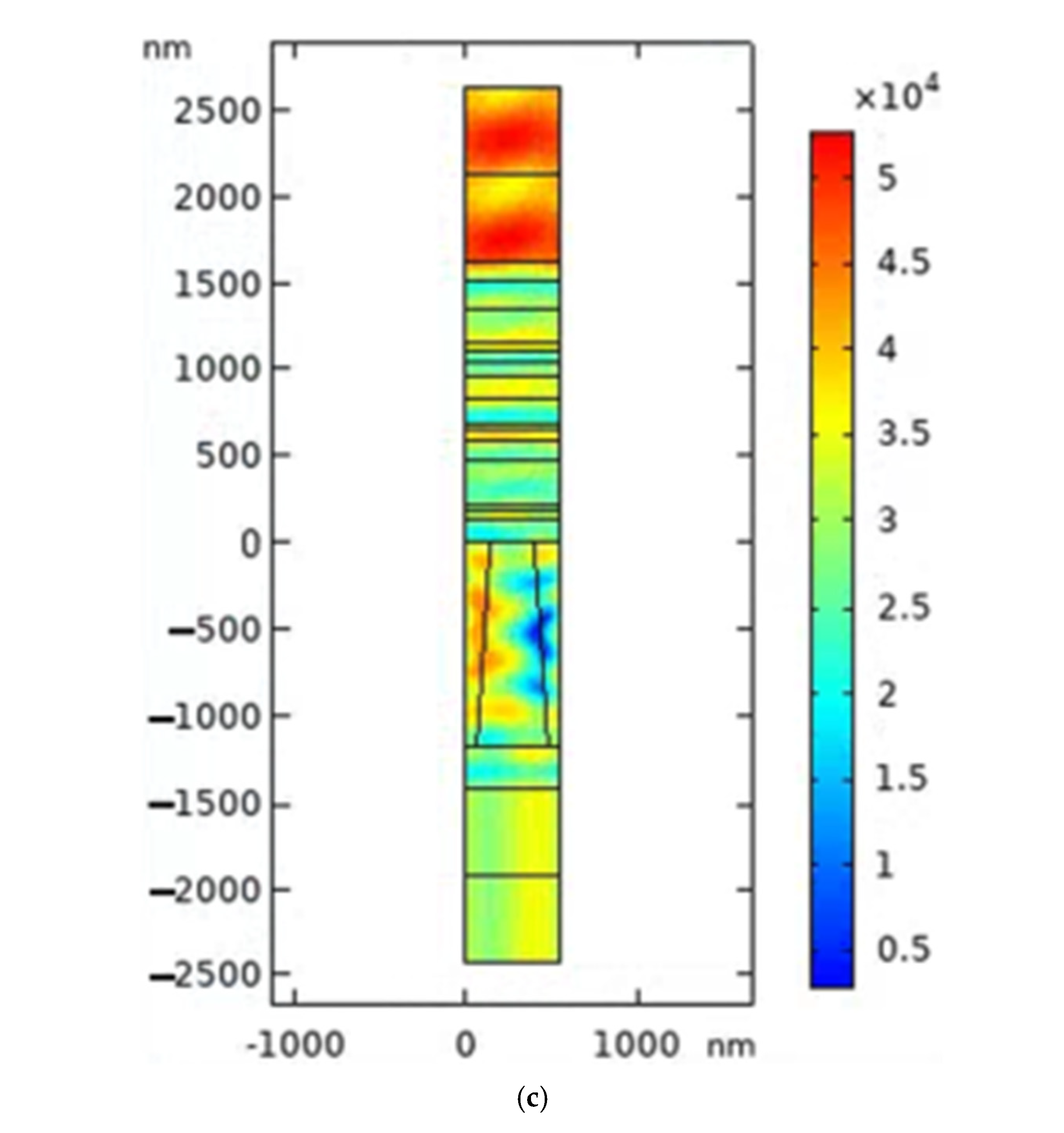
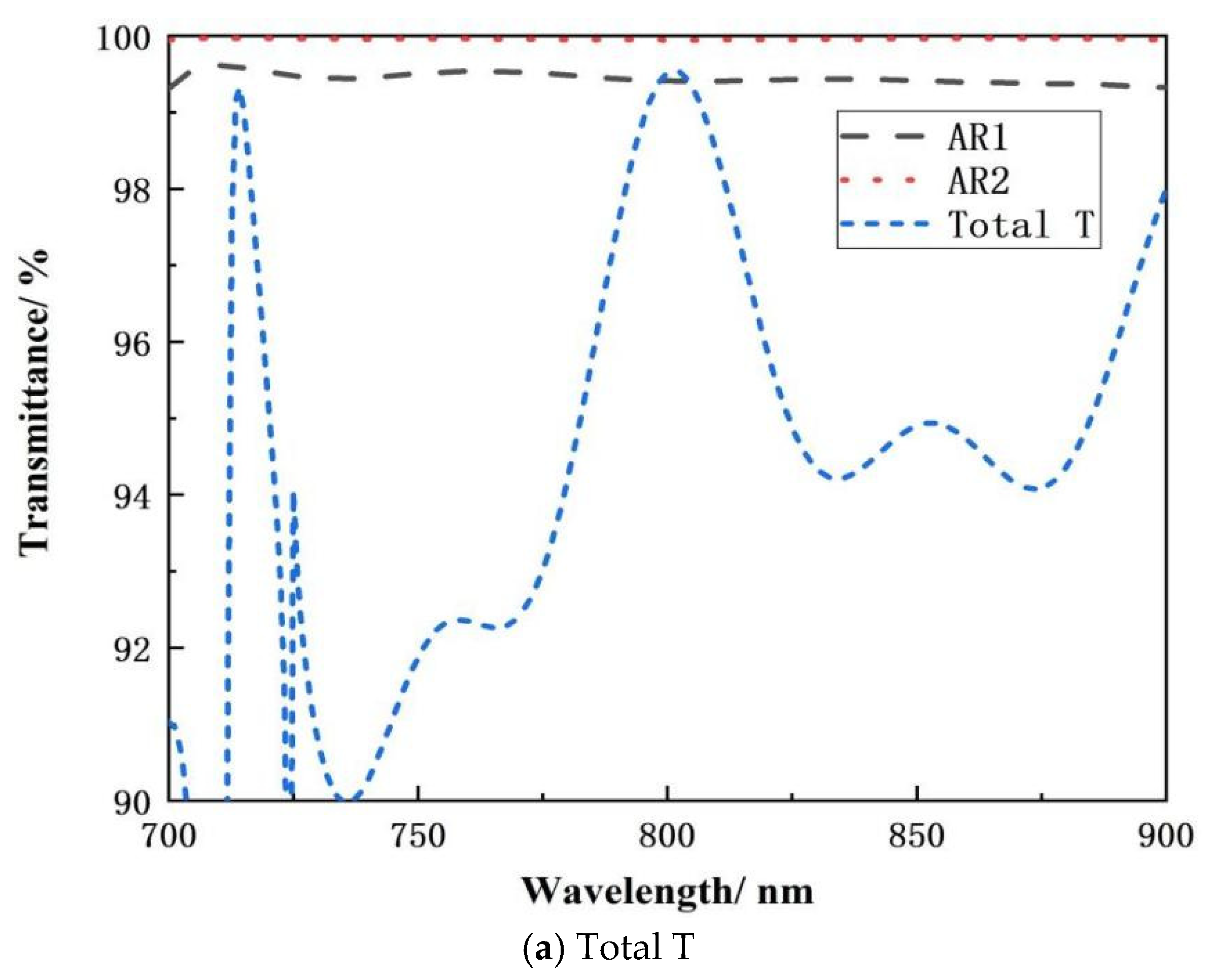
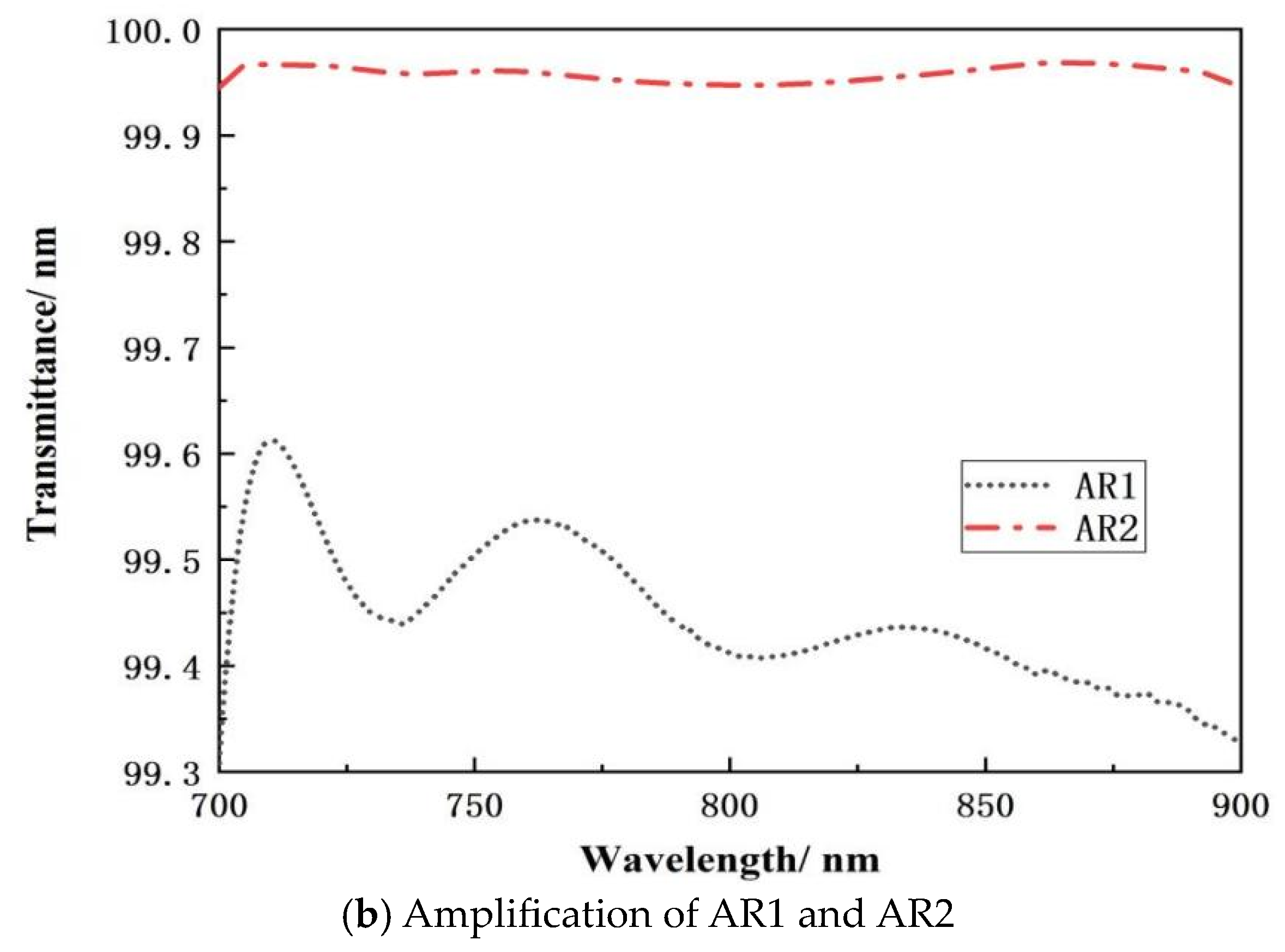
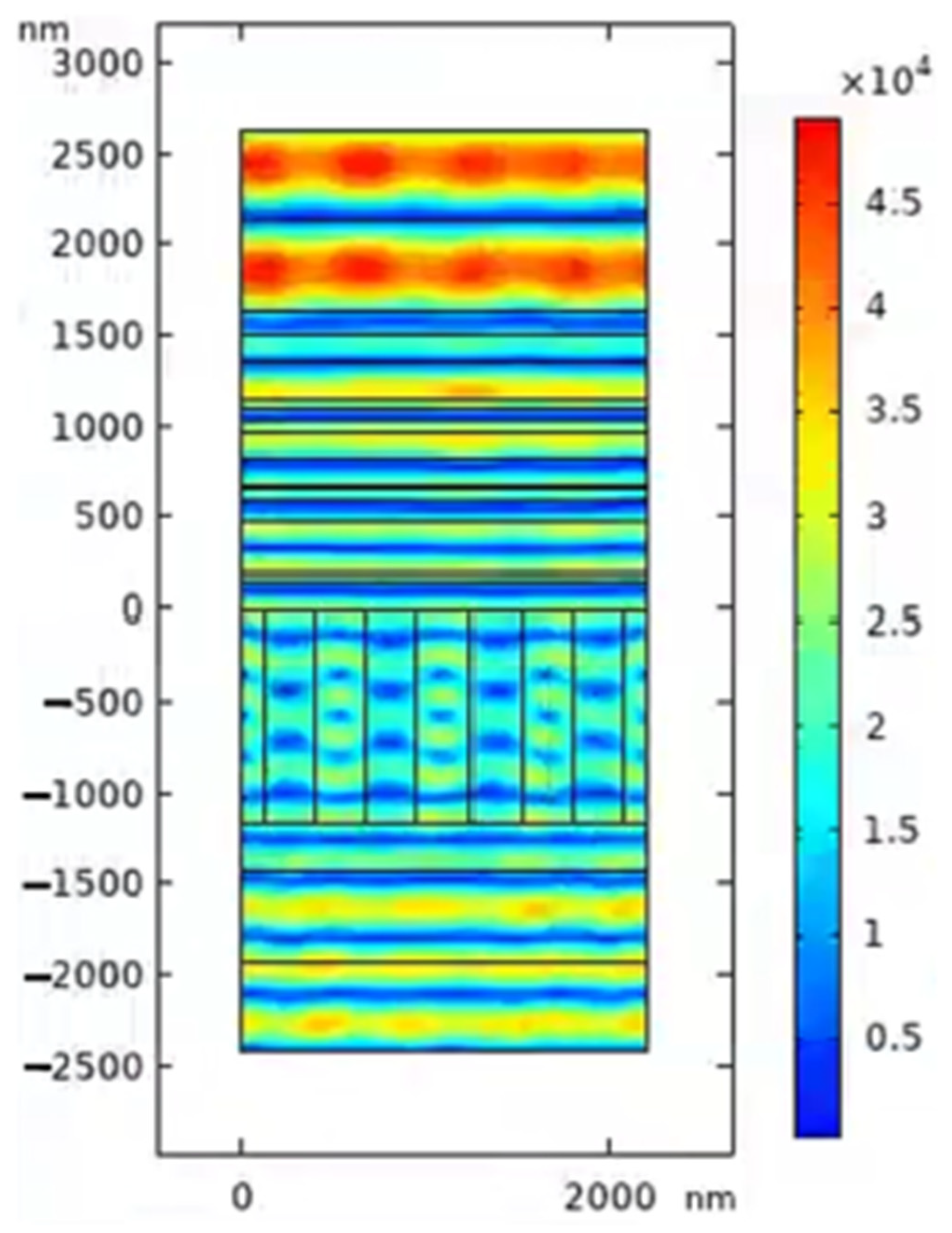
| Spectral Range | 750–850 nm |
|---|---|
| Incidence angle | 46.6° |
| Substrate | Fused Silica |
| Period | 566 nm |
| Filling Factor | 0.5 |
| Background refractive index | 1 |
| (a) AR1 Coating System. | |||||
| AR1, Layer NO. | Layer Material | Layer Thickness/nm | AR1, Layer NO. | Layer Material | Layer Thickness/nm |
| Incidence angle | 46° | 7 | SiO2 | 148 | |
| Incident Medium | Air | 8 | Ta2O5 | 138 | |
| 1 | SiO2 | 38 | 9 | SiO2 | 71 |
| 2 | Ta2O5 | 38 | 10 | Ta2O5 | 64 |
| 3 | SiO2 | 261 | 11 | SiO2 | 50 |
| 4 | Ta2O5 | 118 | 12 | Ta2O5 | 208 |
| 5 | SiO2 | 62 | 13 | SiO2 | 149 |
| 6 | Ta2O5 | 27 | Exit Medium | HfO2 | |
| (b) AR2 Coating System. | |||||
| AR1, Layer NO. | Layer Material | Layer Thickness/nm | AR1, Layer NO. | Layer Material | Layer Thickness/nm |
| Incidence angle | 29° | 14 | SiO2 | 143.6 | |
| Incident Medium | Air | 15 | Ta2O5 | 68.91 | |
| 1 | Ta2O5 | 23.1 | 16 | SiO2 | 75.91 |
| 2 | SiO2 | 99.51 | 17 | Ta2O5 | 247.29 |
| 3 | Ta2O5 | 62.37 | 18 | SiO2 | 382.4 |
| 4 | SiO2 | 96.41 | 19 | Ta2O5 | 214.99 |
| 5 | Ta2O5 | 59.17 | 20 | SiO2 | 115.57 |
| 6 | SiO2 | 108.38 | 21 | Ta2O5 | 46.53 |
| 7 | Ta2O5 | 74.62 | 22 | SiO2 | 41.72 |
| 8 | SiO2 | 104.62 | 23 | Ta2O5 | 65.42 |
| 9 | Ta2O5 | 41.63 | 24 | SiO2 | 270.9 |
| 10 | SiO2 | 115.69 | 25 | Ta2O5 | 106.53 |
| 11 | Ta2O5 | 187.34 | 26 | SiO2 | 137.02 |
| 12 | SiO2 | 96.08 | 27 | ||
| 13 | Ta2O5 | 21.07 | Exit Medium | Fused Silica | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Chen, Y.; Qin, L.; Wang, L. Optimal Design and Analysis of Wide-Band Near-Infrared Hybrid Dielectric Gratings with High Transmission Efficiency. Micromachines 2024, 15, 1290. https://doi.org/10.3390/mi15111290
Wang Y, Chen Y, Qin L, Wang L. Optimal Design and Analysis of Wide-Band Near-Infrared Hybrid Dielectric Gratings with High Transmission Efficiency. Micromachines. 2024; 15(11):1290. https://doi.org/10.3390/mi15111290
Chicago/Turabian StyleWang, Ye, Yongyi Chen, Li Qin, and Lijun Wang. 2024. "Optimal Design and Analysis of Wide-Band Near-Infrared Hybrid Dielectric Gratings with High Transmission Efficiency" Micromachines 15, no. 11: 1290. https://doi.org/10.3390/mi15111290
APA StyleWang, Y., Chen, Y., Qin, L., & Wang, L. (2024). Optimal Design and Analysis of Wide-Band Near-Infrared Hybrid Dielectric Gratings with High Transmission Efficiency. Micromachines, 15(11), 1290. https://doi.org/10.3390/mi15111290








