Numerical Simulation of a Lab-on-Chip for Dielectrophoretic Separation of Circulating Tumor Cells
Abstract
:1. Introduction
2. Materials and Methods
2.1. Target Cell Types
2.2. Modeling and Simulation Setup
2.2.1. Computational Model
- Solve for creeping flow;
- Solve for electric currents;
- Particle tracing based on the previous two physics.
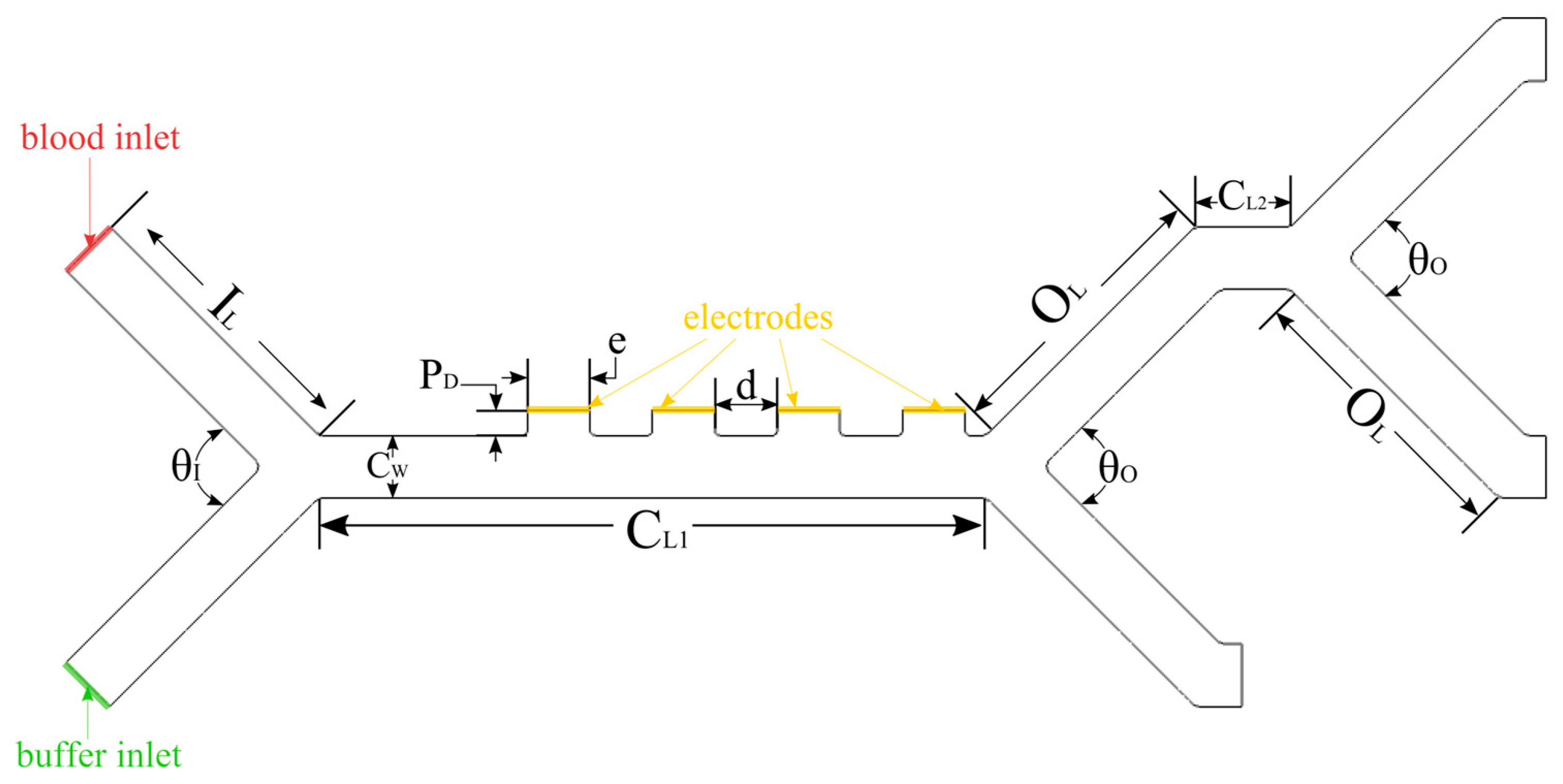
2.2.2. Geometry
2.2.3. Boundary Conditions
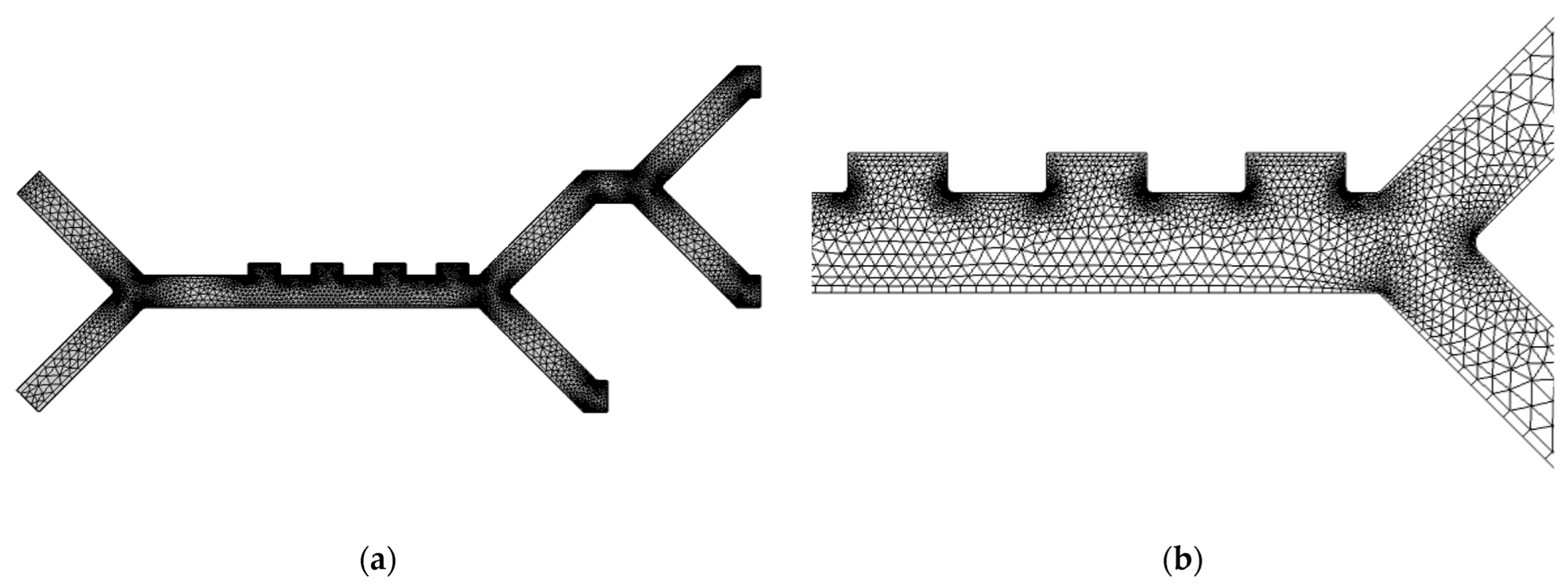
2.2.4. Mesh Refinement
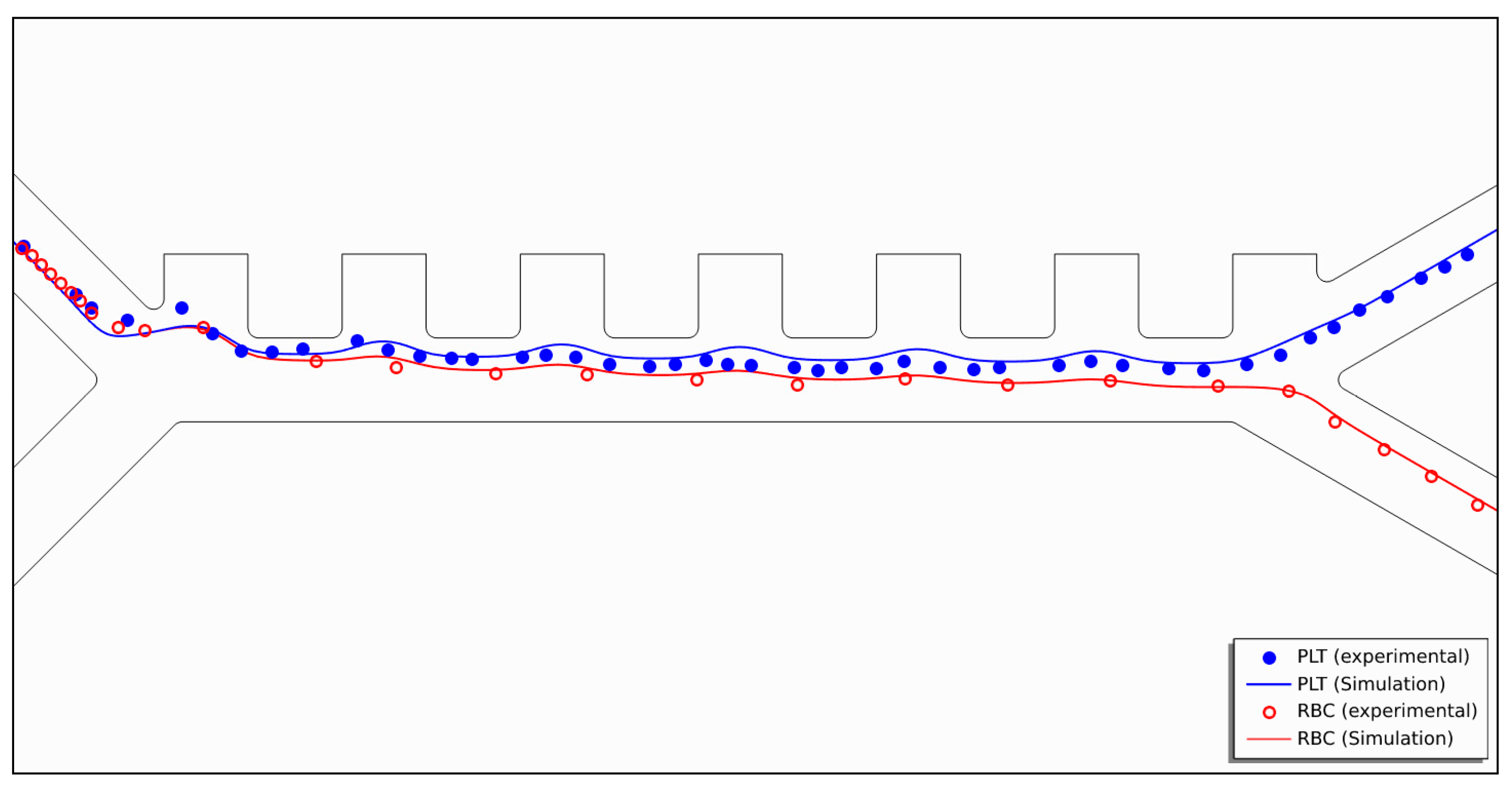
2.3. Numerical Model Validation
2.4. Simulated Design Parameters
3. Results
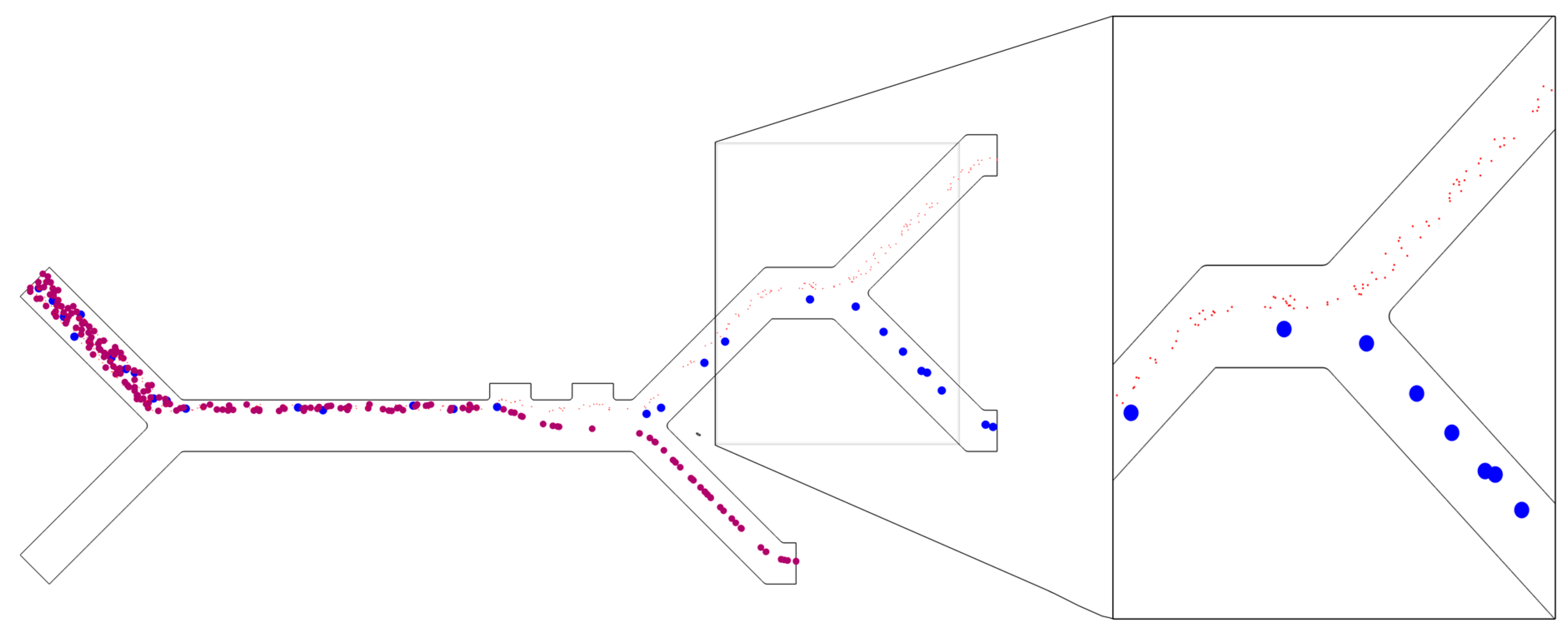
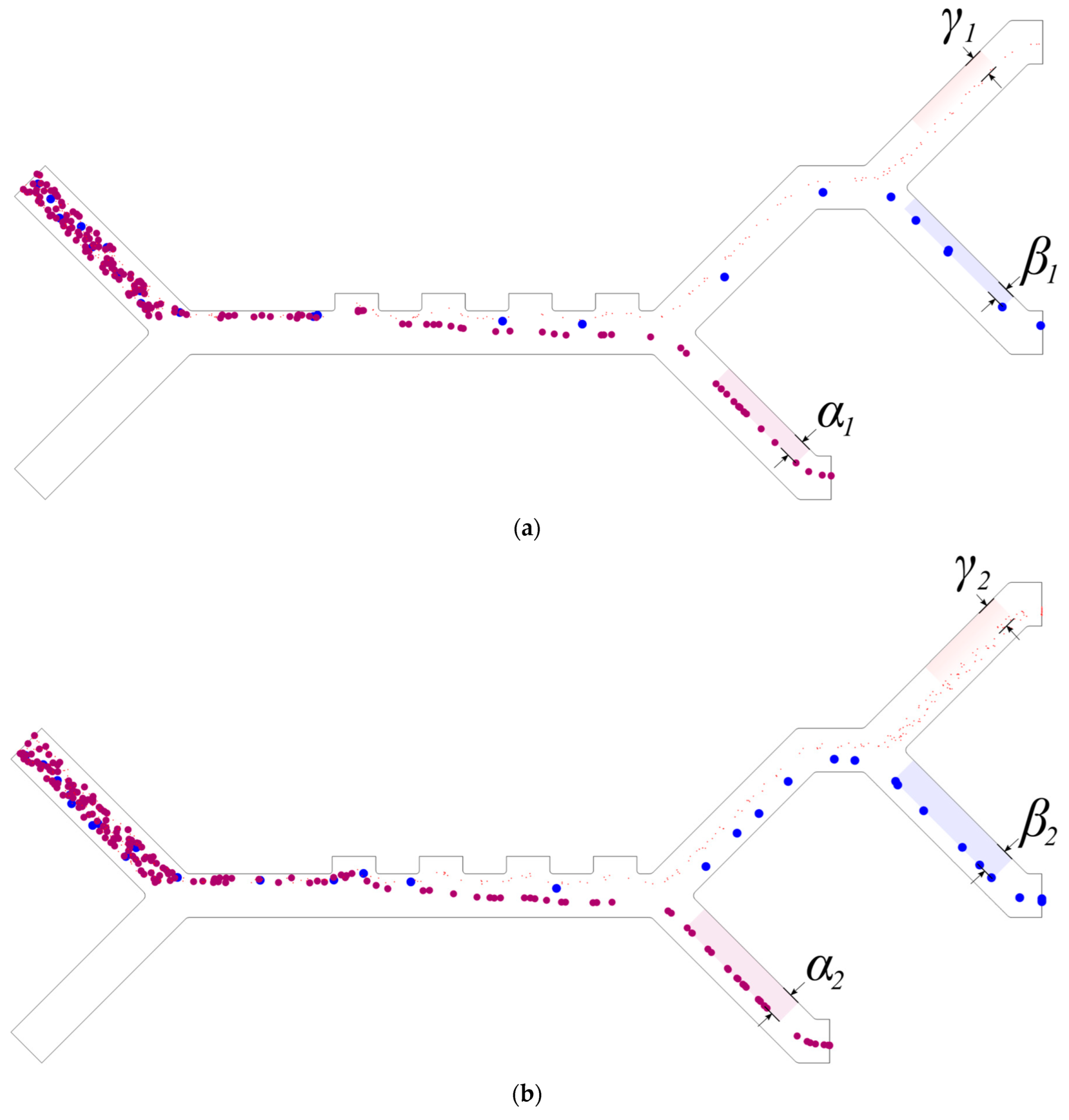
3.1. Separation Efficiency
3.2. Purity
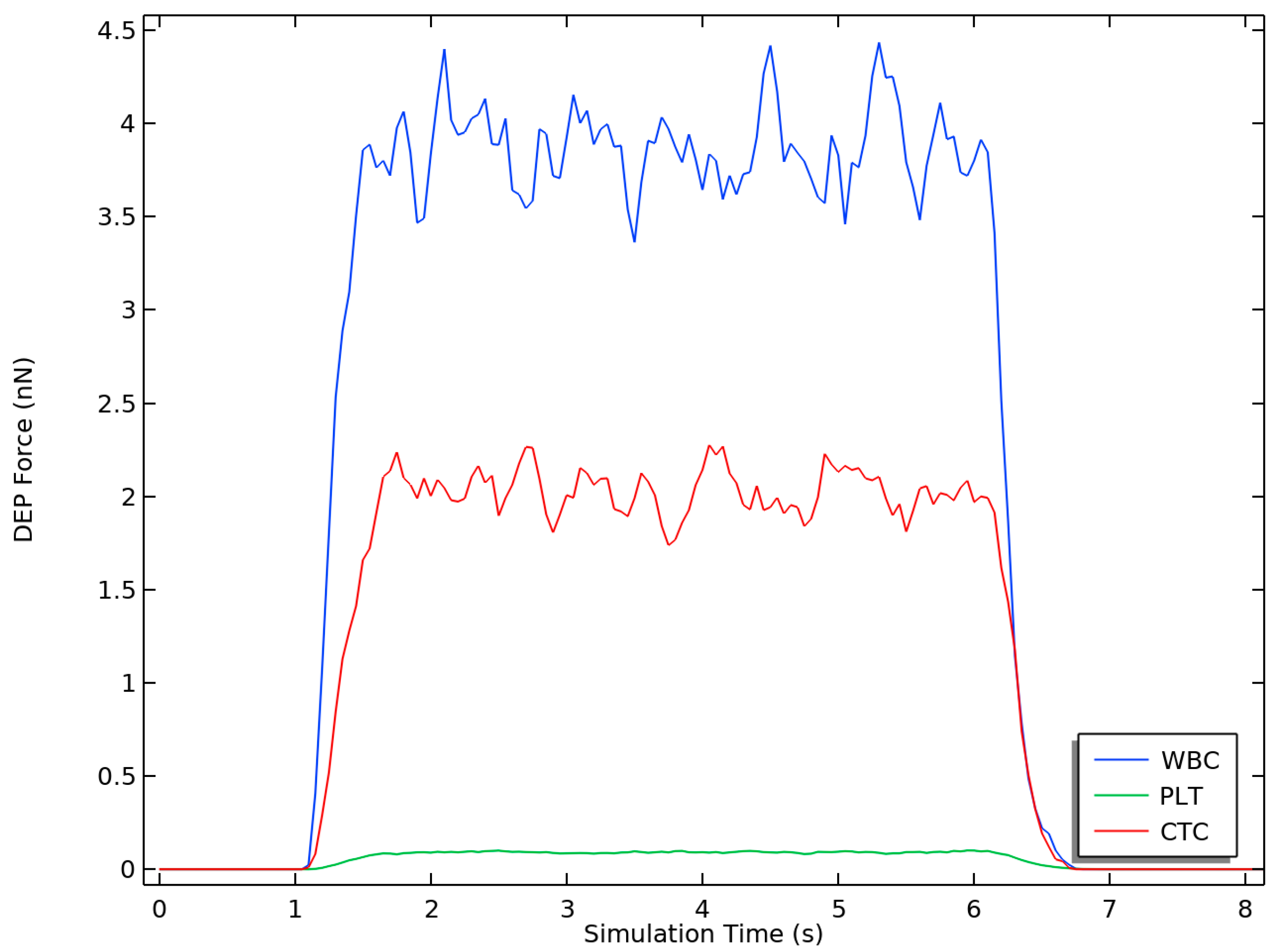
3.3. Dielectrophoretic Force
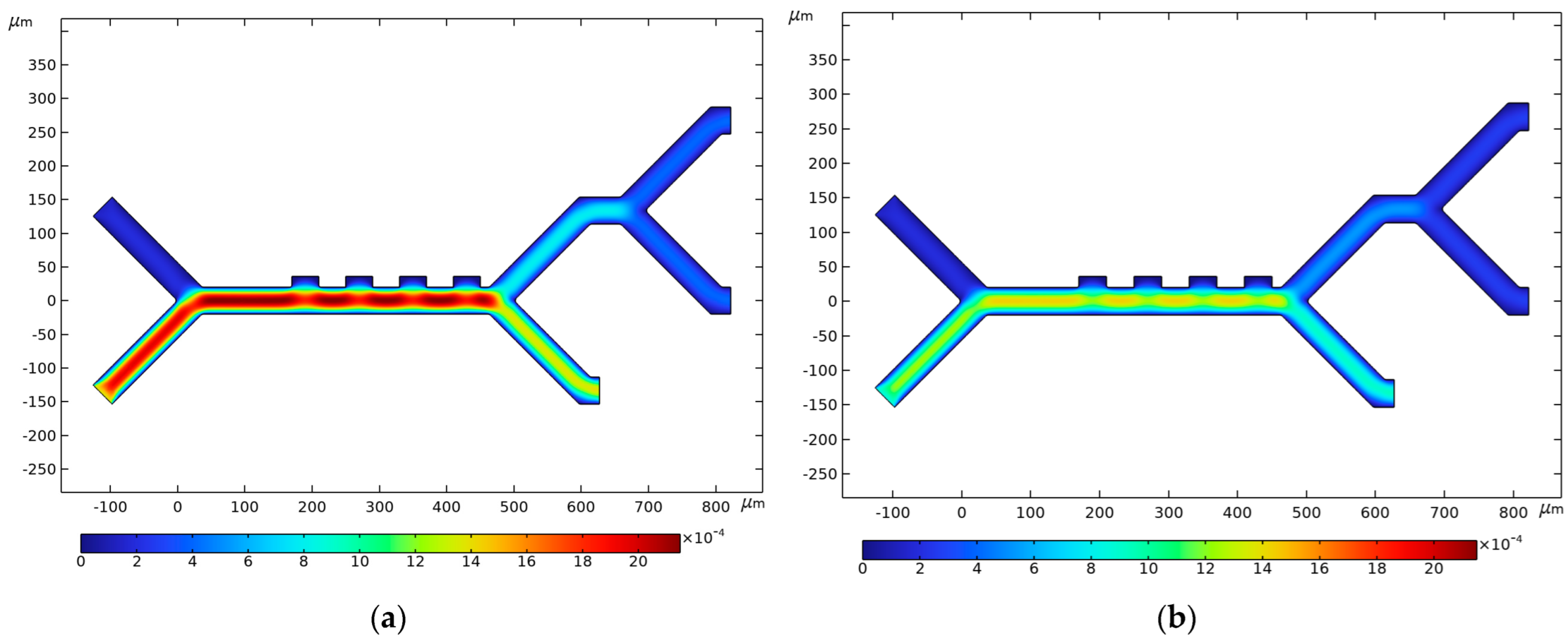
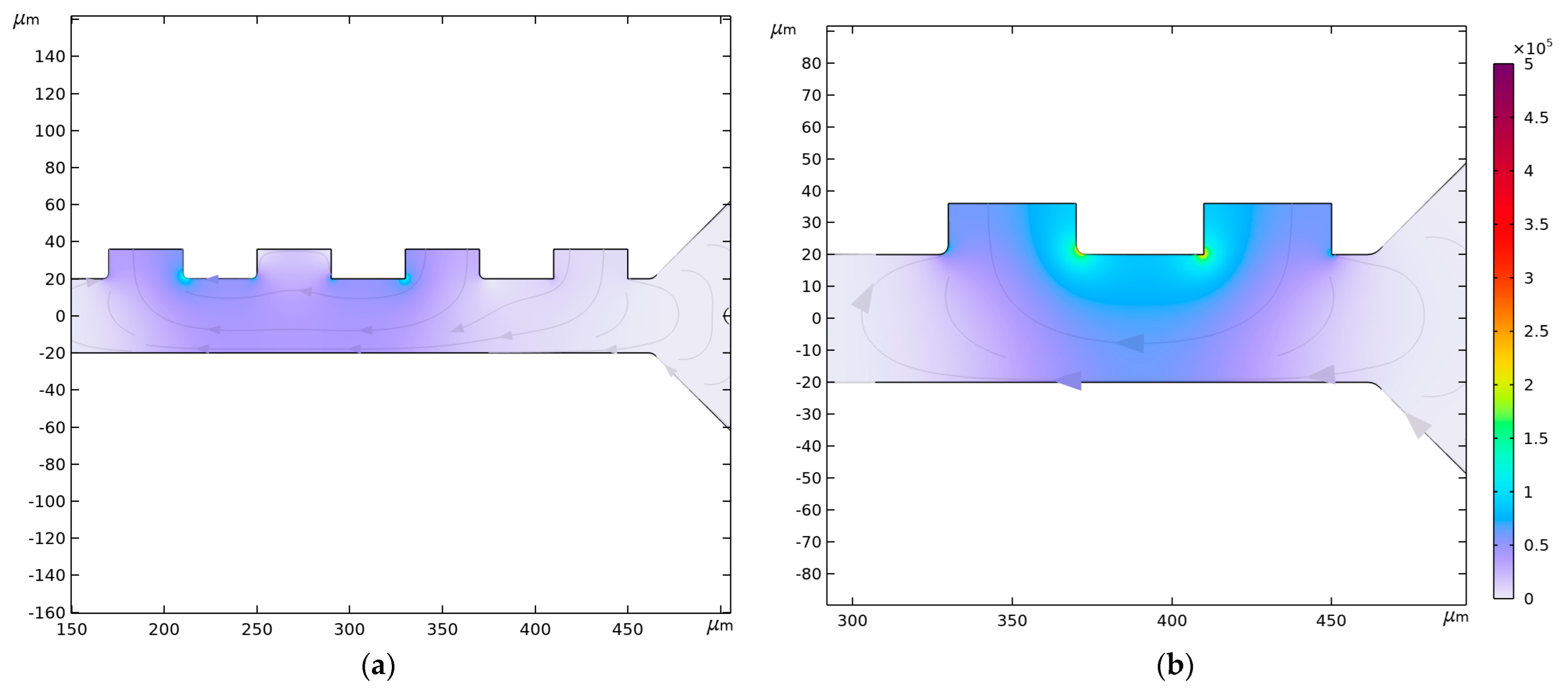
3.4. Fluid Velocity and Pressure
4. Discussion
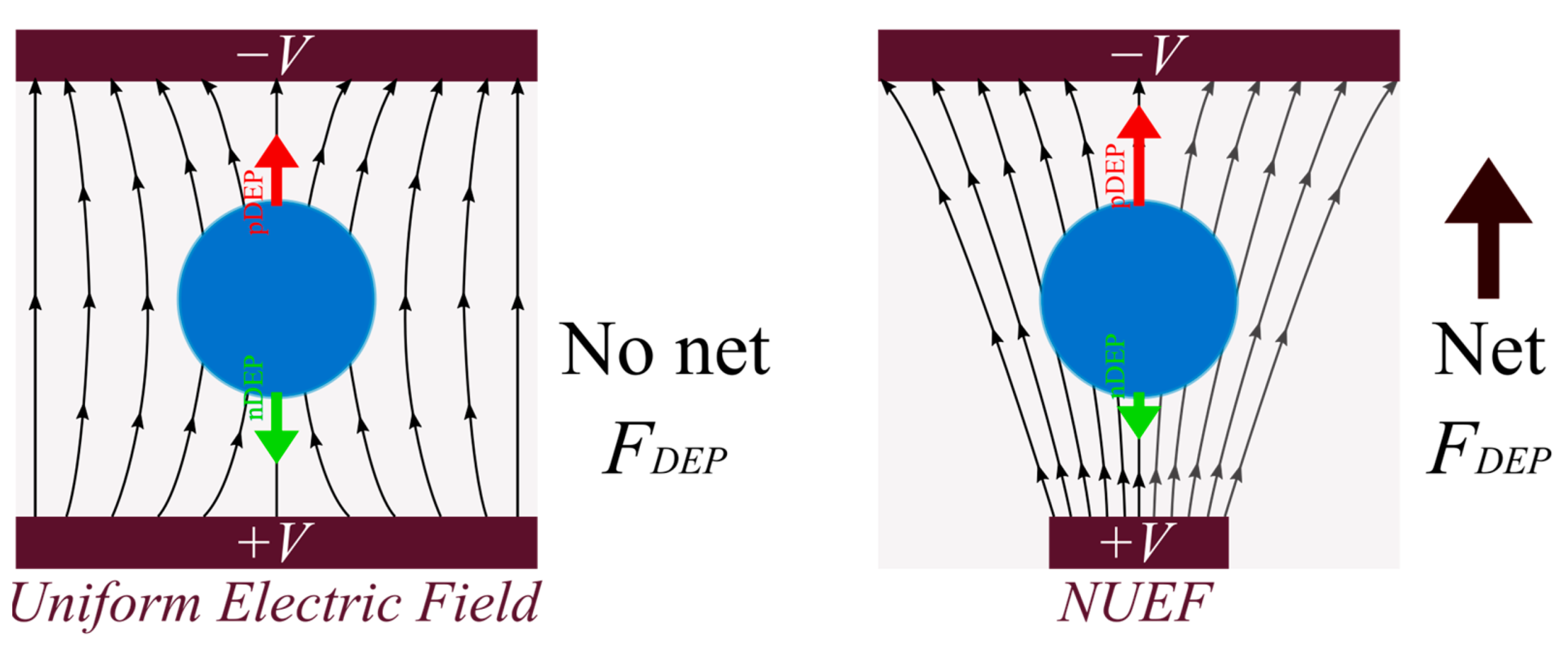
4.1. Dielectrophoretic Force
4.2. Throughput
4.3. Impact of Cell and Buffer Inlet Velocities on the Separation Efficiency
4.4. Impact of Electrodes Configuration and Applied Voltage on the Separation Efficiency
4.5. Impact of Changing Channel Width on Electrode Voltage
4.6. Optimum Design
5. Conclusions
- Increasing the buffer inlet velocity, vin,buffer, can compromise the trajectories of the target cells by forcing the cells to move closer to the electrode and, hence, reducing the overall separation efficiency;
- The use of microchannels with wider widths requires an increase in the applied voltage value to achieve comparable levels of efficiency;
- Using four electrodes allows the usage of lower voltage values compared to using just two electrodes;
- Higher voltage values induce a stronger DEP force that forces the cells to move further from the electrodes.
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Yan, S.; Zhang, J.; Yuan, D.; Li, W. Hybrid Microfluidics Combined with Active and Passive Approaches for Continuous Cell Separation: Microfluidics and Miniaturization. Electrophoresis 2017, 38, 238–249. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Zheng, T.; Wang, L.; Feng, L.; Wang, M.; Zhang, Z.; Feng, H. From Passive to Active Sorting in Microfluidics: A Review. Rev. Adv. Mater. Sci. 2021, 60, 313–324. [Google Scholar] [CrossRef]
- Al-Ali, A.; Waheed, W.; Abu-Nada, E.; Alazzam, A. A Review of Active and Passive Hybrid Systems Based on Dielectrophoresis for the Manipulation of Microparticles. J. Chromatogr. A 2022, 1676, 463268. [Google Scholar] [CrossRef]
- Nagrath, S.; Sequist, L.V.; Maheswaran, S.; Bell, D.W.; Irimia, D.; Ulkus, L.; Smith, M.R.; Kwak, E.L.; Digumarthy, S.; Muzikansky, A.; et al. Isolation of Rare Circulating Tumour Cells in Cancer Patients by Microchip Technology. Nature 2007, 450, 1235–1239. [Google Scholar] [CrossRef]
- Kuan, D.-H.; Wu, C.-C.; Su, W.-Y.; Huang, N.-T. A Microfluidic Device for Simultaneous Extraction of Plasma, Red Blood Cells, and On-Chip White Blood Cell Trapping. Sci. Rep. 2018, 8, 15345. [Google Scholar] [CrossRef] [PubMed]
- Norouzi, N.; Bhakta, H.C.; Grover, W.H. Sorting Cells by Their Density. PLoS ONE 2017, 12, e0180520. [Google Scholar] [CrossRef]
- De Bruijn, D.S.; Jorissen, K.F.A.; Olthuis, W.; Van Den Berg, A. Determining Particle Size and Position in a Coplanar Electrode Setup Using Measured Opacity for Microfluidic Cytometry. Biosensors 2021, 11, 353. [Google Scholar] [CrossRef]
- Geng, Z.; Zhang, L.; Ju, Y.; Wang, W.; Li, Z. A Plasma Separation Device Based on Centrifugal Effect and Zweifach-Fung Effect. In Proceedings of the 15th International Conference on Miniaturized Systems for Chemistry and Life Sciences, Seattle, WA, USA, 2–6 October 2011. [Google Scholar]
- Yeo, J.C.; Kenry; Zhao, Z.; Zhang, P.; Wang, Z.; Lim, C.T. Label-Free Extraction of Extracellular Vesicles Using Centrifugal Microfluidics. Biomicrofluidics 2018, 12, 024103. [Google Scholar] [CrossRef]
- Feshitan, J.A.; Chen, C.C.; Kwan, J.J.; Borden, M.A. Microbubble Size Isolation by Differential Centrifugation. J. Colloid Interface Sci. 2009, 329, 316–324. [Google Scholar] [CrossRef]
- Sun, Y.; Sethu, P. Low-Stress Microfluidic Density-Gradient Centrifugation for Blood Cell Sorting. Biomed. Microdevices 2018, 20, 77. [Google Scholar] [CrossRef]
- Wu, J.; Cui, Y.; Xuan, S.; Gong, X. 3D-Printed Microfluidic Manipulation Device Integrated with Magnetic Array. Microfluid. Nanofluid. 2018, 22, 103. [Google Scholar] [CrossRef]
- Gijs, M.A.M. Magnetic Bead Handling On-Chip: New Opportunities for Analytical Applications. Microfluid. Nanofluid. 2004. [Google Scholar] [CrossRef]
- Lee, H.; Xu, L.; Ahn, B.; Lee, K.; Oh, K.W. Continuous-Flow in-Droplet Magnetic Particle Separation in a Droplet-Based Microfluidic Platform. Microfluid. Nanofluid. 2012, 13, 613–623. [Google Scholar] [CrossRef]
- Zhi, S.; Sun, X.; Feng, Z.; Lei, C.; Zhou, Y. An Innovative Micro Magnetic Separator Based on 3D Micro-Copper-Coil Exciting Soft Magnetic Tips and FeNi Wires for Bio-Target Sorting. Microfluid. Nanofluid. 2019, 23, 43. [Google Scholar] [CrossRef]
- Piacentini, N.; Mernier, G.; Tornay, R.; Renaud, P. Separation of Platelets from Other Blood Cells in Continuous-Flow by Dielectrophoresis Field-Flow-Fractionation. Biomicrofluidics 2011, 5, 034122. [Google Scholar] [CrossRef] [PubMed]
- Kinio, S.; Mills, J.K. Design of Electrode Topologies for Dielectrophoresis through the Use of Genetic Optimization with COMSOL Multiphysics. In Proceedings of the 2015 IEEE International Conference on Mechatronics and Automation (ICMA), Beijing, China, 2–5 August 2015; pp. 1019–1024. [Google Scholar]
- Çetin, B.; Li, D. Dielectrophoresis in Microfluidics Technology. Electrophoresis 2011, 32, 2410–2427. [Google Scholar] [CrossRef]
- Pommer, M.S.; Zhang, Y.; Keerthi, N.; Chen, D.; Thomson, J.A.; Meinhart, C.D.; Soh, H.T. Dielectrophoretic Separation of Platelets from Diluted Whole Blood in Microfluidic Channels. Electrophoresis 2008, 29, 1213–1218. [Google Scholar] [CrossRef]
- Valijam, S.; Salehi, A.; Andersson, M. Design of a Low-Voltage Dielectrophoresis Lab-on-the Chip to Separate Tumor and Blood Cells. Microfluid. Nanofluid. 2023, 27, 22. [Google Scholar] [CrossRef]
- Zhang, H.; Chang, H.; Neuzil, P. DEP-on-a-Chip: Dielectrophoresis Applied to Microfluidic Platforms. Micromachines 2019, 10, 423. [Google Scholar] [CrossRef]
- Puri, P.; Kumar, V.; Belgamwar, S.U.; Sharma, N.N. Microfluidic Device for Cell Trapping with Carbon Electrodes Using Dielectrophoresis. Biomed. Microdevices 2018, 20, 102. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, X. Blood Cells Separation Microfluidic Chip Based on Dielectrophoretic Force. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 206. [Google Scholar] [CrossRef]
- Farahinia, A.; Zhang, W.J.; Badea, I. Novel Microfluidic Approaches to Circulating Tumor Cell Separation and Sorting of Blood Cells: A Review. J. Sci. Adv. Mater. Devices 2021, 6, 303–320. [Google Scholar] [CrossRef]
- Moon, H.-S.; Kwon, K.; Kim, S.-I.; Han, H.; Sohn, J.; Lee, S.; Jung, H.-I. Continuous Separation of Breast Cancer Cells from Blood Samples Using Multi-Orifice Flow Fractionation (MOFF) and Dielectrophoresis (DEP). Lab Chip 2011, 11, 1118. [Google Scholar] [CrossRef] [PubMed]
- Kuan, D.-H.; Huang, N.-T. Recent Advancements in Microfluidics That Integrate Electrical Sensors for Whole Blood Analysis. Anal. Methods 2020, 12, 3318–3332. [Google Scholar] [CrossRef]
- Saha, S.C.; Francis, I.; Nassir, T. Computational Inertial Microfluidics: Optimal Design for Particle Separation. Fluids 2022, 7, 308. [Google Scholar] [CrossRef]
- Shen, S.; Tian, C.; Li, T.; Xu, J.; Chen, S.-W.; Tu, Q.; Yuan, M.-S.; Liu, W.; Wang, J. Spiral Microchannel with Ordered Micro-Obstacles for Continuous and Highly-Efficient Particle Separation. Lab Chip 2017, 17, 3578–3591. [Google Scholar] [CrossRef]
- Bakhshi, M.S.; Rizwan, M.; Khan, G.J.; Duan, H.; Zhai, K. Design of a Novel Integrated Microfluidic Chip for Continuous Separation of Circulating Tumor Cells from Peripheral Blood Cells. Sci. Rep. 2022, 12, 17016. [Google Scholar] [CrossRef]
- Sadeghi, Z.; Esfahany, M.N.; Salehi, H.; Zarezadeh, Z.; Baradaran, A. Clinical Isolation of Breast Cancer Circulating Tumor Cells with an Inertial Microfluidic Chip with a Trapezoidal Cross-Section. In Review. 2023. Available online: https://www.researchsquare.com/article/rs-2881275/v1 (accessed on 18 June 2023).
- Bhagat, A.A.S.; Hou, H.W.; Li, L.D.; Lim, C.T.; Han, J. Pinched Flow Coupled Shear-Modulated Inertial Microfluidics for High-Throughput Rare Blood Cell Separation. Lab Chip 2011, 11, 1870. [Google Scholar] [CrossRef]
- Pødenphant, M.; Ashley, N.; Koprowska, K.; Mir, K.U.; Zalkovskij, M.; Bilenberg, B.; Bodmer, W.; Kristensen, A.; Marie, R. Separation of Cancer Cells from White Blood Cells by Pinched Flow Fractionation. Lab Chip 2015, 15, 4598–4606. [Google Scholar] [CrossRef]
- Laxmi, V.; Tripathi, S.; Joshi, S.S.; Agrawal, A. Separation and Enrichment of Platelets from Whole Blood Using a PDMS-Based Passive Microdevice. Ind. Eng. Chem. Res. 2020, 59, 4792–4801. [Google Scholar] [CrossRef]
- Kim, M.; Mo Jung, S.; Lee, K.-H.; Jun Kang, Y.; Yang, S. A Microfluidic Device for Continuous White Blood Cell Separation and Lysis From Whole Blood: Microfluidic device for wbc separation and lysis from whole blood. Artif. Organs 2010, 34, 996–1002. [Google Scholar] [CrossRef]
- Emmerich, M.E.P.; Sinnigen, A.-S.; Neubauer, P.; Birkholz, M. Dielectrophoretic Separation of Blood Cells. Biomed. Microdevices 2022, 24, 30. [Google Scholar] [CrossRef]
- Yang, S.; Ündar, A.; Zahn, J.D. A Microfluidic Device for Continuous, Real Time Blood Plasma Separation. Lab Chip 2006, 6, 871–880. [Google Scholar] [CrossRef] [PubMed]
- Nam, J.; Namgung, B.; Lim, C.T.; Bae, J.-E.; Leo, H.L.; Cho, K.S.; Kim, S. Microfluidic Device for Sheathless Particle Focusing and Separation Using a Viscoelastic Fluid. J. Chromatogr. A 2015, 1406, 244–250. [Google Scholar] [CrossRef] [PubMed]
- Feng, Z.; Wu, J.; Lu, Y.; Chan, Y.-T.; Zhang, C.; Wang, D.; Luo, D.; Huang, Y.; Feng, Y.; Wang, N. Circulating Tumor Cells in the Early Detection of Human Cancers. Int. J. Biol. Sci. 2022, 18, 3251–3265. [Google Scholar] [CrossRef] [PubMed]
- Deng, Z.; Wu, S.; Wang, Y.; Shi, D. Circulating Tumor Cell Isolation for Cancer Diagnosis and Prognosis. eBioMedicine 2022, 83, 104237. [Google Scholar] [CrossRef]
- Suriyage, M.P.; Asanka, P.V.K.; Cooray, T.M.G.C.S.P.; Liyanage, D.L.F.M.; Pushpakumara, R.A.N.I.; Hendavitharana, D.K.; Fernando, W.W.A.T.I.; Sampath, W.H.P.; Amarasinghe, Y.W.R. Design and Simulation of a Novel MEMS Based Microfluidic Circulating Tumor Cell (CTC) Detection System for a Lab on a Chip Device. IOP Conf. Ser. Mater. Sci. Eng. 2020, 895, 012016. [Google Scholar] [CrossRef]
- Wang, C.; Chen, Y.-G.; Gao, J.-L.; Lyu, G.-Y.; Su, J.; Zhang, Q.; Ji, X.; Yan, J.-Z.; Qiu, Q.-L.; Zhang, Y.-L.; et al. Low Local Blood Perfusion, High White Blood Cell and High Platelet Count Are Associated with Primary Tumor Growth and Lung Metastasis in a 4T1 Mouse Breast Cancer Metastasis Model. Oncol. Lett. 2015, 10, 754–760. [Google Scholar] [CrossRef]
- Grimm, R.H. Prognostic Importance of the White Blood Cell Count for Coronary, Cancer, and All-Cause Mortality. JAMA 1985, 254, 1932. [Google Scholar] [CrossRef]
- Shankar, A.; Wang, J.J.; Rochtchina, E.; Yu, M.C.; Kefford, R.; Mitchell, P. Association Between Circulating White Blood Cell Count and Cancer Mortality: A Population-Based Cohort Study. Arch. Intern. Med. 2006, 166, 188. [Google Scholar] [CrossRef]
- Mabuchi, S.; Matsumoto, Y.; Hamasaki, T.; Kawano, M.; Hisamatsu, T.; Mutch, D.G.; Kimura, T. Elevated White Blood Cell Count at the Time of Recurrence Diagnosis Is an Indicator of Short Survival in Patients With Recurrent Cervical Cancer. Int. J. Gynecol. Cancer 2012, 22, 1545. [Google Scholar] [CrossRef] [PubMed]
- Manouchehri, S.; Ibsen, S.; Wright, J.; Rassenti, L.; Ghia, E.M.; Widhopf, G.F.; Kipps, T.J.; Heller, M.J. Dielectrophoretic Recovery of DNA from Plasma for the Identification of Chronic Lymphocytic Leukemia Point Mutations. Int. J. Hematol. Oncol. 2016, 5, 27–35. [Google Scholar] [CrossRef] [PubMed]
- Abd Rahman, N.; Ibrahim, F.; Yafouz, B. Dielectrophoresis for Biomedical Sciences Applications: A Review. Sensors 2017, 17, 449. [Google Scholar] [CrossRef] [PubMed]
- Hughes, M.P. Strategies for Dielectrophoretic Separation in Laboratory-on-a-Chip Systems. Electrophoresis 2002, 23, 2569–2582. [Google Scholar] [CrossRef]
- Yang, Y.-P.; Giret, T.M.; Cote, R.J. Circulating Tumor Cells from Enumeration to Analysis: Current Challenges and Future Opportunities. Cancers 2021, 13, 2723. [Google Scholar] [CrossRef]
- Alix-Panabières, C.; Pantel, K. Challenges in Circulating Tumour Cell Research. Nat. Rev. Cancer 2014, 14, 623–631. [Google Scholar] [CrossRef]
- Ignatiadis, M.; Lee, M.; Jeffrey, S.S. Circulating Tumor Cells and Circulating Tumor DNA: Challenges and Opportunities on the Path to Clinical Utility. Clin. Cancer Res. 2015, 21, 4786–4800. [Google Scholar] [CrossRef]
- Weyers, J.D.B.; Jones, A.M.; Reed, R. Practical Skills in Biology, 7th ed.; Pearson: Harlow, UK; New York, NY, USA, 2021; ISBN 978-1-292-39707-8. [Google Scholar]
- Khoshmanesh, K.; Nahavandi, S.; Baratchi, S.; Mitchell, A.; Kalantar-zadeh, K. Dielectrophoretic Platforms for Bio-Microfluidic Systems. Biosens. Bioelectron. 2011, 26, 1800–1814. [Google Scholar] [CrossRef]
- Chen, H. A Triplet Parallelizing Spiral Microfluidic Chip for Continuous Separation of Tumor Cells. Sci. Rep. 2018, 8, 4042. [Google Scholar] [CrossRef]
- Yao, J.; Zhu, G.; Zhao, T.; Takei, M. Microfluidic Device Embedding Electrodes for Dielectrophoretic Manipulation of Cells—A Review. Electrophoresis 2019, 40, 1166–1177. [Google Scholar] [CrossRef]
- Li, H.; Zheng, Y.; Akin, D.; Bashir, R. Characterization and Modeling of a Microfluidic Dielectrophoresis Filter for Biological Species. J. Microelectromech. Syst. 2005, 14, 103–112. [Google Scholar] [CrossRef]
- Lin, C.-H.; Lee, G.-B.; Fu, L.-M.; Hwey, B.-H. Vertical Focusing Device Utilizing Dielectrophoretic Force and Its Application on Microflow Cytometer. J. Microelectromech. Syst. 2004, 13, 923–932. [Google Scholar] [CrossRef]
- Challier, L.; Lemarchand, J.; Deanno, C.; Jauzein, C.; Mattana, G.; Mériguet, G.; Rotenberg, B.; Noël, V. Printed Dielectrophoretic Electrode-Based Continuous Flow Microfluidic Systems for Particles 3D-Trapping. Part. Part. Syst. Charact. 2021, 38, 2000235. [Google Scholar] [CrossRef]
- Zhu, H.; Lin, X.; Su, Y.; Dong, H.; Wu, J. Screen-Printed Microfluidic Dielectrophoresis Chip for Cell Separation. Biosens. Bioelectron. 2015, 63, 371–378. [Google Scholar] [CrossRef]
- Altay, R.; Yapici, M.K.; Koşar, A. A Hybrid Spiral Microfluidic Platform Coupled with Surface Acoustic Waves for Circulating Tumor Cell Sorting and Separation: A Numerical Study. Biosensors 2022, 12, 171. [Google Scholar] [CrossRef]
- Dias, L.M.S. Microfabrication of a Microfluidic Device for Cell Sorting: Isolation of Both Circulating Tumour Cell (CTC) and Giant Cancer- Associated Macrophage-like Cells (CAMLs). Ph.D. Thesis, Universidade do Minho, Braga, Portugal, 2020. [Google Scholar]
- Ermolina, I.; Polevaya, Y.; Feldman, Y.; Ginzburg, B.-Z.; Schlesinger, M. Study of Normal and Malignant White Blood Cells by Time Domain Dielectric Spectroscopy. IEEE Trans. Dielect. Electr. Insul. 2001, 8, 253–261. [Google Scholar] [CrossRef]
- Polevaya, Y.; Ermolina, I.; Schlesinger, M.; Ginzburg, B.-Z.; Feldman, Y. Time Domain Dielectric Spectroscopy Study of Human Cells. Biochim. Biophys. Acta (BBA)-Biomembr. 1999, 1419, 257–271. [Google Scholar] [CrossRef]
- Jones, T.B. Basic Theory of Dielectrophoresis and Electrorotation. IEEE Eng. Med. Biol. Mag. 2003, 22, 33–42. [Google Scholar] [CrossRef]
- Honegger, T.; Berton, K.; Picard, E.; Peyrade, D. Determination of Clausius–Mossotti Factors and Surface Capacitances for Colloidal Particles. Appl. Phys. Lett. 2011, 98, 181906. [Google Scholar] [CrossRef]
- Gupta, V.; Jafferji, I.; Garza, M.; Melnikova, V.O.; Hasegawa, D.K.; Pethig, R.; Davis, D.W. ApoStreamTM, a New Dielectrophoretic Device for Antibody Independent Isolation and Recovery of Viable Cancer Cells from Blood. Biomicrofluidics 2012, 6, 024133. [Google Scholar] [CrossRef]
- Hughes, M.P.; Pethig, R.; Wang, X.-B. Dielectrophoretic Forces on Particles in Travelling Electric Fields. J. Phys. D Appl. Phys. 1996, 29, 474–482. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, X.B.; Becker, F.F.; Gascoyne, P.R. Introducing Dielectrophoresis as a New Force Field for Field-Flow Fractionation. Biophys. J. 1997, 73, 1118–1129. [Google Scholar] [CrossRef] [PubMed]
- Ali Othman, N.T.; Sahul Hameed, H.; Rosli, M.I. Simulation on Red Blood Cell’s Separation in Microchannel by Using COMSOL© Multiphysics. J. Teknol. 2022, 84, 103–112. [Google Scholar] [CrossRef]
- Gossett, D.R.; Weaver, W.M.; Mach, A.J.; Hur, S.C.; Tse, H.T.K.; Lee, W.; Amini, H.; Di Carlo, D. Label-Free Cell Separation and Sorting in Microfluidic Systems. Anal. Bioanal. Chem. 2010, 397, 3249–3267. [Google Scholar] [CrossRef] [PubMed]
- Lee, W.; Tseng, P.; Di Carlo, D. (Eds.) Microtechnology for Cell Manipulation and Sorting; Microsystems and Nanosystems; Springer International Publishing: Cham, Switzerland, 2017; ISBN 978-3-319-44137-5. [Google Scholar]
- Pethig, R. Dielectrophoresis: Theory, Methodology, and Biological Applications; John Wiley & Sons, Inc: Hoboken, NJ, USA, 2017; ISBN 978-1-118-67145-0. [Google Scholar]


| Parameter | CTC | WBC | PLTs |
|---|---|---|---|
| Cell diameter | 15 µm | 12 µm | 1.8 µm |
| Cell membrane thickness | 7 nm | 7 nm | 8 nm |
| Cell conductivity | 1 S/m | 0.18 S/m | 0.25 S/m |
| Membrane conductivity | 9 × 10−7 S/m | 9 × 10−6 S/m | 1 × 10−6 S/m |
| Cell relative permittivity | 50 | 80 | 50 |
| Membrane relative permittivity | 12.5 | 10 | 6 |
| Dimension | Value | Description |
|---|---|---|
| IL | 190 µm | Inlet length |
| CL1 | 500 µm | Main channel length |
| CL2 | 60 µm | Secondary channel length |
| CW | 40, 50, 60 µm | Channel width |
| CD | 100 µm | Channel depth |
| OL | 190 µm | Outlet length |
| θI | 90° | Inlet channels angle |
| θO | 90° | Outlet channels angle |
| PD | 16 µm | Electrode protrusion depth |
| e | 40 µm | Electrode width |
| d | 40 µm | Distance between electrodes |
| Cell Type | Coarse and Normal Meshes | Normal and Fine Meshes |
|---|---|---|
| PLT | 50.59% | 0.06% |
| CTC | 0.26% | 0.08% |
| WBC | 395.24% | 0.15% |
| No | Yes | |
| value | 395.24% | 0.15% |
| Four-Electrode Variant vin,buffer = 350 µm/s, 850 µm/s, 1350 µm/s vin,cells = 114 µm/s, 134 µm/s, 154 µm/s | Two-Electrode Variant vin,buffer = 350 µm/s, 850 µm/s, 1350 µm/s vin,cells = 134 µm/s | ||
|---|---|---|---|
| Main Channel Width | Applied Electrode Voltage | Main Channel Width | Applied Electrode Voltage |
| 40 µm | 2.0 V | 40 µm | 2.0 V |
| 40 µm | 2.5 V | 40 µm | 2.5 V |
| 40 µm | 3.0 V | 40 µm | 3.0 V |
| 40 µm | 3.5 V | 40 µm | 3.5 V |
| 40 µm | 4.0 V | 40 µm | 4.0 V |
| 50 µm | 2.0 V | 50 µm | 2.0 V |
| 50 µm | 2.5 V | 50 µm | 2.5 V |
| 50 µm | 3.0 V | 50 µm | 3.0 V |
| 50 µm | 3.5 V | 50 µm | 3.5 V |
| 50 µm | 4.0 V | 50 µm | 4.0 V |
| 60 µm | 2.0 V | 60 µm | 2.0 V |
| 60 µm | 2.5 V | 60 µm | 2.5 V |
| 60 µm | 3.0 V | 60 µm | 3.0 V |
| 60 µm | 3.5 V | 60 µm | 3.5 V |
| 60 µm | 4.0 V | 60 µm | 4.0 V |
| vin,buffer | 850 µm/s | 1350 µm/s | Separation Efficiency | Purity (All Outlets) | ||
|---|---|---|---|---|---|---|
| Number of Electrodes | Channel Width | Electrode Voltage | Channel Width | Electrode Voltage | ||
| 4 | 40 µm | 2.0, 2.5 V | 40 µm | 2.5, 3.0, 3,5 V | 100.00% | 100.00% |
| 4 | 50 µm | 2.5, 3.0 V | 50 µm | 2.5 *, 3.0, 3.5, 4.0 V | ||
| 4 | 60 µm | 2.5 **, 3.0, 3.5, 4.0 V | 60 µm | 3.5, 4.0 V | ||
| 2 | 40 µm | 3.5, 4.0 V | 40 µm | 4.0 V | ||
| 2 | 50 µm | 3.5, 4.0 V | 50 µm | N/A | ||
| Parameter | Value | Description |
|---|---|---|
| N | Four electrodes | Number of electrodes |
| Va | ±2.0 V | Applied voltage |
| CW | 40 µm | Channel width |
| vin,buffer | 850 µm/s | Buffer inlet velocity |
| vin,cells | 134 µm/s | Cell inlet velocity |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alkhaiyat, A.M.; Badran, M. Numerical Simulation of a Lab-on-Chip for Dielectrophoretic Separation of Circulating Tumor Cells. Micromachines 2023, 14, 1769. https://doi.org/10.3390/mi14091769
Alkhaiyat AM, Badran M. Numerical Simulation of a Lab-on-Chip for Dielectrophoretic Separation of Circulating Tumor Cells. Micromachines. 2023; 14(9):1769. https://doi.org/10.3390/mi14091769
Chicago/Turabian StyleAlkhaiyat, Abdallah M., and Mohamed Badran. 2023. "Numerical Simulation of a Lab-on-Chip for Dielectrophoretic Separation of Circulating Tumor Cells" Micromachines 14, no. 9: 1769. https://doi.org/10.3390/mi14091769
APA StyleAlkhaiyat, A. M., & Badran, M. (2023). Numerical Simulation of a Lab-on-Chip for Dielectrophoretic Separation of Circulating Tumor Cells. Micromachines, 14(9), 1769. https://doi.org/10.3390/mi14091769








