A Compact Rat-Race Coupler with Harmonic Suppression for GSM Applications: Design and Implementation Using Artificial Neural Network
Abstract
1. Introduction
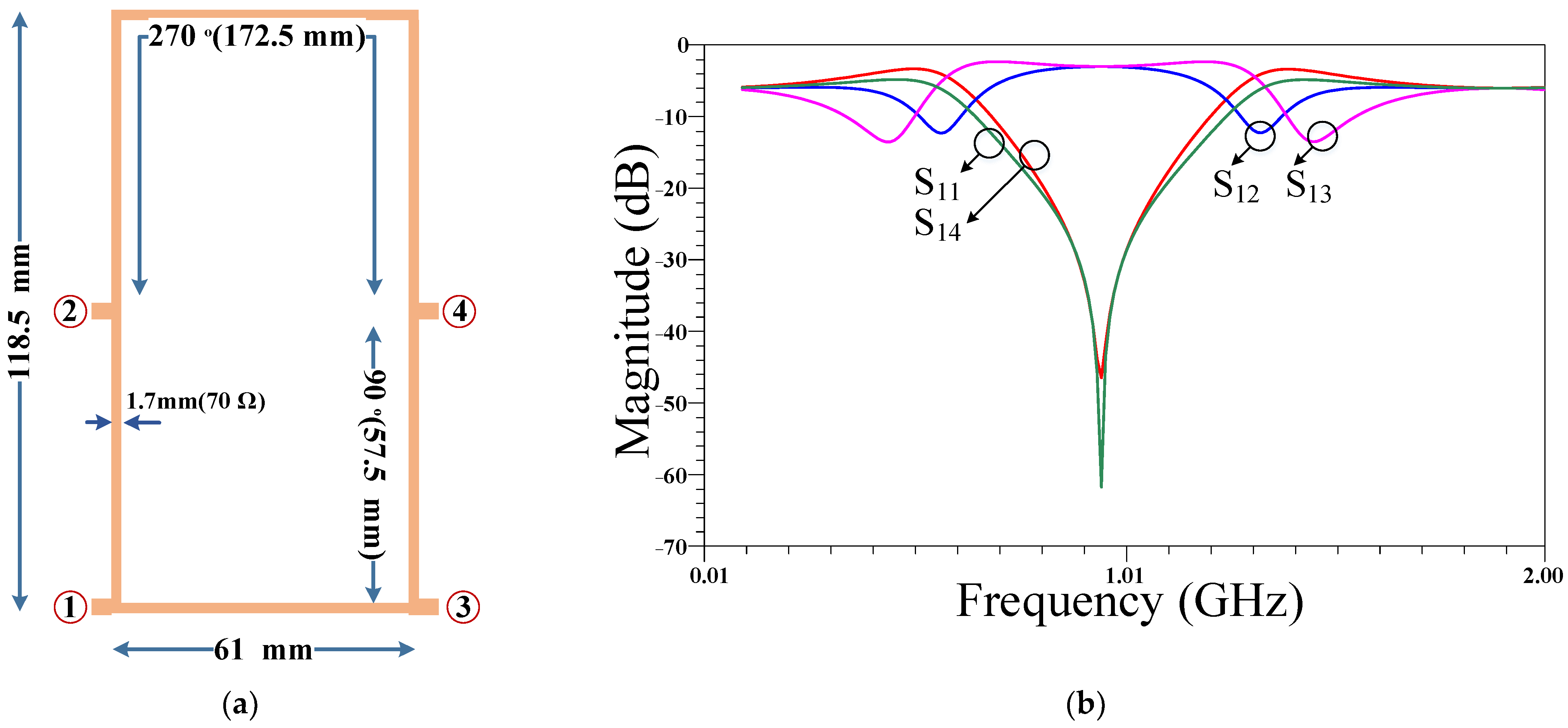
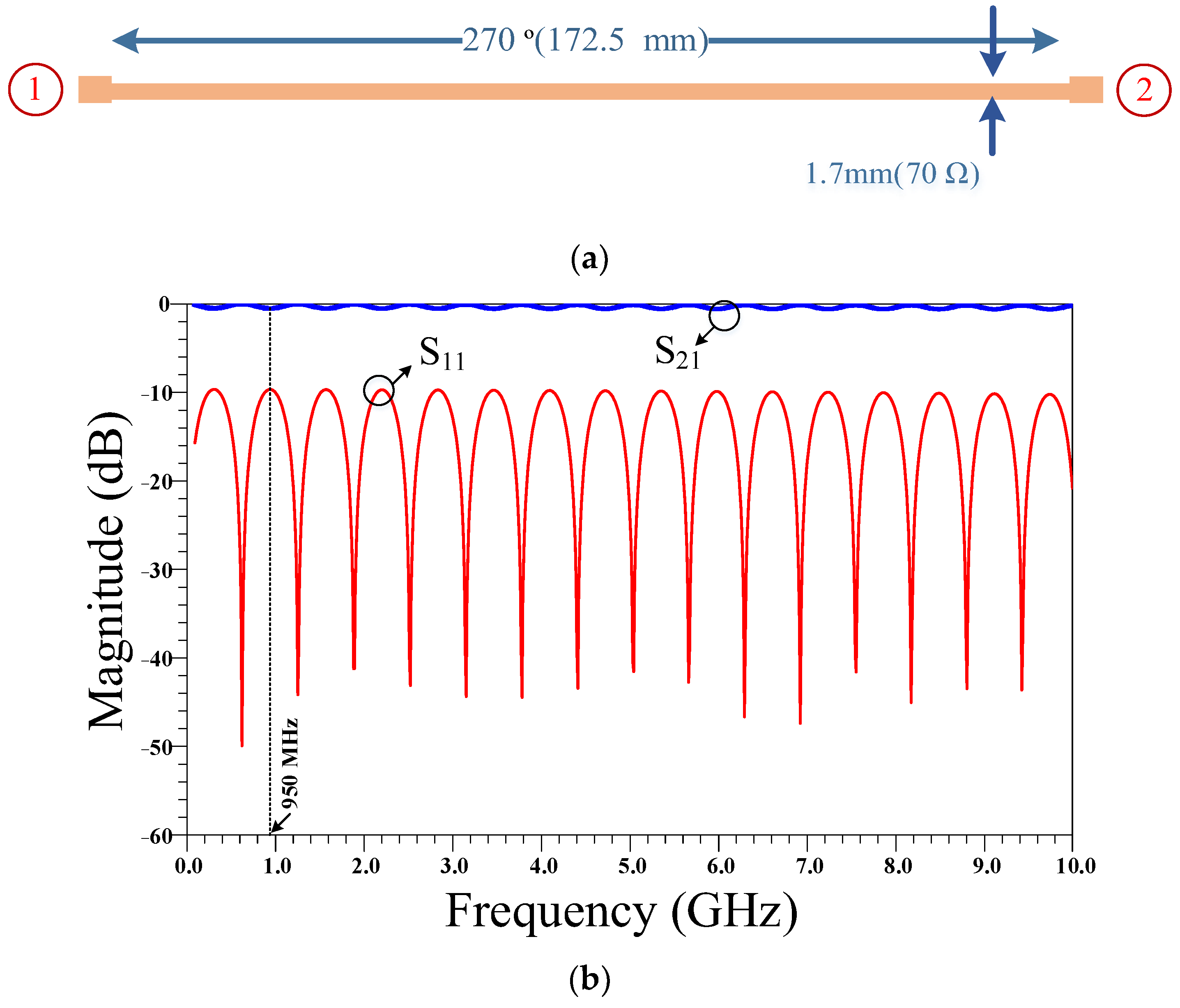
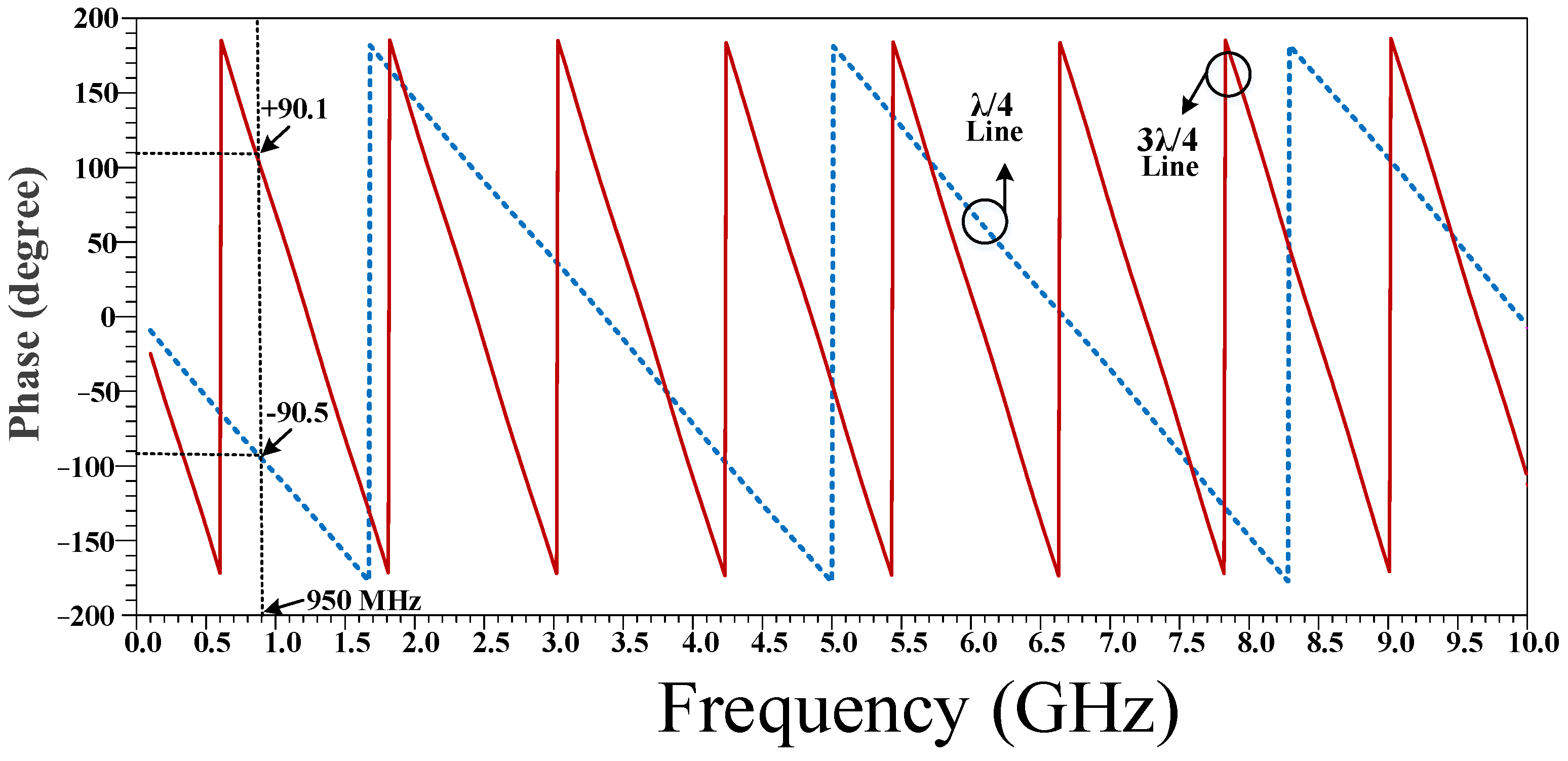
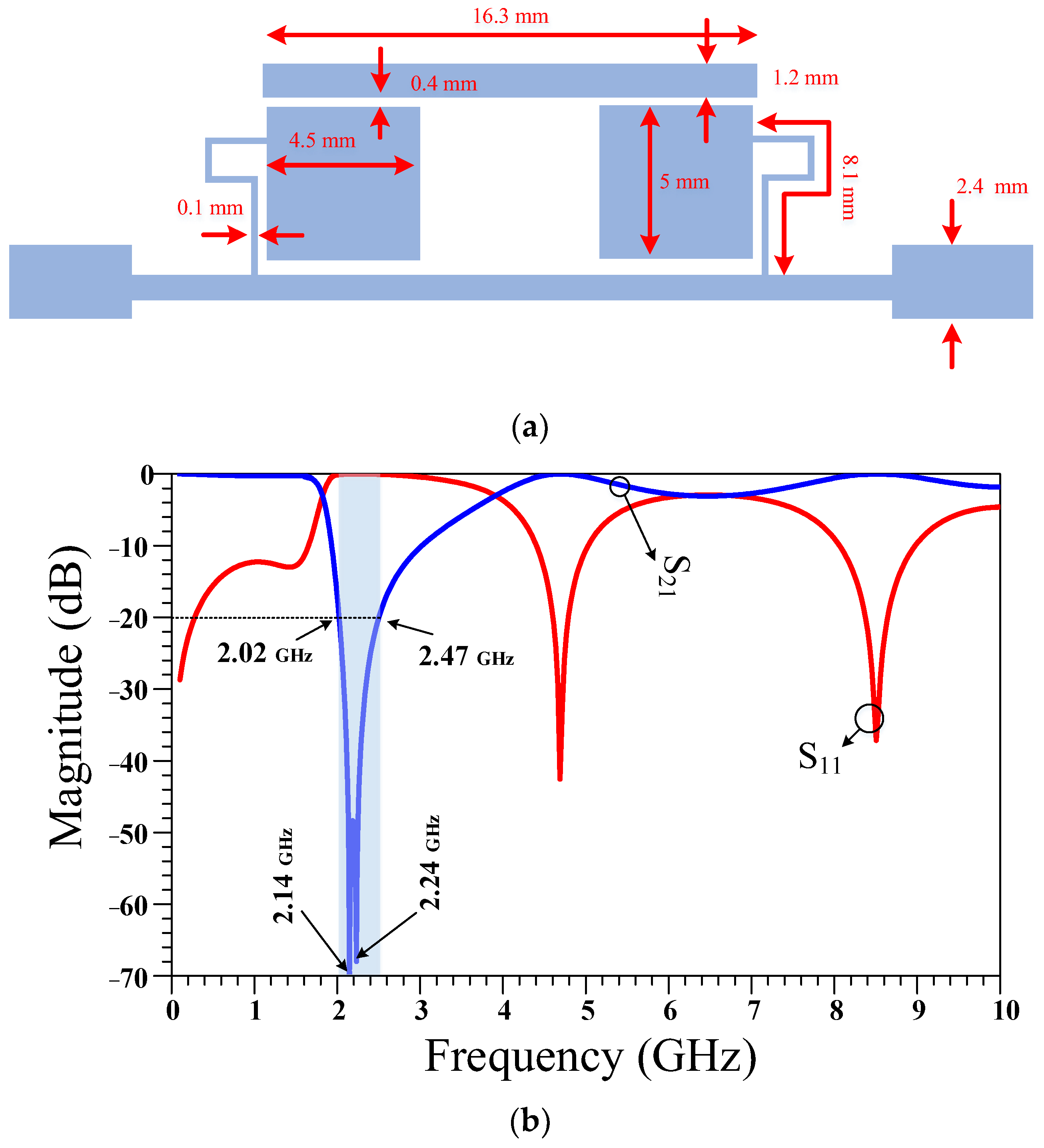
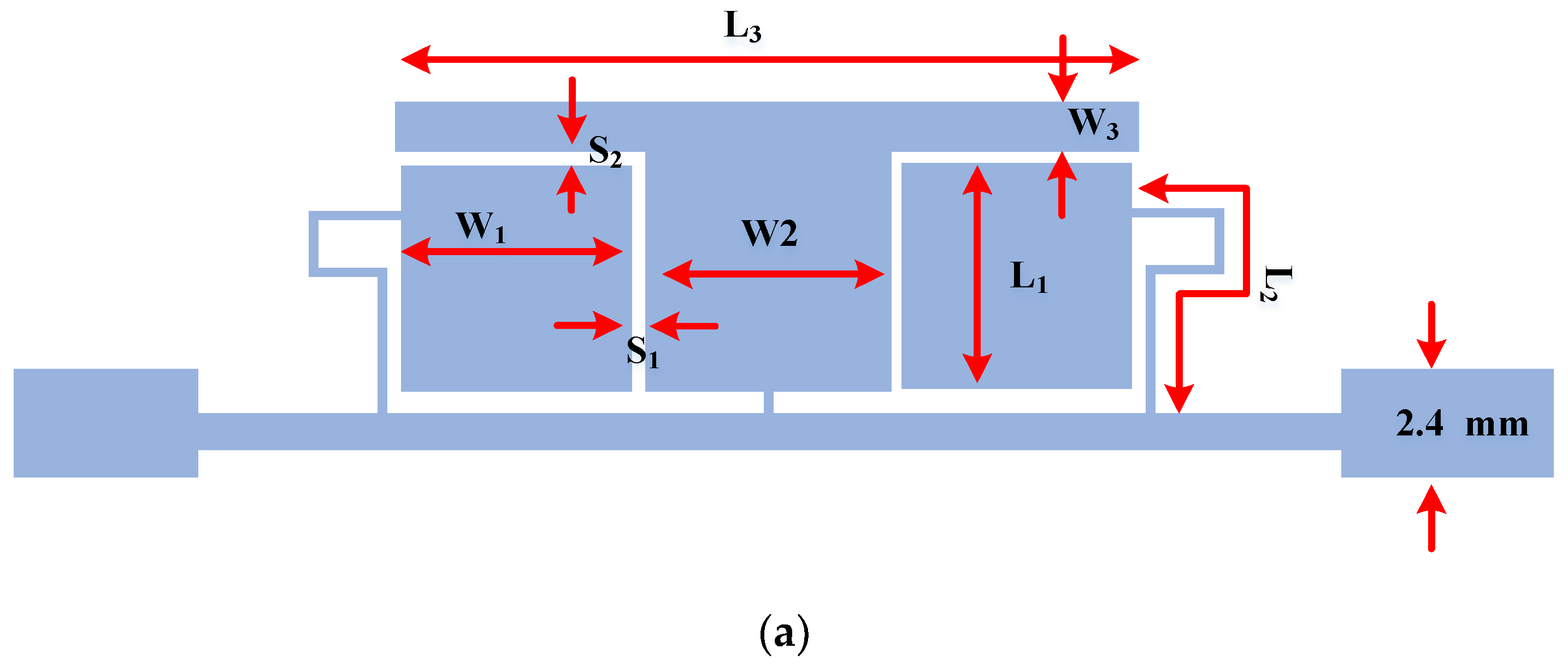
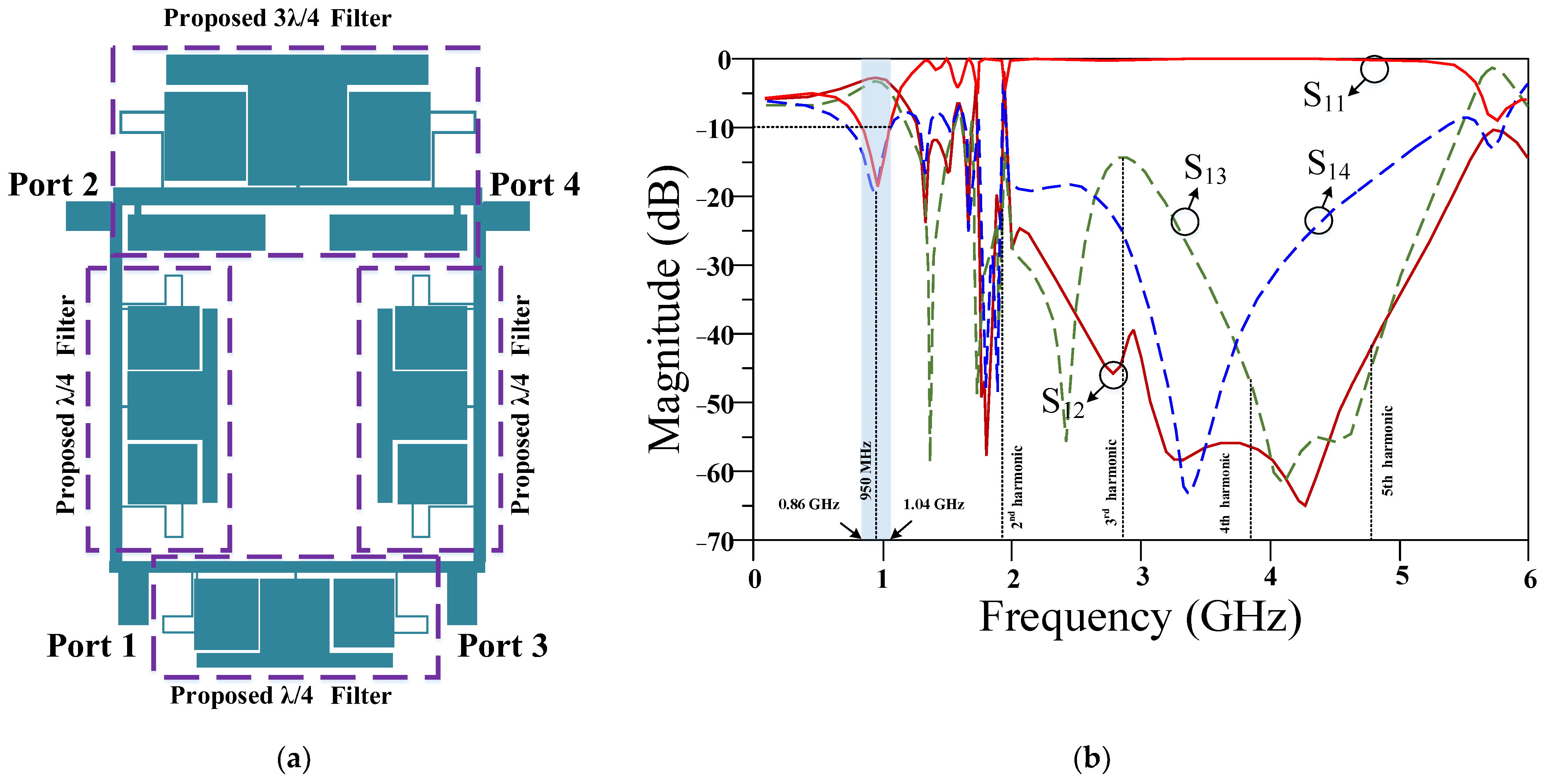
2. Design Procedures
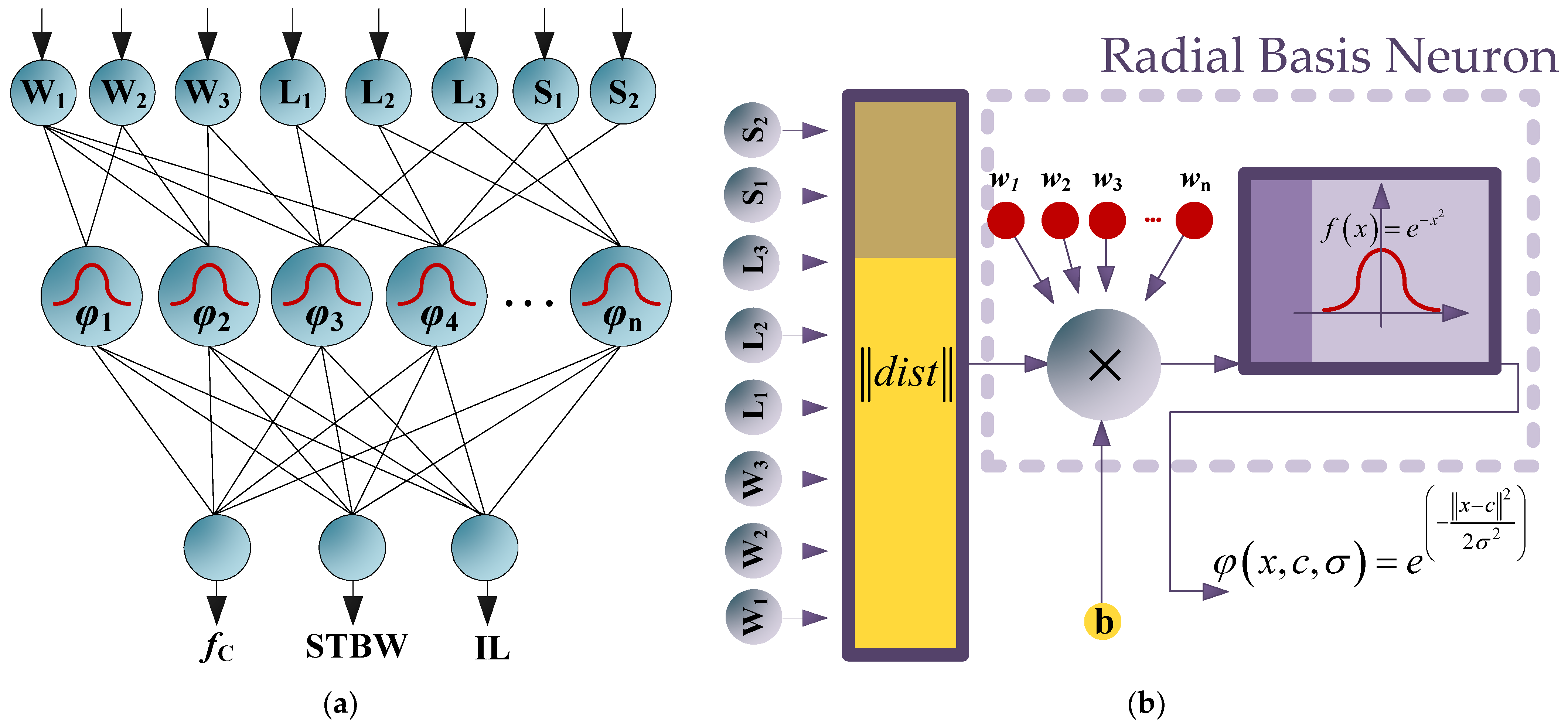
3. The Architecture of the Proposed ANN Model
Results of the Proposed ANN Model
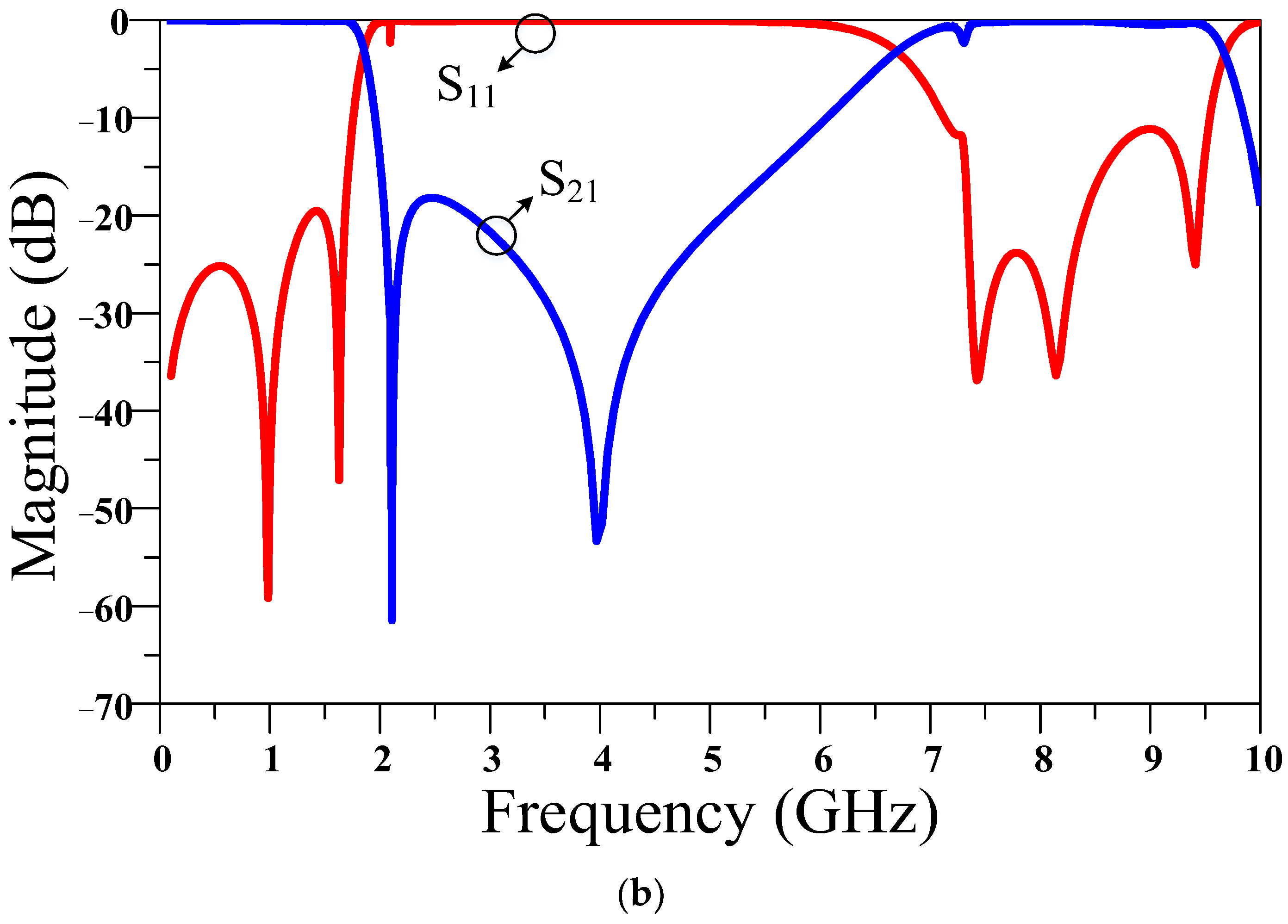
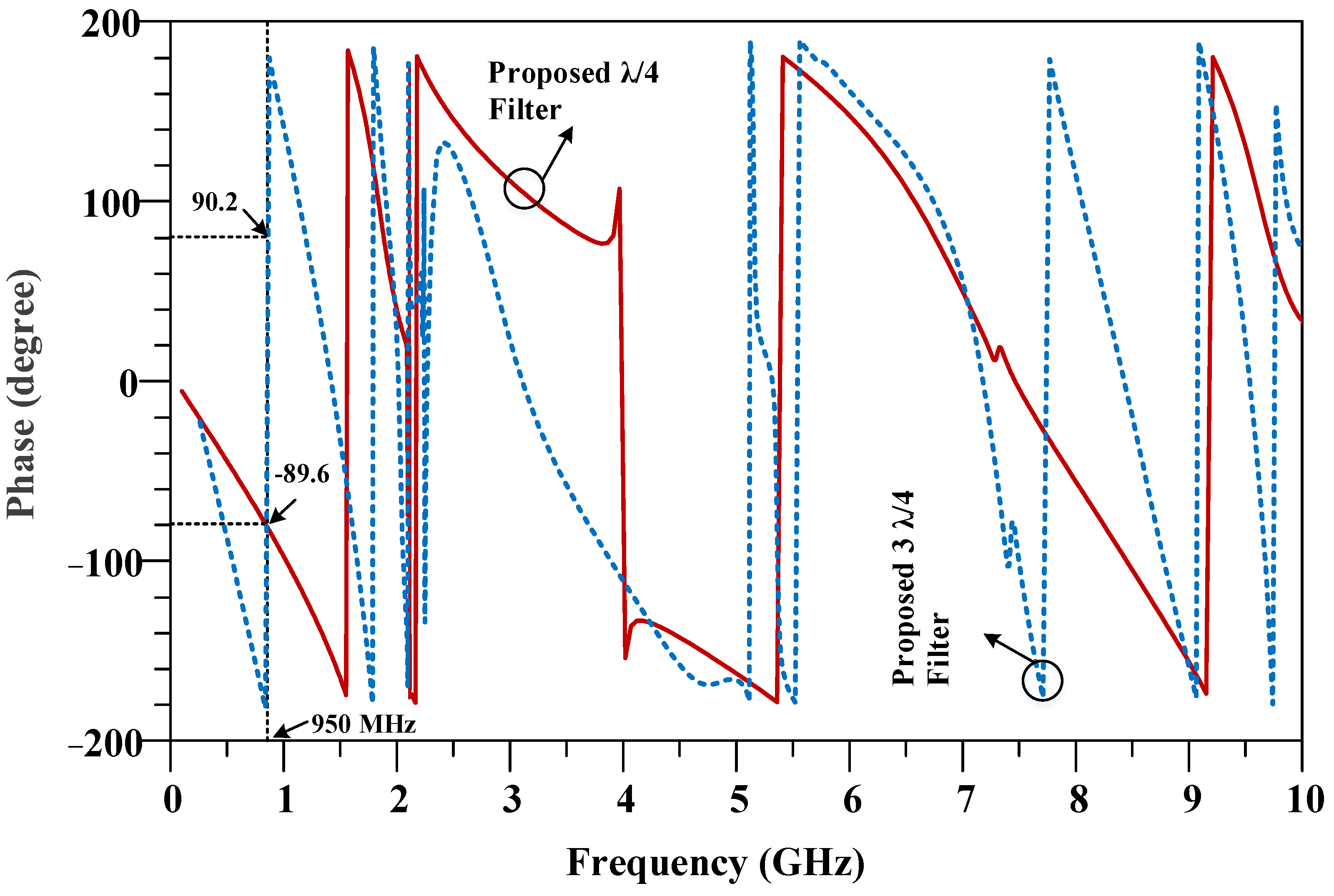
4. Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Roshani, S.; Koziel, S.; Roshani, S.; Jamshidi, M.B.; Parandin, F.; Szczepanski, S. Design of a patch power divider with simple structure and ultra-broadband harmonics suppression. IEEE Access 2021, 9, 165734–165744. [Google Scholar] [CrossRef]
- Rezaei, A.; Yahya, S.I.; Nouri, L. A Comprehensive Review on Microstrip Couplers. Aro-Sci. J. Koya Univ. 2023, 11, 22–31. [Google Scholar] [CrossRef]
- Lalbakhsh, A.; Mohamadpour, G.; Roshani, S.; Ami, M.; Roshani, S.; Sayem, A.S.M.; Alibakhshikenari, M.; Koziel, S. Design of a compact planar transmission line for miniaturized rat-race coupler with harmonics suppression. IEEE Access 2021, 9, 129207–129217. [Google Scholar] [CrossRef]
- Moloudian, G.; Soltani, S.; Bahrami, S.; Buckley, J.L.; O’Flynn, B.; Lalbakhsh, A. Design and fabrication of a Wilkinson power divider with harmonic suppression for LTE and GSM applications. Sci. Rep. 2023, 13, 4246. [Google Scholar] [CrossRef] [PubMed]
- Moloudian, G.; Lalbakhsh, A.; Bahrami, S. A Harmonic-Free Wilkinson Power Divider Using Lowpass Resonators. In Proceedings of the 2022 16th European Conference on Antennas and Propagation (EuCAP), Madrid, Spain, 27 March–1 April 2022; pp. 1–4. [Google Scholar]
- Karimi, G.; Amirian, M.; Lalbakhsh, A.; Ranjbar, M. A new microstrip coupling system for realization of a differential dual-band bandpass filter. AEU-Int. J. Electron. Commun. 2019, 99, 186–192. [Google Scholar] [CrossRef]
- Lalbakhsh, A.; Jamshidi, M.B.; Siahkamari, H.; Ghaderi, A.; Golestanifar, A.; Linhart, R.; Talla, J.; Simorangkir, R.B.; Mandal, K. A compact lowpass filter for satellite communication systems based on transfer function analysis. AEU-Int. J. Electron. Commun. 2020, 124, 153318. [Google Scholar] [CrossRef]
- Xu, J.-X.; Huang, M.; Li, H.-Y.; Yang, Y.; Zhang, X.Y. Design of balanced filtering rat-race coupler based on quad-mode dielectric resonator. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 2267–2271. [Google Scholar] [CrossRef]
- Velan, S.; Kanagasabai, M.; Pakkathillam, J.K.; Palaniswamy, S.K. Compact paper-substrate rat-race coupler deploying modified stepped impedance stub and interdigitated slot resonator for wide-band harmonic suppression. IET Microw. Antennas Propag. 2016, 10, 1667–1672. [Google Scholar] [CrossRef]
- Velidi, V.K.; Shrivastava, S.; Sanyal, S. A compact-size microstrip rat-race coupler with high performance. In Proceedings of the IEEE Technology Students’ Symposium, Chennai, India, 14–16 July 2011; pp. 57–60. [Google Scholar]
- Mondal, P.; Chakrabarty, A. Design of miniaturised branch-line and rat-race hybrid couplers with harmonics suppression. IET Microw. Antennas Propag. 2009, 3, 109–116. [Google Scholar] [CrossRef]
- Gao, S.S.; Sun, S.; Xiao, S. A novel wideband bandpass power divider with harmonic-suppressed ring resonator. IEEE Microw. Wirel. Compon. Lett. 2013, 23, 119–121. [Google Scholar] [CrossRef]
- Kim, J.-S.; Kong, K.-B. Compact branch-line coupler for harmonic suppression. Prog. Electromagn. Res. C 2010, 16, 233–239. [Google Scholar] [CrossRef]
- Chen, C.C.; Sim, C.; Wu, Y.J. Miniaturised dual-band rat-race coupler with harmonic suppression using synthetic transmission line. Electron. Lett. 2016, 52, 1784–1786. [Google Scholar] [CrossRef]
- Lai, C.H.; Ma, T.G. Miniaturised rat-race coupler with second and third harmonic suppression using synthesised transmission lines. Electron. Lett. 2013, 49, 1394–1396. [Google Scholar] [CrossRef]
- Chandra Prasad, V.; Sivasamy, R. Compact Uniform Folded Section Rat-Race Couplers with Harmonic Suppression. IETE J. Res. 2022, 68, 1–11. [Google Scholar] [CrossRef]
- Shao, W.; He, J.; Wang, B.Z. Compact rat-race ring coupler with capacitor loading. Microw. Opt. Technol. Lett. 2010, 52, 7–9. [Google Scholar] [CrossRef]
- Zhang, J.; Sun, X.-W. Harmonic suppression of branch-line and rat-race coupler using complementary spilt ring resonators (CSRR) cell. Prog. Electromagn. Res. Lett. 2008, 2, 73–79. [Google Scholar] [CrossRef]
- Parandin, F.; Olyaee, S.; Kamarian, R.; Jomour, M. Design and simulation of linear all-optical comparator based on square-lattice photonic crystals. Photonics 2022, 9, 459. [Google Scholar] [CrossRef]
- Parandin, F.; Sheykhian, A. Design and simulation of a 2× 1 All-Optical multiplexer based on photonic crystals. Opt. Laser Technol. 2022, 151, 108021. [Google Scholar] [CrossRef]
- Askarian, A.; Parandin, F. A novel proposal for all optical 1-bit comparator based on 2D linear photonic crystal. J. Comput. Electron. 2023, 22, 288–295. [Google Scholar] [CrossRef]
- Parandin, F.; Heidari, F.; Aslinezhad, M.; Parandin, M.M.; Roshani, S.; Roshani, S. Design of 2D photonic crystal biosensor to detect blood components. Opt. Quantum Electron. 2022, 54, 618. [Google Scholar] [CrossRef]
- Parandin, F.; Mahtabi, N. Design of an ultra-compact and high-contrast ratio all-optical NOR gate. Opt. Quantum Electron. 2021, 53, 1–9. [Google Scholar] [CrossRef]
- Parandin, F.; Sheykhian, A.; Bagheri, N. A novel design for an ultracompact optical majority gate based on a ring resonator on photonic crystal substrate. J. Comput. Electron. 2023, 22, 716–722. [Google Scholar] [CrossRef]
- Alanazi, A.K.; Alizadeh, S.M.; Nurgalieva, K.S.; Nesic, S.; Grimaldo Guerrero, J.W.; Abo-Dief, H.M.; Eftekhari-Zadeh, E.; Nazemi, E.; Narozhnyy, I.M. Application of neural network and time-domain feature extraction techniques for determining volumetric percentages and the type of two phase flow regimes independent of scale layer thickness. Appl. Sci. 2022, 12, 1336. [Google Scholar] [CrossRef]
- Nazemi, E.; Feghhi, S.; Roshani, G.; Peyvandi, R.G.; Setayeshi, S. Precise void fraction measurement in two-phase flows independent of the flow regime using gamma-ray attenuation. Nucl. Eng. Technol. 2016, 48, 64–71. [Google Scholar] [CrossRef]
- Roshani, G.H.; Roshani, S.; Nazemi, E.; Roshani, S. Online measuring density of oil products in annular regime of gas-liquid two phase flows. Measurement 2018, 129, 296–301. [Google Scholar] [CrossRef]
- Nazemi, E.; Roshani, G.; Feghhi, S.; Setayeshi, S.; Zadeh, E.E.; Fatehi, A. Optimization of a method for identifying the flow regime and measuring void fraction in a broad beam gamma-ray attenuation technique. Int. J. Hydrog. Energy 2016, 41, 7438–7444. [Google Scholar] [CrossRef]
- Roshani, G.; Nazemi, E.; Roshani, M. Intelligent recognition of gas-oil-water three-phase flow regime and determination of volume fraction using radial basis function. Flow Meas. Instrum. 2017, 54, 39–45. [Google Scholar] [CrossRef]
- Hosseini, S.; Taylan, O.; Abusurrah, M.; Akilan, T.; Nazemi, E.; Eftekhari-Zadeh, E.; Bano, F.; Roshani, G.H. Application of wavelet feature extraction and artificial neural networks for improving the performance of gas–liquid two-phase flow meters used in oil and petrochemical industries. Polymers 2021, 13, 3647. [Google Scholar] [CrossRef] [PubMed]
- Roshani, S.; Azizian, J.; Roshani, S.; Jamshidi, M.; Parandin, F. Design of a miniaturized branch line microstrip coupler with a simple structure using artificial neural network. Frequenz 2022, 76, 255–263. [Google Scholar] [CrossRef]
- Weatherspoon, M.H.; Martinez, H.A.; Langoni, D.; Foo, S.Y. Small-signal modeling of microwave MESFETs using RBF-ANNs. IEEE Trans. Instrum. Meas. 2007, 56, 2067–2072. [Google Scholar] [CrossRef]
- Kabir, H.; Wang, Y.; Yu, M.; Zhang, Q. Applications of artificial neural network techniques in microwave filter modeling, optimization and design. PIERS Online 2007, 3, 1131–1135. [Google Scholar] [CrossRef]
- Yahya, S.I.; Alameri, B.M.; Jamshidi, M.; Roshani, S.; Chaudhary, M.A.; Ijemaru, G.K.; Mezaal, Y.S.; Roshani, S. A New Design Method for Class-E Power Amplifiers Using Artificial Intelligence Modeling for Wireless Power Transfer Applications. Electronics 2022, 11, 3608. [Google Scholar] [CrossRef]
- Roshani, S.; Jamshidi, M.B.; Mohebi, F.; Roshani, S. Design and modeling of a compact power divider with squared resonators using artificial intelligence. Wirel. Pers. Commun. 2021, 117, 2085–2096. [Google Scholar] [CrossRef]
- Chang, W.; Liang, C.; Chang, C.-Y. Wideband high-isolation and perfect-balance microstrip rat-race coupler. Electron. Lett. 2012, 48, 1. [Google Scholar] [CrossRef]
- Ghali, H.; Moselhy, T.A. Miniaturized fractal rat-race, branch-line, and coupled-line hybrids. IEEE Trans. Microw. Theory Tech. 2004, 52, 2513–2520. [Google Scholar] [CrossRef]
- Nie, W.; Luo, S.; Guo, Y.-X.; Fan, Y. Miniaturized rat-race coupler with harmonic suppression. IEEE Microw. Wirel. Compon. Lett. 2014, 24, 754–756. [Google Scholar] [CrossRef]
- Sung, Y.; Ahn, C.; Kim, Y.-S. Size reduction and harmonic suppression of rat-race hybrid coupler using defected ground structure. IEEE Microw. Wirel. Compon. Lett. 2004, 14, 7–9. [Google Scholar] [CrossRef]
- Mohamadzade, B.; Lalbakhsh, A.; Simorangkir, R.B.; Rezaee, A.; Hashmi, R.M. Mutual coupling reduction in microstrip array antenna by employing cut side patches and EBG structures. Prog. Electromagn. Res. M 2020, 89, 179–187. [Google Scholar] [CrossRef]
- Gu, J.; Sun, X. Miniaturization and harmonic suppression rat-race coupler using C-SCMRC resonators with distributive equivalent circuit. IEEE Microw. Wirel. Compon. Lett. 2005, 15, 880–882. [Google Scholar]
- Dong, G.; Wang, W.; Wu, Y.; Liu, Y.; Tentzeris, M.M. Filtering rat-race couplers with impedance transforming characteristics based on terminated coupled line structures. IET Microw. Antennas Propag. 2020, 14, 734–742. [Google Scholar] [CrossRef]
- Bishop, C.M.; Nasrabadi, N.M. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006; Volume 4. [Google Scholar]
- Haykin, S. Neural Networks and Learning Machines, 3rd ed.; Pearson Education: New Delhi, India, 2009. [Google Scholar]
- Chang, W.-S.; Liang, C.-H.; Chang, C.-Y. Slow-wave broadside-coupled microstrip lines and its application to the rat-race coupler. IEEE Microw. Wirel. Compon. Lett. 2015, 25, 361–363. [Google Scholar] [CrossRef]


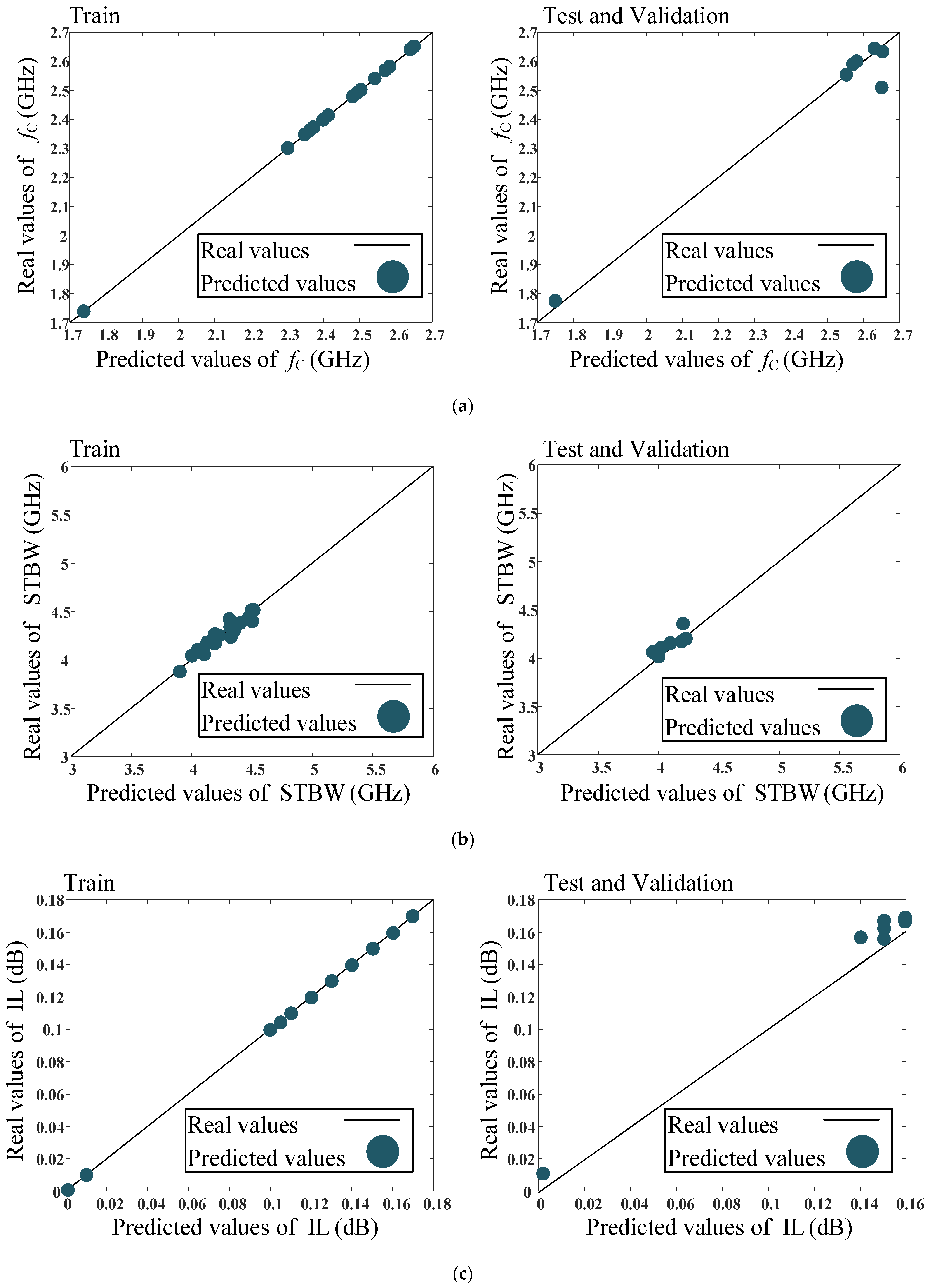
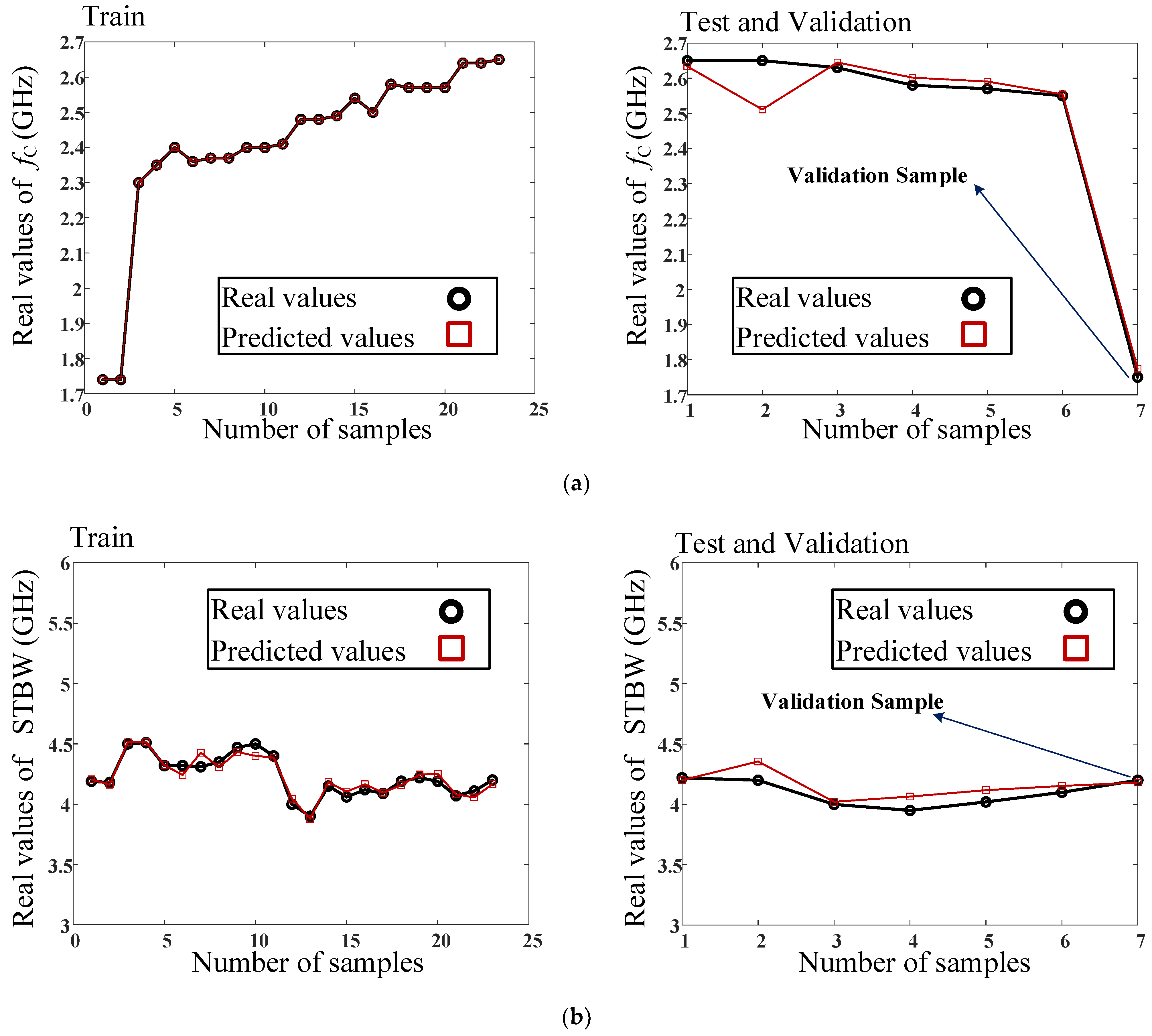
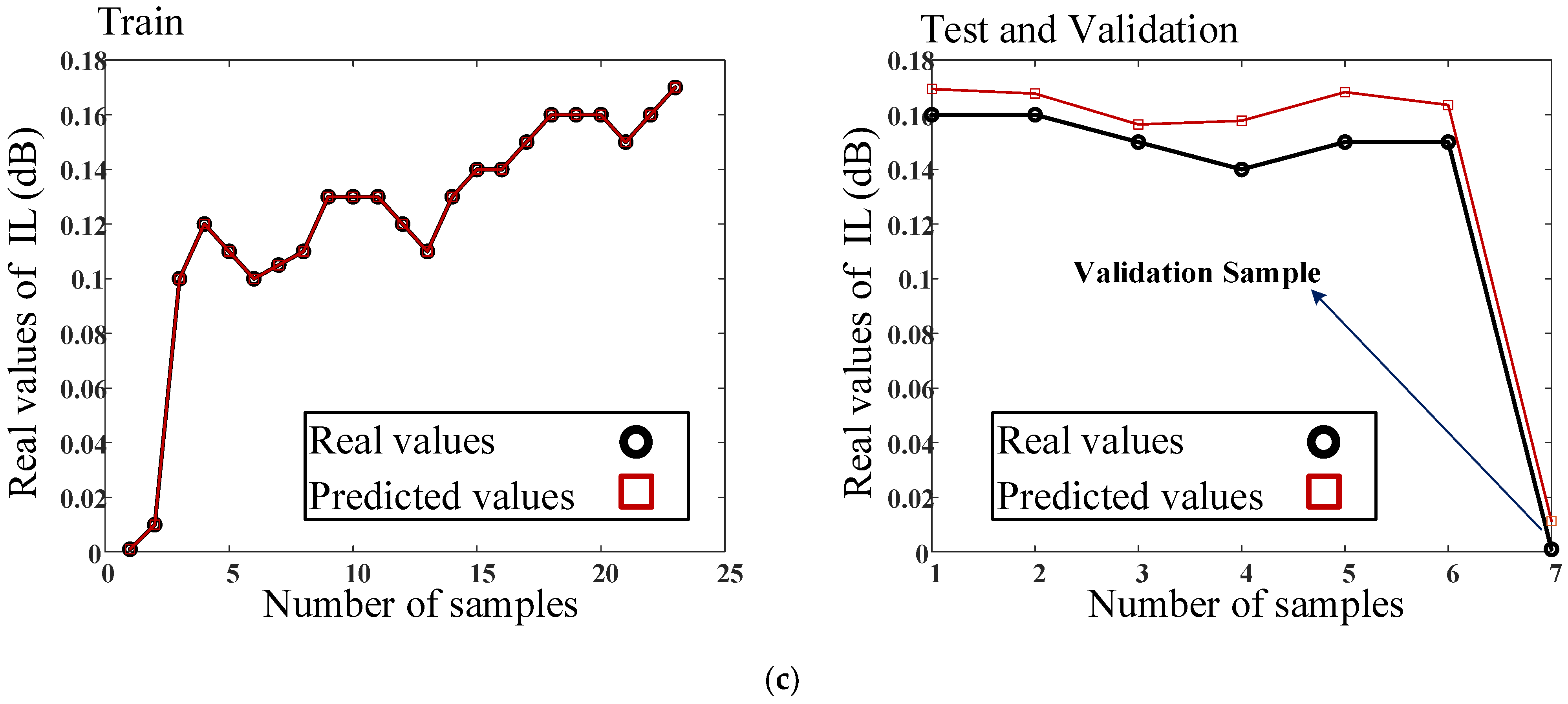



| Training Values and Design Parameters | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Input Parameters | Real Output Param. | Predicted Output Param. | ||||||||||||
| W1 (mm) | W2 (mm) | W3 (mm) | L1 (mm) | L2 (mm) | L3 (mm) | S1 (mm) | S2 (mm) | fc (GHz) | STBW (MHz) | IL (dB) | fc (GHz) | STBW (MHz) | IL (dB) | |
| 1 | 5 | 5.4 | 1.3 | 5 | 8.1 | 16.3 | 0.3 | 0.4 | 1.74 | 4.19 | 0.01 | 1.740 | 4.206 | 0.001 |
| 2 | 5 | 5.2 | 1.3 | 5 | 8.1 | 16.3 | 0.3 | 0.5 | 1.74 | 4.18 | 0.01 | 1.740 | 4.162 | 0.010 |
| 3 | 4 | 4.2 | 0.8 | 4 | 6.7 | 12.9 | 0.3 | 0.3 | 2.3 | 4.5 | 0.1 | 2.300 | 4.513 | 0.100 |
| 4 | 4 | 4.2 | 0.7 | 4 | 6.7 | 12.9 | 0.2 | 0.3 | 2.35 | 4.51 | 0.12 | 2.350 | 4.514 | 0.120 |
| 5 | 4 | 4.2 | 0.7 | 3.8 | 6.7 | 12.9 | 0.2 | 0.4 | 2.4 | 4.32 | 0.11 | 2.400 | 4.323 | 0.110 |
| 6 | 4 | 4.2 | 0.8 | 3.8 | 6.7 | 12.9 | 0.2 | 0.4 | 2.36 | 4.32 | 0.1 | 2.360 | 4.242 | 0.100 |
| 7 | 4 | 4.2 | 0.9 | 3.8 | 6.7 | 12.9 | 0.2 | 0.3 | 2.37 | 4.31 | 0.11 | 2.370 | 4.427 | 0.105 |
| 8 | 4 | 4 | 0.8 | 3.8 | 6.7 | 12.9 | 0.3 | 0.4 | 2.37 | 4.35 | 0.11 | 2.370 | 4.306 | 0.110 |
| 9 | 3.8 | 4 | 0.8 | 3.8 | 6.7 | 12 | 0.2 | 0.3 | 2.4 | 4.47 | 0.13 | 2.400 | 4.432 | 0.130 |
| 10 | 3.8 | 4 | 0.9 | 3.8 | 6.7 | 12 | 0.2 | 0.3 | 2.4 | 4.5 | 0.13 | 2.400 | 4.401 | 0.130 |
| 11 | 3.8 | 3.8 | 0.9 | 3.8 | 6.7 | 12 | 0.3 | 0.3 | 2.41 | 4.4 | 0.13 | 2.410 | 4.385 | 0.130 |
| 12 | 3.8 | 3.8 | 0.9 | 3.8 | 6.7 | 11.8 | 0.2 | 0.4 | 2.48 | 4 | 0.12 | 2.480 | 4.046 | 0.120 |
| 13 | 3.8 | 3.8 | 1 | 3.8 | 6.7 | 11.8 | 0.2 | 0.4 | 2.48 | 3.9 | 0.11 | 2.480 | 3.879 | 0.110 |
| 14 | 3.8 | 3.8 | 0.8 | 3.8 | 6.7 | 11.8 | 0.2 | 0.4 | 2.49 | 4.15 | 0.13 | 2.490 | 4.182 | 0.130 |
| 15 | 3.6 | 3.8 | 0.8 | 3.8 | 6.7 | 11.8 | 0.4 | 0.4 | 2.54 | 4.06 | 0.14 | 2.540 | 4.104 | 0.140 |
| 16 | 3.6 | 3.8 | 0.8 | 3.8 | 6.7 | 11.6 | 0.3 | 0.4 | 2.5 | 4.12 | 0.14 | 2.500 | 4.165 | 0.140 |
| 17 | 3.6 | 3.8 | 0.8 | 3.8 | 6.5 | 11.6 | 0.3 | 0.4 | 2.58 | 4.09 | 0.15 | 2.580 | 4.095 | 0.150 |
| 18 | 3.6 | 3.8 | 0.7 | 3.8 | 6.5 | 11.6 | 0.3 | 0.4 | 2.57 | 4.19 | 0.16 | 2.570 | 4.158 | 0.160 |
| 19 | 3.6 | 3.8 | 0.7 | 3.8 | 6.5 | 11.6 | 0.3 | 0.3 | 2.57 | 4.22 | 0.16 | 2.570 | 4.246 | 0.160 |
| 20 | 3.6 | 4 | 0.7 | 3.8 | 6.5 | 11.6 | 0.2 | 0.3 | 2.57 | 4.19 | 0.16 | 2.570 | 4.252 | 0.160 |
| 21 | 3.4 | 4 | 0.8 | 3.8 | 6.5 | 11.6 | 0.4 | 0.3 | 2.64 | 4.07 | 0.15 | 2.640 | 4.081 | 0.150 |
| 22 | 3.4 | 4 | 0.7 | 3.8 | 6.5 | 11.6 | 0.4 | 0.3 | 2.64 | 4.11 | 0.16 | 2.640 | 4.055 | 0.160 |
| 23 | 3.4 | 4 | 0.7 | 3.8 | 6.5 | 11.2 | 0.2 | 0.3 | 2.65 | 4.2 | 0.17 | 2.650 | 4.166 | 0.170 |
| Testing Values | ||||||||||||||
| Input Parameters | Real Output Param. | Predicted Output Param. | ||||||||||||
| W1 (mm) | W2 (mm) | W3 (mm) | L1 (mm) | L2 (mm) | L3 (mm) | S1 (mm) | S2 (mm) | fc (GHz) | STBW (MHz) | IL (dB) | fc (GHz) | STBW (MHz) | IL (dB) | |
| 1 | 3.4 | 4 | 0.8 | 3.8 | 6.5 | 11.2 | 0.2 | 0.3 | 2.65 | 4.22 | 0.16 | 2.633 | 4.200 | 0.169 |
| 2 | 3.4 | 4 | 0.8 | 3.8 | 6.5 | 11.2 | 0.2 | 0.2 | 2.65 | 4.2 | 0.16 | 2.511 | 4.355 | 0.167 |
| 3 | 3.4 | 3.8 | 0.8 | 3.8 | 6.5 | 11.2 | 0.3 | 0.4 | 2.63 | 4 | 0.15 | 2.644 | 4.021 | 0.156 |
| 4 | 3.4 | 3.8 | 0.8 | 4 | 6.5 | 11.2 | 0.3 | 0.4 | 2.58 | 3.95 | 0.14 | 2.601 | 4.064 | 0.157 |
| 5 | 3.4 | 3.8 | 0.7 | 4 | 6.5 | 11.2 | 0.3 | 0.4 | 2.57 | 4.02 | 0.15 | 2.590 | 4.117 | 0.168 |
| 6 | 3.4 | 3.8 | 0.7 | 4 | 6.6 | 11.2 | 0.3 | 0.4 | 2.55 | 4.1 | 0.15 | 2.554 | 4.152 | 0.163 |
| Validation Values | ||||||||||||||
| Input Parameters | Real Output Param. | Predicted Output Param. | ||||||||||||
| W1 (mm) | W2 (mm) | W3 (mm) | L1 (mm) | L2 (mm) | L3 (mm) | S1 (mm) | S2 (mm) | fc (GHz) | STBW (MHz) | IL (dB) | fc (GHz) | STBW (MHz) | IL (dB) | |
| 1 | 5 | 5.4 | 1.2 | 5 | 8.1 | 16.3 | 0.4 | 0.4 | 1.75 | 4.2 | 0.01 | 1.774 | 4.180 | 0.011 |
| fc (GHz) Errors | STBW (MHz) Errors | IL (dB) Errors | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Train | Test | Valid. | Train | Test | Valid. | Train | Test | Valid. | |
| MRE | 2.45 × 10−15 | 0.0137 | 0.0139 | 0.0088 | 0.0189 | 0.0046 | 7.48 × 10−14 | 0.0816 | 10.3425 |
| RMSE | 6.78 × 10−15 | 0.0587 | 0.0243 | 0.0471 | 0.0918 | 0.0191 | 6.64 × 10−16 | 0.0131 | 0.0103 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yahya, S.I.; Roshani, S.; Ami, M.; Ghadi, Y.Y.; Chaudhary, M.A.; Roshani, S. A Compact Rat-Race Coupler with Harmonic Suppression for GSM Applications: Design and Implementation Using Artificial Neural Network. Micromachines 2023, 14, 1294. https://doi.org/10.3390/mi14071294
Yahya SI, Roshani S, Ami M, Ghadi YY, Chaudhary MA, Roshani S. A Compact Rat-Race Coupler with Harmonic Suppression for GSM Applications: Design and Implementation Using Artificial Neural Network. Micromachines. 2023; 14(7):1294. https://doi.org/10.3390/mi14071294
Chicago/Turabian StyleYahya, Salah I., Saeed Roshani, Mohammad Ami, Yazeed Yasin Ghadi, Muhammad Akmal Chaudhary, and Sobhan Roshani. 2023. "A Compact Rat-Race Coupler with Harmonic Suppression for GSM Applications: Design and Implementation Using Artificial Neural Network" Micromachines 14, no. 7: 1294. https://doi.org/10.3390/mi14071294
APA StyleYahya, S. I., Roshani, S., Ami, M., Ghadi, Y. Y., Chaudhary, M. A., & Roshani, S. (2023). A Compact Rat-Race Coupler with Harmonic Suppression for GSM Applications: Design and Implementation Using Artificial Neural Network. Micromachines, 14(7), 1294. https://doi.org/10.3390/mi14071294









