Highly Reliable Multicomponent MEMS Sensor for Predictive Maintenance Management of Rolling Bearings
Abstract
:1. Introduction
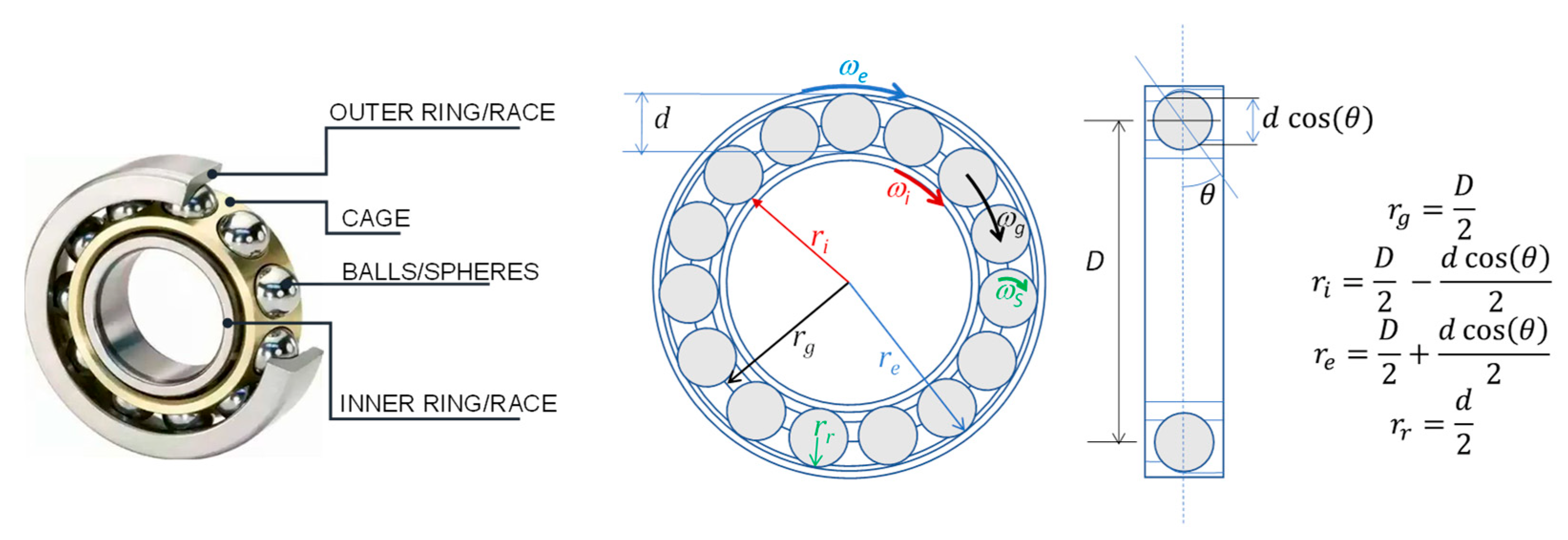
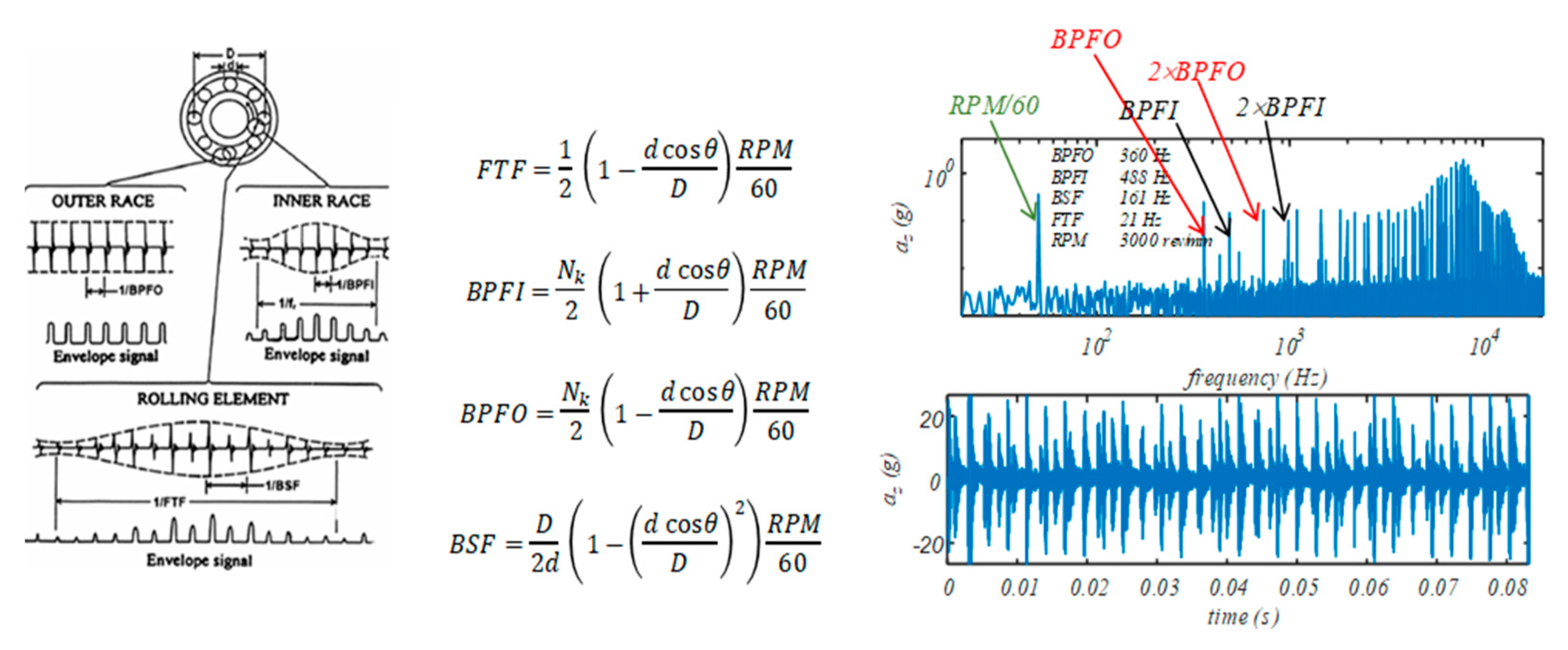
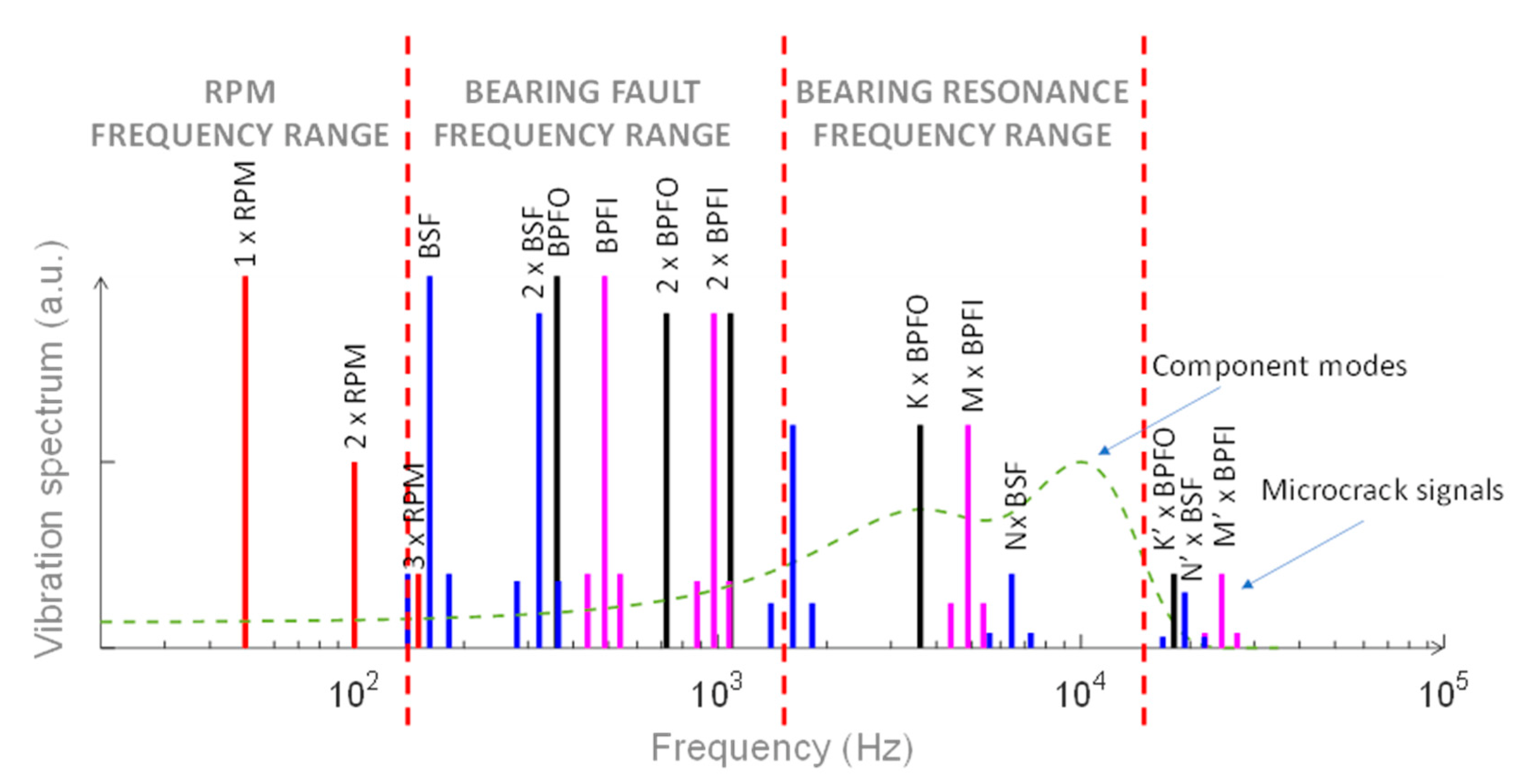
2. Vibration-Based Rolling Bearings Fault Diagnosis: A Brief Survey
3. Materials and Method
3.1. The MDUT and Embedded Sensing Elements
3.2. Calibration Procedures
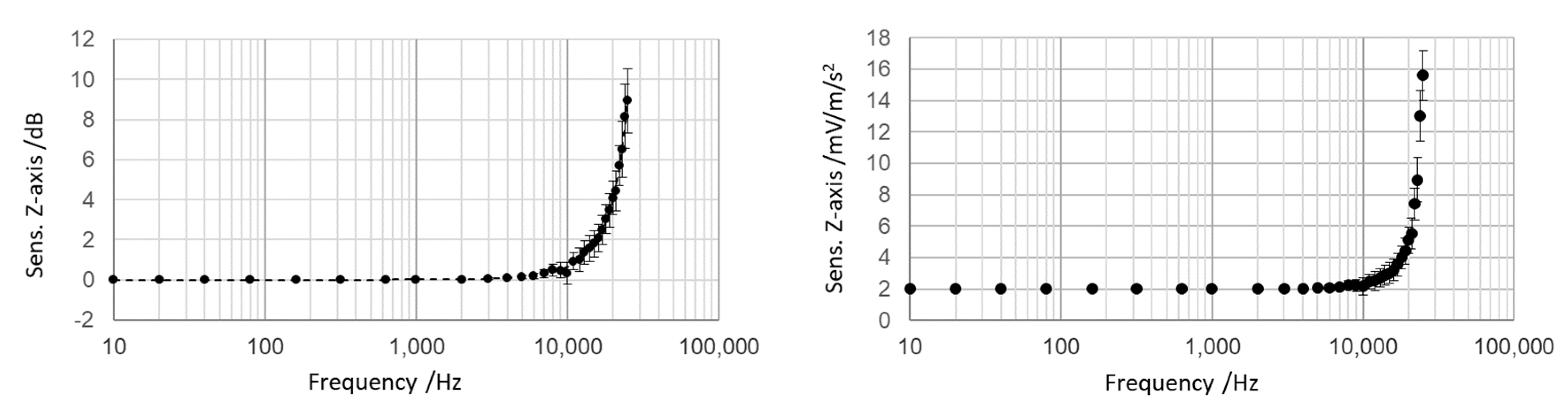
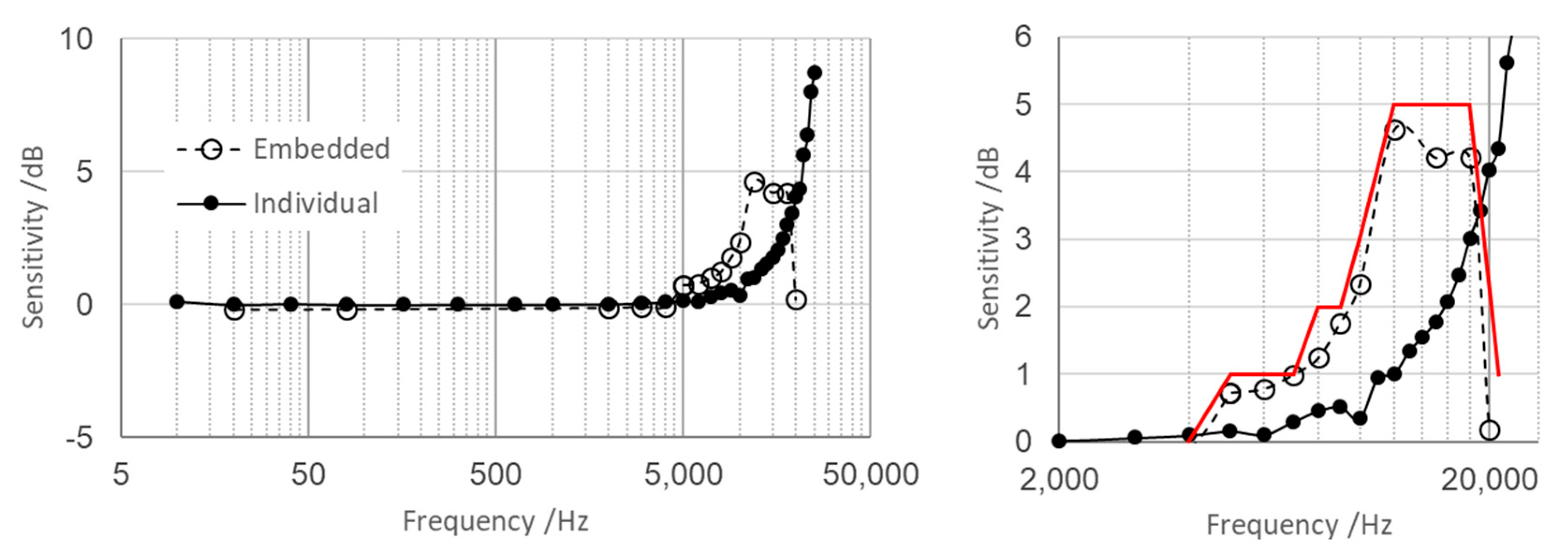
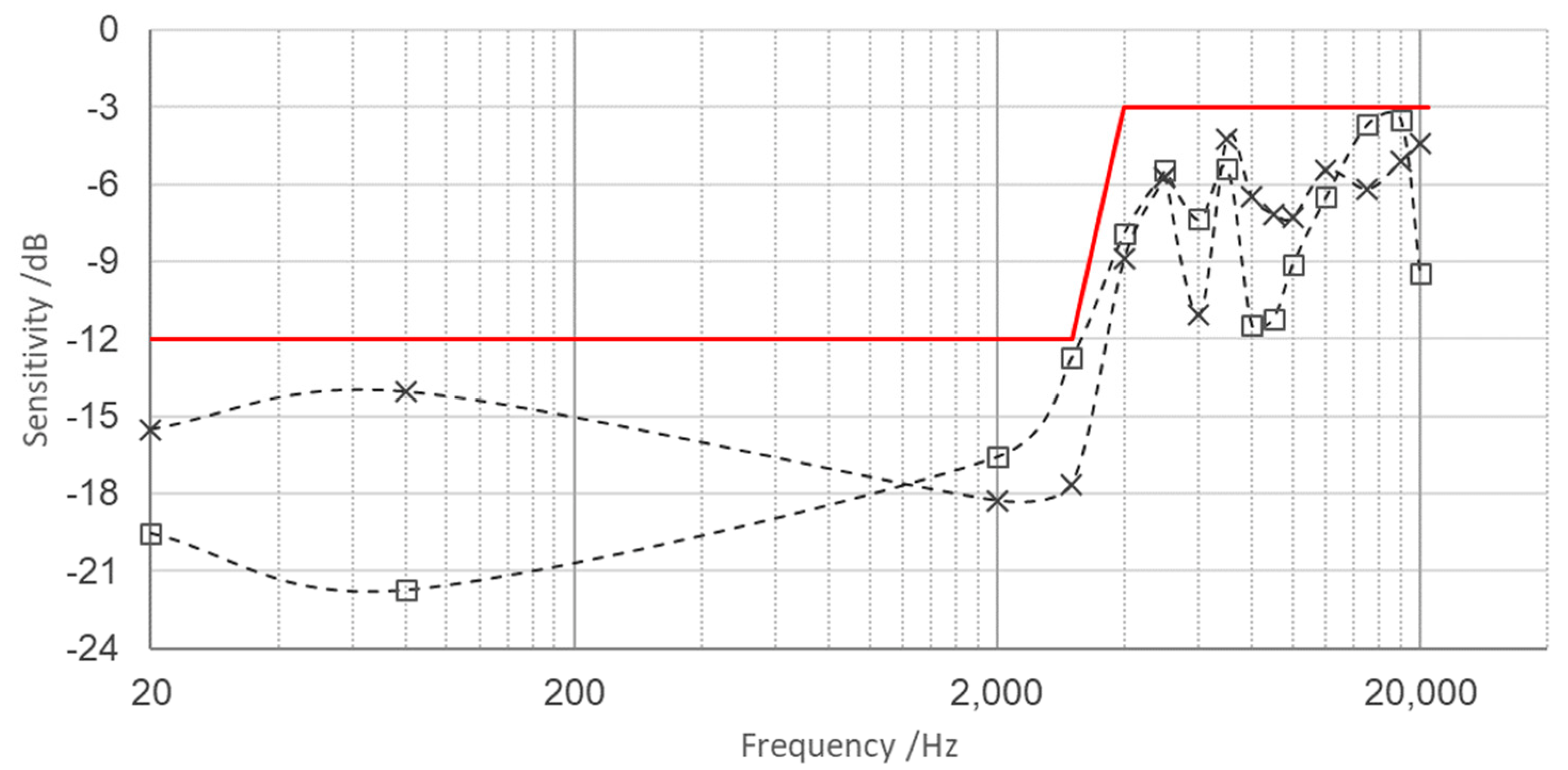
3.3. Calibration Results
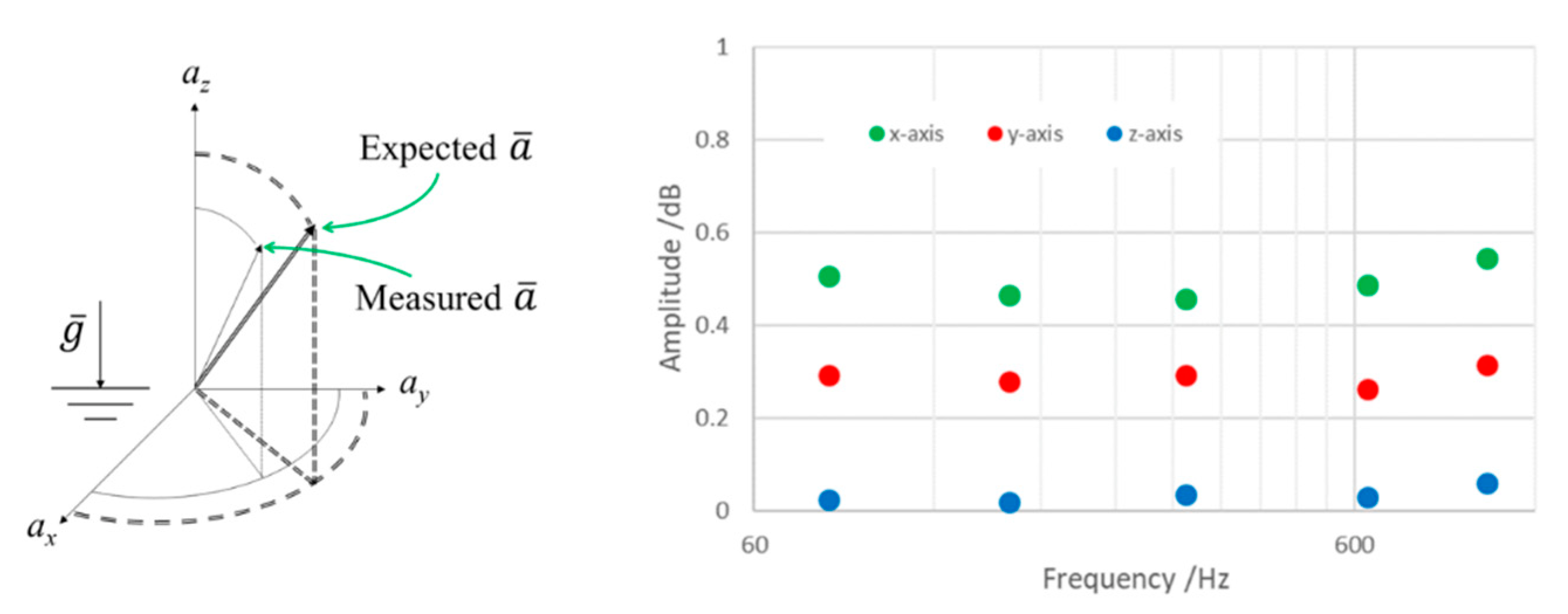
3.4. Metrological Characterization
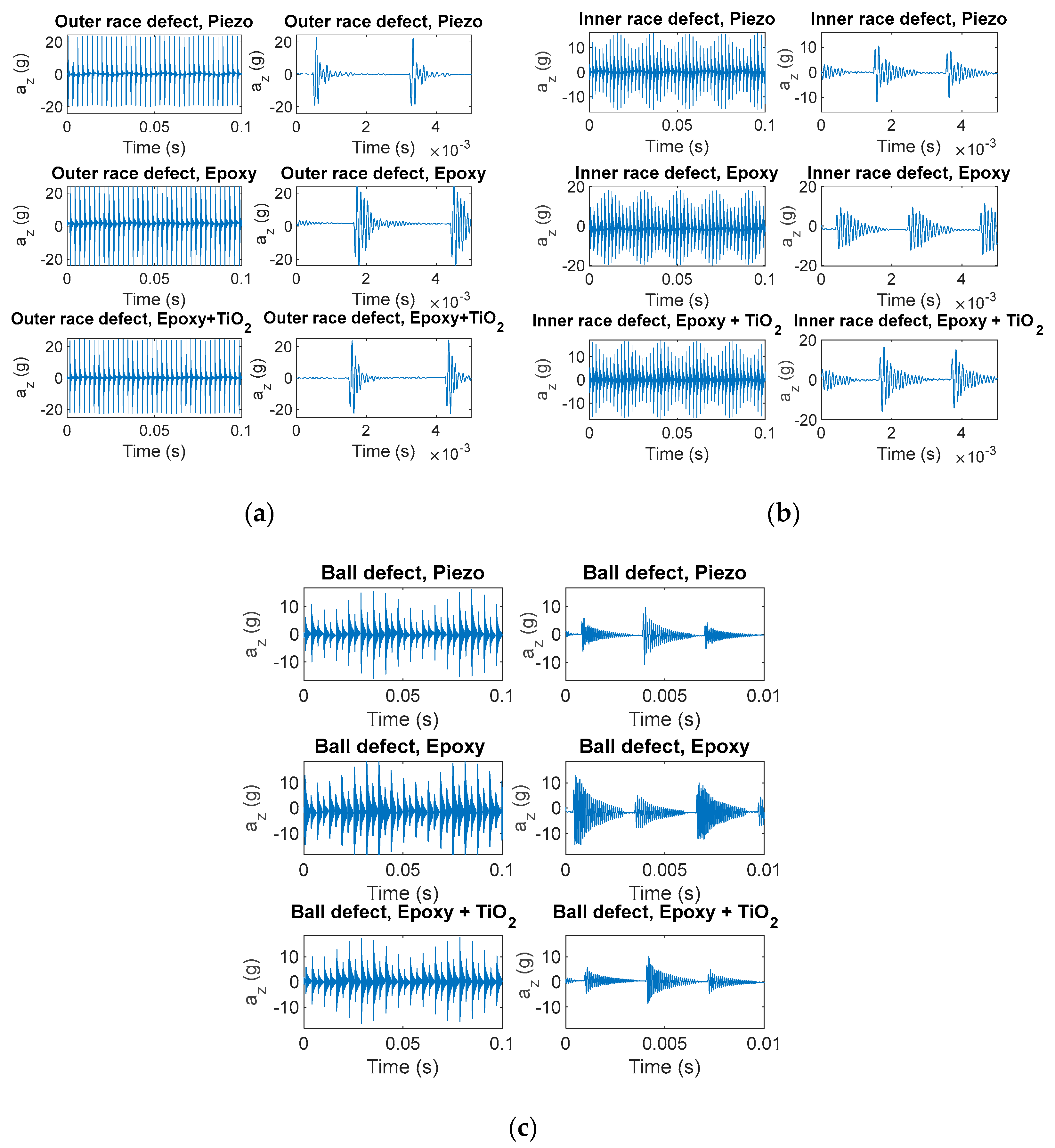
3.5. The Role of the Embedding Resin Case: Actualization of a “Mechanical Filter”
4. Reinforced Resins: MDUTs Realization and Test through Case Studies
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Barai, V.; Ramteke, S.M.; Dhanalkotwar, V.; Nagmote, Y.; Shende, S.; Deshmukh, D. Bearing fault diagnosis using signal processing and machine learning techniques: A review. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2022; Volume 1259, p. 012034. [Google Scholar]
- Cen, J.; Yang, Z.; Liu, X.; Xiong, J.; Chen, H. A Review of Data-Driven Machinery Fault Diagnosis Using Machine Learning Algorithms. J. Vib. Eng. Technol. 2022, 10, 2481–2507. [Google Scholar] [CrossRef]
- Bertocco, M.; Fort, A.; Landi, E.; Mugnaini, M.; Parri, L.; Peruzzi, G.; Pozzebon, A. Roller Bearing Failures Classification with Low Computational Cost Embedded Machine Learning. In 2022 IEEE International Workshop on Metrology for Automotive (MetroAutomotive); IEEE: New York, NY, USA, 2022; pp. 12–17. [Google Scholar]
- Hakim, M.; Omran, A.A.B.; Ahmed, A.N.; Al-Waily, M.; Abdellatif, A. A systematic review of rolling bearing fault diagnoses based on deep learning and transfer learning: Taxonomy, overview, application, open challenges, weaknesses and recommendations. Ain Shams Eng. J. 2022, 14, 101945. [Google Scholar] [CrossRef]
- Mushtaq, S.; Islam, M.M.; Sohaib, M. Deep learning aided Data-Driven fault diagnosis of rotatory machine: A comprehensive review. Energies 2021, 14, 5150. [Google Scholar] [CrossRef]
- Gawde, S.; Patil, S.; Kumar, S.; Kotecha, K. A scoping review on multi-fault diagnosis of industrial rotating machines using multi-sensor data fusion. Artif. Intell. Rev. 2022, 55, 1–54. [Google Scholar] [CrossRef]
- Anwarsha, A.; Narendiranath Babu, T. Recent advancements of signal processing and artificial intelligence in the fault detection of rolling element bearings: A review. J. Vibroengineering 2022, 24, 1027–1055. [Google Scholar] [CrossRef]
- Jiao, J.; Zhao, M.; Lin, J.; Liang, K. A comprehensive review on convolutional neural network in machine fault diagnosis. Neurocomputing 2020, 417, 36–63. [Google Scholar] [CrossRef]
- Jieyang, P.; Kimmig, A.; Dongkun, W.; Niu, Z.; Zhi, F.; Jiahai, W.; Ovtcharova, J. A systematic review of data-driven approaches to fault diagnosis and early warning. J. Intell. Manuf. 2022, 33, 1–28. [Google Scholar] [CrossRef]
- Zhao, Z.; Wu, J.; Li, T.; Sun, C.; Yan, R.; Chen, X. Challenges and opportunities of AI-enabled monitoring, diagnosis & prognosis: A review. Chin. J. Mech. Eng. 2021, 34, 1–29. [Google Scholar]
- Yang, Z.; Xu, B.; Luo, W.; Chen, F. Autoencoder-based representation learning and its application in intelligent fault diagnosis: A review. Measurement 2021, 189, 110460. [Google Scholar] [CrossRef]
- Gonzalez-Jimenez, D.; Del-Olmo, J.; Poza, J.; Garramiola, F.; Madina, P. Data-driven fault diagnosis for electric drives: A review. Sensors 2021, 21, 4024. [Google Scholar] [CrossRef]
- Caiazzo, B.; Di Nardo, M.; Murino, T.; Petrillo, A.; Piccirillo, G.; Santini, S. Towards Zero Defect Manufacturing paradigm: A review of the state-of-the-art methods and open challenges. Comput. Ind. 2022, 134, 103548. [Google Scholar] [CrossRef]
- Wu, G.; Yan, T.; Yang, G.; Chai, H.; Cao, C. A Review on Rolling Bearing Fault Signal Detection Methods Based on Different Sensors. Sensors 2022, 22, 8330. [Google Scholar] [CrossRef]
- Yakhni, M.F.; Cauet, S.; Sakout, A.; Assoum, H.; Etien, E.; Rambault, L.; El-Gohary, M. Variable speed induction motors’ fault detection based on transient motor current signatures analysis: A review. Mech. Syst. Signal Process. 2023, 184, 109737. [Google Scholar] [CrossRef]
- Davari, N.; Veloso, B.; Costa, G.D.A.; Pereira, P.M.; Ribeiro, R.P.; Gama, J. A survey on data-driven predictive maintenance for the railway industry. Sensors 2021, 21, 5739. [Google Scholar] [CrossRef]
- Li, W.; Huang, R.; Li, J.; Liao, Y.; Chen, Z.; He, G.; Gryllias, K. A perspective survey on deep transfer learning for fault diagnosis in industrial scenarios: Theories, applications and challenges. Mech. Syst. Signal Process. 2022, 167, 108487. [Google Scholar] [CrossRef]
- Abbassi, R.; Arzaghi, E.; Yazdi, M.; Aryai, V.; Garaniya, V.; Rahnamayiezekavat, P. Risk-based and predictive maintenance planning of engineering infrastructure: Existing quantitative techniques and future directions. Process. Saf. Environ. Prot. 2022, 165, 776–790. [Google Scholar] [CrossRef]
- Liu, C.; Cichon, A.; Królczyk, G.; Li, Z. Technology development and commercial applications of industrial fault diagnosis system: A review. Int. J. Adv. Manuf. Technol. 2021, 118, 3497–3529. [Google Scholar] [CrossRef]
- Mohd Ghazali, M.H.; Rahiman, W. Vibration analysis for machine monitoring and diagnosis: A systematic review. Shock. Vib. 2021, 2021, 9469318. [Google Scholar] [CrossRef]
- Mohamed, A.; Hassan, M.; M’Saoubi, R.; Attia, H. Tool Condition Monitoring for High-Performance Machining Systems—A Review. Sensors 2022, 22, 2206. [Google Scholar] [CrossRef]
- Fanti, G.; Spinazzè, A.; Borghi, F.; Rovelli, S.; Campagnolo, D.; Keller, M.; Cavallo, D.M. Evolution and applications of recent sensing technology for occupational risk assessment: A rapid review of the literature. Sensors 2022, 22, 4841. [Google Scholar] [CrossRef]
- Tiboni, M.; Remino, C.; Bussola, R.; Amici, C. A Review on Vibration-Based Condition Monitoring of Rotating Machinery. Appl. Sci. 2022, 12, 972. [Google Scholar] [CrossRef]
- Prato, A.; Mazzoleni, F.; D’Emilia, G.; Gaspari, A.; Natale, E.; Schiavi, A. Metrological traceability of a digital 3-axis MEMS accelerometers sensor network. Measurement 2021, 184, 109925. [Google Scholar] [CrossRef]
- BIPM—Consultative Committee for Acoustics, Ultrasound, and Vibration (CCAUV). Strategy Plan 2019 to 2029; BIPM—Consultative Committee for Acoustics, Ultrasound, and Vibration (CCAUV): Paris, France, 2019. [Google Scholar]
- Available online: https://www.analog.com/media/en/technical-documentation/data-sheets/ADXL1001-1002.pdf (accessed on 10 December 2022).
- Den Hartog, J.P. Mechanical Vibrations, 1st ed.; McGraw-Hill Book Company, Inc.: New York, NY, USA, 1934. [Google Scholar]
- Lv, Y.; Zhao, W.; Zhao, Z.; Li, W.; Ng, K.K. Vibration signal-based early fault prognosis: Status quo and applications. Adv. Eng. Inform. 2022, 52, 101609. [Google Scholar] [CrossRef]
- Althubaiti, A.; Elasha, F.; Teixeira, J.A. Fault diagnosis and health management of bearings in rotating equipment based on vibration analysis—A review. J. Vibroeng. 2022, 24, 46–74. [Google Scholar] [CrossRef]
- Tama, B.A.; Vania, M.; Lee, S.; Lim, S. Recent advances in the application of deep learning for fault diagnosis of rotating machinery using vibration signals. Artif. Intell. Rev. 2022, 55, 1–43. [Google Scholar] [CrossRef]
- Ali, A.; Abdelhadi, A. Condition-Based Monitoring and Maintenance: State of the Art Review. Appl. Sci. 2022, 12, 688. [Google Scholar] [CrossRef]
- Yan, G.; Chen, J.; Bai, Y.; Yu, C.; Yu, C. A Survey on Fault Diagnosis Approaches for Rolling Bearings of Railway Vehicles. Processes 2022, 10, 724. [Google Scholar] [CrossRef]
- Ma, J.; Li, C.; Zhang, G. Rolling bearing fault diagnosis based on deep learning and autoencoder information fusion. Symmetry 2021, 14, 13. [Google Scholar] [CrossRef]
- Shi, H.; Li, Y.; Bai, X.; Zhang, K.; Sun, X. A two-stage sound-vibration signal fusion method for weak fault detection in rolling bearing systems. Mech. Syst. Signal Process. 2022, 172, 109012. [Google Scholar] [CrossRef]
- Zhou, Y.; Yan, S.; Ren, Y.; Liu, S. Rolling bearing fault diagnosis using transient-extracting transform and linear discriminant analysis. Measurement 2021, 178, 109298. [Google Scholar] [CrossRef]
- Xu, M.; Wang, Y. An imbalanced fault diagnosis method for rolling bearing based on semi-supervised conditional generative adversarial network with spectral normalization. IEEE Access 2021, 9, 27736–27747. [Google Scholar] [CrossRef]
- Zhang, K.; Xu, Y.; Liao, Z.; Song, L.; Chen, P. A novel Fast Entrogram and its applications in rolling bearing fault diagnosis. Mech. Syst. Signal Process. 2021, 154, 107582. [Google Scholar] [CrossRef]
- Karpat, F.; Kalay, O.C.; Dirik, A.E.; Doğan, O.; Korcuklu, B.; Yüce, C. Convolutional neural networks based rolling bearing fault classification under variable operating conditions. In Proceedings of the 2021 International Conference on INnovations in Intelligent SysTems and Applications (INISTA), Kocaeli, Turkey, 25–27 August 2021; pp. 1–6. [Google Scholar]
- Matsushita, O.; Tanaka, M.; Kobayashi, M.; Keogh, P.; Kanki, H. Vibration of Rolling Element Bearings. In Vibrations of Rotating Machinery; Springer: Tokyo, Japan, 2019; pp. 87–114. [Google Scholar]
- Tom, K.F. A Primer on Vibrational Ball Bearing Feature Generation for Prognostics and Diagnostics Algorithms; Army Research Lab Adelphi Md Sensors and Electron Devices Directorate: Adelphi, MD, USA, 2015. [Google Scholar]
- Kim, S.; An, D.; Choi, J.H. Diagnostics 101: A tutorial for fault diagnostics of rolling element bearing using envelope analysis in matlab. Appl. Sci. 2020, 10, 7302. [Google Scholar] [CrossRef]
- Jain, P.H.; Bhosle, S.P. A Review on Vibration Signal Analysis Techniques Used for Detection of Rolling Element Bearing Defects. SSRG Int. J. Mech. Eng. 2021, 8, 14–29. [Google Scholar] [CrossRef]
- Shakya, P.; Darpe, A.K.; Kulkarni, M.S. Vibration-based fault diagnosis in rolling element bearings: Ranking of various time, frequency and time-frequency domain data-based damage identi cation parameters. Int. J. Cond. Monit. 2013, 3, 53–62. [Google Scholar] [CrossRef]
- ISO 16063-11:1999; Methods for the Calibration of Vibration and Shock Transducers—Part 11: Primary Vibration Calibration by Laser Interferometry. International Organization for Standardization ISO Central Secretariat: Geneva, Switzerland, 1999.
- ISO 16063-21:2003; Methods for the Calibration of Vibration and Shock Transducers—Part 21: Vibration Calibration by Comparison to a Reference Transducer. International Organization for Standardization ISO Central Secretariat: Geneva, Switzerland, 2003.
- Galetto, M.; Schiavi, A.; Genta, G.; Prato, A.; Mazzoleni, F. Uncertainty evaluation in calibration of low-cost digital MEMS accelerometers for advanced manufacturing applications. CIRP Ann. Manuf. Technol. 2019, 68, 535–538. [Google Scholar] [CrossRef]
- D’Emilia, G.; Gaspari, A.; Mazzoleni, F.; Natale, E.; Prato, A.; Schiavi, A. Metrological characterization of MEMS accelerometers by LDV. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2020; Volume 1589, p. 012011. [Google Scholar]
- D’Emilia, G.; Gaspari, A.; Mazzoleni, F.; Natale, E.; Schiavi, A. Calibration of tri-axial MEMS accelerometers in the low-frequency range. Part 2: Uncertainty assessment. J. Sens. Sens. Syst. 2018, 7, 403–410. [Google Scholar] [CrossRef]
- Prato, A.; Mazzoleni, F.; Schiavi, A. Traceability of digital 3-axis MEMS accelerometer: Simultaneous determination of main and transverse sensitivities in the frequency domain. Metrologia 2020, 57, 035013. [Google Scholar] [CrossRef]
- Prato, A.; Mazzoleni, F.; Schiavi, A. Evaluation and correction of systematic effects in a simultaneous 3-axis vibration calibration system. Acta Imeko 2020, 9, 388–393. [Google Scholar] [CrossRef]
- Gaitan, M.; Bautista, I.M.L.; Geist, J. Reduction of calibration uncertainty due to mounting of three-axis accelerometers using the intrinsic properties model. Metrologia 2021, 58, 035006. [Google Scholar] [CrossRef]
- Zega, V.; Nastro, A.; Ferrari, M.; Ardito, R.; Ferrari, V.; Corigliano, A. An Innovative Auxetic Electrically-Tunable Mems Mechanical Filter. In Proceedings of the 2022 IEEE 35th International Conference on Micro Electro Mechanical Systems Conference (MEMS), Tokyo, Japan, 9–13 January 2022; pp. 539–542. [Google Scholar]
- Yao, Z.; Zega, V.; Su, Y.; Corigliano, A. A metaplate in MEMS for innovative applications: Vibration isolation and tunable mechanical filters. In Proceedings of the 2020 IEEE Sensors, Virtual Conference, 25–28 October 2020; pp. 1–4. [Google Scholar]
- Cigada, A.; Lurati, M.; Redaelli, M.; Vanali, M. Mechanical performance and metrological characterization of MEMS accelerometers and application in modal analysis. In Proceedings of the IMAC XXV International Modal Analysis Conference, Orlando, FL, USA, 19–22 February 2007; pp. 19–22. [Google Scholar]
- Addabbo, T.; Fort, A.; Landi, E.; Moretti, R.; Mugnaini, M.; Parri, L.; Vignoli, V. A Characterization system for bearing condition monitoring sensors, a case study with a low power wireless Triaxial MEMS based sensor. In Proceedings of the 2020 IEEE International Workshop on Metrology for Industry 4.0 & IoT, Rome, Italy, 3–5 June 2020; pp. 11–15. [Google Scholar]
- Landi, E.; Parri, L.; Moretti, R.; Fort, A.; Mugnaini, M.; Vignoli, V. High Performance Analog MEMS for IoT Based Condition Monitoring, Characterization with a Bearing Failure Emulation Test Bench. In Proceedings of the 2022 IEEE International Workshop on Metrology for Automotive (MetroAutomotive), Modena, Italy, 4–6 July 2022; pp. 1–5. [Google Scholar]





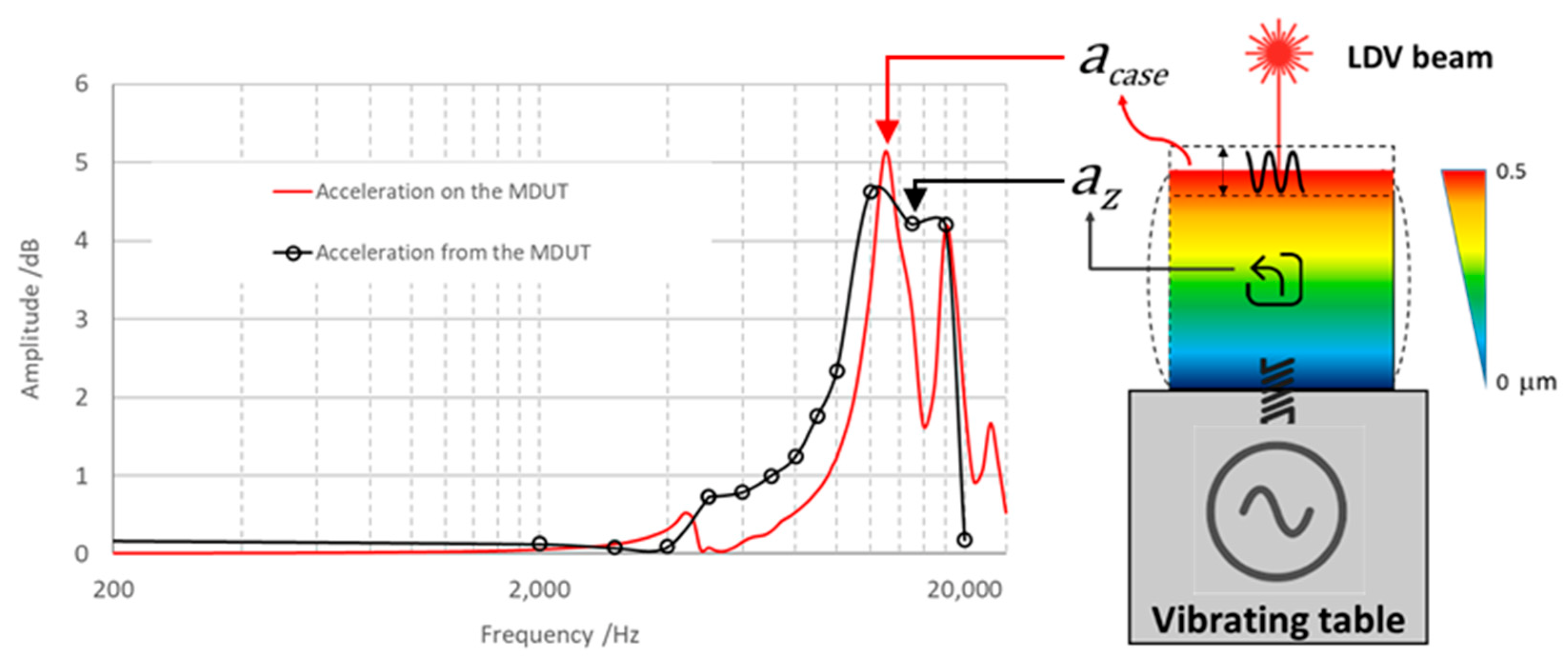
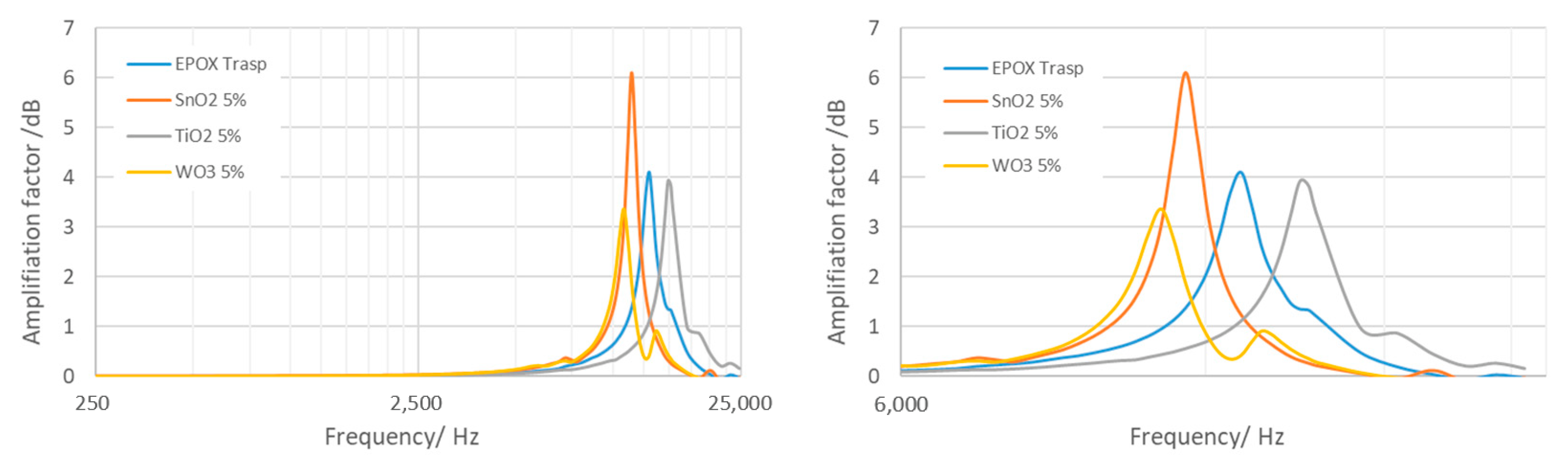

| Resin Case | Resonant Frequency /kHz | Quality Factor /- | Relative Amplification Factor /dB |
|---|---|---|---|
| Epoxy only resin | 13.1 | 3.0 | 4 |
| Epoxy with 5% SnO2 | 11.5 | 13.1 | 6 |
| Epoxy with 5% TiO2 | 15.2 | 2.6 | 4 |
| Epoxy with 5% WO3 | 10.8 | 2.4 | 3.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Landi, E.; Prato, A.; Fort, A.; Mugnaini, M.; Vignoli, V.; Facello, A.; Mazzoleni, F.; Murgia, M.; Schiavi, A. Highly Reliable Multicomponent MEMS Sensor for Predictive Maintenance Management of Rolling Bearings. Micromachines 2023, 14, 376. https://doi.org/10.3390/mi14020376
Landi E, Prato A, Fort A, Mugnaini M, Vignoli V, Facello A, Mazzoleni F, Murgia M, Schiavi A. Highly Reliable Multicomponent MEMS Sensor for Predictive Maintenance Management of Rolling Bearings. Micromachines. 2023; 14(2):376. https://doi.org/10.3390/mi14020376
Chicago/Turabian StyleLandi, Elia, Andrea Prato, Ada Fort, Marco Mugnaini, Valerio Vignoli, Alessio Facello, Fabrizio Mazzoleni, Michele Murgia, and Alessandro Schiavi. 2023. "Highly Reliable Multicomponent MEMS Sensor for Predictive Maintenance Management of Rolling Bearings" Micromachines 14, no. 2: 376. https://doi.org/10.3390/mi14020376
APA StyleLandi, E., Prato, A., Fort, A., Mugnaini, M., Vignoli, V., Facello, A., Mazzoleni, F., Murgia, M., & Schiavi, A. (2023). Highly Reliable Multicomponent MEMS Sensor for Predictive Maintenance Management of Rolling Bearings. Micromachines, 14(2), 376. https://doi.org/10.3390/mi14020376









