A Simple Model of the Energy Harvester within a Linear and Hysteresis Approach
Abstract
1. Introduction
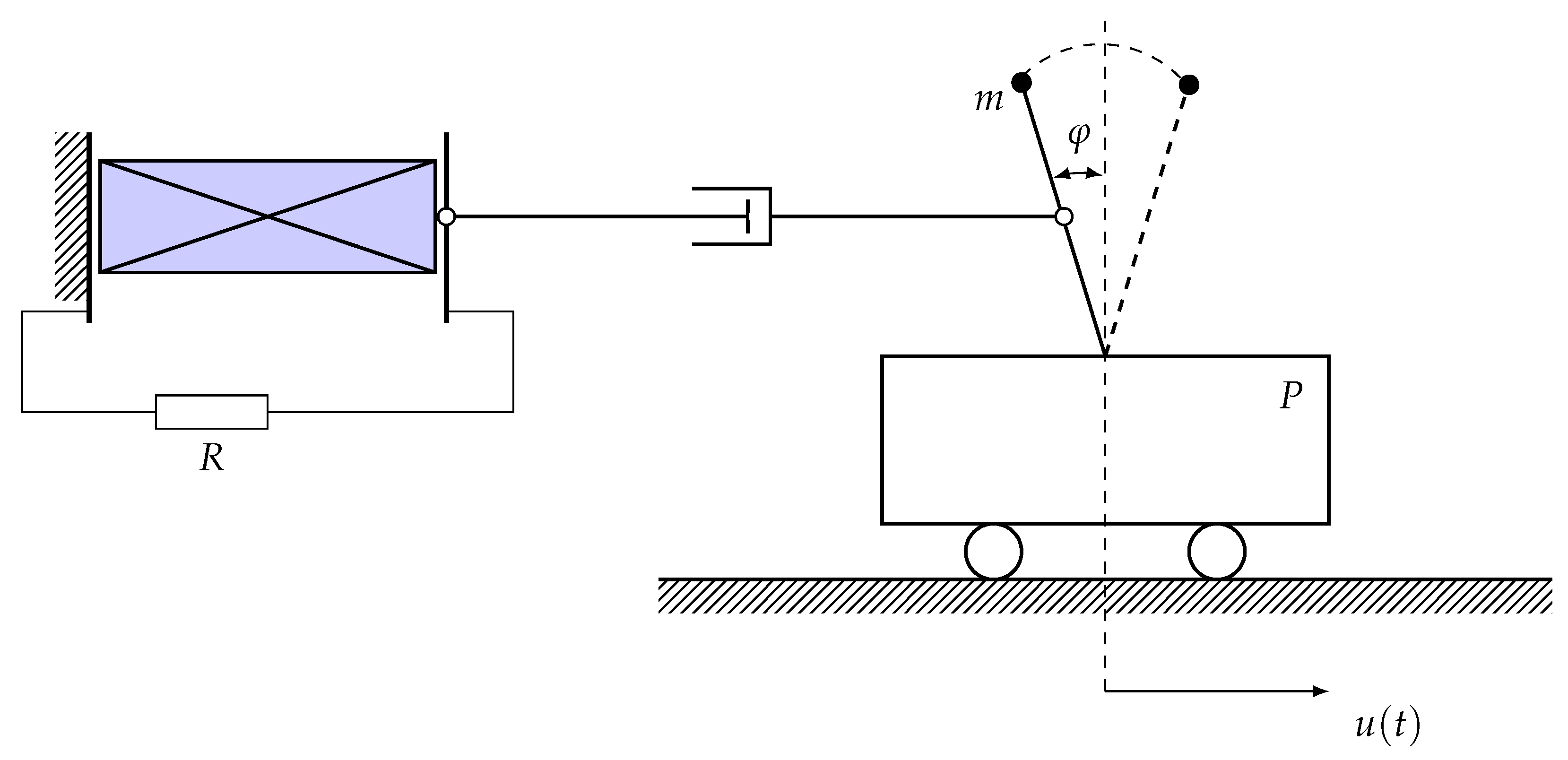
2. Energy Converter Model in Linear Approximation
2.1. Converting the System to a Dimensionless Form
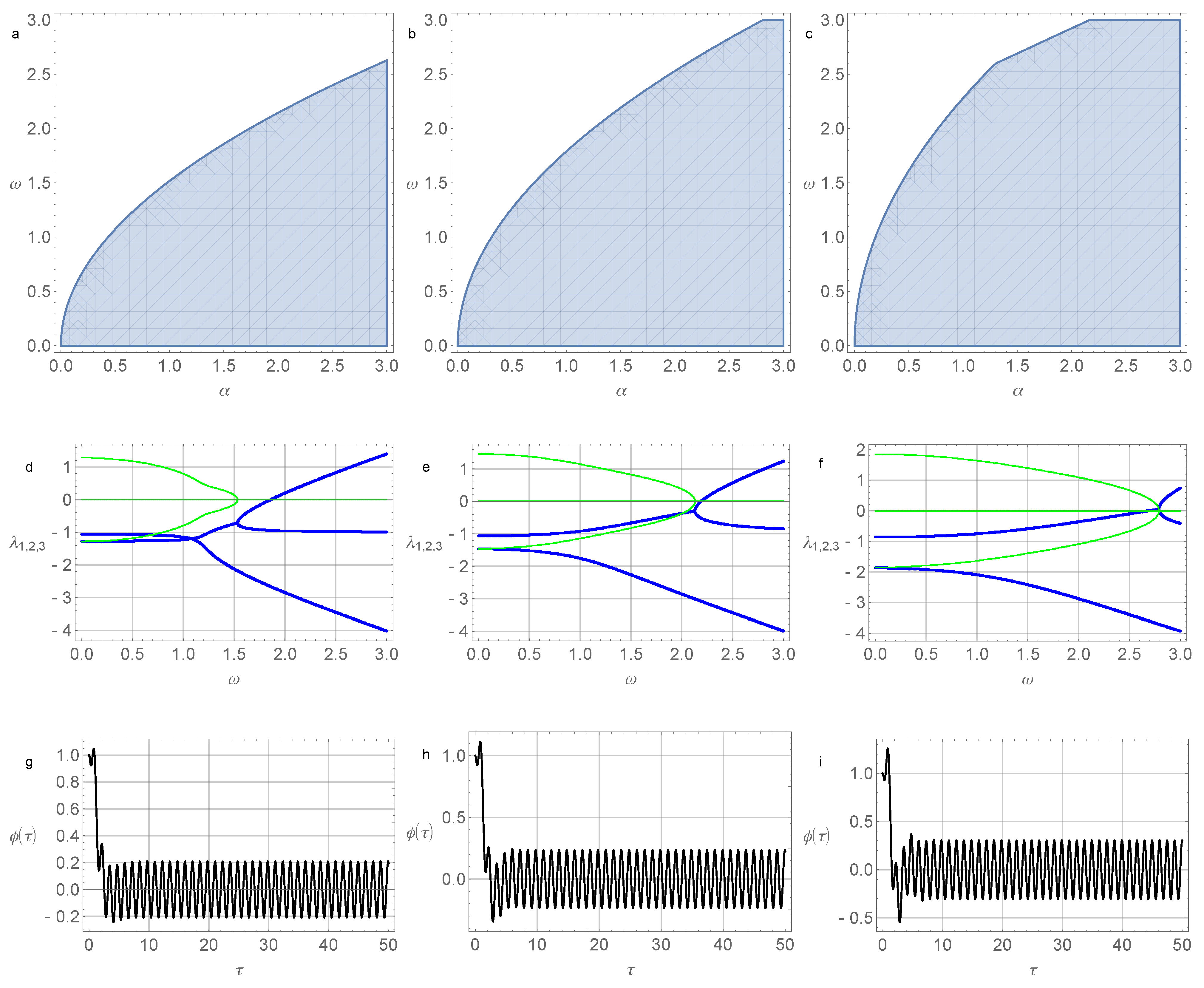
2.2. Investigation of the Stability of a Linearized System
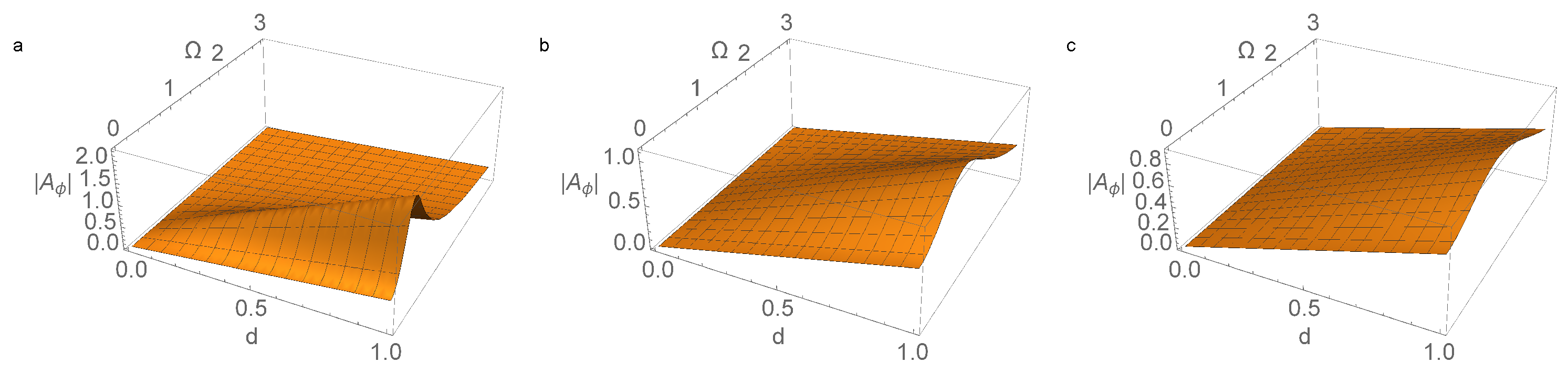
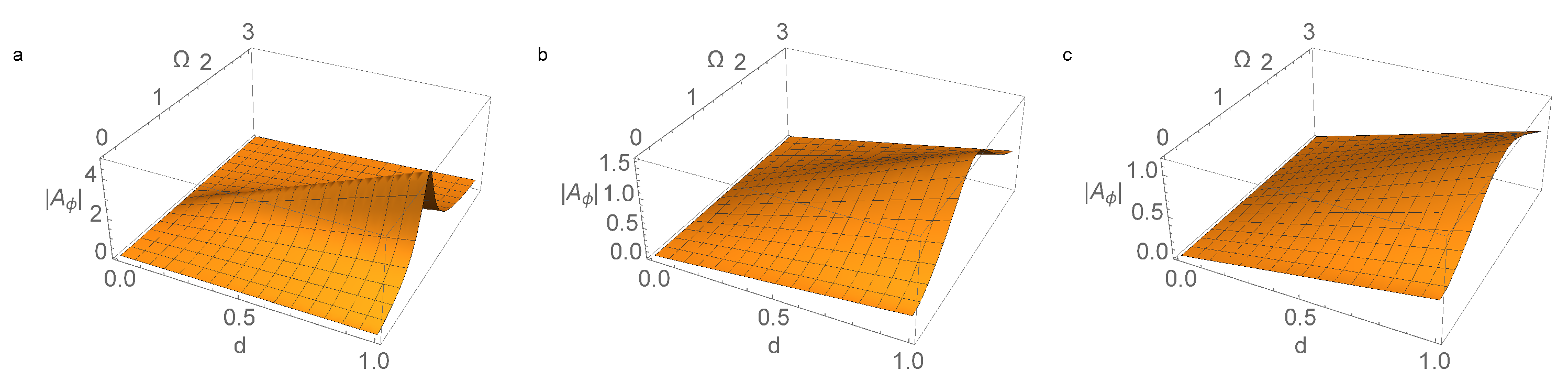
2.3. Amplitude Control of the Pendulum Oscillation
3. Hysteresis Dependencies in the Energy Harvester Model
3.1. System with Hysteresis Friction within the Preisach Model
3.2. Bouc–Wen Model
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Daqaq, M.F. On intentional introduction of stiffness nonlinearities for energy harvesting under white Gaussian excitations. Nonlinear Dyn. 2012, 69, 1063–1079. [Google Scholar] [CrossRef]
- Daqaq, M.F.; Masana, R.; Erturk, A.; Quinn, D.D. On the Role of Nonlinearities in Vibratory Energy Harvesting: A Critical Review and Discussion. Appl. Mech. Rev. 2014, 66, 040801. [Google Scholar] [CrossRef]
- Ghouli, Z.; Belhaq, M. Energy harvesting in a delay-induced parametric van der Pol–Duffing oscillator. Eur. Phys. J. Spec. Top. 2021, 230, 3591–3598. [Google Scholar] [CrossRef]
- Renno, J.M.; Daqaq, M.F.; Inman, D.J. On the optimal energy harvesting from a vibration source. J. Sound Vib. 2009, 320, 386–405. [Google Scholar] [CrossRef]
- Belhaq, M.; Hamdi, M. Energy harvesting from quasi-periodic vibrations. Nonlinear Dyn. 2016, 86, 2193–2205. [Google Scholar] [CrossRef]
- Ghouli, Z.; Hamdi, M.; Belhaq, M. Energy Harvesting in a Duffing Oscillator with Modulated Delay Amplitude, 2021. In IUTAM Symposium on Exploiting Nonlinear Dynamics for Engineering Systems; IUTAM, Bookseries; Kovacic, I., Lenci, S., Eds.; Springer: Cham, Switzerland, 2018; Volume 37. [Google Scholar] [CrossRef]
- Cottone, F.; Vocca, H.; Gammaitoni, L. Nonlinear Energy Harvesting. Phys. Rev. Lett. 2009, 102, 080601-1–080601-4. [Google Scholar] [CrossRef] [PubMed]
- Challa, V.; Prasad, M.; Shi, Y.; Fisher, F. A vibration energy harvesting device with bidirectional resonance frequency tunability. Smart Mater. Struct. 2008, 75, 1–10. [Google Scholar] [CrossRef]
- Duan, G.; Li, Y.; Tan, C. A Bridge-Shaped Vibration Energy Harvester with Resonance Frequency Tunability under DC Bias Electric Field. Micromachines 2022, 13, 1227. [Google Scholar] [CrossRef]
- Ganapathy, S.R.; Salleh, H.; Azhar, M.K.A. Design and optimisation of magnetically-tunable hybrid piezoelectric-triboelectric energy harvester. Sci. Rep. 2021, 11, 4458. [Google Scholar] [CrossRef]
- Ibrahim, P.; Arafa, M.; Anis, Y. An Electromagnetic Vibration Energy Harvester with a Tunable Mass Moment of Inertia. Sensors 2021, 21, 5611. [Google Scholar] [CrossRef]
- Le Scornec, J.; Guiffard, B.; Seveno, R.; Le Camb, V. Frequency tunable, flexible and low cost piezoelectric micro-generator for energy harvesting. Sens.Actuators A Phys. 2020, 312, 112148. [Google Scholar] [CrossRef]
- Wang, Y.; Li, L.; Hofmann, D.; Andrade, J.E.; Daraio, C. Structured fabrics with tunable mechanical properties. Nature 2021, 596, 238–243. [Google Scholar] [CrossRef]
- Xie, L.; Li, J.; Li, X.; Huang, L.; Cai, S. Damping-tunable energy-harvesting vehicle damper with multiple controlled generators: Design, modeling and experiments. Mech. Syst. Signal Process. 2018, 99, 859–872. [Google Scholar] [CrossRef]
- Wang, Z.; He, L.; Zhang, Z.; Zhou, Z.; Zhou, J.; Cheng, G. Research on a Piezoelectric Energy Harvester with Rotating Magnetic Excitation. J. Electron. Mater. 2021, 50, 3228–3240. [Google Scholar] [CrossRef]
- Kovacova, V.; Glinsek, S.; Girod, S.; Defay, E. High Electrocaloric Effect in Lead Scandium Tantalate Thin Films with Interdigitated Electrodes. Sensors 2022, 22, 4049. [Google Scholar] [CrossRef] [PubMed]
- Bouhedma, S.; Hu, S.; Schütz, A.; Lange, F.; Bechtold, T.; Ouali, M.; Hohlfeld, D. Analysis and Characterization of Optimized Dual-Frequency Vibration Energy Harvesters for Low-Power Industrial Applications. Micromachines 2022, 13, 1078. [Google Scholar] [CrossRef]
- Zhang, Y.; Jin, Y. Stochastic dynamics of a piezoelectric energy harvester with correlated colored noises from rotational environment. Nonlinear Dyn. 2019, 98, 501–515. [Google Scholar] [CrossRef]
- Damjanovic, D. Ferroelectric, dielectric and piezoelectric properties of ferroelectric thin films and ceramics. Rep. Prog. Phys. 1998, 61, 1267–1324. [Google Scholar] [CrossRef]
- Dawber, M. Physics of thin-film ferroelectric oxides. Rev. Mod. Phys. 2005, 77, 1083. [Google Scholar] [CrossRef]
- Čeponis, A.; Mažeika, D.; Jūrėnas, V.; Deltuvienė, D.; Bareikis, R. Ring-shaped piezoelectric 5-DOF robot for angular-planar motion. Micromachines 2022, 13, 1763. [Google Scholar] [CrossRef]
- Cheng, C.; Peters, T.; Dangi, A.; Agrawal, S.; Chen, H.; Kothapalli, S.-R.; Trolier-McKinstry, S. Improving PMUT Receive Sensitivity via DC Bias and Piezoelectric Composition. Sensors 2022, 22, 5614. [Google Scholar] [CrossRef]
- Ge, C.; Cretu, E. Simple and Robust Microfabrication of Polymeric Piezoelectric Resonating MEMS Mass Sensors. Sensors 2022, 22, 2994. [Google Scholar] [CrossRef]
- He, Y.; Bahr, B.; Si, M.; Ye, P.; Weinstein, D. A tunable ferroelectric based unreleased RF resonator. Microsyst. Nanoeng. 2020, 6, 8. [Google Scholar] [CrossRef]
- Mažeika, D.; Čeponis, A.; Makutėnienė, D. A cylinder-type multimodal traveling wave piezoelectric actuator. Appl. Sci. 2020, 10, 2396. [Google Scholar] [CrossRef]
- Wang, L.; Hao, B.; Wang, R.; Jin, J.; Xu, Q. A Novel Self-Moving Framed Piezoelectric Actuator. Appl. Sci. 2020, 10, 6682. [Google Scholar] [CrossRef]
- Wang, L.; Wang, J.A.; Jin, J.M.; Yang, L.; Wu, S.W.; Zhou, C.C. Theoretical modeling, verification, and application study on a novel bending-bending coupled piezoelectric ultrasonic transducer. Mech. Syst. Signal Process. 2022, 168, 108644. [Google Scholar] [CrossRef]
- Ghouli, Z.; Litak, G. Effect of High-Frequency Excitation on a Bistable Energy Harvesting System. J. Vib. Eng. Technol. 2022, 11, 99–106. [Google Scholar] [CrossRef]
- Harne, R.L.; Thota, M.; Wang, K.W. Bistable energy harvesting enhancement with an auxiliary linear oscillator. Smart Mater. Struct. 2013, 22, 125028. [Google Scholar] [CrossRef]
- Iliuk, I.; Balthazar, J.M.; Tusset, A.M.; Piqueira, J.R.C. A non-ideal portal frame energy harvester controlled using a pendulum. Eur. Phys. J. Spec. Top. 2013, 222, 1575–1586. [Google Scholar] [CrossRef]
- Chen, J.; Bao, B.; Liu, J.; Wu, Y.; Wang, Q. Piezoelectric energy harvester featuring a magnetic chaotic pendulum. Energy Convers. Manag. 2022, 269, 116155. [Google Scholar] [CrossRef]
- Kumar, R.; Gupta, S.; Ali, S.F. Energy harvesting from chaos in base excited double pendulum. Mech. Syst. Signal Process. 2019, 124, 49–64. [Google Scholar] [CrossRef]
- Litak, G.; Margielewicz, J.; Gąska, D.; Wolszczak, P.; Zhou, S. Multiple Solutions of the Tristable Energy Harvester. Energies 2021, 14, 1284. [Google Scholar] [CrossRef]
- Margielewicz, J.; Gąska, D.; Litak, G.; Wolszczak, P.; Zhou, S. Energy Harvesting in a System with a Two-Stage Flexible Cantilever Beam. Sensors 2022, 22, 7399. [Google Scholar] [CrossRef]
- Juhász, L.; Maas, J.; Borovac, B. Parameter identification and hysteresis compensation of embedded piezoelectric stack actuators. Mechatronics 2011, 21, 329–338. [Google Scholar] [CrossRef]
- Montegiglio, P.; Maruccio, C.; Acciani, G.; Rizzello, G.; Seelecke, S. Nonlinear multi-scale dynamics modeling of piezoceramic energy harvesters with ferroelectric and ferroelastic hysteresis. Nonlinear Dyn. 2020, 100, 1985–2003. [Google Scholar] [CrossRef]
- Kwak, D.-H.; Jang, B.-T.; Cha, S.-Y.; Lee, S.-H.; Lee, H.C.; Yu, B.-G. Hysteresis analysis in capacitance-voltage characteristics of Pt/(Ba, Sr)TiO3/Pt structures. Integr. Ferroelectr. 1996, 13, 121–127. [Google Scholar] [CrossRef]
- Myasnikov, É.N.; Tolstousov, S.V.; Frolenkov, K.Y. Memory Effect in Ba0.85Sr0.15TiO3 Ferroelectric Films on Silicon Substrates. Phys. Solid State 2004, 46, 2268–2274. [Google Scholar] [CrossRef]
- Lin, J.; Gomeniuk, Y.Y.; Monaghan, S.; Povey, I.M.; Cherkaoui, K.; O’Connor, É.; Power, M.; Hurley, P.K. An investigation of capacitance-voltage hysteresis in metal/high-k/In0.53Ga0.47As metal-oxide-semiconductor capacitors. J. Appl. Phys. 2013, 114, 144105. [Google Scholar] [CrossRef]
- Ducharme, S.; Bune, A.V.; Blinov, L.M.; Fridkin, V.M.; Palto, S.P.; Sorokin, A.V.; Yudin, S.G. Critical point in ferroelectric Langmuir-Blodgett polymer films. Phys. Rev. B 1988, 57, 25–28. [Google Scholar] [CrossRef]
- Cross, R.; McNamara, H.; Pokrovskii, A.; Rachinskii, D. A new paradigm for modelling hysteresis in macroeconomic flows. Phys. B Condens. Matter 2008, 403, 231–236. [Google Scholar] [CrossRef]
- Krasnosel’skiǐ, M.A.; Pokrovskiǐ, A.V. Systems with Hysteresis; Springer: Berlin/Heidelberg, Germany, 1989; 410p, ISBN 978-3-642-64782-6. [Google Scholar] [CrossRef]
- Lacarbonara, W.; Talò, M.; Carboni, B.; Lanzara, G. Tailoring of Hysteresis Across Different Material Scales. In Recent Trends in Applied Nonlinear Mechanics and Physics; Belhaq, M., Ed.; Springer Proceedings in Physics: Berlin, Germany, 1999; pp. 227–250. [Google Scholar] [CrossRef]
- Medvedskii, A.L.; Meleshenko, P.A.; Nesterov, V.A.; Reshetova, O.O.; Semenov, M.E.; Solovyov, A.M. Unstable Oscillating Systems with Hysteresis: Problems of Stabilization and Control. J. Comput. Syst. Sci. Int. 2020, 59, 533–556. [Google Scholar] [CrossRef]
- Semenov, M.E.; Solovyov, A.M.; Meleshenko, P.A.; Reshetova, O.O. Efficiency of Hysteresis Damper in Oscillating Systems. Math. Model. Nat. Phenom. 2020, 15, 43-1–43-14. [Google Scholar] [CrossRef]
- Semenov, M.E.; Solovyov, A.M.; Meleshenko, P.A. Stabilization of coupled inverted pendula: From discrete to continuous case. J. Vib. Control 2021, 27, 43–56. [Google Scholar] [CrossRef]
- Ikhouane, F.; Mañosa, V.; Pujol, G. Minor loops of the Dahl and LuGre models. Appl. Math. Model. 2020, 77, 1679–1690. [Google Scholar] [CrossRef]
- Ismail, M.; Ikhouane, F.; Rodellar, J. The hysteresis Bouc–Wen model, a survey. Arch. Comput. Methods Eng. 2009, 16, 161–188. [Google Scholar] [CrossRef]
- Lin, C.-J.; Lin, P.-T. Tracking control of a biaxial piezo-actuated positioning stage using generalized Duhem model. Comput. Math. Appl. 2012, 64, 766–787. [Google Scholar] [CrossRef]
- Krejčí, P.; O’Kane, J.P.; Pokrovskii, A.; Rachinskii, D. Properties of solutions to a class of differential models incorporating Preisach hysteresis operator. Phys. D 2012, 241, 2010–2028. [Google Scholar] [CrossRef]
- Krejčí, P.; Monteiro, G.A. Inverse parameter-dependent Preisach operator in thermo-piezoelectricity modeling. Discret. Contin. Dyn. Syst.—B 2019, 24, 3051–3066. [Google Scholar] [CrossRef]
- Mayergoyz, I.D.; Friedman, G. Generalized Preisach model of hysteresis. IEEE Trans. Magn. 1988, 24, 212–217. [Google Scholar] [CrossRef]
- Preisach, F. Über die magnetische Nachwirkung. Zeitschrift für Physik 1935, 94, 277–302. [Google Scholar] [CrossRef]
- Borzunov, S.V.; Semenov, M.E.; Sel’vesyuk, N.I.; Meleshenko, P.A.; Solovyov, A.M. Stochastic model of the hysteresis converter with a domain structure. Math. Model. Comput. Simulations 2022, 14, 305–321. [Google Scholar] [CrossRef]
- Semenov, M.E.; Borzunov, S.V.; Meleshenko, P.A. Stochastic Preisach operator: Definition within the design approach. Nonlinear Dyn. 2020, 101, 2599–2614. [Google Scholar] [CrossRef]
- Ikhouane, F.; Rodellar, J. On the hysteretic Bouc–Wen model. Nonlinear Dyn. 2005, 42, 63–78. [Google Scholar] [CrossRef]
- Triplett, A.; Quinn, D.D. The effect of nonlinear piezoelectric coupling on vibration-based energy harvesting. In Proceedings of the IMECE2008 ASME International Mechanical Engineering Congress and Exposition, Boston, MA, USA, 31 October–6 November 2008; IMECE2008-66393. pp. 1–6. [Google Scholar] [CrossRef]
- Tusset, A.M.; Rocha, R.T.; Iliuk, I.; Balthazar, J.M.; Litak, G. Dynamics and Control of Energy Harvesting from a Non-ideally Excited Portal Frame System with Fractional Damping. In Vibration Engineering and Technology of Machinery; Mechanisms and Machine Science; Balthazar, J.M., Ed.; Springer: Berlin/Heidelberg, Germany, 2021; Volume 95. [Google Scholar] [CrossRef]
- Pan, J.; Qin, W.; Deng, W.; Zhang, P.; Zhou, Z. Harvesting weak vibration energy by integrating piezoelectric inverted beam and pendulum. Energy 2021, 227, 120374. [Google Scholar] [CrossRef]
- Łygas, K.; Wolszczak, P.; Litak, G. Broadband frequency response of a nonlinear resonator with clearance for energy harvesting. MATEC Web Conf. EDP Sci. 2018, 148, 12003. [Google Scholar] [CrossRef]
- Friswell, M.I.; Ali, S.F.; Bilgen, O.; Adhikari, S.; Lees, A.W.; Litak, G. Non-linear piezoelectric vibration energy harvesting from a vertical cantilever beam with tip mass. J. Intell. Mater. Syst. Struct. 2012, 23, 1505–1521. [Google Scholar] [CrossRef]
- Martin, J.-P.; Li, Q. Design, model, and performance evaluation of a biomechanical energy harvesting backpack. Mech. Syst. Signal Process. 2019, 134, 106318. [Google Scholar] [CrossRef]
- Rome, L.C.; Flynn, L.; Goldman, E.M.; Yoo, T.D. Generating electricity while walking with loads. Science 2005, 309, 1725–1728. [Google Scholar] [CrossRef]
- Gantmacher, F.R. The Theory of Matrices, 2nd ed.; Hirsch, K.A., Ed.; AMS Chelsea Publishing: Providence, RI, USA, 1959; 276p, ISBN 0-8218-2664-6. [Google Scholar]
- Bertotti, G.; Mayergoyz, I.D. The Science of Hysteresis: 3-Volume Set; Elsevier, Academic Press: Amsterdam, The Netherlands, 2005; 2160p, ISBN 9780080540788. [Google Scholar]
- Charalampakis, A.E.; Koumousis, V.K. On the response and dissipated energy of Bouc–Wen hysteretic model. J. Sound Vib. 2008, 309, 887–895. [Google Scholar] [CrossRef]
- Charalampakis, A.E. The response and dissipated energy of Bouc–Wen hysteretic model revisited. Arch. Appl. Mech. 2015, 85, 1209–1223. [Google Scholar] [CrossRef]





| System Parameter Values | Power of External Excitation, | Power Transmitted by the Hysteresis Link, | Electrical Power, | Ratio, |
|---|---|---|---|---|
| , , , | ||||
| , , , | ||||
| , , , | ||||
| , , , | ||||
| , , , | ||||
| , , , |
| System Parameter Values | Power of External Excitation, | Power Transmitted by the Hysteresis Link, | Electrical Power, | Ratio, |
|---|---|---|---|---|
| , , | ||||
| , , | ||||
| , , | ||||
| , , | ||||
| , , | ||||
| , , | ||||
| , , | ||||
| , , | ||||
| , , | ||||
| , , |
| System Parameter Values | Power of External Excitation, | Power Transmitted by the Hysteresis Link, | Electrical Power, | Ratio, |
|---|---|---|---|---|
| , , | ||||
| , , | ||||
| , , | ||||
| , , | ||||
| , , | ||||
| , , | ||||
| , , | ||||
| , , | ||||
| , , | ||||
| , , | ||||
| , , | ||||
| , , |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Semenov, M.E.; Meleshenko, P.A.; Borzunov, S.V.; Reshetova, O.O.; Barsukov, A.I. A Simple Model of the Energy Harvester within a Linear and Hysteresis Approach. Micromachines 2023, 14, 310. https://doi.org/10.3390/mi14020310
Semenov ME, Meleshenko PA, Borzunov SV, Reshetova OO, Barsukov AI. A Simple Model of the Energy Harvester within a Linear and Hysteresis Approach. Micromachines. 2023; 14(2):310. https://doi.org/10.3390/mi14020310
Chicago/Turabian StyleSemenov, Mikhail E., Peter A. Meleshenko, Sergei V. Borzunov, Olga O. Reshetova, and Andrey I. Barsukov. 2023. "A Simple Model of the Energy Harvester within a Linear and Hysteresis Approach" Micromachines 14, no. 2: 310. https://doi.org/10.3390/mi14020310
APA StyleSemenov, M. E., Meleshenko, P. A., Borzunov, S. V., Reshetova, O. O., & Barsukov, A. I. (2023). A Simple Model of the Energy Harvester within a Linear and Hysteresis Approach. Micromachines, 14(2), 310. https://doi.org/10.3390/mi14020310







