A Linear-Arc Composite Beam Piezoelectric Energy Harvester Modeling and Finite Element Analysis
Abstract
:1. Introduction
2. Structure and Theoretical Model of PEH-C
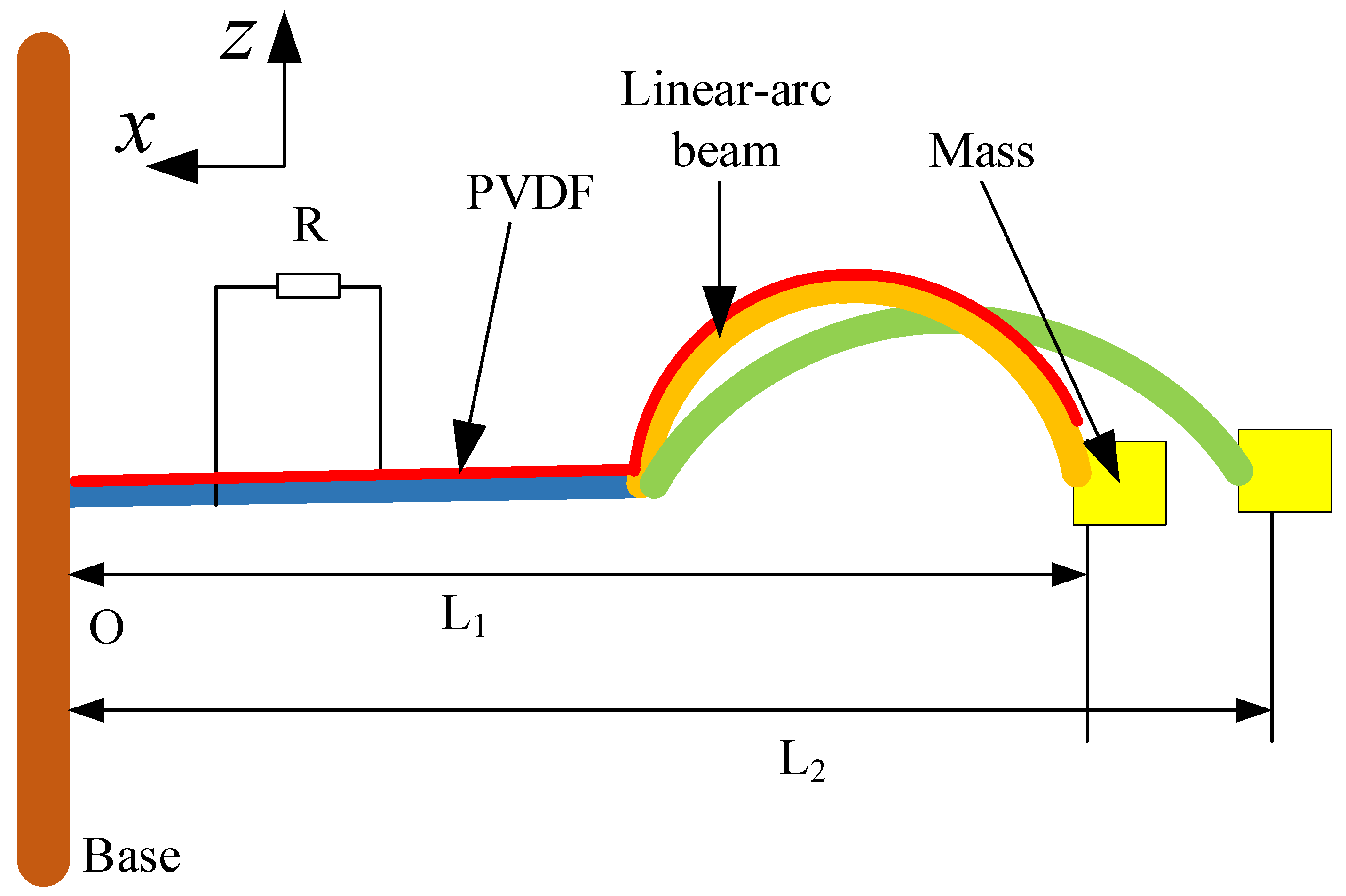
2.1. Structure of PEH-C
2.2. Theoretical Modeling
3. Finite-Element Simulation
3.1. Parameter Settings
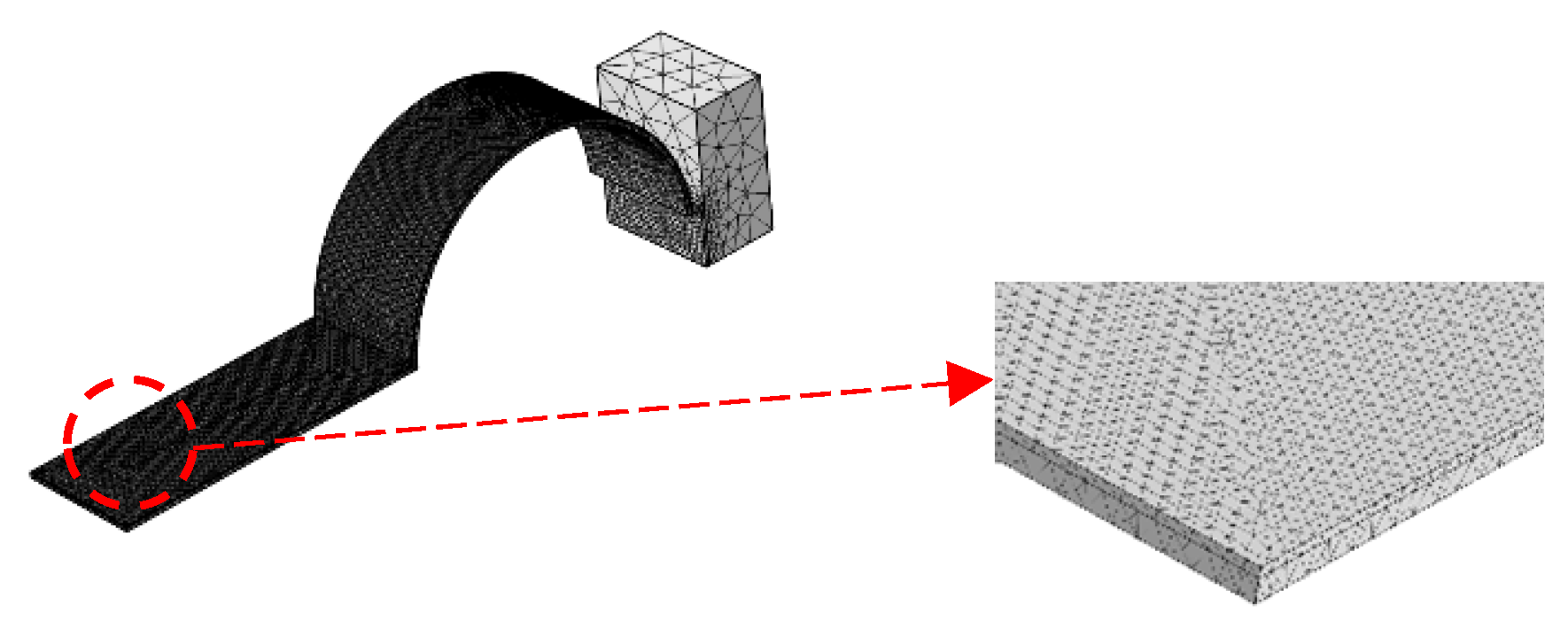
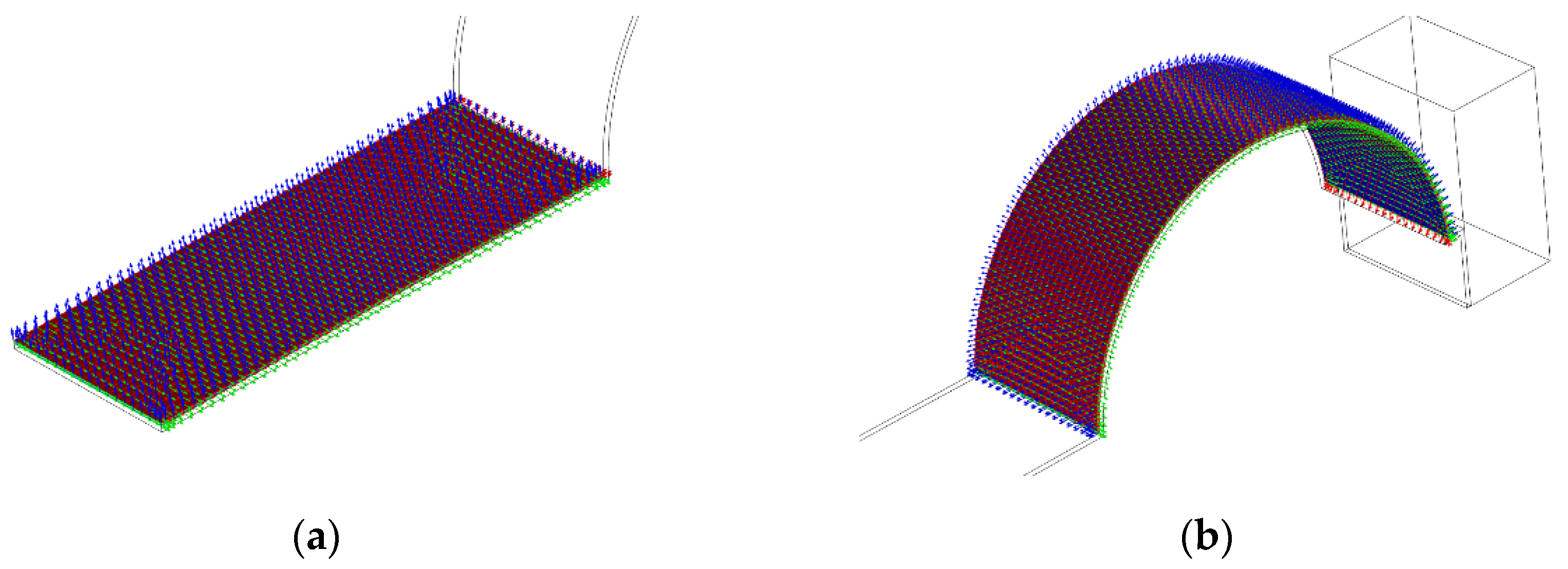
3.2. Finite Element Analysis Mesh Accuracy Verification
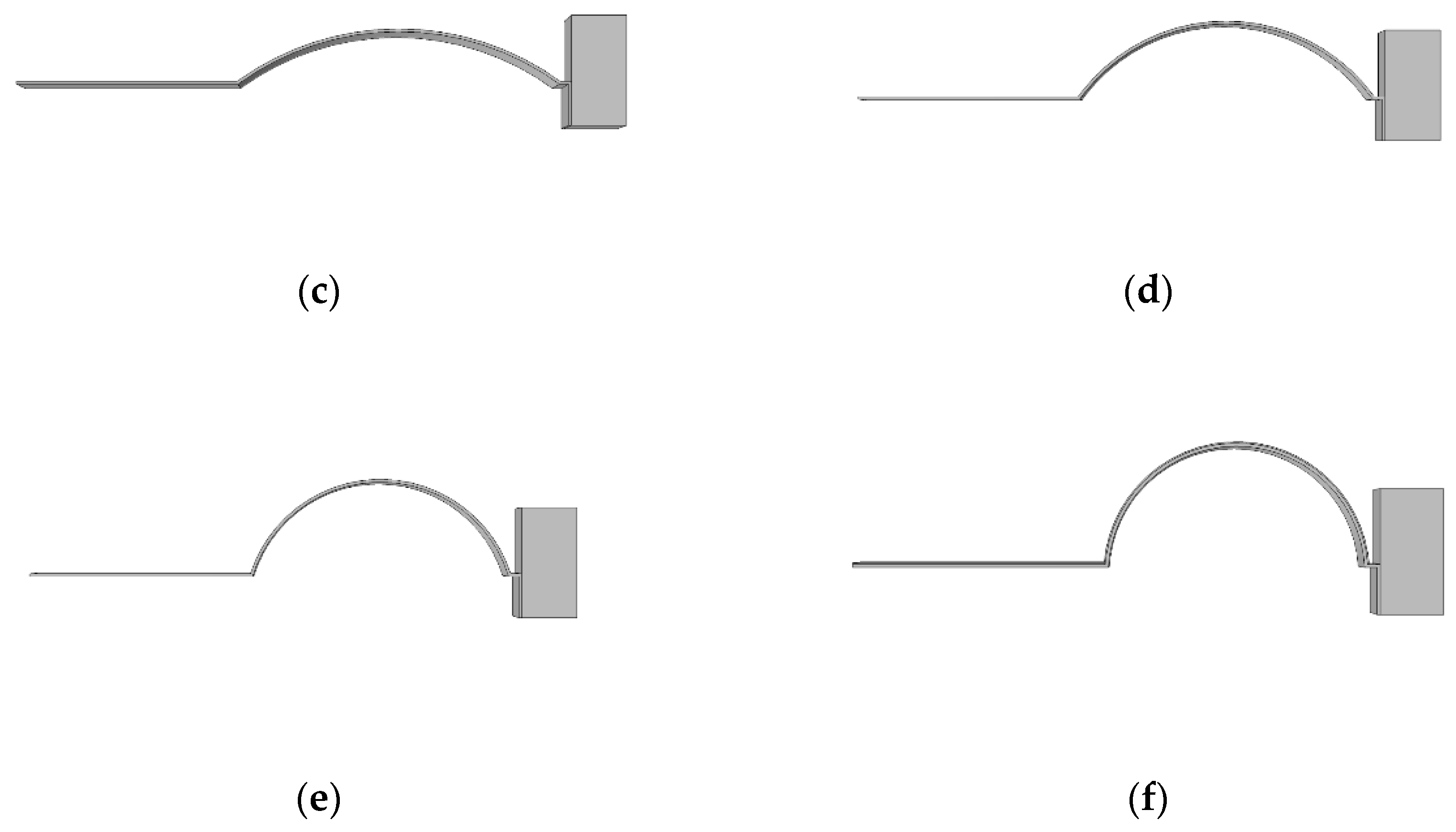
3.3. Nonlinear Restoring Force of the Linear-Arc Beam
3.4. Finite Element Analysis
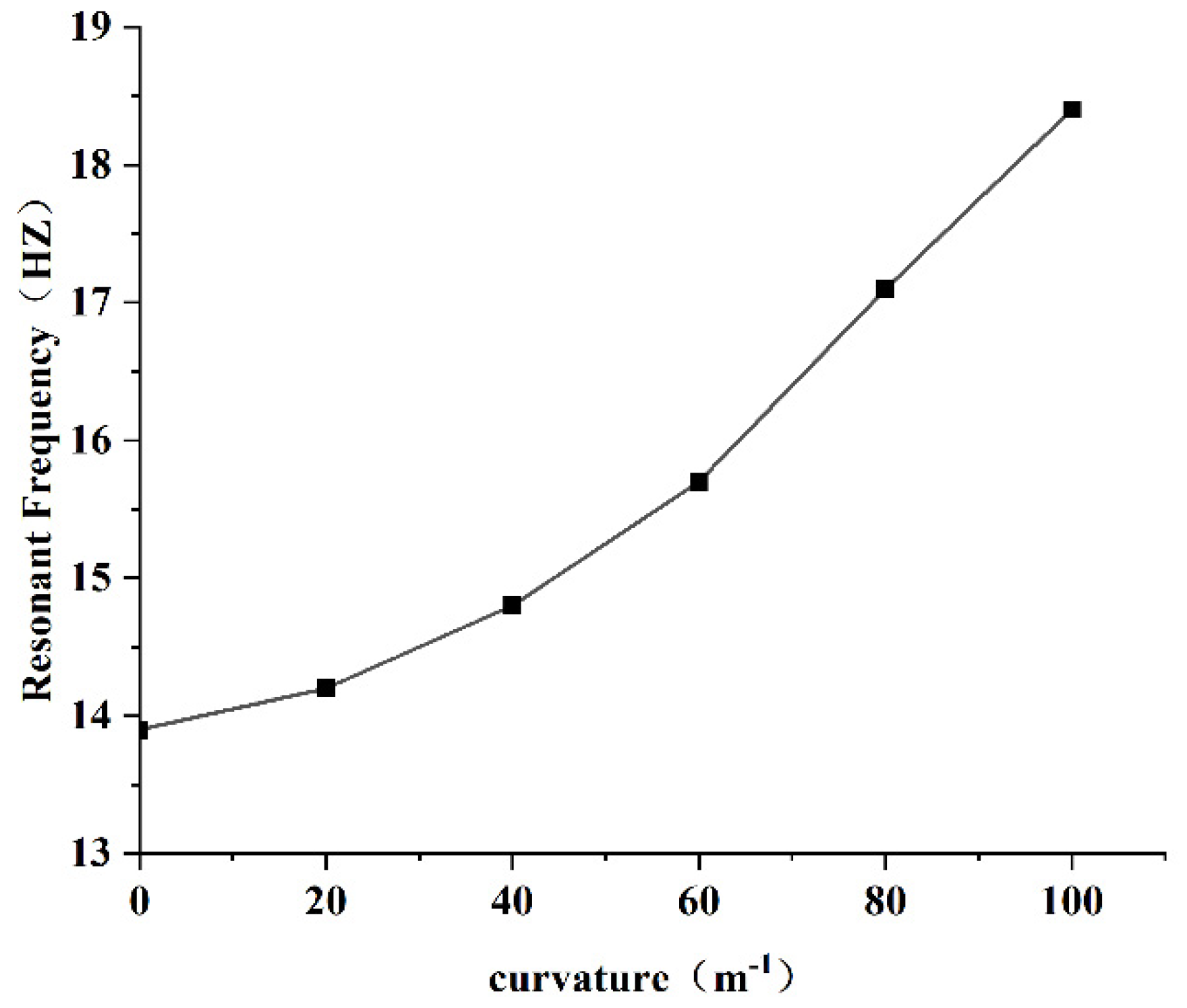
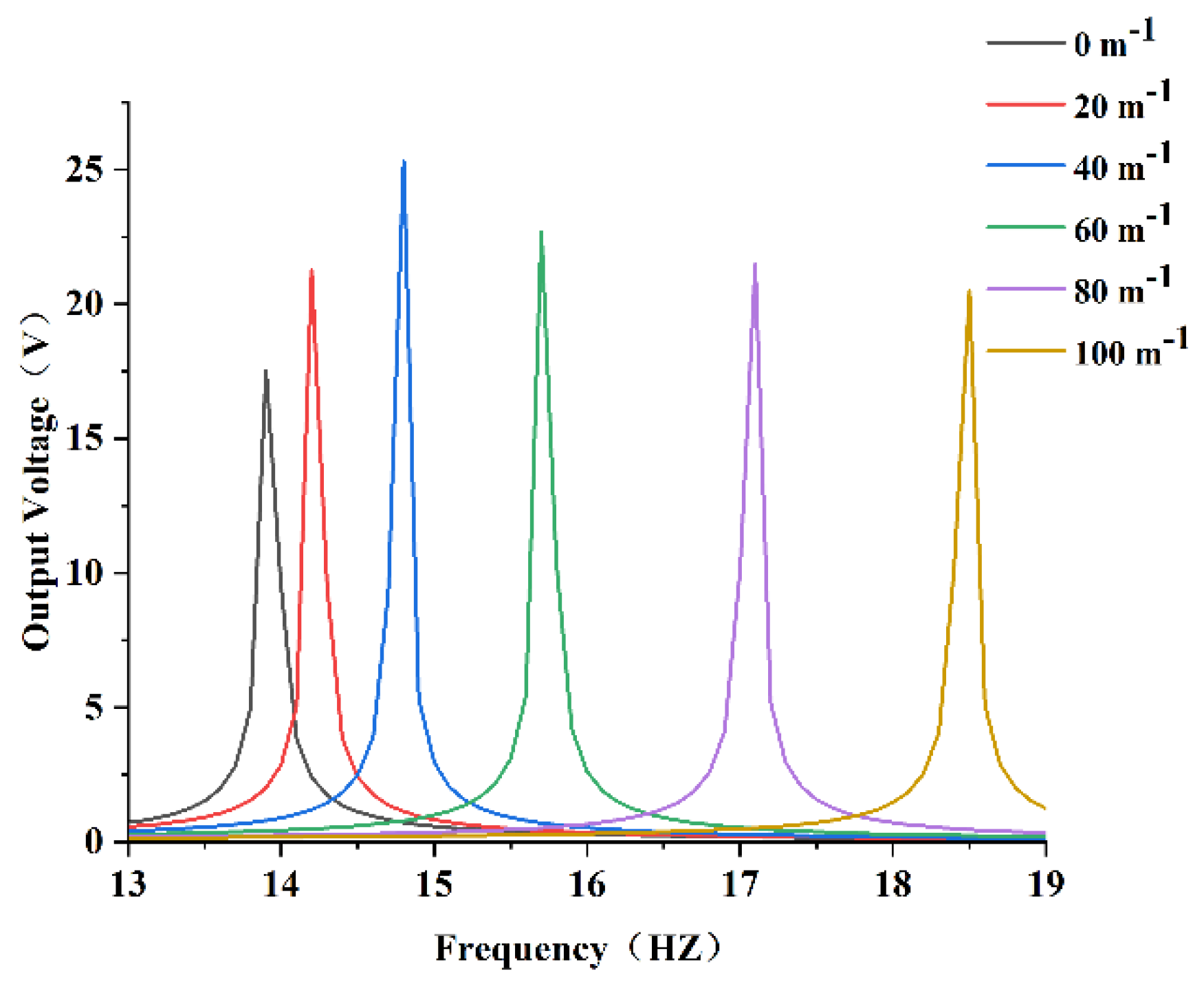
3.4.1. Resonant Frequency
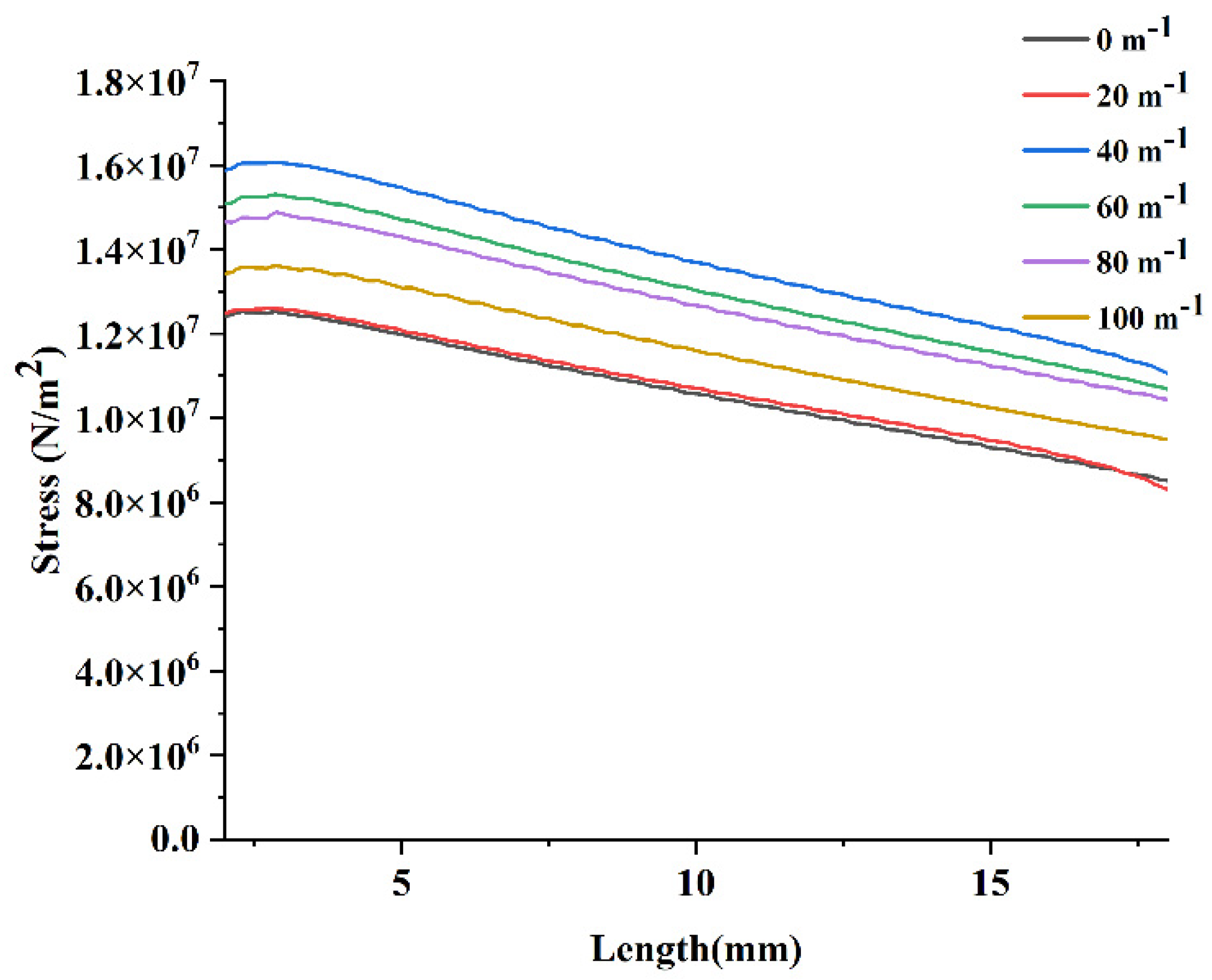
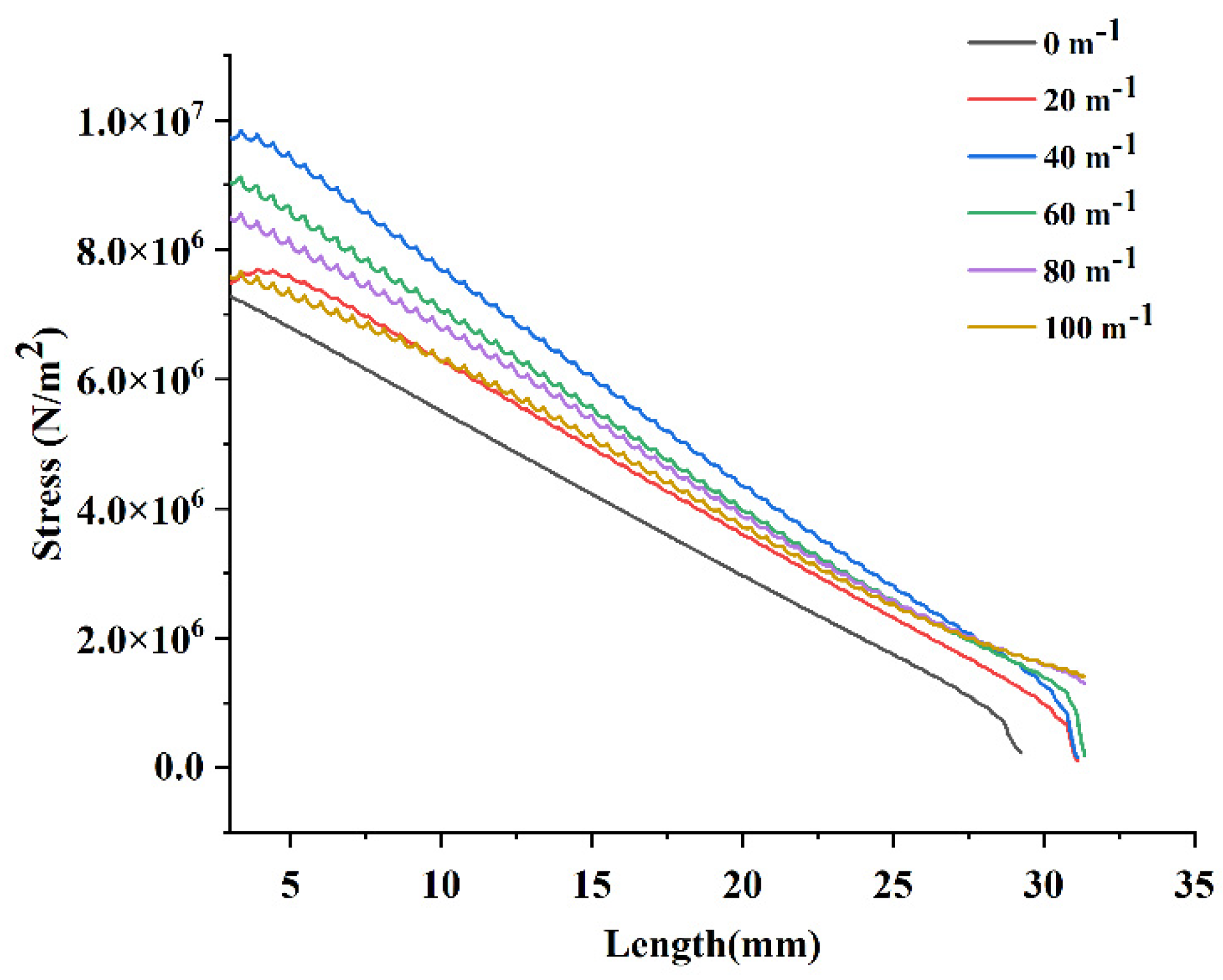
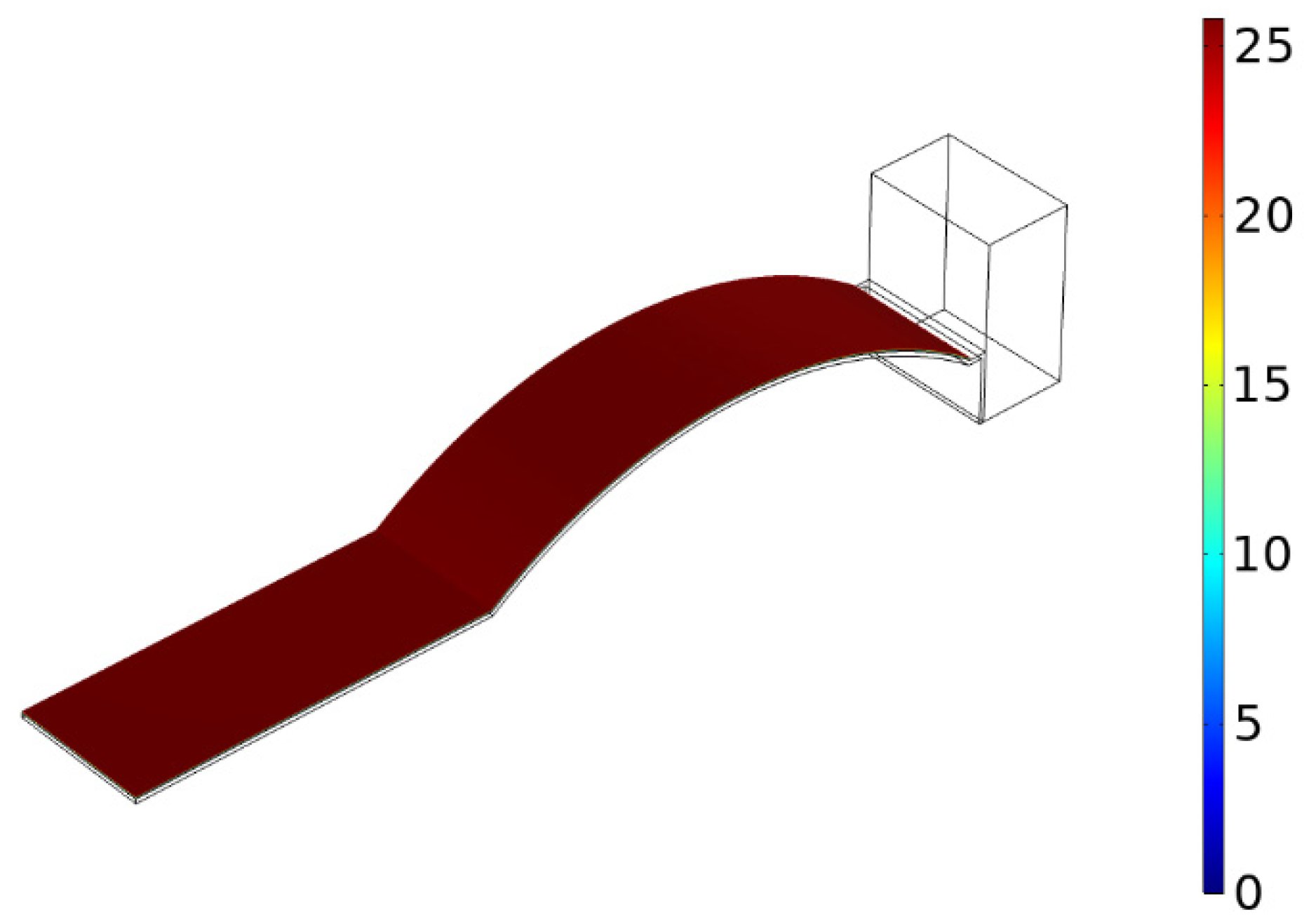
3.4.2. Stress Distribution
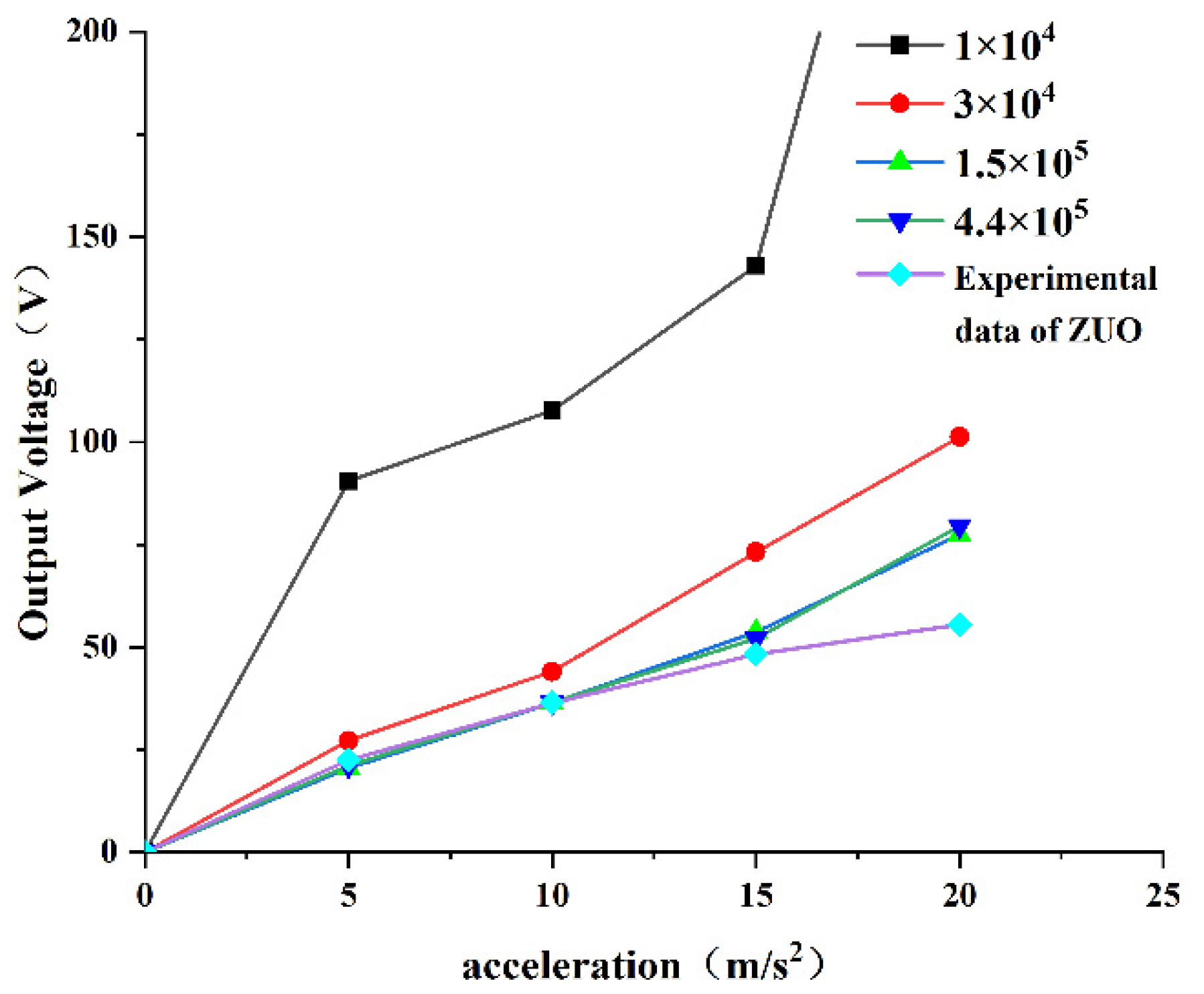
3.4.3. The Output Voltage
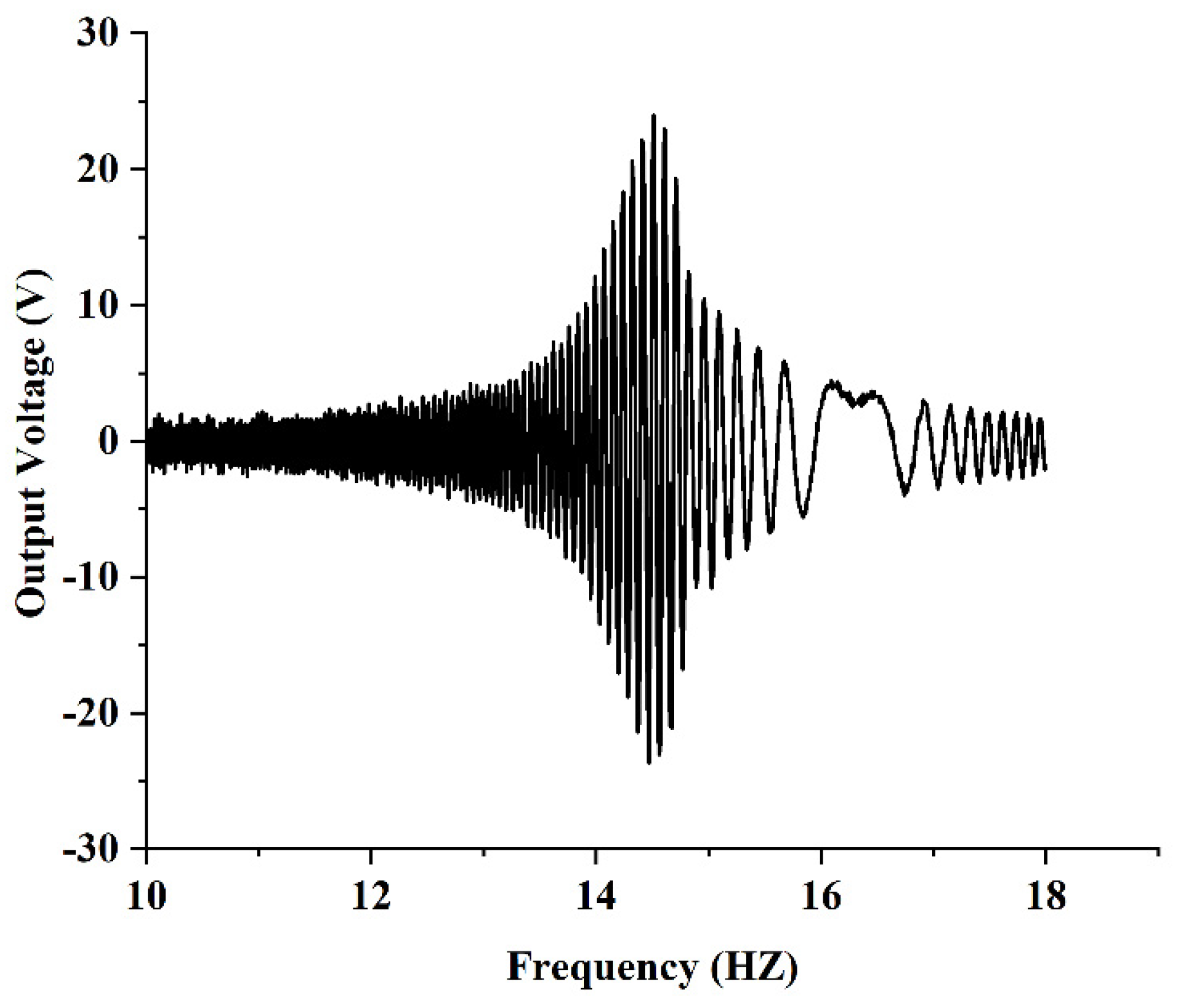
4. Experimental Validation
5. Conclusions
- (1)
- The PEH-C was numerically simulated using COMSOL software to determine the relationship between the nonlinear restoring force and the transverse displacements. Then, curve fitting was performed to obtain the equation for the nonlinear restoring force. Finally, the corresponding coupled governing equations were derived by using the generalized Hamilton principle.
- (2)
- The resonance frequency of the PEH-C gradually increased with an increase in curvature. It was observed that, under the condition of keeping the length unchanged, the curvature of the curved beam part increased, the bending radius decreased, and the corresponding stiffness increased, resulting in an increase in the resonance frequency. Conversely, when the curvature was smaller, the curved beam was closer to the straight beam, the stiffness decreased, and the resonance frequency decreased accordingly.
- (3)
- Compared with the straight beam, the PEH-C introduced into the arc segment was subjected to greater stress under the same excitation. Under the same excitation, the PEH-C with a curvature of 40 had the largest stress and the PEH-C with a curvature of 100 had relatively uniform stress.
- (4)
- The finite element simulation results showed that the PEH-C with a curvature of 40 had the best open-circuit voltage output performance. Experiments showed that the open-circuit voltage output performance of the PEH-C with a curvature of 40 was 9% higher than that of the PEH-C with a curvature of 100 .
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Huang, M.F.; Liu, A.F.; Xiong, N.N.; Wang, T.; Vasilakos, A. A Low-Latency Communication Scheme for Mobile Wireless Sensor Control Systems. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 317–332. [Google Scholar] [CrossRef]
- Numan, M.; Subhan, F.; Khan, W.Z.; Hakak, S.; Haider, S.; Reddy, G.; Jolfaei, A.; Alazab, M. A Systematic Review on Clone Node Detection in Static Wireless Sensor Networks. IEEE Access 2020, 8, 65450–65461. [Google Scholar] [CrossRef]
- Sarkar, A.; Murugan, T.S. Cluster head selection for energy efficient and delay-less routing in wireless sensor network. Wirel. Netw. 2019, 25, 303–320. [Google Scholar] [CrossRef]
- Statista Research Department. Available online: https://www.statista.com/statistics/471264/iot-number-of-connected-devices-worldwide/ (accessed on 29 April 2022).
- Chen, X.Y.; Zhang, X.H.; Wang, L.; Chen, L.Y. An arch-linear composed beam piezoelectric energy harvester with magnetic coupling: Design, modeling and dynamic analysis. J. Sound Vib. 2021, 513, 116394. [Google Scholar] [CrossRef]
- Daqaq, M.F.; Masana, R.; Erturk, A.; Dane Quinn, D. On the role of nonlinearities in vibratory energy harvesting: A critical review and discussion. Appl. Mech. Rev. 2014, 66, 040801. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, S.; Stein, P.; Xu, B.X.; Yang, T. Vibration-based energy harvesting with a clamped piezoelectric circular diaphragm: Analysis and identification of optimal structural parameters. Smart Mater. Struct. 2017, 26, 045011. [Google Scholar] [CrossRef]
- Zhang, X.; Zuo, M.; Yang, W.; Wan, X. A tri-stable piezoelectric vibration energy harvester for composite shape beam: Nonlinear modeling and analysis. Sensors 2020, 20, 1370. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lefeuvre, E.; Badel, A.; Richard, C.; Guyomar, D. Piezoelectric energy harvesting device optimization by synchronous electric charge extraction. J. Intell. Mat. Syst. Str. 2005, 16, 865–876. [Google Scholar] [CrossRef]
- Stanton, S.C.; McGehee, C.; Mann, B.P. Reversible hysteresis for broadband magnetopiezoelastic energy harvesting. Appl. Phys. Lett. 2009, 95, 174103. [Google Scholar] [CrossRef]
- Yu, L.; Tang, L.; Yang, T. Piezoelectric passive self-tuning energy harvester based on a beam-slider structure. J. Sound Vib. 2020, 489, 115689. [Google Scholar] [CrossRef]
- Wang, G.; Liao, W.; Yang, B.; Wang, X.; Xu, W.; Li, X. Dynamic and energetic characteristics of a bistable piezoelectric vibration energy harvester with an elastic magnifier. Mech. Syst. Signal Pr. 2018, 105, 427–446. [Google Scholar] [CrossRef]
- Li, P.; Liu, Y.; Wang, Y.; Luo, C.; Li, G.; Hu, J.; Liu, W.; Zhang, W.J. Low-frequency and wideband vibration energy harvester with flexible frame and interdigital structure. Aip. Adv. 2015, 5, 047151. [Google Scholar] [CrossRef]
- Zhou, S.; Hobeck, J.D.; Cao, J.; Inman, D. Analytical and experimental investigation of flexible longitudinal zigzag structures for enhanced multi-directional energy harvesting. Smart Mater. Struct. 2017, 26, 035008. [Google Scholar] [CrossRef]
- Zhao, S.; Erturk, A. On the stochastic excitation of monostable and bistable electroelastic power generators: Relative advantages and tradeoffs in a physical system. Appl. Phys. Lett. 2013, 102, 103902. [Google Scholar] [CrossRef] [Green Version]
- Zhou, S.; Cao, J.; Inman, D.J.; Lin, J.; Li, D. Harmonic balance analysis of nonlinear tristable energy harvesters for performance enhancement. J. Sound Vib. 2016, 373, 223–235. [Google Scholar] [CrossRef]
- Zhou, S.; Cao, J.; Inman, D.J.; Lin, J.; Liu, S.; Wang, Z. Broadband tristable energy harvester: Modeling and experiment verification. Appl. Energy 2014, 133, 33–39. [Google Scholar] [CrossRef]
- Zhou, S.; Cao, J.; Inman, D.J.; Liu, S.; Wang, W.; Lin, J. Impact-induced high-energy orbits of nonlinear energy harvesters. Appl. Phys. Lett. 2015, 106, 093901. [Google Scholar] [CrossRef]
- Kumar, A.; Ali, S.F.; Arockiarajan, A. Influence of piezoelectric energy transfer on the interwell oscillations of multistable vibration energy harvesters. J. Comput. Nonlin. Dyn. 2019, 14, 031001. [Google Scholar] [CrossRef]
- Panyam, M.; Daqaq, M. Characterizing the effective bandwidth of tri-stable energy harvesters. J. Sound Vib. 2017, 386, 336–358. [Google Scholar] [CrossRef]
- Cao, D.; Gao, Y.; Hu, W. Modeling and power performance improvement of a piezoelectric energy harvester for low-frequency vibration environments. Acta Mech. Sinica-Prc. 2019, 35, 894–911. [Google Scholar] [CrossRef]
- Wang, G.; Liao, W.-H.; Zhao, Z.; Tan, J.; Cui, S.; Wu, H.; Wang, W. Nonlinear magnetic force and dynamic characteristics of a tri-stable piezoelectric energy harvester. Nonlin. Dynam. 2019, 97, 2371–2397. [Google Scholar] [CrossRef]
- Raju, S.S.; Umapathy, M.; Uma, G. Design and analysis of high output piezoelectric energy harvester using non uniform beam. Mech. Adv. Mater. Struct. 2020, 27, 218–227. [Google Scholar] [CrossRef]
- Muthalif, A.G.A.; Nordin, N.H.D. Optimal piezoelectric beam shape for single and broadband vibration energy harvesting: Modeling, simulation and experimental results. Mech. Syst. Signal Process. 2015, 54, 417–426. [Google Scholar] [CrossRef]
- Wang, B.; Luo, X.; Liu, Y.; Yang, Z. Thickness-variable composite beams for vibration energy harvesting. Compos. Struct. 2020, 244, 112232. [Google Scholar] [CrossRef]
- Salem, M.S.; Ahmed, S.; Shaker, A.; Alshammari, M.T.; Al-Dhlan, K.A.; Alanazi, A.; Saeed, A.; Abouelatta, M. Bandwidth broadening of piezoelectric energy harvesters using arrays of a proposed piezoelectric cantilever structure. Micromachines 2021, 12, 973. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Al-Haik, M.; Zakaria, M.; Hajj, M. Piezoelectric energy harvesting using L-shaped structures. J. Intell. Mater. Syst. Struct. 2018, 29, 1206–1215. [Google Scholar] [CrossRef]
- Yang, Z.; Zhou, S.; Zu, J.; Inman, D. High-performance piezoelectric energy harvesters and their applications. Joule 2018, 2, 642–697. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Yang, W.; Zuo, M.; Tan, H.; Fan, H.; Mao, Q.; Wan, X. An arc-shaped piezoelectric bistable vibration energy harvester: Modeling and experiments. Sensors 2018, 18, 4472. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Zuo, M.; Zhang, C.; Wang, L. A Method for Parameter Identification of Composite Beam Piezoelectric Energy Harvester. Sensors 2021, 21, 7213. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. Piezoelectric Energy Harvesting; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Zuo, M. Dynamic Characteristics Analysis and Optimal Design of Thermoelectric-Piezoelectric Dual-Mode Energy Harvester. Master’s Thesis, Xi’an University of Science and Technology, Xi’an, China, 2020. [Google Scholar]






| Parameter | Value | Unit |
|---|---|---|
| Mass density | 7800 | |
| Mass size | 8 × 8 × 5 | |
| PVDF density | 1780 | |
| PVDF Piezoelectric stress | 11.5 | |
| PVDF elastic modulus | 3 | |
| PVDF height | 0.11 | |
| PVDF overall length | 51.4 | |
| PVDF width | 8 | |
| Substrate layer density | 8300 | |
| Substrate layer elastic modulus | 128 | |
| Substrate layer height | 0.2 | |
| Substrate layer overall length | 51.4 | |
| Substrate layer width | 8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Guo, Y.; Zhu, F.; Chen, X.; Tian, H.; Xu, H. A Linear-Arc Composite Beam Piezoelectric Energy Harvester Modeling and Finite Element Analysis. Micromachines 2022, 13, 848. https://doi.org/10.3390/mi13060848
Zhang X, Guo Y, Zhu F, Chen X, Tian H, Xu H. A Linear-Arc Composite Beam Piezoelectric Energy Harvester Modeling and Finite Element Analysis. Micromachines. 2022; 13(6):848. https://doi.org/10.3390/mi13060848
Chicago/Turabian StyleZhang, Xuhui, Yan Guo, Fulin Zhu, Xiaoyu Chen, Hao Tian, and Hengtao Xu. 2022. "A Linear-Arc Composite Beam Piezoelectric Energy Harvester Modeling and Finite Element Analysis" Micromachines 13, no. 6: 848. https://doi.org/10.3390/mi13060848
APA StyleZhang, X., Guo, Y., Zhu, F., Chen, X., Tian, H., & Xu, H. (2022). A Linear-Arc Composite Beam Piezoelectric Energy Harvester Modeling and Finite Element Analysis. Micromachines, 13(6), 848. https://doi.org/10.3390/mi13060848







