The Effects of Viscoelasticity on Droplet Migration on Surfaces with Wettability Gradients
Abstract
:1. Introduction
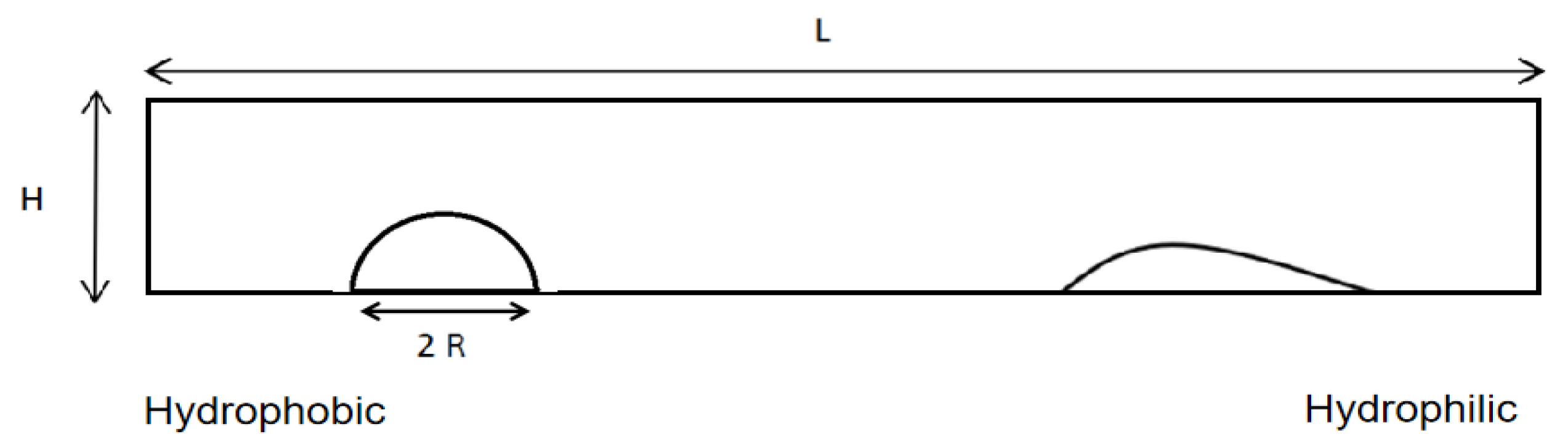
2. Numerical Simulation
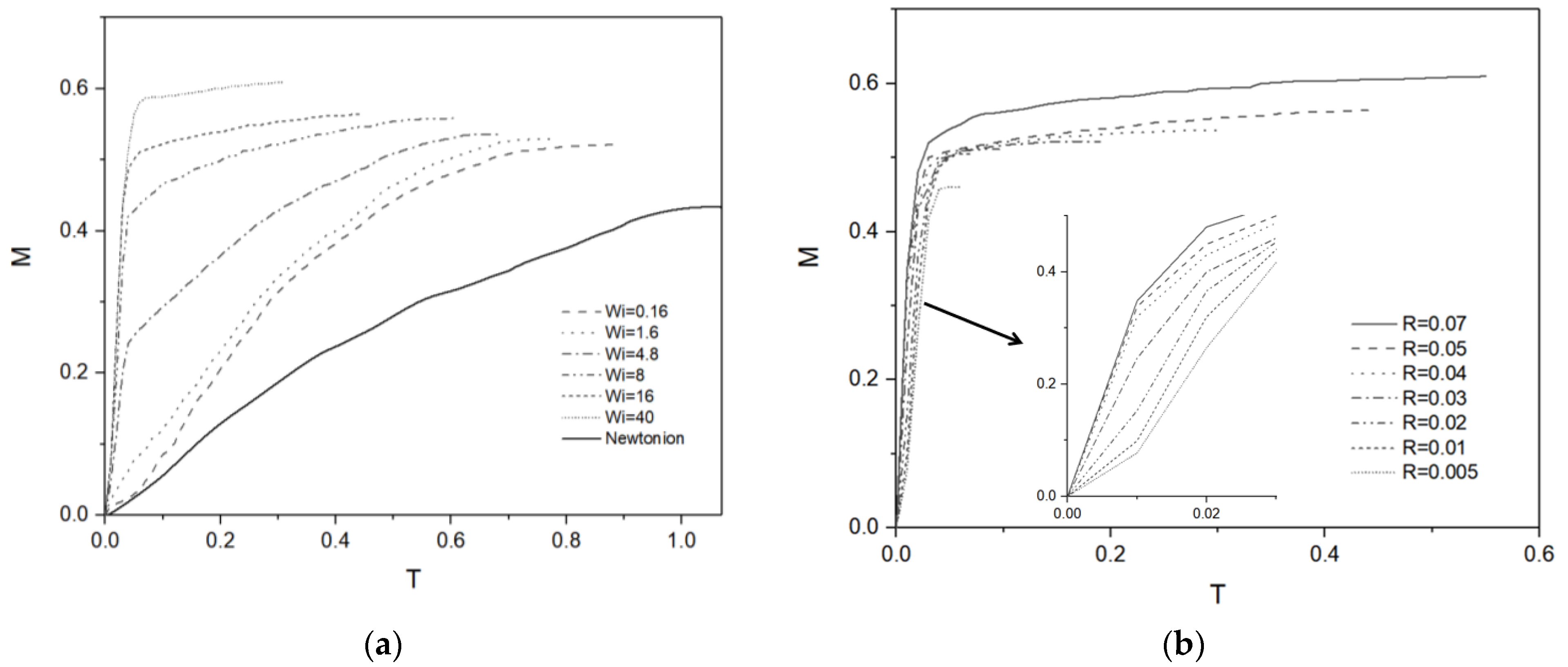
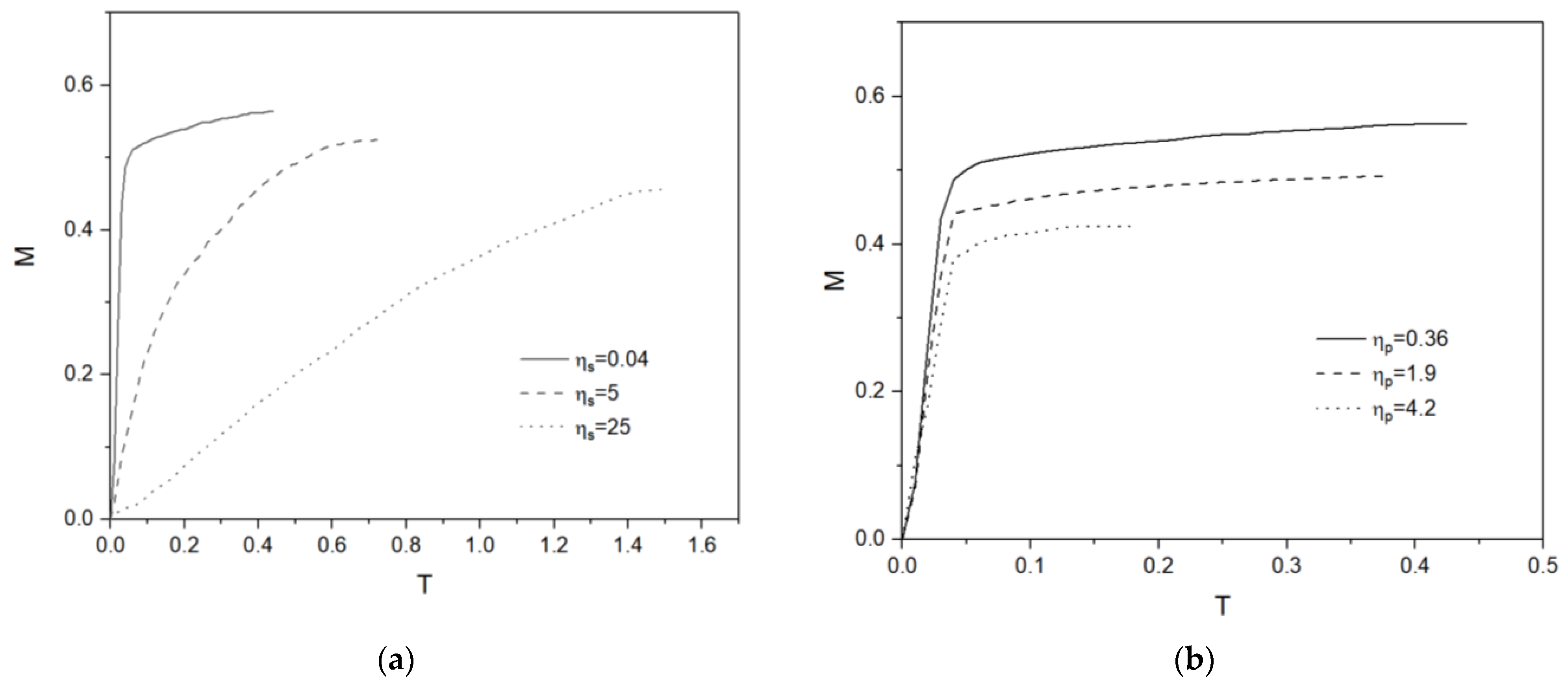
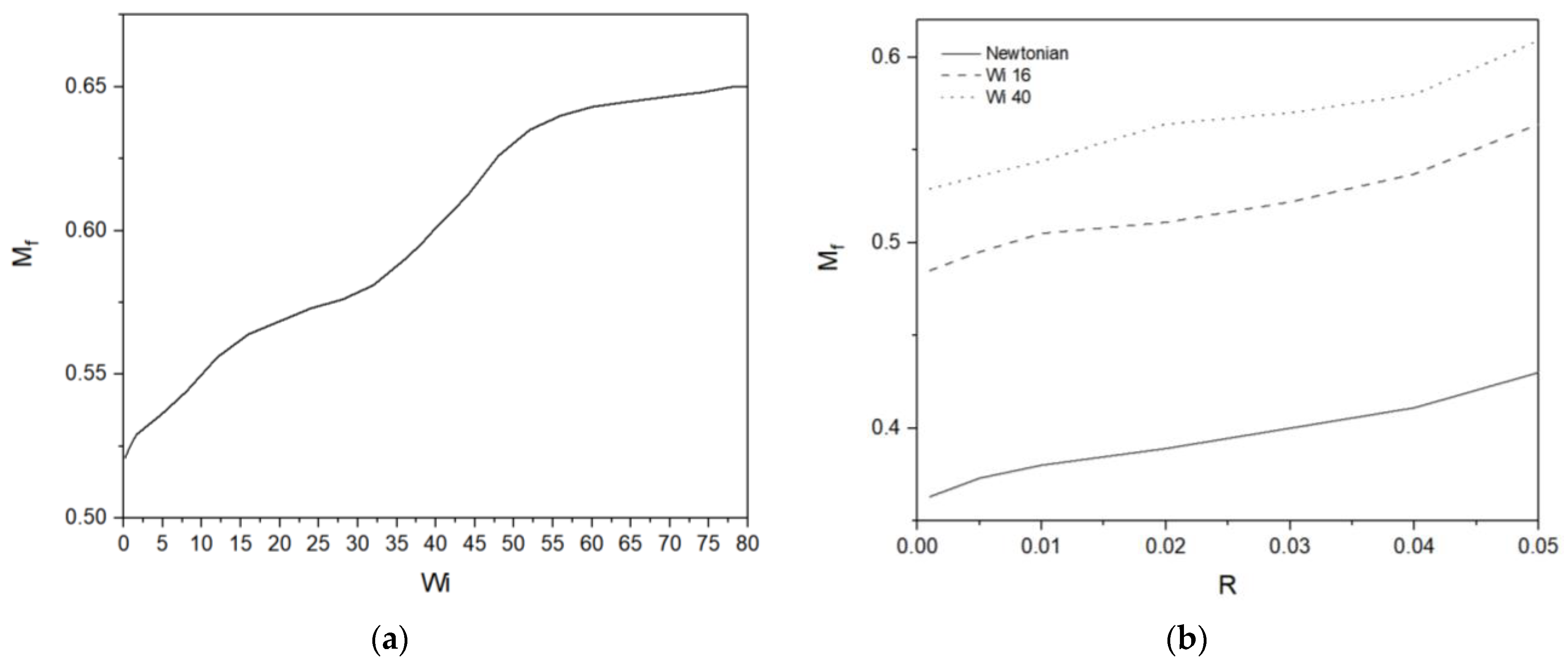
3. Results and Discussion
4. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Yao, X.; Song, Y.; Jiang, L. Applications of bio-inspired special wettablesurfaces. Adv. Mater. 2011, 23, 719–734. [Google Scholar] [CrossRef] [PubMed]
- Darhuber, A.A.; Valentino, J.P.; Troian, S.M.; Wagner, S. Thermocapillary actuation of droplets on chemically patterned surfaces by programmablemicroheater arrays. J. Microelectromech. Syst. 2003, 12, 873–879. [Google Scholar] [CrossRef] [Green Version]
- Mettu, S.; Chaudhury, M.K. Motion of drops on a surface induced bythermal gradient and vibration. Langmuir 2008, 24, 10833–10837. [Google Scholar] [CrossRef] [PubMed]
- Foroutan, M.; Fatemi, S.M.; Esmaeilian, F.; Fadaei Naeini, V.; Baniassadi, M. Contact angle hysteresis and motion behaviors of a water nanodroplet on suspended graphene under temperature gradient. Phys. Fluids 2018, 30, 052101. [Google Scholar] [CrossRef]
- Jaiswal, V.; Harikrishnan, A.; Khurana, G.; Dhar, P. Ionic solubility and solutal advection governed augmented evaporation kinetics of salt solution pendant droplets. Phys. Fluids 2018, 30, 012113. [Google Scholar] [CrossRef] [Green Version]
- Cho, S.K.; Moon, H.; Kim, C.-J. Creating, transporting, cutting, and merging liquid droplets by electrowetting-based actuation for digital microfluidic circuits. J. Microelectromech. Syst. 2003, 12, 70–80. [Google Scholar] [CrossRef] [Green Version]
- Latorre, L.; Kim, J.; Lee, J.; De Guzman, P.-P.; Lee, H.; Nouet, P.; Kim, C.-J. Electrostatic actuation of microscale liquid-metal droplets. J. Microelectromech. Syst. 2002, 11, 302–308. [Google Scholar] [CrossRef]
- Kunti, G.; Mondal, P.K.; Bhattacharya, A.; Chakraborty, S. Electrothermally modulated contact line dynamics of a binary fluid in a patterned fluidicenvironment. Phys. Fluids 2018, 30, 092005. [Google Scholar] [CrossRef]
- Kunti, G.; Bhattacharya, A.; Chakraborty, S. Electrothermally actuatedmoving contact line dynamics over chemically patterned surfaces with resistive heaters. Phys. Fluids 2018, 30, 062004. [Google Scholar] [CrossRef]
- Long, Z.; Shetty, A.M.; Solomon, M.J.; Larson, R.G. Fundamentals ofmagnet-actuated droplet manipulation on an open hydrophobic surface. Lab Chip 2009, 9, 1567–1575. [Google Scholar] [CrossRef]
- Ichimura, K.; Oh, S.-K.; Nakagawa, M. Light-driven motion of liquids on aphotoresponsive surface. Science 2000, 288, 1624–1626. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zheng, Y.; Cheng, J.; Zhou, C.; Xing, H.; Wen, X.; Pi, P.; Xu, S. Droplet Motion on a Shape Gradient Surface. Langmuir 2017, 33, 4172–4177. [Google Scholar] [CrossRef] [PubMed]
- Morrissette, J.M.; Mahapatra, P.S.; Ghosh, A.; Ganguly, R.; Megaridis, C.M. Rapid, Self-driven Liquid Mixing on Open-Surface Microfluidic Platforms. Sci. Rep. 2017, 7, 1800. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dhiman, S.; Jayaprakash, K.S.; Iqbal, R.; Sen, A.K. Self-Transport and Manipulation of Aqueous Droplets on Oil-Submerged Diverging Groove. Langmuir 2018, 34, 12359–12368. [Google Scholar] [CrossRef] [PubMed]
- Petrie, R.J.; Bailey, T.; Gorman, C.B.; Genzer, J. Fast directed motion of fakir droplets. Langmuir 2004, 20, 9893–9896. [Google Scholar] [CrossRef]
- Greenspan, H.P. On the motion of a small viscous droplet that wets a surface. J. Fluid Mech. 1978, 84, 125–143. [Google Scholar] [CrossRef] [Green Version]
- Brochard, F. Motions of droplets on solid surfaces induced by chemical or thermal gradients. Langmuir 1989, 5, 432–438. [Google Scholar] [CrossRef]
- Yang, J.-T.; Chen, J.C.; Huang, K.-J.; Yeh, J.A. Droplet manipulation on a hydrophobic textured surface with roughened patterns. J. Microelectromech. Syst. 2006, 15, 697–707. [Google Scholar] [CrossRef]
- Li, J.; Guo, Z. Spontaneous Directional Transportations of Water Droplets on Surfaces Driven by Gradient Structures. Nanoscale 2018, 10, 13814–13831. [Google Scholar] [CrossRef]
- Moumen, N.; Subramanian, R.S.; McLaughlin, J.B. Experiments on the Motion of Drops on a Horizontal Solid Surface Due to a Wettability Gradient. Langmuir 2006, 22, 2682–2690. [Google Scholar] [CrossRef]
- Chowdhury, I.U.; Mahapatra, P.S.; Sen, A.K. Self-driven droplet transport: Effect of wettability gradient and confinement. Phys. Fluids 2019, 31, 042111. [Google Scholar] [CrossRef]
- Liu, C.; Sun, J.; Li, J.; Xiang, C.; Chenghao, X.; Wang, Z.; Zhou, X. Long-range spontaneous droplet self-propulsion on wettability gradient surfaces. Sci. Rep. 2017, 7, 7552. [Google Scholar] [CrossRef] [PubMed]
- Subramanian, R.S.; Moumen, A.N.; McLaughlin, J.B. Motion of a Drop on a Solid Surface Due to a Wettability Gradient. Langmuir 2005, 21, 11844–11849. [Google Scholar] [CrossRef] [PubMed]
- Chaudhury, M.K.; Chakrabarti, A.; Daniel, S. Generation of Motion of Drops with Interfacial Contact. Langmuir 2015, 31, 9266–9281. [Google Scholar] [CrossRef] [Green Version]
- Xu, X.; Qian, T. Droplet motion in one-component fluids on solid substrates with wettability gradients. Phys. Rev. E 2012, 85, 051601. [Google Scholar] [CrossRef] [Green Version]
- Liu, Q.; Xu, B. A unified mechanics model of wettability gradient-driven motion of water droplet on solid surfaces. Extreme Mech. Lett. 2016, 9, 304–309. [Google Scholar] [CrossRef]
- Raman, K.A. Dynamics of simultaneously impinging drops on a dry surface: Role of inhomogeneous wettability and impact shape. J. Colloid Interface Sci. 2018, 516, 232–247. [Google Scholar] [CrossRef]
- Huang, J.; Shu, C.; Chew, Y. Numerical investigation of transporting droplets by spatiotemporally controlling substrate wettability. J. Colloid Interface Sci. 2008, 328, 124–133. [Google Scholar] [CrossRef]
- Ahmadlouydarab, M.; Feng, J.J. Motion and coalescence of sessile drops driven by substrate wetting gradient and external flow. J. Fluid Mech. 2014, 746, 214–235. [Google Scholar] [CrossRef] [Green Version]
- Nasr, H.; Ahmadi, G.; McLaughlin, J.; Jia, X. Drop motion simulation on a surface due to a wettability gradient. In Proceedings of the ASME 2006 2nd Joint US-European Fluids Engineering Summer Meeting Collocated with the 14th International Conference on Nuclear Engineering, Miami, FL, USA, 17–20 July 2006; American Society of Mechanical Engineers: New York, NY, USA; pp. 547–550. [Google Scholar]
- Chowdhury, I.U.; Mahapatra, P.S.; Sen, A.K. Shape evolution of drops on surfaces of different wettability gradients. Chem. Eng. Sci. 2021, 229, 116136. [Google Scholar] [CrossRef]
- Zielke, P.C.; Subramanian, R.S.; Szymczyk, J.A.; McLaughlin, J.B. Movement of drops on a solid surface due to a contact angle gradient. Proc. Appl. Math. Mech. 2003, 2, 390–391. [Google Scholar] [CrossRef]
- Ji, J.; Qian, S.; Liu, Z. Electroosmotic Flow of Viscoelastic Fluid through a Constriction Microchannel. Micromachines 2021, 12, 417. [Google Scholar] [CrossRef] [PubMed]
- Casas, L.; Ortega, J.A.; Gómez, A.; Escandón, J.; Vargas, R.O. Analytical Solution of Mixed Electroosmotic/Pressure Driven Flow of Viscoelastic Fluids between a Parallel Flat Plates Micro-Channel: The Maxwell Model Using the Oldroyd and Jaumann Time Derivatives. Micromachines 2020, 11, 986. [Google Scholar] [CrossRef] [PubMed]
- Escandón, J.; Torres, D.; Hernández, C.; Vargas, R. Start-Up Electroosmotic Flow of Multi-Layer Immiscible Maxwell Fluids in a Slit Microchannel. Micromachines 2020, 11, 757. [Google Scholar] [CrossRef]
- Mei, L.; Zhang, H.; Meng, H.; Qian, S. Electroosmotic Flow of Viscoelastic Fluid in a Nanoslit. Micromachines 2018, 9, 155. [Google Scholar] [CrossRef] [Green Version]
- Mei, L.; Qian, S. Electroosmotic Flow of Viscoelastic Fluid in a Nanochannel Connecting Two Reservoirs. Micromachines 2019, 10, 747. [Google Scholar] [CrossRef] [Green Version]
- Omori, T.; Ishikawa, T. Swimming of Spermatozoa in a Maxwell Fluid. Micromachines 2019, 10, 78. [Google Scholar] [CrossRef] [Green Version]
- Bai, F.; Li, Y.; Zhang, H.; Joo, S.W. A numerical study on viscoelastic droplet migration on a solid substrate due to wettability gradient. Electrophoresis 2019, 40, 851–858. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Li, Y.; Li, X.; Wu, J.; Qian, S.; Li, F. Dynamic control of particle separation in deterministic lateral displacement separator with viscoelastic fluids. Sci. Rep. 2018, 8, 3618. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, W.; Wu, Z.; Shen, Y.; Wu, H.; Cheng, J.; Zhang, H.; Li, F.; Cai, W. Modulation of viscoelastic fluid response to external body force. Sci. Rep. 2019, 9, 9402. [Google Scholar] [CrossRef]
- Zhang, M.; Wu, Z.; Shen, Y.; Chen, Y.; Lan, C.; Li, F.; Cai, W. Comparison of Micro-Mixing in Time Pulsed Newtonian Fluid and Viscoelastic Fluid. Micromachines 2019, 10, 262. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Figueiredo, R.A.; Oishi, C.M.; Cuminato, J.A.; Azevedo, J.C.; Afonso, A.M.; Alves, M.A. Numerical investigation of three dimensional viscoelastic free surface flows: Impacting drop problem. In Proceedings of the 6th European Conference on Computational Fluid Dynamics (ECFD VI), Barcelona, Spain, 20–25 July 2014; Volume 5. [Google Scholar]

| Fluid | (kg/m3) | (Pa∙s) | (Pa∙s) | (s) | (N/m) |
|---|---|---|---|---|---|
| Oldroyd-B | 1000 | 0.36 | 0.04 | 0.01 | 0.073 |
| Newtonian liquid | 1000 | 0.04 | 0.073 | ||
| Newtonian gas | 1 | 0.073 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, Y.J.; Joo, S.W. The Effects of Viscoelasticity on Droplet Migration on Surfaces with Wettability Gradients. Micromachines 2022, 13, 729. https://doi.org/10.3390/mi13050729
Ren YJ, Joo SW. The Effects of Viscoelasticity on Droplet Migration on Surfaces with Wettability Gradients. Micromachines. 2022; 13(5):729. https://doi.org/10.3390/mi13050729
Chicago/Turabian StyleRen, Ying Jun, and Sang Woo Joo. 2022. "The Effects of Viscoelasticity on Droplet Migration on Surfaces with Wettability Gradients" Micromachines 13, no. 5: 729. https://doi.org/10.3390/mi13050729
APA StyleRen, Y. J., & Joo, S. W. (2022). The Effects of Viscoelasticity on Droplet Migration on Surfaces with Wettability Gradients. Micromachines, 13(5), 729. https://doi.org/10.3390/mi13050729






