Current Progress towards the Integration of Thermocouple and Chipless RFID Technologies and the Sensing of a Dynamic Stimulus
Abstract
:1. Introduction
1.1. Current Need for Extreme Environment Compliant Printable DC Voltage Sensors
1.2. Challenges in Integrating Thermocouple and Chipless RFID Technologies
1.2.1. Liquid Crystal Polymers (LCPs)
1.2.2. Electrostatic Actuators
1.2.3. Ferroelectric Materials
1.2.4. Comparison of Possible Approaches
1.3. Effects of Dynamic Stimulii on Chipless RFID Interrogation
2. Methodology
2.1. Existing BST Varactors
2.2. Test Circuit Design
2.3. Sensor Fabrication
2.4. Circuit Testing
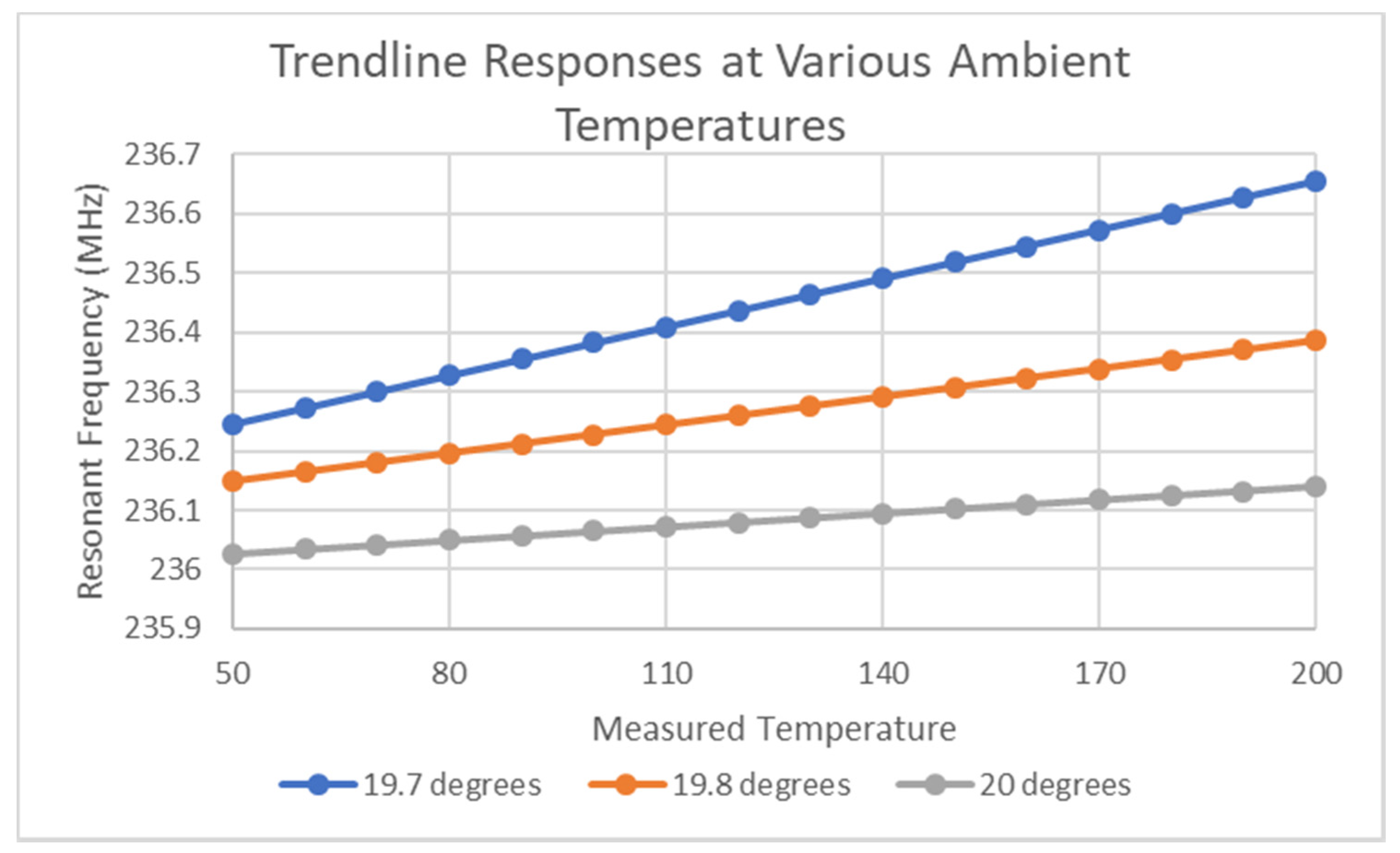
2.4.1. Temperature Testing and Environment Details
2.4.2. Exploration of Stimulus Gradients
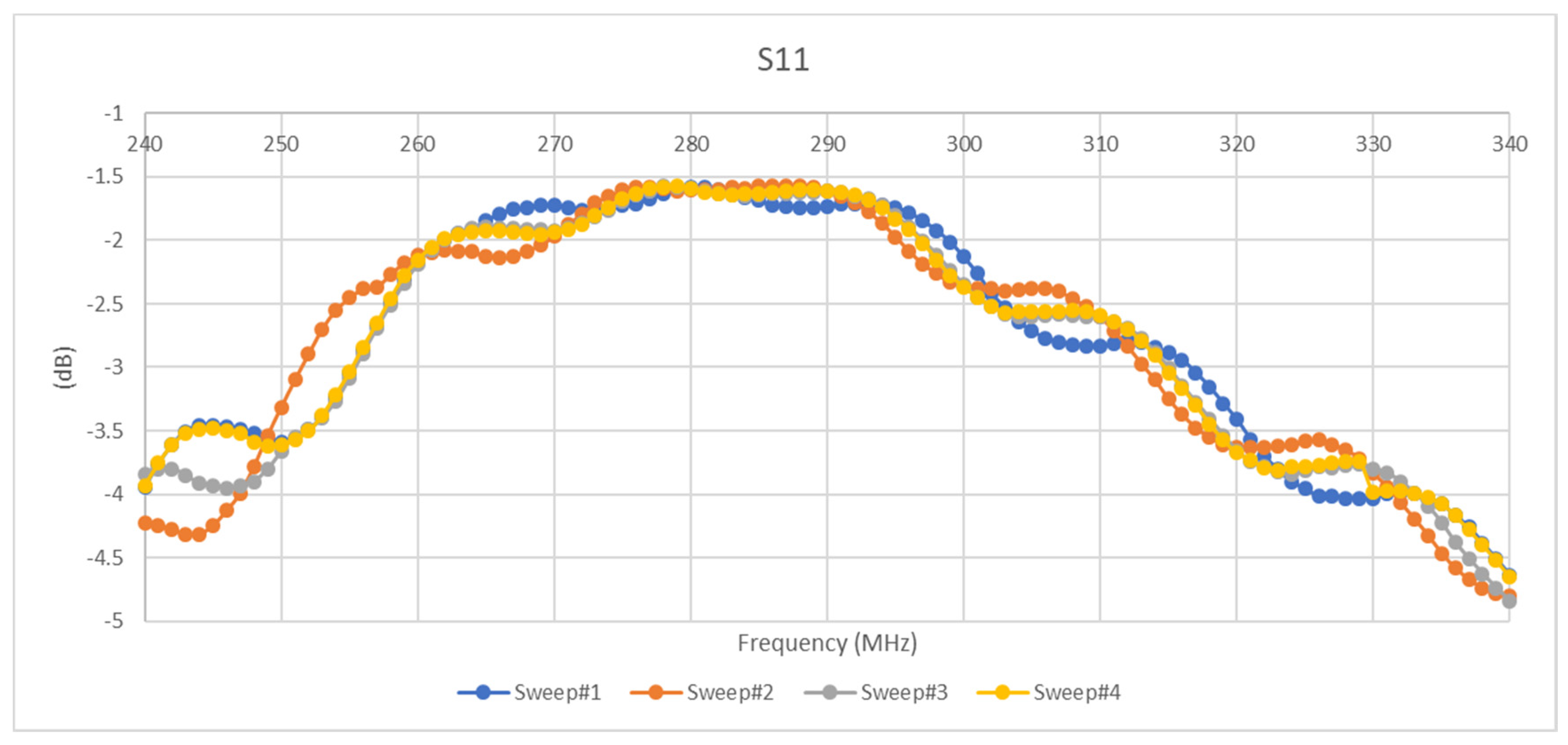
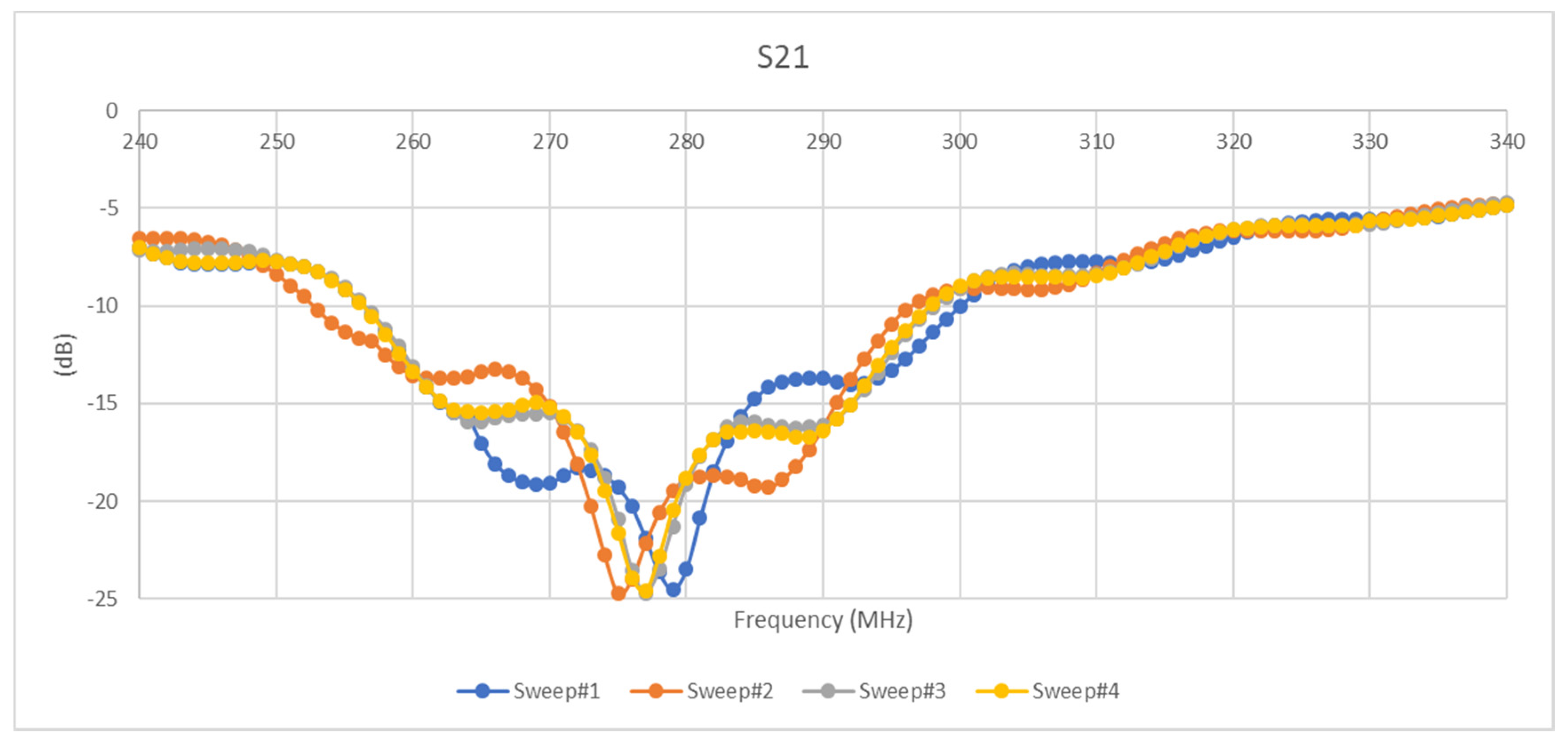
3. Results and Discussion
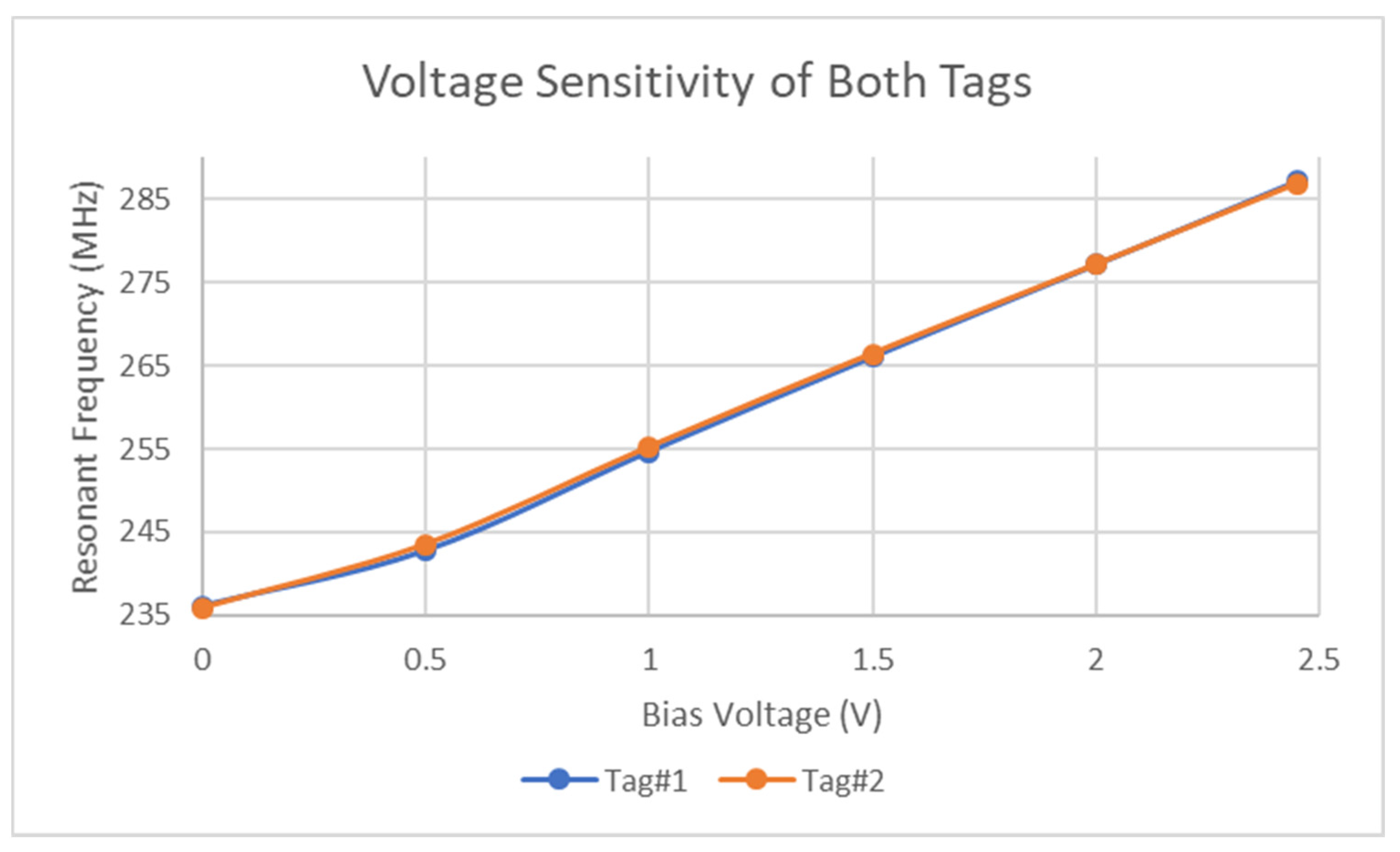
3.1. Large Voltage Biasing of Sensor
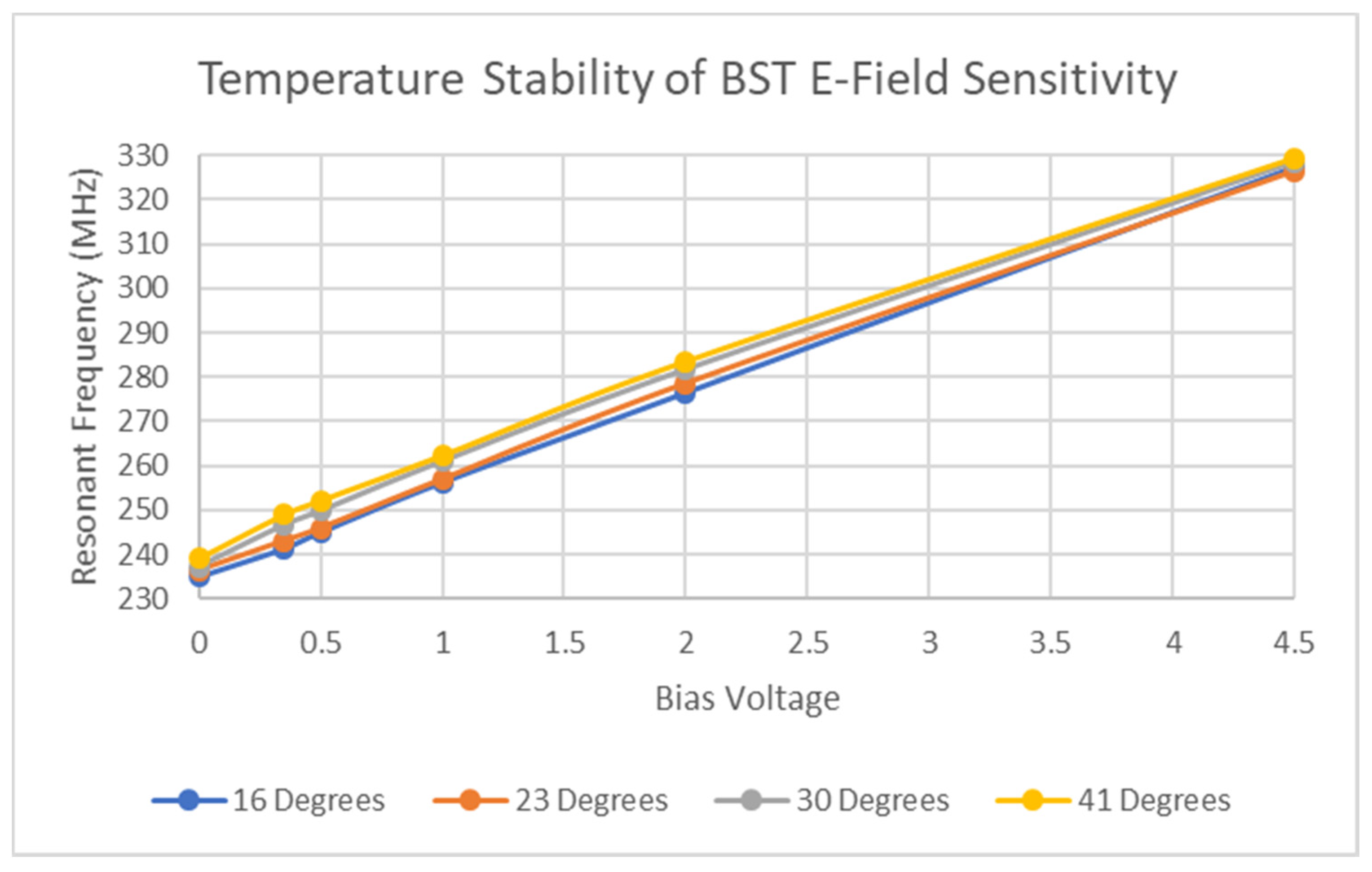
3.2. Thermocouple Biasing of Sensor
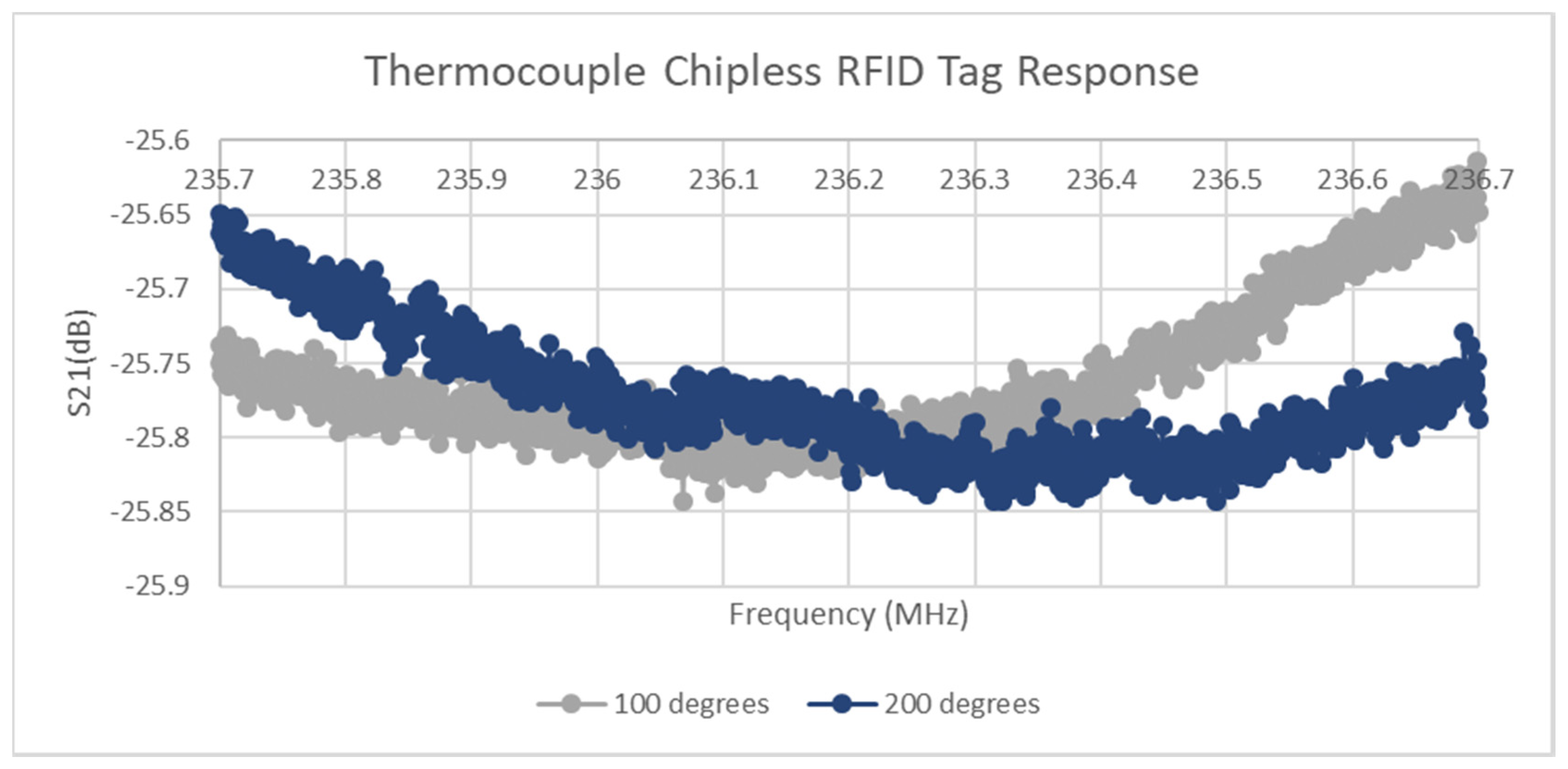
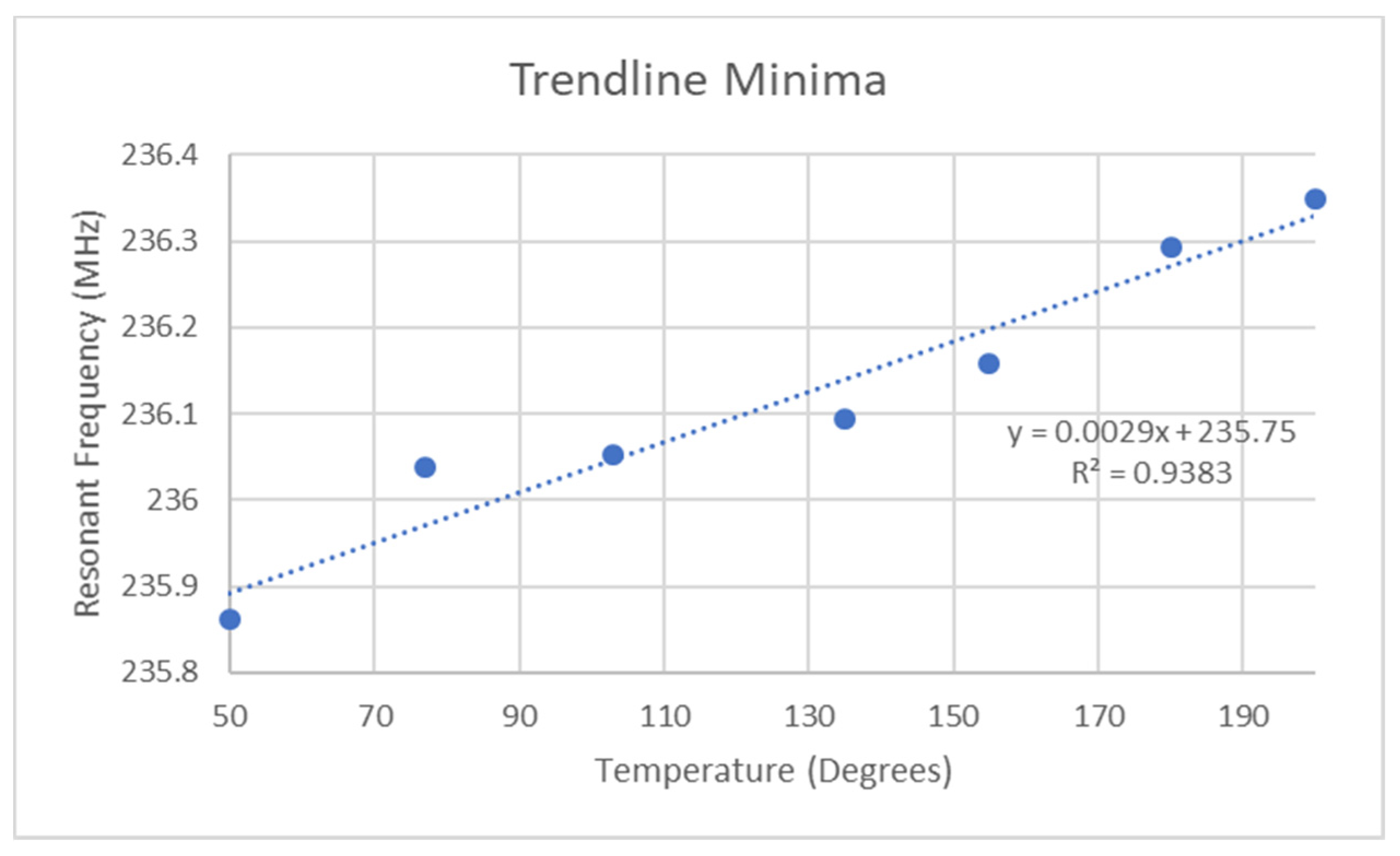
3.3. Results of Dynamic Stimulii
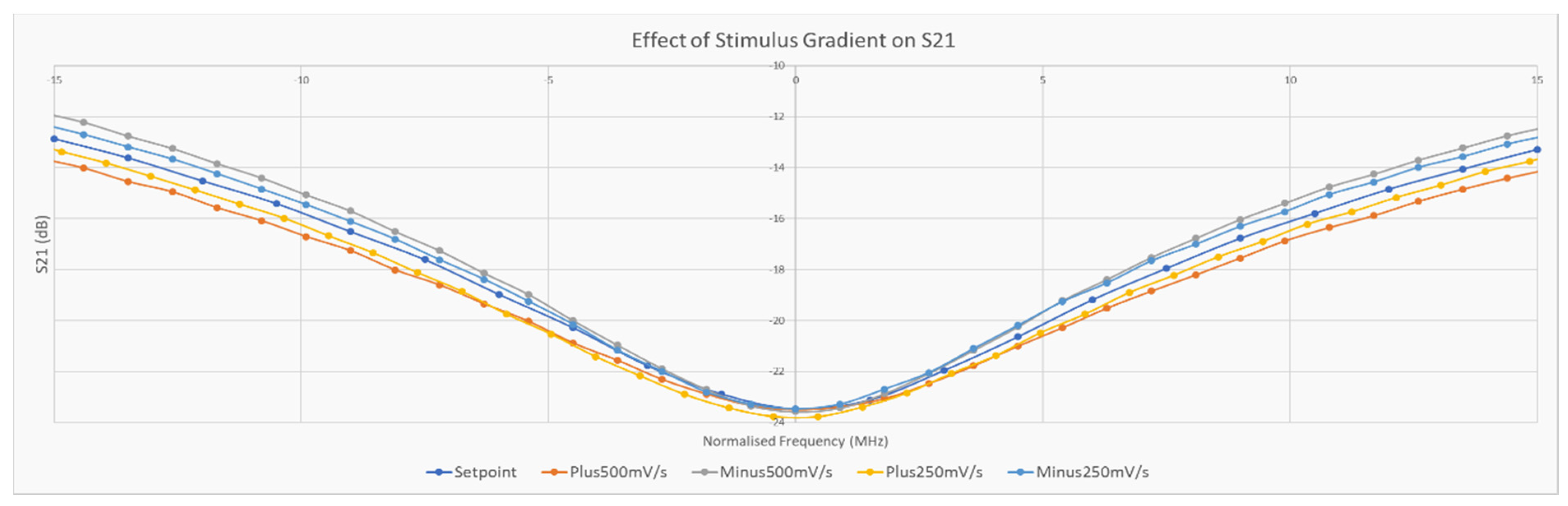
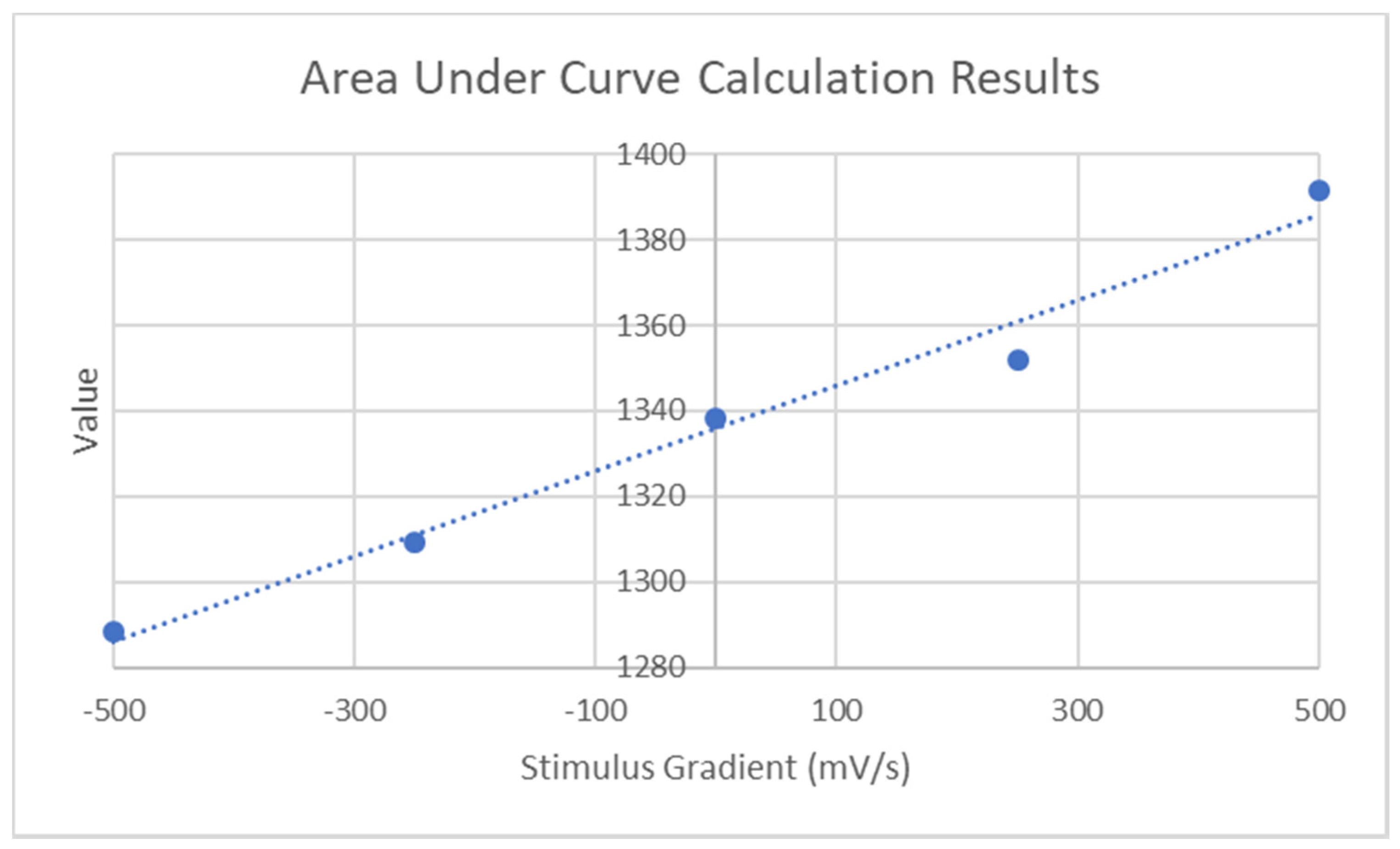
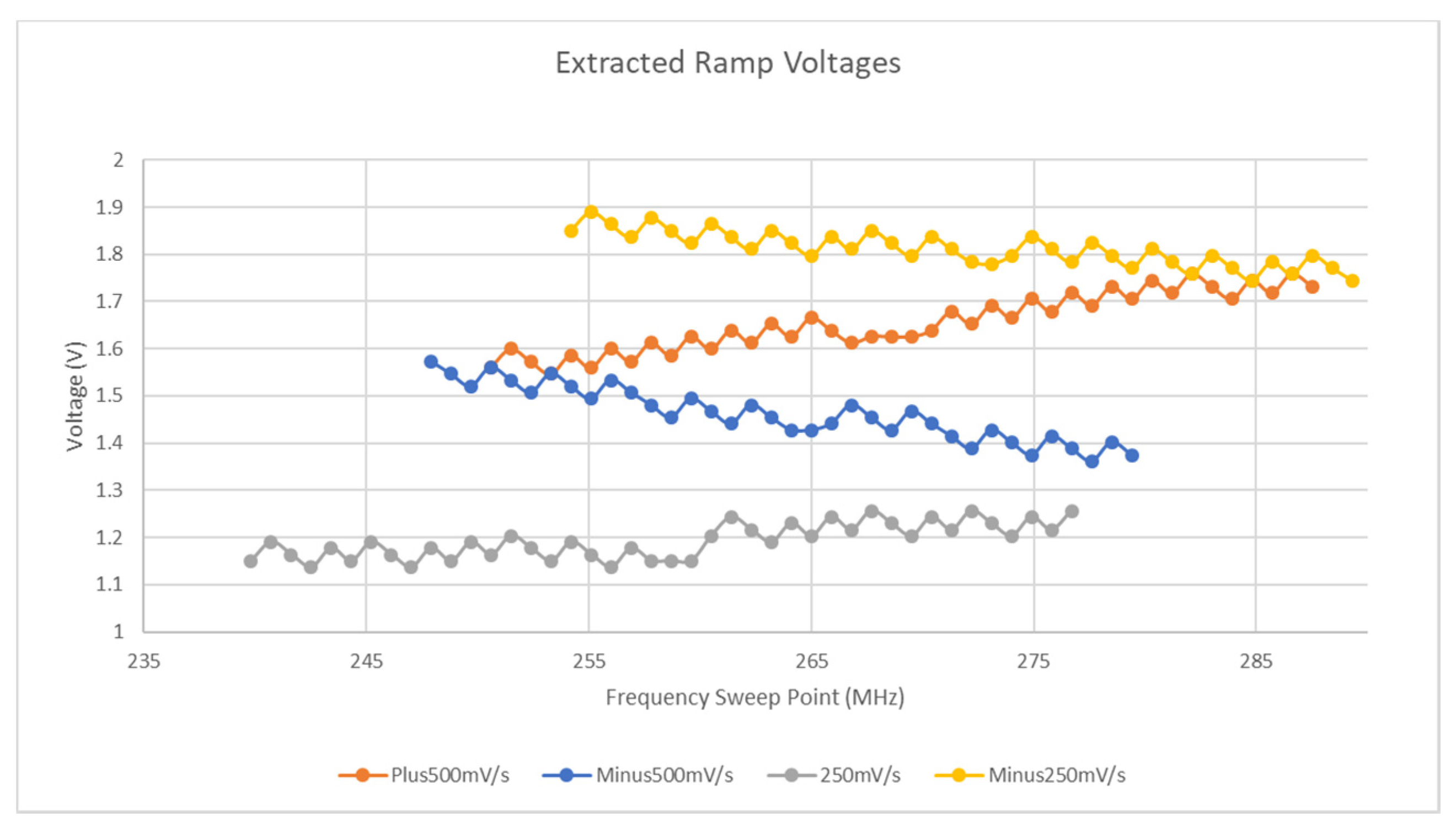
3.3.1. Exploration of Stimulus Gradient Effects
- Sampling rate (Hz).
- Frequency step size (Hz).
- Resonator bandwidth.
- Frequency sweep range.
- Frequency sweep direction.
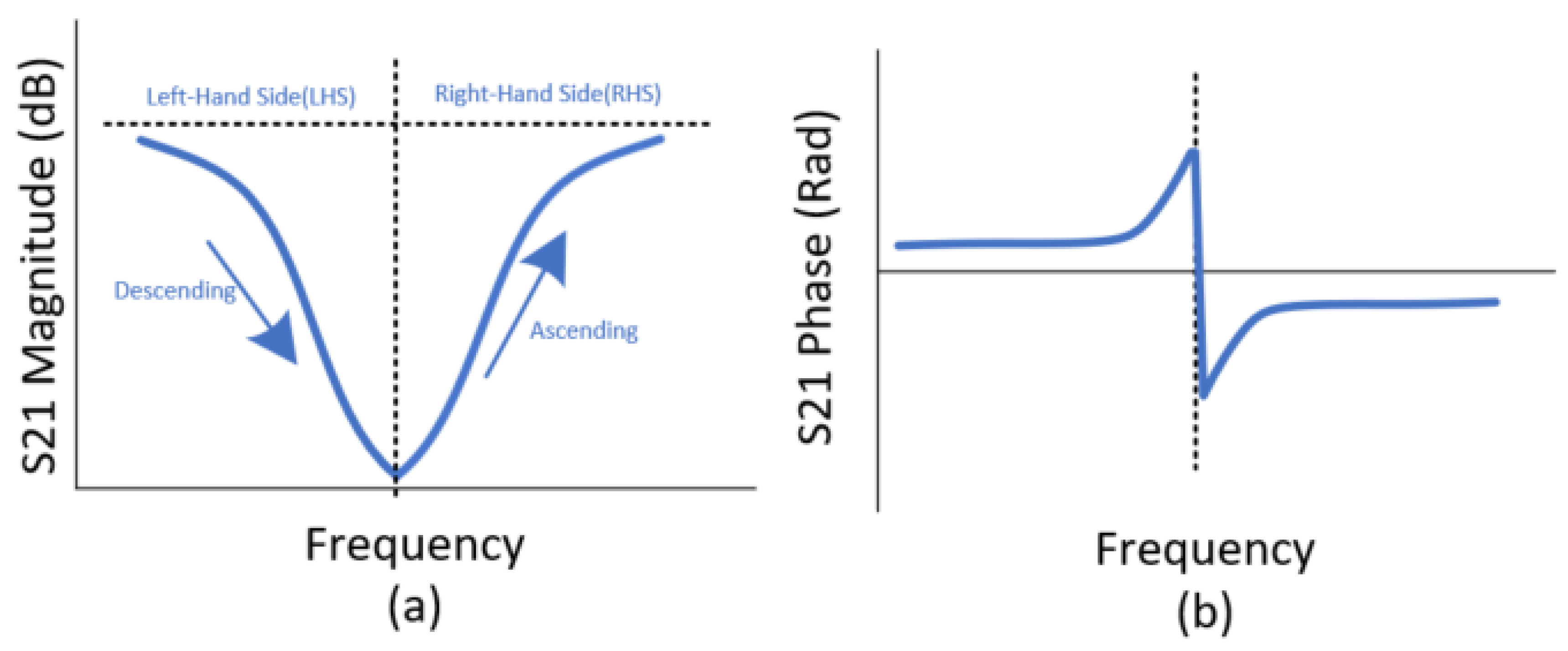
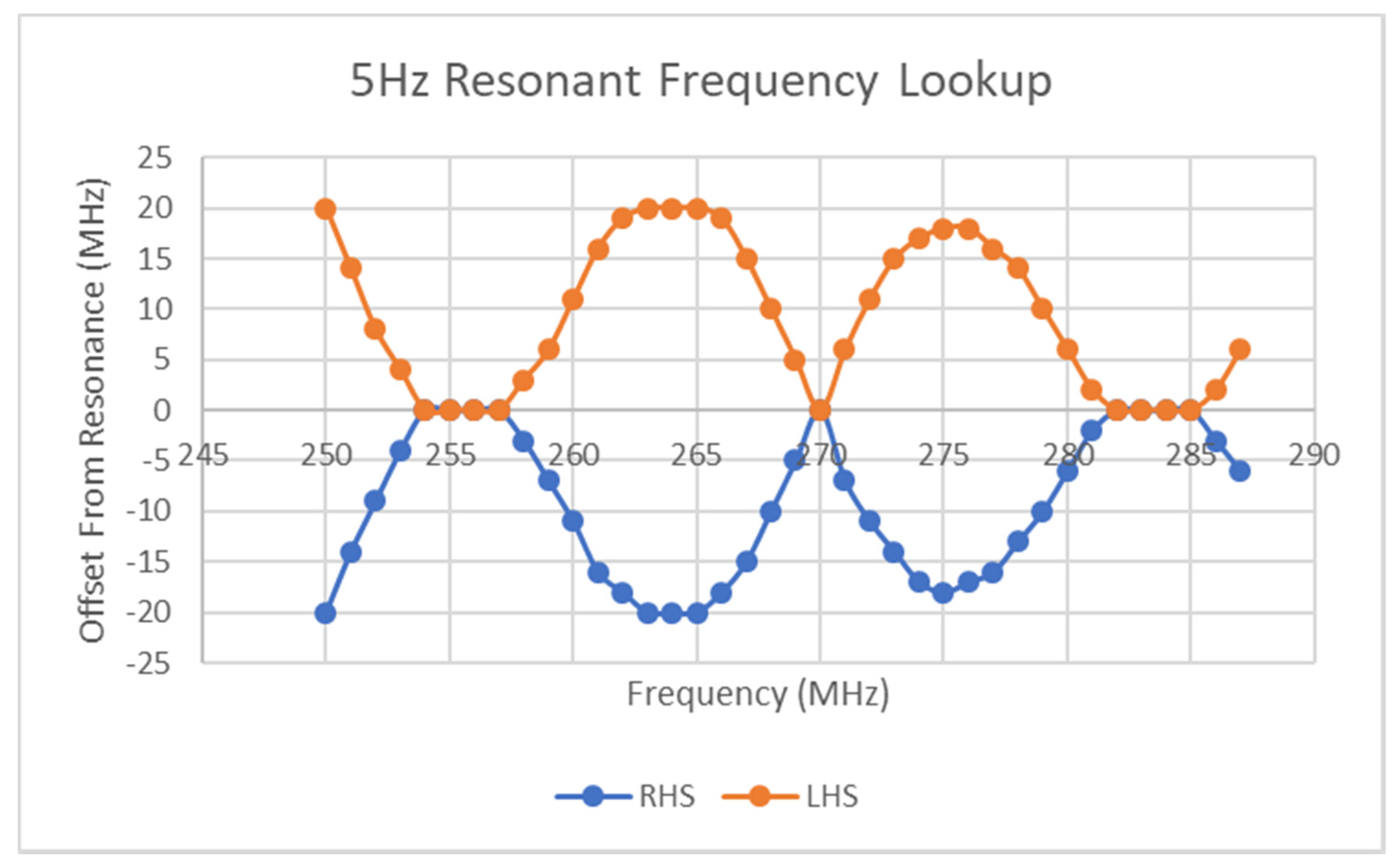
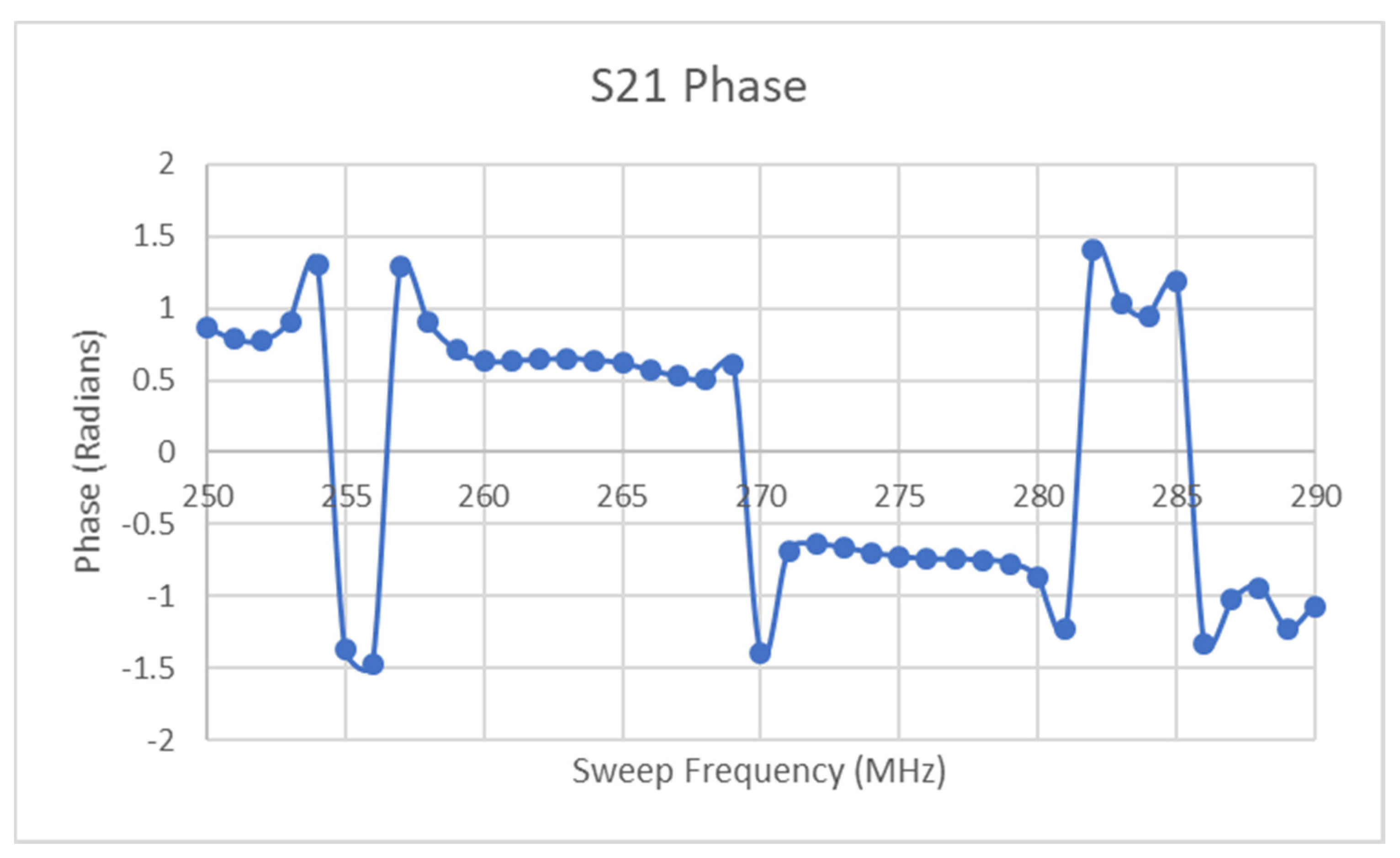
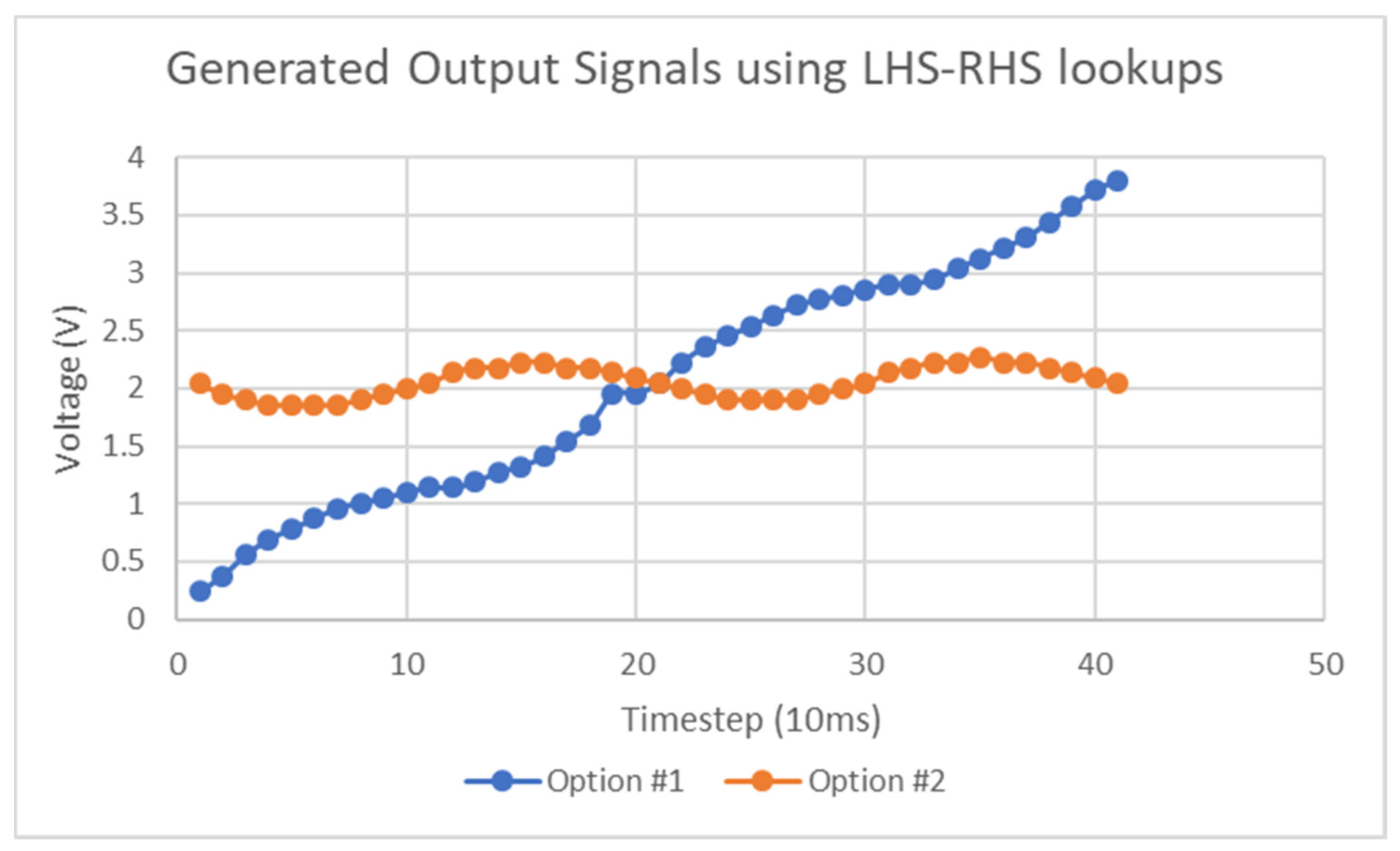
- If the Ramp Direction opposes Sweep Direction:Result: Detection occurs. The minimum point on the curve marks the transition from the sampling of the Left-hand side of the resonant curve (LHS) to the Right-hand side (RHS).
- If the Ramp Direction does not oppose Sweep Direction:Scenario A: Ramp Rate>Sweep Rate or (Initial Ramp Value + Ramp Rate) > Sweep RateResult: Either no resonant response is detected during sweep as the stimulus magnitude has escaped the band or a setpoint-based resonant region is detected at the maximum stimulus level, if saturation occurs within the sensor system.Scenario B: Ramp Rate < Sweep RateResult: Detection occurs. The minimum point on the curve marks the transition from the sampling of the RHS of the resonant curve to the LHS.
- The resolution of all curves will define the accuracy by which the minimum of the curve(s) is measured.
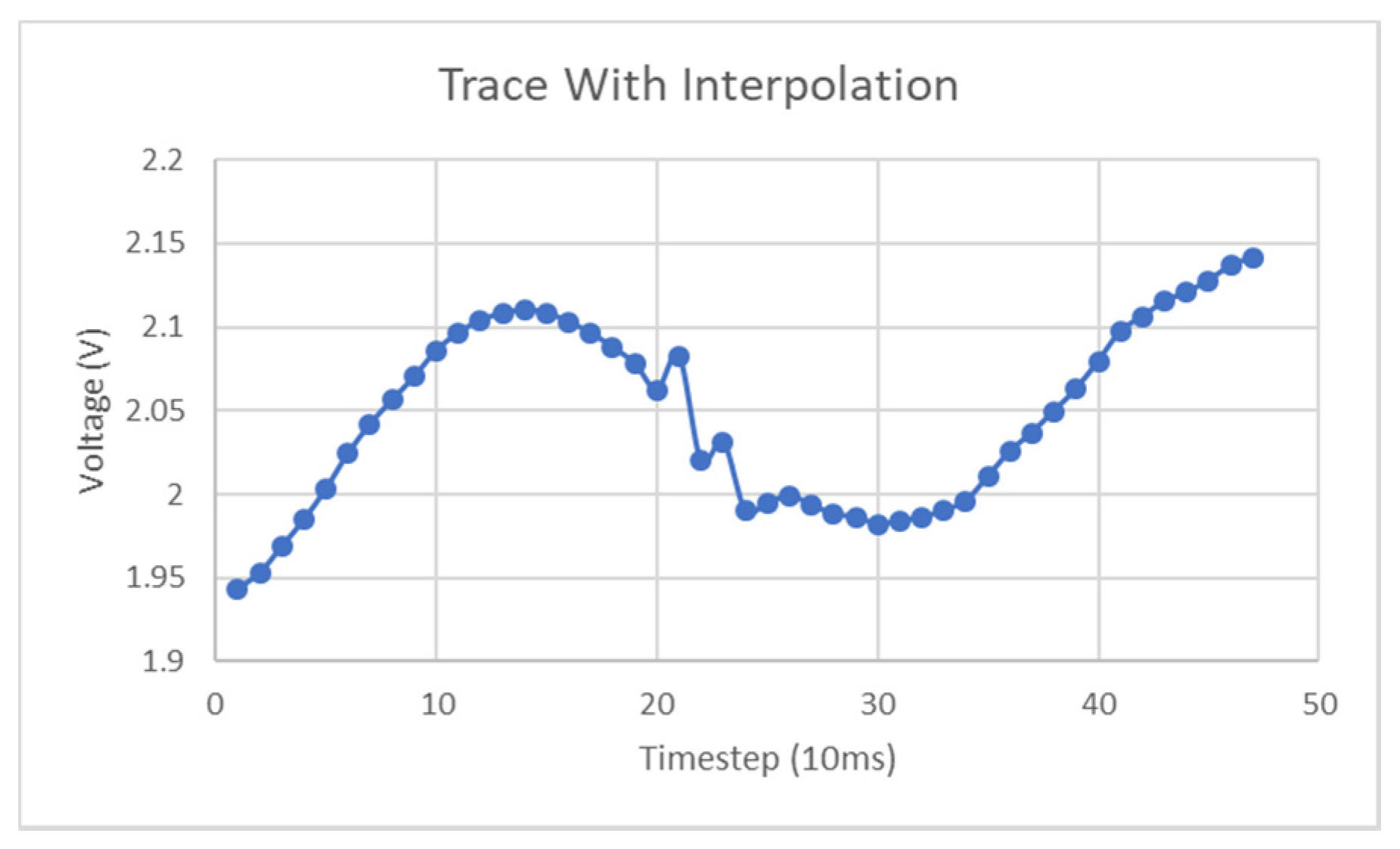
- The resolution of both ramp and setpoint curves will define the accuracy of the inferred voltage at each timestep in the frequency sweep, as even with the addition of linear interpolation, errors will still exist.
- No linear or other form of interpolation was performed on the lookup of the true resonant point on the setpoint curve; thus, the accuracy is totally at the mercy of the setpoint curve resolution.
- Even with interpolation, the setpoint curve had a step size of 1.5 MHz which is quite significant. It is worth noting that the greatest errors induced by this factor will be around the results of the lookup at positions around the minimum value and this poor resolution also hampers the accurate detection of the minimum of the setpoint curve.
- All other sweeps performed consisted of only 100 points, which led to a resolution of 0.9 MHz/step.
- The voltage value that has been inferred is based on the accuracy of the linear relationship between resonant frequency and voltage, displayed in Figure 3.
3.3.2. Exploration of Sinusoidal Stimulus Effects
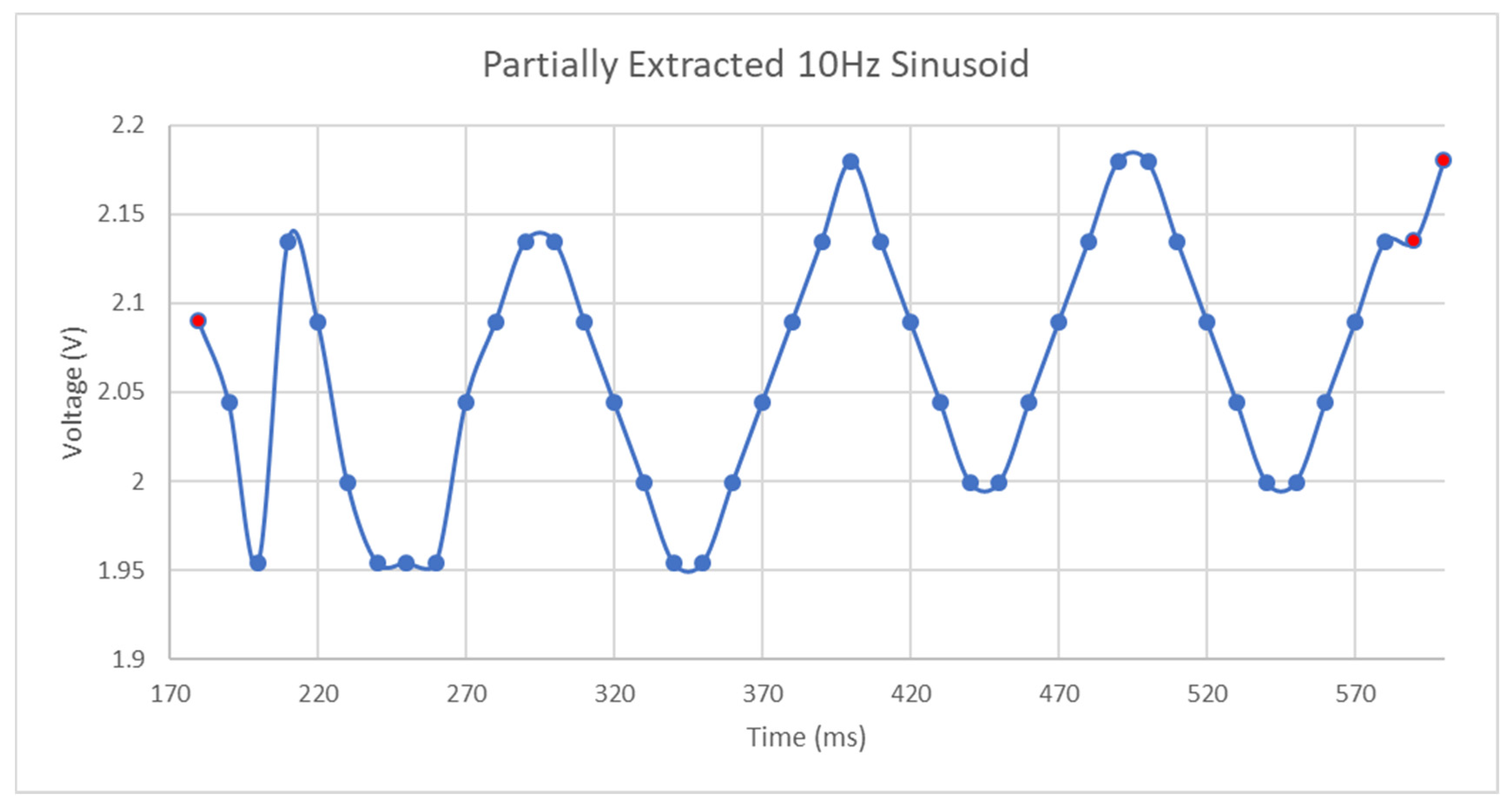
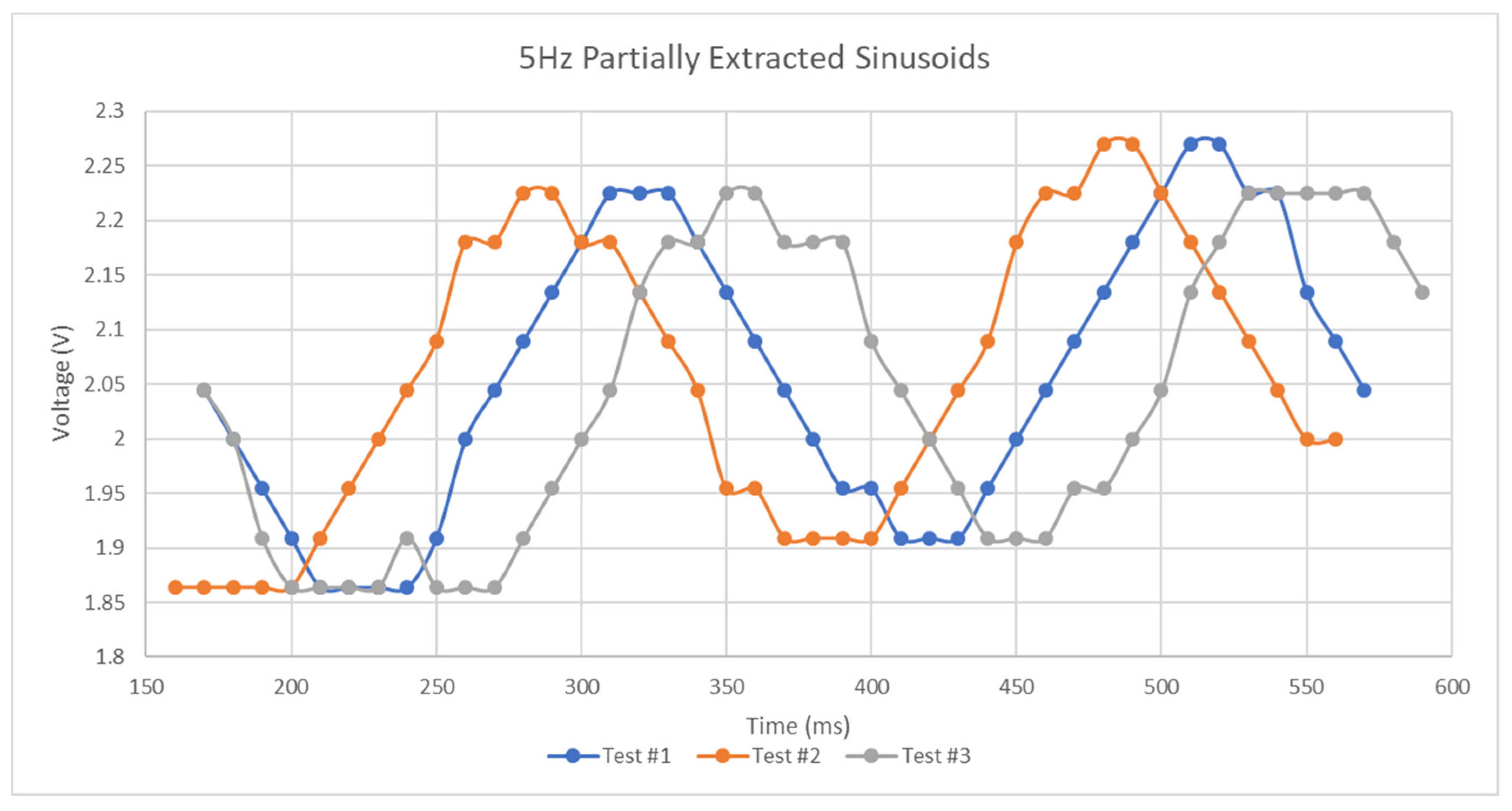
- The frequency sweep can only accurately determine the peak voltage towards the end of the frequency sweep as the bandwidth of the resonant region and that of the lookup function will not always be comparable with the change in resonant frequency caused by an amplitude of this size. A similar effect occurs at the beginning of the sweep with the minimum amplitude of the sinusoid.
- The frequency sweep and that used to generate the mapping function has a finite resolution.
- The spacing between successive points in a discrete setpoint resonant region for a fixed change in S21 magnitude vary nonlinearly in accordance with the nonlinear characteristics of the bandstop response curve.
- The portions of the S21 magnitude outside of the resonant region are not perfectly flat and may have gradients in the direction of this region. This would cause an invalid use of the lookup function at those frequency points.
- Small variations in ambient temperature may exist between this test and that used to develop the voltage-frequency lookup and the impedance behavior of the SIR circuit to a varying bias voltage may not be purely reactive.
4. Conclusions
4.1. Results of This Work
4.2. Future Goals
- How can the electrical sensitivity of this device be enhanced, and its thermal sensitivity lowered?
- What other methods exist that would allow possible successful thermocouple integration into chipless RFID?
- What are the effects of ionizing radiation and general aging on the performance of this device?
- Can a combination of materials such as BST, Polyimide, and a metallic conductor be deposited together into a composite sensor in a sequential fashion onto generic substrates in a timely fashion?
- How well can the dynamic stimulus extraction methodology above perform in a wireless test?
Author Contributions
Funding

Conflicts of Interest
References
- Herrojo, C.; Paredes, F.; Mata-Contreras, J.; Martín, F. Chipless-RFID: A review and recent developments. Sensors 2019, 19, 3385. [Google Scholar] [CrossRef] [Green Version]
- Mc Gee, K.; Anandarajah, P.; Collins, D. A review of chipless remote sensing solutions based on RFID technology. Sensors 2019, 19, 4829. [Google Scholar] [CrossRef] [Green Version]
- Scheick, L.; Johnston, A.; Adell, P.; Irom, F.; McClure, S. Total Ionizing Dose (TID) and Displacement Damage (DD) effects in integrated circuits: Recent results and the implications for emerging technology. In Proceedings of the International Workshop on Radiation Effects on Semiconductor Devices for Space Applications, Tsukuba, Japan, 10–12 December 2013. [Google Scholar]
- French, P.; Krijnen, G.; Roozeboom, F. Precision in harsh environments. In Microsystems and Nanoengineering; Nature Publishing Group: Berlin, Germany, 2016; Volume 2, pp. 1–12. [Google Scholar]
- Scardelletti, M.C.; Jordan, J.L.; Ponchak, G.E.; Zorman, C.A. Wireless capacitive pressure sensor with directional RF chip antenna for high temperature environments. In Proceedings of the IEEE International Conference on Wireless for Space and Extreme Environments, WiSEE 2015, Orlando, FL, USA, 14–16 December 2015; pp. 1–6. [Google Scholar]
- Kim, J.; Wang, Z.; Kim, W.S. Stretchable RFID for wireless strain sensing with silver nano ink. IEEE Sens. J. 2014, 14, 4395–4401. [Google Scholar] [CrossRef]
- Vena, A.; Babar, A.A.; Sydanheimo, L.; Tentzeris, M.M.; Ukkonen, L. A novel near-transparent ASK-reconfigurable inkjet-printed chipless RFID tag. IEEE Antennas Wirel. Propag. Lett. 2013, 12, 753–756. [Google Scholar] [CrossRef]
- Vena, A.; Sydänheimo, L.; Ukkonen, L.; Tentzeris, M.M. A fully inkjet-printed chipless RFID gas and temperature sensor on paper. In Proceedings of the 2014 IEEE RFID Technology and Applications Conference, RFID-TA 2014, Tampere, Finland, 8–9 September 2014; Volume 2, pp. 115–120. [Google Scholar]
- McKerricher, G.; Vaseem, M.; Shamim, A. Fully inkjet-printed microwave passive electronics. Microsyst. Nanoeng. 2017, 3, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Zhang, F.; Tuck, C.; Hague, R.; He, Y.; Saleh, E.; Li, Y.; Sturgess, C.; Wildman, R. Inkjet printing of polyimide insulators for the 3D printing of dielectric materials for microelectronic applications. J. Appl. Polym. Sci. 2016, 133. [Google Scholar] [CrossRef] [Green Version]
- Fang, Y.; Hester, J.G.D.; Su, W.; Chow, J.H.; Sitaraman, S.K.; Tentzeris, M.M. A bio-enabled maximally mild layer-by-layer Kapton surface modification approach for the fabrication of all-inkjet-printed flexible electronic devices. Sci. Rep. 2016, 6, 39909. [Google Scholar] [CrossRef] [Green Version]
- Wilson, W.C.; Juarez, P.D. Emerging needs for pervasive passive wireless sensor networks on aerospace vehicles. Procedia Comput. Sci. 2014, 37, 101–108. [Google Scholar] [CrossRef] [Green Version]
- Wilson, W.C.; Perey, D.F.; Atkinson, G.M.; Barclay, R.O. Passive wireless SAW sensors for IVHM. In Proceedings of the 2008 IEEE International Frequency Control. Symposium, FCS, Honolulu, HI, USA, 18–21 May 2008; pp. 273–277. [Google Scholar]
- Von Moll, A.; Behbahani, A.R.; Fralick, G.C.; Wrbanek, J.D.; Hunter, G.W. A Review of exhaust gas temperature sensing techniques for modern turbine engine controls. In Proceedings of the 50th AIAA/ASME/SAE/ASEE Joint Propulsion Conference 2014, Cleveland, OH, USA, 28–30 July 2014. [Google Scholar]
- ESA. ESA Open Invitation to Tender [FR] AO8922—Direct Printing of Mechanical and Thermal Sensors onto Spacecraft Hardware; ESA: Paris, France, 2017. [Google Scholar]
- Goossens, S.; De Pauw, B.; Geernaert, T.; Salmanpour, M.S.; Khodaei, Z.S.; Karachalios, E.; Saenz-Castillo, M.; Thienpont, H.; Berghmans, F. Aerospace-Grade surface mounted optical fibre strain sensor for structural health monitoring on composite structures evaluated against in-flight conditions. Smart Mater. Struct. 2019, 28, 065008. [Google Scholar] [CrossRef]
- Shen, J.; Zeng, X.; Luo, Y.; Cao, C.; Wang, T. Research on strain measurements of core positions for the Chinese space station. Sensors 2018, 18, 1834. [Google Scholar] [CrossRef] [Green Version]
- Dong, T.; Kim, N.H. Cost-Effectiveness of structural health monitoring in fuselage maintenance of the civil aviation industry. Aerospace 2018, 5, 87. [Google Scholar] [CrossRef] [Green Version]
- Dionne, K.; El Matbouly, H.; Domingue, F.; Boulon, L. A chipless HF RFID tag with signature as a voltage sensor. In Proceedings of the 2012 IEEE International Conference on Wireless Information Technology and Systems (ICWITS), Honolulu, HI, USA, 29 July–3 August 2012; pp. 1–4. [Google Scholar]
- Pollock, D.D. Thermocouples: Theory and Properties, 1st ed.; ASTM International: West Conshohocken, PA, USA, 1991. [Google Scholar]
- Oh, S.-W.; Park, J.-H.; Yoon, T.-H. Near-zero pretilt alignment of liquid crystals using polyimide films doped with UV-curable polymer. Opt. Express 2015, 23, 1044. [Google Scholar] [CrossRef]
- Martin, N.; Laurent, P.; Person, C.; Gelin, P.; Huret, F. Patch antenna adjustable in frequency using liquid crystal. In Proceedings of the 33rd European Microwave Conference, EuMC 2003, Munich, Germany, 7 October 2003; Volume 2, pp. 699–702. [Google Scholar]
- Liu, L.; Langley, R.J. Liquid crystal tunable microstrip patch antenna. Electron. Lett. 2008, 44, 1179–1181. [Google Scholar] [CrossRef]
- Fritzsch, C.; Bildik, S.; Jakoby, R. Ka-band frequency tunable patch antenna. In Proceedings of the IEEE Antennas and Propagation Society, AP-S International Symposium (Digest), Chicago, IL, USA, 8–14 July 2012; pp. 1–2. [Google Scholar]
- Shibaev, P.V.; Wenzlilck, M.; Murray, J.; Tantillo, A.; Howard-Jennings, J. Rebirth of liquid crystals for sensoric applications: Environmental and gas sensors. Adv. Condens. Matter Phys. 2015, 2015, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Hsu, T.-R. MEMS and Microsystems: Design, Manufacture, and Nanoscale Engineering, 2nd ed.; Wiley: Hoboken, NJ, USA, 2008; pp. 55–59, 233. [Google Scholar]
- Liu, C. Foundations of MEMS, 1st ed.; Pearson: Hoboken, NJ, USA, 2005; pp. 127–140. [Google Scholar]
- Thai, T.T.; Chebila, F.; Mehdi, J.M.; Pons, P.; Aubert, H.; DeJean, G.R.; Tentzeris, M.M.; Plana, R. A novel passive ultrasensitive RF temperature transducer for remote sensing and identification utilizing radar cross sections variability. In Proceedings of the 2010 IEEE International Symposium on Antennas and Propagation and CNC-USNC/URSI Radio Science Meeting—Leading the Wave, AP-S/URSI 2010, Toronto, ON, Canada, 11–17 July 2010; pp. 1–4. [Google Scholar]
- Wexler, R.B.; Qi, Y.; Rappe, A.M. Sr-induced dipole scatter in BaxSr1−xTiO3: Insights from a transferable-bond valence-based interatomic potential. Phys. Rev. B 2019, 100, 174109. [Google Scholar] [CrossRef] [Green Version]
- Wang, X. Tunable Microwave Filters using Ferroelectric Thin Films. Ph.D. Thesis, University of Birmingham, Birmingham, UK, 2009. [Google Scholar]
- Saif, A.A.; Jamal, Z.A.Z.; Poopalan, P. Effect of the chemical composition at the memory behavior of Al/BST/SiO2/Si-gate-FET structure. Appl. Nanosci. 2011, 1, 157–162. [Google Scholar] [CrossRef] [Green Version]
- Jeon, J.H. Effect of SrTiO3 concentration and sintering temperature on microstructure and dielectric constant of Ba1−xSrxTiO3. J. Eur. Ceram. Soc. 2004, 24, 1045–1048. [Google Scholar] [CrossRef]
- Nadaud, K.; Borderon, C.; Gillard, R.; Fourn, E.; Renoud, R.; Gundel, H.W. Temperature stable BaSrTiO3 thin films suitable for microwave applications. Thin Solid Films 2015, 591, 90–96. [Google Scholar] [CrossRef] [Green Version]
- Vendik, O.G.; Zubko, S.P. Ferroelectric phase transition and maximum dielectric permittivity of displacement type ferroelectrics (BaxSr1−xTiO3). J. Appl. Phys. 2000, 88, 5343–5350. [Google Scholar] [CrossRef]
- Ioachim, A.; Toacsan, M.I.; Banciu, M.G.; Nedelcu, L.; Dutu, A.; Antohe, S.; Berbecaru, C.; Georgescu, L.; Stoica, G.; Alexandru, H.V. Transitions of barium strontium titanate ferroelectric ceramics for different strontium content. Thin Solid Films 2007, 515, 6289–6293. [Google Scholar] [CrossRef]
- Khalfallaoui, A.; Vélu, G.; Burgnies, L.; Carru, J.C. Characterization of doped BST thin films deposited by sol-gel for tunable microwave devices. In Proceedings of the 2009 IEEE International Frequency Control Symposium Joint with the 22nd European Frequency and Time Forum, Besancon, France, 20–24 April 2009; pp. 295–298. [Google Scholar]
- Vorobiev, A.; Rundqvist, P.; Khamchane, K.; Gevorgian, S. Microwave loss mechanisms in Ba0.25Sr0.75TiO3 thin film varactors. J. Appl. Phys. 2004, 96, 4642–4649. [Google Scholar] [CrossRef]
- Friederich, A.; Kohler, C.; Sazegar, M.; Nikfalazar, M.; Jakoby, R.; Binder, J.R.; Bauer, W. Preparation of integrated passive microwave devices through inkjet printing. In Proceedings of the 9th International Conference and Exhibition on Ceramic Interconnect and Ceramic Microsystems Technologies (CICMT 2013), Orlando, FL, USA, 23–25 April 2013. [Google Scholar]
- Golovina, I.S.; Falmbigl, M.; Hawley, C.J.; Ruffino, A.J.; Plokhikh, A.V.; Karateev, I.A.; Parker, T.C.; Gutierrez-Perez, A.; Vasiliev, A.L.; Spanier, J.E. Controlling the phase transition in nanocrystalline ferroelectric thin films: Via cation ratio. Nanoscale 2018, 10, 21798–21808. [Google Scholar] [CrossRef] [PubMed]
- Pervez, N.K.; Hansen, P.J.; York, R.A. High tunability barium strontium titanate thin films for rf circuit applications. Appl. Phys. Lett. 2004, 85, 4451–4453. [Google Scholar] [CrossRef] [Green Version]
- Itadani, T.; Saito, K. Controlling the molecular orientation of liquid crystalline polymer films deposited by polarized-laser chemical vapor deposition. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 1997, 121, 415–418. [Google Scholar] [CrossRef]
- Torres, J.; García-Cámara, B.; Pérez, I.; Urruchi, V.; Sánchez-Pena, J.M. Wireless temperature sensor based on a nematic liquid crystal cell as variable capacitance. Sensors 2018, 18, 3436. [Google Scholar] [CrossRef] [Green Version]
- Kabir, A.T. Voltage Controlled Oscillators Tuned with BST Ferroelectric Capacitors. Master’s Thesis, University of Colorado Colorado Springs, Colorado Springs, CO, USA, 2012. [Google Scholar]
- Done, A.; Căilean, A.M.; Graur, A. Active frequency stabilization method for sensitive applications operating in variable temperature environments. Adv. Electr. Comput. Eng. 2018, 18, 21–26. [Google Scholar] [CrossRef]
- Microelectronics, S. Datasheet—Parascan™ Tunable Integrated Capacitor. 2015. Available online: https://www.st.com/resource/en/datasheet/stptic-68g2.pdf (accessed on 22 May 2020).
- Amin, E.M.; Karmakar, N.C.; Jensen, B.W. Fully printable chipless RFID multi-parameter sensor. Sens. Actuators A Phys. 2016, 248, 223–232. [Google Scholar] [CrossRef]
- Marindra, A.M.J.; Tian, G.Y. Multiresonance chipless RFID sensor tag for metal defect characterization using principal component analysis. IEEE Sens. J. 2019, 19, 8037–8046. [Google Scholar] [CrossRef]
- Amin, E.M.; Bhattacharyya, R.; Sarma, S.; Karmakar, N.C. Chipless RFID tag for light sensing. In Proceedings of the 2014 IEEE Antennas and Propagation Society International Symposium (APSURSI), Memphis, TN, USA, 6–11 July 2014; pp. 1308–1309. [Google Scholar]
- Pozar, D.M. Microwave Engineering, 4th ed.; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- RS Pro K Type Thermocouple 1/0.2 mm Diameter, −75 °C → +250 °C|RS Components. Available online: https://ie.rs-online.com/web/p/products/3630250/ (accessed on 22 September 2020).
- Kita, J.; Wiegärtner, S.; Moos, R.; Weigand, P.; Pliscott, A.; LaBranche, M.H.; Glicksman, H.D. Screen-printable type S thermocouple for thick-film technology. Procedia Eng. 2015, 120, 828–831. [Google Scholar] [CrossRef] [Green Version]
- Duby, S.; Ramsey, B.; Harrison, D.; Hay, G. Printed thermocouple devices. Proc. IEEE Sens. 2004, 3, 1098–1101. [Google Scholar]
- Offenzeller, C.; Knoll, M.; Jakoby, B.; Hilber, W. Fully screen printed carbon black-only thermocouple and the corresponding seebeck coefficients. Proceedings 2018, 2, 802. [Google Scholar] [CrossRef] [Green Version]
- Mandel, C.; Maune, H.; Maasch, M.; Sazegar, M.; Schüßler, M.; Jakoby, R. Passive wireless temperature sensing with BST-based chipless transponder—IEEE conference publication. In Proceedings of the 2011 German Microwave Conference, Darmstadt, Germany, 14–16 March 2011. [Google Scholar]
- NanoVNA V2 Official Site. Available online: https://nanorfe.com/nanovna-v2.html (accessed on 22 September 2020).
- NanoVNASaver|NanoVNA. Available online: https://nanovna.com/?page_id=90 (accessed on 22 September 2020).
- Corporation, R. RO4000® Series High Frequency Circuit Materials. Available online: http://www.rogerscorp.com (accessed on 22 September 2020).
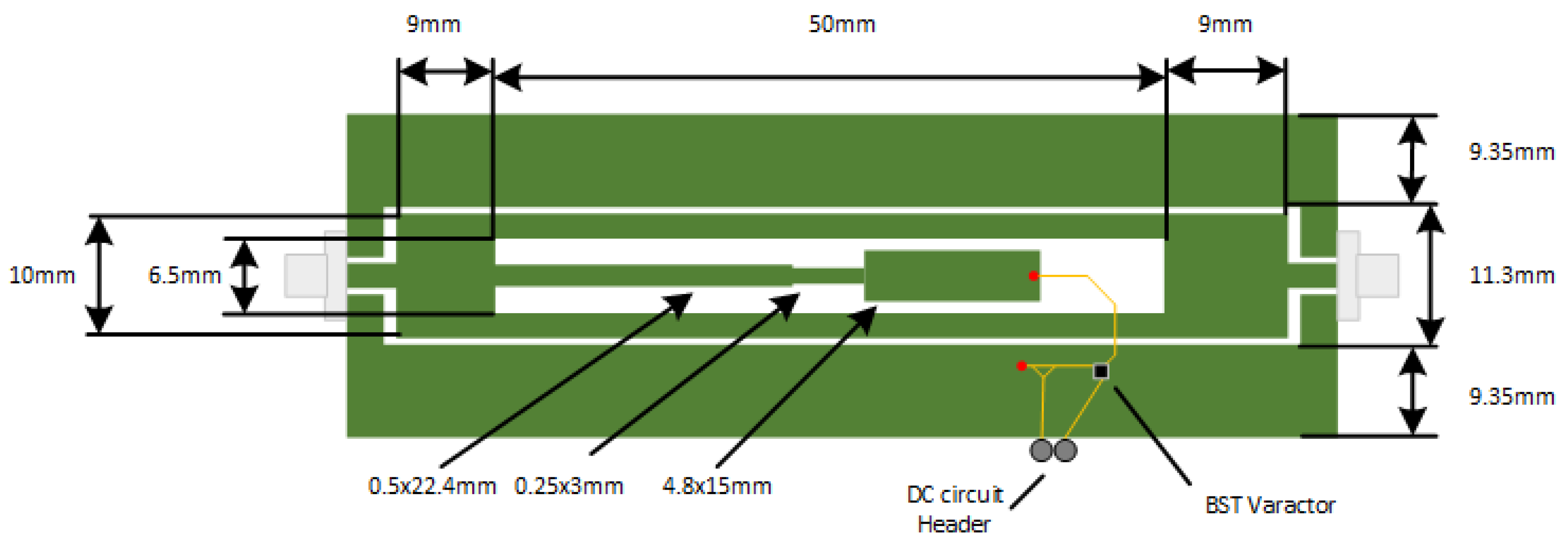

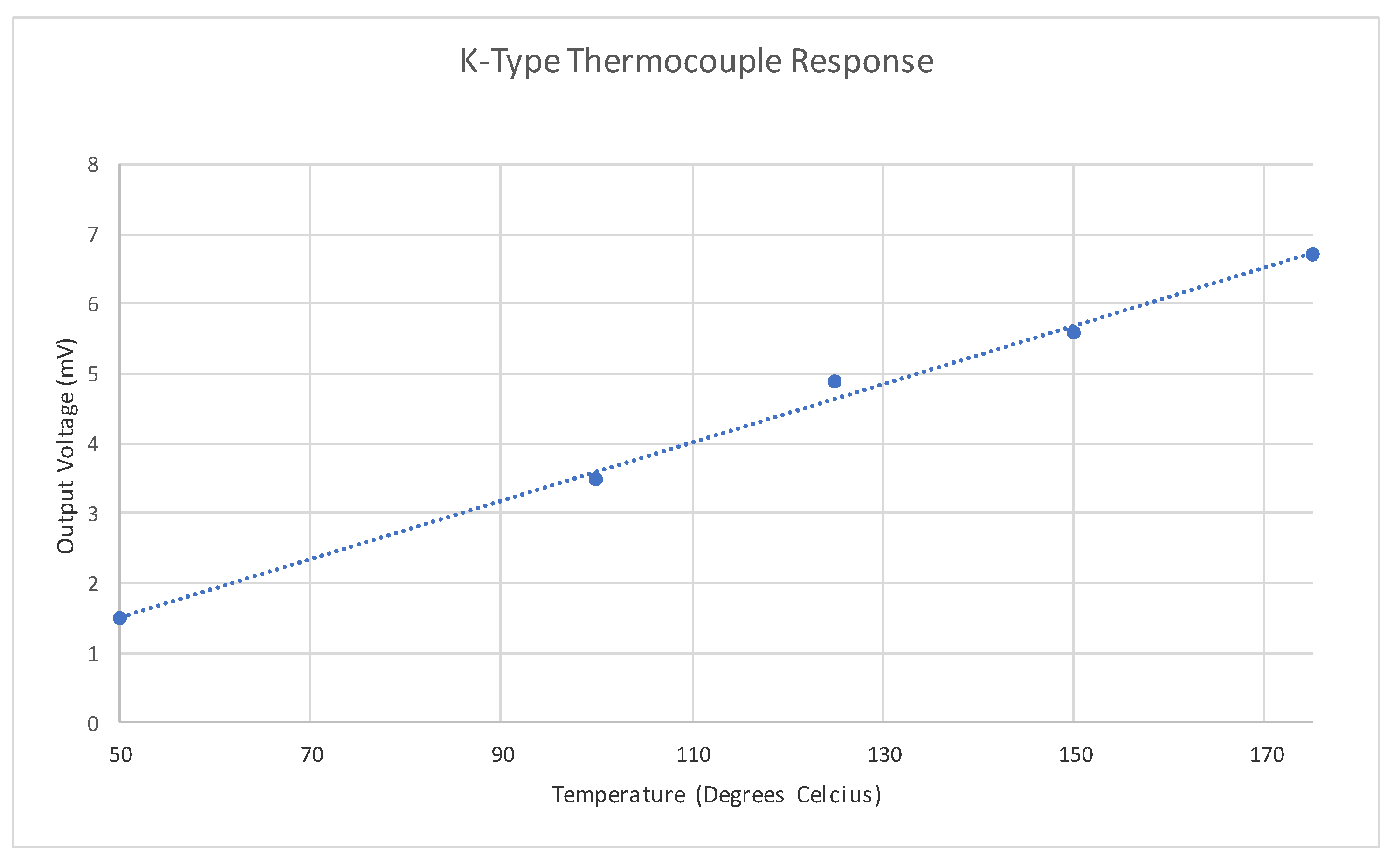
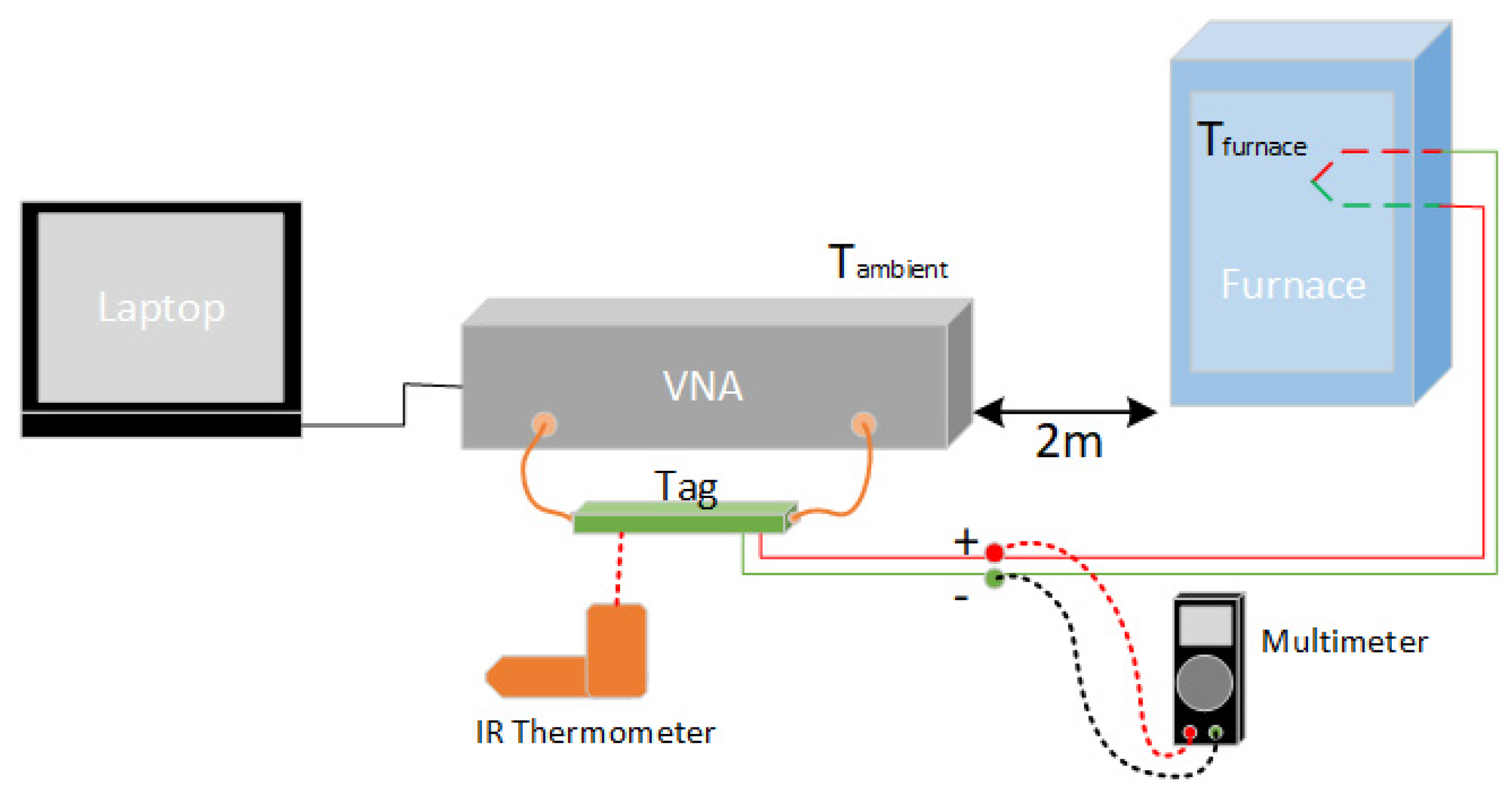
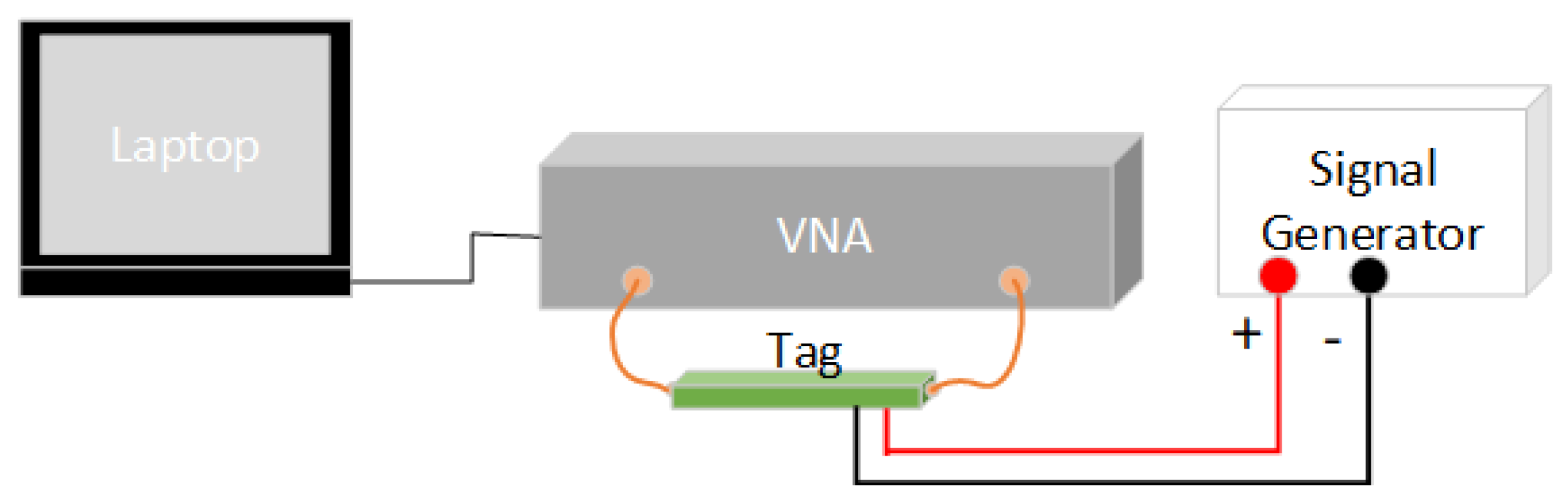

| Method | Merits | Shortcomings |
|---|---|---|
| LCP |
| |
| Electrostatic Actuator |
|
|
| BST |
|
| Specifications |
|---|
|
| Temperature (°C) | Polynomial R2 Value |
|---|---|
| 50 | 0.9713 |
| 77 | 0.9425 |
| 100 | 0.9846 |
| 135 | 0.9784 |
| 155 | 0.9895 |
| 180 | 0.9969 |
| 200 | 0.9948 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mc Gee, K.; Anandarajah, P.; Collins, D. Current Progress towards the Integration of Thermocouple and Chipless RFID Technologies and the Sensing of a Dynamic Stimulus. Micromachines 2020, 11, 1019. https://doi.org/10.3390/mi11111019
Mc Gee K, Anandarajah P, Collins D. Current Progress towards the Integration of Thermocouple and Chipless RFID Technologies and the Sensing of a Dynamic Stimulus. Micromachines. 2020; 11(11):1019. https://doi.org/10.3390/mi11111019
Chicago/Turabian StyleMc Gee, Kevin, Prince Anandarajah, and David Collins. 2020. "Current Progress towards the Integration of Thermocouple and Chipless RFID Technologies and the Sensing of a Dynamic Stimulus" Micromachines 11, no. 11: 1019. https://doi.org/10.3390/mi11111019
APA StyleMc Gee, K., Anandarajah, P., & Collins, D. (2020). Current Progress towards the Integration of Thermocouple and Chipless RFID Technologies and the Sensing of a Dynamic Stimulus. Micromachines, 11(11), 1019. https://doi.org/10.3390/mi11111019






