Abstract
A number of nonlinear acoustic sensing methods exist or are being developed for diverse areas ranging from oceanic sensing of ecosystems, gas bubbles, and submerged objects to medical sensing of the human body. Our approach is to use primary frequency incident waves to generate second order nonlinear sum or difference frequency fields that carry information about an object to be sensed. Here we show that in general nonlinear sensing of an object, many complicated and potentially unexpected mechanisms can lead to sum or difference frequency fields. Some may contain desired information about the object, others may not, even when the intention is simply to probe an object by linear scattering of sum and difference frequency incident waves generated by a parametric array. Practical examples illustrating this in ocean, medical, air and solid earth sensing are given. To demonstrate this, a general and complete second-order theory of nonlinear acoustics in the presence of an object is derived and shown to be consistent with experimental measurements. The total second-order field occurs at sum or difference frequencies of the primary fields and naturally breaks into (A) nonlinear waves generated by wave-wave interactions, and (B) second order waves from scattering of incident wave-wave fields, boundary advection, and wave-force-induced centroidal motion. Wave-wave interactions are analytically shown to always dominate the total second-order field at sufficiently large range and carry only primary frequency response information about the object. As range decreases, the dominant mechanism is shown to vary with object size, object composition, and frequencies making it possible for sum or difference frequency response information about the object to be measured from second-order fields in many practical scenarios. It is also shown by analytic proof that there is no scattering of sound by sound outside the region of compact support intersection of finite-duration plane waves at sum or difference frequencies, to second-order. Analytic expressions for second-order fields due to combinations of planar and far-field wave-wave interactions are also derived as are conditions for when wave-wave interactions will dominate the second order field.
1. Introduction
A number of nonlinear acoustic sensing methods exist or are being developed for diverse areas ranging from oceanic sensing of ecosystems, gas bubbles, and submerged objects to medical sensing of the human body [1,2,3,4,5,6,7]. The approach is to use primary frequency incident waves to generate second order nonlinear sum or difference frequency fields that carry information about an object to be sensed. Here we show that in general nonlinear sensing of an object, many complicated and potentially unexpected mechanisms can lead to sum or difference frequency fields. Some may contain desired information about the object, others may not, even when the intention is simply to probe an object by linear scattering of sum and difference frequency incident waves generated by a parametric array [1,3]. Practical examples illustrating this in ocean, medical, air and solid earth sensing are given. To accomplish this, a general and complete second order theory of nonlinear acoustics in the presence of an object is derived. The theory employs consistent asymptotic analysis of the wave equation and time-dependent boundary conditions to second order, following methods developed in fluid dynamics to quantify second order nonlinear waves found in the presence of floating objects [8,9]. This second order nonlinear acoustic theory is confirmed by quantitative comparison with classic experimental measurements of Jones and Beyer [1]. To our knowledge, no previous nonlinear acoustic theory derived from first principles has been available to explain these measurements. While illustrative examples are computed from exact second order solutions, which may involve integration, analytic solutions and approximate asymptotic expressions are also derived when possible to gain further insight. A detailed discourse on the relationship of this work to previous developments is provided in the Discussion section.
When an object is insonified by two primary frequency incident waves, second order acoustic waves at the sum and difference frequencies of the primary waves arise due to multiple mechanisms. It is found that these generating mechanisms fall into two categories. The first is (A) nonlinear wave-wave interactions of the primary waves, including the interaction between two incident waves (denoted as II), the interaction between two scattered waves (denoted as SS) and the interactions between an incident and scattered wave (denoted as IS and SI). The second is (B) linear scattering of nonlinear waves of the first category due to the presence of the object with radiation from second order boundary advection and wave-force-induced centroidal motion (together denoted as S2). Second order acoustic waves of category (A) contain information about the object’s first order response at the primary frequencies but not at the sum or difference frequency. Second order acoustic waves of category (B) contain information about the object’s linear response to a sum or difference incident wave but this information is often contaminated by complicated nonlinear effects due to primary scattered wave fields at the object boundary so that it cannot typically be extracted simply by factoring from S2 the II amplitudes in analogy to approaches used in linear scattering theory.
We show analytically that wave-wave interactions dominate the total second order field at sufficiently long ranges from the object, but in some scenarios these ranges may be too large to enable practical measurements of this. At shorter ranges, second order scattering may also dominate depending on physical parameters such as object size, object composition, primary frequencies, and range. We show that centroidal motion of a rigid object due to its interaction with acoustic waves can significantly affect the second order field at shorter ranges. In this case, S2 can be decomposed into scattering from a fixed object at its time-averaged position (denoted as D2), and radiation due to the second order centroidal motion (denoted as R2). We also show that resonance effects from elasto-mechanical effects or gas filled bubbles in liquids can dominate the second order field at shorter ranges.
Following experimental practice, we employ a time domain formulation of finite-duration narrow-band incident waves and provide analytic solutions for the resulting second order fields in the presence of an object. Finite-duration incident waves enable nonlinear field components that contain information about the object to be separated in time and space from those that do not, e.g., the II component, for certain sensing geometries. In such a finite-time duration approach, it is important to demonstrate that all potential effects of sound scattering by sound in the II field are accounted for properly. To quantify the scattering of sound by sound inside and outside a bounded interaction region of primary waves with compact support, we derive analytic expressions for the second-order nonlinear field arising from the interaction of plane waves of arbitrary time dependence. In an early investigation of the scattering of sound by sound, Ingard and Pridmore-Brown [10] employed unphysical collimated primary time-harmonic fields, which led to unphysical results as noted by Westervelt [11]. The subsequent time-harmonic plane wave analysis of Westervelt [11] provided no spatial region without interacting primary fields. By analytic proof we show that to second order there is no scattering of sound by sound outside the region of compact support intersection of finite-duration plane waves at sum or difference frequencies in the absence of an object. We also show that non-collinear interaction leads to finite scattering of sound by sound at the primary frequencies only within the region of compact support union through which compact support intersection occurred if the primary waves had zero-frequency spectral components. We rigorously prove that Lamb’s collinear [12] and Westervelt’s non-collinear [11] time-harmonic solutions at the sum or difference frequency for ideal time-harmonic primary plane wave interactions provide good approximations to the second order field arising from the interaction of narrow-band finite-duration primary plane waves with sufficiently long and smooth envelopes, but only in the region of compact support intersection where the primary fields exist. We show such a time-harmonic approximation can be made in many practical scenarios involving the interaction between scattered waves, as well as scattered and incident waves of narrow band.
Applications of practical sensing in the ocean, human body, atmosphere and solid earth using the second order nonlinear acoustic theory derived here are analyzed and evaluated in roughly twenty case studies, where transitions between at least five potentially dominant mechanisms are explored for each. These examples are illustrated and evaluated both in terms of dimensionless parameters and specific frequencies and lengths. The former makes it possible to interpret the results universally over the broadest range of possible applications by scaling the object size, receiver range, and frequencies as necessary. The range of dimensionless parameters considered are chosen to provide a general characterization of regions where important transitions between dominant mechanism occur. The specific cases discussed include object radii spanning hundreds of micrometers to several meters; primary frequencies ranging from tens of Hertz to tens of mega Hertz; difference frequencies ranging from tens of Hertz to hundreds of kilo Hertz and sum frequencies of tens of mega Hertz.
Nonlinear acoustic sensing of oceanic fish at the difference frequency of a parametric array is studied for two representative species: Atlantic herring (Clupea harengus) and Atlantic cod (Gadus morhua). The former are of the plankton feeding Clupeidae family of keystone species that serve as prey to many other fish, mammals and birds. The latter are of the fish-feeding Gadidae family of top level predators. Both families are found throughout the world’s oceans and are important ecologically in circulating biomass between open ocean and coastal waters via feeding to spawning cycles, and as human food sources [13,14]. Traditionally, downward directed echosounders in the tens to hundreds of kilo Hertz range have been used for scientific analysis of fish populations. These frequencies, however, are typically well above the swim-bladder resonance frequencies of most oceanic fish species. Difference frequency sensing with a parametric array has been used to potentially investigate swim bladder resonances [7], which are important for wide area sensing with Ocean Acoustic Waveguide Remote Sensing (OAWRS) [15,16,17,18]. Here we show that potentially unexpected second order nonlinear mechanisms, different from the intended linear scattering of the parametric array’s incident difference frequency field, can mask the difference frequency response of oceanic fish and so make difference frequency sensing of swimbladder resonance difficult or impossible.
Nonlinear acoustic sensing of ocean air bubbles at difference frequencies is also studied. Air bubbles are formed by breaking waves and are ubiquitous in the world’s oceans. Quantifying air bubble distributions in the ocean is important to a number of areas including underwater sensing and communication where bubbles cause attenuation, dispersion and randomization of transmitted signals, and climatology where bubbles are a source of critical gas/aerosol exchanges between the ocean and atmosphere [19,20,21,22]. Oscillating air bubbles are also a major natural source of ambient noise in the ocean [23]. Here it is shown that transitions between dominant nonlinear acoustic mechanisms occur at practical sensing ranges and frequencies and can limit the ability to determine desired bubble parameters.
Applications of nonlinear acoustic difference frequency sensing for medical ultrasound applications [4,5] are investigated for immovable rigid, movable rigid, vacuous, air-filled, and resonating objects. Here, we provide many examples showing that in practical medical applications no single mechanism is always dominant. Instead, a number of mechanisms are found to dominate the received difference frequency field depending on the object composition, size, source and receiver range and orientation, and primary and difference frequencies, which may lead to unexpected consequences for difference frequency sensing.
Nonlinear acoustic difference frequency sensing in the atmosphere for robotic applications, and in the solid earth for detection and sensing of buried structures are also provided, as are opportunities for sensing objects using incident-scattered wave interactions in a variety of media.
2. Linear and Second Order Nonlinear Formulation
Assuming weak nonlinearity, the total pressure field , density field , fluid particle velocity , object boundary displacement and total force on the object due to the acoustic field can be described by [24]
where subscripts 0, 1 and 2 indicate zeroth-, first- and second-order quantities, respectively, with . Here and are ambient pressure and density of the medium without acoustic waves and . The general problem is sketched in Figure 1, where two primary incident fields and are incident on an object, causing two primary scattered fields, and . The second order field generated by wave-wave interactions and second order scattering is measured by a receiver at .
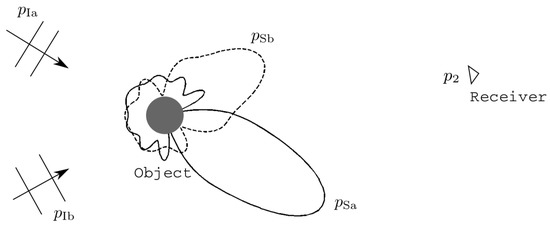
Figure 1.
Two primary incident fields and at respective angular frequencies and are incident on an object, causing two primary scattered fields, and . A receiver at measures the second order field .
In practice, the different orders expressed in Equation (1) can be isolated by slowly increasing the amplitude of an incident time-harmonic primary field. For very small incident amplitude, only the ambient or zeroth order fields will be measurable. As the incident primary field amplitude is slowly increased, it will be possible to measure the first order quantities in Equation (1) above ambient levels at the primary frequency with no other higher order contributions present. Slowly increasing the primary field amplitude further will eventually lead to the addition of only sum and difference frequency fields that are measurable above the ambient levels that correspond to the second order variables of Equation (1). Increasing the incident amplitude further such that there are more frequencies present than the primary, sum and difference frequency introduces nonlinearities beyond the second order, which are not treated in the present paper. In this case, incident amplitudes should be reduced so that only primary, sum and difference frequencies are present. The second order theory presented here is then valid and can be properly used to explain nonlinear phenomena.
2.1. First Order Formulation
The total first order pressure field satisfies the wave equation with source function , via
where is the sound speed, is the Laplacian with respect to the receiver position and t is time. The boundary conditions for pressure release, rigid immovable, or rigid movable objects without rotation are
where the fluid velocity is related to the pressure by the linearized momentum equation , is velocity of the object’s centroidal motion in response to the acoustic field, is the mean reference boundary position, and is the surface outward normal vector of the medium. Pressure release and rigid immovable boundaries are limiting cases of a general locally reacting boundary. It is shown in Appendix C that the solution to the first and second order scattering problems for any locally reacting boundary can be constructed from pressure release and rigid immovable scattering solutions. A rigid movable boundary, however, is a special case of a non-locally reacting boundary because depends on the acoustic field on the whole boundary.
The complete solution for from Green’s theorem is [25,26]
where
Here, the 0 subscript appears on spatial variables of integration and their gradient; is a temporal variable of integration for the first two integrals; is the time at which the source begins to operate; is a time much larger than the period of any harmonic source in operation; is the known incident wave, is the scattered wave, which depends on the object boundary condition; and represents the transient effect associated with initial conditions at . The time domain Green function is where is the Dirac delta function and .
For pressure release or rigid immovable objects, the scattered wave can be obtained by solving the integral equation (8) with boundary conditions
where and .
For rigid movable objects, let the total scattered wave be decomposed as
where subscript D1 represents first order scattering from the rigid object whose boundary is fixed, and subscript R1 represents first order radiation due to centroidal motion of the rigid object. By definition, is the same as for the rigid immovable object. The radiated wave depends on the , and it satisfies the boundary condition
where . The centroidal velocity is determined by the equation of motion
where M is the mass of the object and the integral on the right-hand side of Equation (14) represents the total force on the object. The inertial term on the left-hand side of Equation (14) can be written as with operator . Since the radiated wave is a linear function of the centroidal motion, the force on the body due to radiation can be written as , where the linear operator depends on the object geometry and the medium properties. Then becomes
where the wave-exciting force is defined as
which is completely determined by and . Once in Equation (13) is determined, can be obtained with the same procedure as that for .
The formulation for time-harmonic first-order scattering including centroidal motion of the object is provided in the online supplementary material.
2.2. Second Order Formulation
The governing equation for the second order acoustic pressure field in a homogeneous, inviscid medium is [11]
where
and is the momentum tensor [24], and and are constants from the equation of state. The second order fluid velocity is related to via
To find the second order boundary condition on the body, we expand the boundary condition on the exact boundary in a Taylor series with respect to [8]. After substituting the perturbation expansions for p, and into the series and collecting terms at each order, the second order boundary conditions are obtained as
where is the second order centroidal velocity for rigid objects without rotation, and are first order boundary and centroidal displacements, respectively. The second order boundary condition for a general locally reacting boundary is derived in Appendix C, where it is shown that solution to the second order scattering problem for any locally reacting boundary can also be constructed from pressure release and rigid immovable scattering solutions.
As in the first order problem, the total second order wave field is given by Green theorem, as
where
Here is the second order incident wave, which is due to wave-wave interactions of the first order field, is the second order scattered field determined by the second order boundary condition, and accounts for the initial conditions.
When the primary wave field consists of incident and scattered waves, we have
Substituting and from (27) into Equation (18) then into Equation (24) leads to a decomposition of as
where
in which , , , and are functions of and , is the gradient operator with respect to , II represents contributions from incident-incident interactions, SS from scattered-scattered interactions, and IS and SI from incident-scattered interactions.
The procedure to obtain for pressure release or rigid immovable objects is similar to that for (Section 2.1 and online supplementary material), but the boundary conditions are
where is the second order fluid velocity due to , which is given by Equation (19) with . The fluid velocity . The pressure component describes contributions from wave-boundary interactions due to first order boundary motion.
Following the approach used in first order for rigid movable objects, is decomposed as
where is the second order scattered wave from a rigid object whose centroid is fixed at second order, i.e., , and is the second order radiated wave due to any second order centroidal motion .
The procedure to obtain is similar to that for and , but the boundary condition is
where . The velocity component also describes contributions from wave-boundary interactions due to first order boundary motion.
To obtain , the procedure is again similar to that for , but with boundary condition
where . The centroidal velocity is determined by the second order equation of motion
where the second order pressure component arises from Taylor series expansion of the total pressure p at the instantaneous boundary with respect to . By defining the second order wave-exciting force as
becomes
When the primary incident field has two components , the primary scattered field is , and the total first order field is . This leads to
and can be expressed in the same manner. Substituting and into in Equation (18) and then Equation (24) leads to
The first parenthetical group of terms in Equation (42) is due to II interaction, the second to SS interaction, and the last to IS and SI interactions. The II components , , and , SS components , , and , and IS and SI components , , and correspond to self-interactions of each incident wave. The II components and , SS components and , and IS and SI components , , and are due to cross-interactions between the and incident fields.
When has two harmonic components at angular frequencies and , , the variables , , , , and also contain these harmonic components, i.e.,
Then , , , and in Equation (28) contain static and double frequency ( and ) components due to self-interactions, and sum () and difference () frequency components due to cross-interactions. Specifically, the components for , , , and are
where
in which the asterisk denotes complex conjugation that applies to the difference frequency case only. Equations (45)–(48) are obtained by substituting , , and from (43) into Equations (29)–(32) and integrating over .
The components of , , , and can be written as
where the complex amplitudes , , , and can then be determined by further analysis. Specifically, substituting into Equation (25) and integrating over yields
where and . The scattered wave for pressure release or rigid immovable objects can be obtained from Equation (50) with boundary conditions
where , , and are the second-order complex fluid velocity amplitudes associated with , , and respectively, and are first order complex pressure field amplitudes at frequencies and respectively, and . In the pressure release boundary Equation (51), the term leads to linear sum or difference frequency scattering of incident wave-wave fields II, SS, IS and SI, while the last two terms lead to nonlinear radiation from boundary advection that will involve II, SS, IS and SI type components, where SS or SS-type boundary components dominate the amplitude of for In the rigid immovable boundary Equation (51), there is only linear sum or difference frequency scattering of incident wave-wave fields.
For rigid movable objects, can be obtained from Equation (50) with and boundary condition
where , and are first order fluid velocities at frequencies and respectively.
The wave-exciting force is
The centroidal velocity for a rigid movable object attached to a spring and damper in the direction of motion is
where is the undamped natural frequency, is the dimensionless damping ratio, is the Fourier transform of and is the Fourier transform of , which is sometimes referred to as the radiation impedance [24,27,28] and is determined from its elements by
where are the first order radiated fields from an object due to unit amplitude velocity oscillation at frequency in directions (online supplementary material). In terms of , the second order radiated field is
2.3. Summary
In summary, the total second order field from any object insonified by acoustic waves is generated by wave-wave interactions, including II, SS, IS and SI, and by second order scattering S2, as
which, for the sum and difference frequency amplitudes, leads to
The interaction components , , and are given by Equations (29)–(32). The S2 component is given by Equation (25) with boundary conditions (33) and (34) for pressure release and rigid immovable objects, respectively. The general solution for objects with non-rigid locally reacting boundaries is given in Appendix C in terms of the pressure release and rigid immovable solutions of this section. For rigid movable objects, S2 is decomposed into D2 and R2. The D2 component is given by Equation (25) with boundary condition (36). The R2 component is given by Equation (25) with boundary condition (37), where the centroidal motion is determined from the wave-exciting force by Equation (39).
From the sensing perspective, the II interaction only depends on the primary incident waves and it contains no information about the object. The SS, IS and SI interactions depend on the first order scattered waves and , and they contain primary frequency scattering information of the object. S2 contains the object’s second order scattering information at the sum or difference frequency. For example for the rigid object, D2 depends on the geometry of the object and R2 depends on the second order motion of the object.
The present theory provides a complete and self-consistent treatment of second order interaction and scattering in the presence of an object, including the effect of second order centroidal motion. More details about the wave-exciting force formulation are provided in Appendix D.
3. Solutions for Wave-Wave Interactions
3.1. Direct Integration
3.1.1. General Approach
Let of Equation (23) and the associated second order velocity due to wave-wave interactions be further decomposed as [29]
where and are nonzero only when the primary field exists and can be directly evaluated from first order pressure and velocity , as
and satisfies
where . As in Equation (24), solution for is
Finite-duration incident plane waves propagating at directions and with center frequencies and respectively can be written as
where
are harmonic plane waves with amplitudes and , respectively, and is a window function with compact support of duration T, which is here assumed to have unit height within the window except at each end where smooth transitions to zero occur over time periods much less than T.
When the object is small compared to the spacial extent of the incident plane wave window, the dominant scattering components are within the narrow band of the incident waves, and the window functions are sufficiently smooth, the primary scattered waves can be approximated as
which correspond to harmonic scattered waves and at frequencies and , where compact support is preserved by moving windows.
Like in Equation (42), and have self-interaction and cross-interaction components due to II, SS, IS and SI mechanisms. By substituting Equations (65) and (67) into Equation (64) and integrating over , the cross-interaction components for are
where
When the primary incident and scattered waves are purely time harmonic, . Equations (68)–(71) become
where
The cross-interaction components of are denoted by , , and . They can be determined by substituting appropriate first-order field products into equation (61). When the primary fields are time harmonic,
where , , and are the complex amplitudes at the sum and difference frequency for the cross-interactions, which again can be directly obtained from Equation (61).
3.2. Analytic Solutions
While time domain and frequency domain solutions for wave-wave interactions can be directly evaluated numerically via Equations (68)–(71) and Equations (77)–(80) respectively, which is the approach we have used in all rigid and pressure release simulations presented in this paper, we have obtained analytic solutions for some cases not considered previously. We also provide approximate analytic expressions for the S2 pressure for small pressure release or gas filled bubbles.
3.2.1. Incident-Incident Interaction of Plane Waves of General Time Dependence
For two collinear time harmonic plane waves given by Equation (66) with , was derived by Lamb [12], who showed that it grows linearly with range. For zero second order normal velocity at , is
Here the complex conjugate and the “−” sign in “±” apply to the difference frequency case only. For two non-collinear time harmonic plane waves given by Equation (66) with and , Westervelt [11] found that
where and is the angle between and .
These time-harmonic results are here generalized to plane waves with arbitrary time dependence to investigate the scattering of sound by sound and also properly model typical experimental scenarios. For two collinear plane waves of arbitrary time dependence and , the second order fields due to their cross-interaction are (online supplementary material).
where the complex conjugates only apply to . For narrow-band waves with compact support given by Equation (65) with , and a sufficiently smooth temporal window , Equation (84) becomes (online supplementary material)
where the term in the square brackets corresponds to and the other term in the square brackets corresponds to . It can be seen from Equations (84) and (85) that sum and difference frequency components of only exist within the region of compact support intersection. For narrow-band primary waves with sufficiently smooth windows, the second order field in the intersection corresponds to Lamb’s solution with boundary condition at .
For two non-collinear intersecting plane waves of arbitrary time dependence and , the second order fields due to their cross-interaction are found to be (online supplementary material).
which is the full solution including both and components. Sum and difference frequency components of only exist within the region of compact support intersection, so that no scattering of sound by sound at sum or difference frequencies is found outside the region of compact support intersection to second order. Primary frequency components in exist within the region of compact support union through which compact support intersection occurred if the primary waves had non-zero zero-frequency components. There is no scattering of sound by sound at any frequency outside the region of compact support union through which compact support intersection occurred.
For narrow-band plane waves with compact support given by Equation (65) with and , where window is sufficiently long and smooth, Equation (86) becomes (online supplementary material)
which shows that a time-harmonic approximation involving Westervelt’s time harmonic solution (Equation (83)) can be made in the region of compact support intersection for narrow-band plane waves with sufficiently long and smooth windows.
3.2.2. Scattered-Scattered Interaction
Let and be the far field ranges [30] for the primary scattered fields and respectively, such that beyond and , far field approximations [31] apply
where , , l is the length scale of the object, are the wavelengths of the incident fields, and are the amplitudes of the incident fields, and are the far field scatter functions, and .
The integral representation of , Equation (78), can then be decomposed into
where is due to the SS interaction within and is due to SS interaction beyond , and satisfies and . The term for can then be analytically approximated via a stationary phase or spherical wave expansion approach (online supplementary material), yielding
where is the exponential integral [32,33] and for sufficiently small objects is the object radius. For , since the logarithmic function dominates the exponential integrals in Equation (90), falls off by . The component falls off by and by . The total second order field due to the SS interaction can be approximated by
which is consistent with a general diverging waveform suggested by Westervelt and Radue [34] but without explicit derivation or interpretation.
When the two primary fields radiating from a sphere with radius a are spherically symmetric, , and . Equation (90) reduces exactly to Baxter’s solution [33]. Compared to Baxter’s solution, it is found that Dean’s earlier solution [29] has an extra term proportional to the spherical Bessel function so violates the Sommerfeld radiation condition (online supplementary material). A further approximation made by Dean for the far field and a small object , however, satisfies the Sommerfeld radiation condition because it contains only the dominant term. Jones and Beyer [1,35] developed a heuristic formula based on the radial dependence of Dean’s omnidirectional solution with far field and small object approximations, and applied it to model the sum frequency interaction of two scattered fields from a large sphere (), where they found good agreement in angular dependence with data by introducing an arbitrary scaling factor.
3.2.3. Incident-Scattered Interaction
For incident plane waves and given by Equation (66) and scattered waves and given by Equation (88), the second order fields and in the forward directions are analytically derived (online supplementary material) from Equations (79) and (80). At large range, and have constant magnitude in range while and fall off by . The total second order fields due to the IS and SI interactions are then
Unlike the interaction of collinear plane waves where growth is found along the propagation path, collinearity between planar and spherical wavefronts within an equivalent Fresnel area about the forward direction, together with spreading of the spherical wave, balances out second-order wave growth. For , the term in Equation (93) is due to the additional contribution from a stationary phase point at range in the forward direction.
The backscatter directions and for the IS and SI interactions respectively lack collinearity and stationary phase contributions so that and fall off in range by as do and , and have much lower magnitude than and in the forward directions. Detailed derivations for IS and SI interactions are provided in the online supplementary material.
3.3. Sound Pressure Level of the IS and SS interactions
The Sound Pressure Level (SPL) of in the forward direction is determined from Equations (92) and (93) as
which depends on the SPL of incident waves, the frequencies , the far field scatter function and constants and A.
At long range and away from the forward direction, is dominant. The SPL for for can be determined from Equation (91) as
Compared to the SPL of in Equation (95), it can be seen that a higher incident SPL is required for to compensate for its falloff.
3.3.1. S2 for Small Pressure Release or Gas Filled Bubbles
Consider small pressure release objects with . The righthand side of Equation (51), is dominated by the SS component of from Equation (61) and the last two advective terms of Equation (51) are dominated by SS-type components, so that
where and for the pressure release case. If the small object is a gas filled bubble, or a fish swim bladder, an additional constraining equation at the boundary is necessary, which makes the dimensionless coefficients and dependent on sum, difference and primary frequencies as well as parameters of medium and object such as resonance frequency, damping, and radius as shown in Appendix B via Equations (B28) and (B29) respectively. In these cases, may attain maxima for probing frequencies at resonance, and approaches the pressure release case for high probing frequencies and zero for low probing frequencies.
4. Confirmation of Theory with Measurements
The exact second order theory presented here without approximation (Equation (59)) is computationally confirmed by comparison with experimental data from Jones and Beyer [1,35] for second-order sum-frequency pressure at range mm due to a large rigid sphere of radius mm in water insonified by two perpendicular incident beams at frequencies = 7 MHz and MHz, such that , and = 152.6 which are all large. Good quantitative agreement is found between theory and measurements with 0.98 correlation across scattered angle and overall mean square difference of less than 0.3 dB (Figure 2) as shown in the online supplementary material.
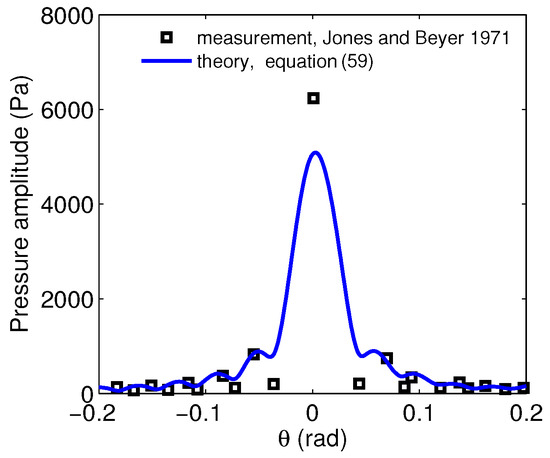
Figure 2.
Comparison between Jones and Beyer’s experiment [1,35] and exact theory obtained computationally for the sum frequency second order pressure. Good quantitative agreement is found between measurement and theory with 0.98 correlation across scattered angle and overall mean square difference of less than 0.3 dB.
5. Transitions Between Dominant Mechanisms in Sum or Difference Frequency Sensing of an Object
At sufficiently long range, the SS, IS and SI interactions always dominate, as seen from the asymptotic behavior given by Equations (90) and (92)–(94) compared to the inverse radial far field fall-off of S2 dictated by Equation (50). At such long ranges, only the object’s response at the primary frequencies can be measured from the second order field, if the field is large enough to be measured. Our analysis here (Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8) shows that at shorter ranges, however, depending on frequencies, receiver range and the object’s scattering properties, the S2 mechanism can also dominate, where the object’s response at the sum or difference frequency may be deduced from the second order field at the sum or difference frequency. While it is possible to exploit these complicated transitions between dominant mechanisms for novel remote sensing applications, difficulties also arise in many cases, as we will show.
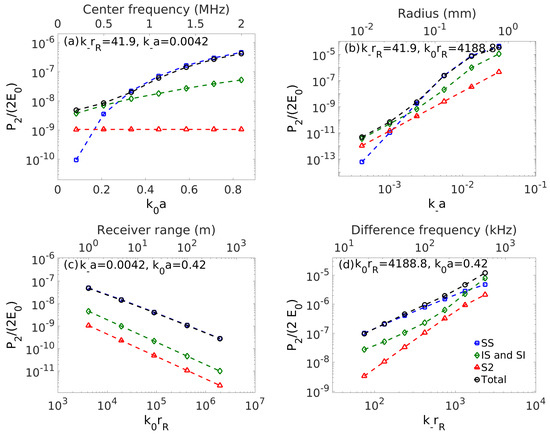
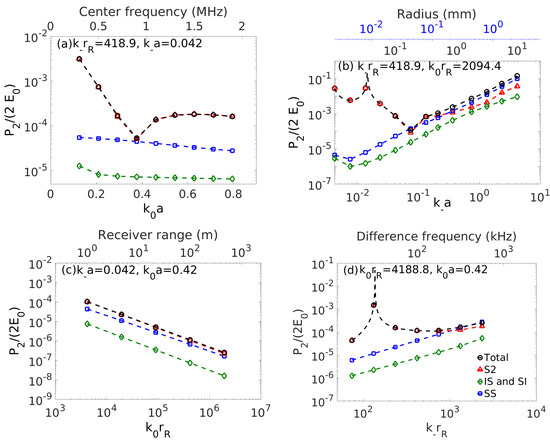
Figure 3.
A rigid immovable sphere with collinear incident waves propagating at . The difference frequency component of is calculated at as a function of (a) center frequency or , (b) object radius or , (c) receiver range or and (d) difference frequency or . The lower dimensionless abscissas are for general interpretations. The upper abscissas are for a medical or underwater sensing example with 1 MHz primary and 10 kHz difference frequencies, 0.1 mm sphere radius at range 1 m from the receiver with 1500 m/s sound speed. In (a), dominates for large , while dominates for small . In (b), dominates for large , dominates for small . In (c), is dominant and has the most gradual roll-off with range. In (d), dominates for small while dominates for large . The nonlinear parameter is . The normalization employs .
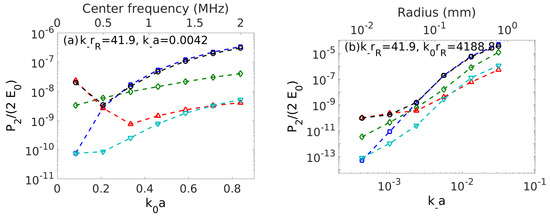
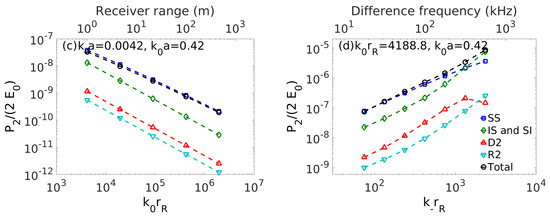
Figure 4.
A rigid movable sphere with collinear incident waves propagating at . The difference frequency component of is calculated at as a function of (a) center frequency or , (b) object radius or , (c) receiver range or and (d) difference frequency or . In (a), dominates for large , while dominates for small . In (b), dominates for large and dominates for small . In (c), is dominant has the most gradual roll-off with range. In (d), dominates for small and dominates for large . The nonlinear parameter is , and the density ratio between the object and medium is . Lower dimensionless abscissas are for general interpretations. Upper abscissas are for a medical or underwater sensing example as in Figure 3, except the rigid object is movable.
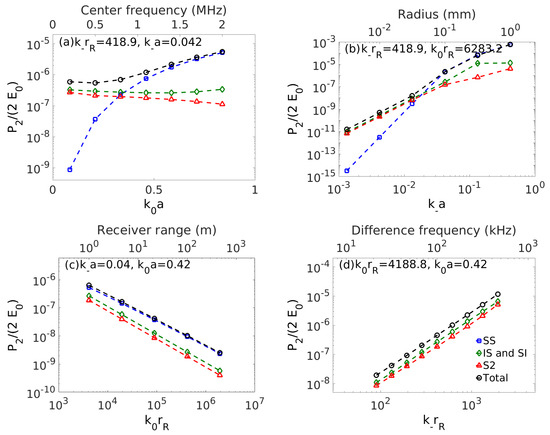
Figure 5.
A rigid immovable sphere with perpendicular incident waves propagating at and direction, respectively. The difference frequency component of is calculated at as a function of (a) center frequency or , (b) object radius or , (c) receiver range or , and (d) difference frequency or . Lower dimensionless abscissas are for general interpretations. Upper abscissas are for a medical sensing or underwater example of perpendicular primary waves with 1 MHz primary and 100 kHz difference frequencies, sphere radius of 0.1 mm at range 1 m from the receiver with sound speed 1500 m/s sound speed. In (a), dominates for large , while and dominate for small . In (b), dominates for large , and dominate for small . In (c), is dominant and has the most gradual roll-off with range. In (d), and dominate and SS is too small to be shown but appears in Figures S13 or S18. The nonlinear parameter is .
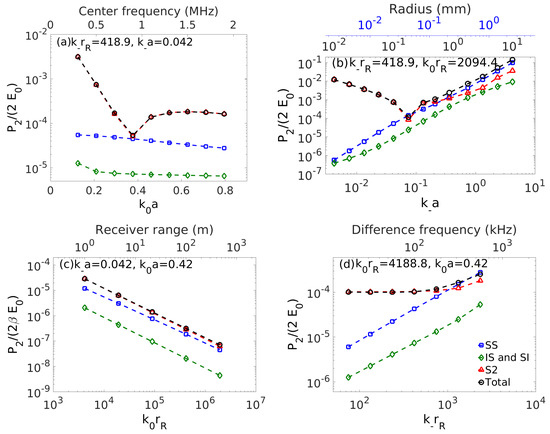
Figure 6.
A pressure release sphere with collinear incident waves propagating in . The difference frequency component of is calculated at as a function of (a) center frequency or , (b) object radius or , (c) receiver range or , and (d) difference frequency or . Lower dimensionless abscissas are for general interpretations. Upper black abscissas are for a medical or underwater sensing example of 1 MHz primary and 100 kHz difference frequencies with 0.1 mm sphere radius at 1 m range from the receiver with 1500 m/s sound speed. The upper blue abscissa in (b) is for different medical or underwater sensing example of 2 MHz primary and 400 kHz difference frequencies with 0.1 mm sphere radius at 0.25 m range with 1500 m/s sound speed. In (a), is dominant. In (b), dominates for small , becomes comparable to for near 1 then transitions to dominance for . In (c), is dominant, but will dominate as range increases. In (d), dominates for small , and becomes comparable to for large . The nonlinear parameter is .
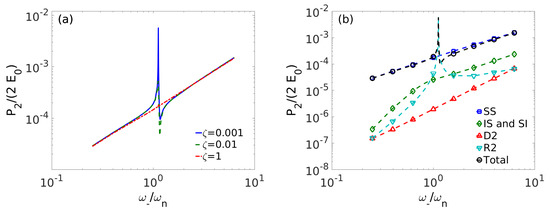
Figure 8.
A resonating rigid movable sphere with collinear incident waves propagating in direction. is calculated in . In (a), total difference frequency component of is plotted as a function of difference frequency near resonance for damping ratio . In (b), , , , and are shown near resonance for . When the object’s resonance is excited at the difference frequency, is amplified and it becomes dominant for small enough damping. The object radius a, receiver range and the center frequency are fixed so and . The nonlinear parameter is and the density ratio between the object and the medium is 2.4.
Examples are computed from the exact governing equations which allow general object shapes and sizes compared to the wavelength, but for simplicity scenarios involving spherical objects are presented. The geometry is shown in Figure E2, which does not include measurements in forward scatter where IS and SI are larger. These forward scattered cases are treated in online material. With the harmonic wave approximation, is given by Equation (82) with or (83), , and are determined from Equations (78)–(80) respectively, and from spherical wave expansions (online supplementary material). The results represent difference frequency wave amplitudes in the time domain between and for narrow-band incident fields, as discussed in Appendix E. In all examples a practical object-centered coordinate system is used where for the II component in Equation (82). A normalization is used in the examples.
To generalize the analysis, dimensionless parameters , , and are used, where is the center frequency wavenumber, is the difference frequency wavenumber, a is the radius of the object and is the receiver range. The values for the parameters are chosen based on the following considerations: (1) , so that the II interaction can be time separated from the other mechanisms, (2) the difference frequency is lower than the primary frequencies, and (3) important transitions between mechanisms can be seen. Illustrative examples are presented and discussed for medical imaging, various ocean sensing applications as well as for sensing in air and the solid earth. Some general observations on the transitions between mechanisms found for rigid and pressure release cases are noted in Appendix F.
By matching the relevant dimensionless parameters and properly scaling the nonlinear parameter , results presented in Section 5 can be applied to various sensing scenarios in air, water and solid earth. Depending on the actual dominant mechanism, the response of the object at the primary frequencies or difference frequency can then be deduced from . It is useful to clearly define the II component of S2, corresponding to the mechanism, via
5.1. Medical and Fine-Scale Underwater Sensing
For nonlinear medical ultrasound sensing applications [28,36,37], which are portable to fine-scale high frequency underwater sensing, a transition between nonlinear mechanisms can be seen for rigid (Figure 3, Figure 4 and Figure 5) and vacuous objects (Figure 6) sensed at the difference frequency in a watery environment. The SS mechanism is dominant (top right point of Figure 3b and Figure 4b) for a 0.5 mm rigid object in a water environment sensed at a range of 1 m in backscatter for 1 MHz primary and 10 kHz difference frequency, and stands above noise with typical incident and received levels. As the object diameter is reduced IS and SI in backscatter become dominant for the immovable collinear case, so that no difference frequency information can be obtained due to lack of a measurable S2 component. When perpendicular waves are incident on the immovable object, the dominant mechanisms are similar to those of the collinear case except S2 is as dominant as the IS and SI as object diameter decreases (Figure 5b). Allowing the rigid object’s centroid to move in response to the wave fields for the same parameters enables S2 to become dominant through D2 as the object radius is reduced by two orders of magnitude from 0.5 mm (Figure 4b). The R2 component, due to radiation from object centroidal motion is negligible and unmeasurable for this example when S2 dominates (Figure 4b). If the rigid object was attached to sufficiently underdamped springy material, it is possible that a resonance effect could make R2 and consequently S2 dominant and detectable at resonance even for large object radii, as shown in Figure 8. It may be difficult to extract the difference frequency response at resonance, however, if R2 is not dominated by the response to II as is the case for the example in Figure 8 as shown in Figure S15.
Continuing the medical ultrasound and high frequency underwater analysis with a vacuous bubble of 0.1 mm radius in water, first in backscatter, the S2 and SS contributions are equally dominant with the bubble sensed well above noise at 0.25 m range with a 2.0 MHz primary and 400 kHz difference frequency (Figure 6b, ) for typical incident levels. This makes it challenging to extract difference frequency response information from the second order field, since this information is not contained in the contaminating SS component. All frequencies in this example are well above the bubble’s resonace frequency ( near the water-atmosphere surface), so pressure release theory is accurate. For smaller bubble diameters () the S2 mechanism becomes dominant but the contribution becomes increasingly negligible (Figure S14) so that a complicated inversion involving primary frequency scattering information is necessary to extract the object’s difference frequency response information from S2 especially for and near unity. Dominance of S2 in backscatter occurs when and begin to decrease below unity and SS and SS-type effects at the object boundary begin to dominate S2 which then obeys Equation (97) for and much less than unity. As the difference frequency approaches the air bubble resonance frequency from above, the S2 field (Figure 7b) becomes significantly different from that of the pressure release case (Figure 6b), but the transition from SS to S2 dominance is seen to occur at frequencies above where resonance effects matter and where pressure release theory is sufficient. The S2 pressure peaks at resonance but then eventually decreases to zero as frequency decreases (Figure 7b). The minima in S2 seen in Figure 6a,b occur when SS effects at the boundary become less dominant as and approach unity from below. As the bubble radius increases above 0.1 mm, the SS mechanism transitions to dominance and masks difference frequency responses from the object (Figure 6b and Figure 7b) . For the same 2 MHz primary and 400 kHz difference frequencies and 0.1 mm radius gas filled or pressure release bubble, but with reception in the forward direction at 1 m range, IS and SI are dominant and become increasingly so for larger bubble radii so masking difference frequency information from the object (Figure S19). (Typical primary wave incident levels in medical ultrasound are 240 dB re 1 Pa in water with noise levels in the noise levels in the 50 to 65 dB re 1 Pa range for the difference frequencies considered.)
The examples are illustrated and evaluated both in terms of dimensionless parameters and specific frequencies and lengths. The former makes it possible to interpret the results universally over the broadest range of possible applications by scaling the object size, receiver range, and frequencies as necessary. In this way, for example, Figure 3b with 1 MHz primary and 10 kHz difference frequencies at range 1 m from the receiver can be interpreted for lower or higher frequency cases. Consider increasing the frequencies by a factor of fifteen, from 1 MHz to 15 MHz for the primary and 10 kHz to 150 kHz for the difference which are also used in ultrasound, and correspondingly decreasing the receiver range by a factor of fifteen. The nondimensional axes of the same figure show that the object radius where the SS mechanism begins to dominate must then correspondingly be reduced by a factor of fifteen. Similar analysis of scaling up or down frequencies and length scales can be performed readily for all figures with nondimensional axes.
Depending on one’s perspective and the physical scenario, the difference frequency responses from an object sought in the medical vibro-acoustics (e.g., [4,5]) may be extractable from some or all S2 field components with varying amount of difficulty, and would certainly exist in an R2 subcomponent of S2 since this corresponds well with the mechanism discussed in Greenleaf et al. [4] and referred to as an “acoustic emission”, but would not be available in SS, IS or SI fields.
5.2. Sensing Ocean Bubbles
The preceding example of a pressure release bubble in water applies directly to near-surface air bubbles in the ocean of the same size, primary and difference frequencies, and receiver ranges, and can be scaled to other similar cases using the non-dimensional parameters in (Figure 7) in correspondence with Equation (97). Other examples of the dominance of SS IS and SI at ranges of practical interest can be seen in Figure 9a where for a 1 mm bubble with primary frequency 430 kHz and difference frequency 43 kHz, SS will dominate the total second order difference frequency field at 4.88 m range from the object in backscatter, while IS and SI forward will dominate at much shorter ranges in forward scatter (Figure 9b). Scaling up, with a 10 mm bubble at 43 kHz primary and 4.3 kHz difference frequency SS will dominate at 48.8 m range in backscatter with IS and SI dominating at much shorter ranges in forward scatter. In the ocean context, these examples show that for primary and difference frequencies well above the bubble’s resonance frequency, wave-wave interactions SS, IS and SI become important and will dominate the difference frequency field from an air bubble even at relatively close sensing ranges. In this regime where wave-wave interactions are important, the total second order field from an aggregate of bubbles is not the superposition of the individual second order bubble fields.
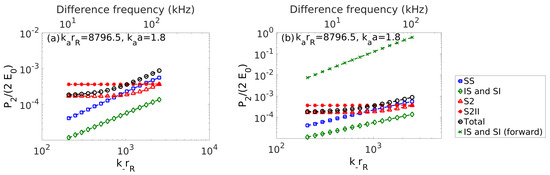
Figure 9.
(a) A near surface air bubble in water with collinear incident waves propagating at . The difference frequency component of is calculated in backscatter at as a function of difference frequency or . Lower dimensionless abscissas are for general interpretations. Upper abscissas are for 430 kHz primary and 43 kHz difference frequencies with bubble radius 0.1 mm radius at 4.88 m range from the receiver in water. A transition between mechanisms is seen where is dominant for while is dominant for above and near resonance. The nonlinear parameter is . (b) Same as (a) but with in the forward direction also included for which is seen to dominate the field over the entire range shown.
In the analysis of air bubbles in water using a primary pump frequency at the air bubble resonance (with wavenumber ) and a variable primary image frequency (with wavenumber ) moving from to well above resonance (e.g., [2]), Figure 10 shows that wave-wave fields from a bubble are not significant at a receiver in backscatter for many practical sensing ranges and primary image frequencies. The same Figure 10 shows, however, that as approaches unity the wave-wave IS and SI backscatter components can attain similar levels as S2 and become dominant. This transition occurs for smaller as range increases. It also occurs for smaller for receivers in the forward direction (Figure S21). Analytic conditions for when SS, and forward IS and SI are negligible compared to S2 are given in Appendix B. Due to the complicated nature of IS and SI in nonforward directions such conditions are available only through computations such as in Figure 10 and Figure S21. In the other contexts, such as the previous medical and the following ocean fisheries examples, as well as cases where parametric arrays or related approaches are intended to employ II incidence, primary frequencies are typically not used at the frequencies of the desired response from an object otherwise linear acoustic sensing would be employed.
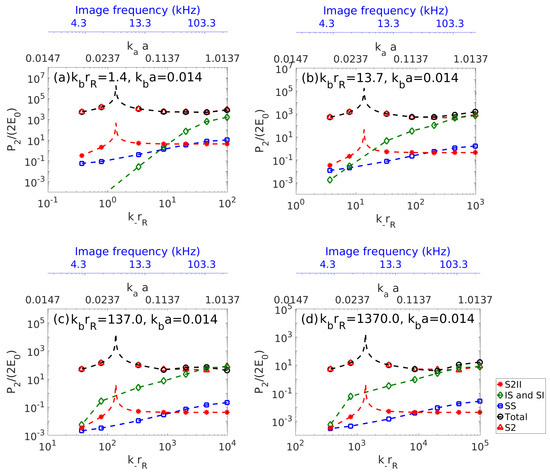
Figure 10.
An acoustically compact near surface air bubble in water will resonate at roughly (Equation (B19)). Primary pump wave frequency is then set to roughly the bubble resonance frequency which is determined by . For collinear incident waves propagating at , the difference frequency component of is calculated in backscatter at as a function of difference frequency through . This nondimensional example may be interpreted for a 1 mm radius underwater bubble with 3.34 kHz primary pump wave frequency and image wave frequency varying through from the vicinity of 0.0167 to 1.0137 for receiver ranges (a) m, (b) m, (c) m, and (d) m as in the upper black abscissas. The upper blue abscissas are for the corresponding primary image wave frequency for this example calculated by with sound speed m/s. For image wave well below unity, S2 dominates and a localized peak is seen at difference frequency resonance. For image wave , wave-wave effects dominate at shorter receiver ranges as increases.
5.3. Ocean Fisheries Sensing
In ocean fisheries applications, difference frequency sensing has been used in ocean line-transect surveys to potentially probe the near-resonance frequency response of herring schools in the Nordic Seas via a parametric array sonar [7]. The linear near resonance response of fish has relevance to linear ecosystem-scale sensing techniques [15,16,38]. In the nonlinear work [7], the parametric sonar transmits high intensity primary frequency waves that lead to combined incident primary 15–21 kHz and difference frequency 0.5–6.0 kHz fields at the herring shoals, roughly 50–100 m below the research vessel [7]. Herring swimbladder equivalent radii are between roughly 0.8–1.0 cm for herring in the 100–50 m depth range. Our analysis shows that the SS component, which has no difference frequency information and is essentially a nuisance contamination in this context, begins to make a non-negligible contribution to the total received second order field from any herring in the 50–100 m depth range for difference frequencies above 2 to 3 kHz (Figure 11 and Figure 12). For difference frequencies below 2 kHz S2 is dominant, but not always equal to as see in Figure 11 and Figure 12 which means that a complicated inversion involving knowledge of the herring scattering response at the primary frequencies and wave-wave boundary effects will be necessary to extract the linear difference frequency response of the herring for difference frequencies this range. This is because and are near unity so that a delicate balance between II, SS, IS and SI boundary values and second order boundary advection may affect the radiated S2 amplitude. It is noteworthy, however, that some of the necessary information for this inversion may be obtained from primary frequency scattered returns that could be received simultaneously from parametric array survey. Similar analysis for cod, (Figure 13) which typically shoal in the 100–150 m range during spawning in Lofoten Norway and have corresponding swimbladder equivalent radii of roughly 4.2 cm where they are neutrally buoyant, shows SS is either dominant or a significant contaminant over the entire difference frequency range from 0.5 to 6 kHz making it impossible or difficult to obtain difference frequency response information from the second order field in this scenario. The relative amplitudes of difference to primary frequency waves radiating from a parametric array may differ from those assumed here, depending on array geometry and other factors [1] which may alter some results.
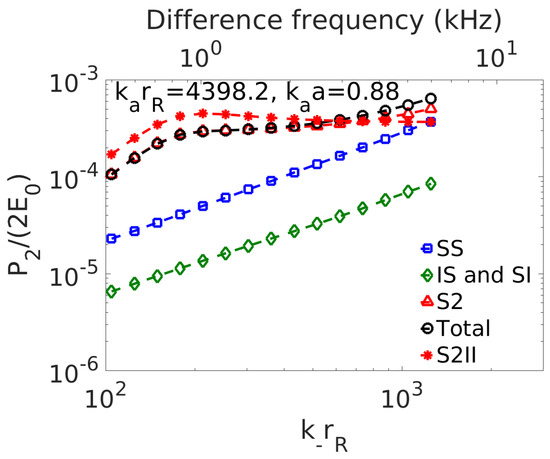
Figure 11.
Equivalent to a herring at 50 m depth modeled as swimbladder with equivalent radius of roughly 1 cm with collinear incident waves of 21 kHz primary and varying difference frequencies propagating at using resonant bubble Equation (97) with herring damping. The difference frequency component of is calculated in backscatter at as a function of difference frequency through or . Upper abscissa shows the difference frequency for the current example.
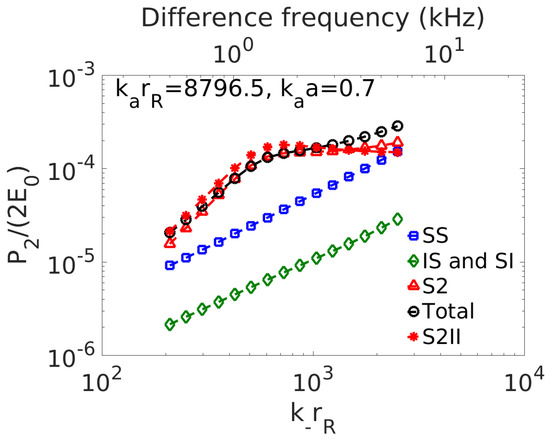
Figure 12.
Same as Figure 11 but for herring at 100 m depth with equivalent bubble radius of 0.80 cm.
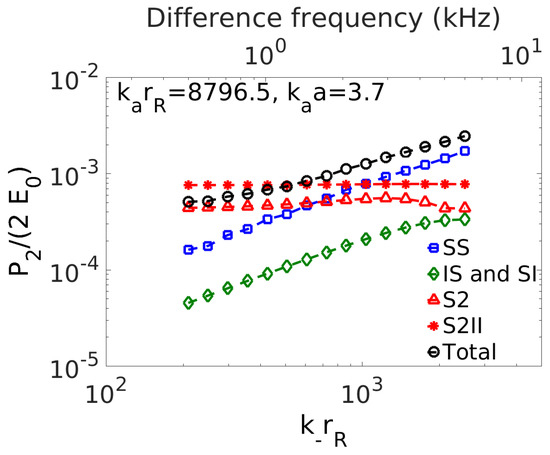
Figure 13.
Equivalent to a cod at 100 m depth modeled as swimbladder with equivalent radius of roughly 4.2 cm with collinear incident waves of 21 kHz primary and varying difference frequencies propagating at using resonant bubble equation Equation (97) with cod damping. The difference frequency component of is calculated in backscatter at as a function of difference frequency through or . Upper abscissa shows the difference frequency for the current example.
5.4. Sensing Objects From IS Interactions
The IS mechanism can lead to robust sum or difference frequency detection and sensing of objects in air or water over extended ranges since asymptotically IS is constant in range. Perfectly reflecting objects, for example, with circumferences that are on the order of the primary wavelength or larger () and incident sound pressure levels on the order of that for a 1 watt monopolar point source at 1 m ( 171 dB re 1 at 1 m in water and 108 dB re 20 at 1 m in air) are seen to have IS levels (Figure 14) that stand above typical ambient noise ambient noise levels (Figure S8). A trip wire employing perpendicular primary beams could be used, for example, so that when an object crosses the beam of a primary field, a sum or difference frequency IS would trigger its presence at a sensor in the forward direction of the primary beam crossed by the object. The advantage is the sensor could be well past the primary shadow of the object where detection at primary frequencies would be difficult since the received primary field would be dominated by the incident primary field. In another example, it is seen from Equations (92)–(94) that stealthy long range sensing of an object’s primary frequency response via sum and difference frequency measurements is possible. For example, if an object scatters or radiates an outward propagating wave at angular frequency , a beam could be transmitted at a different frequency forward scattering past the object to a receiver. By continuing this for angles about the object, it is possible to reconstruct the directivity pattern of from , for primary frequency object classification at the difference frequency.
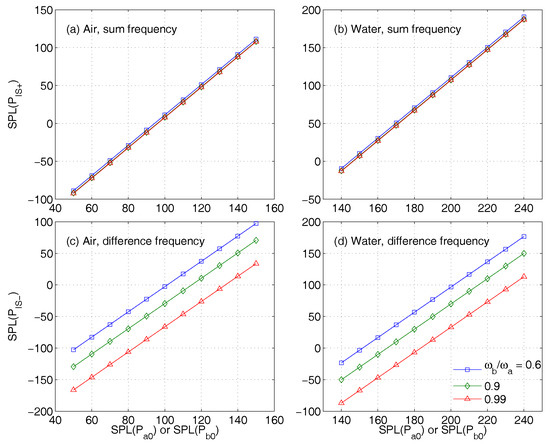
Figure 14.
Sound Pressure Level (SPL) of in the forward direction as a function of incident SPL at large range in air and water for , and assuming and . The SPL in air, (a,c), is referenced to 20 Pa and the SPL in water, (b,d), is referenced to 1 Pa. In (a,c) for air, high frequency incident SPL between 120 dB and 140 dB re 20 Pa gives sum frequency SPL between 48 dB to 88 dB re 20 Pa, and difference frequency SPL between 38 dB and 77 dB re 20 Pa respectively, for . Similarly, in (b,d) for water, high frequency incident SPL between 170 dB and 190 dB re 1 Pa gives sum frequency SPL between 48 dB to 90 dB, and difference frequency SPL between 37 dB and 77 dB respectively, for . With moderate to high incident SPLs, these sum and difference frequency second order waves can be measurable at long range.
5.5. Sensing Objects in Air
In air, the SS mechanism can lead to robust sum or difference frequency detections from objects large compared to the primary wavelength. Consider, for example, nonlinear acoustic sensing of a 4 cm diameter rigid sphere with a primary frequency of 40 kHz and a difference frequency of 4 kHz with bat sonar incident levels of 140 dB re 20 [39] which has relevance to robot sonar. Received levels of at least 53 dB re 20 are expected at 2 m range at the difference frequency and at nearly an order of magnitude greater range at the sum frequency, which are well above noise levels at those frequencies (Figure S8) using Equation (90) or (91). As the radius of object increases, so will the detection range.
5.6. Sensing in the Solid Earth
Difference frequency sensing of buried structures in the solid earth, such as archaeological remains, is also possible. A 4-m scale rigid structure, for example, can be robustly detected by the S2 mechanism for 50 Hz primary and 10 Hz difference frequency waves at distances greater than 1 km (Figure S7) for standard ground vibrators within tens of meters of the feature, e.g., a 240 dB re 1 Pa incident SPL can be generated from a 150 kN vibrator 30 m away with , kg/m, m/s.
6. Discussion
Unique opportunities exist for sensing an object at the sum or difference frequency of primary incident waves. Many of these have been discussed in a variety of contexts, as for example through the use of parametric source arrays and related approaches in ocean fishery, gas bubble and submerged object sensing and medical ultrasonic imaging [1,2,3,4,5,6,7], but in the absence of a complete theory for the second order field in the presence of an object. Here we examine some practical sensing scenarios in water, air and solid earth. In the context of using parametric arrays, for example, to probe an object’s sum or difference frequency response, a problem we find is that in many practical scenarios, SS, IS and SI incidence on the object and boundary advection responses from the object contribute more than II incidence to S2, which may not have been expected. This can make accurate extraction of the object’s linear response to sum or difference frequency waves from S2 far more complicated than may have been anticipated. The other problem is that the field at the receiver may be dominated by SS, IS or SI, which also may not have been expected, and these contain no such sum or difference frequency linear response information. For parametric arrays and related approaches, these issues arise because the primary fields needed to form the sum or difference frequency incident field (II) typically interact with the object to be sensed in a manner that cannot be ignored when analyzing the second order field.
Inspired by 18th-century accounts of difference frequency waves propagating from musical instruments [1], Lamb developed solutions for the II interaction of collinear time-harmonic primary planewaves [12]. Westervelt later solved the time-harmonic non-collinear planewave case [11] and estimated the second order field of an endfire array so inventing the parametric array [3] which is a wave-wave based instrument with mature and well tested theory [1]. Then Dean and Baxter obtained time-harmonic solutions for the omnidirectional cylindrical [29] and spherical [29,33] wave cases, and Tjotta et al., investigated II interaction for time-harmonic incident beams [40,41,42]. Jones and Beyer measured the second-order acoustic field at the sum frequency caused by an object in the overlap region of two primary incident waves [1,35] and proposed a heuristic formula consistent with an SS-type mechanism based on Dean’s solution. Greenleaf et al., proposed measuring an object’s difference frequency response from primary wave insonification for applications in medical ultrasound where significant interest in this exists [4,5]. Without a complete theoretical formulation for the second order field in the presence of a movable object, it was noted that the interaction of primary scattered waves may dominate the second order field [36,43,44] and mask information about the object’s difference frequency response contained in weaker field components. Such a complete theory, as presented here, is necessary to investigate the conditions under which an object’s difference frequency response may be detectable and when each of the various second order mechanisms may dominate. To treat the case of a movable object, we define a complete and self-consistent second order acoustic wave-exciting force, and find previous helpful formulations [28,45,46,47] missed the effects of some second order field components and overcounted others. (An analytic solution for the SS field arising from a rigid immovable sphere was dervied by Silva and Bandeira [48].) Approximate analytic solutions for the second order nonlinear wave fields found in the presence of low-impedance contrast inhomogeneities, that apply to one or many inhomogeneities, are also derived in Appendix A.
Since the SS, IS and SI interactions always dominate the field components that carry object information at sufficiently long range, exact and asymptotic analytic solutions are rigorously obtained for them, which put previous heuristic estimates [1,34,35] of SS into perspective. For spherically symmetric interacting waves, our analytic solution is exact and reduces to Baxter’s [33] for this special case, where we show that Baxter’s solution satisfies the Sommerfeld radiation condition but Dean’s [29] does not. Analytic solutions are derived for the second-order field due to the interaction of a plane and spherical wave. These lead to analytic expressions for IS and SI in the far field of any arbitrarily shaped scatterer.
A number of investigations on the nonlinear acoustics of air bubbles in water are based on leading order approximations near and below resonance frequency where the bubble’s circumference is very small compared to the primary field’s wavelength [2,49,50]. In these approaches SS, IS and SI fields are neglected, and are typically negligible away from the bubble for practical receiver ranges in this low frequency regime. Even in these scenarios, however, we find the leading order effect of SS, IS and SI on S2 through wave-wave boundary incidence can be significant and so are included here as well as the boundary advection effects included in the other approaches [49,50,51], which are of similar order. Our formulation then is consistent to leading order with these previous formulations in this low frequency regime near and below resonance. We find that for primary and difference frequencies well above bubble resonance, however, as the bubble circumference to primary frequency wavelength approaches and exceeds unity, SS, IS and SI wave-wave fields begin to significantly affect and eventually dominate the second order field propagating outward from an air bubble in water at ranges and frequencies important to many practical sensing scenarios and so cannot be neglected. In this case, linear superposition of individual bubble fields in an ensemble, which is valid and sometimes theoretically relied upon for primary frequencies near bubble resonance [49,51], is not valid in this higher frequency regime where wave-wave interaction effects are important. Other approaches [52] heuristically treated bubble and water or seabed mixtures as effective media in a second order wave equation formulation to investigate nonlinear acoustic scattering, but these cannot be applied to or built up from a single scatterer since they lack fundamental boundary conditions at an inhomogeneity and have not been clearly verified experimentally.
Sum and difference frequency methods for detecting and analyzing bubbles in water with one primary wave (the ‘pump’) near the bubble resonance, and primary wave (the ‘image’) at much higher frequency (e.g., [2]) also depend on wave-wave interactions away from the bubbles to be negligible. A cautionary note in an introductory paper on this topic “the transducers were also kept at a short distance (less than an inch) from the bubble stream so as to avoid the generation of sum or difference frequencies due to nonlinearity of the medium” [2] refers to possible contamination by wave-wave interactions citing Westervelt [11] and Beyer [1]. Here we show that for typical scenarios in this pump-image approach, while SS, IS and SI received fields are significant as incident fields at the bubble boundary, they are usually not significant away from the object in practical implementations of the pump-image approach due to the fact that the pump wavelength is always roughly two orders of magnitude larger than the bubble circumference to pump near resonance, the image wavelength is typically less than the bubble circumference, and sensing ranges are not large. The use of such a long primary pump wavelength, however, may be impractical for other applications involving parametric arrays or related approaches [1,3,4,5,7] where much of the merit rests on the avoidance of traditional primary sources that transmit at such long wavelengths.
7. Conclusions
For applications in nonlinear acoustic sensing of objects by sum or difference frequency fields, a general second order theory of nonlinear interaction and scattering of acoustic waves in the presence of an object is derived and confirmed by comparison with experimental measurements. Practical guidance on designing experiments and interpreting measurements to sense objects with second order nonlinear acoustics have been provided, including approaches to determine whether wave-wave interaction effects, second order boundary scattering and advection, object resonance, or radiation from wave-induced object centroidal motion are dominant in a given scenario. We show that the wave-wave fields propagating from the object contain only primary wave frequency information about the object, while the remaining components contain sum and difference frequency information, with the latter typically being more desirable in many applications of nonlinear acoustic sensing. In the latter case, we show that a complicated inversion may be necessary to extract this sum or difference frequency information.
In the use of parametric arrays, for example, we find it is often not possible to simply assume the only incident field on the object is the difference frequency field generated by the parametric array. This is because intense primary frequency waves are needed to generate this incident difference frequency field. We show that in many practical examples of sensing objects these primary fields in fact lead to the dominant difference frequency response from the object by mechanisms other than linear scattering of the incident difference frequency field of the parametric array.
In general, we analytically find that at long ranges from the object, wave-wave interactions always dominate the second order field, but the required ranges in some cases may be too large to enable practical measurements. We find at shorter ranges, any of a number of second order nonlinear mechanisms may dominate, depending on frequencies, object size, object composition, and source and receiver positions with respect to the object. We show that in diverse applications ranging from ocean fishery and bubble to medical sensing, careful analysis using complete and self-consistent nonlinear theory is necessary to determine which mechanism or mechanisms are dominant in a given scenario.
Since finite-duration waveforms are typically used in practical sensing scenarios, we analytically show that there is no scattering of sound by sound outside a region of interacting primary plane waves of compact support. This makes it possible to readily distinguish incident-incident wave interactions from those involving an object by appropriate choice of measurement geometry.
Supplementary Materials
The following are available online at www.mdpi.com/2072-4292/9/9/954/s1.
Acknowledgments
This research was partially supported by the Office of Naval Research.
Author Contributions
The research was conceived by Makris, developed by Makris, Ratilal, Liu and Zhang, and numerically implemented by Zhang and Cho. The paper was primarily written by Makris and Zhang with many contributions from all authors including full appendices from Ratilal and Liu. The Supplementary Online Material was primarily written by Zhang and Makris with many contributions from all authors.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Second Order Nonlinear Acoustic Wave Equation in Medium with Volume Inhomogeneities
Let be the ambient density without inhomogeneities or the acoustic wave, be the change of density due to inhomogeneities without the acoustic wave, and be the change of density due to the acoustic wave. The total density can be written as
Without the acoustic wave, the total derivative of ambient density vanishes,
The exact continuity and momentum equations are
Applying Equation (A2) to Equations (A3) and (A4) leads to
Now perturbation expansions are introduced to , p and in Equations (A5) and (A6). Canceling the first order velocity from Equations (A5) and (A6) leads to
Similarly, eliminating the second order velocity from Equations (A5) and (A6) yields
For the equation of state, it is assumed that the density is a function of pressure only and can be expressed as a Taylor series expansion about the ambient pressure,
Taylor series expansion leads to
where the compressibility and .
Substituting Equation (A10) into Equation (A7) to eliminate and assuming the inhomogeneities and are stationary in time yields
which is the classical wave equation for space containing inhomogeneities [24].
Substituting Equation (A11) into Equation (A8) to eliminate and further assuming is stationary in time yields
By adding on both sides and then multiplying by , Equation (A13) can be rewritten as
where and are the fractional changes in compressibility and density of the medium due to inhomogeneities, is the mean compressibility and is the mean sound speed of the medium. For a homogeneous medium, , , , , and the above equation reduces to Equation (17).
Consider time harmonic fields incident on a single target. Let the incident wave consist of two harmonic components, and with frequencies and . The corresponding Helmholtz equation for the second order pressure at the sum or difference frequency is
where
The solution to Equation (A15) is
which has five components corresponding to the five parenthetical groups in curly brackets in of Equation (A16). Components in the first three sets of curly brackets in Equation (A16) are nonzero in or on the inhomogeneity and describe second order scattering S2. As in the linear case, the changes of compressibility in the medium, , scatter as monopoles while the changes of density, , scatter as dipoles. Components in the last two sets of curly brackets in equation (A16) are nonzero where the primary waves are nonzero and describe nonlinear wave-wave interactions, including II, SS and IS, where only II exists if the medium has no inhomogeneities.
Appendix B. Second Order Pressure Field from a Small Resonant Air Bubble
Consider a small spherical gas bubble in an infinite fluid subject to the action of two collinear harmonic plane incident waves. The incident waves have frequencies and and amplitudes and . The bubble has a radius of a at rest. We derive the asymptotic solution for . By including the bubble’s damping and restoring effects into the equation of motion for a pressure release sphere, we obtain an approximate equation governing the motion of the bubble wall in the radial direction, which takes the first order form
where the damping constant includes dissipation from thermal phenomena, viscosity, acoustic radiation, and surface tension, and is the natural frequency of the bubble volume pulsation, which is determined from
where is surface tension, is the ambient pressure, and is the polytropic constant [2].
For the given incident waves, the first order scattered field from a small pressure release sphere can be determined from the boundary condition, Equation (10). The amplitude of first-order motion of the bubble wall is obtained from Equation (B18):
where the amplification factors and are defined by
The first order scattered field will be monopolar as given by
The results in Equations (B20) and (B22) approach the solution of a pressure release sphere at large frequencies .
The equation governing the second-order motion of the bubble wall is obtained from Equation (19):
where denotes the second-order interaction terms associated with surface tension, thermal phenomena and viscous effects, given by
For small bubbles with , the second-order incident wave (Equation (44)), which contains II, SS, IS and SI components, is dominated by on the bubble wall
In the vicinity of the bubble, is dominated by the velocity components due to first order scattering, and , which are determined by use of Equation (B22) and near the bubble surface take the form
The second-order S2 pressure component from a pressure release sphere can be obtained by solving the linear scattering problem with the boundary condition given by Equation (51). With determined from Equation (B23), the S2 pressure is
where the amplification factor is
and the coefficient is defined by
represents the effect of the second-order interactions associated with surface tension and fluid viscosity, which is found to be insignificant compared to the other effects. Equation (B27) becomes the second-order solution for a pressure release sphere when and . If the second-order incident wave , which contains all II, SS, IS and SI wave-wave fields at the boundary, is omitted in (B23), the solution in Equation (B27) becomes equal to that obtained by Newhouse & Shankar [2]. We find, however, in our examples that is of similar order as the other terms in (B23) and should not be ommitted.
In the far field , can be determined from Equation (91), and and in the forward scatter direction can be determined from Equations (92)–(94). Their ratios to are found to be
which, when the ratios are small, become conditions on receiver range, probing frequencies, and parameters of the object and medium for which these wave-wave fields at the receiver will be negligible, and when the ratios become large become conditions on when these wave-wave fields at the receiver are dominant. It is noteworthy that no simple expression has been obtained for IS + SI in nonforward directions, so computations of this have been provided in Section 5.
Appendix C. Locally Reacting Boundary
The normal velocity is a function of pressure p on a locally reacting boundary S as
where the nonlinear function h can be expanded with respect to ambient pressure as
This boundary condition on can be further expanded with respect to the reference mean boundary , as
Substituting the perturbation expansions for , and p to the above equation and collecting terms of the same order, we obtain first and second order boundary conditions for the general locally reacting boundary, as
Here is the same as the acoustic impedance z in reference [24].
The first and second order fields for a pressure release boundary problem are denoted as and respectively. They satisfy the boundary conditions
The first and second order fields for a fixed rigid boundary problem are denoted as and respectively. They satisfy the boundary conditions
On , the first and second order waves for a general locally reacting boundary problem are
The coefficients and are functions of position on , and they can be determined from the first or second order boundary conditions (C39) and (C40), as
The first order scattered wave from a general locally reacting boundary can be obtained by evaluating Equation (8), with Equations (C43) and (C45). The second order scattered wave from a general locally reacting boundary can be obtained by evaluating Equation (25) with Equations (C44) and (C46).
Appendix D. Static and Dynamic Force
Starting from , the total second order force acting on an object can be written as [45]
where is the difference between the volume occupied by the exact boundary and time-averaged boundary . is the Lagrangian density, where is the kinetic energy density and is the potential energy density. Components of the second order potential are explicitly written out following our convention as
Similarly, .
The first two terms on the right-hand side of Equation (D47) have zero zero-frequency component due to the time derivative, so the static radiation force is determined by the zero-frequency component of the last two terms. This, for example, enables King [53] to calculate on a rigid movable sphere for plane wave incidence without solving . The radiation force here has its counterpart in hydrodynamics as the second order drifting force on an object [54].
In the dynamic case, all terms in Equation (D47) must be included. As in Equation (38), the centroidal motion of the object, , is determined by the equation of motion
Substituting Equations (D47) and (D48) into Equation (D49) and combining the contribution of R2 as the radiation impedance , we obtain
where
is equivalent to Equation (39), and
which contains the wave-wave interactions and the corresponding D2 components.
The object’s centroidal velocity can be determined from Equations (D50)–(D52). A derivation along these lines found in references [28,45,46,47], however, uses instead of where omits terms , , , , and , and adds an extraneous , and so does not equal of Equation (D52) as it must to quantify all second order effects in a general manner. Low difference frequency measurements [28] show that converges to , which also occurs if is used. Using instead of in Equation (D51), however, does not generally lead to the correct relation between and centroidal velocity as in Equation (D50) across frequency.
Appendix E. Space-Time Isolation of Second Order Field Components that Carry Information About an Object
Here we consider sum and difference frequency sensing of an object by measurement of the second order nonlinear fields arising from SS, IS, SI and S2 mechanisms. When the primary waves have compact support, we show here for and via Equations (69) and (70) and for via Equations (84)–(87) that the second order waves also have compact support (Figure E1). Given this, we show that it is possible to isolate in time and space field components , and that carry information about the object from that does not contain such information by the appropriate choice of receiver location (Figure E2).
The compact support of as analytically derived in Equation (86) is confirmed by direct numerical integration of the full time domain Green theorem solution ( from (68) plus from (61)) and shown in Figure E1a. Compact support of and components is also shown by direct numerical integration of the respective time domain Green theorem solutions ( from (69), from (70), and and from (61)) and shown in Figure E1b–d. Within these regions of compact support, the and can be well approximated by a number of time harmonic approximations including the asymptotic solutions (90), (93), online supplementary material Equation (S156), and direct numerical integration of the harmonic wave Green theorem solutions (78) and (79), plus the respective components from (61). The backscattered IS (Figure E1d) is much smaller than the forward scattered IS component (Figure E1c) as expected from Section 3.2, and the component is zero because the primary incident and scattered waves do not intersect at the receiver in the backscatter direction for this case (Figure E2).
Figure E1.
Second order wave due to the interaction of (a) incident waves of compact support (II), (b) scattered waves (SS) of compact support, (c) incident and scattered waves (IS) of compact support in the forward (c), and backscatter (d) direction by direct numerical integration of the indicated full time domain solutions (solid lines). The second order waves have compact support within which the indicated harmonic approximations are shown to be valid. The top panels show the real pressure and the bottom panels show the pressure amplitude at the difference frequency. Here kHz, kHz, s, m/s and . The pressure is normalized by , where . In (a), the pressure is calculated at the origin; in (b–d), the pressure is calculated at m from the center of a pressure release sphere of radius m and the scattered waves are approximately spherically symmetric with scatter functions .
The II, SS, IS and SI overlap regions of compact support are shown in Figure E2. If a receiver is placed in any location where the II overlap region (gray in Figure E2) and the SS overlap region (blue in Figure E2) do not intersect, as in the example shown in Figure E2, it will measure between and with no component, where occurs when the fronts of the incident waves simultaneously arrive at the object center. The II overlap region entirely passes the receiver before the SS overlap region arrives for the examples shown in Figure E2 if for the collinear case, and if for the perpendicular case. If a receiver is placed in the forward direction in the collinear case, cannot be separated from the other components regardless of the duration of the incident waves, and will mask information about the object carried in , , and .
Since second order scattering (S2) occurs at the object between and when all narrow-band primary waves of compact support overlap, the component has compact support via
where is the time harmonic complex-amplitude of the second order scattered wave of Equation (50) and has compact support, and following , has duration T with unit height within the window except at the ends where smooth transitions to zero occur over periods much less than T.
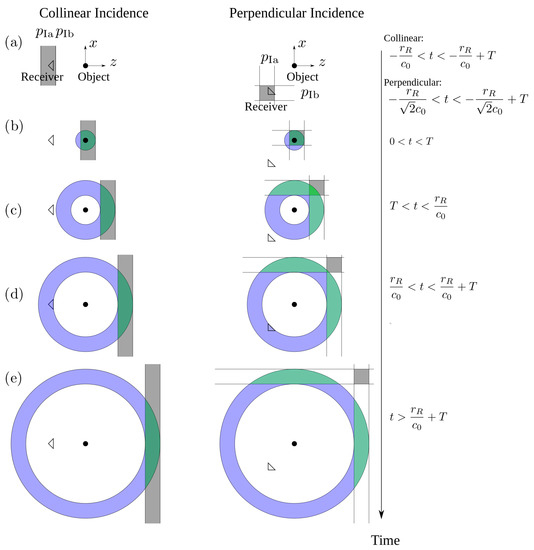
Figure E2.
Primary incident and scattered waves of compact support and regions of compact support overlap, at different time instances (a–e). The left column is for the collinear incidence case, and the right column is for the perpendicular incidence case. The overlap regions for the incident waves, scattered waves, and incident and scattered wave are volumes in 3-D, and they are projected and shown on a 2-D plane as the gray, blue and green areas, respectively.
Appendix F. Transitions Between Mechanisms for Rigid and Pressure Release Objects
Some general patterns of behavior for various mechanisms and transitions between dominant mechanisms are observed at the difference frequency when the receiver range is not asymptotically large, and the receivers are not in forward scatter where IS and SI are more significant:
For rigid objects, it is found that: (1) is dominant for high primary frequencies and large objects, as seen in Figure 3a,b and Figure 4a,b for collinear incidence, and in Figure 5a,b for perpendicular incidence; (2) is most sensitive to the changes of primary frequency and object size, because it is a function of the product of primary scattered fields which depend strongly on and ; (3) when the primary frequency or object size decreases, the dominant mechanism transitions from SS to D2, IS and SI. Specifically, for movable objects, due to the wave-boundary interaction can become dominant as seen in Figure 4a,b. For immovable objects, and are comparable, as seen in Figure 3a,b and Figure 5a,b; (4) is dominant at large difference frequency, as seen in Figure 3d, Figure 4d and Figure 5d; and (5) , which arises from the second order centroidal motion, has very little contribution to the total second order field, as seen in Figure 4. For rigid objects attached to springy material, however, the centroidal motion can be amplified such that becomes dominant when the difference frequency is close to a resonance frequency, as shown in Figure 8.
For pressure release objects, it is found that (1) is dominant at small primary frequencies, for small objects or at small difference frequency, as seen in Figure 6a,b,d, and is mainly due to SS and SS-type boundary effects from the first term of (Equation (61)) and the wave-boundary interaction (Equation (51)); (2) is sensitive to changes in object size but not to the primary frequency for small objects, as seen in Figure 6a,b, because and do not depend on frequency for small pressure release objects; and (3) is insensitive to changes in difference frequency when it is small, as seen in Figure 6d, because and the wave-boundary interaction depend on the primary frequencies, which converge to the center frequency as the difference frequency decreases.
For all rigid, pressure release and rigid-mass-spring-resonating cases, falls off in range more gradually than in the non-forward direction and do, as seen in Figure 3c, Figure 4c, Figure 5c and Figure 6c. This is consistent with the asymptotic behavior of each component discussed in Section 3.2.
References
- Beyer, R. Nonlinear Acoustics; Acoustical Society of America: Melville, NY, USA, 1997. [Google Scholar]
- Newhouse, V.; Shankar, P.M. Bubble size measurements using the nonlinear mixing of two frequencies. J. Acoust. Soc. Am. 1984, 75, 1473–1477. [Google Scholar] [CrossRef]
- Westervelt, P.J. Parametric Acoustic Array. J. Acoust. Soc. Am. 1963, 35, 535–537. [Google Scholar] [CrossRef]
- Fatemi, M.; Greenleaf, J.F. Ultrasound-Stimulated Vibro-Acoustic Spectrography. Science 1998, 280, 82–85. [Google Scholar] [CrossRef] [PubMed]
- Fatemi, M.; Greenleaf, J.F. Vibro-acoustography: An imaging modality based on ultrasound-stimulated acoustic emission. Proc. Natl. Acad. Sci. USA 1999, 96, 6603–6608. [Google Scholar] [CrossRef] [PubMed]
- Mitri, F.; Silva, G.; Greenleaf, J.F.; Fatemi, M. Simultaneous sum-frequency and vibro-acoustography imaging for nondestructive evaluation and testing applications. J. Appl. Phys. 2007, 102, 114911. [Google Scholar] [CrossRef]
- Godø, O.R.; Foote, K.G.; Dybedal, J.; Tenningen, E.; Patel, R. Detecting Atlantic herring by parametric sonar. J. Acoust. Soc. Am. 2010, 127, EL153–EL159. [Google Scholar] [CrossRef] [PubMed]
- Ogilvie, T.F. Second-order hydrodynamic effects on ocean platforms. In Proceedings of the International Workshop on Ship and Platform Motions, California, CA, USA, 26–28 October 1983. [Google Scholar]
- Faltinsen, O. Sea Loads on Ships and Offshore Structures; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Ingard, U.; Pridmore-Brown, D.C. Scattering of Sound by Sound. J. Acoust. Soc. Am. 1956, 28, 367–369. [Google Scholar] [CrossRef]
- Westervelt, P.J. Scattering of Sound by Sound. J. Acoust. Soc. Am. 1957, 29, 199–203. [Google Scholar] [CrossRef]
- Lamb, H. The Dynamical Theory of Sound; E. Arnold & Co.: London, UK, 1931. [Google Scholar]
- Duarte, C.M.; Holmer, M.; Olsen, Y.; Soto, D.; Marbà, N.; Guiu, J.; Black, K.; Karakassis, I. Will the oceans help feed humanity? BioScience 2009, 59, 967–976. [Google Scholar] [CrossRef]
- Food and Agriculture Organization. Yearbook of Fishery Statistics Summary Tables 2013. Available online: ftp://ftp.fao.org/FI/STAT/summary/a1d.pdf (accessed on 14 September 2017).
- Makris, N.C.; Ratilal, P.; Symonds, D.T.; Jagannathan, S.; Lee, S.; Nero, R.W. Fish population and behavior revealed by instantaneous continental shelf-scale imaging. Science 2006, 311, 660–663. [Google Scholar] [CrossRef] [PubMed]
- Makris, N.C.; Ratilal, P.; Jagannathan, S.; Gong, Z.; Andrews, M.; Bertsatos, I.; Godø, O.R.; Nero, R.W.; Jech, J.M. Critical population density triggers rapid formation of vast oceanic fish shoals. Science 2009, 323, 1734–1737. [Google Scholar] [CrossRef] [PubMed]
- Jagannathan, S.; Bertsatos, I.; Symonds, D.; Chen, T.; Nia, H.T.; Jain, A.D.; Andrews, M.; Gong, Z.; Nero, R.; Ngor, L.; et al. Ocean acoustic waveguide remote sensing (OAWRS) of marine ecosystems. Mar. Ecol. Prog. Ser. 2009, 395, 137–160. [Google Scholar] [CrossRef]
- Gong, Z.; Andrews, M.; Jagannathan, S.; Patel, R.; Jech, J.M.; Makris, N.C.; Ratilal, P. Low-frequency target strength and abundance of shoaling Atlantic herring (Clupea harengus) in the Gulf of Maine during the Ocean Acoustic Waveguide Remote Sensing 2006 Experiment. J. Acoust. Soc. Am. 2010, 127, 104–123. [Google Scholar] [CrossRef] [PubMed]
- Haywood, J.; Ramaswamy, V.; Soden, B. Tropospheric aerosol climate forcing in clear-sky satellite observations over the oceans. Science 1999, 283, 1299–1303. [Google Scholar] [CrossRef] [PubMed]
- Monahan, E.C.; Spiel, D.E.; Davidson, K.L. A model of marine aerosol generation via whitecaps and wave disruption. In Oceanic Whitecaps; Springer: New York, NY, USA, 1986; pp. 167–174. [Google Scholar]
- Hoppel, W.; Frick, G.; Fitzgerald, J. Surface source function for sea-salt aerosol and aerosol dry deposition to the ocean surface. J. Geophys. Res. Atmos. 2002, 107, AAC 7-1–AAC 7-17. [Google Scholar] [CrossRef]
- Wanninkhof, R.; McGillis, W.R. A cubic relationship between air-sea CO2 exchange and wind speed. Geophys. Res. Lett. 1999, 26, 1889–1892. [Google Scholar] [CrossRef]
- Wenz, G.M. Acoustic ambient noise in the ocean: Spectra and sources. J. Acoust. Soc. Am. 1962, 34, 1936–1956. [Google Scholar] [CrossRef]
- Morse, P.; Ingard, K. Theoretical Acoustics; Princeton University Press: Princeton, NJ, USA, 1986. [Google Scholar]
- Morse, P.; Feshbach, H. Methods of Theoretical Physics; International Series in Pure and Applied Physics; McGraw-Hill: New York, NY, USA, 1953. [Google Scholar]
- Lai, Y.; Makris, N.C. Spectral and modal formulations for the Doppler-shifted field scattered by an object moving in a stratified medium. J. Acoust. Soc. Am. 2003, 113, 223–244. [Google Scholar] [CrossRef] [PubMed]
- Oestreicher, H.L. Field and Impedance of an Oscillating Sphere in a Viscoelastic Medium with an Application to Biophysics. J. Acoust. Soc. Am. 1951, 23, 707–714. [Google Scholar] [CrossRef]
- Chen, S.; Silva, G.T.; Kinnick, R.R.; Greenleaf, J.F.; Fatemi, M. Measurement of dynamic and static radiation force on a sphere. Phys. Rev. E 2005, 71, 056618. [Google Scholar] [CrossRef] [PubMed]
- Dean, L.W. Interactions between Sound Waves. J. Acoust. Soc. Am. 1962, 34, 1039–1044. [Google Scholar] [CrossRef]
- Steinberg, B. Principles of Aperture and Array System Design: Including Random and Adaptive Arrays; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1976. [Google Scholar]
- Bowman, J.J.; Senior, T.B.A.; Uslenghi, P.L.E. Electromagnetic and Acoustic Scattering by Simple Shapes (Revised Edition); Hemisphere Publishing Corporation: New York, NY, USA, 1987. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. (Eds.) Handbook of Mathematical Functions; Dover Publications Inc.: Mineola, NY, USA, 1972. [Google Scholar]
- Baxter, S. The first order non-linear sound field of a two-frequency spherical source. J. Sound Vib. 1984, 94, 337–349. [Google Scholar] [CrossRef]
- Westervelt, P.J.; Radue, J. Nonlinear Diverging Waves. J. Acoust. Soc. Am. 1961, 33, 1672. [Google Scholar] [CrossRef]
- Jones, J.P. On the Scattering of Sound by Sound. Ph.D. Thesis, Brown University, Providence, RI, USA, 1971. [Google Scholar]
- Silva, G.T.; Mitri, F.G. Difference-frequency generation in vibro-acoustography. Phys. Med. Biol. 2011, 56, 5985–5993. [Google Scholar] [CrossRef] [PubMed]
- Morgan, K.E.; Allen, J.S.; Dayton, P.A.; Chomas, J.E.; Klibaov, A.L.; Ferrara, K.W. Experimental and theoretical evaluation of microbubble behavior: Effect of transmitted phase and bubble size. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2000, 47, 1494–1509. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Garcia, H.; Huang, W.; Tran, D.D.; Jain, A.D.; Yi, D.H.; Gong, Z.; Jech, J.M.; Godø, O.R.; Makris, N.C.; et al. Vast assembly of vocal marine mammals from diverse species on fish spawning ground. Nature 2016, 531, 366–370. [Google Scholar] [CrossRef] [PubMed]
- Koblitz, J.C.; Stilz, P.; Schnitzler, H.U. Source levels of echolocation signals vary in correlation with wingbeat cycle in landing big brown bats (Eptesicus fuscus). J. Exp. Biol. 2010, 213, 3263–3268. [Google Scholar] [CrossRef] [PubMed]
- Tjotta, J.N.; Tjotta, S. Interaction of sound waves. Part II: Plane wave and real beam. J. Acoust. Soc. Am. 1987, 82, 1429–1435. [Google Scholar] [CrossRef]
- Tjotta, J.N.; Tjotta, S. Interaction of sound waves. Part III: Two real beams. J. Acoust. Soc. Am. 1988, 83, 487–495. [Google Scholar] [CrossRef]
- Jarle Berntsen, J.N.T.; Tjotta, S. Interaction of sound waves. Part IV: Scattering of sound by sound. J. Acoust. Soc. Am. 1989, 86, 1968–1983. [Google Scholar] [CrossRef]
- Makris, N.C.; Ratilal, P.; Thierman, J. Coherent nonlinear scattering mechanisms for ultrasound-stimulated vibro-acoustic spectrography. J. Acoust. Soc. Am. 2002, 112, 2405. [Google Scholar] [CrossRef]
- Thierman, J. Sources of Difference Frequency Sound in a Dual-Frequency Imaging System with Implications for monitoring Thermal Surgery. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2004. [Google Scholar]
- Silva, G.T.; Chen, S.; Greenleaf, J.F.; Fatemi, M. Dynamic ultrasound radiation force in fluids. Phys. Rev. E 2005, 71, 056617. [Google Scholar] [CrossRef] [PubMed]
- Mitri, F.G.; Chen, S. Theory of dynamic acoustic radiation force experienced by solid cylinders. Phys. Rev. E 2005, 71, 016306. [Google Scholar] [CrossRef] [PubMed]
- Silva, G.T.; Chen, S.; Viana, L.P. Parametric Amplification of the Dynamic Radiation Force of Acoustic Waves in Fluids. Phys. Rev. Lett. 2006, 96, 234301. [Google Scholar] [CrossRef] [PubMed]
- Silva, G.T.; Bandeira, A. Difference-frequency generation in nonlinear scattering of acoustic waves by a rigid sphere. Ultrasonics 2013, 53, 470–478. [Google Scholar] [CrossRef] [PubMed]
- Plekanov, G.; Soluyan, S. Emission of harmonic and combination frequency waves by air bubbles. Sov. Phys. Acoust. 1971, 18, 396–398. [Google Scholar]
- Keller, J.B.; Miksis, M. Bubble oscillations of large amplitude. J. Acoust. Soc. Am. 1980, 68, 628–633. [Google Scholar] [CrossRef]
- Kluzek, Z.; Soustova, I.; Sutin, A. Nonlinear incoherent scattering of acoustic waves by a bubble layer. Acoust. Phys. 1996, 42, 568–575. [Google Scholar]
- Ostrovsky, L.A.; Sutin, A.M.; Soustova, I.A.; Matveyev, A.L.; Potapov, A.I.; Kluzek, Z. Nonlinear scattering of acoustic waves by natural and artificially generated subsurface bubble layers in sea. J. Acoust. Soc. Am. 2003, 113, 741–749. [Google Scholar] [CrossRef] [PubMed]
- King, L. On the acoustic radiation pressure on spheres. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1934, 147, 212. [Google Scholar] [CrossRef]
- Newman, J. Marine Hydrodynamics; The MIT Press: Cambridge, MA, USA, 1977. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).