Spatial Disaggregation of Latent Heat Flux Using Contextual Models over India
Abstract
:1. Introduction
- Disaggregate satellite estimated EF and Rg from 1000 m into 250 m and subsequently convert the disaggregated EF and Rg into daytime integrated latent heat flux (λEday) at 250 m resolution; and
2. Study Sites and Datasets
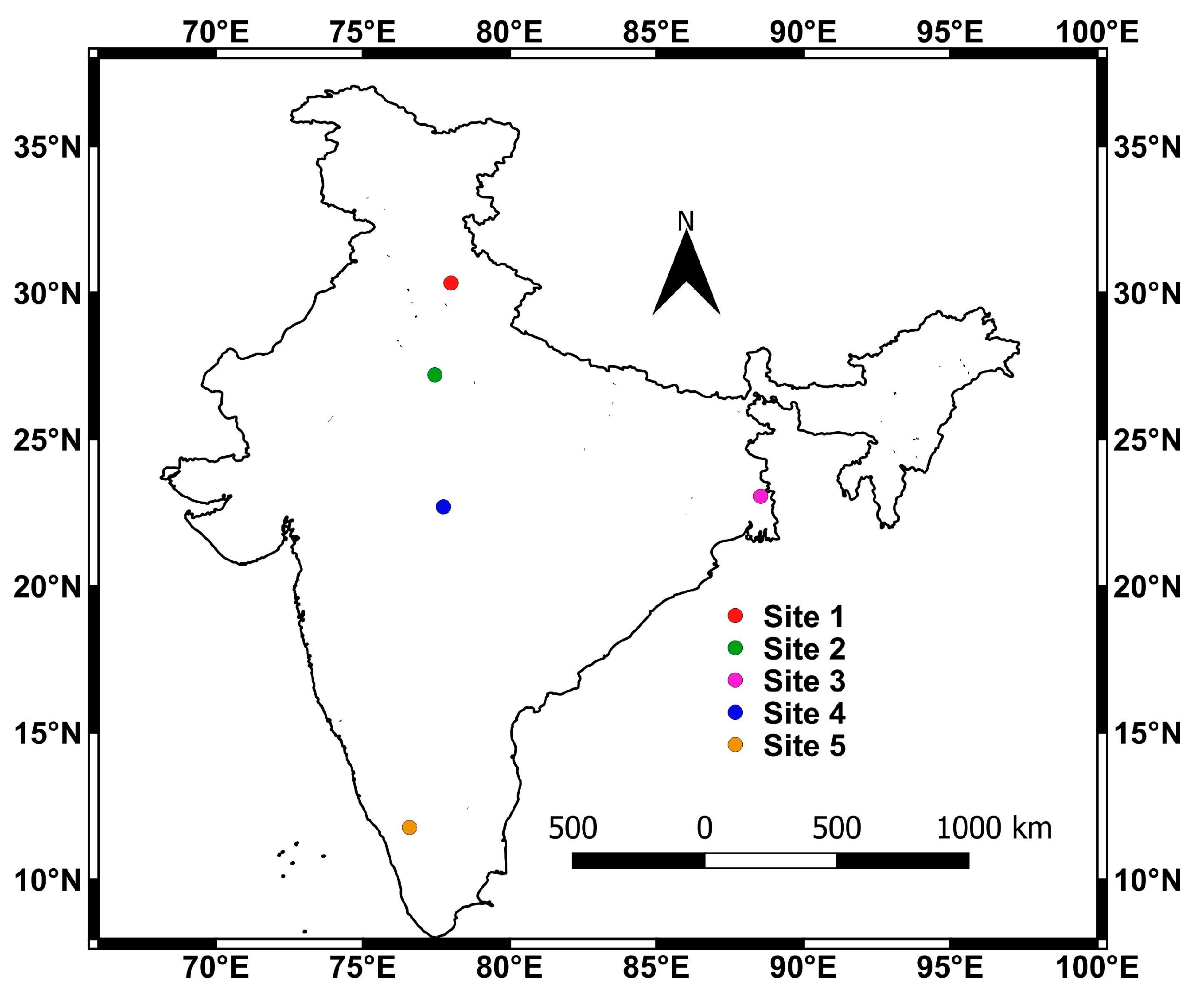
2.1. Study Sites and In Situ Data
2.2. Satellite Data
3. Methodology
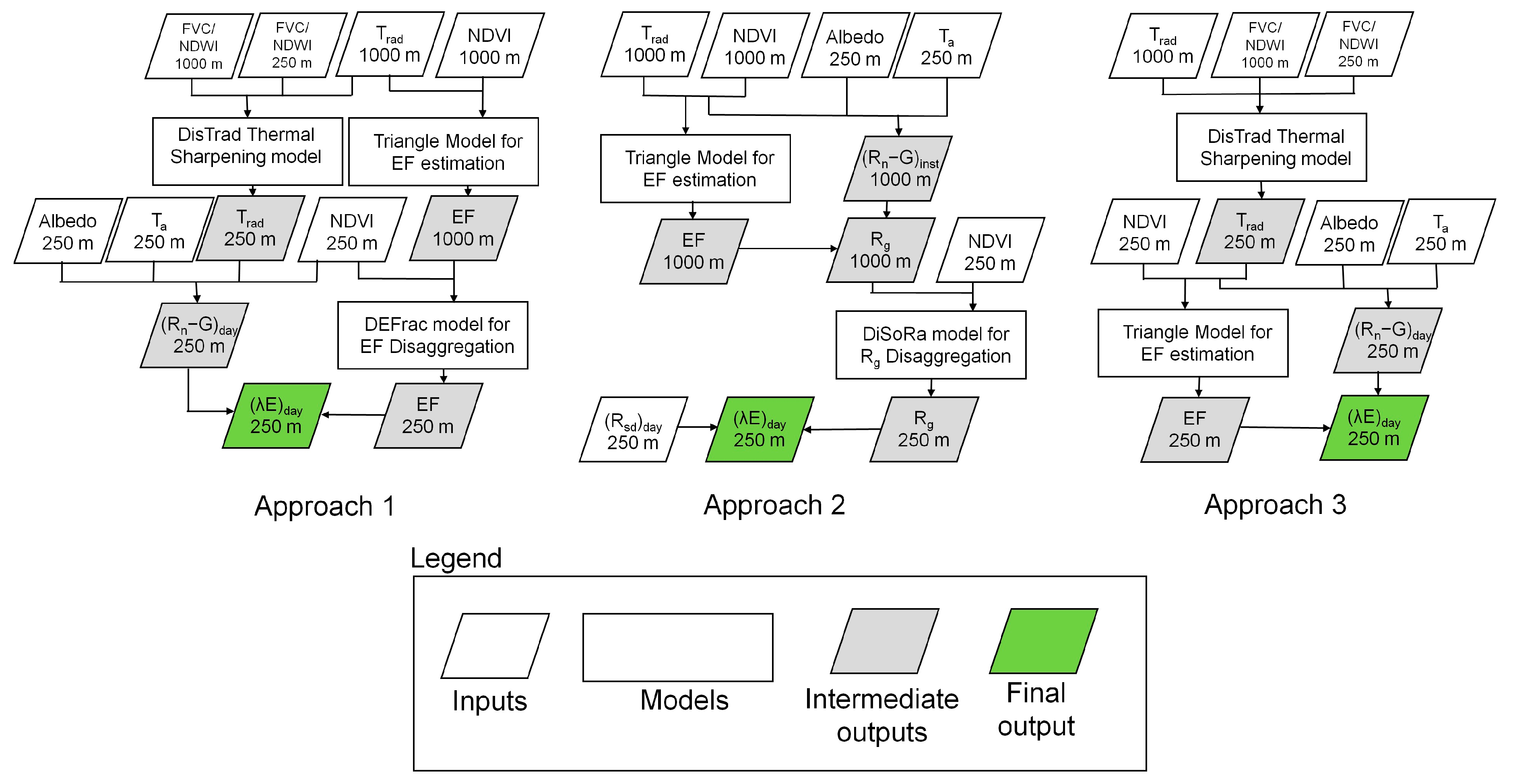
3.1. Brief Overview of the Disaggregation Approaches
3.2. Estimation of EF and Rg from Satellite Data
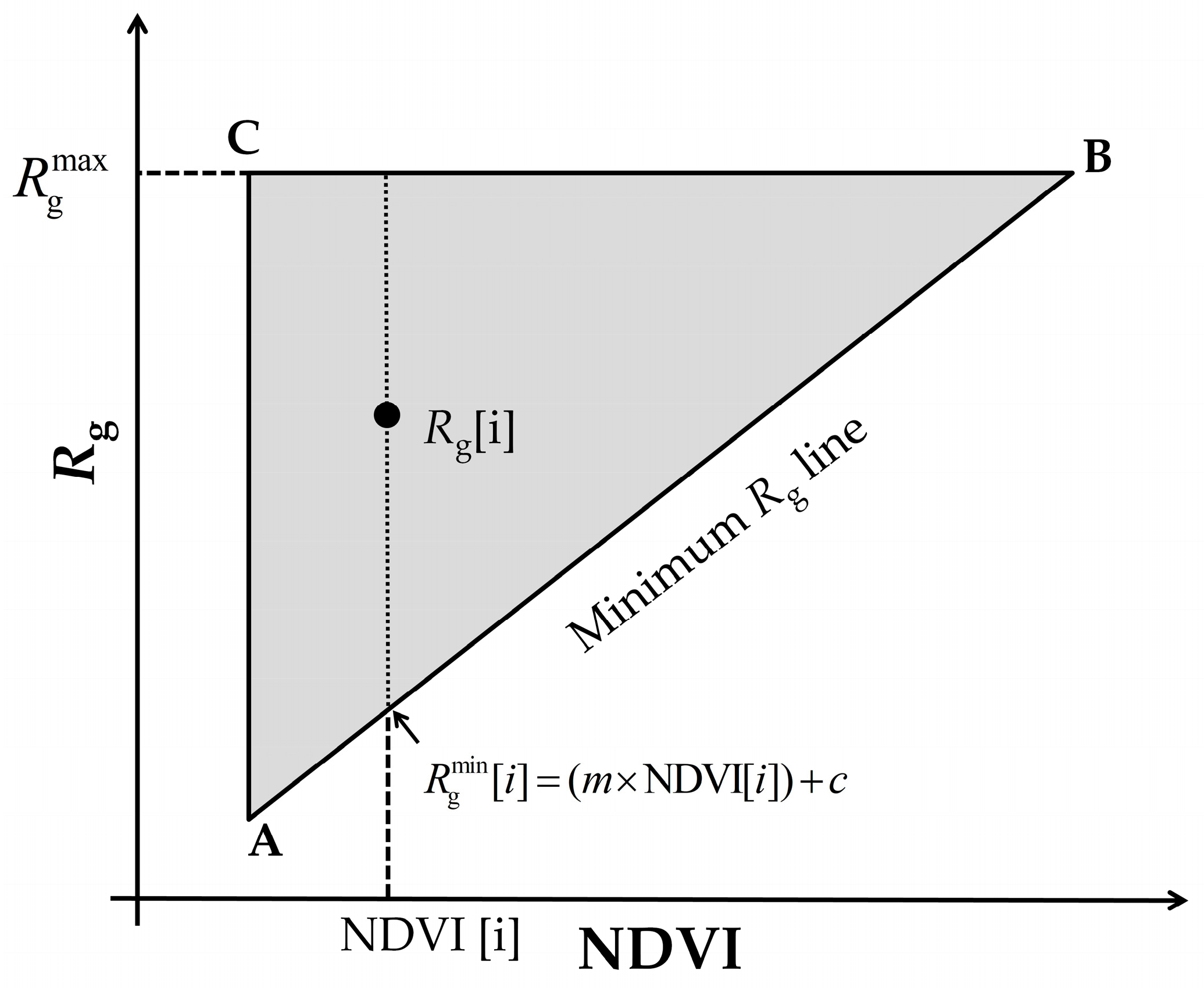
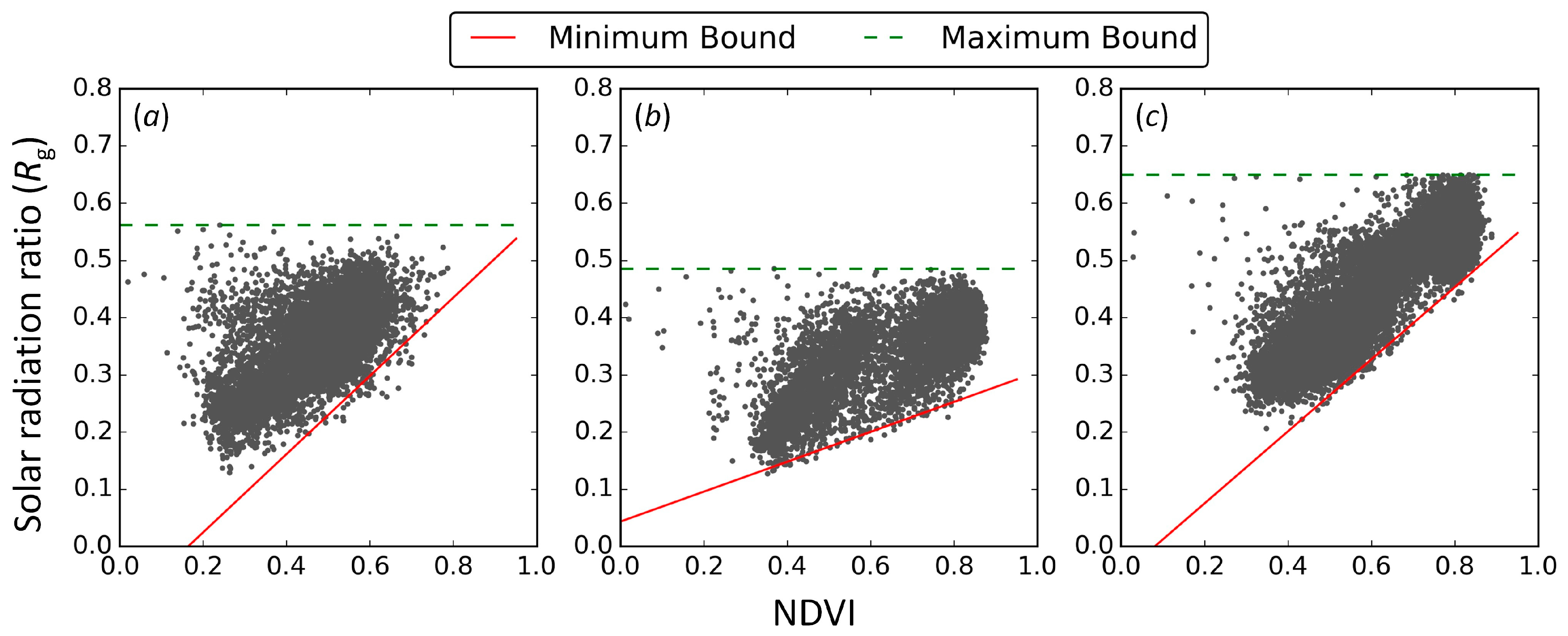
3.3. Disaggregation of Rg and EF
3.4. Disaggregation of TRad
3.5. Estimation of λEday at 250 m Resolution
3.6. In Situ Data Processing
4. Results and Discussion
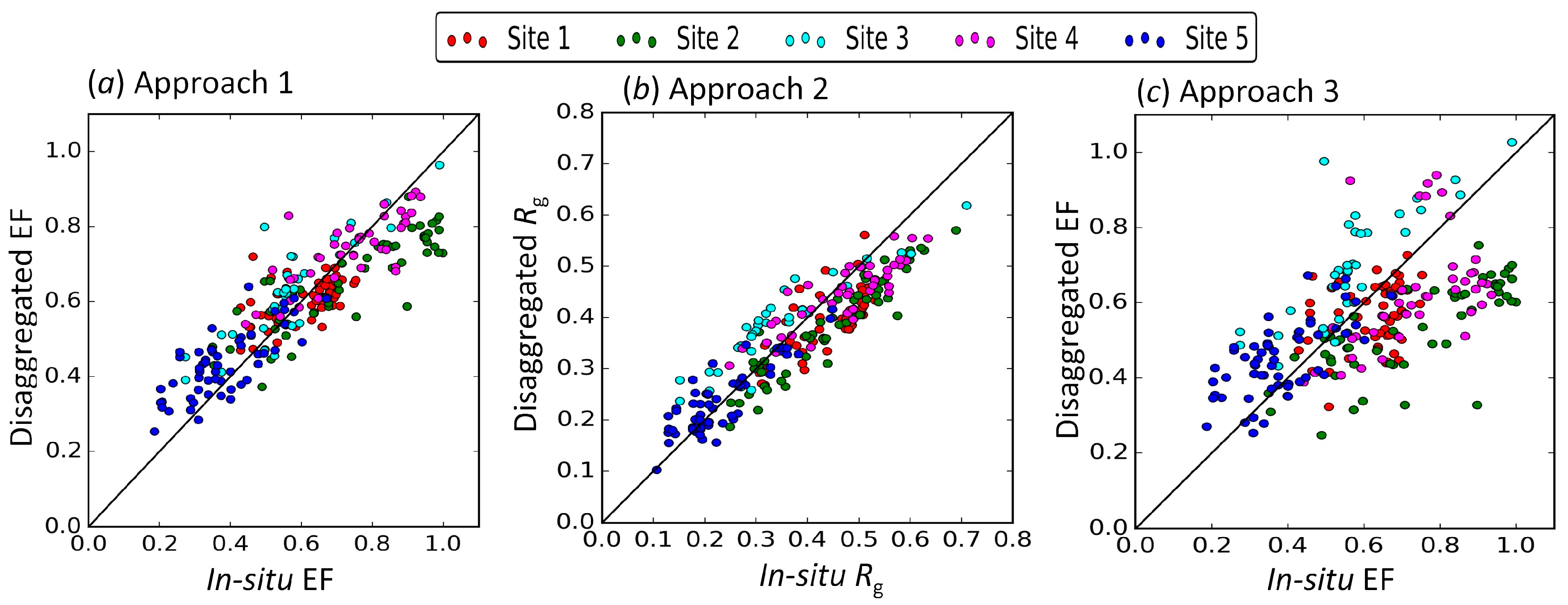
4.1. Validation of Disaggregated EF and Rg at 250 m
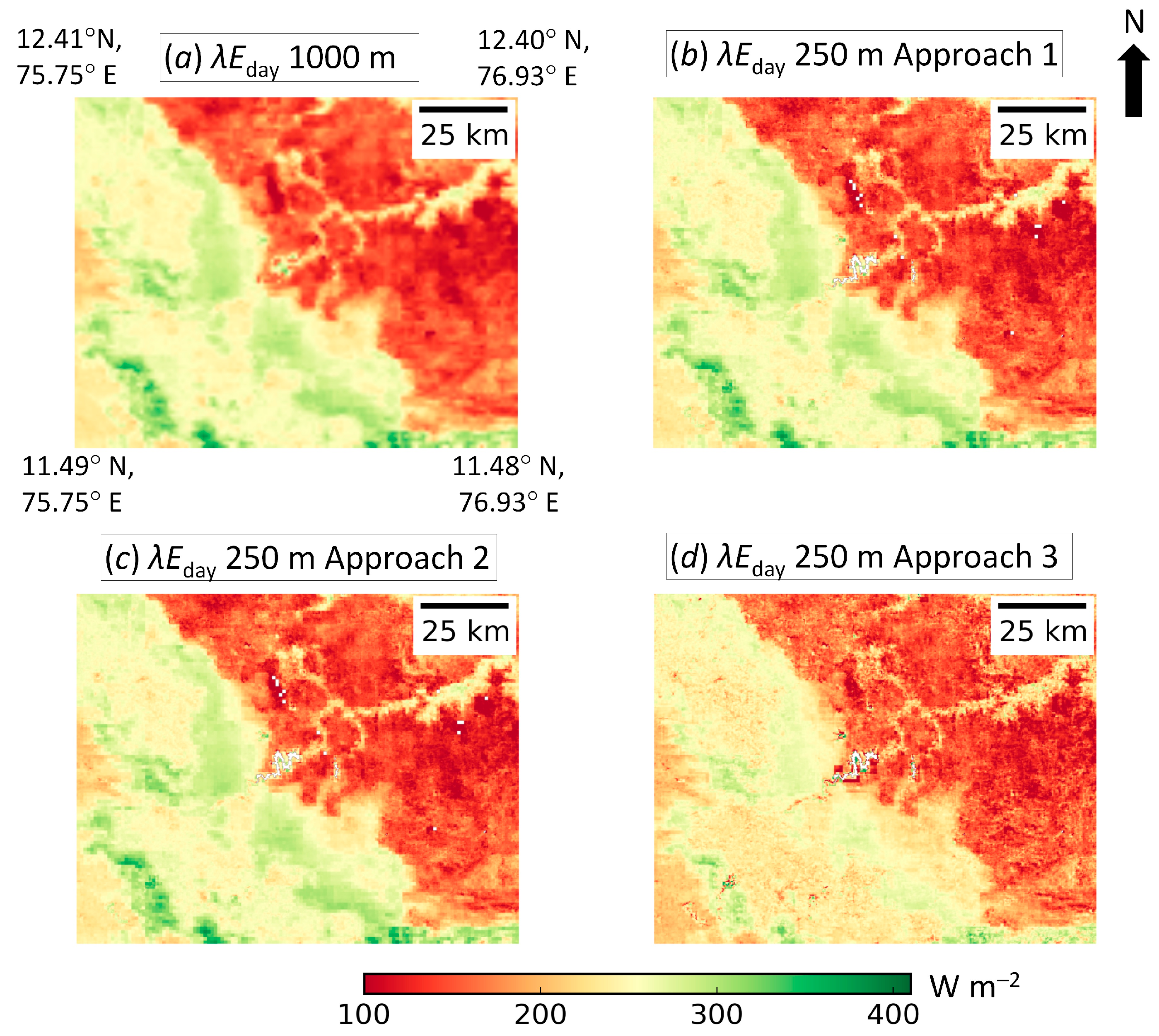
4.2. Validation of Disaggregated λEday at 250 m
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bastiaanssen, W.G.M.; Menenti, M.; Feddes, R.A.; Holstlag, A.A.M. A remote sensing surface energy balance algorithm for land (SEBAL). 1: Formulation. J. Hydrol. 1998, 213, 198–212. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Trezza, R. Satellite-Based Energy Balance for Mapping Evapotranspiration with Internalized Calibration (METRIC)—Model. J. Irrig. Drain. Eng. 2007, 133, 380–394. [Google Scholar] [CrossRef]
- Allen, R.G.; Morse, A.; Tasumi, M.; Trezza, R.; Bastiaanssen, W.; Wright, J.L.; Kramer, W. Evapotranspiration from a Satellite-Based Surface Energy Balance for the Snake Plain Aquifer in Idaho. California Water Plan 2005, 4, 161–175. [Google Scholar]
- Anderson, M.C.; Allen, R.G.; Morse, A.; Kustas, W.P. Use of Landsat thermal imagery in monitoring evapotranspiration and managing water resources. Remote Sens. Environ. 2012, 122, 50–65. [Google Scholar] [CrossRef]
- Kustas, W.P.; Norman, J.M.; Anderson, M.C.; French, A.N. Estimating subpixel surface temperatures and energy fluxes from the vegetation index-radiometric temperature relationship. Remote Sens. Environ. 2003, 85, 429–440. [Google Scholar] [CrossRef]
- Agam, N.; Kustas, W.P.; Anderson, M.C.; Li, F.; Neale, C.M.U. A vegetation index based technique for spatial sharpening of thermal imagery. Remote Sens. Environ. 2007, 107, 545–558. [Google Scholar] [CrossRef]
- Agam, N.; Kustas, W.P.; Anderson, M.C.; Li, F.; Colaizzi, P.D. Utility of thermal image sharpening for monitoring field-scale evapotranspiration over rainfed and irrigated agricultural regions. Geophys. Res. Lett. 2008, 35, L02402. [Google Scholar] [CrossRef]
- Bindhu, V.M.; Narasimhan, B.; Sudheer, K.P. Development and verification of a non-linear disaggregation method (NL-DisTrad) to downscale MODIS land surface temperature to the spatial scale of Landsat thermal data to estimate evapotranspiration. Remote Sens. Environ. 2013, 135, 118–129. [Google Scholar] [CrossRef]
- Eswar, R.; Sekhar, M.; Bhattacharya, B.K. A simple model for spatial disaggregation of evaporative fraction: Comparative study with thermal sharpened land surface temperature data over India. J. Geophys. Res. Atmos. 2013, 118, 12,029–12,044. [Google Scholar] [CrossRef]
- Hong, S.H.; Hendrickx, J.M.H.; Borchers, B. Down-scaling of SEBAL derived evapotranspiration maps from MODIS (250 m) to Landsat (30 m) scales. Int. J. Remote Sens. 2011, 32, 6457–6477. [Google Scholar] [CrossRef]
- Mallick, K.; Bhattacharya, B.K.; Rao, V.; Reddy, D.R.; Banerjee, S.; Venkatesh, H.; Pandey, V.; Kar, G.; Mukherjee, J.; Vyas, S.P.; et al. Latent heat flux estimation in clear sky days over Indian agroecosystems using noon-time satellite remote sensing data. Agric. For. Meteorol. 2009, 149, 1646–1665. [Google Scholar] [CrossRef]
- Bhattacharya, B.K.; Mallick, K.; Patel, N.K.; Parihar, J.S. Regional clear sky evapotranspiration over agricultural land using remote sensing data from Indian geostationary meteorological satellite. J. Hydrol. 2010, 387, 65–80. [Google Scholar] [CrossRef]
- Eswar, R.; Sekhar, M.; Bhattacharya, B.K. Comparison of three remote sensing based models for the estimation of latent heat flux over India. Hydrol. Sci. 2017. accepted. [Google Scholar]
- Cammalleri, C.; Anderson, M.C.; Kustas, W.P. Upscaling of evapotranspiration fluxes from instantaneous to daytime scales for thermal remote sensing applications. Hydrol. Earth Syst. Sci. 2014, 18, 1885–1894. [Google Scholar] [CrossRef] [Green Version]
- Tang, R.; Li, Z.L.; Sun, X. Temporal upscaling of instantaneous evapotranspiration: An intercomparison of four methods using eddy covariance measurements and MODIS data. Remote Sens. Environ. 2013, 138, 102–118. [Google Scholar] [CrossRef]
- Van Niel, T.G.; McVicar, T.R.; Roderick, M.L.; van Dijk, A.I.J.M.; Beringer, J.; Hutley, L.B.; van Gorsel, E. Upscaling latent heat flux for thermal remote sensing studies: Comparison of alternative approaches and correction of bias. J. Hydrol. 2012, 468–469, 35–46. [Google Scholar] [CrossRef]
- Eswar, R.; Sekhar, M.; Bhattacharya, B.K. Disaggregation of LST over India: Comparative analysis of different vegetation indices. Int. J. Remote Sens. 2016, 37, 1035–1054. [Google Scholar] [CrossRef]
- Jiang, L.; Islam, S. A methodology for estimation of surface evapotranspiration over large areas using remote sensing observations. Geophys. Res. Lett. 1999, 26, 2773–2776. [Google Scholar] [CrossRef]
- Venturini, V.; Bisht, G.; Islam, S.; Jiang, L. Comparison of evaporative fractions estimated from AVHRR and MODIS sensors over South Florida. Remote Sens. Environ. 2004, 93, 77–86. [Google Scholar] [CrossRef]
- Batra, N.; Islam, S.; Venturini, V.; Bisht, G.; Jiang, L. Estimation and comparison of evapotranspiration from MODIS and AVHRR sensors for clear sky days over the Southern Great Plains. Remote Sens. Environ. 2006, 103, 1–15. [Google Scholar] [CrossRef]
- Tang, R.; Li, Z.L.; Tang, B. An application of the Ts–VI triangle method with enhanced edges determination for evapotranspiration estimation from MODIS data in arid and semi-arid regions: Implementation and validation. Remote Sens. Environ. 2010, 114, 540–551. [Google Scholar] [CrossRef]
- Tang, R.; Li, Z.L.; Chen, K.S. Validating MODIS—Derived land surface evapotranspiration with in situ measurements at two AmeriFlux sites in a semiarid region. J. Geophys. Res. Atmos. 2011, 116, D04106. [Google Scholar] [CrossRef]
- Laxmi, K.; Nandagiri, L. Latent heat flux estimation using trapezoidal relationship between MODIS land surface temperature and fraction of vegetation–application and validation in a humid tropical region. Remote Sens. Lett. 2014, 5, 981–990. [Google Scholar] [CrossRef]
- Martínez Pérez, J.Á.; García-Galiano, S.G.; Martin-Gorriz, B.; Baille, A. Satellite-Based Method for Estimating the Spatial Distribution of Crop Evapotranspiration: Sensitivity to the Priestley-Taylor Coefficient. Remote Sens. 2017, 9, 611. [Google Scholar] [CrossRef]
- Petropoulos, G.; Carlson, T.N.; Wooster, M.J.; Islam, S. A review of Ts/VI remote sensing based methods for the retrieval of land surface energy fluxes and soil surface moisture. Prog. Phys. Geogr. 2009, 33, 224–250. [Google Scholar] [CrossRef]
- Liang, S. Narrowband to broadband conversions of land surface albedo: I. Algorithms. Remote Sens. Environ. 2000, 76, 213–238. [Google Scholar] [CrossRef]
- Jin, M.; Liang, S. An Improved Land Surface Emissivity Parameter for Land Surface Models Using Global Remote Sensing Observations. J. Clim. 2006, 19, 2867–2881. [Google Scholar] [CrossRef]
- Campbell, G.S.; Norman, J.M. An Introduction to Environmental Biophysics, 2nd ed.; Springer: New York, NY, USA, 1998; p. 164. [Google Scholar]
- Bisht, G.; Venturini, V.; Islam, S.; Jiang, L. Estimation of net radiation using MODIS (Moderate Resolution Imaging Spectroradiometer) data for clear sky days. Remote Sens. Environ. 2005, 97, 52–67. [Google Scholar] [CrossRef]
- Valor, E.; Caselles, V. Mapping land surface emissivity from NDVI: application to European, African and South American areas. Remote Sens. Environ. 1996, 57, 167–184. [Google Scholar] [CrossRef]
- Perez, P.J.; Castellvi, F.; Ibanez, M.; Rosell, J.I. Assessment of reliability of Bowen ratio method for partitioning fluxes. Agric. For. Meteorol. 1999, 97, 141–150. [Google Scholar] [CrossRef]
| Variables | Data Source with Available Resolution | Method Adopted to Get the Variable at 250 m Resolution |
|---|---|---|
| Solar zenith angle (θ) | Available from MODIS 7-band surface reflectance product at 1000 m resolution. | Assumed the same value for all the 250 m pixels within a single 1000 m pixel. |
| Surface albedo (α) | Estimated from MODIS 7-band surface reflectance product at 500 m resolution [28]. | Bilinear interpolation to 250 m |
| NDVI | Estimated from MODIS 7-band/2-band surface reflectance product at 500 m and 250 m, respectively. | Available from MODIS at 250 m |
| Surface emissivity (εs) | Available at 1000 m resolution from MODIS LST product. But not used for disaggregation | Estimated using NDVI at 250 m following [30] |
| Air temperature (Ta) | Available at 5000 m resolution from MODIS atmospheric profile product. | Assumed the same value for all the 250 m pixels within a single 5000 m pixel. |
| TRad | Available at 1000 m resolution from MODIS LST product. | Disaggregated to 250 m using the DisTrad thermal sharpening model [17] |
| Satellite overpass time (tpass) | Available at 1000 m resolution from MODIS LST product. | Assumed the same value for all the 250 m pixels within a single 1000 m pixel. |
| Site | RMSE | ||||
|---|---|---|---|---|---|
| EF 1000 m | EF 250 m DEFrac | EF 250 m DisTrad | Rg 1000 m | Rg 250 m DiSoRa | |
| Site 1 | 0.08 | 0.08 | 0.11 | 0.08 | 0.07 |
| Site 2 | 0.14 | 0.13 | 0.24 | 0.08 | 0.07 |
| Site 3 | 0.09 | 0.09 | 0.16 | 0.07 | 0.07 |
| Site 4 | 0.08 | 0.08 | 0.18 | 0.05 | 0.05 |
| Site 5 | 0.09 | 0.09 | 0.11 | 0.04 | 0.04 |
| Site | RMSE for λEday 1000 m (W m−2) | RMSE for λEday at 250 m (W m−2) | ||
|---|---|---|---|---|
| Approach 1 | Approach 2 | Approach 3 | ||
| Site 1 | 33 | 31 | 31 | 40 |
| Site 2 | 39 | 38 | 36 | 62 |
| Site 3 | 44 | 40 | 40 | 58 |
| Site 4 | 30 | 27 | 25 | 47 |
| Site 5 | 25 | 25 | 25 | 31 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eswar, R.; Sekhar, M.; Bhattacharya, B.K.; Bandyopadhyay, S. Spatial Disaggregation of Latent Heat Flux Using Contextual Models over India. Remote Sens. 2017, 9, 949. https://doi.org/10.3390/rs9090949
Eswar R, Sekhar M, Bhattacharya BK, Bandyopadhyay S. Spatial Disaggregation of Latent Heat Flux Using Contextual Models over India. Remote Sensing. 2017; 9(9):949. https://doi.org/10.3390/rs9090949
Chicago/Turabian StyleEswar, Rajasekaran, Muddu Sekhar, Bimal K. Bhattacharya, and Soumya Bandyopadhyay. 2017. "Spatial Disaggregation of Latent Heat Flux Using Contextual Models over India" Remote Sensing 9, no. 9: 949. https://doi.org/10.3390/rs9090949
APA StyleEswar, R., Sekhar, M., Bhattacharya, B. K., & Bandyopadhyay, S. (2017). Spatial Disaggregation of Latent Heat Flux Using Contextual Models over India. Remote Sensing, 9(9), 949. https://doi.org/10.3390/rs9090949





