SCOPE-Based Emulators for Fast Generation of Synthetic Canopy Reflectance and Sun-Induced Fluorescence Spectra
Abstract
:1. Introduction
2. Emulation Theory
2.1. Machine Learning Regression Algorithms (MLRAs)
2.2. Dimensionality Reduction Algorithms
3. ARTMO Modules: Emulator Toolbox, SCOPE and A-SGM
3.1. SCOPE
3.2. Automated Scene Generator Module (A-SGM)
4. Experimental Setup
- The selected MLRAs are first analyzed for the default training LUT of 500 samples and using 20 PCA for emulating R spectra and 5 PCA for emulating SIF spectra.
- For the best-performing MLRA, the roles of PCA and PLS are analyzed.
- For the best-performing MLRA and DR method, the following number of components are evaluated: 10, 20, 30 and 40 components for R spectra, and 2 up to 10 components for SIF spectra.
- Additionally, the role of LUT size is analyzed for the best-performing emulator. A new LUT of 1000 samples according to LHS has been generated and evaluated.
4.1. Emulation Validation
4.2. Scene Definition
5. Results
5.1. SCOPE Reflectance (R) Spectra
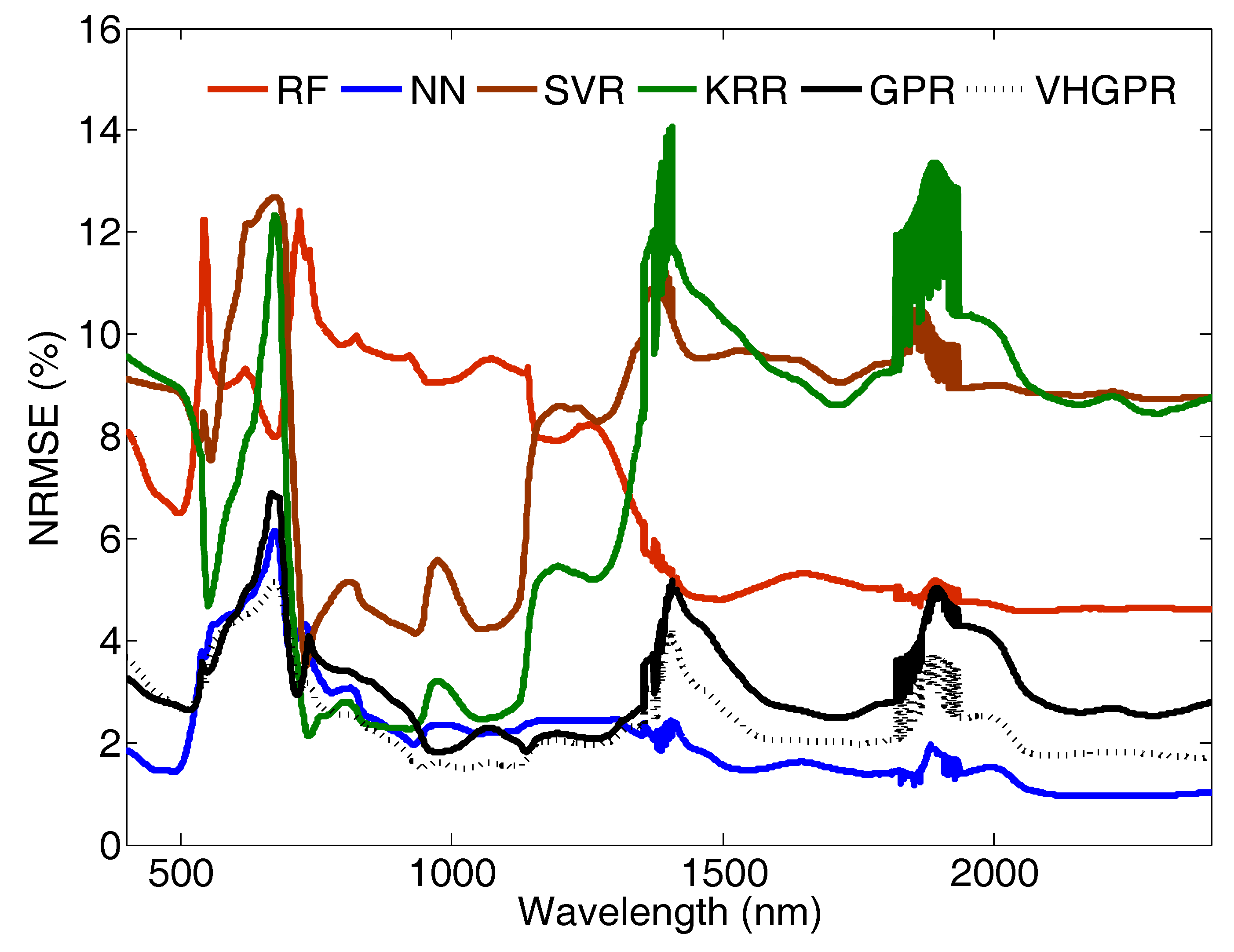
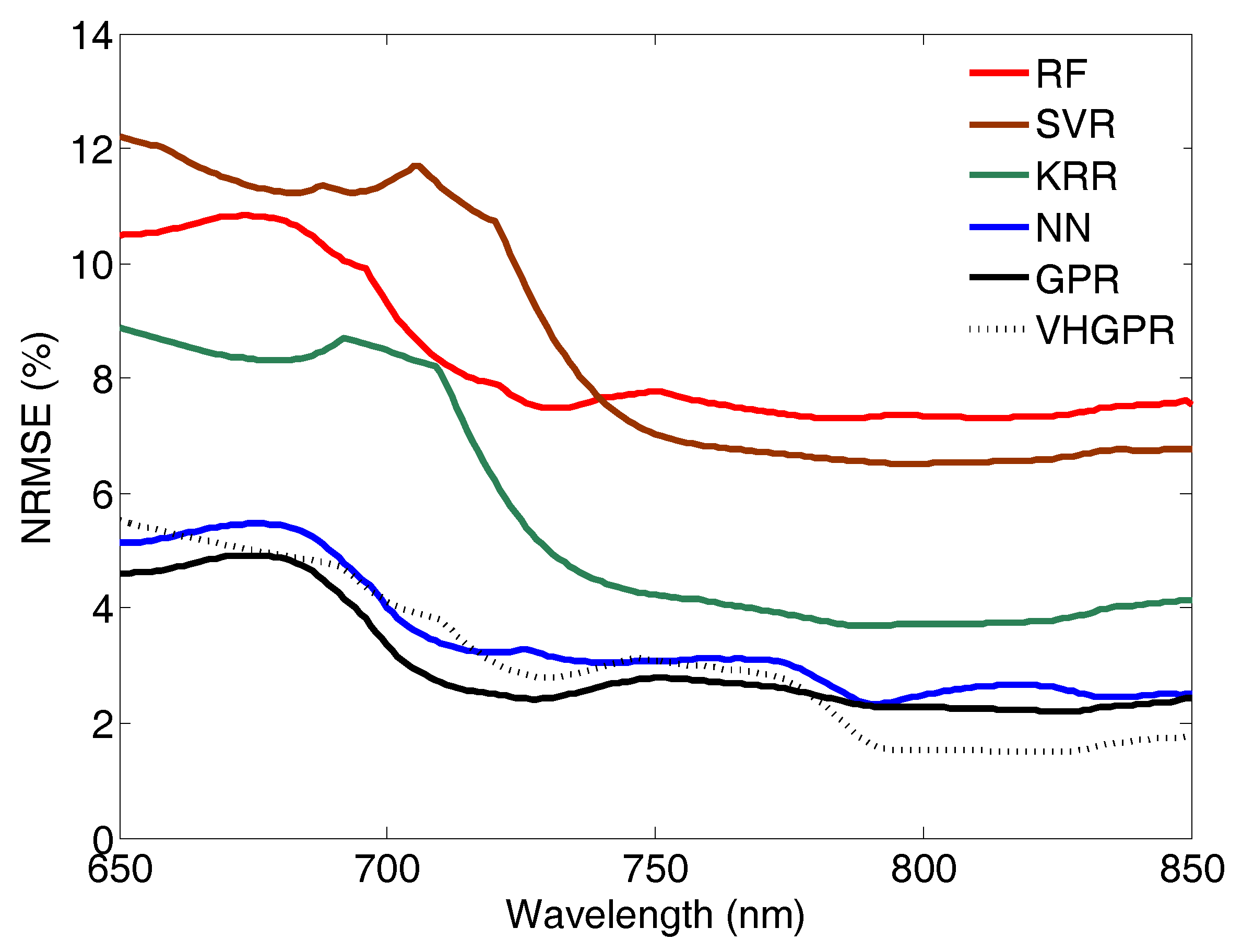
5.1.1. On the Role of Used MLRA
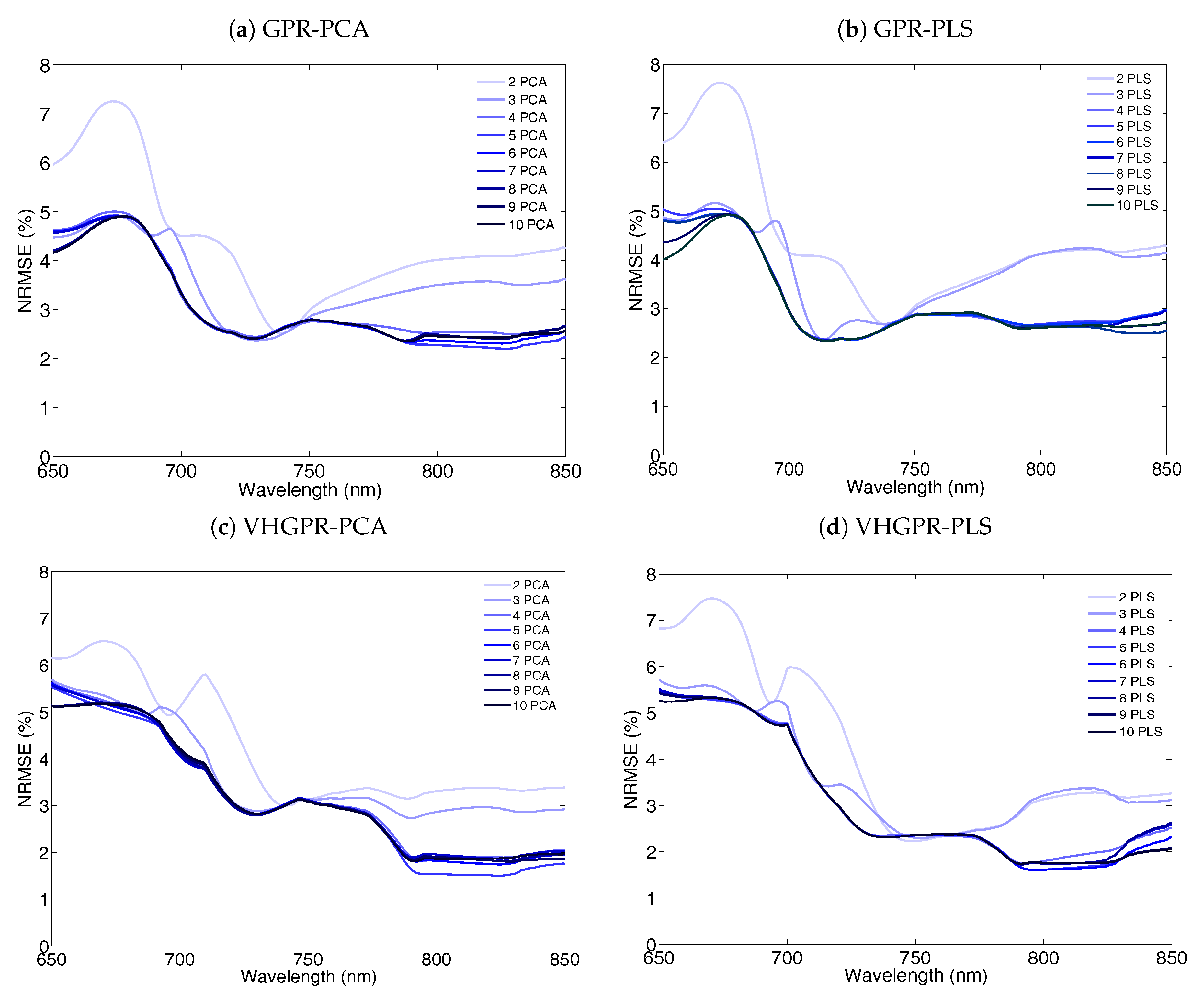
5.1.2. On the Role of Dimensionality Reduction (DR) Methods
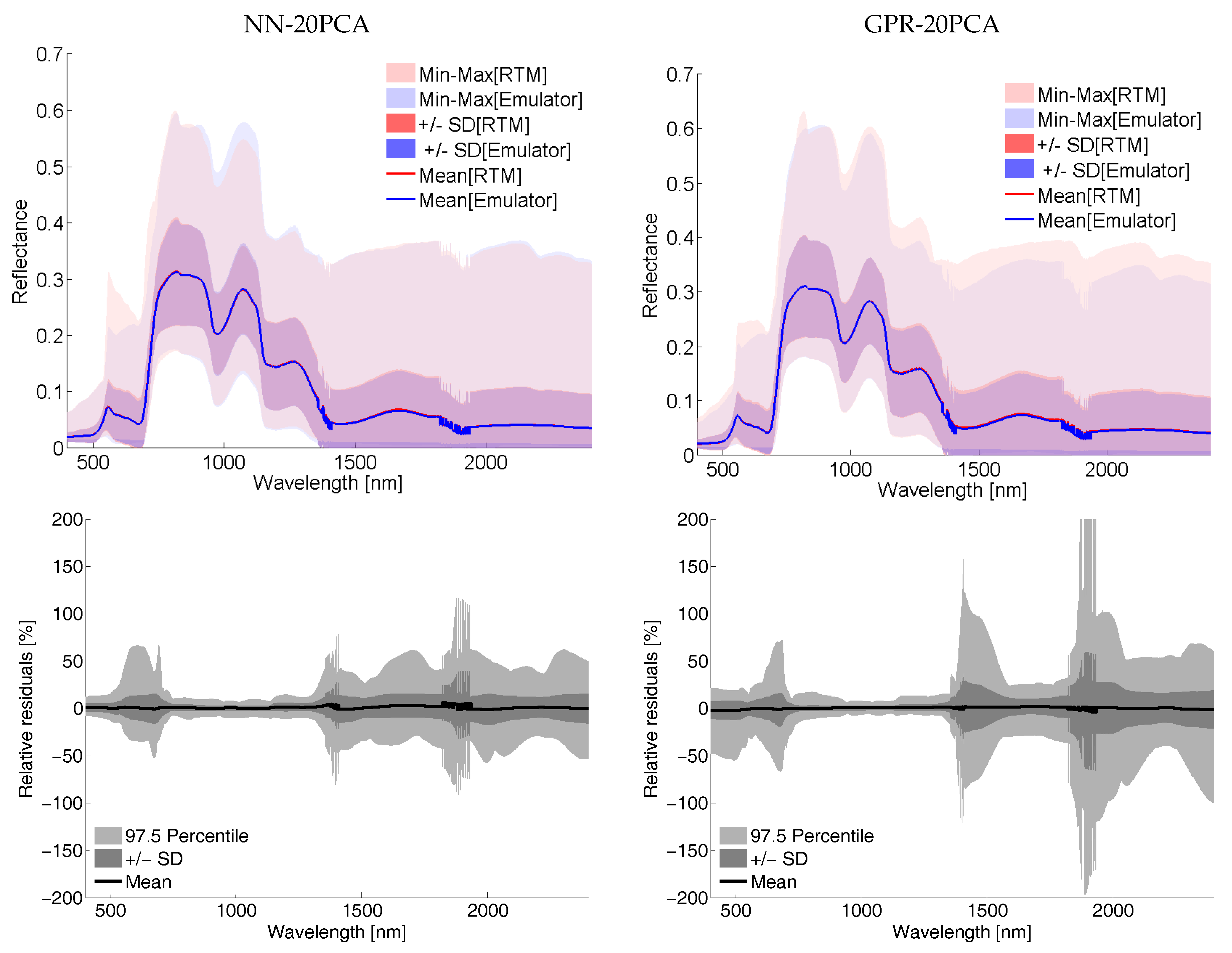
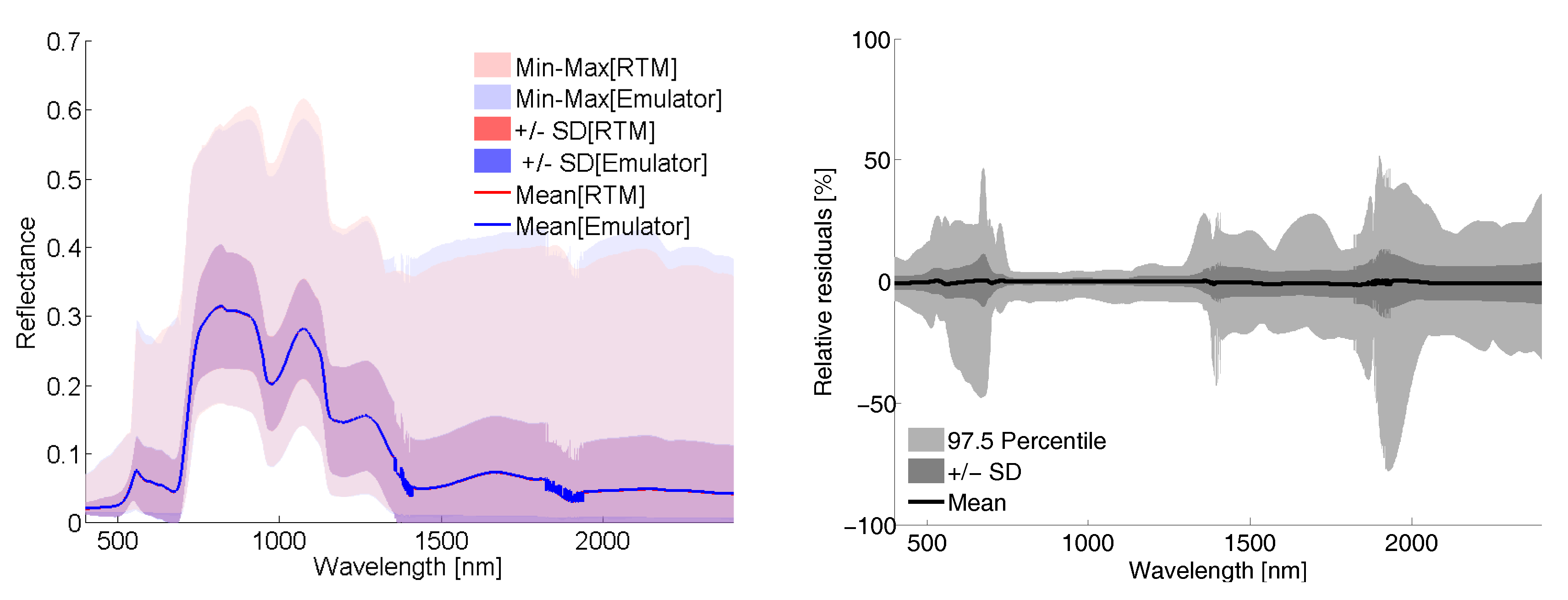
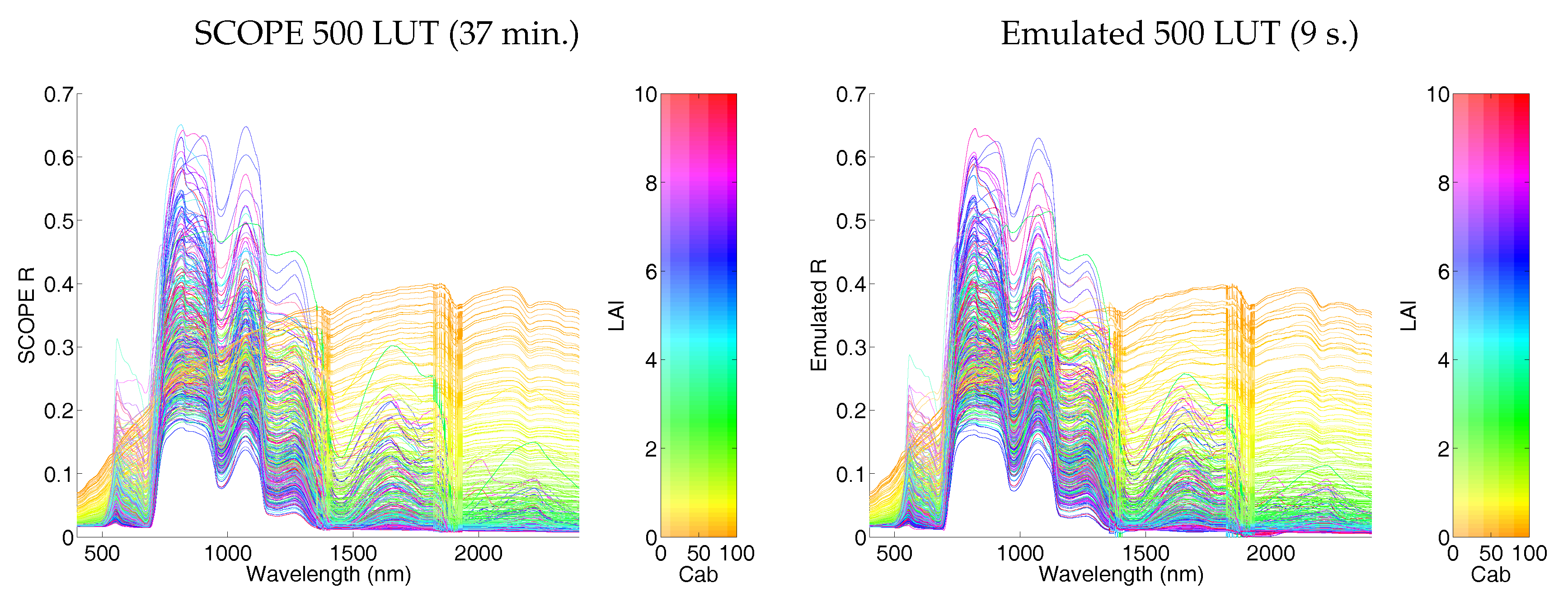
5.1.3. On the Role of LUT Size and Visualizing 500 LUT Emulator R Spectra
5.2. SCOPE Sun-Induced Fluorescence (SIF) Output
On the Role of Used MLRA
5.3. On the Role of Dimensionality Reduction (DR) Methods
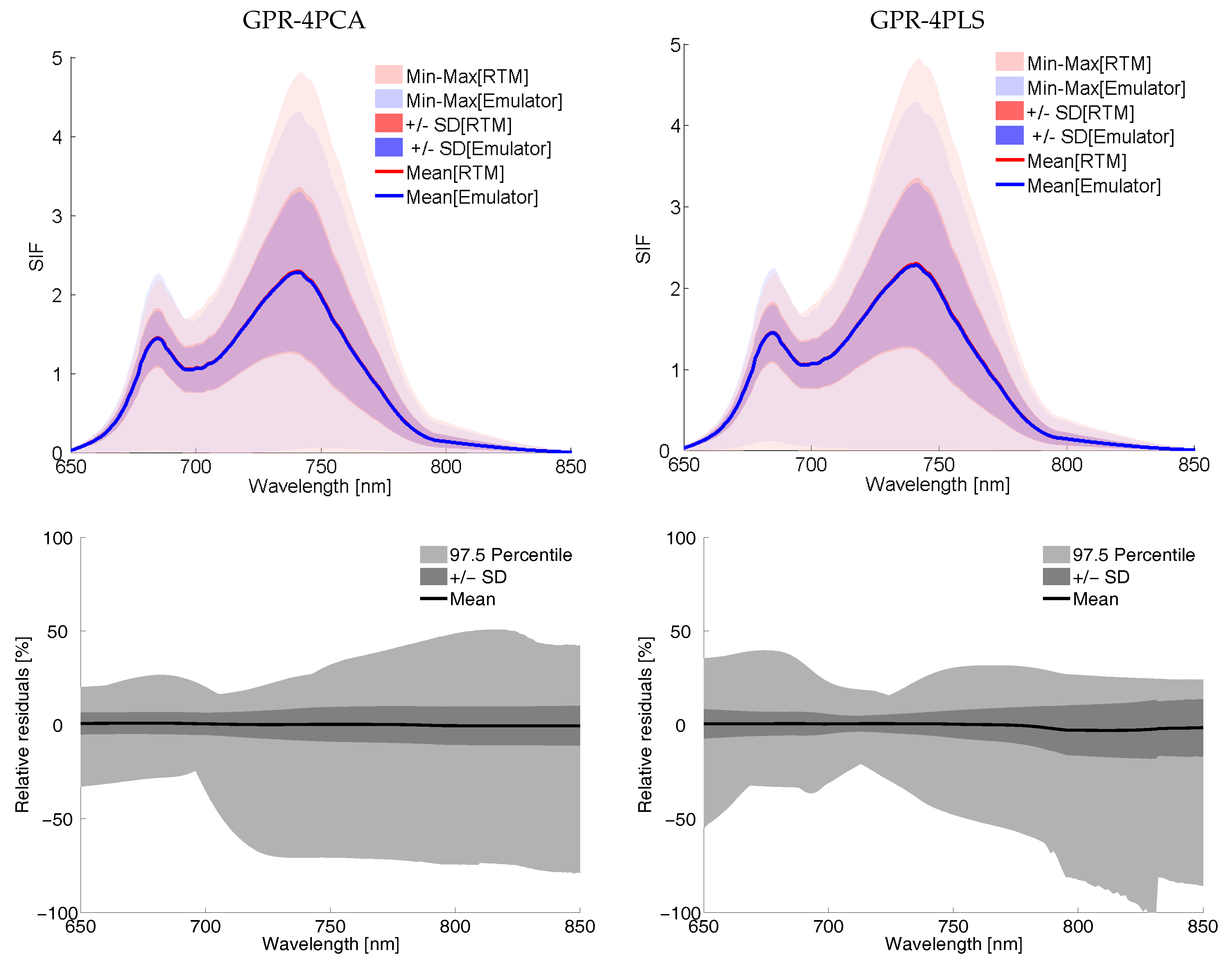
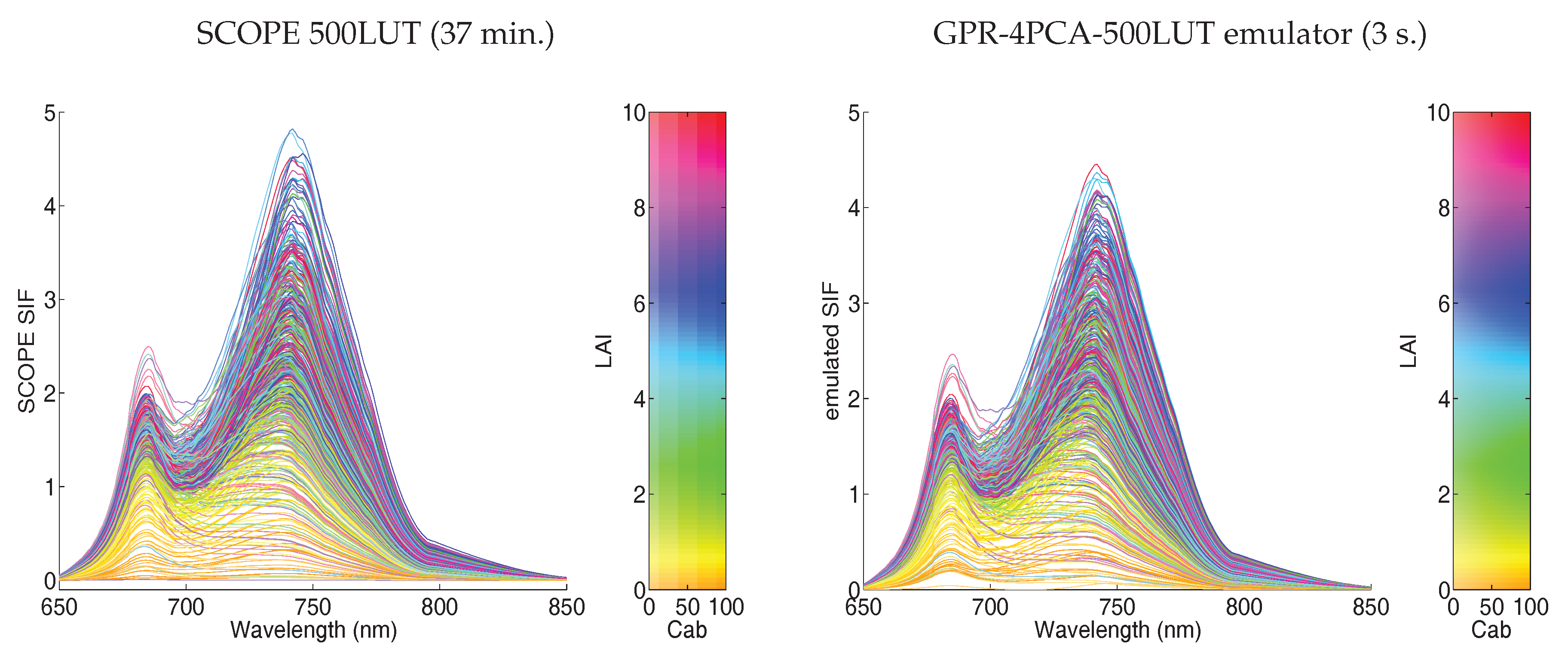
Visualizing 500 LUT Emulator SIF Spectra
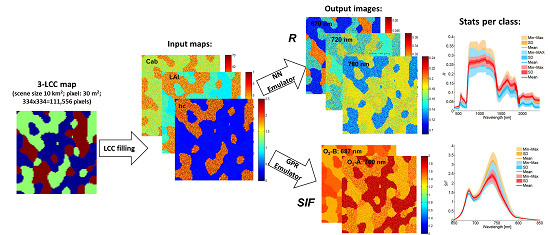
5.4. Scene Generation
6. Discussion
6.1. Interpreting Emulator Results
6.2. Opportunities for Fast Scene Generation
6.3. New Processing Opportunities with Emulators
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| Broadband Incoming Shortwave Radiation (0.4–2.5 m) [W m] | 600 |
|---|---|
| air temperature [T] | 20 |
| air pressure [hPa] | 970 |
| atmospheric vapour pressure [hPa] | 15 |
| wind speed at height z [m s] | 2 |
| atmospheric CO concentration [ppm] | 380 |
| atmospheric O concentration [per mille] | 209 |
| carotenoid content [g cm] | 20 |
| leaf width [m] | 0.1 |
| soil boundary layer resistance [s m] | 10 |
| within canopy layer resistance [s m] | 0 |
| leaf boundary resistance [s m] | 10 |
| observation zenith angle [] | 0 |
| solar zenith angle [] | 30 |
| azimuthal difference between solar and observation angle [] | 0 |
| soil resistance for evaporation from the pore space [s m] | 500 |
| spectrum number (column in the database soil file) [] | 1 |
| maximum carboxylation capacity (at optimum temperature) [mol m s] | 30 |
| Ball-Berry stomatal conductance parameter [] | 8 |
| extinction coefficient for Vcmax in the vertical (maximum at the top). 0 for uniform Vcmax [] | 0.6396 |
| Respiration = Rdparam*Vcmcax [] | 0.0150 |
| fluorescence model | Collatz-TB12 |
| measurement height of meteorological data-[m] | 10 |
| broadband thermal transmittance | 0.01 |
| photochemical pathway | C3 |
| fluorescence quantum yield efficiency at photosystem level | 0.02 |
| broadband soil reflectance in the thermal range (1-emissivity) | 0.06 |
| leaf drag coefficient | 0.3 |
| leaf inclination distribution | spherical |
References
- Schaepman, M.E.; Ustin, S.L.; Plaza, A.J.; Painter, T.H.; Verrelst, J.; Liang, S. Earth system science related imaging spectroscopy—An assessment. Remote Sens. Environ. 2009, 113, S123–S137. [Google Scholar] [CrossRef]
- Li, L.; Zhang, Q.; Huang, D. A review of imaging techniques for plant phenotyping. Sensors 2014, 14, 20078–20111. [Google Scholar] [CrossRef] [PubMed]
- Asner, G.; Martin, R. Spectranomics: Emerging science and conservation opportunities at the interface of biodiversity and remote sensing. Glob. Ecol. Conserv. 2016, 8, 212–219. [Google Scholar] [CrossRef]
- Rossini, M.; Meroni, M.; Migliavacca, M.; Manca, G.; Cogliati, S.; Busetto, L.; Picchi, V.; Cescatti, A.; Seufert, G.; Colombo, R. High resolution field spectroscopy measurements for estimating gross ecosystem production in a rice field. Agric. For. Meteorol. 2010, 150, 1283–1296. [Google Scholar] [CrossRef]
- Daumard, F.; Champagne, S.; Fournier, A.; Goulas, Y.; Ounis, A.; Hanocq, J.F.; Moya, I. A field platform for continuous measurement of canopy fluorescence. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3358–3368. [Google Scholar] [CrossRef]
- Rascher, U.; Alonso, L.; Burkart, A.; Cilia, C.; Cogliati, S.; Colombo, R.; Damm, A.; Drusch, M.; Guanter, L.; Hanus, J.; et al. Sun-induced fluorescence—A new probe of photosynthesis: First maps from the imaging spectrometer HyPlant. Glob. Chang. Biol. 2015, 21, 4673–4684. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Drusch, M.; Moreno, J.; Del Bello, U.; Franco, R.; Goulas, Y.; Huth, A.; Kraft, S.; Middleton, E.M.; Miglietta, F.; Mohammed, G.; et al. The FLuorescence EXplorer mission concept-ESA’s Earth Explorer 8. IEEE Trans. Geosci. Remote Sens. 2016, 55, 1273–1284. [Google Scholar] [CrossRef]
- Ball, J.T.; Woodrow, I.E.; Berry, J.A. A Model Predicting Stomatal Conductance and Its Contribution to the Control of Photosynthesis under Different Environmental Conditions; Springer: Dordrecht, The Netherlands, 1987; pp. 221–224. [Google Scholar]
- Collatz, G.J.; Ball, J.T.; Grivet, C.; Berry, J.A. Physiological and environmental regulation of stomatal conductance, photosynthesis and transpiration: A model that includes a laminar boundary layer. Agric. For. Meteorol. 1991, 54, 107–136. [Google Scholar] [CrossRef]
- Collatz, G.J.; Ribas-Carbo, M.; Berry, J. Coupled photosynthesis-stomatal conductance model for leaves of C4 plants. Funct. Plant Biol. 1992, 19, 519–538. [Google Scholar]
- Gausman, H.; Allen, W.; Cardenas, R.; Richardson, A. Relation of light reflectance to histological and physical evaluations of cotton leaf maturity. Appl. Opt. 1970, 9, 545–552. [Google Scholar] [CrossRef] [PubMed]
- Jacquemoud, S.; Baret, F. PROSPECT: A model of leaf optical properties spectra. Remote Sens. Environ. 1990, 34, 75–91. [Google Scholar] [CrossRef]
- Berk, A.; Anderson, G.; Acharya, P.; Bernstein, L.; Muratov, L.; Lee, J.; Fox, M.; Adler-Golden, S.; Chetwynd, J.; Hoke, M.; et al. MODTRANTM5: 2006 Update. SPIE 2006, 6233. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.; Asner, G.; François, C.; Ustin, S. PROSPECT + SAIL models: A review of use for vegetation characterization. Remote Sens. Environ. 2009, 113, S56–S66. [Google Scholar] [CrossRef]
- Pedrós, R.; Goulas, Y.; Jacquemoud, S.; Louis, J.; Moya, I. FluorMODleaf: A new leaf fluorescence emission model based on the PROSPECT model. Remote Sens. Environ. 2010, 114, 155–167. [Google Scholar] [CrossRef]
- Vilfan, N.; van der Tol, C.; Muller, O.; Rascher, U.; Verhoef, W. Fluspect-B: A model for leaf fluorescence, reflectance and transmittance spectra. Remote Sens. Environ. 2016, 186, 596–615. [Google Scholar] [CrossRef]
- Van der Tol, C.; Berry, J.A.; Campbell, P.K.E.; Rascher, U. Models of fluorescence and photosynthesis for interpreting measurements of solar-induced chlorophyll fluorescence. J. Geophys. Res. Biogeosci. 2014, 119, 2312–2327. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gastellu-Etchegorry, J.; Lauret, N.; Yin, T.; Landier, L.; Kallel, A.; Malenovský, Z.; Al Bitar, A.; Aval, J.; Benhmida, S.; Qi, J.; et al. DART: Recent advances in remote sensing data modeling with atmosphere, polarization, and chlorophyll fluorescence. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2640–2649. [Google Scholar] [CrossRef]
- Hernández-Clemente, R.; North, P.; Hornero, A.; Zarco-Tejada, P. Assessing the effects of forest health on sun-induced chlorophyll fluorescence using the FluorFLIGHT 3-D radiative transfer model to account for forest structure. Remote Sens. Environ. 2017, 193, 165–179. [Google Scholar] [CrossRef]
- Verrelst, J.; Rivera, J.P.; van der Tol, C.; Magnani, F.; Mohammed, G.; Moreno, J. Global sensitivity analysis of the SCOPE model: What drives simulated canopy-leaving sun-induced fluorescence? Remote Sens. Environ. 2015, 166, 8–21. [Google Scholar] [CrossRef]
- Verrelst, J.; van der Tol, C.; Magnani, F.; Sabater, N.; Rivera, J.; Mohammed, G.; Moreno, J. Evaluating the predictive power of sun-induced chlorophyll fluorescence to estimate net photosynthesis of vegetation canopies: A SCOPE modeling study. Remote Sens. Environ. 2016, 176, 139–151. [Google Scholar] [CrossRef]
- Kennedy, M.; O’Hagan, A. Predicting the output from a complex computer code when fast approximations are available. Biometrika 2000, 87, 1–13. [Google Scholar] [CrossRef]
- O’Hagan, A. Bayesian analysis of computer code outputs: A tutorial. Reliab. Eng. Syst. Saf. 2006, 91, 1290–1300. [Google Scholar] [CrossRef]
- Gómez-Dans, J.L.; Lewis, P.E.; Disney, M. Efficient emulation of radiative transfer codes using Gaussian Processes and application to land surface parameter inferences. Remote Sens. 2016, 8, 119. [Google Scholar] [CrossRef]
- Verrelst, J.; Sabater, N.; Rivera, J.P.; Muñoz Marí, J.; Vicent, J.; Camps-Valls, G.; Moreno, J. Emulation of leaf, canopy and atmosphere radiative transfer models for fast global sensitivity analysis. Remote Sens. 2016, 8, 673. [Google Scholar] [CrossRef]
- Rivera, J.P.; Verrelst, J.; Gómez-Dans, J.; Muñoz Marí, J.; Moreno, J.; Camps-Valls, G. An emulator toolbox to approximate radiative transfer models with statistical learning. Remote Sens. 2015, 7, 9347–9370. [Google Scholar] [CrossRef]
- Verrelst, J.; Romijn, E.; Kooistra, L. Mapping vegetation density in a heterogeneous river floodplain ecosystem using pointable CHRIS/PROBA data. Remote Sens. 2012, 4, 2866–2889. [Google Scholar] [CrossRef]
- Vicent, J.; Sabater, N.; Tenjo, C.; Acarreta, J.; Manzano, M.; Rivera, J.; Jurado, P.; Franco, R.; Alonso, L.; Verrelst, J.; et al. FLEX End-to-End mission performance simulator. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4215–4223. [Google Scholar] [CrossRef]
- Cogliati, S.; Verhoef, W.; Kraft, S.; Sabater, N.; Alonso, L.; Vicent, J.; Moreno, J.; Drusch, M.; Colombo, R. Retrieval of sun-induced fluorescence using advanced spectral fitting methods. Remote Sens. Environ. 2015, 169, 344–357. [Google Scholar] [CrossRef]
- Damm, A.; Guanter, L.; Paul-Limoges, E.; van der Tol, C.; Hueni, A.; Buchmann, N.; Eugster, W.; Ammann, C.; Schaepman, M. Far-red sun-induced chlorophyll fluorescence shows ecosystem-specific relationships to gross primary production: An assessment based on observational and modeling approaches. Remote Sens. Environ. 2015, 166, 91–105. [Google Scholar] [CrossRef]
- Van der Tol, C.; Rossini, M.; Cogliati, S.; Verhoef, W.; Colombo, R.; Rascher, U.; Mohammed, G. A model and measurement comparison of diurnal cycles of sun-induced chlorophyll fluorescence of crops. Remote Sens. Environ. 2016, 186, 663–677. [Google Scholar] [CrossRef]
- Zhang, Y.; Guanter, L.; Berry, J.; van der Tol, C.; Yang, X.; Tang, J.; Zhang, F. Model-based analysis of the relationship between sun-induced chlorophyll fluorescence and gross primary production for remote sensing applications. Remote Sens. Environ. 2016, 187, 145–155. [Google Scholar] [CrossRef]
- Petropoulos, G.; Wooster, M.; Carlson, T.; Kennedy, M.; Scholze, M. A global Bayesian sensitivity analysis of the 1D SimSphere soil vegetation atmospheric transfer (SVAT) model using Gaussian model emulation. Ecol. Model. 2009, 220, 2427–2440. [Google Scholar] [CrossRef]
- Rohmer, J.; Foerster, E. Global sensitivity analysis of large-scale numerical landslide models based on Gaussian-Process meta-modeling. Comput. Geosci. 2011, 37, 917–927. [Google Scholar] [CrossRef]
- Carnevale, C.; Finzi, G.; Guariso, G.; Pisoni, E.; Volta, M. Surrogate models to compute optimal air quality planning policies at a regional scale. Environ. Model. Softw. 2012, 34, 44–50. [Google Scholar] [CrossRef]
- Villa-Vialaneix, N.; Follador, M.; Ratto, M.; Leip, A. A comparison of eight metamodeling techniques for the simulation of N 2 O fluxes and N leaching from corn crops. Environ. Model. Softw. 2012, 34, 51–66. [Google Scholar] [CrossRef] [Green Version]
- Castelletti, A.; Galelli, S.; Ratto, M.; Soncini-Sessa, R.; Young, P. A general framework for dynamic emulation modelling in environmental problems. Environ. Model. Softw. 2012, 34, 5–18. [Google Scholar] [CrossRef]
- Lee, L.; Pringle, K.; Reddington, C.; Mann, G.; Stier, P.; Spracklen, D.; Pierce, J.; Carslaw, K. The magnitude and causes of uncertainty in global model simulations of cloud condensation nuclei. Atmos. Chem. Phys. 2013, 13, 8879–8914. [Google Scholar] [CrossRef]
- Bounceur, N.; Crucifix, M.; Wilkinson, R. Global sensitivity analysis of the climate—Vegetation system to astronomical forcing: An emulator-based approach. Earth Syst. Dyn. Discuss. 2014, 5, 901–943. [Google Scholar] [CrossRef]
- Ireland, G.; Petropoulos, G.; Carlson, T.; Purdy, S. Addressing the ability of a land biosphere model to predict key biophysical vegetation characterisation parameters with Global Sensitivity Analysis. Environ. Model. Softw. 2015, 65, 94–107. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Bruzzone, L. (Eds.) Kernel Methods for Remote Sensing Data Analysis; Wiley & Sons: Chichester, UK, 2009. [Google Scholar]
- Razavi, S.; Tolson, B.A.; Burn, D.H. Numerical assessment of metamodelling strategies in computationally intensive optimization. Environ. Model. Softw. 2012, 34, 67–86. [Google Scholar] [CrossRef]
- McKay, M.; Beckman, R.; Conover, W. Comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 1979, 21, 239–245. [Google Scholar]
- Baret, F.; Clevers, J.; Steven, M. The robustness of canopy gap fraction estimates from red and near-infrared reflectances: A comparison of approaches. Remote Sens. Environ. 1995, 54, 141–151. [Google Scholar] [CrossRef]
- Combal, B.; Baret, F.; Weiss, M.; Trubuil, A.; Macé, D.; Pragnère, A.; Myneni, R.; Knyazikhin, Y.; Wang, L. Retrieval of canopy biophysical variables from bidirectional reflectance using prior information to solve the ill-posed inverse problem. Remote Sens. Environ. 2003, 84, 1–15. [Google Scholar] [CrossRef]
- Verrelst, J.; Muñoz, J.; Alonso, L.; Delegido, J.; Rivera, J.; Camps-Valls, G.; Moreno, J. Machine learning regression algorithms for biophysical parameter retrieval: Opportunities for Sentinel-2 and -3. Remote Sens. Environ. 2012, 118, 127–139. [Google Scholar] [CrossRef]
- Rivera, J.; Verrelst, J.; Delegido, J.; Veroustraete, F.; Moreno, J. On the semi-automatic retrieval of biophysical parameters based on spectral index optimization. Remote Sens. 2014, 6, 4924–4951. [Google Scholar] [CrossRef]
- Verrelst, J.; Camps Valls, G.; Muñoz Marí, J.; Rivera, J.; Veroustraete, F.; Clevers, J.; Moreno, J. Optical remote sensing and the retrieval of terrestrial vegetation bio-geophysical properties—A review. ISPRS J. Photogramm. Remote Sens. 2015, 108, 273–290. [Google Scholar] [CrossRef]
- Hankin, R.K. Introducing BACCO, an R package for Bayesian analysis of computer code output. J. Stat. Softw. 2005, 14, 1–21. [Google Scholar] [CrossRef]
- Hughes, G. On the mean accuracy of statistical pattern recognizers. IEEE Trans. Inf. Theory 1968, 14, 55–63. [Google Scholar] [CrossRef]
- Wold, S.; Esbensen, K.; Geladi, P. Principal component analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks—A Comprehensive Foundation, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Shawe-Taylor, J.; Cristianini, N. Kernel Methods for Pattern Analysis; Cambridge University Press: New York, NY, USA, 2004. [Google Scholar]
- Vapnik, V.; Golowich, S.; Smola, A. Support vector method for function approximation, regression estimation, and signal processing. Adv. Neural Inf. Process. Syst. 1997, 9, 281–287. [Google Scholar]
- Suykens, J.; Vandewalle, J. Least squares support vector machine classifiers. Neural Process. Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; The MIT Press: New York, NY, USA, 2006. [Google Scholar]
- Lázaro-Gredilla, M.; Titsias, M.K.; Verrelst, J.; Camps-Valls, G. Retrieval of biophysical parameters with heteroscedastic Gaussian processes. IEEE Geosci. Remote Sens. Lett. 2014, 11, 838–842. [Google Scholar] [CrossRef]
- Rivera Caicedo, J.; Verrelst, J.; Muñoz-Marí, J.; Moreno, J.; Camps-Valls, G. Toward a semiautomatic machine learning retrieval of biophysical parameters. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1249–1259. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Gómez-Chova, L.; Muñoz-Marí, J.; Lázaro-Gredilla, M.; Verrelst, J. SimpleR: A Simple Educational Matlab Toolbox for Statistical Regression, V2.1. 2013. Available online: http://www.uv.es/gcamps/software.html (accessed on 6 September 2017).
- Wold, H.O.A. Non-Linear Estimation by Iterative Least Squares Procedures. In Research Papers in Statistics, Festschrift for J. Neyman; David, F.J., Neyman, J., Eds.; Wiley: London, UK, 1966. [Google Scholar]
- Van Der Tol, C.; Verhoef, W.; Timmermans, J.; Verhoef, A.; Su, Z. An integrated model of soil-canopy spectral radiances, photosynthesis, fluorescence, temperature and energy balance. Biogeosciences 2009, 6, 3109–3129. [Google Scholar] [CrossRef]
- Timmermans, J.; Su, Z.; Van Der Tol, C.; Verhoef, A.; Verhoef, W. Quantifying the uncertainty in estimates of surface-atmosphere fluxes through joint evaluation of the SEBS and SCOPE models. Hydrol. Earth Syst. Sci. 2013, 17, 1561–1573. [Google Scholar] [CrossRef]
- Duffour, C.; Olioso, A.; Demarty, J.; Van der Tol, C.; Lagouarde, J.P. An evaluation of SCOPE: A tool to simulate the directional anisotropy of satellite-measured surface temperatures. Remote Sens. Environ. 2015, 158, 362–375. [Google Scholar] [CrossRef]
- Zhang, Y.; Guanter, L.; Berry, J.; Joiner, J.; van der Tol, C.; Huete, A.; Gitelson, A.; Voigt, M.; Kahler, P. Estimation of vegetation photosynthetic capacity from space-based measurements of chlorophyll fluorescence for terrestrial biosphere models. Glob. Chang. Biol. 2014, 20, 3727–3742. [Google Scholar] [CrossRef] [PubMed]
- Feret, J.B.; François, C.; Asner, G.P.; Gitelson, A.A.; Martin, R.E.; Bidel, L.P.R.; Ustin, S.L.; le Maire, G.; Jacquemoud, S. PROSPECT-4 and 5: Advances in the leaf optical properties model separating photosynthetic pigments. Remote Sens. Environ. 2008, 112, 3030–3043. [Google Scholar] [CrossRef]
- Rivera, J.; Sabater, N.; Tenjo, C.; Vicent, J.; Alonso, L.; Moreno, J. Synthetic scene simulator for hyperspectral spaceborne passive optical sensors. Application to ESA’s FLEX/Sentinel-3 tandem mission. In Proceedings of the 6th Workshop on Hyperspectral Image and Signal Processing, Lausane, Switzerland, 24–27 June 2014. [Google Scholar]
- Conti, S.; O’Hagan, A. Bayesian emulation of complex multi-output and dynamic computer models. J. Stat. Plan. Inference 2010, 140, 640–651. [Google Scholar] [CrossRef]
- Verrelst, J.; Rivera, J.; Moreno, J.; Camps-Valls, G. Gaussian processes uncertainty estimates in experimental Sentinel-2 LAI and leaf chlorophyll content retrieval. ISPRS J. Photogram. Remote Sens. 2013, 86, 157–167. [Google Scholar] [CrossRef]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Schmidhuber, J. Deep Learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [PubMed]
- Vicent, J.; Sabater, N.; Verrelst, J.; Alonso, L.; Moreno, J. Assessment of approximations in aerosol optical properties and vertical distribution into FLEX atmospherically-corrected surface reflectance and retrieved Sun-Induced Fluorescence. Remote Sens. 2017, 9, 675. [Google Scholar] [CrossRef]
- Mousivand, A.; Menenti, M.; Gorte, B.; Verhoef, W. Multi-temporal, multi-sensor retrieval of terrestrial vegetation properties from spectral-directional radiometric data. Remote Sens. Environ. 2015, 158, 311–330. [Google Scholar] [CrossRef]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis: The Primer; John Wiley & Sons: Chichester, UK, 2008. [Google Scholar]
- Nossent, J.; Elsen, P.; Bauwens, W. Sobol’sensitivity analysis of a complex environmental model. Environ. Model. Softw. 2011, 26, 1515–1525. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Baret, F.; Andrieu, B.; Danson, F.; Jaggard, K. Extraction of vegetation biophysical parameters by inversion of the PROSPECT + SAIL models on sugar beet canopy reflectance data. Application to TM and AVIRIS sensors. Remote Sens. Environ. 1995, 52, 163–172. [Google Scholar] [CrossRef]
- Kuusk, A. Monitoring of vegetation parameters on large areas by the inversion of a canopy reflectance model. Int. J. Remote Sens. 1998, 19, 2893–2905. [Google Scholar] [CrossRef]
- Myneni, R.; Hoffman, S.; Knyazikhin, Y.; Privette, J.; Glassy, J.; Tian, Y.; Wang, Y.; Song, X.; Zhang, Y.; Smith, G.; et al. Global products of vegetation leaf area and fraction absorbed PAR from year one of MODIS data. Remote Sens. Environ. 2002, 83, 214–231. [Google Scholar] [CrossRef]
- Richter, R. A spatially adaptive fast atmospheric correction algorithm. Int. J. Remote Sens. 1996, 17, 1201–1214. [Google Scholar] [CrossRef]
- Thome, K.; Palluconi, F.; Takashima, T.; Masuda, K. Atmospheric correction of ASTER. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1199–1211. [Google Scholar] [CrossRef]
- Kotchenova, S.; Vermote, E.; Matarrese, R.; Klemm, F., Jr. Validation of a vector version of the 6S radiative transfer code for atmospheric correction of satellite data. Part I: Path radiance. Appl. Opt. 2006, 45, 6762–6774. [Google Scholar] [CrossRef] [PubMed]
- Guanter, L.; Alonso, L.; Moreno, J. CHRIS Proba Atmospheric Correction Module. In Algorithm Theoretical Basis Document; ESA ESRIN Contract No. 20442; ESA ESRIN: Frascati, Italy, 2007. [Google Scholar]
- Hagolle, O.; Huc, M.; Pascual, D.; Dedieu, G. A multi-temporal and multi-spectral method to estimate aerosol optical thickness over land, for the atmospheric correction of FormoSat-2, LandSat, VENμS and Sentinel-2 images. Remote Sens. 2015, 7, 2668–2691. [Google Scholar] [CrossRef]
- Lefévre, M.; Oumbe, A.; Blanc, P.; Espinar, B.; Gschwind, B.; Qu, Z.; Wald, L.; Schroedter-Homscheidt, M.; Hoyer-Klick, C.; Arola, A.; et al. McClear: A new model estimating downwelling solar radiation at ground level in clear-sky conditions. Atmos. Meas. Tech. 2013, 6, 2403–2418. [Google Scholar] [CrossRef] [Green Version]
- Richter, R.; Heege, T.; Kiselev, V.; Schläpfer, D. Correction of ozone influence on TOA radiance. Int. J. Remote Sens. 2014, 35, 8044–8056. [Google Scholar] [CrossRef]


| Model Variables | Units | Minimum | Maximum | |
|---|---|---|---|---|
| Leaf variables: | ||||
| N | Leaf structure index | unitless | 1.0 | 4.0 |
| Cw | Leaf water content | [cm] | 0.001 | 0.05 |
| Cab | Leaf chlorophyll content | [g/cm] | 0.1 | 100 |
| Cm | Leaf dry matter content | [g/cm] | 0.0001 | 0.05 |
| Cs | Senescent material | unitless | 0.0001 | 0.3 |
| Canopy variables: | ||||
| LAI | Leaf area index | [m/m] | 0.01 | 10 * |
| hc | plant height | [m] | 0 | 2 |
| SMC | volumetric soil moisture content | unitless | 0.01 | 0.7 |
| Model Variables | Units | Vegetation Class 1 Mean (% SD) | Vegetation Class 2 Mean (% SD) | Vegetation Class 3 Mean (% SD) |
|---|---|---|---|---|
| Leaf variables: | ||||
| N | unitless | 1.2 (30%) | 1.4 (30%) | 1.1 (10%) |
| Cw | [cm] | 0.02 (30%) | 0.01 (30%) | 0.01 (10%) |
| Cab | [g/cm] | 40 (30%) | 50 (30%) | 30 (10%) |
| Cm | [g/cm] | 0.02 (30%) | 0.03 (30%) | 0.03 (10%) |
| Cs | unitless | 0.001 (30%) | 0.001 (30%) | 0.001 (10%) |
| Canopy variables: | ||||
| LAI | [m/m] | 3 (30%) | 5 (30%) | 2.5 (10%) |
| hc | [m] | 0.3 (30%) | 2 (30%) | 0.3 (10%) |
| SMC | unitless | 0.02 (30%) | 0.02 (30%) | 0.02 (30%) |
| MLRA | RMSE | NRMSE (%) | CPU (s) |
|---|---|---|---|
| RF | 0.022 | 6.763 | 46.6 |
| NN | 0.007 | 2.066 | 266.6 |
| SVR | 0.027 | 8.317 | 810.4 |
| KRR | 0.025 | 7.538 | 2.2 |
| GPR | 0.011 | 3.106 | 114.7 |
| VHGPR | 0.008 | 2.433 | 1006.8 |
| MLRA | RMSE | NRMSE (%) | CPU (s) |
|---|---|---|---|
| RF | 0.135 | 8.241 | 12.0 |
| NN | 0.081 | 5.031 | 44.7 |
| SVR | 0.126 | 7.349 | 293.9 |
| KRR | 0.108 | 6.723 | 1.5 |
| GPR | 0.049 | 3.303 | 27.9 |
| VHGPR | 0.055 | 3.064 | 102.4 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Verrelst, J.; Rivera Caicedo, J.P.; Muñoz-Marí, J.; Camps-Valls, G.; Moreno, J. SCOPE-Based Emulators for Fast Generation of Synthetic Canopy Reflectance and Sun-Induced Fluorescence Spectra. Remote Sens. 2017, 9, 927. https://doi.org/10.3390/rs9090927
Verrelst J, Rivera Caicedo JP, Muñoz-Marí J, Camps-Valls G, Moreno J. SCOPE-Based Emulators for Fast Generation of Synthetic Canopy Reflectance and Sun-Induced Fluorescence Spectra. Remote Sensing. 2017; 9(9):927. https://doi.org/10.3390/rs9090927
Chicago/Turabian StyleVerrelst, Jochem, Juan Pablo Rivera Caicedo, Jordi Muñoz-Marí, Gustau Camps-Valls, and José Moreno. 2017. "SCOPE-Based Emulators for Fast Generation of Synthetic Canopy Reflectance and Sun-Induced Fluorescence Spectra" Remote Sensing 9, no. 9: 927. https://doi.org/10.3390/rs9090927
APA StyleVerrelst, J., Rivera Caicedo, J. P., Muñoz-Marí, J., Camps-Valls, G., & Moreno, J. (2017). SCOPE-Based Emulators for Fast Generation of Synthetic Canopy Reflectance and Sun-Induced Fluorescence Spectra. Remote Sensing, 9(9), 927. https://doi.org/10.3390/rs9090927