Characteristics of Evapotranspiration of Urban Lawns in a Sub-Tropical Megacity and Its Measurement by the ‘Three Temperature Model + Infrared Remote Sensing’ Method
Abstract
:1. Introduction
2. Materials and Methods
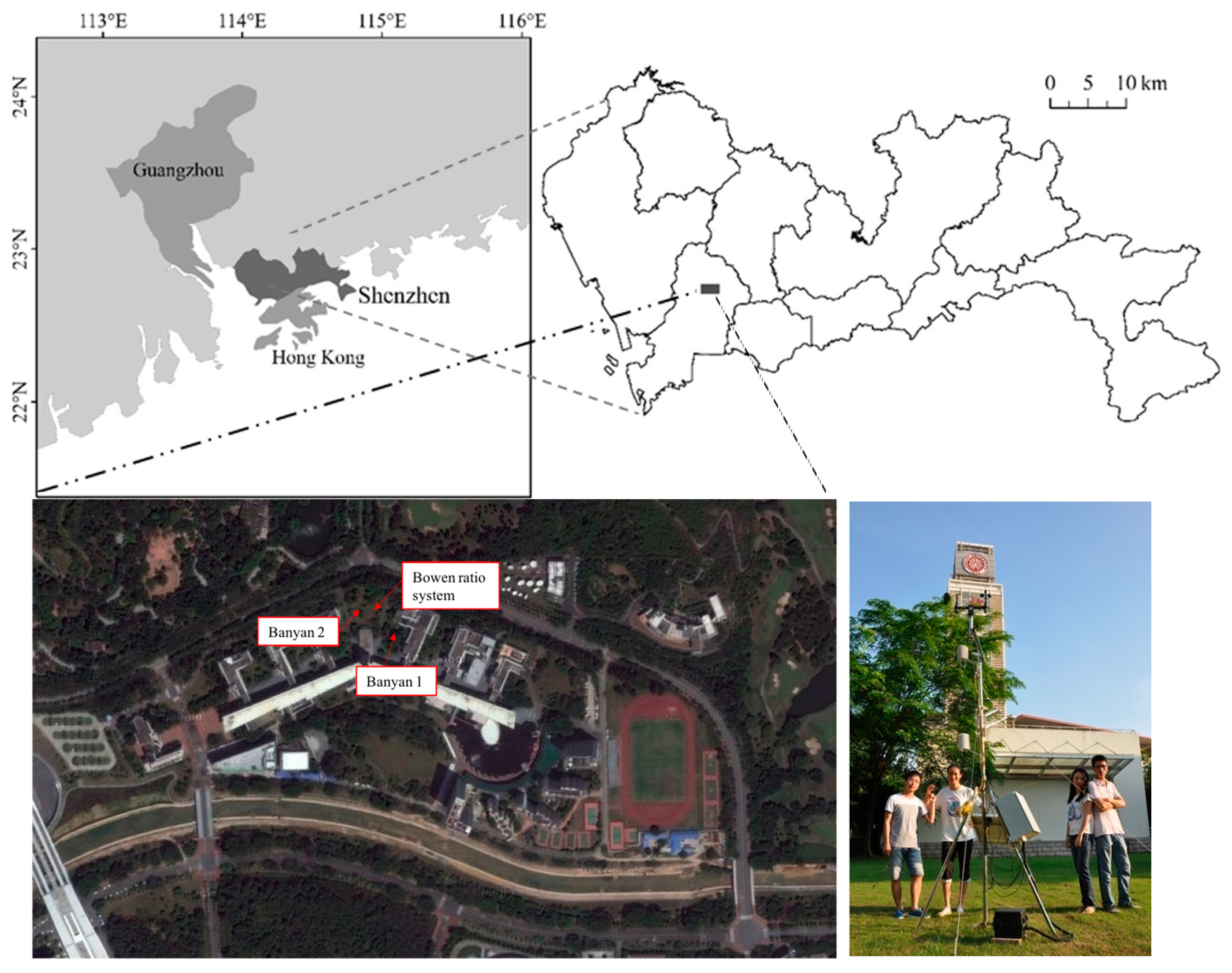
2.1. Study Site and Measurements
2.2. Data Analysis
2.2.1. Estimation of ET by Bowen Ratio Energy Balance (BREB) Method
2.2.2. Estimation of ET by Using Three Temperature Model (3T Model) + Infrared Remote Sensing (Infrared RS) Method
3. Results
3.1. Meteorological Characteristics in the Studied Urban Area
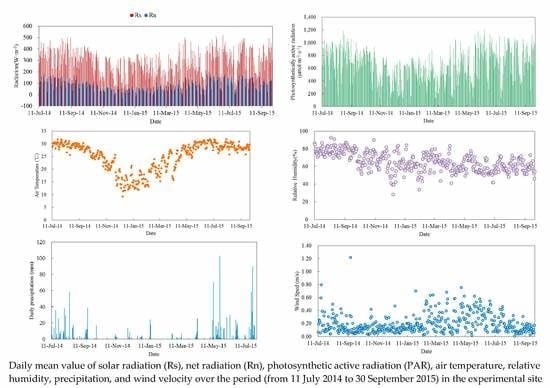
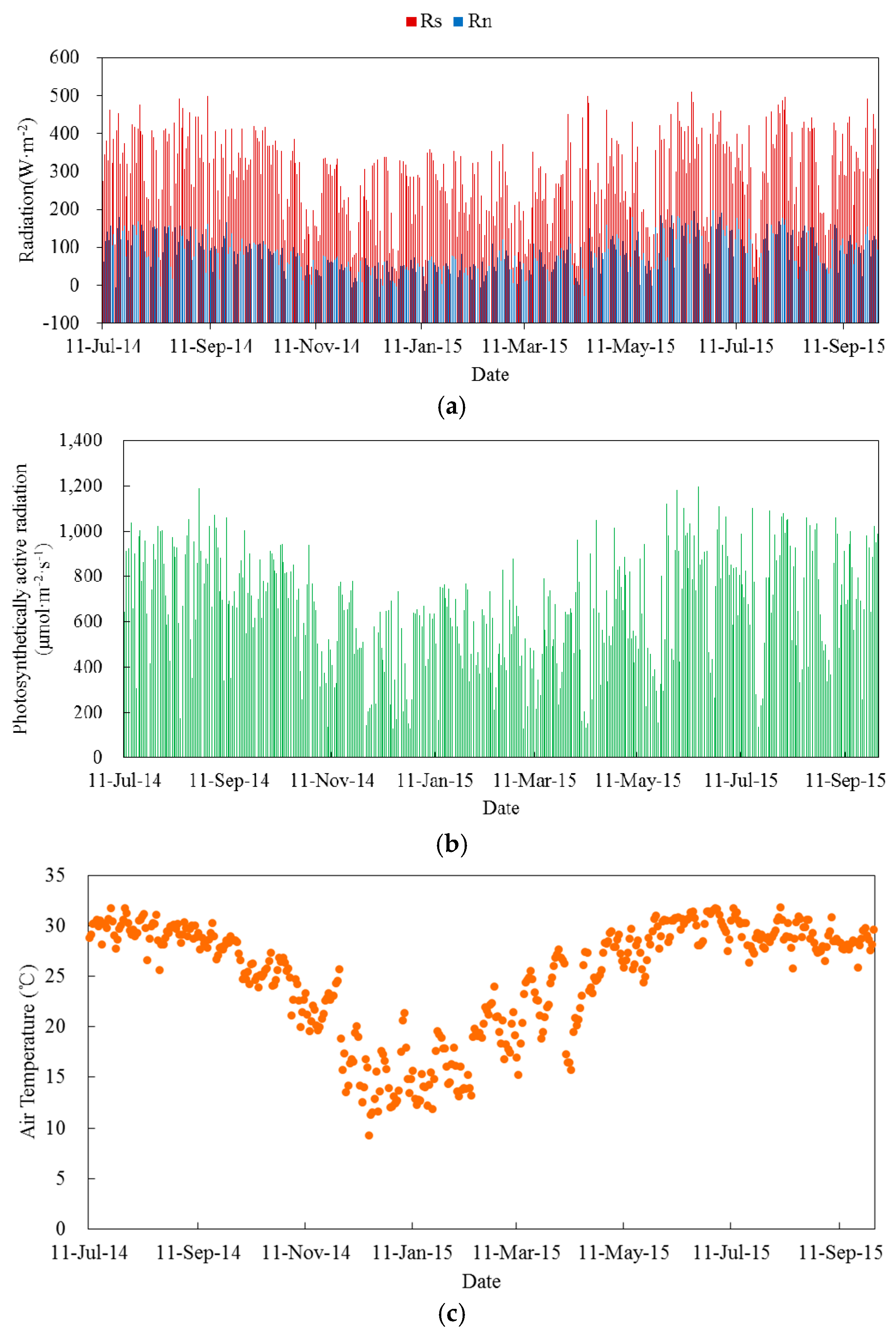
3.1.1. Radiation Characteristics
3.1.2. Air Temperature
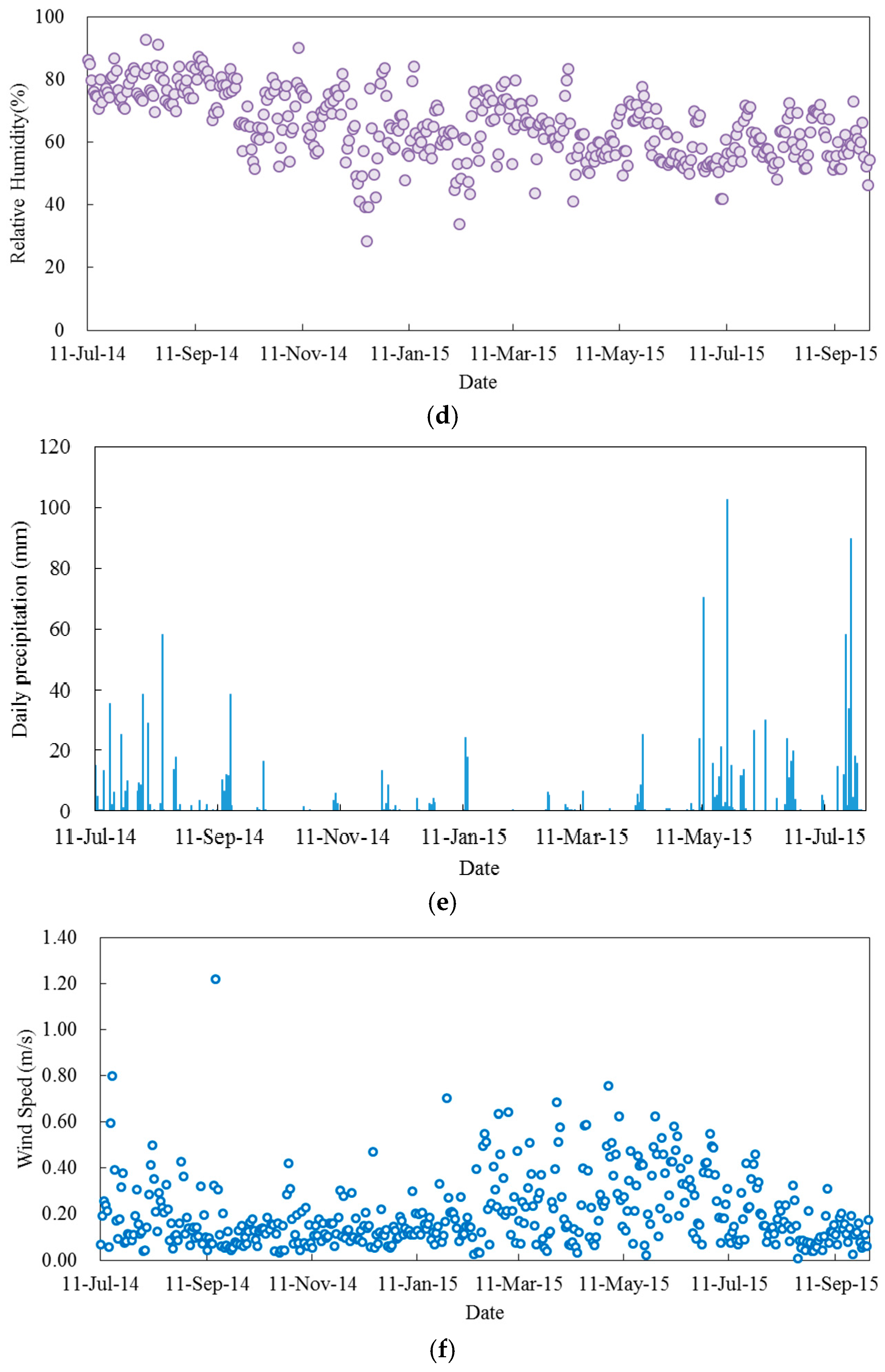
3.1.3. Relative Humidity
3.1.4. Precipitation
3.1.5. Wind Velocity
3.1.6. Summary for Section 3.1
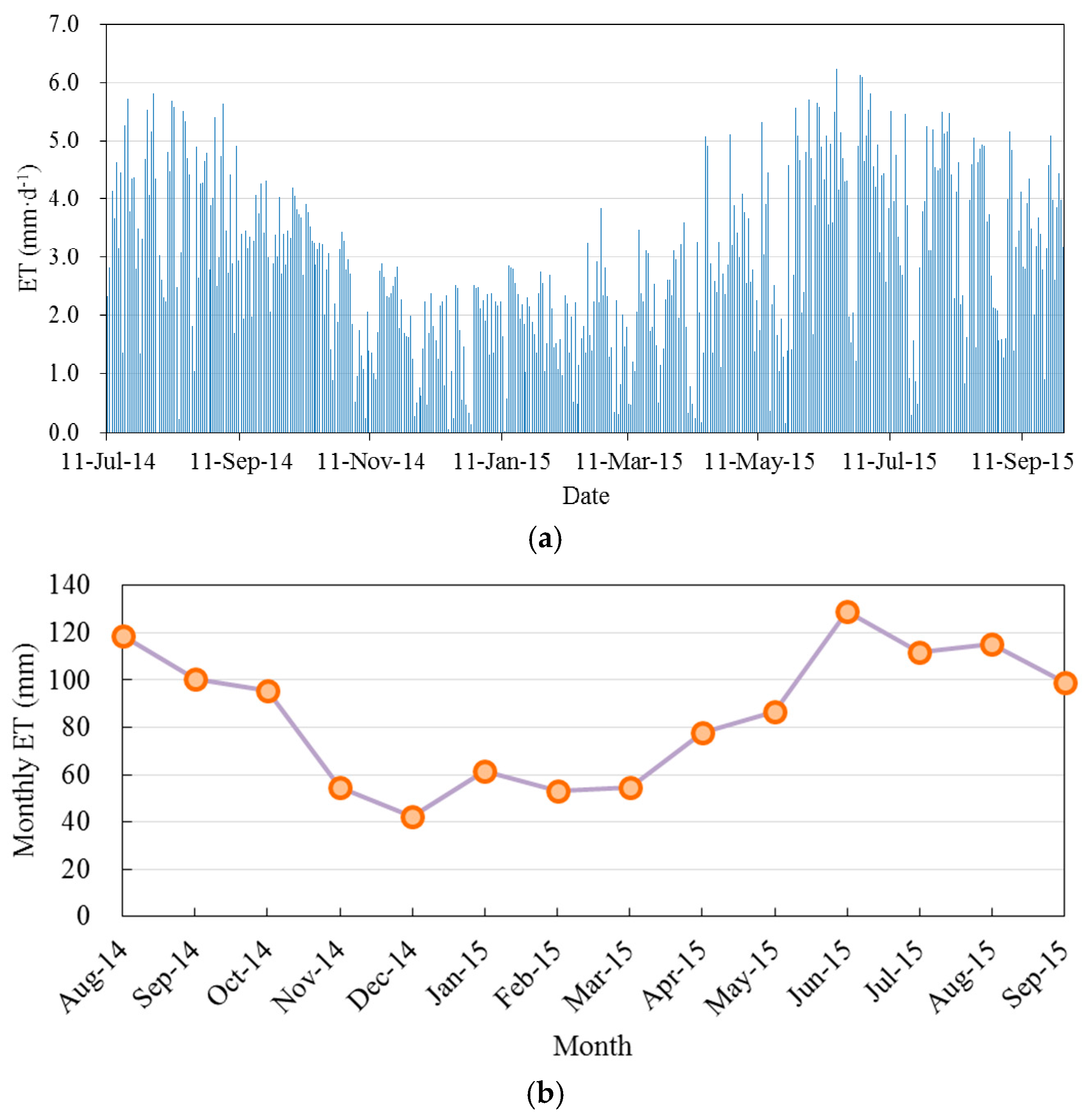
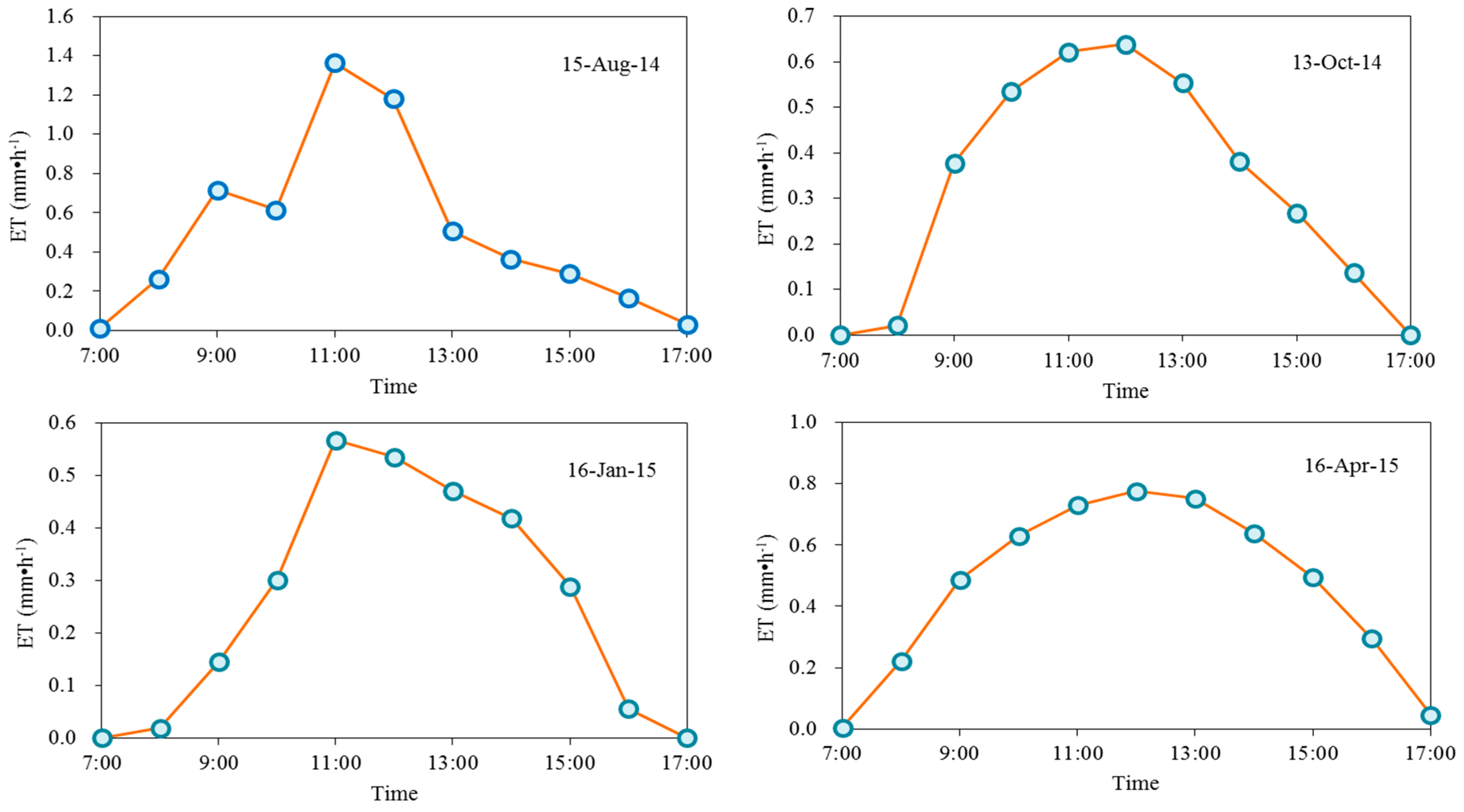
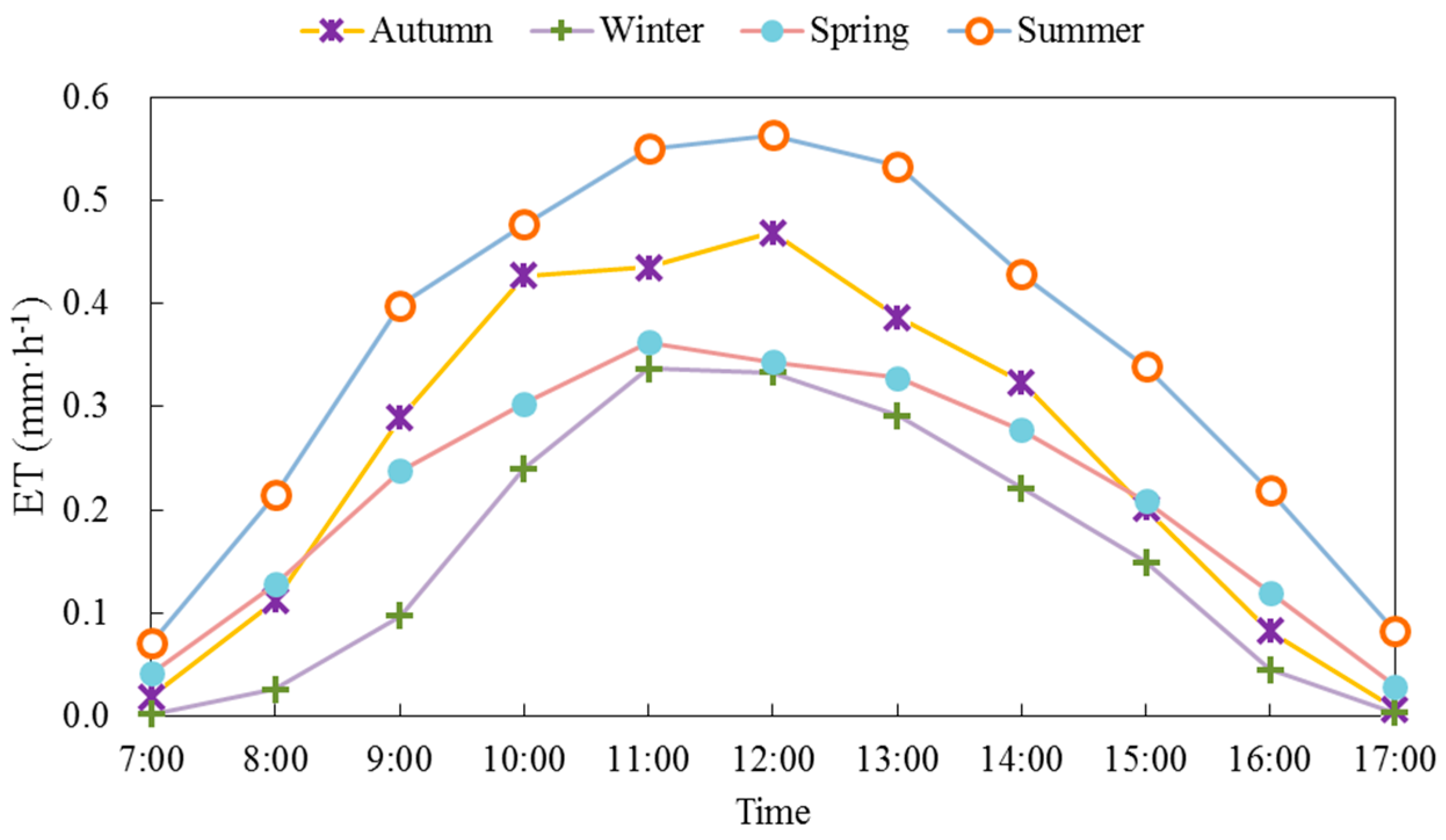
3.2. Magnitude and Variation Trends of Hourly, Daily, and Seasonal ET
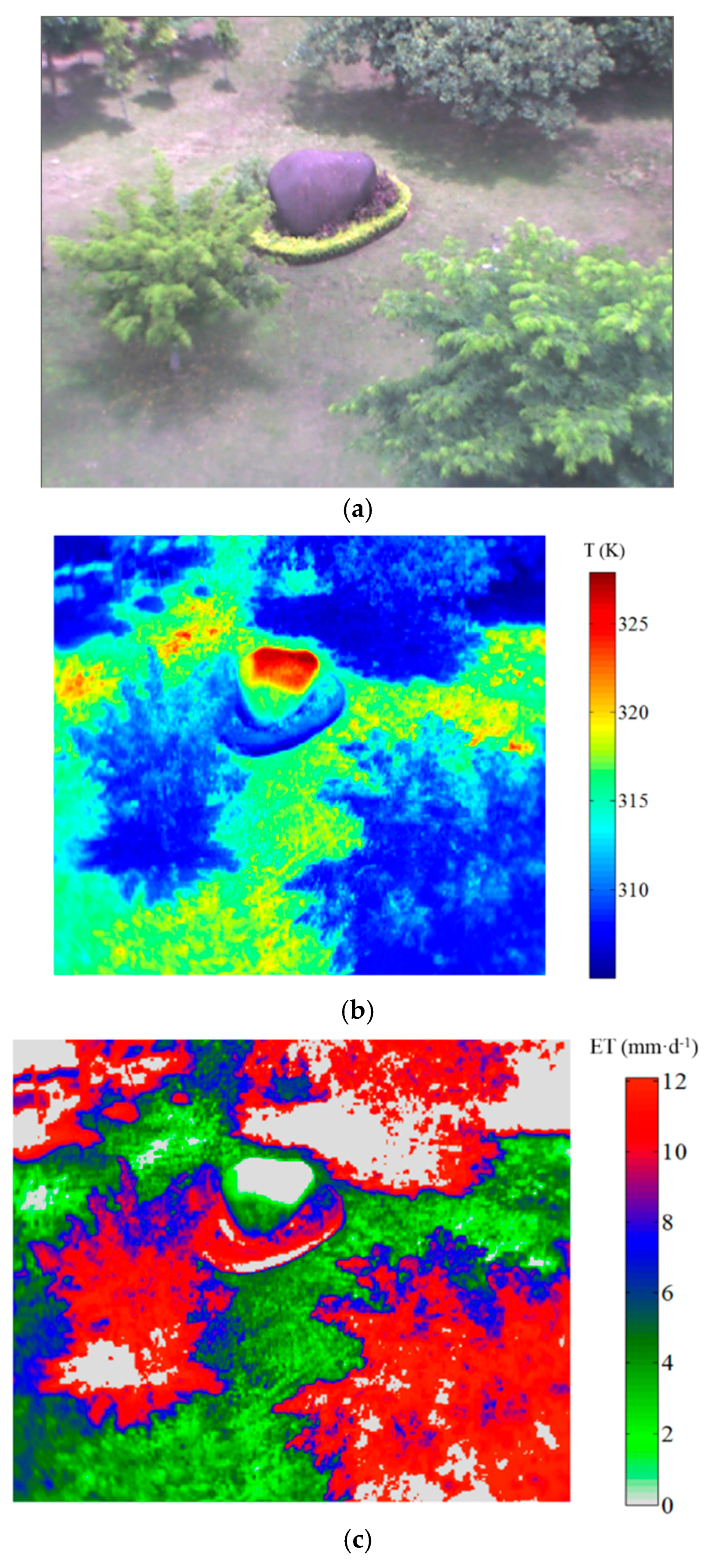
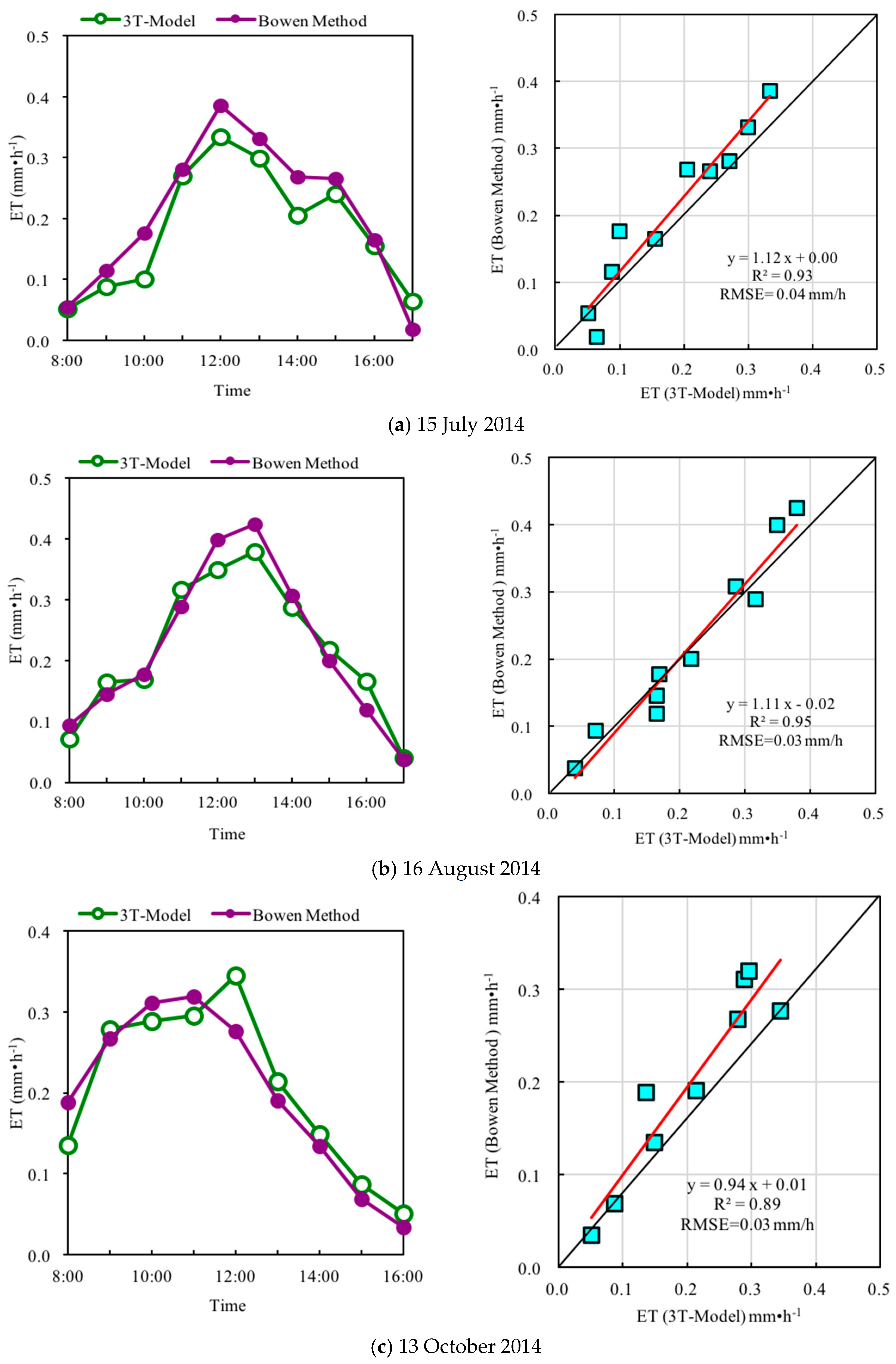
3.3. Urban ET Estimated by ‘3T Model + Infrared RS’ Method
4. Discussion
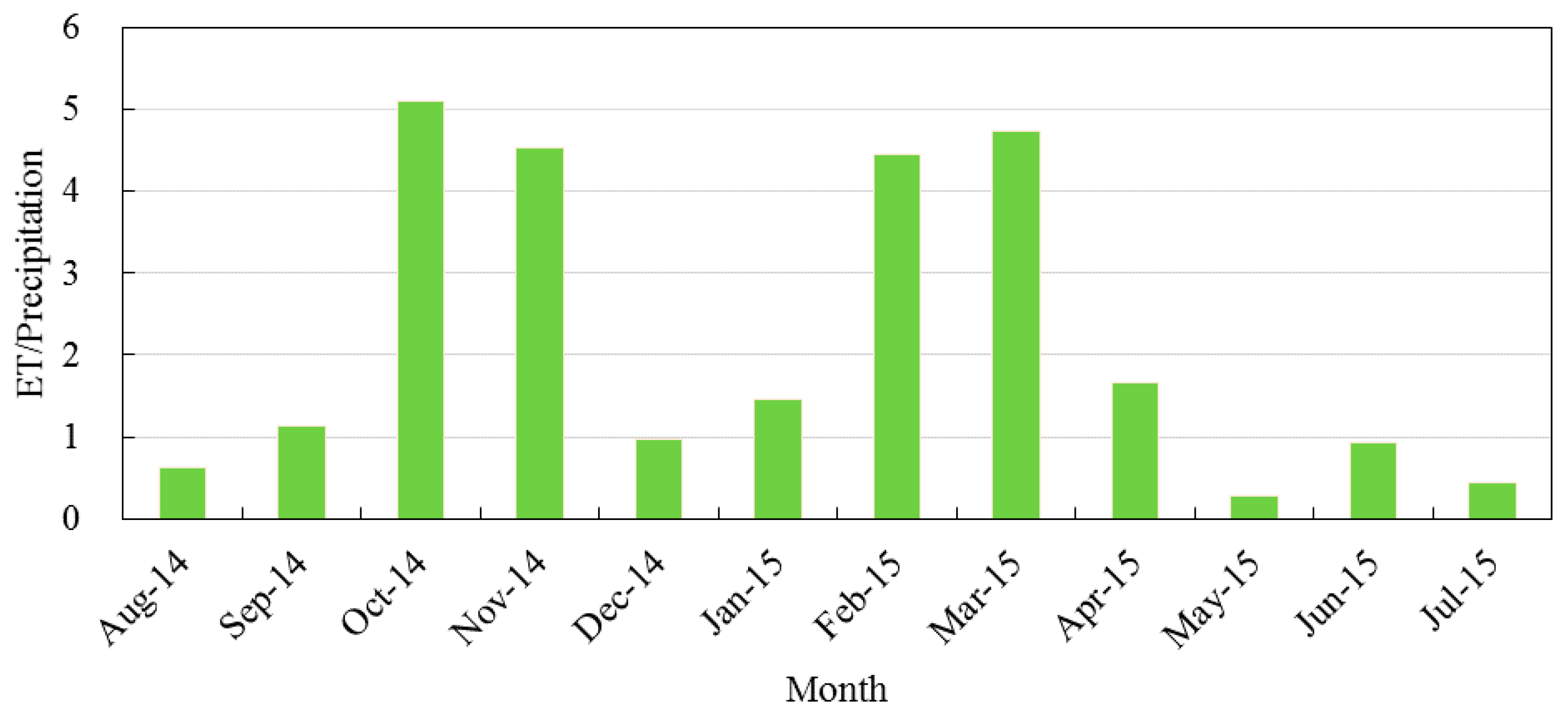
4.1. Relationship between Urban ET and Precipitation (P)
4.2. Main Impact Factor of Urban ET
4.3. Evaluation of the ‘3T Model + Infrared RS’ Method for Urban ET Estimation
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Morini, E.; Touchaei, A.G.; Castellani, B.; Rossi, F.; Cotana, F. The impact of albedo increase to mitigate the urban heat island in Terni (Italy) using the WRF model. Sustainability 2016, 8, 999. [Google Scholar] [CrossRef]
- Morini, E.; Castellani, B.; Presciutti, A.; Filipponi, M.; Nicolini, A.; Rossi, F. Optic-energy performance improvement of exterior paints for buildings. Energy Build. 2017, 139, 690–701. [Google Scholar] [CrossRef]
- Qiu, G.Y.; Yang, B.; Li, X.; Guo, Q.; Tan, S. Cooling effect of evapotranspiration (ET) and ET measurement by thermal remote sensing in urban. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 14–18 December 2015. [Google Scholar]
- Grimmond, C.S.B.; Oke, T.R. Evapotranspiration Rates in Urban Areas; IAHS Press: Wallingford, UK, 1999; Volume 259, pp. 235–244. [Google Scholar]
- Berthier, E.; Dupont, S.; Mestayer, P.G.; Andrieu, H. Comparison of two evapotranspiration schemes on a sub-urban site. J. Hydrol. 2006, 328, 635–646. [Google Scholar] [CrossRef]
- Willems, P. Revision of urban drainage design rules after assessment of climate change impacts on precipitation extremes at Uccle, Belgium. J. Hydrol. 2013, 496, 166–177. [Google Scholar] [CrossRef]
- Mancipe-Munoz, N.A.; Buchberger, S.G.; Suidan, M.T.; Lu, T. Calibration of rainfall-runoff model in urban watersheds for stormwater management assessment. J. Water Resour. Plan. Manag. 2014, 140, 05014001. [Google Scholar] [CrossRef]
- Grimm, N.B.; Faeth, S.H.; Golubiewski, N.E.; Redman, C.L.; Wu, J.; Bai, X.; Briggs, J.M. Global change and the ecology of cities. Science 2008, 319, 756–760. [Google Scholar] [CrossRef] [PubMed]
- Arnfield, A.J. Two decades of urban climate research: A review of turbulence, exchanges of energy and water, and the urban heat island. Int. J. Climatol. 2003, 23, 1–26. [Google Scholar] [CrossRef]
- Rossi, F.; Pisello, A.L.; Nicolini, A.; Filipponi, M.; Palombo, M. Analysis of retro-reflective surfaces for urban heat island mitigation: A new analytical model. Appl. Energy 2014, 114, 621–631. [Google Scholar] [CrossRef]
- Min, S.K.; Zhang, X.; Zwiers, F.W.; Hegerl, G.C. Human contribution to more-intense precipitation extremes. Nature 2011, 470, 378–381. [Google Scholar] [CrossRef] [PubMed]
- Huang, G.R.; He, H.J. Impact of urbanization on features of rainfall during flood period in Jinan city. J. Nat. Disasters 2011, 3, 7–12. [Google Scholar]
- Yang, Z.; Dominguez, F.; Gupta, H.V. Urban effects on regional climate: A case study in the Phoenix-Tucson Corridor. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 15–19 December 2014. [Google Scholar]
- Oke, T.R.; Zeuner, G.; Jauregui, E. The surface energy balance in Mexico City. Atmos. Environ. Part B Urban Atmos. 1992, 26, 433–444. [Google Scholar] [CrossRef]
- Grimmond, C.S.B. The suburban energy balance: Methodological considerations and results for a mid-latitude west coast city under winter and spring conditions. Int. J. Climatol. 1992, 12, 481–497. [Google Scholar] [CrossRef]
- Grimmond, C.S.B.; Oke, T.R. Turbulent heat fluxes in urban areas: Observations and a local-scale urban meteorological parameterization scheme (LUMPS). J. Appl. Meteorol. 2002, 41, 792–810. [Google Scholar] [CrossRef]
- Jim, C.Y.; Chen, W. Assessing the ecosystem service of air pollutant removal by urban trees in Guangzhou (China). J. Environ. Manag. 2008, 88, 665–676. [Google Scholar] [CrossRef] [PubMed]
- Jim, C.Y.; Chen, W.Y. Ecosystem services and valuation of urban forests in China. Cities 2009, 26, 187–194. [Google Scholar] [CrossRef]
- DiGiovanni, K.; Gaffin, S.; Montalto, F.; Rosenzweig, C. Applicability of classical predictive equations for the estimation of evapotranspiration from urban green spaces: Green roof results. J. Hydrol. Eng. 2013, 18, 99–107. [Google Scholar] [CrossRef]
- Voyde, E.; Fassman, E.; Simcock, R. Hydrology of an extensive living roof under sub-tropical climate conditions in Auckland, New Zealand. J. Hydrol. 2010, 394, 384–395. [Google Scholar] [CrossRef]
- Ouldboukhitine, S.E.; Andrade, H.; Vaz, T. Assessment of green roof thermal behavior: A coupled heat and mass transfer model. Build. Environ. 2011, 46, 2624–2631. [Google Scholar] [CrossRef]
- Neukrug, H. A Triple Bottom Line Assessment of Traditional and Green Infrastructure Options for Controlling CSO Events in Philadelphia’s Watersheds; Philadelphia Water Department and Office of Watersheds: Philadelphia, PA, USA, 2009. [Google Scholar]
- Bloomberg, M.; Holloway, C. NYC Green Infrastructure Plan; Office of the Mayor: New York, NY, USA, 2010. [Google Scholar]
- Xu, C.Y.; Chen, D. Comparison of seven models for estimation of evapotranspiration and groundwater recharge using lysimeter measurement data in Germany. Hydrol. Process. 2005, 19, 3717–3734. [Google Scholar] [CrossRef]
- Bedient, P.B.; Huber, W.C. Hydrology and Floodplain Analysis, 3rd ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Denich, C.; Bradford, A. Estimation of evapotranspiration from bioretention areas using weighing lysimeters. J. Hydrol. Eng. 2010, 15, 522–530. [Google Scholar] [CrossRef]
- Pataki, D.E.; McCarthy, H.R.; Litvak, E.; Pincetl, S. Transpiration of urban forests in the Los Angeles metropolitan area. Ecol. Appl. 2011, 21, 661–677. [Google Scholar] [CrossRef] [PubMed]
- Peters, E.B.; Hiller, R.V.; McFadden, J.P. Seasonal contributions of vegetation types to suburban evapotranspiration. J. Geophys. Res. Biogeosci. 2011, 116. [Google Scholar] [CrossRef]
- Jacobs, C.; Elbers, J.; Brolsma, R.; Hartogensisc, O.; Moors, E.; María, T.R.M.; Hove, B. Assessment of evaporative water loss from Dutch cities. Build. Environ. 2015, 83, 27–38. [Google Scholar] [CrossRef]
- Ward, H.C.; Evans, J.G.; Grimmond, C.S.B. Infrared and millimetre-wave scintillometry in the suburban environment–Part 2: Large-area sensible and latent heat fluxes. Atmos. Meas. Tech. 2015, 8, 1407–1424. [Google Scholar] [CrossRef]
- Kim, S.J. Influence of micrometeorological factors for actual evapotranspiration in the coastal urban area. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 14–18 December 2015. [Google Scholar]
- Litvak, E. Evapotranspiration of the urban forest at the municipal scale in Los Angeles, CA. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 14–18 December 2015. [Google Scholar]
- Miller, G.R.; Long, M.R.; Fipps, G.; Swanson, C.; Traore, S. Spatiotemporal variability in potential evapotranspiration across an urban monitoring network. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 14–18 December 2015. [Google Scholar]
- Nouri, H.; Nagler, P.L. Evapotranspiration estimation in heterogeneous urban vegetation. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 14–18 December 2015. [Google Scholar]
- Lazzarin, R.M.; Castellotti, F.; Busato, F. Experimental measurements and numerical modelling of a green roof. Energy Build. 2005, 37, 1260–1267. [Google Scholar] [CrossRef]
- Bowen, I.S. The ratio of heat losses by conduction and by evaporation from any water surface. Phys. Rev. 1926, 27, 779–789. [Google Scholar] [CrossRef]
- Andreas, E.L.; Cash, B.A. A new formulation for the Bowen ratio over saturated surfaces. J. Appl. Meteorol. 1996, 35, 1279–1289. [Google Scholar] [CrossRef]
- Pauwels, V.R.N.; Samson, R. Comparison of different methods to measure and model actual evapotranspiration rates for a wet sloping grassland. Agric. Water Manag. 2006, 82, 1–24. [Google Scholar] [CrossRef]
- Qiu, G.Y.; Momii, K.; Yano, T. Estimation of plant transpiration by imitation leaf temperature. I. Theoretical consideration and field verification. Trans. Jpn. Soc. Irrig. Drain. Reclam. Eng. 1996, 64, 47–56. [Google Scholar]
- Yan, C.; Qiu, G.Y. The three-temperature model to estimate evapotranspiration and its partitioning at multiple scales—A review. Trans. ASABE 2015, 59, 661–670. [Google Scholar]
- Yang, Y.; Zou, Z.; Zhao, W.; Li, R.; Qiu, G.Y. The study of optical properties and thermal performance of thin layer concrete pavement commonly used in the urban environment’s external surface. Ecol. Environ. Sci. 2016, 25, 835–841, (In Chinese with English Abstract). [Google Scholar]
- Li, X.; Li, H.; Zhang, Q.; Qiu, G.Y. Study on reducing effect of different urban landscapes on urban temperature. Ecol. Environ. Sci. 2014, 23, 106–112, (In Chinese with English Abstract). [Google Scholar]
- Qiu, G.Y.; Omasa, K.; Sase, S. An infrared-based coefficient to screen plant environmental stress: Concept, test and applications. Funct. Plant Biol. 2009, 36, 990–997. [Google Scholar] [CrossRef]
- Song, L.; Liu, S.; Zhang, X.; Zhou, J. Estimating and validating soil evaporation and crop transpiration during the HiWATER-MUSOEXE. IEEE Geosci. Remote Sens. Lett. 2015, 12, 334–338. [Google Scholar] [CrossRef]
- Qiu, G.Y.; Zhao, M. Remotely monitoring evaporation rate and soil water status using thermal imaging and “three-temperatures model (3T Model)” under field-scale conditions. J. Environ. Monit. 2010, 12, 716–723. [Google Scholar] [CrossRef] [PubMed]
- Xiong, Y.J.; Qiu, G.Y. Simplifying the revised three-temperature model for remotely estimating regional evapotranspiration and its application to a semi-arid steppe. Int. J. Remote Sens. 2014, 35, 2003–2027. [Google Scholar]
- Tian, F.; Qiu, G.Y.; Lü, Y.H.; Yang, Y.H.; Xiong, Y. Use of high-resolution thermal infrared remote sensing and “three-temperature model” for transpiration monitoring in arid inland river catchment. J. Hydrol. 2014, 515, 307–315. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Xiong, Y.J.; Qiu, G.Y.; Zhang, Q.T. Is scale really a challenge in evapotranspiration estimation? A multi-scale study in the Heihe oasis using thermal remote sensing and the three-temperature model. Agric. For. Meteorol. 2016, 230–231, 128–141. [Google Scholar] [CrossRef]
| Parameter | Sensor Type | Measuring Height (m) | Sensor Resolution |
|---|---|---|---|
| Humidity & temperature | 225-050YA, Novalynx, Grass Valley, CA, USA | 2.0; 1.5 | ±3%, ±0.6 °C |
| Wind velocity & direction | 200-WS-02, Novalynx, Grass Valley, CA, USA | 2.0 | ±0.2 m s−1, ±3° |
| Solar radiation | PYP-PA, Apogee, Santa Monica, CA, USA | 2.0 | 10–40 μV/W/m2 |
| Photosynthetic active radiation | QSOA-S, Apogee, Santa Monica, CA USA | 2.0 | <3% |
| Net radiation | 240-100, Novalynx, Grass Valley, CA, USA | 2.0 | <4% |
| Soil heat flux | HFP01, Hukseflux, Center Moriches, NY, USA | −0.05; −0.02 | 50 μV/W/m2 |
| Temperature (°C) | Humidity (%) | Solar Radiation (W m−2) | Net Radiation (W m−2) | PAR (μmol m−2 s−1) | Wind Velocity (m s−1) | ||
|---|---|---|---|---|---|---|---|
| 2014 | August | 29.54 | 78.05 | 338.37 | 114.50 | 811.67 | 0.20 |
| September | 28.71 | 78.76 | 328.72 | 99.55 | 742.48 | 0.15 | |
| October | 25.84 | 67.69 | 330.94 | 87.70 | 752.03 | 0.14 | |
| November | 22.43 | 69.74 | 218.73 | 48.85 | 512.17 | 0.13 | |
| December | 15.02 | 61.05 | 185.56 | 30.16 | 410.66 | 0.13 | |
| 2015 | January | 15.46 | 63.31 | 255.55 | 47.21 | 593.47 | 0.18 |
| February | 17.95 | 61.27 | 229.06 | 52.06 | 534.66 | 0.23 | |
| March | 20.99 | 66.51 | 189.85 | 51.55 | 454.87 | 0.23 | |
| April | 23.73 | 60.19 | 267.57 | 75.51 | 600.84 | 0.25 | |
| May | 27.89 | 63.81 | 244.54 | 87.11 | 593.97 | 0.34 | |
| June | 30.20 | 57.10 | 350.27 | 134.23 | 825.46 | 0.34 | |
| July | 29.50 | 58.25 | 296.17 | 111.68 | 717.60 | 0.24 | |
| August | 29.24 | 60.31 | 331.55 | 112.52 | 789.94 | 0.12 | |
| September | 28.42 | 59.37 | 324.23 | 97.43 | 768.37 | 0.12 |
| Month | Temperature | RH | PAR | Wind Velocity |
|---|---|---|---|---|
| August 2014 | 0.257 | 0.244 | 0.653 | 0.194 |
| September 2014 | 0.034 | 0.018 | 0.917 | −0.182 |
| October 2014 | 0.105 | −0.006 | 0.792 | 0.307 |
| November 2014 | −0.157 | −0.130 | 0.758 | −0.012 |
| December 2014 | 0.079 | −0.023 | 0.665 | −0.092 |
| January 2015 | −0.289 | −0.263 | 0.772 | 0.157 |
| February 2015 | 0.014 | 0.046 | 0.784 | −0.225 |
| March 2015 | −0.087 | −0.031 | 0.850 | 0.158 |
| April 2015 | −0.157 | −0.093 | 0.892 | 0.067 |
| May 2015 | 0.598 | 0.582 | 0.885 | −0.316 |
| June 2015 | −0.072 | −0.022 | 0.862 | −0.028 |
| July 2015 | −0.255 | −0.272 | 0.769 | 0.045 |
| August 2015 | −0.213 | −0.229 | 0.815 | −0.161 |
| September 2015 | −0.275 | −0.273 | 0.764 | −0.121 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, G.; Tan, S.; Wang, Y.; Yu, X.; Yan, C. Characteristics of Evapotranspiration of Urban Lawns in a Sub-Tropical Megacity and Its Measurement by the ‘Three Temperature Model + Infrared Remote Sensing’ Method. Remote Sens. 2017, 9, 502. https://doi.org/10.3390/rs9050502
Qiu G, Tan S, Wang Y, Yu X, Yan C. Characteristics of Evapotranspiration of Urban Lawns in a Sub-Tropical Megacity and Its Measurement by the ‘Three Temperature Model + Infrared Remote Sensing’ Method. Remote Sensing. 2017; 9(5):502. https://doi.org/10.3390/rs9050502
Chicago/Turabian StyleQiu, Guoyu, Shenglin Tan, Yue Wang, Xiaohui Yu, and Chunhua Yan. 2017. "Characteristics of Evapotranspiration of Urban Lawns in a Sub-Tropical Megacity and Its Measurement by the ‘Three Temperature Model + Infrared Remote Sensing’ Method" Remote Sensing 9, no. 5: 502. https://doi.org/10.3390/rs9050502
APA StyleQiu, G., Tan, S., Wang, Y., Yu, X., & Yan, C. (2017). Characteristics of Evapotranspiration of Urban Lawns in a Sub-Tropical Megacity and Its Measurement by the ‘Three Temperature Model + Infrared Remote Sensing’ Method. Remote Sensing, 9(5), 502. https://doi.org/10.3390/rs9050502