Learning Dual Multi-Scale Manifold Ranking for Semantic Segmentation of High-Resolution Images
Abstract
:1. Introduction
2. Related Work
3. Manifold Ranking Formulation
3.1. Binary Manifold Ranking
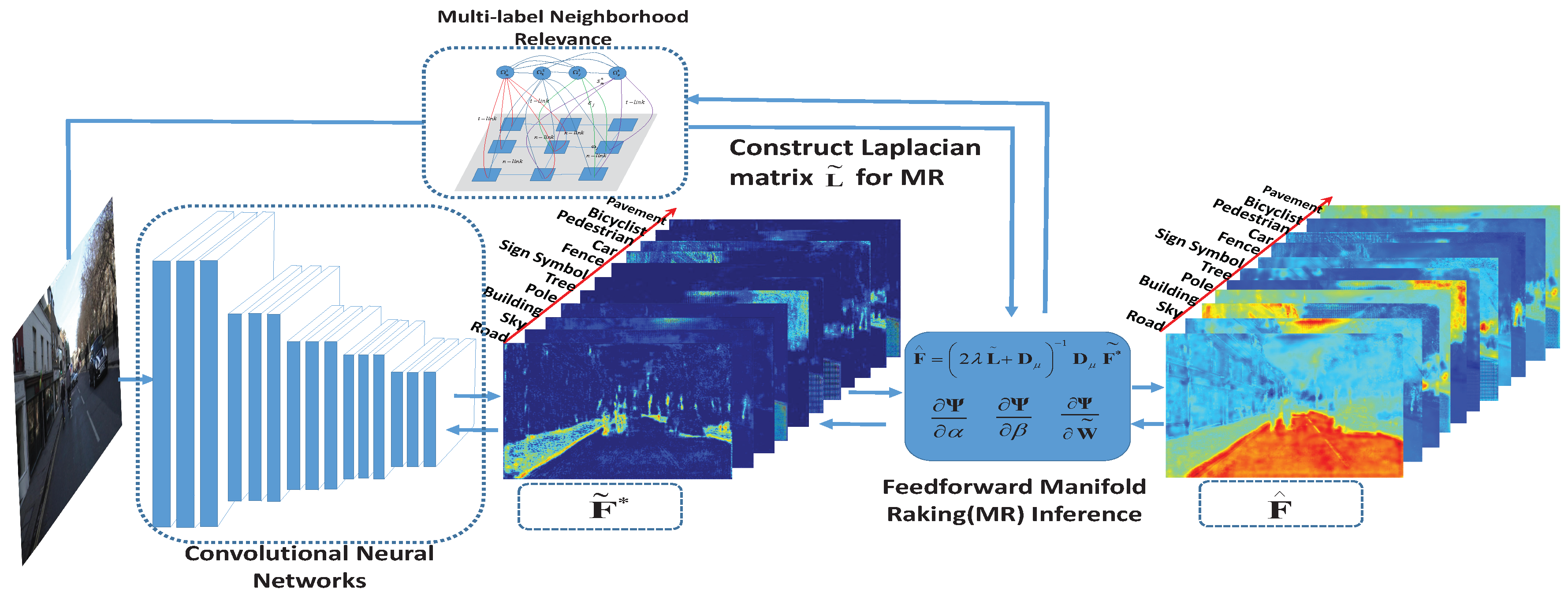
3.2. Multi-Label Manifold Ranking
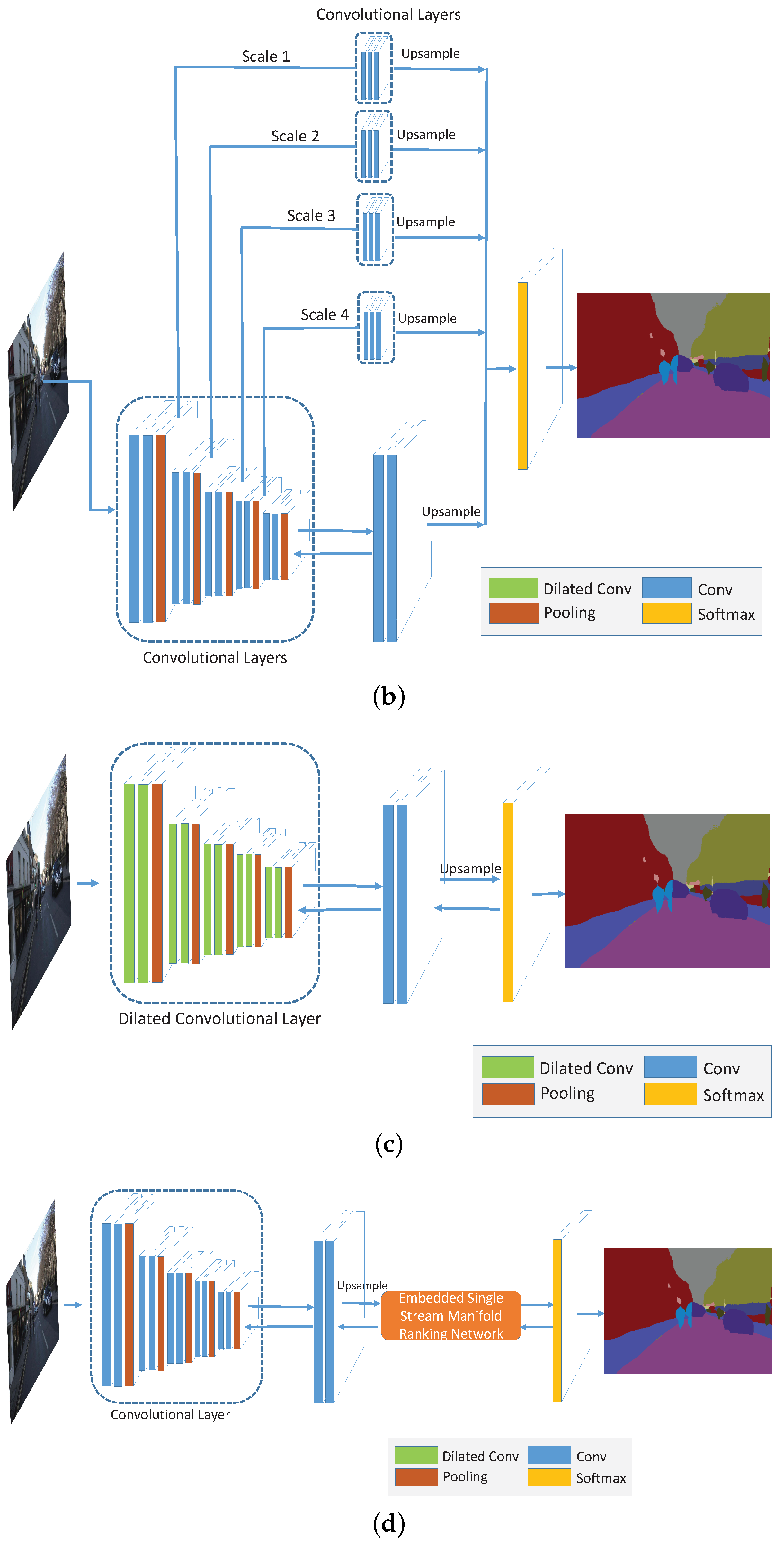
4. Deep Multi-Scale Manifold Ranking Network
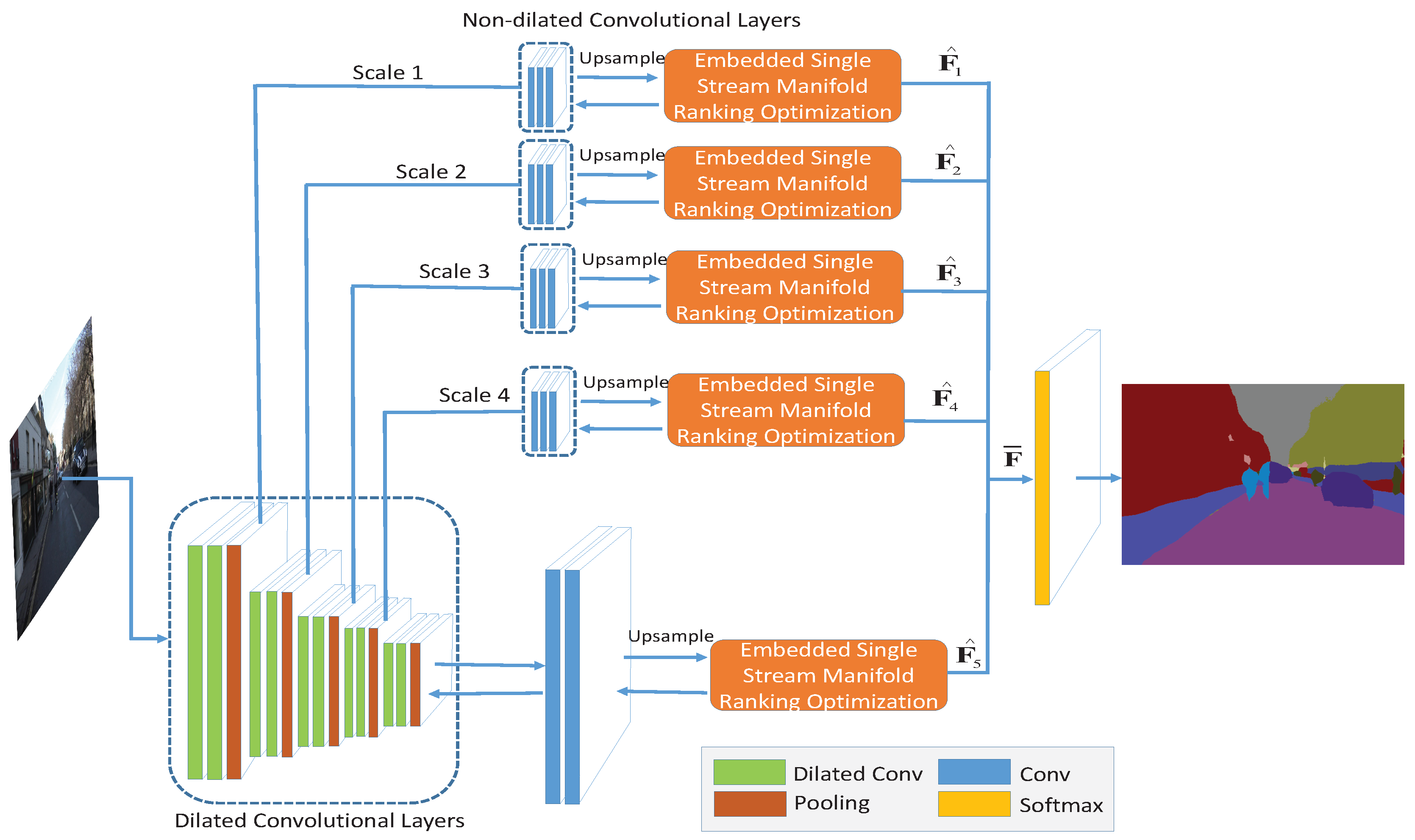
4.1. Embedded Feedforward Single Stream Manifold Ranking Optimization
4.1.1. Manifold Ranking Inference
4.1.2. Derivative to Smoothness Coefficients
4.1.3. Derivative to Compatibility Matrix
4.2. Dual Multi-Scale Manifold Ranking Network
5. Experiments
5.1. Experiment on Close-Range Dataset
5.1.1. Evaluation on PASCAL VOC
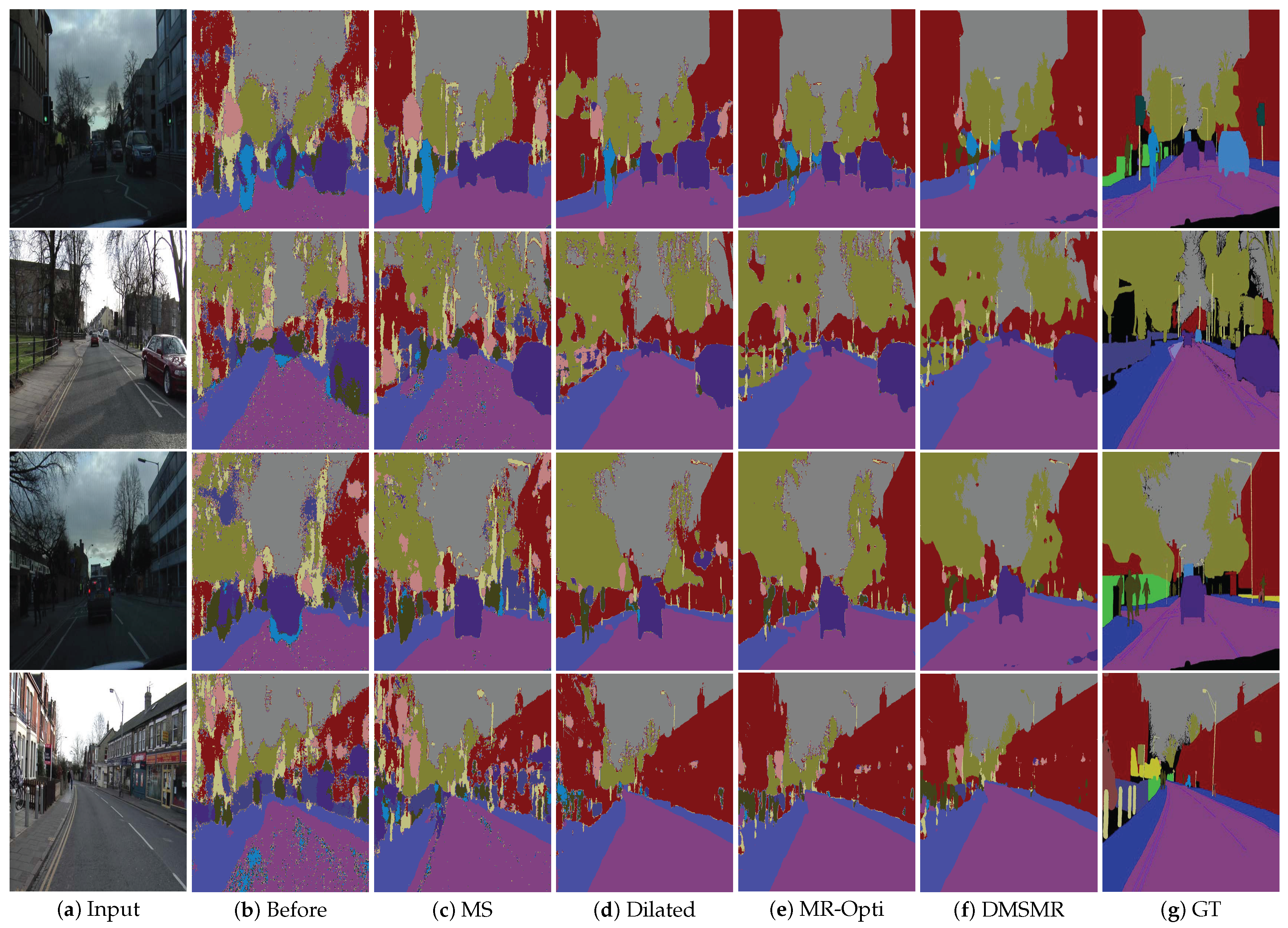
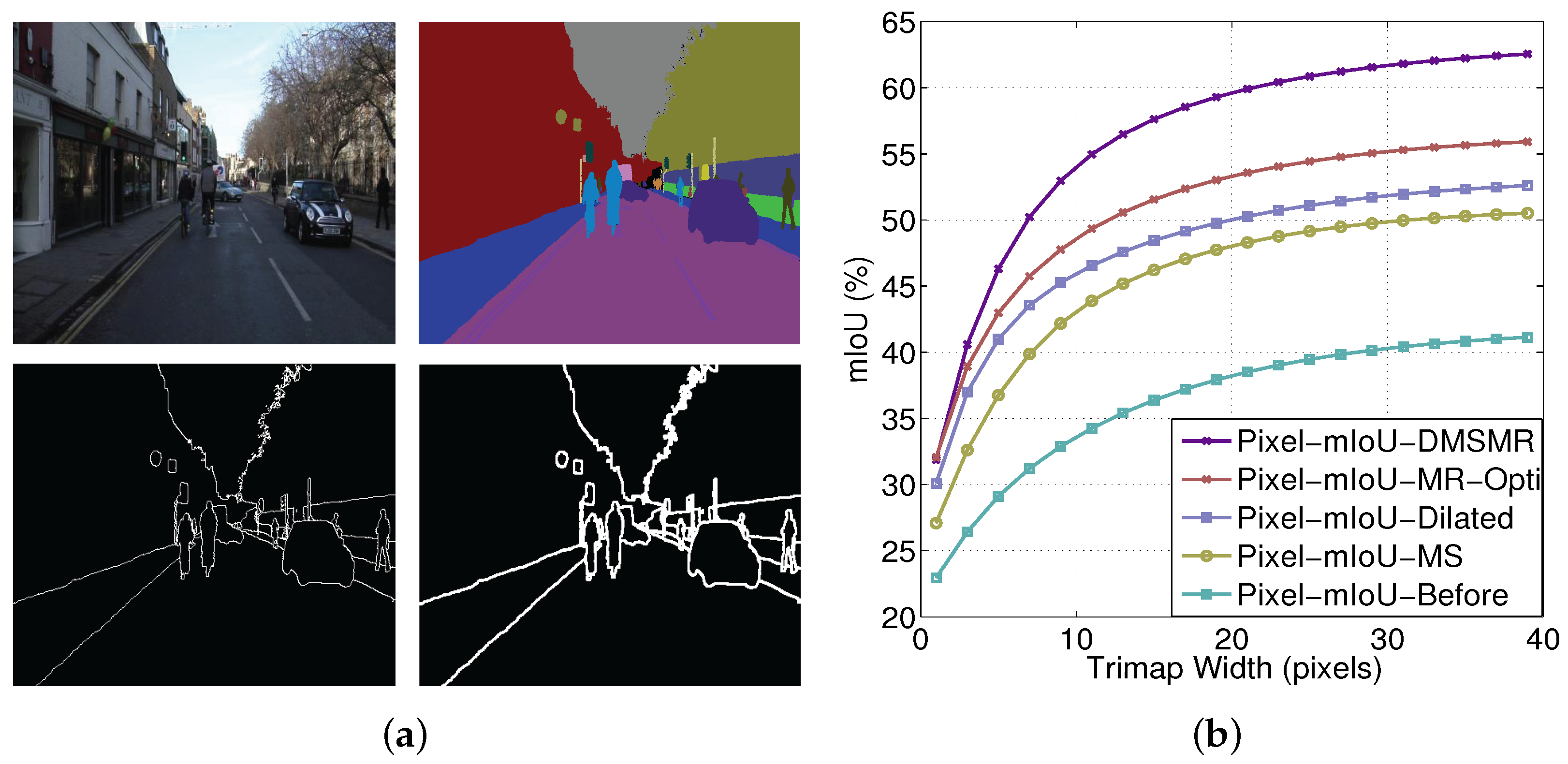
5.1.2. Evaluation on CamVid
5.2. Experiment on High Resolution Remote Sensing Dataset
5.2.1. Evaluation on Vaihingen Dataset
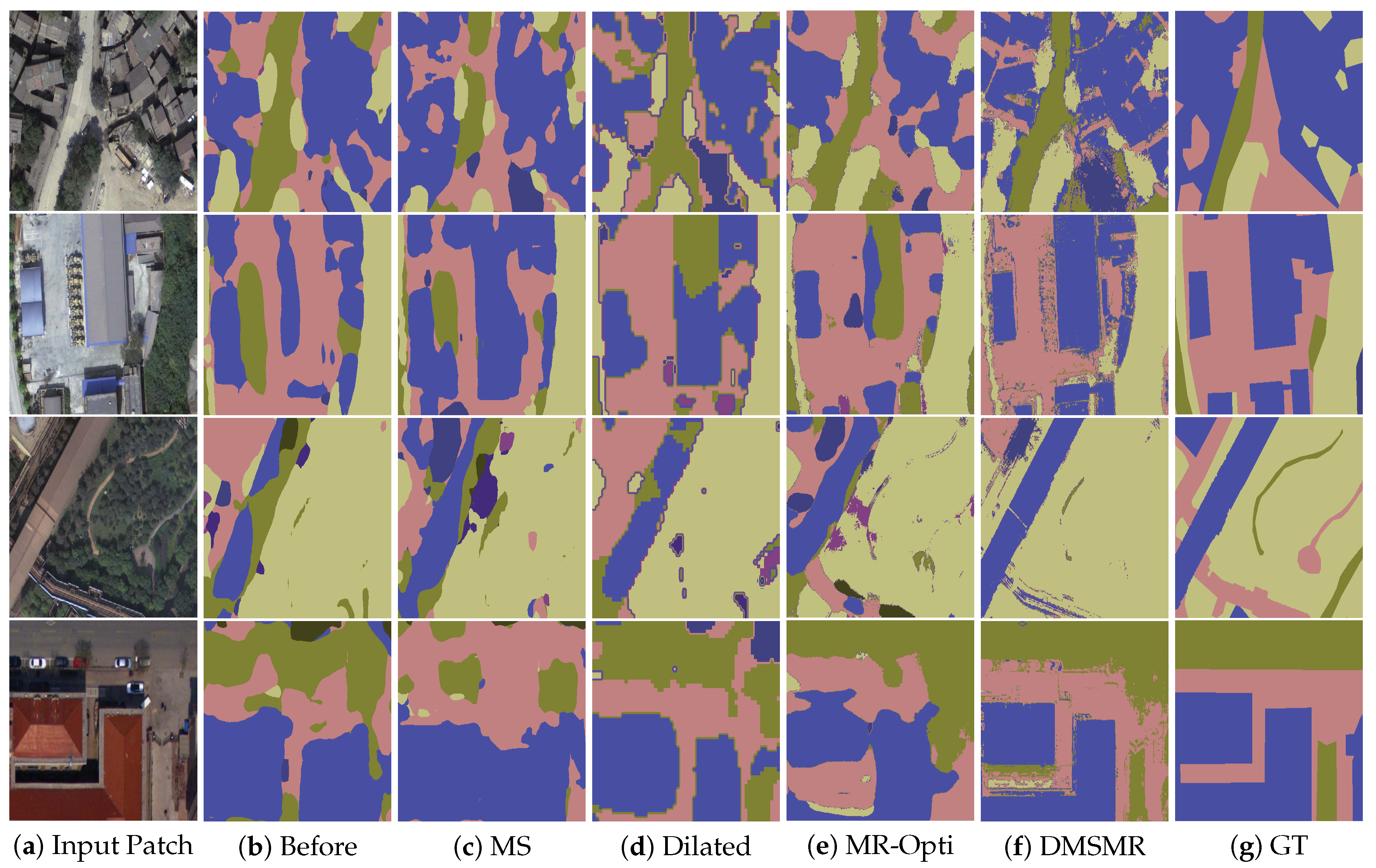
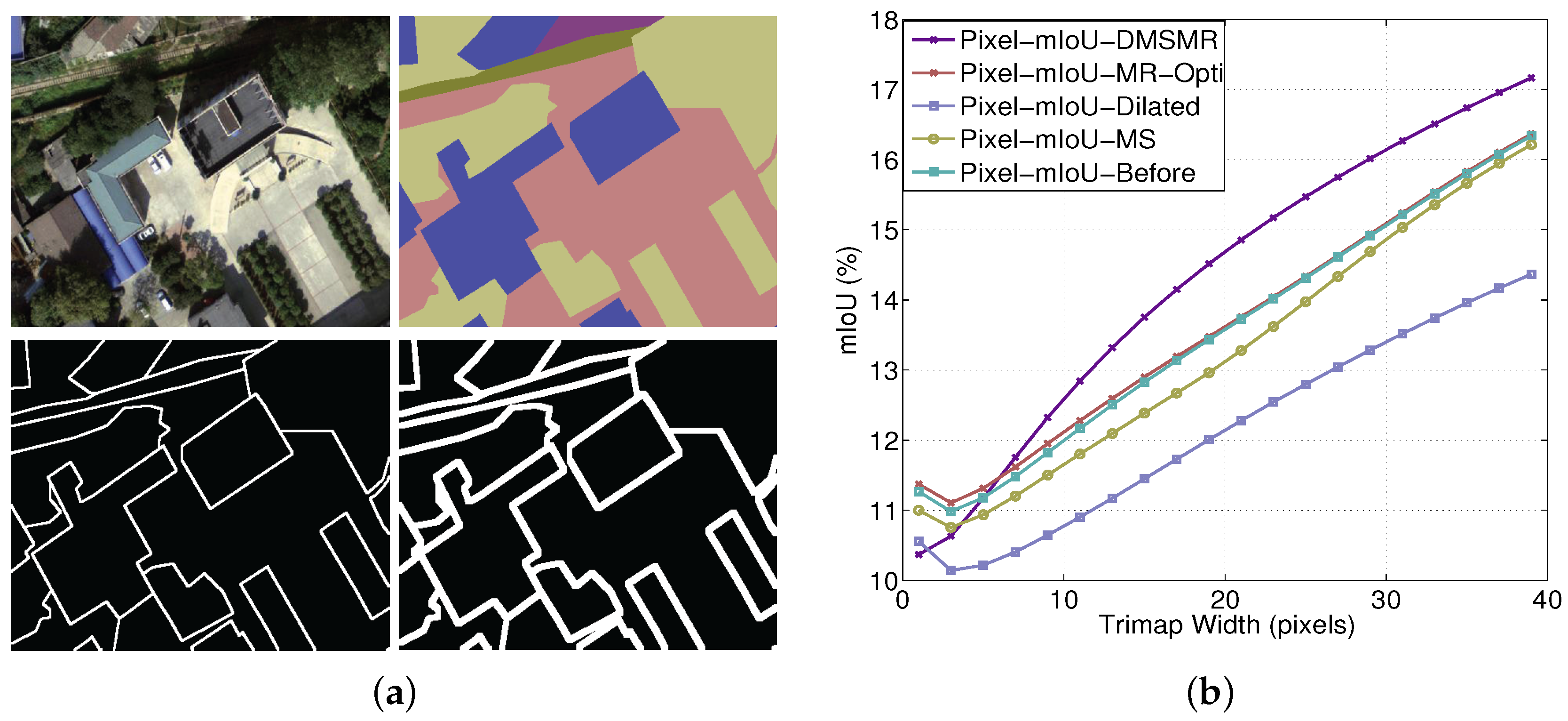
5.2.2. Evaluation on EvLab-SS Dataset
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
Appendix A.1. Learning Parameter α and β
Appendix A.2. Learning Compatibility Matrix
Appendix A.3. Network with Different Strategies
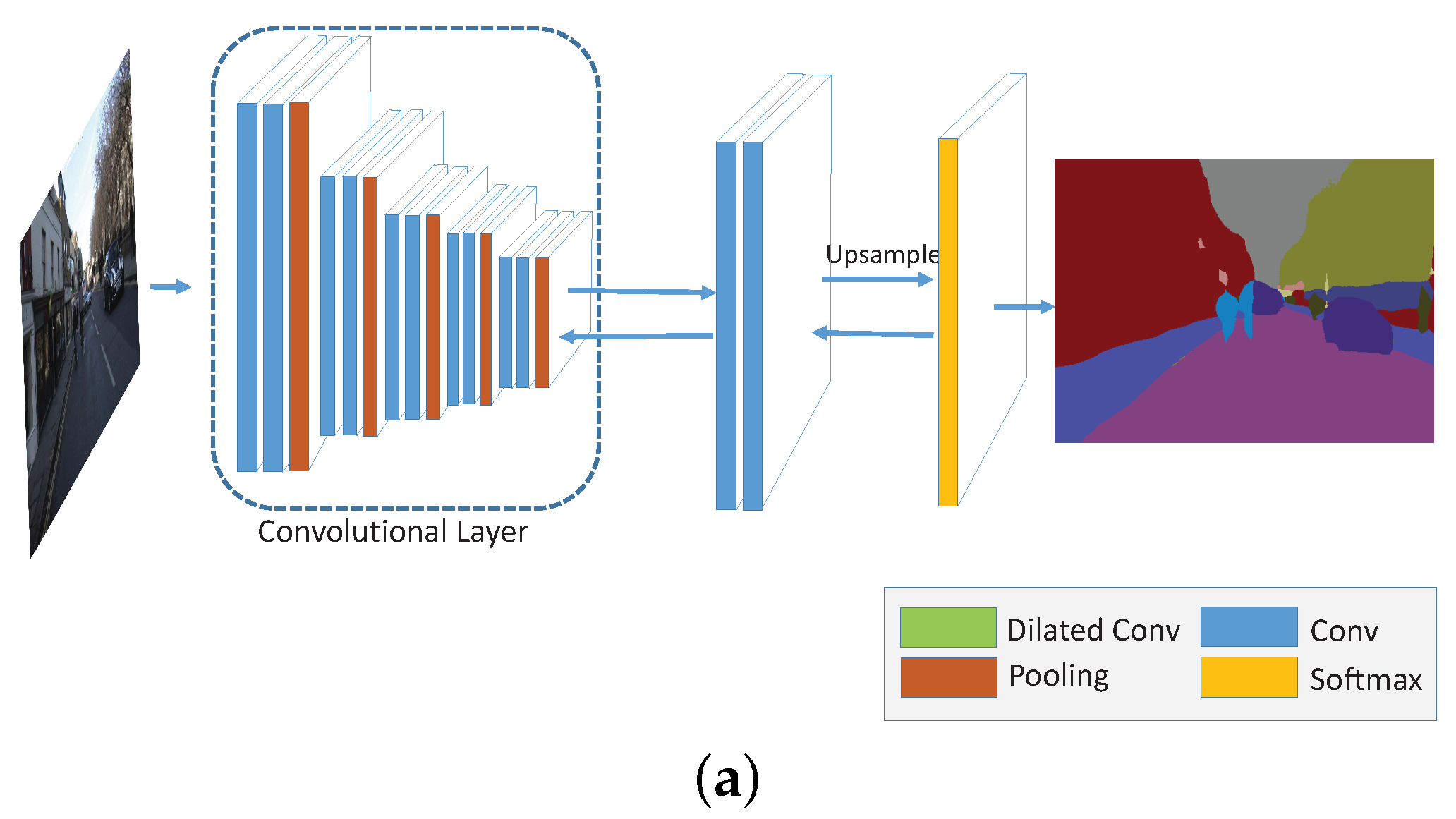
| (a) Networks before Employing the Strategies (Before) | ||||||
| Block | Name | Kernel Size | Pad | Dilation | Stride | Number of Output |
| 0 | input | - | - | - | - | 3 |
| 1 | conv1-1 | 3 × 3 | 1 | 1 | 1 | 64 |
| conv1-2 | 3 × 3 | 1 | 1 | 1 | 64 | |
| pool1 | 3 × 3 | 1 | 0 | 1 | 64 | |
| 2 | conv2-1 | 3 × 3 | 1 | 1 | 1 | 128 |
| conv2-2 | 3 × 3 | 1 | 1 | 1 | 128 | |
| pool2 | 3 × 3 | 1 | 0 | 2 | 128 | |
| 3 | conv3-1 | 3 × 3 | 1 | 1 | 1 | 256 |
| conv3-2 | 3 × 3 | 1 | 1 | 1 | 256 | |
| pool3 | 3 × 3 | 1 | 0 | 2 | 256 | |
| 4 | conv4-1 | 3 × 3 | 1 | 1 | 1 | 512 |
| conv4-2 | 3 × 3 | 1 | 1 | 1 | 512 | |
| pool4 | 3 × 3 | 1 | 0 | 1 | 512 | |
| 5 | conv5-1 | 5 × 5 | 2 | 1 | 1 | 512 |
| conv5-2 | 5 × 5 | 2 | 1 | 1 | 512 | |
| pool5 | 3 × 3 | 1 | 0 | 1 | 512 | |
| - | fc6 | 3 × 3 | 1 | 1 | 1 | 1024 |
| fc7 | 1 × 1 | 0 | 1 | 1 | 1024 | |
| * | fc8 | 1 × 1 | 0 | 1 | 1 | 12 |
| - | output | 1 × 1 | 0 | 1 | 1 | 12 |
| (b) Networks Using Multi-Scale Strategy (MS) | ||||||
| Scale (Block) | Name | Kernel Size | Pad | Dilation | Stride | Number of Output |
| 0 | input | - | - | - | - | 3 |
| 1 | conv1-1 | 3 × 3 | 1 | 1 | 1 | 64 |
| conv1-2 | 3 × 3 | 1 | 1 | 1 | 64 | |
| pool1 | 3 × 3 | 1 | 0 | 2 | 64 | |
| 2 | conv2-1 | 3 × 3 | 1 | 1 | 1 | 128 |
| conv2-2 | 3 × 3 | 1 | 1 | 1 | 128 | |
| pool2 | 3 × 3 | 1 | 0 | 2 | 128 | |
| 3 | conv3-1 | 3 × 3 | 1 | 1 | 1 | 256 |
| conv3-2 | 3 × 3 | 1 | 1 | 1 | 256 | |
| pool3 | 3 × 3 | 1 | 0 | 2 | 256 | |
| 4 | conv4-1 | 3 × 3 | 1 | 1 | 1 | 512 |
| conv4-2 | 3 × 3 | 1 | 1 | 1 | 512 | |
| pool4 | 3 × 3 | 1 | 0 | 1 | 512 | |
| 5 | conv5-1 | 5 × 5 | 2 | 1 | 1 | 512 |
| conv5-2 | 5 × 5 | 2 | 1 | 1 | 512 | |
| pool5 | 3 × 3 | 1 | 0 | 1 | 512 | |
| - | fc6 | 3 × 3 | 1 | 1 | 1 | 1024 |
| fc7 | 1 × 1 | 0 | 1 | 1 | 1024 | |
| * | fc8 | 1 × 1 | 0 | 1 | 1 | 12 |
| 1 | pool1-conv-1 | 3 × 3 | 1 | 1 | 4 | 128 |
| pool1-conv-2 | 1 × 1 | 0 | 1 | 1 | 128 | |
| pool1-conv-3 | 1 × 1 | 0 | 1 | 1 | 12 | |
| 2 | pool2-conv-1 | 3 × 3 | 1 | 1 | 2 | 128 |
| pool2-conv-2 | 1 × 1 | 0 | 1 | 1 | 128 | |
| pool2-conv-3 | 1 × 1 | 0 | 1 | 1 | 12 | |
| 3 | pool3-conv-1 | 3 × 3 | 1 | 1 | 1 | 128 |
| pool3-conv-2 | 1 × 1 | 0 | 1 | 1 | 128 | |
| pool3-conv-3 | 1 × 1 | 0 | 1 | 1 | 12 | |
| 4 | pool4-conv-1 | 3 × 3 | 1 | 1 | 1 | 128 |
| pool4-conv-2 | 1 × 1 | 0 | 1 | 1 | 128 | |
| pool4-conv-3 | 1 × 1 | 0 | 1 | 1 | 12 | |
| - | output | 1 × 1 | 0 | 1 | 1 | 12 |
| (c) Networks Using Dilated Method (Dilated) | ||||||
| Block | Name | Kernel Size | Pad | Dilation | Stride | Number of Output |
| 0 | input | - | - | - | - | 3 |
| 1 | conv1-1 | 3 × 3 | 6 | 6 | 1 | 64 |
| conv1-2 | 3 × 3 | 6 | 6 | 1 | 64 | |
| pool1 | 3 × 3 | 1 | 0 | 2 | 64 | |
| 2 | conv2-1 | 3 × 3 | 4 | 4 | 1 | 128 |
| conv2-2 | 3 × 3 | 4 | 4 | 1 | 128 | |
| pool2 | 3 × 3 | 1 | 0 | 2 | 128 | |
| 3 | conv3-1 | 3 × 3 | 2 | 2 | 1 | 256 |
| conv3-2 | 3 × 3 | 2 | 2 | 1 | 256 | |
| pool3 | 3 × 3 | 1 | 0 | 2 | 256 | |
| 4 | conv4-1 | 3 × 3 | 2 | 2 | 1 | 512 |
| conv4-2 | 3 × 3 | 2 | 2 | 1 | 512 | |
| pool4 | 3 × 3 | 1 | 0 | 1 | 512 | |
| 5 | conv5-1 | 3 × 3 | 2 | 2 | 1 | 512 |
| conv5-2 | 3 × 3 | 2 | 2 | 1 | 512 | |
| pool5 | 3 × 3 | 1 | 0 | 1 | 512 | |
| - | fc6 | 3 × 3 | 1 | 1 | 1 | 1024 |
| fc7 | 1 × 1 | 0 | 1 | 1 | 1024 | |
| * | fc8 | 1 × 1 | 0 | 1 | 1 | 12 |
| - | output | 1 × 1 | 0 | 1 | 1 | 12 |
| (d) Networks Using Manifold Ranking Optimization (MR-Opti) | ||||||
| Block | Name | Kernel Size | Pad | Dilation | Stride | Number of Output |
| 0 | input | - | - | - | - | 3 |
| 1 | conv1-1 | 3 × 3 | 1 | 1 | 1 | 64 |
| conv1-2 | 3 × 3 | 1 | 1 | 1 | 64 | |
| pool1 | 3 × 3 | 1 | 0 | 1 | 64 | |
| 2 | conv2-1 | 3 × 3 | 1 | 1 | 1 | 128 |
| conv2-2 | 3 × 3 | 1 | 1 | 1 | 128 | |
| pool2 | 3 × 3 | 1 | 0 | 2 | 128 | |
| 3 | conv3-1 | 3 × 3 | 1 | 1 | 1 | 256 |
| conv3-2 | 3 × 3 | 1 | 1 | 1 | 256 | |
| pool3 | 3 × 3 | 1 | 0 | 2 | 256 | |
| 4 | conv4-1 | 3 × 3 | 1 | 1 | 1 | 512 |
| conv4-2 | 3 × 3 | 1 | 1 | 1 | 512 | |
| pool4 | 3 × 3 | 1 | 0 | 1 | 512 | |
| 5 | conv5-1 | 5 × 5 | 2 | 1 | 1 | 512 |
| conv5-2 | 5 × 5 | 2 | 1 | 1 | 512 | |
| pool5 | 3 × 3 | 1 | 0 | 1 | 512 | |
| - | fc6 | 3 × 3 | 1 | 1 | 1 | 1024 |
| fc7 | 1 × 1 | 0 | 1 | 1 | 1024 | |
| * | fc8 | 1 × 1 | 0 | 1 | 1 | 12 |
| - | Manifold Ranking Optimization | 12 | ||||
| - | output | 1 × 1 | 0 | 1 | 1 | 12 |
References
- Ladicky, L.; Torr, P.; Zisserman, A. Human Pose Estimation using a Joint Pixel-wise and Part-wise Formulation. In Proceedings of the 2013 IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013. [Google Scholar]
- Romera, E.; Bergasa, L.; Arroyo, R. Can we unify monocular detectors for autonomous driving by using the pixel-wise semantic segmentation of CNNs? arXiv, 2016; arXiv:1607.00971. [Google Scholar]
- Barrnes, D.; Maddern, W.; Posner, I. Find Your Own Way: Weakly-Supervised Segmentation of Path Proposals for Urban Autonomy. arXiv, 2016; arXiv:1610.01238. [Google Scholar]
- Kendall, A.; Cipolla, R. Modelling Uncertainty in Deep Learning for Camera Relocalization. arXiv, 2015; arXiv:1509.05909. [Google Scholar]
- Xiao, J.; Quan, L. Multiple View Semantic Segmentation for Street View Images. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009. [Google Scholar]
- Floros, G.; Leibe, B. Joint 2D-3D Temporally Consistent Semantic Segmentation of Street Scenes. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012. [Google Scholar]
- Huval, B.; Wang, T.; Tandon, S.; Kiske, J.; Song, W.; Pazhayampallil, J.; Mujica, F. An empirical evaluation of deep learning on highway driving. arXiv, 2015; arXiv:1504.01716. [Google Scholar]
- Chen, C.; Seff, A.; Kornhauser, A.; Xiao, J. Deepdriving: Learning affordance for direct perception in autonomous driving. In Proceedings of the 2015 IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015. [Google Scholar]
- Toshev, A.; Szegedy, C. DeepPose: Human Pose Estimation via Deep Neural Networks. arXiv, 2014; arXiv:1312.4659. [Google Scholar]
- Tompson, J.J.; Jain, A.; LeCun, Y.; Bregler, C. Joint training of a convolutional network and a graphical model for human pose estimation. arXiv, 2014; arXiv:1406.2984. [Google Scholar]
- Jackson, A.; Valstar, M.; Tzimiropoulos, G. A CNN Cascade for Landmark Guided Semantic Part Segmentation. arXiv, 2016; arXiv:1609.09642. [Google Scholar]
- Maggiori, E.; Tarabalka, Y.; Charpiat, G.; Alliez, P. High-Resolution Semantic Labeling with Convolutional Neural Networks. arXiv, 2016; arXiv:1611.01962. [Google Scholar]
- Kampffmeyer, M.; Salberg, A.B.; Jenssen, R. Semantic segmentation of small objects and modeling of uncertainty in urban remote sensing images using deep convolutional neural networks. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Las Vegas, NV, USA, 26 June–1 July 2016. [Google Scholar]
- Audebert, N.; Saux, B.L.; Lefèvre, S. Semantic Segmentation of Earth Observation Data Using Multimodal and Multi-scale Deep Networks. arXiv, 2016; arXiv:1609.06846. [Google Scholar]
- Längkvist, M.; Kiselev, A.; Alirezaie, M.; Loutfi, A. Classification and segmentation of satellite orthoimagery using convolutional neural networks. Remote Sens. 2016, 8, 329. [Google Scholar] [CrossRef]
- Muruganandham, S. Semantic Segmentation of Satellite Images Using Deep Learning. Master’s Thesis, Department of Computer Science, Electrical and Space Engineering, Luleå University of Technology, Luleå, Sweden, 2016. [Google Scholar]
- Wu, Z.; Song, S.; Khosla, A.; Yu, F.; Zhang, L.; Tang, X.; Xiao, J. 3d Shapenets: A Deep Representation for Volumetric Shapes; Princeton University: Princeton, NJ, USA, 2015. [Google Scholar]
- Kendall, A.; Grimes, M.; Cipolla, R. PoseNet: A Convolutional Network for Real-Time 6-DOF Camera Relocalization. arXiv, 2016; arXiv:1505.07427. [Google Scholar]
- Barron, J.T.; Poole, B. The fast bilateral solver. arXiv, 2016; arXiv:1511.03296. [Google Scholar]
- Mostajabi, M.; Yadollahpour, P.; Shakhnarovich, G. Feedforward semantic segmentation with zoom-out features. arXiv, 2015; arXiv:1412.0774v1. [Google Scholar]
- Dai, J.; He, K.; Sun, J. Instance-aware Semantic Segmentation via Multi-task Network Cascades. arXiv, 2015; arXiv:1512.04412. [Google Scholar]
- Shelhamer, E.; Long, J.; Darrell, T. Fully Convolutional Networks for Semantic Segmentation. arXiv, 2015; arXiv:1605.06211. [Google Scholar]
- Yu, F.; Koltun, V. Multi-Scale Context Aggregation by Dilated Convolutions. arXiv, 2016; arXiv:1511.07122. [Google Scholar]
- Chen, L.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A. DeepLab: Semantic Image Segmentation with Deep Convolutional Nets, Atrous Convolution, and Fully Connected CRFs. arXiv, 2015; arXiv:1606.00915. [Google Scholar]
- Zheng, S.; Jayasumana, S.; Paredes, B.; Vineet, V.; Su, Z.; Du, D.; Huang, C.; Torr, P. Conditional Random Fields as Recurrent Neural Networks. arXiv, 2015; arXiv:1502.03240. [Google Scholar]
- Chandra, S.; Kokkinos, I. Fast, Exact and Multi-Scale Inference for Semantic Image Segmentation with Deep Gaussian CRFs. arXiv, 2016; arXiv:1603.08358. [Google Scholar]
- Badrinarayanan, V.; Handa, A.; Cipolla, R. SegNet: A Deep Convolutional Encoder-Decoder Architecture for Image Segmentation. arXiv, 2015; arXiv:1511.00561. [Google Scholar]
- Hyeonwoo, N.; Hong, S.; Han, B. Learning deconvolution network for semantic segmentation. arXiv, 2015; arXiv:1505.04366. [Google Scholar]
- Lin, G.; Shen, C.; Hengel, A.; Reid, I. Efficient piecewise training of deep structured models for semantic segmentation. arXiv, 2016; arXiv:1504.01013. [Google Scholar]
- Eigen, D.; Fergus, R. Predicting Depth, Surface Normals and Semantic Labels with a Common Multi-Scale Convolutional Architecture. arXiv, 2015; arXiv:1411.4734. [Google Scholar]
- Chen, L.; Schwing, A.; Yuille, A.; Urtasun, R. Learning Deep Structured Models. arXiv, 2015; arXiv:1407.2538. [Google Scholar]
- Chen, L.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A. Semantic Image Segmentation with Deep Convolutional Nets and Fully Connected CRFs. arXiv, 2015; arXiv:1412.7062. [Google Scholar]
- Krähenbühl, P.; Koltun, V. Efficient Inference in Fully Connected CRFs with Gaussian Edge Potentials. arXiv, 2012; arXiv:1210.5644. [Google Scholar]
- Arnab, A.; Jayasumana, S.; Zheng, S.; Torr, P. Higher Order Conditional Random Fields in Deep Neural Networks. arXiv, 2016; arXiv:1511.08119. [Google Scholar]
- Vemulapalli, R.; Tuzel, O.; Liu, M.; Chellappa, R. Gaussian Conditional Random Field Network for Semantic Segmentation. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Zhou, D.; Weston, J.; Gretton, A.; Bousquent, O.; Scholkopf, B. Ranking on data manifolds. In Proceedings of the 16th International Conference on Neural Information Processing Systems, Whistler, BC, Canada, 9–11 December 2003. [Google Scholar]
- Zhou, D.; Bousquent, O.; Lal, T.; Weston, J.; Scholkopf, B. Learning with Local and Global Consistency. In Proceedings of the 16th International Conference on Neural Information Processing Systems, Whistler, BC, Canada, 9–11 December 2003. [Google Scholar]
- Yang, C.; Zhang, L.; Lu, H.; Ruan, X.; Yang, M. Saliency Detection via Graph-Based Manifold Ranking. In Proceedings of the 2013 IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013. [Google Scholar]
- Bencherif, M.A.; Bazi, Y.; Guessoum, A.; Alajlan, N.; Melgani, F.; AlHichri, H. Fusion of Extreme Learning Machine and Graph-Based Optimization Methods for Active Classification of Remote Sensing Images. IEEE Geosci. Remote Sens. Lett. 2015, 12, 527–531. [Google Scholar] [CrossRef]
- Krähenbühl, P.; Koltun, V. Parameter Learning and Convergent Inference for Dense Random Fields. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013. [Google Scholar]
- Gupta, S.; Girshick, R.; Arbeláez, P.; Malik, J. Learning Rich Features from RGB-D Images for Object Detection and Segmentation. arXiv, 2014; arXiv:1407.5736. [Google Scholar]
- Hariharan, B.; Arbeláez, P.; Girshick, R.; Malik, J. Simultaneous Detection and Segmentation. arXiv, 2014; arXiv:1407.1808. [Google Scholar]
- Dai, J.; He, K.; Sun, J. Convolutional Feature Masking for Joint Object and Stuff Segmentation. arXiv, 2015; arXiv:1412.1283. [Google Scholar]
- Farabet, C.; Couprie, C.; Najman, L.; LeCun, Y. Learning Hierarchical Features for Scene Labeling. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1915–1929. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Yang, Y.; Wang, J.; Xu, W.; Yuille, A. Attention to Scale: Scale-aware Semantic Image Segmentation. arXiv, 2016; arXiv:1511.03339. [Google Scholar]
- Bearman, A.; Russakovsky, O.; Ferrari, V.; Li, F.F. What’s the Point: Semantic Segmentation with Point Supervision. arXiv, 2016; arXiv:1506.02106. [Google Scholar]
- Romero, A.; Gatta, C.; Camps-Valls, G. Unsupervised Deep Feature Extraction for Remote Sensing Image Classification. IEEE Trans. Geosci. Remote Sens. 2015, 54, 1349–1362. [Google Scholar] [CrossRef]
- Campos-Taberner, M.; Romero-Soriano, A.; Gatta, C.; Camps-Valls, G.; Lagrange, A.; Le Saux, B.; Randrianarivo, H. Processing of Extremely High-Resolution LiDAR and RGB Data: Outcome of the 2015 IEEE GRSS Data Fusion Contest–Part A: 2-D Contest. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 5547–5559. [Google Scholar] [CrossRef]
- Tschannen, M.; Cavigelli, L.; Mentzer, F.; Wiatowski, T.; Benini, L. Deep Structured Features for Semantic Segmentation. arXiv, 2016; arXiv:1609.07916. [Google Scholar]
- Piramanayagam, S.; Schwartzkopf, W.; Koehler, F.W.; Saber, E. Classification of remote sensed images using random forests and deep learning framework. SPIE Remote Sens. Int. Soc. Opt. Photonics 2016. [Google Scholar] [CrossRef]
- Marcu, A.; Leordeanu, M. Dual Local-Global Contextual Pathways for Recognition in Aerial Imagery. arXiv, 2016; arXiv:1605.05462. [Google Scholar]
- Yuan, Y.; Lin, J.; Wang, Q. Dual-clustering-based hyperspectral band selection by contextual analysis. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1431–1445. [Google Scholar] [CrossRef]
- Kendall, A.; Badrinarayanan, V.; Cipolla, R. Bayesian SegNet: Model Uncertainty in Deep Convolutional Encoder-Decoder Architectures for Scene Understanding. arXiv, 2015; arXiv:1511.02680. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv, 2015; arXiv:1409.1556. [Google Scholar]
- Hong, S.; Noh, H.; Han, B. Decoupled Deep Neural Network for Semi-supervised Semantic Segmentation. arXiv, 2015; arXiv:1506.04924. [Google Scholar]
- Audebert, N.; Saux, B.L.; Lefèvre, S. Segment-before-Detect: Vehicle Detection and Classification through Semantic Segmentation of Aerial Images. Remote Sens. 2017, 9, 368. [Google Scholar] [CrossRef]
- Huang, Z.; Cheng, G.; Wang, H.; Li, H.; Shi, L.; Pan, C. Building extraction from multi-source remote sensing images via deep deconvolution neural networks. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016. [Google Scholar]
- Audebert, N.; Boulch, A.; Lagrange, A.; Le Saux, B.; Lefevre, S. Deep Learning for Remote Sensing; Technical Report; ONERA The French Aerospace Lab, DTIM & Univ. Bretagne-Sud & ENSTA ParisTech: Palaiseau, France, 2016. [Google Scholar]
- Paisitkriangkrai, S.; Sherrah, J.; Janney, P.; Hengel, V.D. Effective semantic pixel labelling with convolutional networks and conditional random fields. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition Workshops, Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Alam, F.I.; Zhou, J.; Liew, A.W.C.; Jia, X. CRF learning with CNN features for hyperspectral image segmentation. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Beijing, China, 10–15 July 2016. [Google Scholar]
- He, X.; Cai, D.; Niyogi, P. Laplacian Score for Feature Selection. In Proceedings of the 18th International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 5–8 December 2005. [Google Scholar]
- Quan, R.; Han, J.; Zhang, D.; Nie, F. Object co-segmentation via graph optimized-flexible manifold ranking. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Wang, Q.; Lin, J.; Yuan, Y. Salient band selection for hyperspectral image classification via manifold ranking. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 1279–1289. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Zhang, L.; Lu, H. Graph-regularized saliency detection with convex-hull-based center prior. IEEE Signal Process. Lett. 2013, 20, 637–640. [Google Scholar] [CrossRef]
- Xu, B.; Bu, J.; Chen, C.; Cai, D.; He, X.; Liu, W.; Luo, J. Efficient Manifold Ranking for Image Retrieval. In Proceedings of the 34th international ACM SIGIR Conference on Research and Development in Information Retrieval, Beijing, China, 24–28 July 2011. [Google Scholar]
- Hsieh, C.; Han, C.; Shih, J.; Lee, C.; Fan, K. 3D Model Retrieval Using Multiple Features and Manifold Ranking. In Proceedings of the 2015 8th International Conference on Ubi-Media Computing (UMEDIA), Colombo, Sri Lanka, 24–26 August 2015. [Google Scholar]
- Zhou, T.; He, X.; Xie, K.; Fu, K.; Zhang, J.; Yang, J. Robust visual tracking via efficient manifold ranking with low-dimensional compressive features. Pattern Recognit. 2015, 48, 2459–2473. [Google Scholar] [CrossRef]
- Brostow, G.; Shotton, J.; Fauqueur, J.; Cipolla, R. Segmentation and Recognition Using Structure from Motion Point Clouds. In Proceedings of the 10th European Conference on Computer Vision, Marseille, France, 12–18 October 2008. [Google Scholar]
- Brostow, G.; Fauqueur, J.; Cipolla, R. Semantic object classes in video: A high-definition ground truth database. Pattern Recognit. Lett. 2009, 30, 88–97. [Google Scholar] [CrossRef]
- Ruder, S. An overview of gradient descent optimization algorithms. arXiv, 2016; arXiv:1609.04747. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv, 2015; arXiv:1512.03385. [Google Scholar]
- Everingham, M.; Gool, L.; Williams, C.K.I.; Winn, J.; Zisserman, A. The Pascal Visual Object Classes (VOC) Challenge. Int. J. Comput. Vis. 2010, 88, 303–338. [Google Scholar] [CrossRef]
- Rottensteiner, F.; Sohn, G.; Jung, J.; Gerke, M.; Baillard, C.; Benitez, S.; Breitkopf, U. The ISPRS benchmark on urban object classification and 3D building reconstruction. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, I-3, 293–298. [Google Scholar] [CrossRef]
- Glorot, X.; Bordes, A.; Bengio, Y. Deep Sparse Rectifier Neural Networks. In Proceedings of the 14th International Conference on Artificial Intelligence and Statistics, Fort Lauderdale, FL, USA, 11–13 April 2011; Volume 15, pp. 315–323. [Google Scholar]
- Jia, Y.; Shelhamer, E.; Donahue, J.; Karayev, S.; Long, J.; Girshick, R.; Guadarrama, S.; Darrell, T. Caffe: Convolutional Architecture for Fast Feature Embedding. In Proceedings of the 22nd ACM International Conference on Multimedia, Orlando, FL, USA, 3–7 November 2014. [Google Scholar]
- Marmanis, D.; Wegner, J.D.; Galliani, S.; Schindler, K.; Datcu, M.; Stilla, U. Semantic Segmentation of Aerial Images with an Ensemble of CNSS. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 3, 473–480. [Google Scholar] [CrossRef]
- Hariharan, B.; Arbeláez, P.; Bourdev, L.; Maji, S.; Malik, J. Semantic Contours from Inverse Detectors. In Proceedings of the 2011 IEEE International Conference on Computer Vision (ICCV), Barcelona, Spain, 6–13 November 2011. [Google Scholar]
- Zoran, D.; Weiss, Y. From Learning Models of Natural Image Patches to Whole Image Restoration. In Proceedings of the 2011 IEEE International Conference on Computer Vision (ICCV), Barcelona, Spain, 6–13 November 2011. [Google Scholar]
- Lin, T.; Maire, M.; Belongie, S.; Bourdev, L.; Girshick, R.; Hays, J.; Perona, P.; Ramanan, D.; Zitnick, C.; Dollár, P. Microsoft coco: Common objects in context. arXiv, 2014; arXiv:1405.0312. [Google Scholar]
- Lin, G.; Milan, A.; Shen, C.; Reid, I. RefineNet: Multi-Path Refinement Networks with Identity Mappings for High-Resolution Semantic Segmentation. arXiv, 2016; arXiv:1611.06612. [Google Scholar]
- Kohli, P.; Torr, P.H. Robust higher order potentials for enforcing label consistency. Int. J. Comput. Vis. 2009, 82, 302–324. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the 25th International Conference on Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012. [Google Scholar]
- Quang, N.T.; Thuy, N.T.; Sang, D.V.; Binh, H.T.T. An efficient framework for pixel-wise building segmentation from aerial images. In Proceedings of the Sixth International Symposium on Information and Communication Technology, Hue City, Vietnam, 3–4 December 2015. [Google Scholar]
- Boulch, A. DAG of Convolutional Networks for Semantic Labeling; Technical Report; Office National d’études et de Recherches Aérospatiales: Palaiseau, France, 2015. [Google Scholar]
- Gerke, M.; Speldekamp, T.; Fries, C.; Gevaert, C. Automatic semantic labelling of urban areas using a rule-based approach and realized with mevislab. Unpublished 2015. [Google Scholar] [CrossRef]
- Sherrah, J. Fully convolutional networks for dense semantic labelling of high-resolution aerial imagery. arXiv, 2016; arXiv:1606.02585. [Google Scholar]
- Gerke, M. Use of the Stair Vision Library within the ISPRS 2D Semantic Labeling Benchmark (Vaihingen); Technical Report; University of Twente: Enschede, The Netherlands, 2015. [Google Scholar]
- Petersen, K.; Pedersen, M. The Matrix Cookbook; Technical University of Denmark: Kongens Lyngby, Denmark, 2008. [Google Scholar]
- The National Survey of Geographical Conditions Leading Group Office, Sate Council, P.R.C. General Situation and Index of Geographical Conditions (Chinese Manual, GDPJ 01-2013); The National Survey of Geographical Conditions Leading Group Office, Sate Council, P.R.C.: Beijing, China, 2013. [Google Scholar]
- Immitzer, M.; Atzberger, C.; Koukal, T. Tree species classification with random forest using very high spatial resolution 8-band WorldView-2 satellite data. Remote Sens. 2012, 4, 2661–2693. [Google Scholar] [CrossRef]
- Dribault, Y.; Chokmani, K.; Bernier, M. Monitoring seasonal hydrological dynamics of minerotrophic peatlands using multi-date GeoEye-1 very high resolution imagery and object-based classification. Remote Sens. 2012, 4, 1887–1912. [Google Scholar] [CrossRef]
- Onojeghuo, A.O.; Blackburn, G.A. Mapping reedbed habitats using texture-based classification of QuickBird imagery. Int. J. Remote Sens. 2011, 32, 8121–8138. [Google Scholar] [CrossRef]
- Junwei, S.; Youjing, Z.; Xinchuan, L.; Wenzhi, Y. Comparison between GF-1 and Landsat-8 images in land cover classification. Prog. Geogr. 2016, 35, 255–263. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Advances in Neural Information Processing Systems; The MIT Press: Cambridge, MA, USA, 2014; pp. 2672–2680. [Google Scholar]
- Mirza, M.; Osindero, S. Conditional generative adversarial nets. arXiv, 2014; arXiv:1411.1784. [Google Scholar]
- Luc, P.; Couprie, C.; Chintala, S.; Verbeek, J. Semantic Segmentation using Adversarial Networks. arXiv, 2016; arXiv:1611.08408. [Google Scholar]


| (a) Dilated Convolutional Layers | ||||||
|---|---|---|---|---|---|---|
| Scale (Block) | Name | Kernel Size | Pad | Dilation | Stride | Number of Output |
| 0 | input | - | - | - | - | 3 |
| 1 | conv1-1 | 3 × 3 | 6 | 6 | 1 | 64 |
| conv1-2 | 3 × 3 | 6 | 6 | 1 | 64 | |
| pool1 | 3 × 3 | 1 | 0 | 2 | 64 | |
| 2 | conv2-1 | 3 × 3 | 4 | 4 | 1 | 128 |
| conv2-2 | 3 × 3 | 4 | 4 | 1 | 128 | |
| pool2 | 3 × 3 | 1 | 0 | 2 | 128 | |
| 3 | conv3-1 | 3 × 3 | 2 | 2 | 1 | 256 |
| conv3-2 | 3 × 3 | 2 | 2 | 1 | 256 | |
| pool3 | 3 × 3 | 1 | 0 | 2 | 256 | |
| 4 | conv4-1 | 3 × 3 | 2 | 2 | 1 | 512 |
| conv4-2 | 3 × 3 | 2 | 2 | 1 | 512 | |
| pool4 | 3 × 3 | 1 | 0 | 1 | 512 | |
| 5 | conv5-1 | 3 × 3 | 2 | 2 | 1 | 512 |
| conv5-2 | 3 × 3 | 2 | 2 | 1 | 512 | |
| pool5 | 3 × 3 | 1 | 0 | 1 | 512 | |
| - | fc6 | 3 × 3 | 1 | 1 | 1 | 1024 |
| fc7 | 1 × 1 | 0 | 1 | 1 | 1024 | |
| * | fc8 | 1 × 1 | 0 | 1 | 1 | 12 |
| - | Manifold Ranking Optimization | 12 | ||||
| (b) Non-Dilated Convolutional Layers | ||||||
| Scale (Block) | Name | Kernel Size | Pad | Dilation | Stride | Output Size |
| 1 | pool1-conv-1 | 3 × 3 | 1 | 1 | 4 | 128 |
| pool1-conv-2 | 1 × 1 | 0 | 1 | 1 | 128 | |
| pool1-conv-3 | 1 × 1 | 0 | 1 | 1 | 12 | |
| - | Manifold Ranking Optimization | 12 | ||||
| 2 | pool2-conv-1 | 3 × 3 | 1 | 1 | 2 | 128 |
| pool2-conv-2 | 1 × 1 | 0 | 1 | 1 | 128 | |
| pool2-conv-3 | 1 × 1 | 0 | 1 | 1 | 12 | |
| - | Manifold Ranking Optimization | 12 | ||||
| 3 | pool3-conv-1 | 3 × 3 | 1 | 1 | 1 | 128 |
| pool3-conv-2 | 1 × 1 | 0 | 1 | 1 | 128 | |
| pool3-conv-3 | 1 × 1 | 0 | 1 | 1 | 12 | |
| - | Manifold Ranking Optimization | 12 | ||||
| 4 | pool4-conv-1 | 3 × 3 | 1 | 1 | 1 | 128 |
| pool4-conv-2 | 1 × 1 | 0 | 1 | 1 | 128 | |
| pool4-conv-3 | 1 × 1 | 0 | 1 | 1 | 12 | |
| - | Manifold Ranking Optimization | 12 | ||||
| Aeroplane | Bicycle | Bird | Boat | Bottle | Bus | Car | Cat | Chair | Cow | Diningtable | Dog | Horse | Motorbike | Person | Pottedplant | Sheep | Sofa | Train | Tvmonitor | Mean IoU | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SegNet [27] | 73.6 | 37.6 | 62.0 | 46.8 | 58.6 | 79.1 | 70.1 | 65.4 | 23.6 | 60.4 | 45.6 | 61.8 | 63.5 | 75.3 | 74.9 | 42.6 | 63.7 | 42.5 | 67.8 | 52.7 | 59.9 |
| FCN-8s [22] (Multi-stage training) | 76.8 | 34.2 | 68.9 | 49.4 | 60.3 | 75.3 | 74.7 | 77.6 | 21.4 | 62.5 | 46.8 | 71.8 | 63.9 | 76.5 | 73.9 | 45.2 | 72.4 | 37.4 | 70.9 | 55.1 | 62.2 |
| DeepLab-Msc [24] (VGG-16 initialization) | 74.9 | 34.1 | 72.6 | 52.9 | 61.0 | 77.9 | 73.0 | 73.7 | 26.4 | 62.2 | 49.3 | 68.4 | 64.1 | 74.0 | 75.0 | 51.7 | 72.7 | 42.5 | 67.2 | 55.7 | 62.9 |
| DilatedConv Front end [28] (VGG-16 initialization) | 82.2 | 37.4 | 72.7 | 57.1 | 62.7 | 82.8 | 77.8 | 78.9 | 28 | 70 | 51.6 | 73.1 | 72.8 | 81.5 | 79.1 | 56.6 | 77.1 | 49.9 | 75.3 | 60.9 | 67.6 |
| DeconvNet + CRF [28] (Region Proposals) | 87.8 | 41.9 | 80.6 | 63.9 | 67.3 | 88.1 | 78.4 | 81.3 | 25.9 | 73.7 | 61.2 | 72.0 | 77.0 | 79.9 | 78.7 | 59.5 | 78.3 | 55.0 | 75.2 | 61.5 | 70.5 |
| CRF-RNN [25] (Multi-stage training) | 87.5 | 39.0 | 79.7 | 64.2 | 68.3 | 87.6 | 80.8 | 84.4 | 30.4 | 78.2 | 60.4 | 80.5 | 77.8 | 83.1 | 80.6 | 59.5 | 82.8 | 47.8 | 78.3 | 67.1 | 72.0 |
| DMSMR | 87.6 | 40.3 | 80.6 | 62.9 | 71.3 | 88.1 | 84.4 | 84.7 | 29.6 | 77.8 | 58.5 | 79.9 | 80.9 | 85.4 | 82.1 | 54.9 | 83.8 | 48.2 | 80.2 | 65.3 | 72.4 |
| G-CRF [35] (Unary Initialized with DeepLab CNN) | 85.2 | 43.9 | 83.3 | 65.2 | 68.3 | 89.0 | 82.7 | 85.3 | 31.1 | 79.5 | 63.3 | 80.5 | 79.3 | 85.5 | 81.0 | 60.5 | 85.5 | 52.0 | 77.3 | 65.1 | 73.2 |
| Building | Tree | Sky | Car | Sign | Road | Pedestrian | Fence | Pole | Sidewalk | Bicyclist | Mean IoU | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Before | 45.5 | 73.5 | 78.0 | 23.7 | 14.5 | 87.2 | 11.3 | 36.9 | 2.5 | 74.3 | 13.1 | 41.9 |
| MS | 81.4 | 88.1 | 80.3 | 40.1 | 16.3 | 95.6 | 26.2 | 40.0 | 3.7 | 82.0 | 37.4 | 53.7 |
| Dilated | 59.8 | 82.8 | 79.5 | 29.0 | 19.4 | 91.0 | 17.5 | 48.0 | 6.7 | 81.2 | 44.7 | 50.9 |
| MR-Opti | 90.6 | 95.1 | 74.6 | 94.6 | 21.9 | 98.2 | 53.1 | 64.3 | 9.8 | 92.6 | 42.1 | 54.8 |
| DMSMR | 93.1 | 94.5 | 82.9 | 92.7 | 45.5 | 97.4 | 72.5 | 77.2 | 7.2 | 94.5 | 68.9 | 63.6 |
| Imp.surf. | Building | Low veg. | Tree | Car | Overall F1 | Overall Acc. | |
|---|---|---|---|---|---|---|---|
| SVL [87] (Feature based) | 86.1 | 90.9 | 77.6 | 84.9 | 59.9 | 79.88 | 84.7 |
| ADL [59] (CRF post-processing) | 89.0 | 93.0 | 81.0 | 87.8 | 59.5 | 82.06 | 87.3 |
| UT_Mev [85] (DSM supported) | 84.3 | 88.7 | 74.5 | 82.0 | 9.9 | 67.88 | 81.8 |
| HUST [83] (CRF post-processing) | 86.9 | 92.0 | 78.3 | 86.9 | 29.0 | 74.62 | 85.9 |
| ONE [84] (VGG-16 pre-trained model) | 87.8 | 92.0 | 77.8 | 86.2 | 50.7 | 78.90 | 85.9 |
| DLR [76] (VGG-16 pre-trained model) | 90.3 | 92.3 | 82.5 | 89.5 | 76.3 | 86.18 | 88.5 |
| UOA [29] (VGG-16 pre-trained model) | 89.8 | 92.1 | 80.4 | 88.2 | 82.0 | 86.50 | 87.6 |
| RIT [50] (DSM supported, VGG-16 pre-trained model) | 88.1 | 93.0 | 80.5 | 87.2 | 41.9 | 78.14 | 86.3 |
| ETH_C [86] (DSM supported) | 87.2 | 92.0 | 77.5 | 87.1 | 54.5 | 79.66 | 85.9 |
| DST [49] (DSM supported) | 90.3 | 93.5 | 82.5 | 88.8 | 73.9 | 85.80 | 88.7 |
| DMSMR | 90.4 | 93.0 | 81.4 | 88.6 | 74.5 | 85.58 | 88.4 |
| Background | Farmland | Garden | Woodland | Grassland | Building | Road | Structures | Digging Pile | Desert | Waters | Overall Accuracy | Mean IoU | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Before | 75.16 | 35.73 | 0.0 | 51.65 | 8.99 | 66.59 | 35.12 | 46.19 | 19.05 | 3.56 | 3.13 | 49.76 | 21.35 |
| MS | 75.73 | 39.36 | 0.0 | 49.33 | 11.89 | 65.85 | 32.80 | 46.94 | 12.91 | 16.69 | 5.87 | 48.93 | 21.42 |
| Dilated | 40.59 | 29.18 | 0.0 | 46.48 | 11.36 | 61.74 | 40.46 | 42.54 | 18.10 | 11.57 | 19.84 | 46.8 | 19.03 |
| MR-Opti | 79.44 | 20.52 | 0.0 | 57.84 | 2.95 | 74.29 | 28.96 | 49.60 | 17.55 | 0.10 | 0.99 | 53.51 | 21.85 |
| DMSMR | 40.59 | 22.14 | 0.0 | 62.47 | 8.11 | 68.84 | 39.80 | 51.06 | 14.56 | 16.52 | 19.45 | 54.15 | 22.17 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Hu, X.; Zhao, L.; Lv, Y.; Luo, M.; Pang, S. Learning Dual Multi-Scale Manifold Ranking for Semantic Segmentation of High-Resolution Images. Remote Sens. 2017, 9, 500. https://doi.org/10.3390/rs9050500
Zhang M, Hu X, Zhao L, Lv Y, Luo M, Pang S. Learning Dual Multi-Scale Manifold Ranking for Semantic Segmentation of High-Resolution Images. Remote Sensing. 2017; 9(5):500. https://doi.org/10.3390/rs9050500
Chicago/Turabian StyleZhang, Mi, Xiangyun Hu, Like Zhao, Ye Lv, Min Luo, and Shiyan Pang. 2017. "Learning Dual Multi-Scale Manifold Ranking for Semantic Segmentation of High-Resolution Images" Remote Sensing 9, no. 5: 500. https://doi.org/10.3390/rs9050500
APA StyleZhang, M., Hu, X., Zhao, L., Lv, Y., Luo, M., & Pang, S. (2017). Learning Dual Multi-Scale Manifold Ranking for Semantic Segmentation of High-Resolution Images. Remote Sensing, 9(5), 500. https://doi.org/10.3390/rs9050500





